Unsupervised Change Detection Using Fuzzy Topology-Based Majority Voting
Abstract
:1. Introduction
1.1. Pixel-Level Fusion CD Methods
1.2. Decision-Level Fusion CD Methods
1.3. Our Method
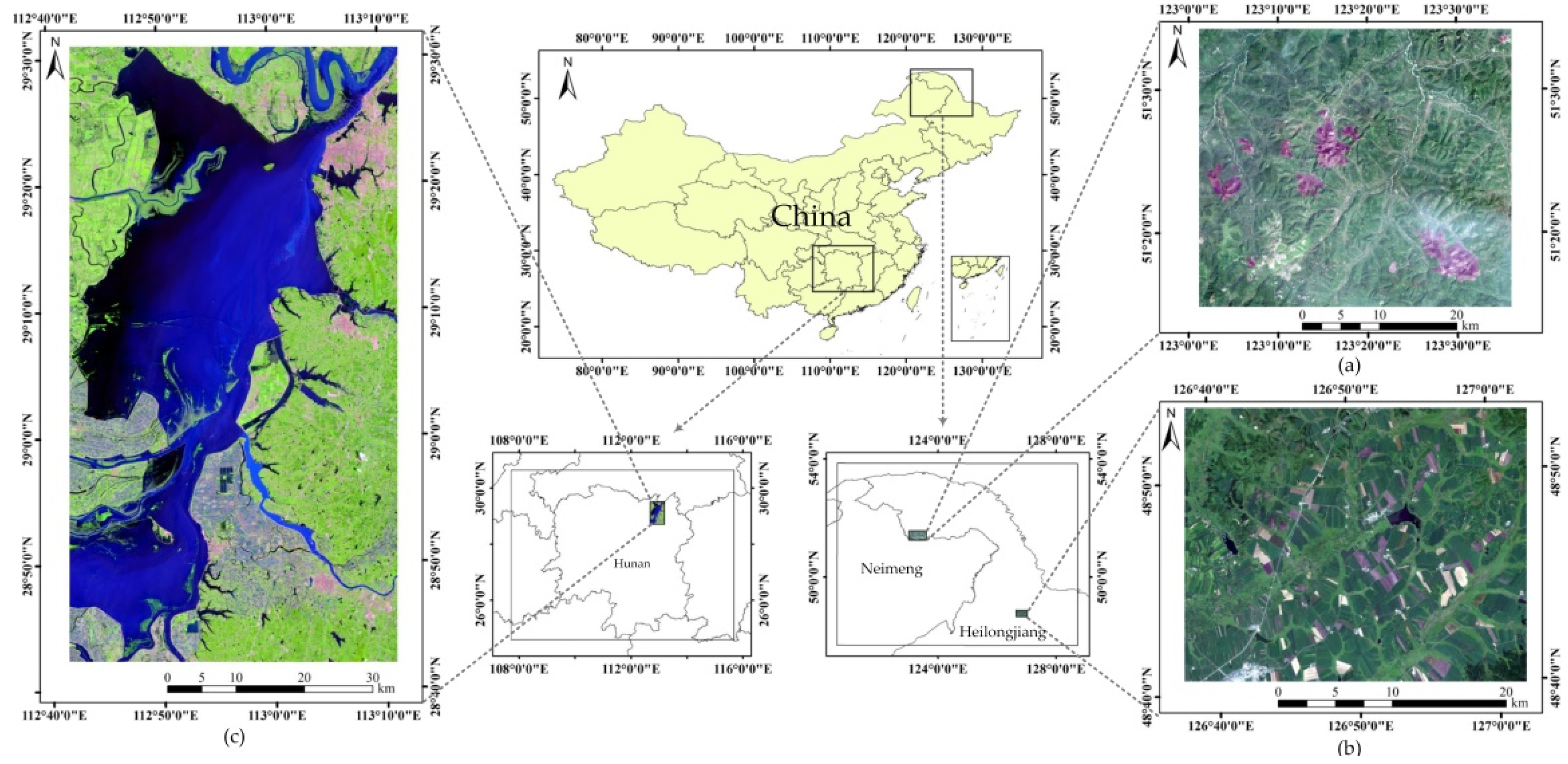
2. Study Site and Materials
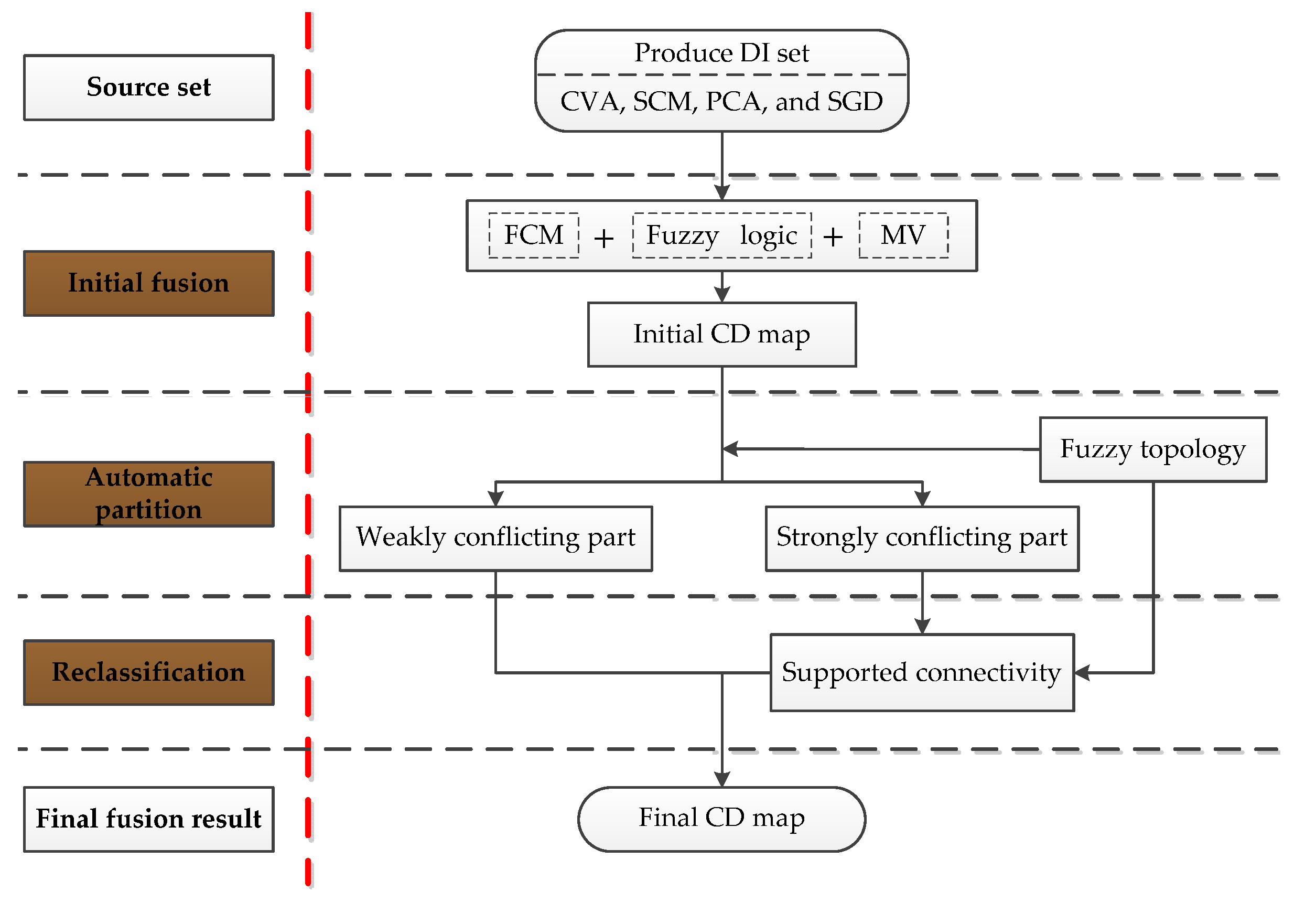
3. Proposed FTMV Fusion CD Method
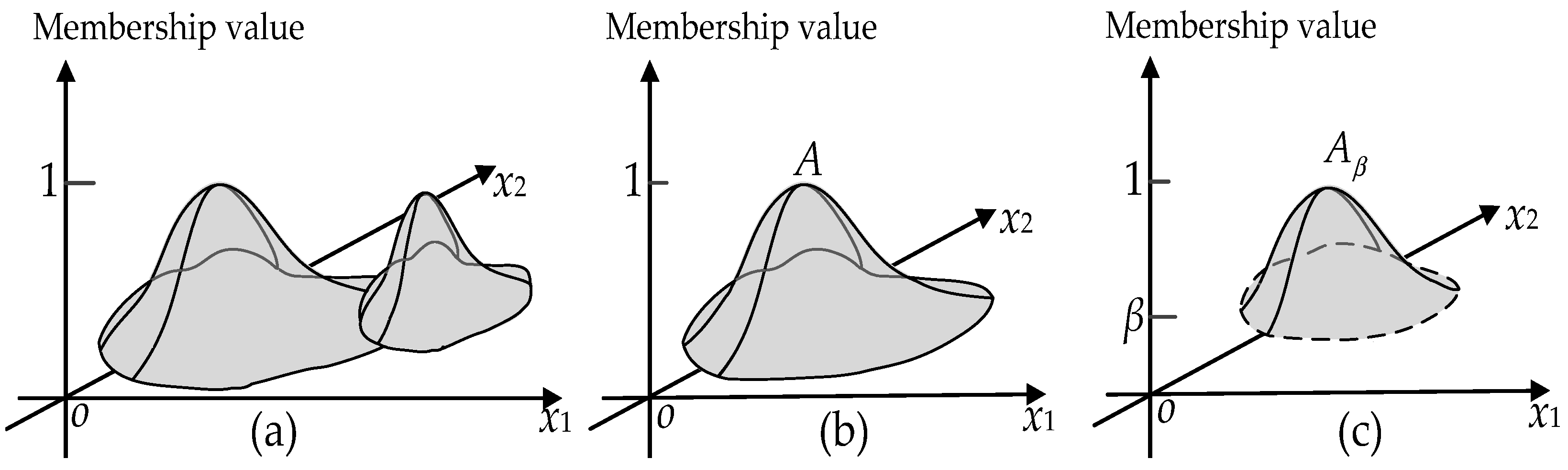
3.1. Mathematical Basis for the Proposed FTMV
- (1)
- Ø, U∈δ.
- (2)
- If A, B∈δ, then A∩B∈δ.
- (3)
- Let δ, where J is an index set, then ∈δ.
3.2. Initial Fusion
3.2.1. Improve MV Using Fuzzy Logic
3.2.2. Analyze DI Images
3.2.3. Generate an Initial Fusion CD Map by FMV
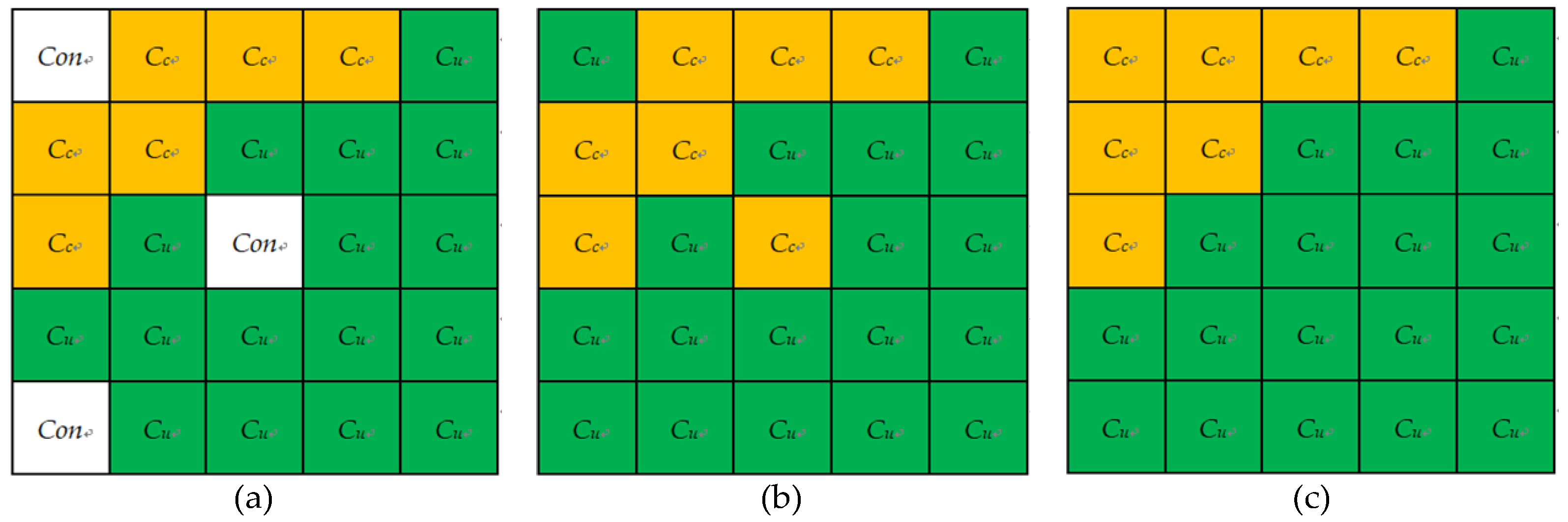
3.3. Automatic Partition
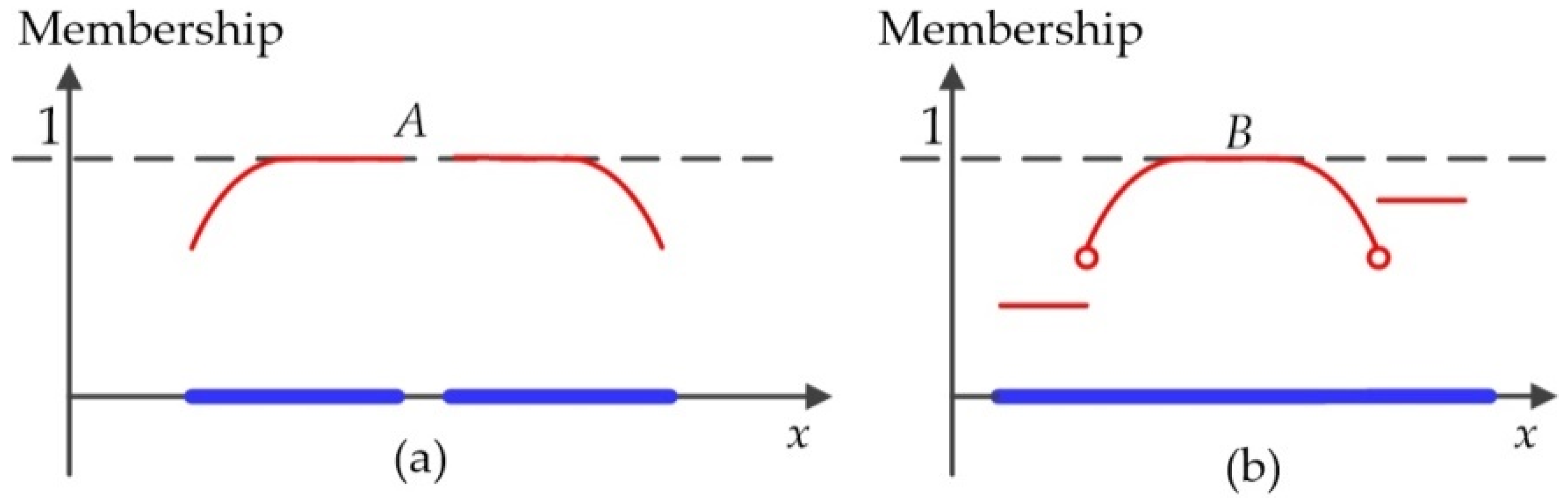
3.3.1. Partition the Initial Fusion CD Map Conceptually
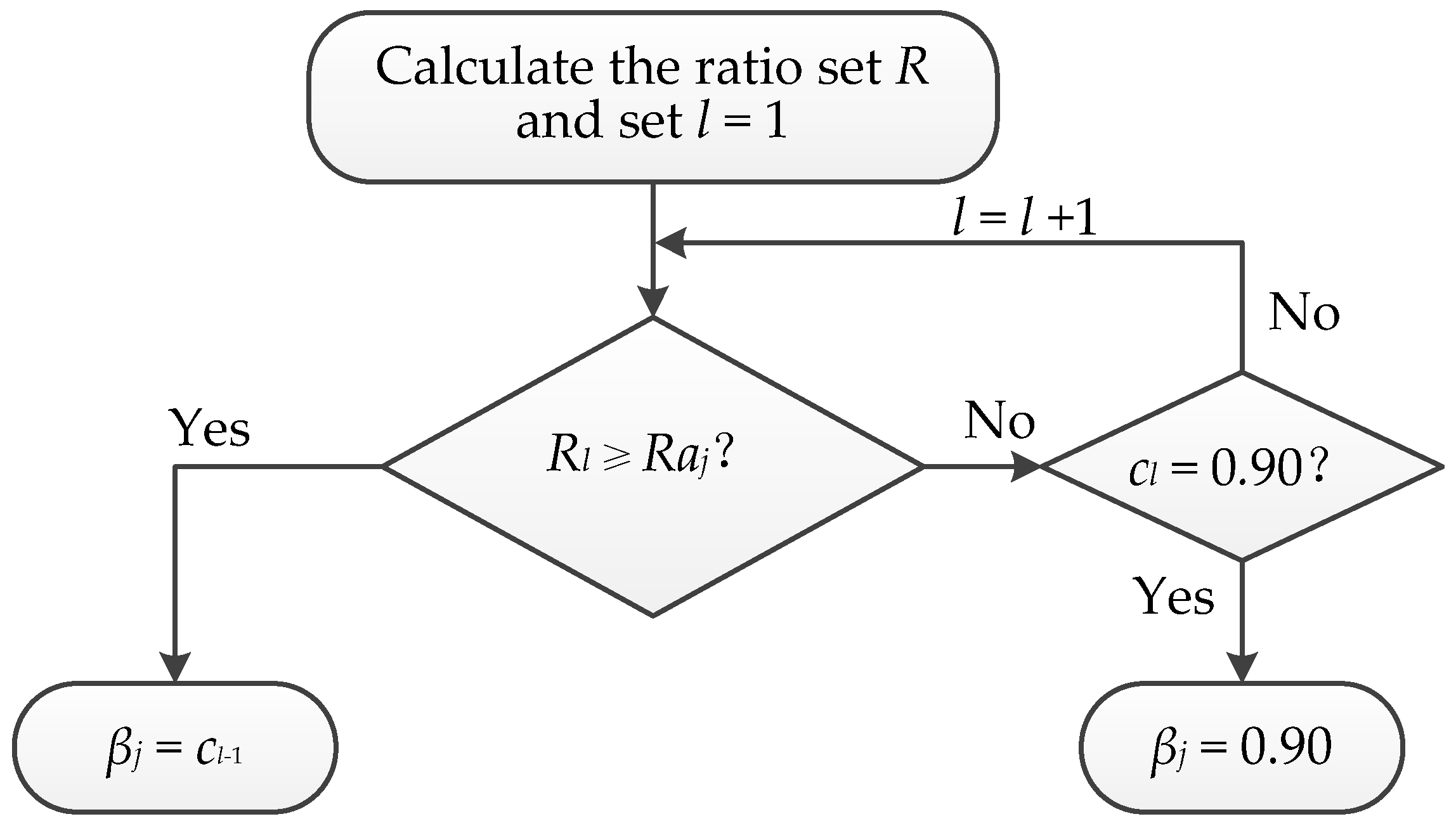
3.3.2. Determine the Optimal Threshold βj
3.4. Reclassification
4. Results
4.1. Experiment Setup and Evaluation Criteria
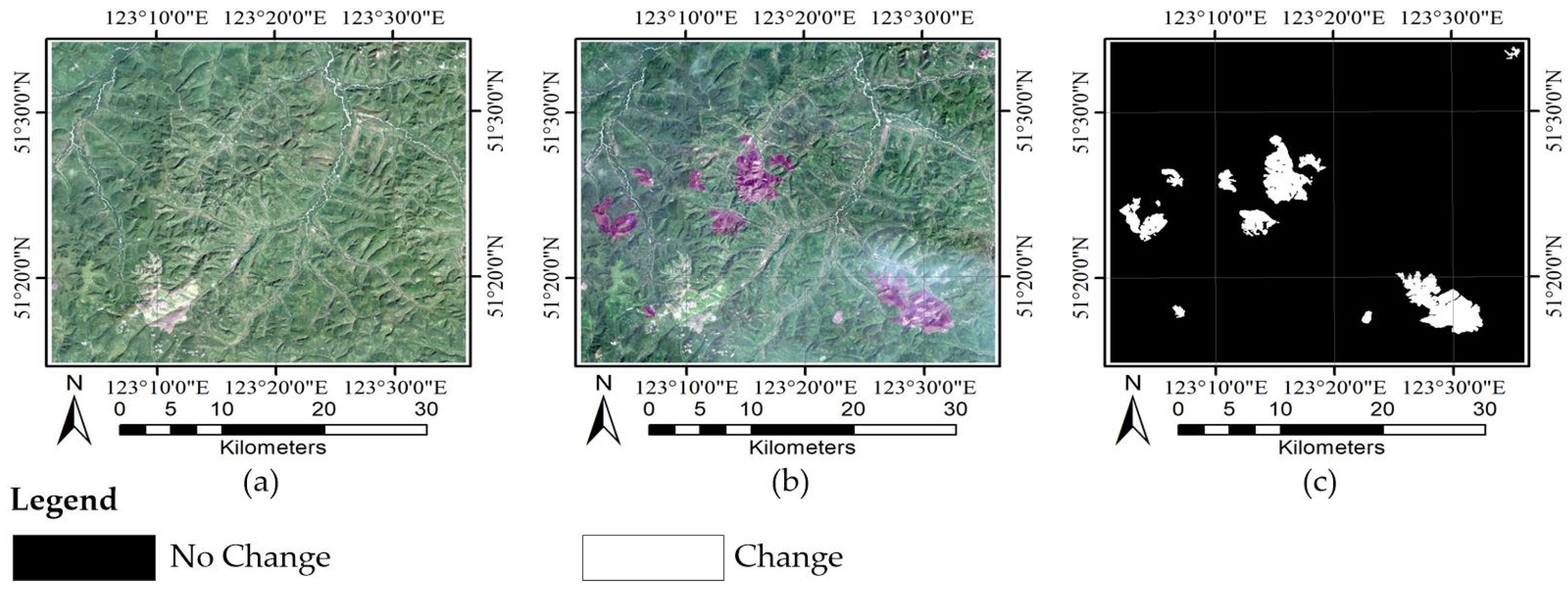
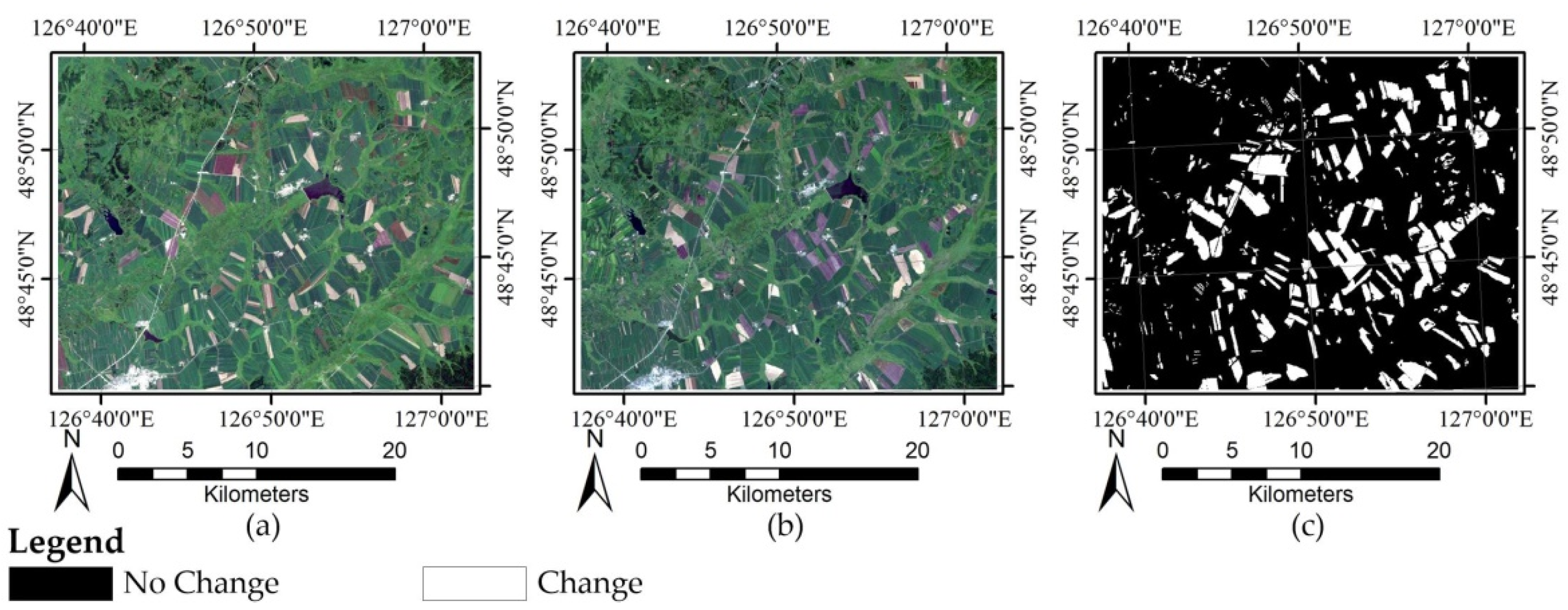
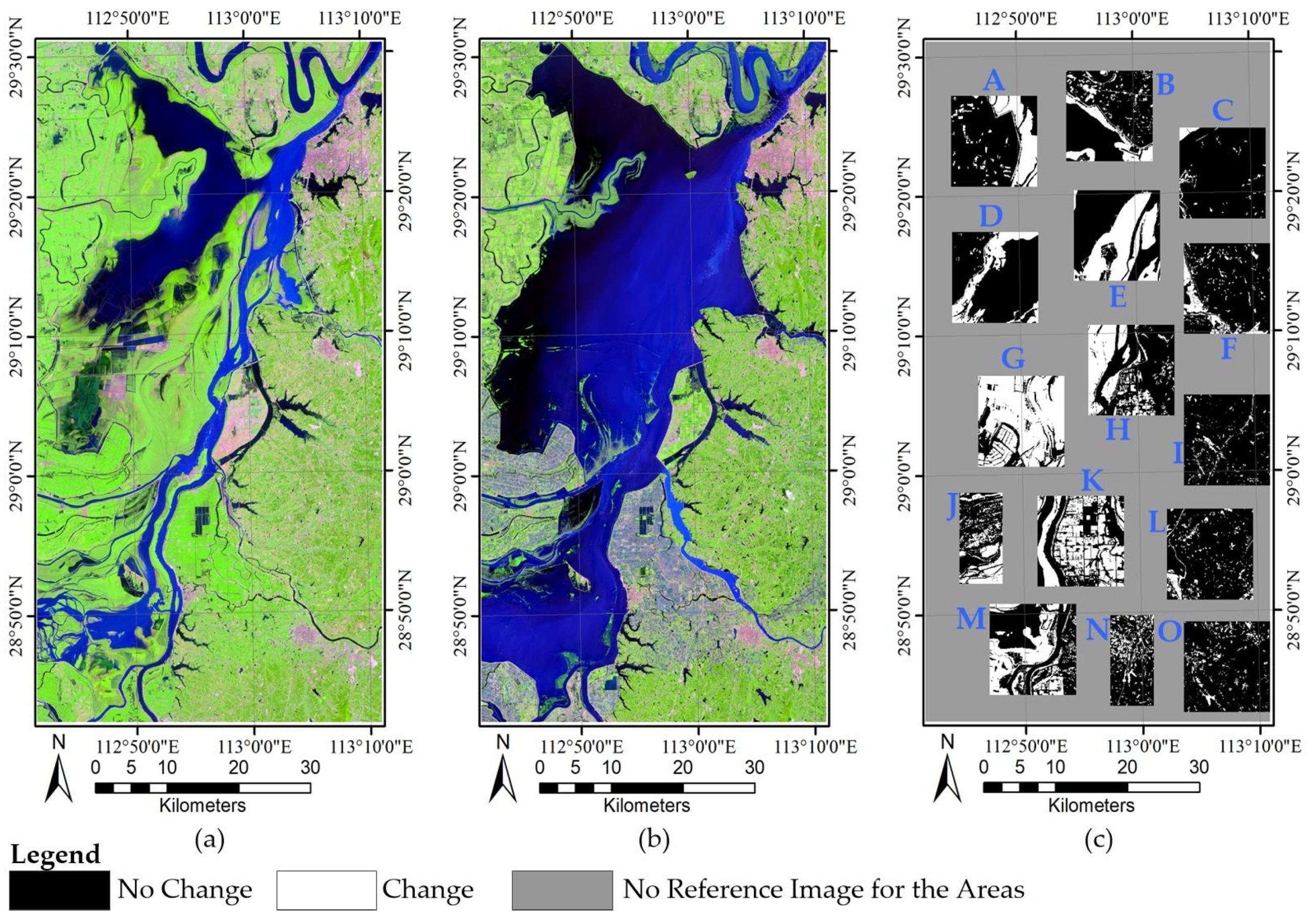
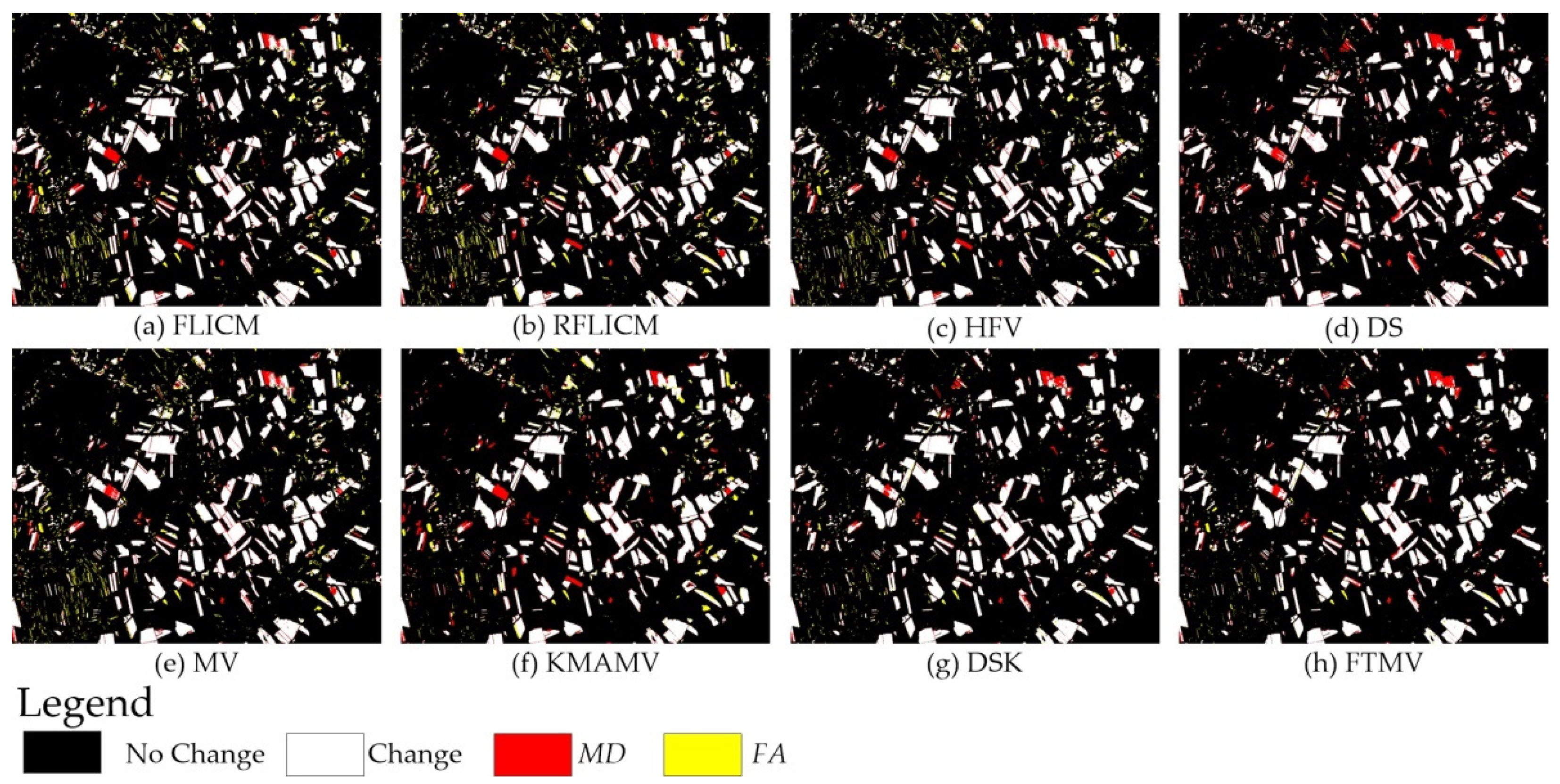
4.2. Experiment Results
5. Discussion
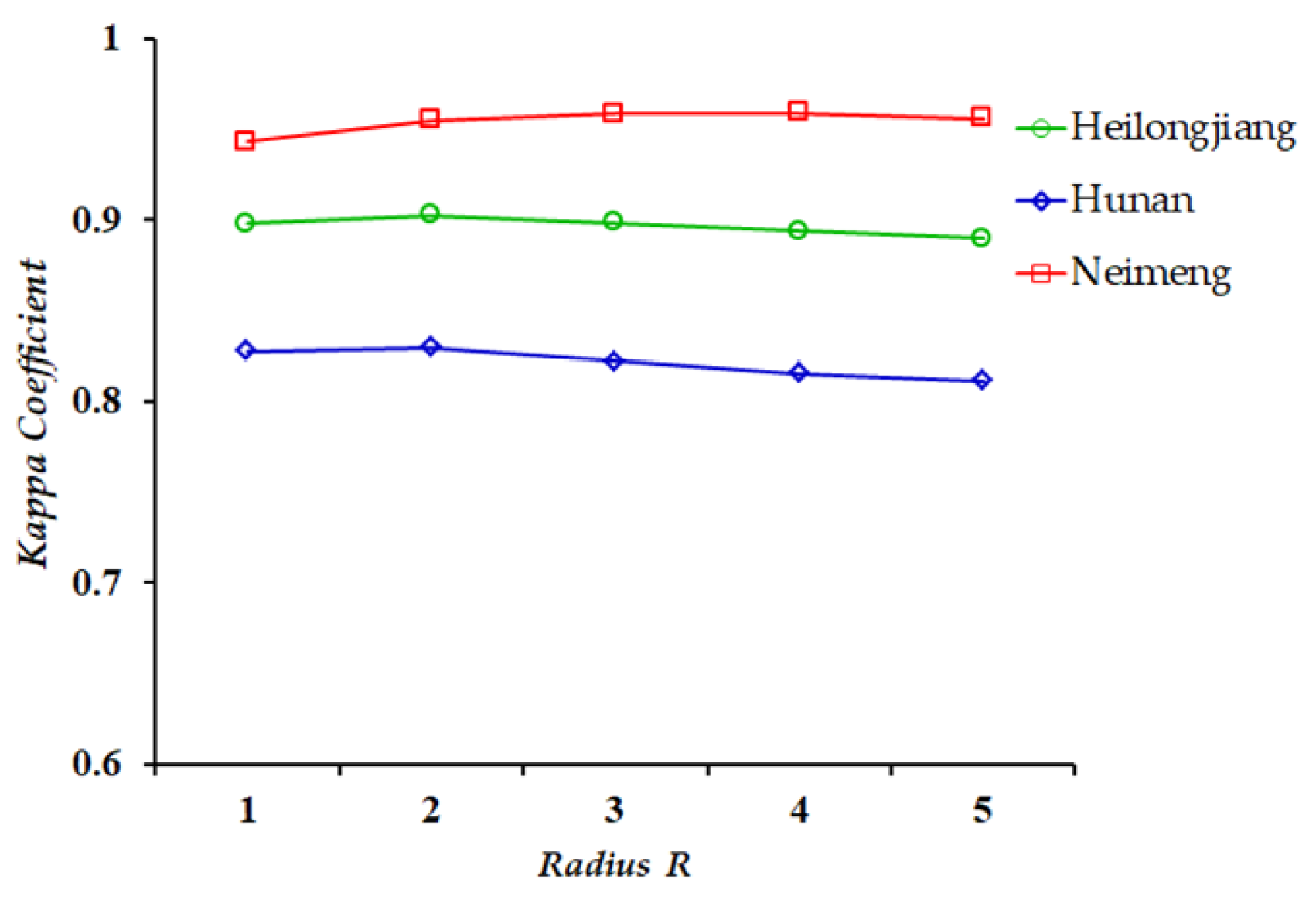
5.1. Robustness of Neighbourhood Window Size
5.2. Effectiveness of the Proposed AAM
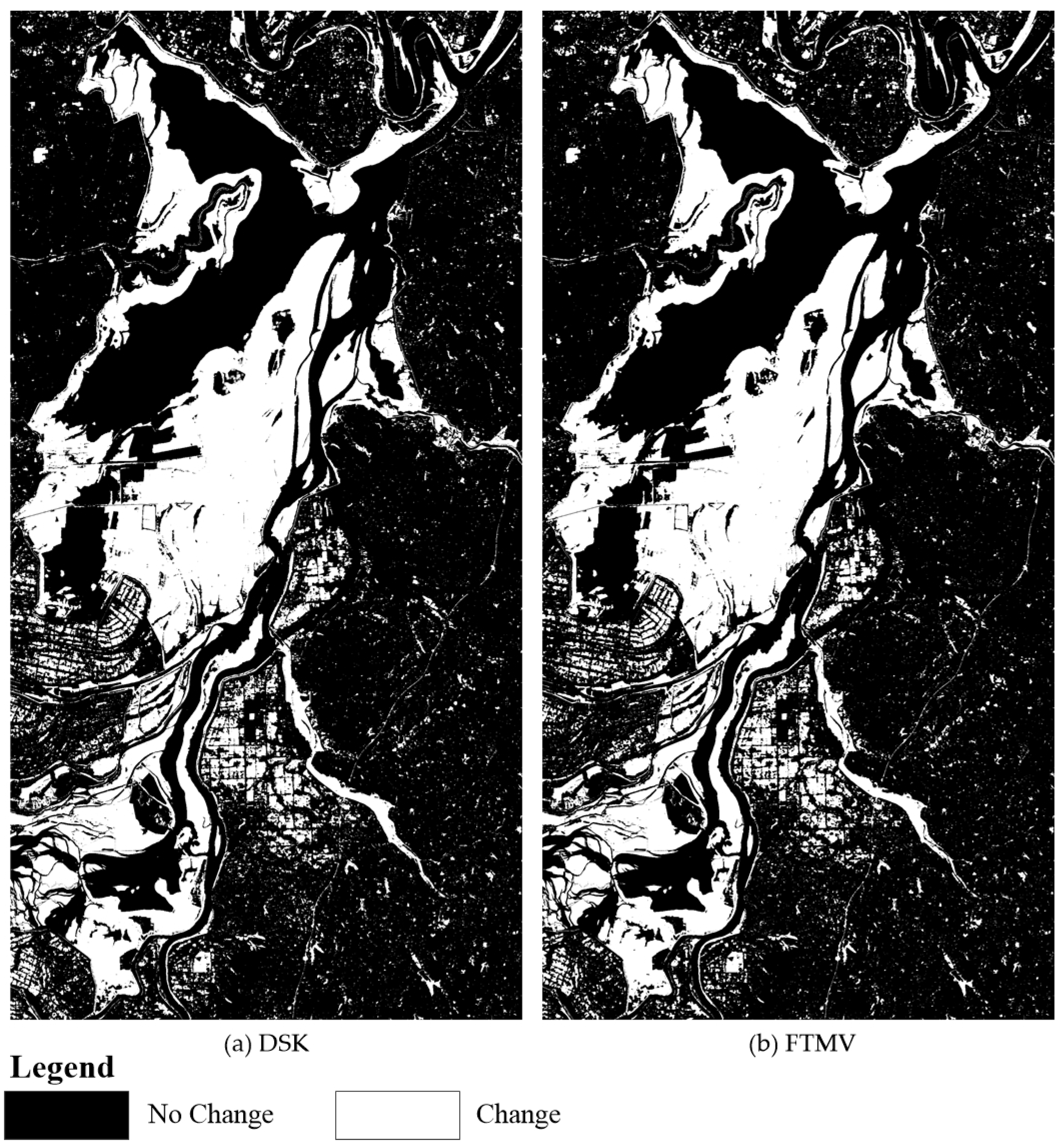
5.3. Advantages of FTMV over DSK
5.4. Future Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef] [Green Version]
- Patra, S.; Ghosh, S.; Ghosh, A. Histogram thresholding for unsupervised change detection of remote sensing images. Int. J. Remote Sens. 2011, 32, 6071–6089. [Google Scholar] [CrossRef]
- Shao, P.; Shi, W.Z.; He, P.F.; Hao, M.; Zhang, X.K. Novel Approach to Unsupervised Change Detection Based on a Robust Semi-Supervised FCM Clustering Algorithm. Remote Sens. 2016, 8, 264. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, A.; Mishra, N.S.; Ghosh, S. Fuzzy clustering algorithms for unsupervised change detection in remote sensing images. Inform. Sciences 2011, 181, 699–715. [Google Scholar] [CrossRef]
- Gong, M.; Zhou, Z.; Ma, J. Change detection in synthetic aperture radar images based on image fusion and fuzzy clustering. IEEE Trans. Image Process. 2012, 21, 2141–2151. [Google Scholar] [CrossRef] [PubMed]
- Bovolo, F.; Bruzzone, L.; Marconcini, M. A novel approach to unsupervised change detection based on a semisupervised SVM and a similarity measure. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2070–2082. [Google Scholar] [CrossRef] [Green Version]
- Celik, T.; Ma, K.K. Unsupervised change detection for satellite images using dual-tree complex wavelet transform. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1199–1210. [Google Scholar] [CrossRef]
- Shi, W.Z.; Shao, P.; Hao, M.; He, P.F.; Wang, J.M. Fuzzy topology-based method for unsupervised change detection. Remote Sens. Lett. 2016, 7, 81–90. [Google Scholar] [CrossRef]
- Mura, M.D.; Prasad, S.; Pacifici, F.; Gamba, P.; Chanussot, J.; Benediktsson, J.A. Challenges and Opportunities of Multimodality and Data Fusion in Remote Sensing. Proc. IEEE 2015, 103, 1585–1601. [Google Scholar] [CrossRef] [Green Version]
- Du, P.J.; Liu, S.C.; Xia, J.S.; Zhao, Y.D. Information fusion techniques for change detection from multi-temporal remote sensing images. Inform. Fusion 2013, 14, 19–27. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. An adaptive semiparametric and context-based approach to unsupervised change detection in multitemporal remote-sensing images. IEEE Trans. Image Process. 2002, 11, 452–466. [Google Scholar] [CrossRef]
- Liu, L.Y.; Jia, Z.H.; Yang, J.; Kasabov, N.K. SAR Image Change Detection Based on Mathematical Morphology and the K-Means Clustering Algorithm. IEEE Access 2019, 7, 43970–43978. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Zhang, X.R.; Hou, B.; Liu, G.C. Using Combined Difference Image and k-Means Clustering for SAR Image Change Detection. IEEE Geosci. Remote Sens. Lett. 2014, 11, 691–695. [Google Scholar] [CrossRef]
- Bovolo, F. A Multilevel Parcel-Based Approach to Change Detection in Very High Resolution Multitemporal Images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 33–37. [Google Scholar] [CrossRef] [Green Version]
- Inglada, J.; Mercier, G. A New Statistical Similarity Measure for Change Detection in Multitemporal SAR Images and Its Extension to Multiscale Change Analysis. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1432–1445. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, H.F.; Deng, K.Z.; Fan, H.D.; Yu, M. Strategies Combining Spectral Angle Mapper and Change Vector Analysis to Unsupervised Change Detection in Multispectral Images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 681–685. [Google Scholar] [CrossRef]
- Le Hegarat-Mascle, S.; Seltz, R. Automatic change detection by evidential fusion of change indices. Remote Sens. Environ. 2004, 91, 390–404. [Google Scholar] [CrossRef]
- Du, P.J.; Liu, S.C.; Gamba, P.; Tan, K.; Xia, J.S. Fusion of Difference Images for Change Detection Over Urban Areas. IEEE J. Sel. Top. Appl. Obs. Earth Remote Sens. 2012, 5, 1076–1086. [Google Scholar] [CrossRef]
- Longbotham, N.; Pacifici, F.; Glenn, T.; Zare, A.; Volpi, M.; Tuia, D.; Christophe, E.; Michel, J.; Inglada, J.; Chanussot, J.; et al. Multi-Modal Change Detection, Application to the Detection of Flooded Areas: Outcome of the 2009–2010 Data Fusion Contest. IEEE J. Sel. Top. Appl. Obs. Earth Remote Sens. 2012, 5, 331–342. [Google Scholar] [CrossRef]
- Liu, S.; Du, Q.; Tong, X.; Samat, A.; Bruzzone, L.; Bovolo, F. Multiscale Morphological Compressed Change Vector Analysis for Unsupervised Multiple Change Detection. IEEE J. Sel. Top. Appl. Obs. Earth Remote Sens. 2017, 10, 4124–4137. [Google Scholar] [CrossRef]
- Hedjam, R.; Kalacska, M.; Mignotte, M.; Nafchi, H.Z.; Cheriet, M. Iterative Classifiers Combination Model for Change Detection in Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6997–7008. [Google Scholar] [CrossRef]
- Lv, Z.Y.; Liu, T.F.; Shi, C.; Benediktsson, J.A.; Du, H.J. Novel Land Cover Change Detection Method Based on k-Means Clustering and Adaptive Majority Voting Using Bitemporal Remote Sensing Images. IEEE Access 2019, 7, 34425–34437. [Google Scholar] [CrossRef]
- Shao, P.; Shi, W.; Hao, M. Indicator-Kriging-Integrated Evidence Theory for Unsupervised Change Detection in Remotely Sensed Imagery. IEEE J. Sel. Top. Appl. Obs. Earth Remote Sens. 2018, 11, 4649–4663. [Google Scholar] [CrossRef]
- Mase, S. GeoStatistics and Kriging Predictors. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 609–612. [Google Scholar]
- Chen, J.; Lu, M.; Chen, X.; Chen, J.; Chen, L. A spectral gradient difference based approach for land cover change detection. ISPRS J. Photogramm. Remote Sens. 2013, 85, 1–12. [Google Scholar] [CrossRef]
- Nemmour, H.; Chibani, Y. Multiple support vector machines for land cover change detection: An application for mapping urban extensions. ISPRS J. Photogramm. Remote Sens. 2006, 61, 125–133. [Google Scholar] [CrossRef]
- Falco, N.; Mura, M.D.; Bovolo, F.; Benediktsson, J.A.; Bruzzone, L. Change Detection in VHR Images Based on Morphological Attribute Profiles. IEEE Geosci. Remote Sens. Lett. 2013, 10, 636–640. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, T.; Benediktsson, J.A.; Falco, N. Land Cover Change Detection Techniques: Very-High-Resolution Optical Images: A Review. IEEE Geosci. and Remote Sens. Mag. 2021, 2–21. [Google Scholar] [CrossRef]
- Liu, K.; Shi, W. Computing the fuzzy topological relations of spatial objects based on induced fuzzy topology. Int. J. Geogr. Inf. Sci. 2006, 20, 857–883. [Google Scholar] [CrossRef]
- Kittler, J.; Hatef, M.; Duin, R.P.W.; Matas, J. On combining classifiers. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 226–239. [Google Scholar] [CrossRef] [Green Version]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Plenum: New York, NY, USA, 1981. [Google Scholar]
- Ma, J.; Gong, M.; Zhou, Z. Wavelet fusion on ratio images for change detection in SAR images. IEEE Geosci. Remote Sens. Lett. 2012, 9, 1122–1126. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, T.; Shi, C.; Benediktsson, J.A. Local Histogram-Based Analysis for Detecting Land Cover Change Using VHR Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1284–1287. [Google Scholar] [CrossRef]
- Lv, Z.; Li, G.; Jin, Z.; Benediktsson, J.A.; Foody, G.M. Iterative Training Sample Expansion to Increase and Balance the Accuracy of Land Classification From VHR Imagery. IEEE Trans. Geosci. Remote Sens. 2021, 59, 139–150. [Google Scholar] [CrossRef]
- Gong, M.; Su, L.; Jia, M.; Chen, W. Fuzzy clustering with a modified MRF energy function for change detection in synthetic aperture radar images. IEEE Trans. Fuzzy Syst. 2014, 22, 98–109. [Google Scholar] [CrossRef]
- Cai, W.L.; Chen, S.C.; Zhang, D.Q. Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation. Pattern Recognit. 2007, 40, 825–838. [Google Scholar] [CrossRef] [Green Version]



| 1 | Initial fusion |
|
| 2 | Automatic partition |
|
| 3 | Reclassification |
|
| 1 Four single-DI detectors used to generate the input of FTMV: | CVA, SCM, PCA, and SGD |
| 2 Five similar fusion CD methods: | The pixel-level fusion approach HFV [17]. The decision-level fusion approaches MV [19], DS [19], KMAMV [23], and DSK [24]. |
| 3 Two advanced non-fusion CD techniques: | The fuzzy local information C-means clustering algorithm (FLICM) [33]. The reformulated FLICM (RFLICM) [6]. |
| Methods | MD | FA | OE | KC | T/Second |
|---|---|---|---|---|---|
| CVA | 3400 | 87,835 | 91,235 | 0.6037 | 8.37 |
| SCM | 12,280 | 1174 | 13,454 | 0.9067 | 5.24 |
| PCA | 11,534 | 7989 | 19,523 | 0.8708 | 8.23 |
| SGD | 5521 | 12,956 | 18,477 | 0.8852 | 5.62 |
| FLICM | 4507 | 48,331 | 52,838 | 0.7272 | 29.25 |
| RFLICM | 4356 | 53,102 | 57,458 | 0.7099 | 30.32 |
| HFV | 4594 | 31,556 | 36,150 | 0.7975 | 6.27 |
| DS | 6384 | 8447 | 14,831 | 0.9049 | 29.12 |
| MV | 5703 | 16,354 | 22,057 | 0.8654 | 28.69 |
| KMAMV | 5454 | 10,220 | 15,674 | 0.9011 | / |
| DSK | 3362 | 2528 | 5890 | 0.9616 | 67.42 |
| FTMV | 2790 | 3569 | 6359 | 0.9590 | 33.48 |
| Methods | MD | FA | OE | KC | T/Second |
|---|---|---|---|---|---|
| CVA | 14,854 | 20,301 | 35,155 | 0.8335 | 2.65 |
| SCM | 34,319 | 1758 | 36,077 | 0.8047 | 2.71 |
| PCA | 41,724 | 3681 | 45,405 | 0.7491 | 2.86 |
| SGD | 15,270 | 14,635 | 29,905 | 0.8555 | 3.13 |
| FLICM | 15,920 | 15,875 | 31,795 | 0.8467 | 10.09 |
| RFLICM | 15,676 | 16,389 | 32,065 | 0.8458 | 11.60 |
| HFV | 14,223 | 14,172 | 28,395 | 0.8631 | 2.95 |
| DS | 23,411 | 3507 | 26,918 | 0.8610 | 14.12 |
| MV | 14,386 | 14,425 | 28,811 | 0.8611 | 13.23 |
| KMAMV | 17,222 | 10,442 | 27,664 | 0.8635 | / |
| DSK | 13,500 | 5264 | 18,764 | 0.9070 | 32.42 |
| FTMV | 14,379 | 5290 | 19,669 | 0.9022 | 15.89 |
| Methods | MD | FA | OE | KC | T/Second |
|---|---|---|---|---|---|
| CVA | 144,075 | 69,971 | 214,046 | 0.7552 | 15.10 |
| SCM | 217,350 | 9527 | 226,877 | 0.7220 | 13.89 |
| PCA | 196,697 | 24,042 | 220,739 | 0.7345 | 13.30 |
| SGD | 125,686 | 106,307 | 231,993 | 0.7418 | 14.55 |
| FLICM | 159,887 | 49,210 | 209,097 | 0.7564 | 63.85 |
| RFLICM | 148,525 | 59,116 | 207,641 | 0.7607 | 67.76 |
| HFV | 137,523 | 54,602 | 192,125 | 0.7793 | 14.36 |
| DS | 175,590 | 13,446 | 189,036 | 0.7739 | 60.32 |
| MV | 135,334 | 63,804 | 199,138 | 0.7725 | 58.85 |
| KMAMV | 167,081 | 39,183 | 206,264 | 0.7576 | / |
| DSK | 113,873 | 32,437 | 146,310 | 0.8321 | 127.58 |
| FTMV | 120,348 | 27,337 | 147,685 | 0.8295 | 62.39 |
| Proposed AAM | Optimal Values | |||||
|---|---|---|---|---|---|---|
| βu | βc | KC | βu | βc | KC | |
| Neimeng | 0.90 | 0.65 | 0.9590 | 0.89 | 0.69 | 0.9608 |
| Heilongjiang | 0.90 | 0.55 | 0.9022 | 0.92 | 0.51 | 0.9059 |
| Hunan | 0.85 | 0.55 | 0.8295 | 0.88 | 0.51 | 0.8403 |
| DSK | FTMV | ||
|---|---|---|---|
| 1 | FCM clustering for four DIs | 1 | FCM clustering for four DIs |
| 2 | Compute mass functions for four DIs | × | |
| 3 | DS fusion | 2 | FMV fusion |
| 4 | Compute conflict degree for each pixel | × | |
| 5 | Divide initial CD map by manually tuning two key threshold parameters | 3 | Divide initial CD map automatically |
| 6 | Compute an experimental covariance function for each class | × | |
| 7 | Indicator kriging interpolation | 4 | Connectivity analysis |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, P.; Shi, W.; Liu, Z.; Dong, T. Unsupervised Change Detection Using Fuzzy Topology-Based Majority Voting. Remote Sens. 2021, 13, 3171. https://doi.org/10.3390/rs13163171
Shao P, Shi W, Liu Z, Dong T. Unsupervised Change Detection Using Fuzzy Topology-Based Majority Voting. Remote Sensing. 2021; 13(16):3171. https://doi.org/10.3390/rs13163171
Chicago/Turabian StyleShao, Pan, Wenzhong Shi, Zhewei Liu, and Ting Dong. 2021. "Unsupervised Change Detection Using Fuzzy Topology-Based Majority Voting" Remote Sensing 13, no. 16: 3171. https://doi.org/10.3390/rs13163171
APA StyleShao, P., Shi, W., Liu, Z., & Dong, T. (2021). Unsupervised Change Detection Using Fuzzy Topology-Based Majority Voting. Remote Sensing, 13(16), 3171. https://doi.org/10.3390/rs13163171








