An Adaptive Weighted Phase Optimization Algorithm Based on the Sigmoid Model for Distributed Scatterers

Abstract

Distributed scatterers (DSs) have been widely used in the time series interferometric synthetic aperture radar technique, which compensates for the insufficient density of persistent scatterers (PSs) in nonurban areas. In contrast to PS, DS is vulnerable to temporal and geometric decorrelation effects. Thus, phase optimization processing for DS is essential for reliable deformation parameter estimation. Advanced research has revealed that the application of all possible interferometric pairs will be more conducive to the reduction in phase biases. However, the low-coherence pixels will inevitably increase the difficulty of phase optimization and introduce unpredictable negative effects, which will reduce the effect of phase optimization. Therefore, this study proposed an advanced adaptive weighted phase optimization algorithm (AWPOA). In the AWPOA, the adaptive weighting strategy based on the sigmoid model was first proposed to assign more reasonable weights to pixels of different quality, which can efficiently reduce the negative influence of low-coherence pixels and improve the optimization performance. Moreover, coherence bias correction based on the second-kind statistics and an efficient solution strategy based on eigenvalue decomposition were derived and applied to achieve optimal phase series retrieval. The experimental results validated against both simulated and two sets of TerraSAR-X data demonstrated the overall superiority of the AWPOA over traditional phase optimization algorithms (POAs). Specifically, the processing efficiency of the eigenvalue decomposition solution strategy used in AWPOA was nearly 20 times faster than that of the PTA iterative solution strategy under the case without bias correction. Although bias correction increased the processing time, the optimization effect was significantly improved. Moreover, in terms of the quantitative evaluation indexes with the residual and the sum of the phase difference, the mean value of the improvement percentage of the AWPOA was increased by more than 12%, and the standard deviation was reduced by more than 1% over the traditional POAs, indicating its superior optimization performance and noise robustness.

1. Introduction

In recent decades, the interferometric synthetic aperture radar (InSAR) technique has played an important role in geophysics and geodesy with the benefits of wide coverage and high precision under all weather conditions. The differential InSAR (DInSAR) technique developed on this basis has also yielded broad application prospects in the field of surface deformation monitoring [1,2,3] and geological disaster monitoring [4,5]. However, the DInSAR technique is limited by temporal and geometric decorrelation, atmospheric delay, and other factors [6]. To overcome these limits, the time series InSAR (TSInSAR) technique based on time series SAR image analysis was subsequently developed [7,8,9], which mainly focuses on time series analysis of coherent radar targets instead of ensembles of image pixels. According to the different scattering mechanisms of coherent radar targets adopted in the TSInSAR technique, they can be divided into two categories: persistent scatterers (PSs) and distributed scatterers (DSs).

Among them, PSs are scatterers whose scattering characteristics remain stable even over long time intervals and under large baseline separation, such as houses, bridges, and other manmade buildings and exposed surface rocks. Because PS pixels always maintain a high coherence in long time series SAR images, the TSInSAR technique based on PSs usually adopts the combination mode of a single-master interferometric pair, such as the persistent scatterer InSAR (PSInSAR) technique [8], the spatiotemporal unwrapping network (STUN) [10], the PS pair (PSP) interferometry technique [11], and the Geodesy and Earth Observing Systems persistent scatterer interferometry (GEOS-PSI) technique [12]. However, there are various limitations attributed to the insufficient density of PSs in nonurban areas, which restricts the accuracy and reliability of deformation field information recognition and interpretation.

DSs compensate for this shortcoming and are widely distributed in bare soil areas, sparsely vegetated or desert areas, and rural areas. However, in contrast to PSs with the dominant scatterer in the resolution cell, DSs include many random scatterers with similar scattering characteristics in the resolution cell, which makes it vulnerable to temporal and geometric decorrelation effects. Therefore, improvement of the signal-to-noise ratio (SNR) of the observed phase is an indispensable step in the TSInSAR technique based on DSs. The classic small baseline subset (SBAS) technique [7] enhances the phase SNR via the construction of an interferometric pair network with small temporal and spatial baselines and multilook interferogram processing. Subsequently, the SqueeSAR technique [13] achieves this objective through spatial averaging of the statistically homogeneous pixel (SHP) neighborhood and estimates the optimal phase series based on the corresponding sample covariance matrix (SCM). Notably, the SqueeSAR technique considers all possible interferometric pair information, and researchers have further verified that even weak coherent phase information may facilitate phase history retrieval [14]. Hence, numerous extended techniques have been proposed on the basis of the SqueeSAR technique, whose fundamental difference involves the phase optimization algorithm (POA) [15,16].

In regard to the POA, research has focused on three aspects: SCM estimation, the weighting strategy, and the solution strategy. The SCM or complex coherence matrix, i.e., the normalized SCM, is crucial to balance the quality of time series phase observations [17]. Accurate SCM estimation better guarantees the optimization performance of the algorithm. However, due to limited samples and inevitable heterogeneous pixels, the SCM estimated via maximum-likelihood estimation is suboptimal. Although the advanced coherence estimation method based on the convolutional neural network joint model shows the better results, its estimation accuracy is still limited by the number of samples [18]. Advanced research has demonstrated that there are two ways to reduce the impact of this problem. On the one hand, a more accurate SHP recognition algorithm [19,20] could be adopted to avoid heterogeneous pixels. On the other hand, a robust SCM estimation method [21] or a coherence bias correction approach [17,22] could be adopted to improve the estimation accuracy. In terms of the weighting strategy, Cao et al. [23] and Samiei [24] unified partial optimization algorithms into a generic mathematical model under the condition of the same SCM estimator, and the only difference was the weight factor assigned to the residual phase. Weighting strategies based on the Hadamard product of the inverse of coherence and coherence [13,25], equal weight [23], coherence [15,26], coherence power [27], and Fisher information [28,29] have been proposed and verified to achieve good performance. Advanced research has revealed that even low-coherence pixels provide useful information. However, if the low-coherence pixels are assigned unreasonable weights, it will increase the difficulty of phase optimization, introduce unpredictable negative effects, and ultimately reduce the optimization effect. Therefore, it is essential to allocate reasonable weights for different quality pixels. Currently, the solution strategies for POAs mainly include the quasi-Newton method and the eigenvalue decomposition (EVD) method. The former method is aimed at the nonlinear optimization problem of maximum-likelihood estimation. Research has indicated that the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm realizes a better effect [30], but the method is time-consuming, and the number of iterations is affected by initialization [25]. The latter method is suitable for specific phase optimization models, such as the component extraction and selection SAR (CAESAR) algorithm [31] relying on SCM decomposition and the phase-decomposition-based PS InSAR (PD-PSInSAR) technique [32] based on complex coherence matrix decomposition. However, these two optimization algorithms based on EVD are more inclined to the tomographic separation of multiple scattering mechanisms, and the optimization performance is inferior to that of optimization algorithms based on maximum-likelihood estimation. The subsequently developed eigen-decomposition-based maximum-likelihood-estimator of the interferometric phase (EMI) algorithm considers both the optimization performance of the maximum-likelihood estimator and the solution performance of EVD.

In view of the current research hotspots and the existing problems in POAs, this study proposed an adaptive weighted POA based on the sigmoid model (AWPOA). Note that the proposed AWPOA comprehensively considers the three key research points mentioned above. First, coherence bias correction based on the second-kind statistics is introduced and carried out in regard to the SCM derived via maximum-likelihood estimation of the SHP neighborhood. Then, an adaptive weighting strategy based on the sigmoid model is first proposed and applied for the generic optimization function model, which can adaptively allocate reasonable weights for different quality pixels. Finally, an efficient solution strategy based on the EMI framework is derived and used to estimate the optimal phase series, which can effectively improve the processing efficiency. Simulated data and two sets of TerraSAR-X real data jointly verify the effectiveness of the proposed AWPOA.

The article is organized as follows. In Section 2, the proposed AWPOA is described in detail, including coherence bias correction, an adaptive weighting strategy based on the sigmoid model and an efficient solution strategy based on the EMI framework. In Section 3, the optimization performance of the AWPOA is evaluated with simulated data. In Section 4, the effectiveness of the proposed AWPOA is further evaluated with two sets of TerraSAR-X real data. Finally, conclusions are outlined in Section 5.

2. Proposed Method

2.1. Coherence Bias Correction

The sample covariance matrix is the basis of all phase optimization methods for distributed scatterers, which is mainly derived through maximum-likelihood estimation for the SHP neighborhood. On the basis of advanced research, this study adopted the fast SHP selection (FaSHPS) algorithm [33] to identify the SHP neighborhood set. For given N images, the L-look amplitude vector of pixel p is $A=\left[\begin{array}{cccc}{A}_1& A_2& \cdots & A_N\end{array}\right]$, and the estimator of the mean value $\mu (p)$ of pixel p can be expressed as $\overline{A}(p)={\displaystyle \sum A_i}/N$. In view of the statistical characteristics of scatterers, amplitude A satisfies a Rayleigh distribution. Therefore, the coefficient of variation (CV) of the corresponding pixel is only related to the number of looks, i.e., $\mathrm{CV}\left(A(p)\right)=\sqrt{Var\left(A(p)\right)}/E\left(A(p)\right)=0.52/\sqrt{L}$. On this basis, the confidence interval of $\overline{A}(p)$ at a confidence level of $1-\alpha$ is expressed as:

$$P\left\{\mu (p)-z_{1-\alpha /2}\cdot 0.52\cdot \mu (p)/\sqrt{N\cdot L}<\overline{A}(p)<\mu (p)+z_{1-\alpha /2}\cdot 0.52\cdot \mu (p)/\sqrt{N\cdot L}\right\}=1-\alpha ,$$

(1)

where $z_{1-\alpha /2}$ is the $1-\alpha /2$ percentile of the standard normal probability density function.

Based on the determined SHP neighborhood sets, the sample covariance matrix is derived through maximum-likelihood estimation. However, to avoid the influence of the unbalanced backscattered power among the SAR images, the complex coherence matrix is considered instead of the sample covariance matrix.

$$\widehat{T}=\frac{1}{M}{\displaystyle \sum _{y\in \Omega }y{y}^H}=|\widehat{T}|\circ \Phi ,$$

(2)

where $\widehat{T}$ is the complex coherence matrix; M is the number of pixels in SHP neighborhood set $\Omega$; $y$ is an N×1 normalized complex observation vector; ${(\cdot )}^H$ indicates the conjugate transpose operation; $|\widehat{T}|$ is the coherence matrix, i.e., the absolute value of the complex coherence matrix; $\circ$ indicates the Hadamard product; and $\Phi =\exp (j{\phi }_{i,j})$ is the phase observation. Limited samples and the inevitable heterogeneous pixels in the SHP neighborhood bias the coherence estimation, especially over low-coherence pixels. Therefore, the second-kind statistics defined with the Mellin transform (log-moment) [34] are applied in coherence bias correction, and the refined complex coherence matrix can be obtained as:

$$\tilde{T}=|\tilde{T}|\circ \Phi \mathrm{with} |\tilde{T}|=\exp \left(\frac{1}{M}{\displaystyle \sum _{i\in \Omega }\ln \left(|\widehat{T}{|}_i\right)}\right),$$

(3)

where $\tilde{T}$ is the refined complex coherence matrix and $|\widehat{T}|$ and $|\tilde{T}|$ are the coherence values before and after bias correction, respectively.

2.2. The Adaptive Weight Based on the Sigmoid Model

Initially, the optimized phase series can be estimated via maximization of the joint probability density function of the SHP neighborhood or the absolute value of the logarithm of this probability density function:

$$\widehat{\varphi }=\arg \underset{T}{\max }\left\{\hspace{1em}\ln \left(pdf(\tilde{T}|T)\right)\hspace{1em}\right\}=\arg \underset{T}{\max }\left\{\hspace{1em}-tr\left(T^{-1}\tilde{T}\right)-\ln \left(Det(T)\right)\hspace{1em}\right\},$$

(4)

where $\widehat{\varphi }$ is the estimator of the optimized phase, $tr(\cdot )$ is the trace of the matrix, $Det(\cdot )$ is the matrix determinant, and $T$ is the real covariance matrix of the N-dimensional complex circular Gaussian distribution vector, which can be expressed with the real coherence and the real phase.

$$T=\mathsf{\psi }\mathsf{\gamma }{\mathsf{\psi }}^H=\mathsf{\gamma }\circ \mathsf{\theta }{\mathsf{\theta }}^H \mathrm{with} \mathsf{\psi }=diag(\mathsf{\theta })=diag\left(\begin{array}{cccc}\exp (j{\varphi }_1)& \exp (j{\varphi }_2)& \cdots & \exp (j{\varphi }_N)\end{array}\right),$$

(5)

where $\gamma$ is the real coherence matrix and $\varphi$ is the real phase vector. Through detailed derivation, Equation (4) can be further expressed as a generic mathematical function model:

$$\widehat{\varphi }=\arg \underset{\varphi }{\max }\left\{\hspace{1em}{\mathsf{\theta }}^H\left(\mathbf{w}\circ \Phi \right)\hspace{1em}\mathsf{\theta }\hspace{1em}\right\}=\arg \underset{\varphi }{\max }\left\{\hspace{1em}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j>i}^N{w}_{ij}\cos \left({\phi }_{i,j}-({\varphi }_i-{\varphi }_j)\right)}}\hspace{1em}\right\},$$

(6)

where w is the weight factor corresponding to the residual phase, which is also the main difference from many POAs. In principle, the optimal phase reconstruction process actually determines the maximum summation of $\cos \left({\phi }_{i,j}-({\varphi }_i-{\varphi }_j)\right)$ with the corresponding weight term w, which minimizes the difference between the estimators and observations.

The POA considers all possible interferometric pair information, and advanced research has revealed that even low-coherence pixels provide useful information. However, when a high weight is assigned to low-quality pixels, this reduces or even mitigates the role of high-quality pixels in the phase optimization process, resulting in a nonideal optimized phase in the SNR improvement. Therefore, it is essential to allocate reasonable weights to pixels of different qualities. This is consistent with the conclusion that the optimization effect of the equal-weight strategy is inferior to that of the coherence weighted strategy, as reported in [23].

Therefore, an adaptive weighting strategy based on the sigmoid model was proposed to allocate reasonable weights for different quality pixels and to further improve the quality of the optimized phase. Considering that the coherence coefficient effectively characterizes the degree of signal decorrelation and the phase quality, it was adopted as the medium of the proposed adaptive weighting strategy. In addition, the proposed adaptive weight can be described as

$$w_{sig}=\frac{1}{1+\exp \left(k(-|\tilde{T}|+b)\right)}.$$

(7)

There are two main parameters involved in the above equation: b indicates the inflection point, and k indicates the intensity of the data changes before and after the inflection point. This can be understood more intuitively through Figure 1a. Here, the full coherence matrix $|\tilde{T}|$ is regarded as a band matrix, and the bandwidth of the matrix is defined by parameter Bw, as shown in Figure 1b. Moreover, b is set to the mean value of the diagonal element in the Bw column, i.e., the mean value of the red diagonal elements, as shown in Figure 1b.

When the coherence value is low, this algorithm allocates a lower weight to reduce the proportion of the low-quality phase in the process of phase optimization, which weakens the negative impact of the low-quality phase on phase optimization. When the coherence of pixels is high, this algorithm allocates a higher weight to enhance the role of the high-quality phase in phase optimization. Therefore, the adaptive weighting strategy based on the sigmoid model proposed in this study not only ensures the consideration of all possible interferometric phase information but also reduces the negative impact of the phase corresponding to a low coherence on phase optimization.

2.3. An Efficient Solution Strategy Based on the EMI Framework

To solve the nonlinear optimization problem described in Equation (4), the quasi-Newton method based on the BFGS algorithm is usually applied. However, this process is highly time consuming. Therefore, this study adopted an efficient EVD solution strategy similar to the EMI algorithm.

Substituting Equation (5) into Equation (4), the following is obtained:

$$\widehat{\varphi }=\arg \underset{\varphi }{\max }\left\{\hspace{1em}-tr\left(\mathsf{\psi }{\mathsf{\gamma }}^{-1}{\mathsf{\psi }}^H\tilde{T}\right)\hspace{1em}\right\}=\arg \underset{\varphi }{\max }\left\{\hspace{1em}{\mathsf{\theta }}^H\left(-{\mathsf{\gamma }}^{-1}\circ \tilde{T}\right)\mathsf{\theta }\hspace{1em}\right\}.$$

(8)

Compared to the generic mathematical function model described in Equation (6), we can obtain:

$$w=-{\mathsf{\gamma }}^{-1}\circ |\tilde{T}|.$$

(9)

Considering that the coherence matrix is fixed, the fundamental difference between the various weighting strategies lies in the setting of the real coherence matrix $\gamma$. When $\gamma$ is replaced by the sample coherence matrix, the optimal solution can be obtained theoretically. However, due to the inevitable coherence bias, the optimized result is always suboptimal. Therefore, a series of different weighting strategies was proposed to improve the optimization performance, and the ultimate goal of the adaptive weighting strategy based on the sigmoid model was the same. The adaptive weighting strategy described in Equation (7) is substituted into Equation (9), $\gamma ={\gamma }_{\mathrm{sig}}={\left(-\frac{W_{sig}}{|\tilde{T}|}\right)}^{-1}$, where the division operation is an elementwise operation. Notably, $\gamma$ is replaced by ${\gamma }_{\mathrm{sig}}$.

In contrast to Equation (5), two calibration factors were introduced in the EMI solution framework, which act on the real phase $\mathsf{\psi }$.

$$\mathsf{\psi }\prime =\alpha diag(\mathsf{\eta }\circ \mathsf{\theta })=\alpha diag\left(\begin{array}{cccc}{\eta }_1\exp (j{\varphi }_1)& {\eta }_2\exp (j{\varphi }_2)& \cdots & {\eta }_N\exp (j{\varphi }_N)\end{array}\right),$$

(10)

where $\alpha$ is a real number and $\mathsf{\eta }$ is an N×1 real vector. Substituting Equation (10) into Equation (5), the following was obtained:

$$T\prime =\mathsf{\psi }\prime \mathsf{\gamma }\mathsf{\psi }{\prime }^H={\alpha }^2\mathsf{\gamma }\circ \mathsf{\eta }{\mathsf{\eta }}^T\circ \mathsf{\theta }{\mathsf{\theta }}^H.$$

(11)

Under the condition of Equation (11), the maximum joint probability density function was derived again:

$$\begin{array}{ll}\widehat{\varphi }& =\arg \underset{\varphi ,\alpha ,\eta }{\max }\left\{\hspace{1em}-tr\left(T{\prime }^{-1}\tilde{T}\right)-\ln \left(Det(T\prime )\right)\hspace{1em}\right\}\\ & =\arg \underset{\varphi ,\alpha ,\eta }{\max }\left\{\hspace{1em}-tr\left({\alpha }^{-2}({\gamma }^{-1}\circ \tilde{T})\zeta {\zeta }^H\right)-2\ln \left({\displaystyle \prod \alpha {\eta }_i}\right)-\ln \left(Det(\mathsf{\gamma })\right)\hspace{1em}\right\}\\ & =\arg \underset{\varphi ,\alpha ,\eta }{\max }\left\{\hspace{1em}-{\alpha }^{-2}{\zeta }^H({\gamma }^{-1}\circ \tilde{T})\zeta -{\displaystyle \sum \ln {\left(\alpha {\eta }_i\right)}^2}\hspace{1em}\right\}\end{array}, \mathrm{with} \mathsf{\zeta }={\mathsf{\eta }}^{\circ -1}\circ \mathsf{\theta },$$

(12)

To solve Equation (12), Taylor expansion was carried out under ${\left(\alpha {\eta }_i\right)}^2\approx 1$, and the first-order equation was adopted to accelerate the convergence of the objective function:

$$\widehat{\varphi }=\arg \underset{\varphi ,\alpha ,\eta }{\max }\left\{\hspace{1em}-{\alpha }^{-2}{\zeta }^H({\gamma }^{-1}\circ \tilde{T})\zeta -{\displaystyle \sum _{i=1}^N{(\alpha {\eta }_i)}^2}\hspace{1em}\right\}=\arg \underset{\varphi ,\alpha ,\eta }{\min }\left\{\hspace{1em}{\alpha }^{-2}{\zeta }^H({\gamma }^{-1}\circ \tilde{T})\zeta -{\displaystyle \sum _{i=1}^N{(\alpha {\eta }_i)}^{-2}}\hspace{1em}\right\}.$$

(13)

Furthermore, Lagrange multiplication was applied to realize the equality constraint of the ${\mathsf{\eta }}^{\circ -1}$ vector norm, i.e., ${‖{\mathsf{\eta }}^{\circ -1}‖}_2{}^2={\displaystyle \sum _{i=1}^N{({\eta }_i)}^{-2}=}\hspace{1em}{\zeta }^H\zeta =N$. Substituting it into Equation (13), the following was obtained:

$$\begin{array}{ll}\widehat{\varphi }& =\arg \underset{\varphi ,\alpha ,\eta }{\min }\left\{\hspace{1em}{\alpha }^{-2}{\zeta }^H({\gamma }^{-1}\circ \tilde{T})\zeta -{\alpha }^{-2}{\zeta }^H\zeta \hspace{1em}\right\}\\ & =\arg \underset{\varphi ,\alpha ,\eta ,\mu }{\min }\left\{\hspace{1em}{\alpha }^{-2}{\zeta }^H({\gamma }^{-1}\circ \tilde{T})\zeta -{\alpha }^{-2}{\zeta }^H\zeta -\mu ({\zeta }^H\zeta -N)\hspace{1em}\right\}\\ & =\arg \underset{\varphi ,\alpha ,\eta ,\mu }{\min }\left\{\hspace{1em}{\alpha }^{-2}{\zeta }^H({\gamma }^{-1}\circ \tilde{T})\zeta -{\alpha }^{-2}{\zeta }^H\zeta -\mu {\zeta }^H\zeta \hspace{1em}\right\}\end{array}$$

(14)

This minimum objective function can be further expressed as:

$$\begin{gathered} {\alpha }^{-2}{\zeta }^H({\gamma }^{-1}\circ \tilde{T})\zeta ={\alpha }^{-2}{\zeta }^H(\zeta +{\alpha }^2\mu \zeta )\hspace{1em}, \\ ({\gamma }^{-1}\circ \tilde{T})\zeta =\lambda \hspace{1em}\zeta \mathrm{with} \lambda =1+{\alpha }^2\mu . \end{gathered}$$

(15)

Therefore, the eigenvector corresponding to the minimum eigenvalue of ${\gamma }^{-1}\circ \tilde{T}$ is the solution of Equation (14), i.e., the optimized phase series. Through the above derivation, it was found that the two-step solution strategy described in Equations (13) and (14) is aimed at the second term of the objective function, which is independent of the setting of $\gamma$. That is, the above solution strategy is not affected by the weight. Therefore, within the EMI solution framework, the optimized phase solution of the different weighting strategies is the eigenvector corresponding to the minimum eigenvalue of $-w\circ \Phi$.

Therefore, on the basis of the above coherence bias correction, the adaptive weighting strategy and the effective solution strategy, the optimized phase series of the proposed algorithm is the eigenvector corresponding to the minimum eigenvalue of $-w_{sig}\circ \Phi$. Note that the optimized phase is relative to a specific image, which is similar to traditional POAs.

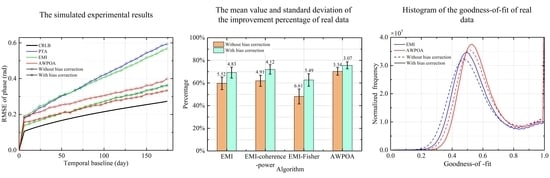
3. Experimental Results with the Simulated Data

3.1. Influence of Coherence Bias Correction on Phase Optimization

In this study, simulation analysis was first implemented to verify the performance of the proposed AWPOA, and state-of-the-art POAs were compared. In this section, the influence of coherence bias correction on the performance of the considered POAs is analyzed in detail. Here, the generic decorrelation model [35] was employed for real coherence matrix simulation:

$${\gamma }_{i,j}=({\gamma }_0-{\gamma }_{\infty })\exp \left(\frac{-\Delta t_{i,j}}{\tau }\right)+{\gamma }_{\infty },$$

(16)

where ${\gamma }_0$ and ${\gamma }_{\infty }$ indicate the short- and long-term coherence, respectively; $\Delta t_{i,j}$ corresponds to the temporal baseline between the i-th and j-th acquisitions; and $\tau$ is the signal correlation length. When ${\gamma }_{\infty }=0$, it is referred to as the exponential decay, and when ${\gamma }_{\infty }\ne 0$, it is referred to as the long-term coherence. This study adopted the exponential decay model with ${\gamma }_0=0.6$ and ${\gamma }_{\infty }=0$ and the long-term coherence model with ${\gamma }_0=0.6$ and ${\gamma }_{\infty }=0.1$ for experimental analysis and sets $\tau =50$. Moreover, an equal time interval of six days, similar to that of Sentinel-1, was adopted. Furthermore, 30 images with 100 SHPs were simulated [36], the topographic and atmospheric phase components were set to zero, and the displacement rate was 2 mm/yr.

Figure 2 shows a comparison of the coherence matrix estimators before and after bias correction. Comparing Figure 2a,b, obvious deviation was found, especially in the low-coherence region. However, after bias correction based on the second-kind statistics, the coherence estimation effect was effectively improved, and the resulting matrix was closer to the real coherence matrix. Furthermore, the subsequent optimization effect will be improved using the refined coherence matrix. Figure 2d shows a histogram of the different coherence estimation errors, which reflects the performance of bias correction more intuitively. Undeniably, there were still some residual estimation errors after using coherence bias correction, which needs to be further studied.

To quantitatively analyze the influence of bias correction on phase optimization, the root mean squared error (RMSE) of the optimized phase is defined as follows:

$$RMSE=\sqrt{\frac{{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{\left({\widehat{\varphi }}_{i,j}-{\varphi }_{i,j}\right)}^2}}}{MN}},$$

(17)

where $\widehat{\varphi }$ and $\varphi$ are the optimized phase and simulated real phase, respectively, and M and N refer to the row and column lengths of the simulated data. Figure 3 shows the RMSE of the optimized phase before and after coherence bias correction considering different coherence models and three different POAs with 2000 simulations. In terms of no-bias correction with the exponential decay model, the RMSE of the phase obtained by the traditional EMI algorithm was slightly smaller than that of the traditional phase triangulation algorithm (PTA). It indicates that the optimization effect of the traditional EMI algorithm was slightly better than that of the traditional PTA, which is consistent with previous studies. This is because two calibration factors were introduced in the EMI algorithm, which provides the possibility of calibration in the presence of coherence error. However, the calibration effectiveness was slight. Notably, the AWPOA proposed in this study obtains obvious advantages in its optimization performance over the PTA and EMI algorithms. Specifically, compared with the other two algorithms, the maximum increment of RMSE obtained by AWPOA was about 0.2. After coherence bias correction, the RMSE of the optimized phase of all algorithms was significantly improved and gradually approached the Cramér–Rao lower bound (CRLB) [37]. Among them, the PTA and EMI algorithms attained the most prominent improvement effect, the maximum improvement value of RMSE was about 0.23, and the optimized results were basically the same. However, the RMSE obtained by these two algorithms was still 0.03 higher than that of AWPOA, indicating that the performance of these two algorithms was still worse than AWPOA. Because the coherence simulated by the long-term coherence model was generally higher than that of the exponential decay model, especially in the case of the long temporal baseline, the RMSE of the optimized phase obtained by the long-term coherence model was smaller than that of the exponential decay model. Under the case of no-bias correction, it can be found that the optimization effects of the PTA and EMI algorithms were similar, but they were also inferior to AWPOA. After adopting the coherence bias correction, these three optimization algorithms showed a similar optimization effect, and they all showed significant improvement over the case of no-bias correction.

Generally, the experimental results with the different coherence simulation models all verified the necessity and reliability of coherence bias correction for the POA and further confirmed the superiority of the proposed AWPOA over the considered traditional algorithms.

3.2. Influence of the Weight on Phase Optimization

To further verify the effectiveness of the adaptive weighting strategy based on the sigmoid model in the proposed AWPOA, the influence of the weight on phase optimization was independently analyzed. To avoid any mixed influence of the bias correction factor, coherence bias correction was not performed in the experiment. In addition, combined with the efficient solution strategy described in Section 2.3, this study integrated certain traditional weighting strategies into this efficient solution framework, such as equal-weight, coherence, coherence power [38], and Fisher information strategies, to compare and analyze the optimization performance under the different weights. Given a pixel, the corresponding weights can be expressed as follows:

$$w_{equal}=1, w_{coherence}=|\widehat{T}|, w_{coherence-power}=|\widehat{T}{|}^2, w_{Fisher}=\frac{2L|\widehat{T}{|}^2}{1-|\widehat{T}{|}^2},$$

(18)

where L is the number of looks.

Note that the weight of the PTA and EMI algorithm is the Hadamard product of the inverse of coherence and coherence, i.e., $w=-|\widehat{T}{|}^{-1}\circ |\widehat{T}|$. As shown in Figure 4a, in the case of the exponential decay model, the optimization effect of the EMI algorithm was similar to that of the PTA or even slightly better. However, the efficiency of the EMI algorithm was much higher than that of the PTA because it does not require complicated iterative processing. Comparing the different weighting strategies, the performance of the equal-weight strategy was the worst because it assigns the same weight to all pixels. The other weighting strategies all consider the coherence of pixels, so the performance levels are higher than that of the equal-weight strategy. Among them, the performance of the weighting strategy based on coherence was basically consistent with that of the EMI algorithm. Additionally, the optimization effect of the weighting strategy based on coherence power was similar to that of the weighting strategy based on Fisher information, and they were superior to the previous weighting strategies. However, the RMSE of the optimized phase estimated with the adaptive weighting strategy based on the sigmoid model was obviously the best. Under the case of the maximum temporal baseline, the RMSE obtained by the adaptive weighting strategy was improved by at least 0.12 compared to the other weighting strategy. That is because this method assigns a more reasonable weight to pixels of different quality. Specifically, the adaptive weighting strategy assigns a lower weight to low-coherence pixels, which reduces their negative impact on phase optimization processing. Meanwhile, it assigns a higher weight to high-coherence pixels, which expands their positive role in phase optimization processing.

The RMSE values of different POAs under the long-term coherence model were generally lower than those of the exponential decay model by more than 0.15. However, we can obtain the same conclusion with the exponential decay model. In detail, the optimization performance with the equal weighting strategy was still the worst, and the performances with the coherence weighting strategy, EMI, and PTA were similar. Moreover, the optimization performance with the coherence power and the Fisher information weighting strategy was basically the same and better than the former weighting strategies. The adaptive weighting strategy always had the best optimization effect.

Generally, the experimental results with the different coherence simulation models all demonstrate the superiority of the adaptive weighting strategy based on the sigmoid model over the traditional weighting strategies in optimization performance.

3.3. Efficiency

On the basis of the above simulation data, the computational time of different POAs was statistically analyzed, as summarized

Table 1. Computational time (in seconds) for the different POAs.

Methods	Without Bias Correction	With Bias Correction
PTA	61.385	231.367
EMI	3.247	182.028
AWPOA	3.013	170.300

. Notably, all algorithms were conducted using MATLAB R2021a software with an i7-9750H 2.60-GHz CPU and 16 GB of RAM.

The processing efficiency of the proposed AWPOA was basically the same as that of the EMI algorithm, and they were nearly 20 times faster than that of the PTA under the case without bias correction. In fact, the efficient solution strategy described in Section 2.3 was similar to that of EMI, which are all based on the EVD. However, PTA uses the BFGS algorithm, which needs a large number of iterative operations and is very time consuming. Notably, compared with the EMI algorithm, the AWPOA adopts the adaptive weighing strategy based on the sigmoid, which avoids the inversion operation. Therefore, in theory, the AWPOA is slightly more efficient than the EMI algorithm. Unfortunately, coherence bias correction processing is relatively time consuming. However, it will significantly improve the optimization performance of the algorithm, as shown in Figure 3.

4. Experimental Results with the Real Data

4.1. Real Data 1

To evaluate the effectiveness of the proposed AWPOA for DS phase history retrieval, 12 TerraSAR-X images with ascending orbits, an incidence of 35.28 degrees, a resolution of 0.91 m (range) × 1.89 m (azimuth), a size of 3000 (range) × 4000 (azimuth), covering the Capital International Airport were employed for experimental analysis in this study. These SAR images were acquired from 30 January 2018 to 28 January 2019, and the temporal interval was 33 days. Notably, all possible interference pairs were adopted for experimental analysis. Meanwhile, according to the experimental results obtained with the simulated data, the more representative algorithms were selected among the above comparison algorithms to realize experimental comparison and analysis of the real data.

An interferogram with a temporal baseline of 66 days was used as an example for visual analysis. Notably, the smoother the optimized phase and the less residual noise, the better the optimization performance of the algorithm. Considering the influence of the temporal and geometric decorrelation factors, the quality of the interferogram was poor, and a large amount of phase noise masked the effective phase information, as shown in Figure 5a,f. Figure 5b–e shows the optimized interferometric phase obtained by EMI, POA with coherence-power weight, POA with Fisher weight, and AWPOA. Notably, POAs with coherence power and Fisher weight combine these weighting strategies with the efficient solution strategy derived in this study. Compared with the original interferogram, these POAs all showed an obvious noise suppression effect, and the optimized phases were all smoother. Among them, the optimized phase processed by the Fisher weight still retained many obvious noise points. That is, the optimization performance of POA with the Fisher weight was the worst, followed by the EMI algorithm. Compared with the former two POAs, the POA with the coherence-power weight showed a better effect, and the phase noise was effectively suppressed. However, the optimized phase obtained by the AWPOA was smoothest, especially in the middle runway area, which indicates that the overall optimization performance of the AWPOA was better than that of the other algorithms. Moreover, the coherence maps corresponding to the optimized interferogram obtained by different POAs were calculated respectively, which can more intuitively evaluate the quality of the optimized phase. The larger the coherence value, the better the quality of the interferometric phase, and the better the optimization performance of the algorithm. It can be found that the coherence map calculated by the AWPOA, shown in Figure 5j, shows the large value in a wide range, which was significantly better than that of other algorithms. It further indicates the best optimized phase quality and the best optimization performance of the AWPOA.

Furthermore, the black rectangular area marked in Figure 5 was enlarged for detailed analysis, as shown in Figure 6. Obviously, the phase fringes optimized by the proposed AWPOA are clearer than those optimized by other algorithms, and the corresponding coherence map was also the best. Additionally, combined with the coherence map, the optimized phase obtained by the POA with the coherence-power weight was slightly inferior to that of the AWPOA; however, it was obviously superior to the EMI and the POA with the Fisher weight. Generally, this local magnification analysis further verified the effectiveness of the proposed AWPOA in improving the phase quality.

Additionally, all possible interferograms obtained based on the optimized phase were further quantitatively evaluated and analyzed. Here, two common indexes were considered to evaluate the quality of the phase, i.e., the number of residues and the sum of the phase difference (SPD).

$$SPD={\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N\left(\frac{1}{8}{\displaystyle \sum _{l=-1}^1{\displaystyle \sum _{k=-1}^1\left|{\widehat{\varphi }}_{i,j}-{\widehat{\varphi }}_{i+l,j+k}\right|}}\right)}}$$

(19)

Moreover, the influences of coherence bias correction and the weighting strategy on phase optimization are considered in the same way as simulated data verification.

To show the improvement of the phase quality of the optimized phase more intuitively, the improvement percentage of the number of residues and the SPD were calculated. Taking the SPD index as an example, the improvement percentage of SPD was defined as follows:

$$improvement=\left(1-\frac{SP{D}_{POA}}{SP{D}_{ori}}\right)\times 100\%$$

(20)

where $SP{D}_{POA}$ and $SP{D}_{ori}$ are the SPD of the optimized interferogram by different POAs and the original interferogram, respectively. Figure 7 shows the improvement percentage of these two indexes obtained by different POAs. In terms of the number of residues index, it can be found that the improvement percentage processed by the coherence-power weighting strategy was slightly better than that of the EMI algorithms, which is consistent with the conclusion derived by the above simulated data. Interestingly, the improvement of the phase quality obtained by the Fisher weighting strategy was the worst, which may have resulted from the poor coherence. However, the AWPOA proposed in this study maintained the highest improvement percentage regardless of the low-coherence interferogram or high-coherence interferogram. In addition, compared with no bias correction, coherence bias correction processing can further improve the quality of the optimized interferogram, i.e., the performance of phase optimization. Nevertheless, the AWPOA always shows better optimization performance than other POAs. In terms of the SPD index, although the specific values of this index are different from those of the former index, the distribution trend of the improvement percentage of all interferograms is extremely similar to that of the former index. Therefore, the same conclusion can be derived.

Furthermore, the mean value and standard deviation (STD) of the improvement percentage of the phase quality in terms of the number of residues and SPD was calculated and analyzed, as shown in

Table 2. Mean value and standard deviation of the improvement percentage of the phase quality corresponding to real data 1.

Methods	Residues				SPD
	Without Bias Correction		With Bias Correction		Without Bias Correction		With Bias Correction
	Mean	STD	Mean	STD	Mean	STD	Mean	STD
EMI	59.75%	5.52%	69.26%	4.83%	32.23%	5.86%	41.10%	5.89%
Coherence-power weight	62.02%	4.91%	72.03%	4.12%	35.82%	5.71%	44.06%	5.54%
Fisher weight	48.13%	6.61%	62.70%	5.49%	27.00%	5.90%	36.80%	5.95%
AWPOA	70.30%	3.31%	75.62%	3.07%	41.88%	4.91%	47.56%	4.70%

. Choosing the evaluation results of the number of residues as an example, regardless of the POA used, the mean value of the improvement percentage after coherence bias correction was significantly improved by more than 5% over that achieved without bias correction. Moreover, the standard deviation was slightly reduced, which further verifies that coherence bias correction effectively enhances the performance of the POA. In terms of the different weighting strategies, the adaptive weighting strategy based on the sigmoid model attained the optimal performance, and its noise reduction rate was significantly higher than that of the other weighting strategies. In particular, in the case without bias correction, the mean value of the improvement percentage of the AWPOA was at least 8% higher than that of the other algorithms. In addition, the performance of the coherence-power weighting strategy was suboptimal but slightly better than that of the EMI algorithm. Considering the different weighting strategies and processing methods, the AWPOA proposed in this study provided the minimum standard deviation, at least 1% lower than other algorithms, which demonstrates that this algorithm achieved a higher noise robustness than that achieved with the other algorithms.

By analyzing the evaluation results of the SPD, the same conclusion is drawn, i.e., coherence bias correction processing effectively increases the optimization performance, and the adaptive weighting strategy based on the sigmoid model was obviously better than the traditional weighting strategies. In fact, the traditional POAs do not include the bias correction. Therefore, in terms of the above indexes, the mean value of the improvement percentage obtained by the AWPOA was increased by at least 12%, and the standard deviation was reduced by at least 1% over the traditional POAs. Comprehensive analysis revealed that the proposed AWPOA, which combines bias correction and the adaptive weighting strategy, attained a better optimization performance and noise robustness.

Additionally, the quality of the optimized phase estimator obtained by different POAs can also be evaluated with the goodness-of-fit, which directly determines the number of selected DS candidates.

$${\gamma }_{PTA}=\frac{2}{N(N-1)}\mathrm{Re}\left({\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j>i}^N\exp \left(j\left({\phi }_{i,j}-({\widehat{\varphi }}_i-{\widehat{\varphi }}_j)\right)\right)}}\right)$$

(21)

Figure 8a,b show histograms of the goodness-of-fit corresponding to the different weighting strategies with and without bias correction processing, respectively. In terms of no bias correction processing, the normalized frequency of the goodness-of-fit estimated with the coherence-power weighting strategy was similar to that of the Fisher weighting strategy when the goodness-of-fit was higher than 0.5, which was slightly better than that of the EMI algorithm. After bias correction processing, the optimization performance of the EMI algorithm was significantly improved, and the gap between the coherence-power weighting and the Fisher weighting strategy was narrowed. However, at a goodness-of-fit higher than 0.5, the normalized frequency of the AWPOA was significantly higher than that of the other three algorithms, which further verifies the effectiveness of the AWPOA. Moreover, considering that the pixels with goodness-of-fit values higher than the threshold were selected as DS candidates, the number of DS candidates obtained with the AWPOA was notably larger than that obtained with the other algorithms. Furthermore, the higher density of the DS candidates promotes the subsequent three-dimensional phase unwrapping and improves the reliability of deformation parameter interpretation. Figure 8c more intuitively shows the improvement effect of the optimized phase before and after bias correction and the notable advantages of the proposed AWPOA.

4.2. Real Data 2

In addition, real data 2 with TerraSAR-X images covering the Beijing Daxing International Airport were employed for further experimental analysis. Specifically, 12 SAR scenes acquired from 12 March 2018 to 23 December 2018 (the temporal interval was 22 days) along an ascending orbit, with an incidence of 31.04 degrees, a resolution of 0.91 m (range) × 2.05 m (azimuth), and a size of 5100 (range) × 3400 (azimuth) were processed. Similarly, all possible interference pairs were adopted for experimental analysis.

Considering that the airport was under construction during this period and that there was much forest vegetation around it, the decorrelation phenomenon was more of a series. A large amount of phase noise existed in the original interferogram shown in Figure 9a. The coherence was generally less than 0.4, which is not conducive to the subsequent time series analysis. Therefore, the phase optimization process was necessary to improve the quality of the interferogram. The optimized interferograms processed by different POAs are shown in Figure 9b–e. We found that there remained some noise in the results obtained by the EMI and the POA with the Fisher weight. The optimized phase obtained by the AWPOA was the smoothest, which was slightly better than that of the POA with the coherence-power weight. Moreover, the coherence obtained by the AWPOA, shown in Figure 9j, was generally greater than 0.7, which was significantly higher than that of other algorithms. That is, the AWPOA proposed in this study showed the best optimization performance compared to the other traditional POAs. The above conclusion can also be drawn more intuitively by analyzing the black rectangular area.

To comprehensively evaluate the optimization performance of the POA under the influence of different decorrelations, quantitative evaluation analysis was further performed. Similar to real data 1, the improvement percentage of the phase quality obtained by different POAs was calculated, and the number of residues and SPD indexes were also adopted for evaluating the phase quality. The mean value and standard deviation of the improvement percentage of all impossible interferograms are shown in

Table 3. Mean value and standard deviation of the improvement percentage of the phase quality corresponding to real data 2.

Methods	Residues				SPD
	Without Bias Correction		With Bias Correction		Without Bias Correction		With Bias Correction
	Mean	STD	Mean	STD	Mean	STD	Mean	STD
EMI	52.73%	3.60%	64.95%	3.45%	26.44%	3.65%	35.75%	4.18%
Coherence-power weight	52.11%	3.62%	66.69%	3.36%	27.33%	3.90%	37.37%	4.36%
Fisher weight	45.98%	4.17%	61.80%	3.84%	23.93%	3.89%	33.91%	4.43%
AWPOA	61.87%	2.55%	69.21%	2.59%	33.38%	3.37%	39.25%	3.64%

. In terms of no bias correction, the results of these two indexes show a similar distribution trend, and both of them come to the same conclusion. Specifically, the mean value obtained by the POA with the Fisher weight was the lowest, indicating that its optimization performance was the worst. The optimization performance of the POA with the coherence-power weight was similar to that of the EMI and even slightly better than that of the latter. Obviously, the mean value of the improvement percentage obtained by the AWPOA was the highest, and it improved by more than 9% for the residues index and 6% for the SPD index over other algorithms. This indicates that the optimization performance of the AWPOA was better than that of other POAs in the case without bias correction; that is, the adaptive weighting strategy based on the sigmoid model adopted in the AWPOA was better than other traditional weighting strategies. Moreover, the STD value obtained by the AWPOA was the lowest, and it was reduced by at least 1% over other POAs, indicating that the AWPOA has the highest noise robustness. Notably, the mean values of the improvement percentage obtained by POAs are all further improved when the bias correction process is carried out, which verifies the effectiveness of the bias correction in improving the optimization performance. However, the AWPOA proposed in this study, which combines bias correction and the adaptive weighting strategy, always shows the best optimization performance and noise robustness compared to other POAs. Specifically, in terms of the above two indexes, the mean value of the improvement percentage obtained by the AWPOA was increased by at least 12% over the traditional POAs, which have no bias correction.

Furthermore, the goodness-of-fit index was calculated to evaluate the quality of the optimized phase. Similar to the results of real data 1, the adaptive weighting strategy adopted in the AWPOA always shows the best performance with or without bias correction. Moreover, Figure 10c shows more intuitively that the bias correction process can further improve the value of goodness-of-fit and the quality of the optimized phase. Generally, the above experimental results all verify that the proposed AWPOA combined with bias correction and the adaptive weighting strategy based on the sigmoid model has the best optimization performance, which is consistent with the conclusion drawn by the previous experimental results of real data 1.

5. Conclusions

In this study, an advanced adaptive weighted phase optimization algorithm was proposed to improve the SNR of the phase corresponding to DS pixels, which were conducive to the interpretation of the deformation signal. Specifically, the proposed AWPOA adopted the adaptive weighting strategy based on the sigmoid model, which can assign a more reasonable weight to pixels of different quality. Moreover, coherence bias correction based on the second-kind statistics was introduced to reduce the coherence estimation error, and an efficient solution strategy based on EVD was derived to further improve the processing efficiency of the algorithm.

The experimental results obtained with simulated data and two sets of TerraSAR-X real data suggest that the AWPOA proposed in this study attained a better optimization performance and a higher noise robustness than those of the traditional algorithm. Compared with the traditional POAs, the mean value of the improvement percentage obtained by the AWPOA was improved by at least 12% for the residual and SPD indexes, indicating the better optimization performance of the AWPOA. Additionally, the standard deviation of the improvement percentage obtained by the AWPOA was reduced by at least 1% over other POAs, indicating the higher noise robustness of the AWPOA. Moreover, this study analyzed the influence of the adaptive weighting strategy based on the sigmoid model and coherence bias correction on the optimization performance in detail. They all provide a better effect than that provided by the traditional weighting strategies and processing involving no bias correction. Furthermore, this superior phase optimization effect will promote the improvement of the quantity and quality of DS and will be more conducive to the subsequent deformation parameter calculation.