Deformation Estimation Using Beidou GEO-Satellite-Based Reflectometry
Abstract
:1. Introduction
2. Theoretical Deformation Model
2.1. Reflect Geometry
2.2. Deformation Retrieval Model
3. Data Acquisition Devices and Software Processing
3.1. Data Acquisition Devices
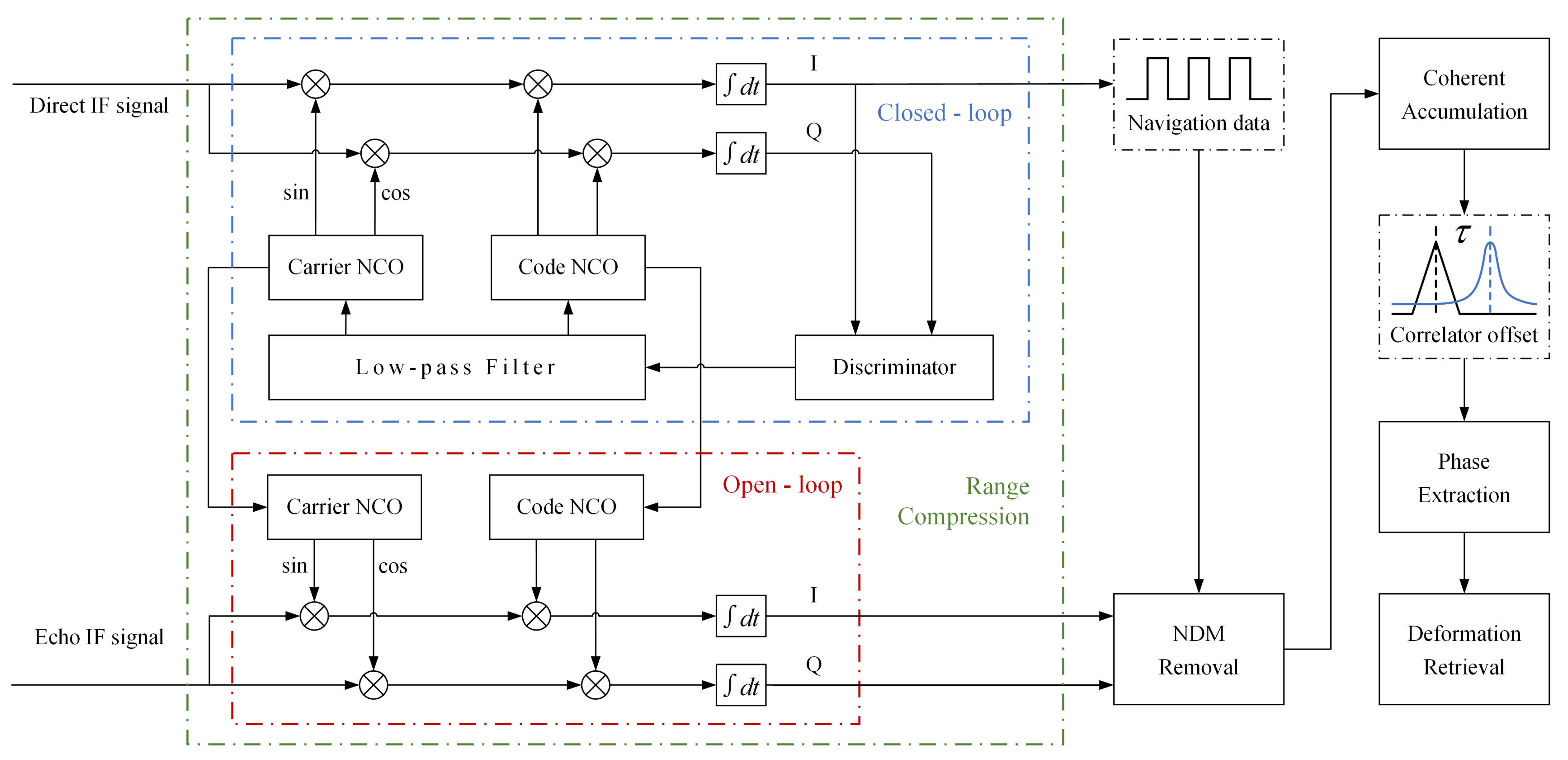
3.2. Software Processing
3.2.1. Range Compression
3.2.2. Navigation Data Modulation Removal
3.2.3. Coherent Accumulation
3.2.4. Phase Extraction and Deformation Retrieval
4. Experiment
4.1. Experimental Scenario
4.2. Experimental Artificial Deformation
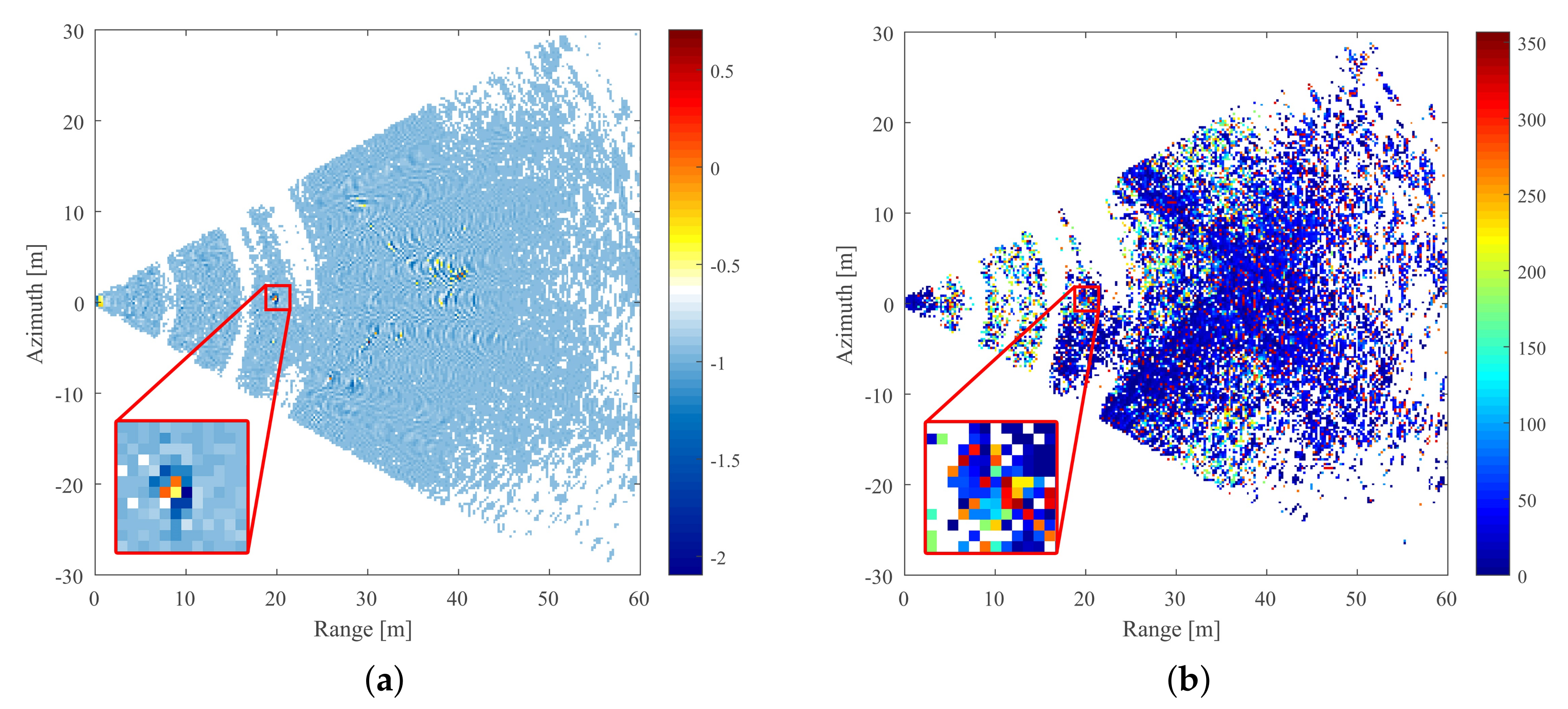
4.3. Data Processing Results
- (1)
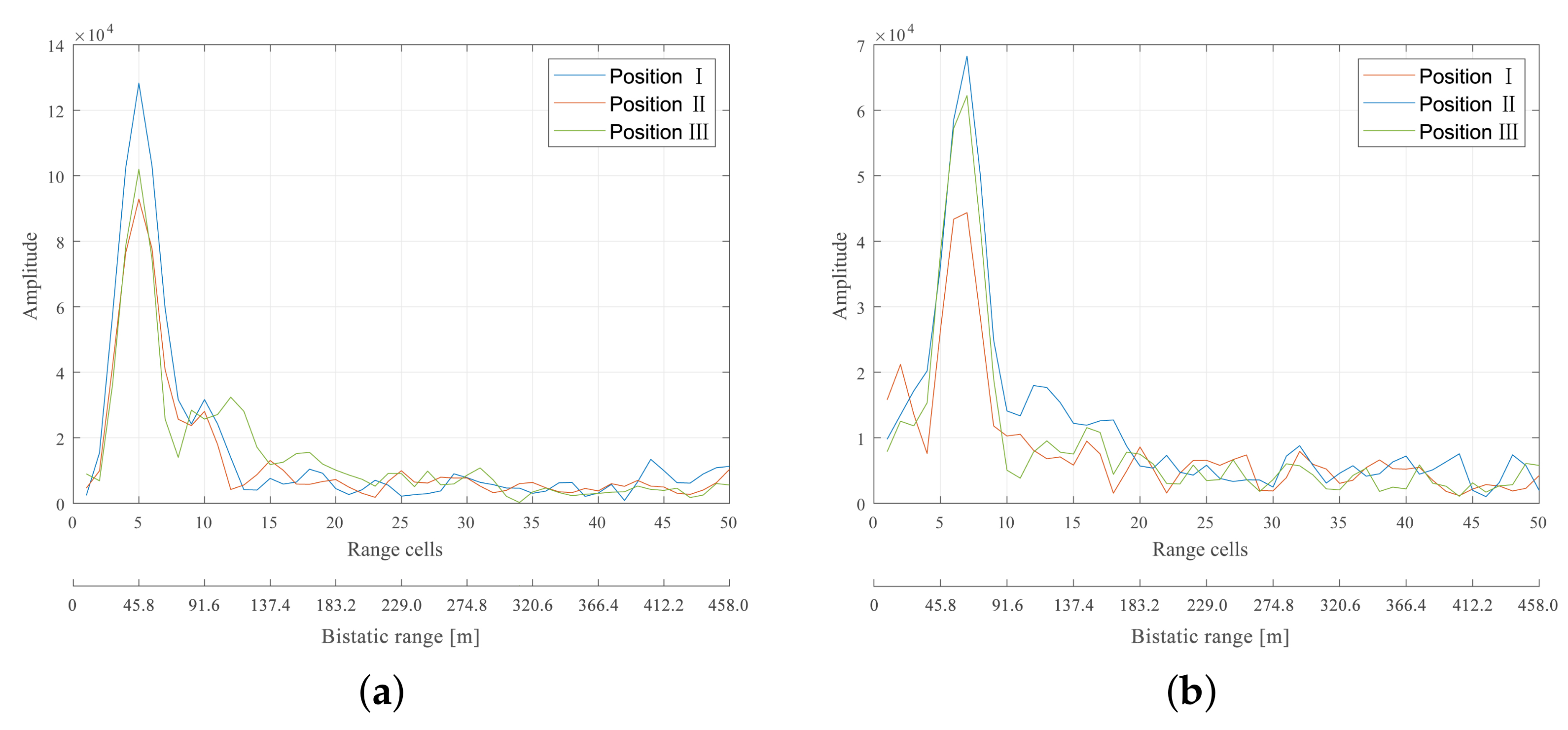
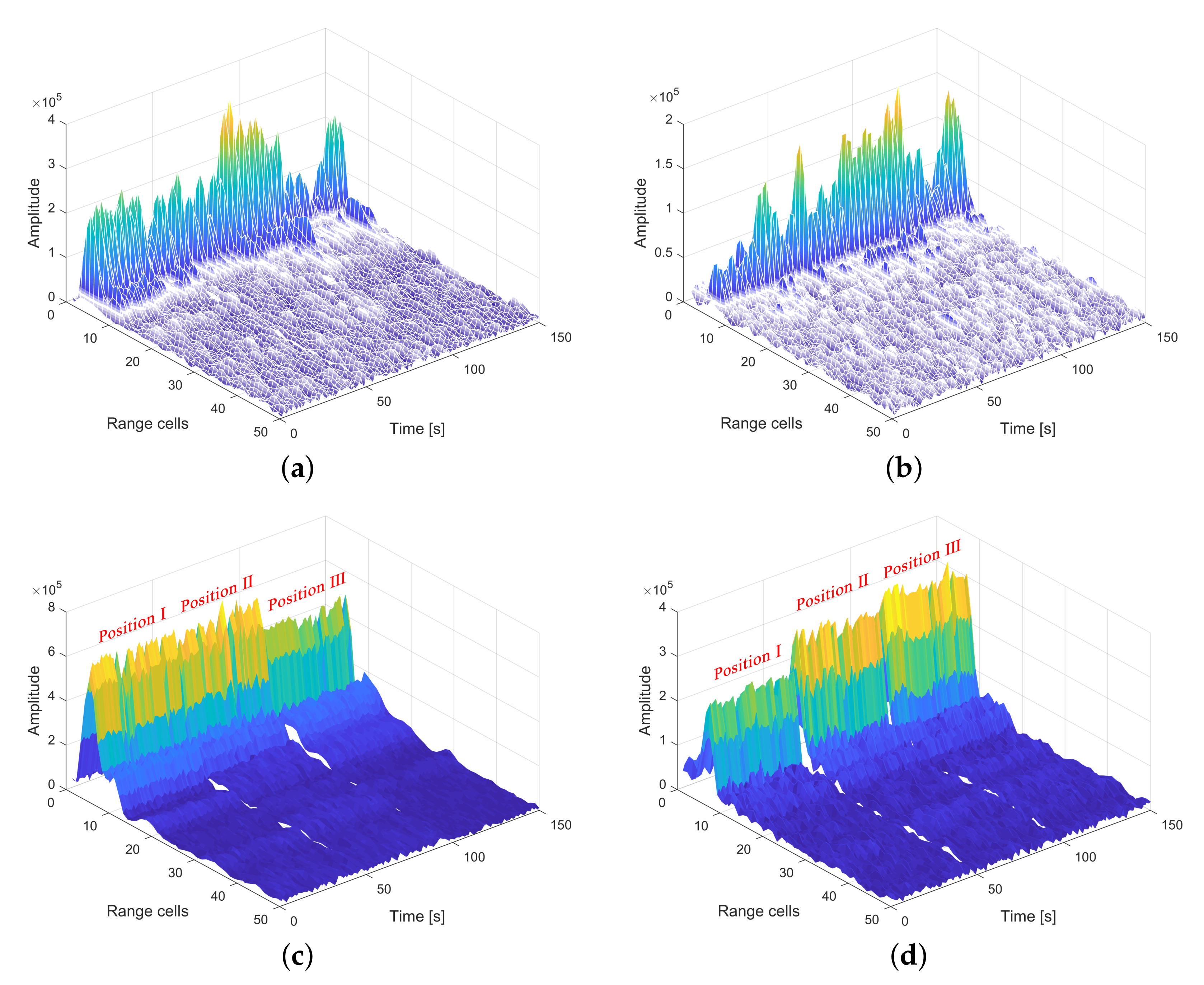
- Results of Range Compression
- (2)
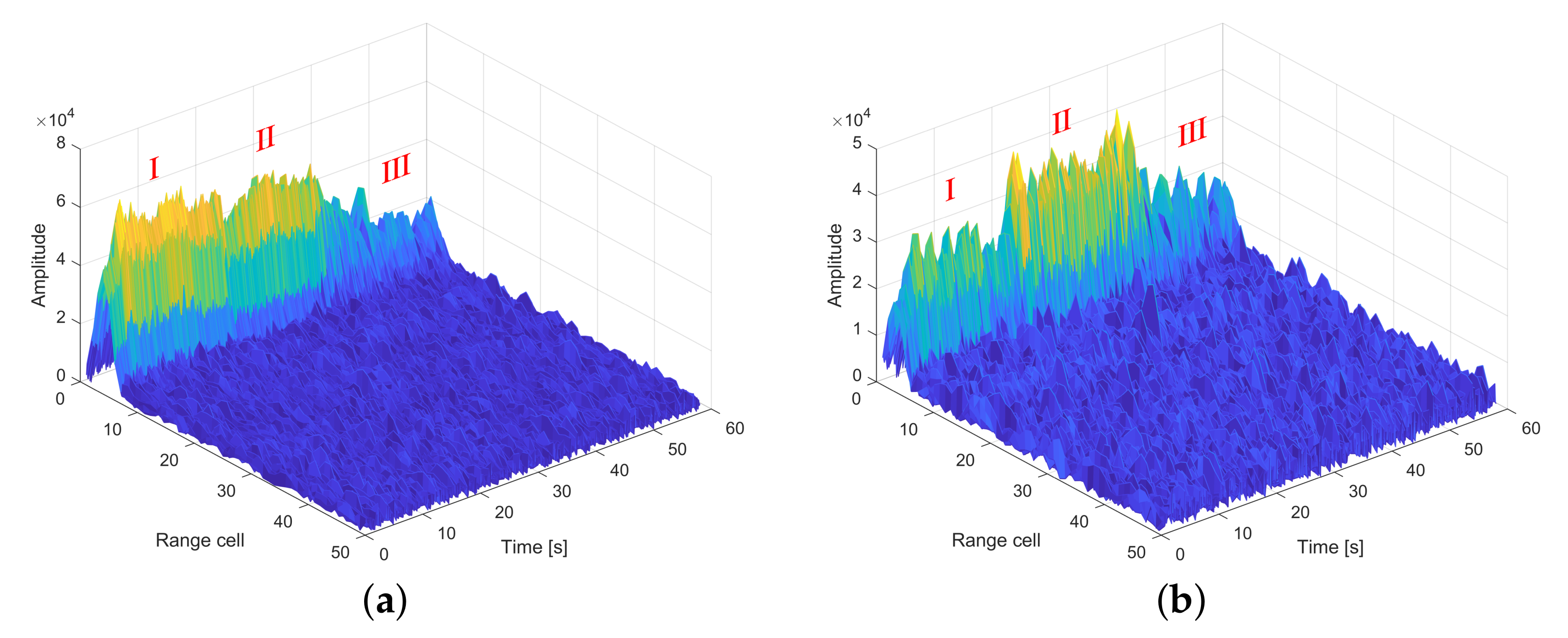
- Results of NDM Removal and Coherent Accumulation
- (3)
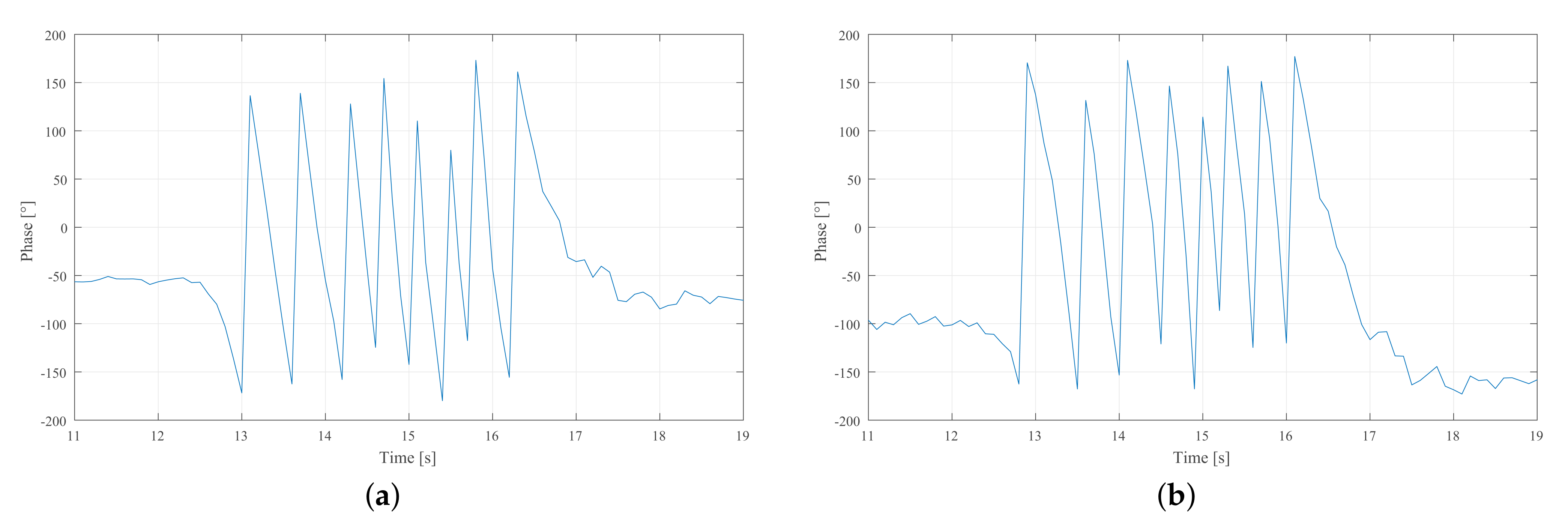
- Results of Phase Extraction
4.4. Deformation Estimation Results
5. Discussion
5.1. Result Comparison with Ground-Based SAR
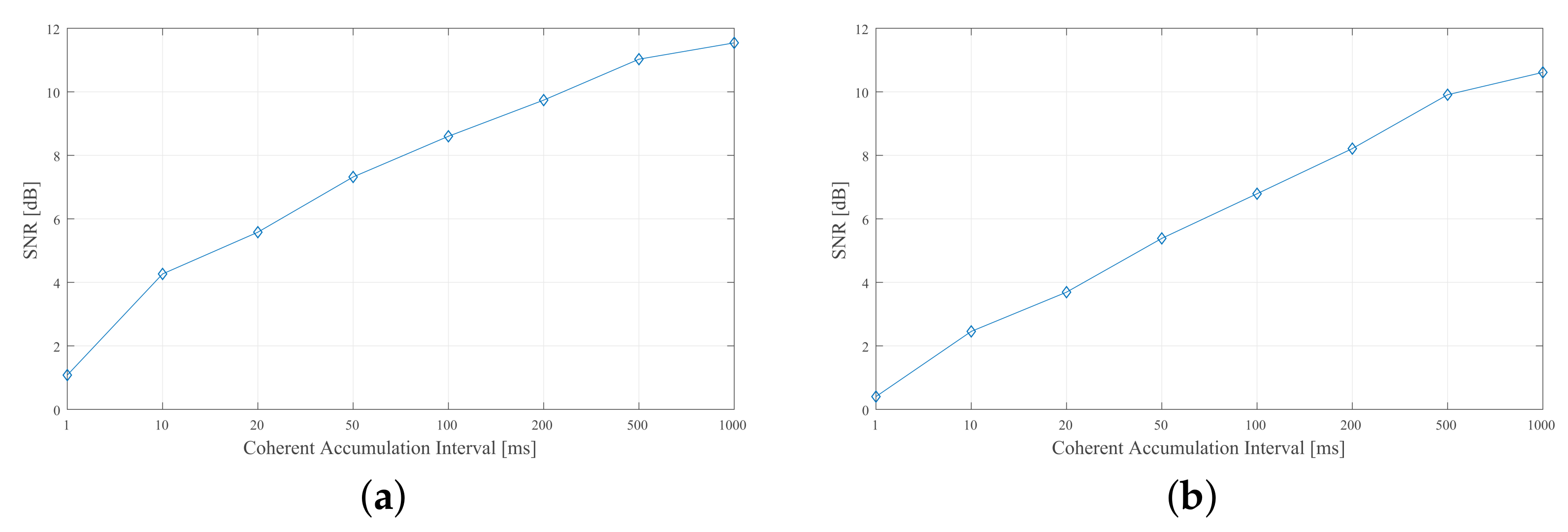
5.2. Effect of SNR on Phase Stability and Deformation Retrieval
5.3. Study on Estimation Range Extension
- (1)
- Continuously record the GNSS direct and echo signals.
- (2)
- Perform phase extractions over the entire processing period, detect the deviants in phase (assuming that only one deviant exists within one certain time segment), and take the time segment in which the deviant arises into further analysis.
- (3)
- Retrieve the fractional part of deformation quantity with the sums of phase variations at the beginning and the ending segments .
- (4)
- Retrieve the integer part of deformation quantity with the amount of complete cycles, which can be derived by subtracting one from the number of phase reversals N. Consequently, the overrange deformation quantity could be expressed as:where denotes the fractional part of deformation quantity and denotes the integer part of deformation quantity.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, R.; Fan, X. The landslide story. Nat. Geosci. 2013, 6, 325–326. [Google Scholar] [CrossRef]
- Jia, H.; Zhang, H.; Liu, L.; Liu, G. Landslide Deformation Monitoring by Adaptive Distributed Scatterer Interferometric Synthetic Aperture Radar. Remote Sens. 2019, 11, 2273. [Google Scholar] [CrossRef] [Green Version]
- Luo, T.; Li, F.; Pan, B.; Zhou, W.; Chen, H.; Shen, G.; Hao, W. Deformation Monitoring of Slopes With a Shipborne InSAR System: A Case Study of the Lancang River Gorge. IEEE Access 2021, 9, 5749–5759. [Google Scholar] [CrossRef]
- Yang, S.S.; Potirakis, S.M.; Sasmal, S.; Hayakawa, M. Natural Time Analysis of Global Navigation Satellite System Surface Deformation: The Case of the 2016 Kumamoto Earthquakes. Entropy 2020, 22, 674. [Google Scholar] [CrossRef]
- Rezvani, M.H.; Watson, C.S.; King, M.A. Estimating Vertical Land Motion and Residual Altimeter Systematic Errors Using a Kalman-Based Approach. J. Geophys. Res. Ocean. 2021, 126, e2020JC017106. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Hu, J.; Wang, Y.J.; Chen, G.L. InSAR-Based Model Parameter Estimation of Probability Integral Method and Its Application for Predicting Mining-Induced Horizontal and Vertical Displacements. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4818–4832. [Google Scholar] [CrossRef]
- Parizzi, A.; Brcic, R.; De Zan, F. InSAR Performance for Large-Scale Deformation Measurement. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Hong, S.; Liu, M. Postseismic Deformation and Afterslip Evolution of the 2015 Gorkha Earthquake Constrained by InSAR and GPS Observations. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020230. [Google Scholar] [CrossRef]
- Qiu, Z.; Jiao, M.; Jiang, T.; Zhou, L. Dam Structure Deformation Monitoring by GB-InSAR Approach. IEEE Access 2020, 8, 123287–123296. [Google Scholar] [CrossRef]
- Xiao, R.; Shi, H.; He, X.; Li, Z.; Jia, D.; Yang, Z. Deformation Monitoring of Reservoir Dams Using GNSS: An Application to South-to-North Water Diversion Project, China. IEEE Access 2019, 7, 54981–54992. [Google Scholar] [CrossRef]
- Arnoso, J.; Riccardi, U.; Benavent, M.; Tammaro, U.; Montesinos, F.G.; Blanco-Montenegro, I.; Vélez, E. Strain Pattern and Kinematics of the Canary Islands from GNSS Time Series Analysis. Remote Sens. 2020, 12, 3297. [Google Scholar] [CrossRef]
- Zou, X.; Li, Z.; Li, Y.; Wang, Y.; Tang, W.; Deng, C.; Cui, J.; Fu, R. A Novel Method to Mitigate the Multipath Error for BDS-2 Dam Deformation Monitoring. Remote Sens. 2021, 13, 1787. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, Y.; Yu, W.; Chen, W.; Weng, D. Deformation monitoring using GNSS-R technology. Adv. Space Res. 2019, 63, 3303–3314. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Vall-llossera, M.; Valencia, E.; Marchan-Hernandez, J.F.; Ramos-Perez, I. Soil Moisture Retrieval Using GNSS-R Techniques: Experimental Results Over a Bare Soil Field. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3616–3624. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CYGNSS Data for Soil Moisture Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S.; Jales, P.; Gommenginger, C. Spaceborne GNSS-R Minimum Variance Wind Speed Estimator. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6829–6843. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Roselló, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef] [Green Version]
- Jacobson, M.D. Dielectric-Covered Ground Reflectors in GPS Multipath Reception—Theory and Measurement. IEEE Geosci. Remote Sens. Lett. 2008, 5, 396–399. [Google Scholar] [CrossRef]
- Vey, S.; Güntner, A.; Wickert, J.; Blume, T.; Thoss, H.; Ramatschi, M. Monitoring Snow Depth by GNSS Reflectometry in Built-up Areas: A Case Study for Wettzell, Germany. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4809–4816. [Google Scholar] [CrossRef] [Green Version]
- Tabibi, S.; Geremia-Nievinski, F.; van Dam, T. Statistical Comparison and Combination of GPS, GLONASS, and Multi-GNSS Multipath Reflectometry Applied to Snow Depth Retrieval. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3773–3785. [Google Scholar] [CrossRef]
- Liu, F.; Fan, X.; Zhang, T.; Liu, Q. GNSS-Based SAR Interferometry for 3-D Deformation Retrieval: Algorithms and Feasibility Study. IEEE Trans. Geosci. Remote Sens. 2018. [Google Scholar] [CrossRef]
- Li, W.; Fabra, F.; Yang, D.; Rius, A.; Martín-Neira, M.; Yin, C.; Wang, Q.; Cao, Y. Initial Results of Typhoon Wind Speed Observation Using Coastal GNSS-R of BeiDou GEO Satellite. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4720–4729. [Google Scholar] [CrossRef]
- Ban, W.; Yu, K.; Zhang, X. GEO-Satellite-Based Reflectometry for Soil Moisture Estimation: Signal Modeling and Algorithm Development. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1829–1838. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Y.; Gao, F.; Guo, P.; Wang, X.; Niu, X.; Wu, M.; Fu, N. Sea Surface Height Estimation by Ground-Based BDS GEO Satellite Reflectometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5550–5559. [Google Scholar] [CrossRef]
- Nogues-Correig, O.; Cardellach Gali, E.; Sanz Campderros, J.; Rius, A. A GPS-Reflections Receiver That Computes Doppler/Delay Maps in Real Time. IEEE Trans. Geosci. Remote Sens. 2007, 45, 156–174. [Google Scholar] [CrossRef]
- Chiu, T.C.; Liou, Y.A.; Yeh, W.H.; Huang, C.Y. NCURO Data-Retrieval Algorithm in FORMOSAT-3 GPS Radio-Occultation Mission. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3395–3405. [Google Scholar] [CrossRef]
- Pany, T.; Riedl, B.; Winkel, J.; Woerz, T.; Schweikert, R.; Niedermeier, H.; Lagrasta, S.; Lopez-Risueno, G.; Jiménez-Baños, D. Coherent integration time: The longer, the better. Inside GNSS 2009, 4, 52–61. [Google Scholar]
- Liu, W.; Beckheinrich, J.; Semmling, M.; Ramatschi, M.; Vey, S.; Wickert, J.; Hobiger, T.; Haas, R. Coastal Sea-Level Measurements Based on GNSS-R Phase Altimetry: A Case Study at the Onsala Space Observatory, Sweden. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5625–5636. [Google Scholar] [CrossRef]
- Feng, W.; Nico, G.; Sato, M. GB-SAR Interferometry Based on Dimension-Reduced Compressive Sensing and Multiple Measurement Vectors Model. IEEE Geosci. Remote Sens. Lett. 2019, 16, 70–74. [Google Scholar] [CrossRef]
- Zebker, H.A.; Lu, Y. Phase unwrapping algorithms for radar interferometry: Residue-cut, least-squares, and synthesis algorithms. J. Opt. Soc. Am. A 1998, 15, 586. [Google Scholar] [CrossRef]









| C01/Reflecting Plate I | C04/Reflecting Plate II | |
|---|---|---|
| Sampling frequency | 32.738 MHz | |
| Signal Bandwidth | 10.23 MHz | |
| Central frequency | 0.1271125 MHz | |
| Satellite azimuth | 137 | 117 |
| Satellite elevation | 43 | 28 |
| Tilt angle | 69 | 76 |
| bistatic range | 36 m | 47 m |
| Deformation I | Deformation II | |
|---|---|---|
| Reflecting plate I (C01 event) | 2 cm | 4 cm |
| Reflecting plate II (C04 event) | 2 cm | 5 cm |
| Satellite | Event | Estimation (cm) | Ground Truth (cm) | RMSE (cm) |
|---|---|---|---|---|
| C01 | Deformation I | 0.51 | 1.88 | 0.85 |
| Deformation II | 4.27 | 3.75 | ||
| C04 | Deformation I | 0.89 | 1.93 | 1.04 |
| Deformation II | 10.34 | 4.83 | ∖ |
| Parameters | Value |
|---|---|
| Central frequency | 5.6 GHz (Waveband C) |
| Wavelength | 5.6 cm |
| Signal bandwidth | 600 MHz |
| Range resolution | 0.25 m |
| Azimuth resolution | 0.25 m |
| Satellite | Period Class | SNR (dB) | Phase RMSE () | Deformation RMSE (cm) |
|---|---|---|---|---|
| 3C01 | Superior | 8.61 | 2.77 | 0.09 |
| Mediocre | 8.44 | 6.56 | 0.22 | |
| Inferior | 8.35 | 8.29 | 0.28 | |
| 3C04 | Superior | 8.16 | 2.49 | 0.08 |
| Mediocre | 8.14 | 7.30 | 0.25 | |
| Inferior | 7.95 | 11.38 | 0.39 |
| Event | Ground Truth (cm) | RMSE (cm) | |||
|---|---|---|---|---|---|
| 2Dataset 1 | Deformation I | 99.00 | 100.41 | 97.03 | 2.77 |
| Deformation II | 96.78 | 94.90 | 97.03 | 1.52 | |
| 2Dataset 2 | Deformation I | 9.65 | 9.37 | 9.70 | 0.24 |
| Deformation II | 186.99 | 187.03 | 184.36 | 2.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Yan, S.; Gong, J. Deformation Estimation Using Beidou GEO-Satellite-Based Reflectometry. Remote Sens. 2021, 13, 3285. https://doi.org/10.3390/rs13163285
Chen Y, Yan S, Gong J. Deformation Estimation Using Beidou GEO-Satellite-Based Reflectometry. Remote Sensing. 2021; 13(16):3285. https://doi.org/10.3390/rs13163285
Chicago/Turabian StyleChen, Yongqian, Songhua Yan, and Jianya Gong. 2021. "Deformation Estimation Using Beidou GEO-Satellite-Based Reflectometry" Remote Sensing 13, no. 16: 3285. https://doi.org/10.3390/rs13163285
APA StyleChen, Y., Yan, S., & Gong, J. (2021). Deformation Estimation Using Beidou GEO-Satellite-Based Reflectometry. Remote Sensing, 13(16), 3285. https://doi.org/10.3390/rs13163285







