InSAR Coherence Analysis for Wetlands in Alberta, Canada Using Time-Series Sentinel-1 Data
Abstract
1. Introduction
2. Material and Method
2.1. Study Area
2.2. Reference Data
2.3. Satellite Data
2.4. InSAR Processing and Coherence Values Extraction
2.5. Scenarios for Wetland Coherence Assessment
3. Results
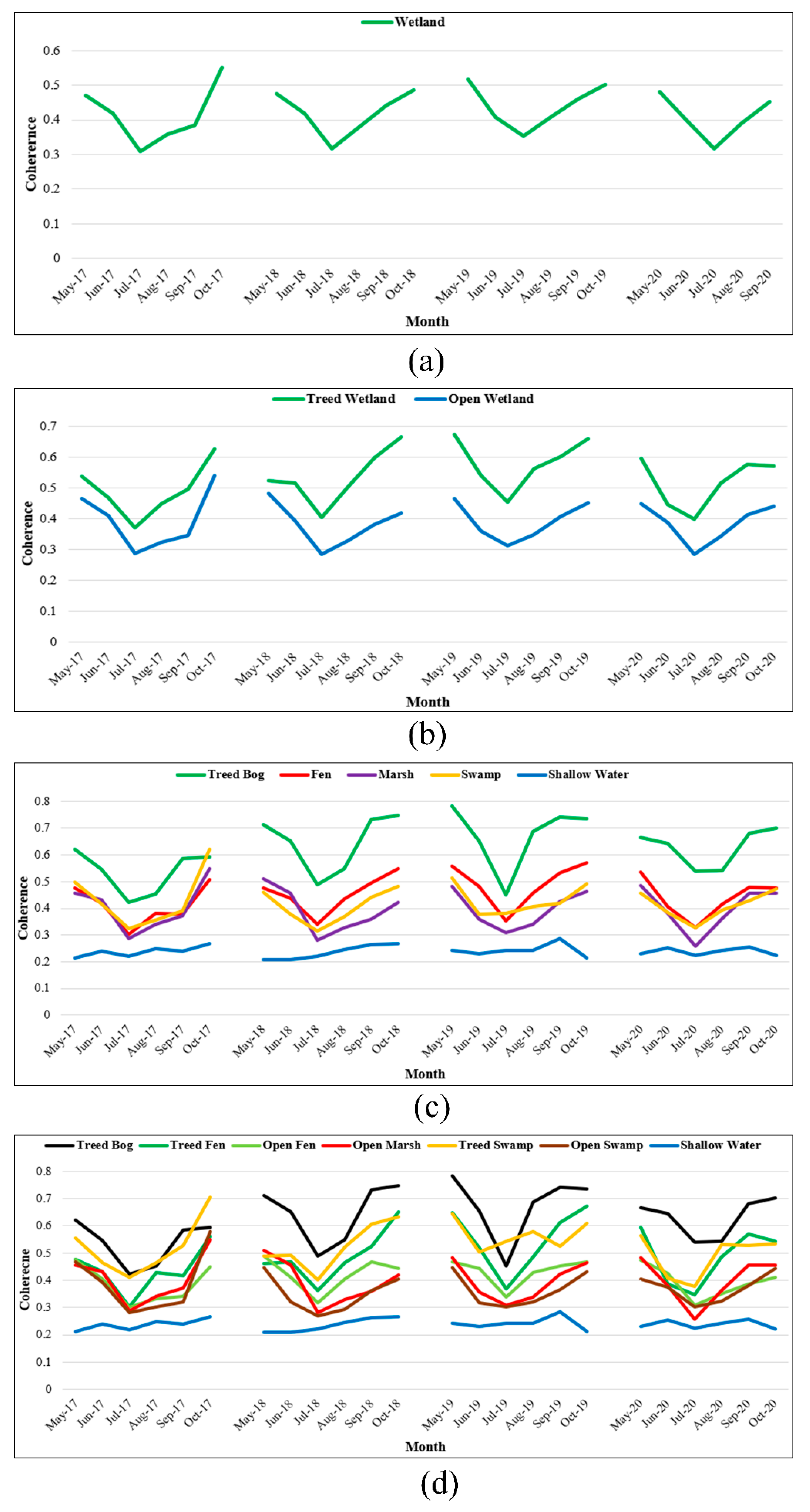
3.1. Monthly Coherence Change
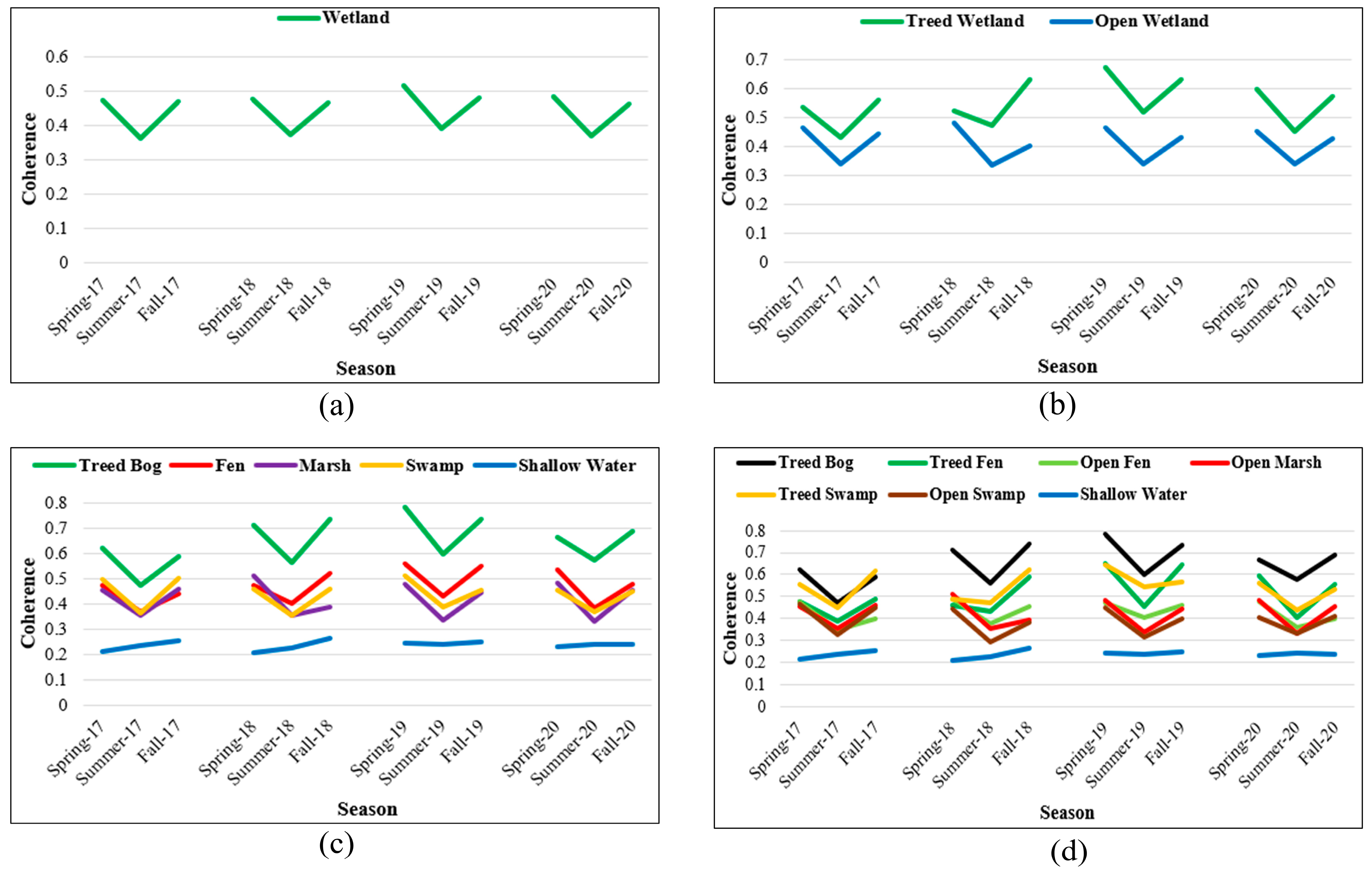
3.2. Seasonal Coherence Change
3.3. Leaf-On/Off Coherence Change
4. Discussion
4.1. Findings
4.2. Future Works
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Riley, W.J.; Subin, Z.M.; Lawrence, D.M.; Swenson, S.C.; Torn, M.S.; Meng, L.; Mahowald, N.M.; Hess, P. Barriers to predicting changes in global terrestrial methane fluxes: Analyses using CLM4Me, a methane biogeochemistry model integrated in CESM. Biogeosciences 2011, 8, 1925–1953. [Google Scholar] [CrossRef]
- Mahdavi, S.; Salehi, B.; Huang, W.; Amani, M.; Brisco, B. A PolSAR change detection index based on neighborhood information for flood mapping. Remote Sens. 2019, 11, 1854. [Google Scholar] [CrossRef]
- Mahdavi, S.; Salehi, B.; Granger, J.; Amani, M.; Brisco, B.; Huang, W. Remote sensing for wetland classification: A comprehensive review. GISci. Remote Sens. 2018, 55, 623–658. [Google Scholar] [CrossRef]
- Schmitt, A.; Brisco, B. Wetland monitoring using the curvelet-based change detection method on polarimetric SAR imagery. Water 2013, 5, 1036–1051. [Google Scholar] [CrossRef]
- Adeli, S.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.J.; Brisco, B.; Tamiminia, H.; Shaw, S. Wetland monitoring using SAR data: A meta-analysis and comprehensive review. Remote Sens. 2020, 12, 2190. [Google Scholar] [CrossRef]
- Elhadi, M.I.A.; Mutanga, O.; Rugege, D.; Ismail, R. Field spectrometry of papyrus vegetation (Cyperus papyrus L.) in swamp wetlands of St Lucia, South Africa. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 4, p. 260. [Google Scholar]
- Amani, M.; Mahdavi, S.; Afshar, M.; Brisco, B.; Huang, W.; Mohammad Javad Mirzadeh, S.; White, L.; Banks, S.; Montgomery, J.; Hopkinson, C. Canadian Wetland Inventory using Google Earth Engine: The First Map and Preliminary Results. Remote Sens. 2019, 11, 842. [Google Scholar] [CrossRef]
- Kaplan, G.; Avdan, U. Monthly analysis of wetlands dynamics using remote sensing data. ISPRS Int. J. Geo-Inf. 2018, 7, 411. [Google Scholar] [CrossRef]
- Zhao, J.; Niu, Y.; Lu, Z.; Yang, J.; Li, P.; Liu, W. Applicability Assessment of Uavsar Data in Wetland Monitoring: A Case Study of Louisiana Wetland. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 2375–2378. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Brisco, B. Separability analysis of wetlands in Canada using multi-source SAR data. GISci. Remote Sens. 2019, 56, 1233–1260. [Google Scholar] [CrossRef]
- Hird, J.; DeLancey, E.; McDermid, G.; Kariyeva, J. Google Earth Engine, Open-Access Satellite Data, and Machine Learning in Support of Large-Area Probabilistic Wetland Mapping. Remote Sens. 2017, 9, 1315. [Google Scholar] [CrossRef]
- Salvia, M.; Franco, M.; Grings, F.; Perna, P.; Martino, R.; Karszenbaum, H.; Ferrazzoli, P. Estimating flow resistance of wetlands using SAR images and interaction models. Remote Sens. 2009, 1, 992–1008. [Google Scholar] [CrossRef]
- DeLancey, E.R.; Kariyeva, J.; Cranston, J.; Brisco, B. Monitoring Hydro Temporal Variability in Alberta, Canada with Multi-Temporal Sentinel-1 SAR Data. Can. J. Remote Sens. 2018, 44, 1–10. [Google Scholar] [CrossRef]
- Brisco, B.; Shelat, Y.; Murnaghan, K.; Montgomery, J.; Fuss, C.; Olthof, I.; Hopkinson, C.; Deschamps, A.; Poncos, V. Evaluation of C-Band SAR for Identification of Flooded Vegetation in Emergency Response Products. Can. J. Remote Sens. 2019, 45, 73–87. [Google Scholar] [CrossRef]
- Brisco, B.; Ahern, F.; Murnaghan, K.; White, L.; Canisus, F.; Lancaster, P. Seasonal change in wetland coherence as an aid to wetland monitoring. Remote Sens. 2017, 9, 158. [Google Scholar] [CrossRef]
- Tsyganskaya, V.; Martinis, S.; Marzahn, P.; Ludwig, R. SAR-based detection of flooded vegetation—A review of characteristics and approaches. Int. J. Remote Sens. 2018, 39, 2255–2293. [Google Scholar] [CrossRef]
- Canisius, F.; Brisco, B.; Murnaghan, K.; Van Der Kooij, M.; Keizer, E. SAR Backscatter and InSAR Coherence for Monitoring Wetland Extent, Flood Pulse and Vegetation: A Study of the Amazon Lowland. Remote Sens. 2019, 11, 720. [Google Scholar] [CrossRef]
- DeLancey, E.R.; Brisco, B.; Canisius, F.; Murnaghan, K.; Beaudette, L.; Kariyeva, J. The Synergistic Use of RADARSAT-2 Ascending and Descending Images to Improve Surface Water Detection Accuracy in Alberta, Canada. Can. J. Remote Sens. 2019, 45, 759–769. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Smith, L.C.; Melack, J.M. Amazon floodplain water level changes measured with interferometric SIR-C radar. IEEE Trans. Geosci. Remote Sens. 2001, 39, 423–431. [Google Scholar] [CrossRef]
- Lee, H.; Yuan, T.; Yu, H.; Jung, H.C. Interferometric SAR for wetland hydrology: An overview of methods, challenges, and trends. IEEE Geosci. Remote Sens. Mag. 2020, 8, 120–135. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Melack, J.M.; Dunne, T.; Mertes, L.A.K.; Hess, L.L.; Smith, L.C. Interferometric radar measurements of water level changes on the Amazon flood plain. Nature 2000, 404, 174–177. [Google Scholar] [CrossRef]
- Foroughnia, F.; Nemati, S.; Maghsoudi, Y.; Perissin, D. An iterative PS-InSAR method for the analysis of large spatio-temporal baseline data stacks for land subsidence estimation. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 248–258. [Google Scholar] [CrossRef]
- Ranjgar, B.; Razavi-Termeh, S.V.; Foroughnia, F.; Sadeghi-Niaraki, A.; Perissin, D. Land Subsidence Susceptibility Mapping Using Persistent Scatterer SAR Interferometry Technique and Optimized Hybrid Machine Learning Algorithms. Remote Sens. 2021, 13, 1326. [Google Scholar] [CrossRef]
- Olen, S.; Bookhagen, B. Applications of SAR interferometric coherence time series: Spatiotemporal dynamics of geomorphic transitions in the south-central Andes. J. Geophys. Res. Earth Surf. 2020, 125, e2019JF005141. [Google Scholar] [CrossRef]
- Yuan, M.; Xie, C.; Shao, Y.; Xu, J.; Cui, B.; Liu, L. Retrieval of water depth of coastal wetlands in the Yellow River Delta from ALOS PALSAR backscattering coefficients and interferometry. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1517–1521. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Agram, P.S.; Simons, M. A noise model for InSAR time series. J. Geophys. Res. Solid Earth 2015, 120, 2752–2771. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Wetland water level monitoring using interferometric synthetic aperture radar (InSAR): A review. Can. J. Remote Sens. 2018, 44, 247–262. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Multi-temporal, multi-frequency, and multi-polarization coherence and SAR backscatter analysis of wetlands. ISPRS J. Photogramm. Remote Sens. 2018, 142, 78–93. [Google Scholar] [CrossRef]
- Santoro, M.; Wegmuller, U.; Askne, J.I.H. Signatures of ERS–Envisat interferometric SAR coherence and phase of short vegetation: An analysis in the case of maize fields. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1702–1713. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Wegmüller, U.; Labrière, N.; Chave, J. Sentinel-1 Coherence for Mapping Above-Ground Biomass in Semiarid Forest Areas. IEEE Geosci. Remote Sens. Lett. 2021. [Google Scholar] [CrossRef]
- Santoro, M.; Askne, J.I.H.; Wegmuller, U.; Werner, C.L. Observations, modeling, and applications of ERS-ENVISAT coherence over land surfaces. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2600–2611. [Google Scholar] [CrossRef]
- Mirzaee, S.; Motagh, M.; Arefi, H.; Nooryazdan, A. Phenological tracking og agricultural feilds investigated by using dual polarimetry tanDEM-X images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 73. [Google Scholar] [CrossRef]
- Hong, S.H.; Wdowinski, S.; Kim, S.W.; Won, J.S. Multi-temporal monitoring of wetland water levels in the Florida Everglades using interferometric synthetic aperture radar (InSAR). Remote Sens. Environ. 2010, 114, 2436–2447. [Google Scholar] [CrossRef]
- Xie, C.; Xu, J.; Shao, Y.; Cui, B.; Goel, K.; Zhang, Y.; Yuan, M. Long term detection of water depth changes of coastal wetlands in the Yellow River Delta based on distributed scatterer interferometry. Remote Sens. Environ. 2015, 164, 238–253. [Google Scholar] [CrossRef][Green Version]
- Minotti, P.G.; Rajngewerc, M.; Santoro, V.A.; Grimson, R. Evaluation of SAR C-band interferometric coherence time-series for coastal wetland hydropattern mapping. J. S. Am. Earth Sci. 2021, 106, 102976. [Google Scholar] [CrossRef]
- Liao, T.H.; Simard, M.; Denbina, M.; Lamb, M.P. Monitoring water level change and seasonal vegetation change in the coastal wetlands of louisiana using L-band time-series. Remote Sens. 2020, 12, 2351. [Google Scholar] [CrossRef]
- By, C.; Pettapiece, D.J.D. and W.W. Natural Regions and Subregions of Alberta: Natural Regions Committee; Government of Alberta: Edmonton, AB, Canada, 2016; ISBN 0778545725. [Google Scholar]
- DeLancey, E.R.; Simms, J.F.; Mahdianpari, M.; Brisco, B.; Mahoney, C.; Kariyeva, J. Comparing Deep Learning and Shallow Learning for Large-Scale Wetland Classification in Alberta, Canada. Remote Sens. 2019, 12, 2. [Google Scholar] [CrossRef]
- NASA. ASF. Available online: https://search.asf.alaska.edu (accessed on 15 March 2021).
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: New York, NY, USA, 2001; Volume 2, ISBN 0792369459. [Google Scholar]
- CPOD. Sentinel-1 POD Products Performance; Copernicus Sentinel-1, -2 and -3 Precise Orbit Determination Service (Sentinelspod); European Space Agency: Paris, France, 2019; Available online: https://sentinel.esa.int/documents/247904/3455957/Sentinel-1-POD-Products-Performance.pdf (accessed on 15 March 2021).
- Mallorquí, J.; Mora, O.; Blanco, P.; Broquetas, A. Linear and Non-Linear Long-Term Terrain Deformation with Dinsar (CPT: Coherent Pixels Technique). In Proceedings of the Fringe 2003 Workshop, Frascati, Italy, 1–5 December 2003. [Google Scholar]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Pepe, A.; Calò, F. A Review of Interferometric Synthetic Aperture RADAR (InSAR) Multi-Track Approaches for the Retrieval of Earth’s Surface Displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Marinkovic, P.; Ketelaar, G.; Leijen, F.V.; Hanssen, R. InSAR Quality Control: Analysis of Five Years of Corner Reflector Time Series. In Proceedings of the Fringe 2007 Workshop, Frascati, Italy, 26–30 November 2007. [Google Scholar]
- Gatelli, F.; Monti Guamieri, A.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The wavenumber shift in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1994, 32, 855–865. [Google Scholar] [CrossRef]
- Yague-Martinez, N.; De Zan, F.; Prats-Iraola, P. Coregistration of Interferometric Stacks of Sentinel-1 TOPS Data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1002–1006. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Brisco, B. Spectral analysis of wetlands using multi-source optical satellite imagery. ISPRS J. Photogramm. Remote Sens. 2018, 144, 119–136. [Google Scholar] [CrossRef]
- Lu, Z.; Kwoun, O. Radarsat-1 and ERS InSAR Analysis over Southeastern Coastal Louisiana: Implications for Mapping Water-Level Changes Beneath Swamp Forests. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2167–2184. [Google Scholar] [CrossRef]
- Mahdavi, S.; Salehi, B.; Amani, M.; Granger, J.E.; Brisco, B.; Huang, W.; Hanson, A. Object-Based Classification of Wetlands in Newfoundland and Labrador Using Multi-Temporal PolSAR Data. Can. J. Remote Sens. 2017, 43, 432–450. [Google Scholar] [CrossRef]
- Kim, S.-W.; Wdowinski, S.; Amelung, F.; Dixon, T.H.; Won, J.-S. Interferometric Coherence Analysis of the Everglades Wetlands, South Florida. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5210–5224. [Google Scholar] [CrossRef]
- Shang, J.; Liu, J.; Poncos, V.; Geng, X.; Qian, B.; Chen, Q.; Dong, T.; Macdonald, D.; Martin, T.; Kovacs, J.; et al. Detection of Crop Seeding and Harvest through Analysis of Time-Series Sentinel-1 Interferometric SAR Data. Remote Sens. 2020, 12, 1551. [Google Scholar] [CrossRef]
- Battaglia, M.J.; Banks, S.; Behnamian, A.; Bourgeau-Chavez, L.; Brisco, B.; Corcoran, J.; Chen, Z.; Huberty, B.; Klassen, J.; Knight, J.; et al. Multi-Source EO for Dynamic Wetland Mapping and Monitoring in the Great Lakes Basin. Remote Sens. 2021, 13, 599. [Google Scholar] [CrossRef]



| Treed Bog | Treed Fen | Open Fen | Open Marsh | Treed Swamp | Open Swamp | Shallow Open Water | |
|---|---|---|---|---|---|---|---|
| # polygons (area) | 2564 (298.05) | 2925 (322.26) | 12,970 (1455.48) | 3421 (160.81) | 12.035 (836.73) | 2247 (191.44) | 1993 (51.33) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amani, M.; Poncos, V.; Brisco, B.; Foroughnia, F.; DeLancey, E.R.; Ranjbar, S. InSAR Coherence Analysis for Wetlands in Alberta, Canada Using Time-Series Sentinel-1 Data. Remote Sens. 2021, 13, 3315. https://doi.org/10.3390/rs13163315
Amani M, Poncos V, Brisco B, Foroughnia F, DeLancey ER, Ranjbar S. InSAR Coherence Analysis for Wetlands in Alberta, Canada Using Time-Series Sentinel-1 Data. Remote Sensing. 2021; 13(16):3315. https://doi.org/10.3390/rs13163315
Chicago/Turabian StyleAmani, Meisam, Valentin Poncos, Brian Brisco, Fatemeh Foroughnia, Evan R. DeLancey, and Sadegh Ranjbar. 2021. "InSAR Coherence Analysis for Wetlands in Alberta, Canada Using Time-Series Sentinel-1 Data" Remote Sensing 13, no. 16: 3315. https://doi.org/10.3390/rs13163315
APA StyleAmani, M., Poncos, V., Brisco, B., Foroughnia, F., DeLancey, E. R., & Ranjbar, S. (2021). InSAR Coherence Analysis for Wetlands in Alberta, Canada Using Time-Series Sentinel-1 Data. Remote Sensing, 13(16), 3315. https://doi.org/10.3390/rs13163315










