Generalized Dechirp-Keystone Transform for Radar High-Speed Maneuvering Target Detection and Localization
Abstract
:1. Introduction
1.1. Prior Work
1.2. Contribution
1.3. Organization
2. Signal Model and Problem Formulation
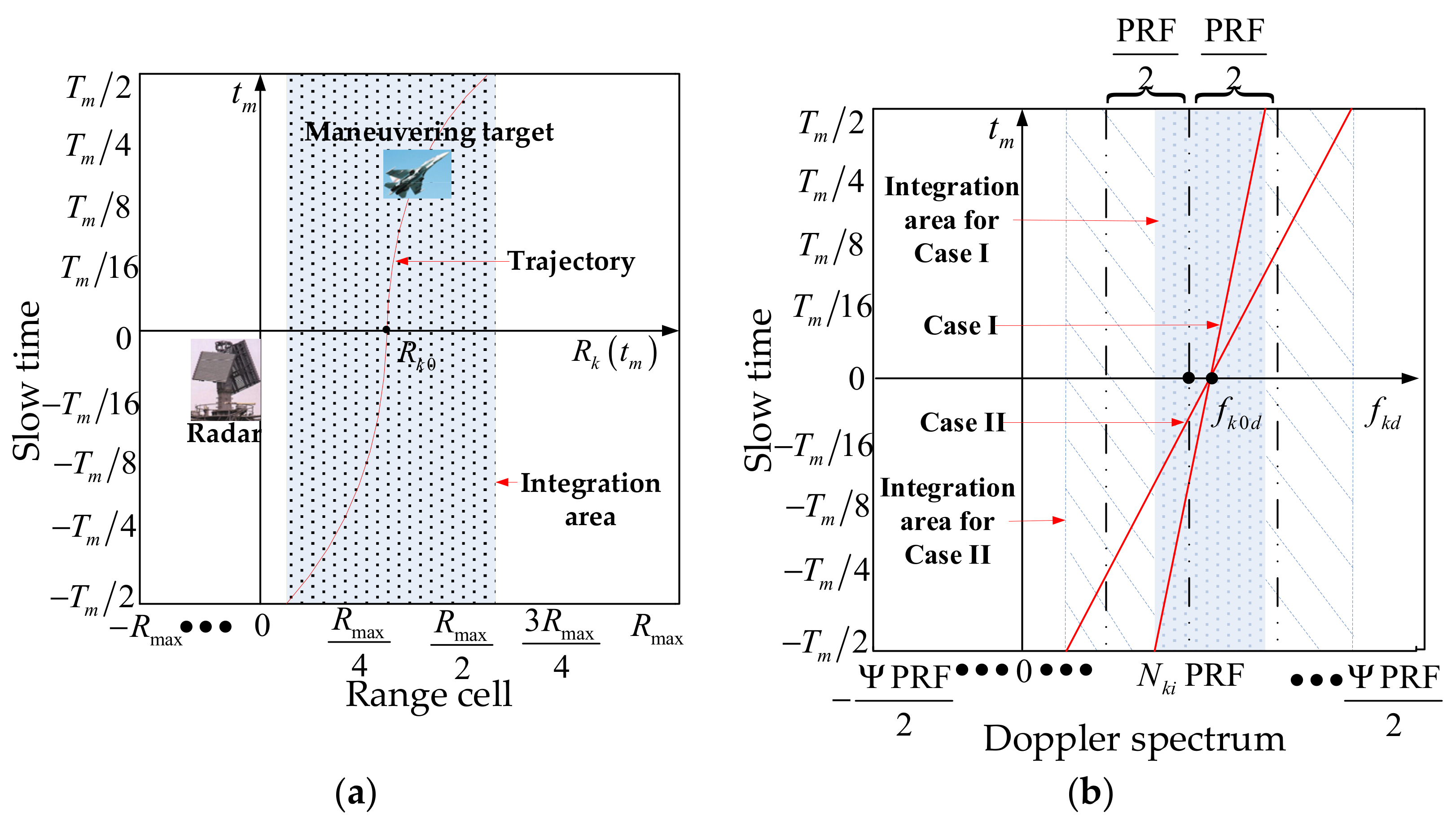
2.1. RCM and DFM
2.2. Doppler Ambiguity Integer
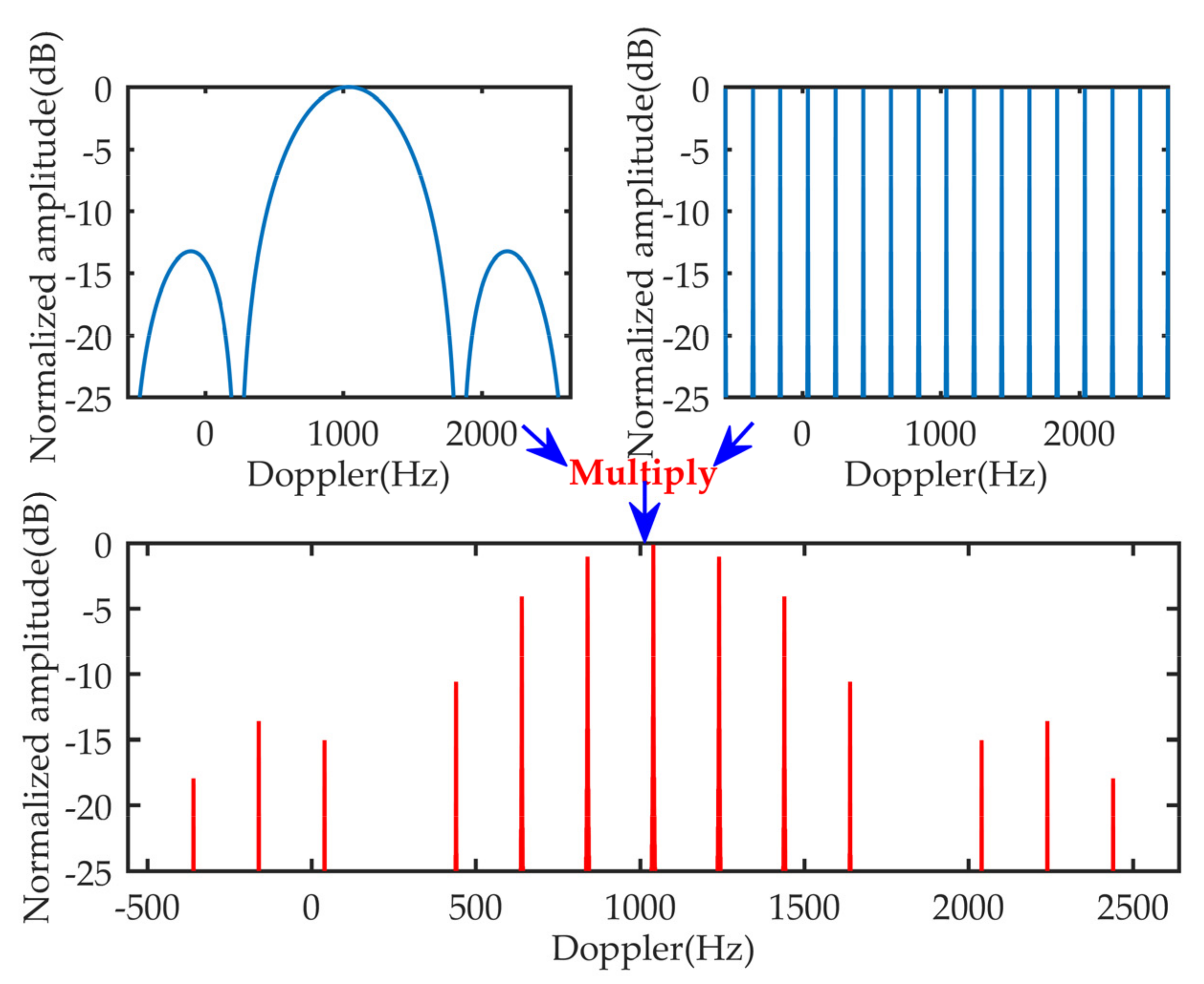
2.3. Doppler Spectrum Coupling and Half-Blind-Velocity Effect
3. PU Mode and PS Mode
3.1. PU Mode
3.2. PS Mode
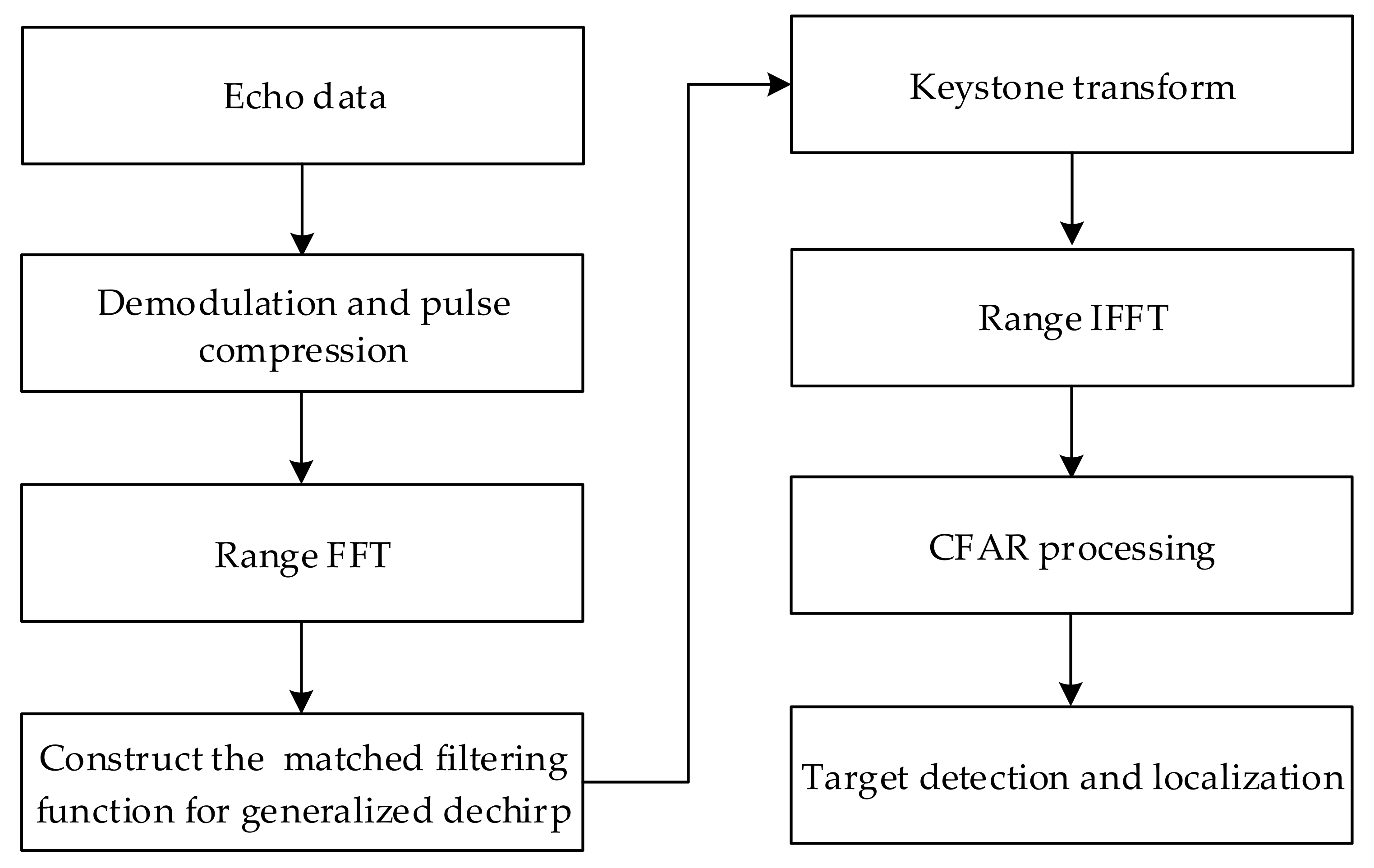
4. GDKT and Implementation
4.1. GDKT
- The GDKT uses and to separately process the linear RCM and inter-pulse energy integration. Similar to the KTD method, the GDKT is more computationally efficient than the MLE method;
- In the GDKT, the KT is employed after eliminating the influence of the Doppler spectrum coupling and half-blind-velocity effect. Therefore, same as the MLE method, the GDKT is statistically optimal.
4.2. Implementation of the GDKT
5. Theoretical Comparisons and Numerical Illustrations
5.1. Computational Cost
5.2. Energy Integration
5.3. Resolution and PSL
5.4. Anti-Noise Performance
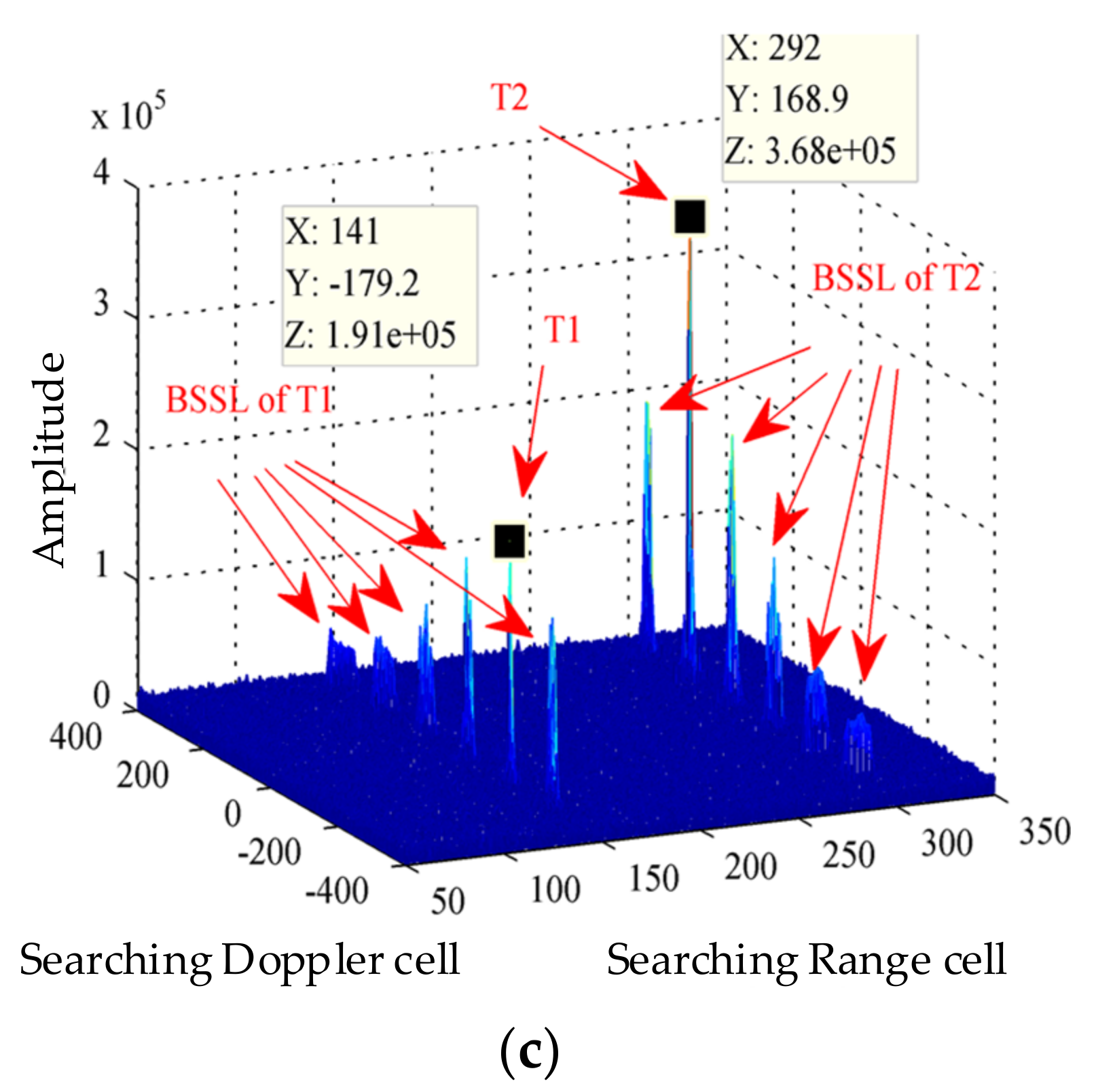
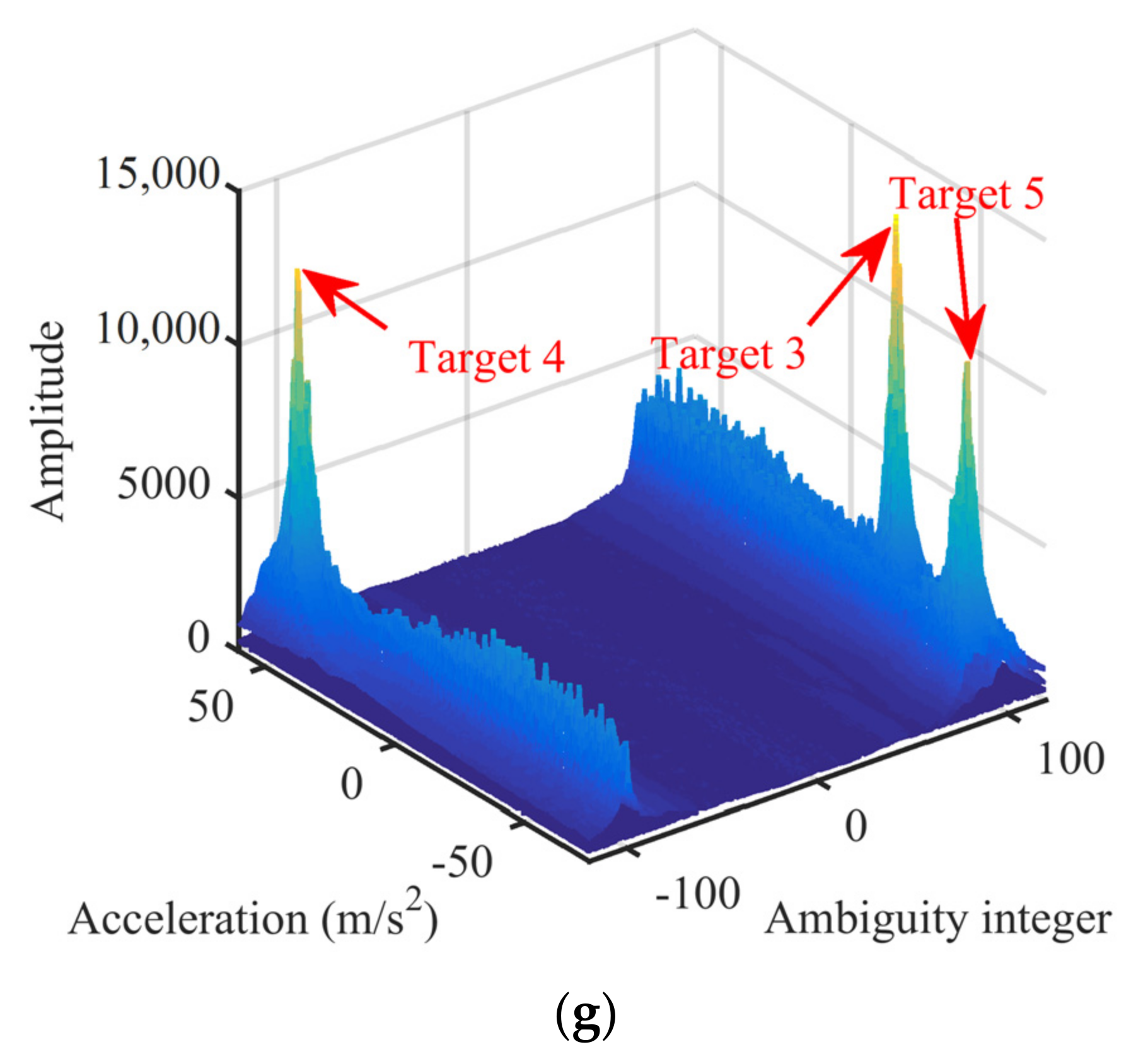
5.5. Practicability under Multicomponent High-Speed Maneuvering Targets
6. Real Radar Data Validation
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Moses, P.L.; Rausch, V.L.; Nguyen, L.T.; Hill, J.R. NASA hypersonic flight demonstrators—Overview, status, and future plans. Acta Astronaut. 2004, 55, 619–630. [Google Scholar] [CrossRef]
- De Miao, A.; Farina, A.; Gertach, K. Adaptive detection of range spread targets with orthogonal rejection. IEEE Trans. Aerosp. Electron. Syst. 1999, 47, 1522–1531. [Google Scholar]
- Gini, F.; Greco, M.; Farina, A. Clairvoyant and adaptive signal detection in non-Gaussian clutter: A data-dependent threshold interpretation. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar] [CrossRef]
- Orlando, D.; Frank, E.; Giuseppe, R. Track-before-detect algorithms for bistatic sonars. In Proceedings of the 2010 2nd IEEE International Workshop on Cognitive Information Processing, Elba, Italy, 14–16 June 2010; pp. 180–185. [Google Scholar]
- Jia, X.; Peng, Y.N.; Xia, X.G.; Farina, A. Focus-before-detection radar signal processing: Part i—Challenges and methods. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 48–59. [Google Scholar]
- Jia, X.; Peng, Y.N.; Xia, X.G.; Long, T.; Mao, E.-K. Focus-before-detection radar signal processing: Part ii—Recent developments. IEEE Aerosp. Electron. Syst. Mag. 2018, 33, 34–49. [Google Scholar]
- Ehlers, F.; Orlando, D.; Ricci, G. Batch tracking algorithm for multistatic sonars. IET Radar Sonar Navig. 2012, 6, 746–752. [Google Scholar] [CrossRef]
- Jin, K.; Li, G.; Lai, T.; Jin, T.; Zhao, Y. A Novel Long-Time Coherent Integration Algorithm for Doppler-Ambiguous Radar Maneuvering Target Detection. IEEE Sens. J. 2020, 20, 9394–9407. [Google Scholar] [CrossRef]
- Sun, Z.; Li, X.; Cui, G.; Yi, W.; Kong, L. Hypersonic Target Detection and Velocity Estimation in Coherent Radar System Based on Scaled Radon Fourier Transform. IEEE Trans. Veh. Technol. 2020, 69, 6525–6540. [Google Scholar] [CrossRef]
- Carlson, B.; Evans, E.; Wilson, S. Search radar detection and track with the Hough transform. I. system concept. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 102–108. [Google Scholar] [CrossRef]
- Carlson, B.; Evans, E.; Wilson, S. Search radar detection and track with the Hough transform. II. Detection statistics. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 109–115. [Google Scholar] [CrossRef]
- Carlson, B.D.; Evans, E.D.; Wilson, S.L. Search radar detection and track with the Hough transform. III. Detection performance with binary integration. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 116–125. [Google Scholar] [CrossRef]
- Carretero-Moya, J.; Gismero-Menoyo, J.; Asensio-Lopez, A.; Blanco-del-Campo, A. Application of the radon transform to detect small-targets in sea clutter. IET Radar Sonar Navig. 2009, 3, 155–166. [Google Scholar] [CrossRef]
- Copeland, A.C.; Ravichandran, G.; Trivedi, M.M. Localized Radon transform-based detection of ship wakes in SAR images. IEEE Trans. Geosci. Remote. Sens. 1995, 33, 35–45. [Google Scholar] [CrossRef]
- Tandra, R.; Sahai, A. SNR walls for signal detection. IEEE J. Sel. Top. Signal Process. 2008, 2, 4–17. [Google Scholar] [CrossRef] [Green Version]
- Abatzoglou, T.J.; Gheen, G.O. Range, radial velocity, and acceleration MLE using radar LFM pulse train. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 1070–1083. [Google Scholar] [CrossRef]
- Xu, J.; Xia, X.-G.; Peng, S.-B.; Yu, J.; Peng, Y.-N.; Qian, L.-C. Radar maneuvering target motion estimation based on generalized Radon-Fourier transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar]
- Chen, X.; Guan, J.; Liu, N.; He, Y. Maneuvering target detection via Radon-fractional Fourier transform-based long-time coherent integration. IEEE Trans. Signal Process. 2014, 62, 939–953. [Google Scholar] [CrossRef]
- Wu, W.; Wang, G.H.; Sun, J.P. Polynomial Radon-polynomial Fourier transform for near space hypersonic maneuvering target detection. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 1306–1322. [Google Scholar] [CrossRef]
- Perry, R.; Dipietro, R.; Fante, R. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Wang, C.; Jiu, B.; Liu, H. Maneuvering target detection in random pulse repetition interval radar via resampling-keystone transform. Signal Process. 2021, 181, 107899. [Google Scholar] [CrossRef]
- Fang, X.; Xiao, G.; Cao, Z.; Min, R.; Pi, Y. Migration Correction Algorithm for Coherent Integration of Low-Observable Target With Uniform Radial Acceleration. IEEE Trans. Instrum. Meas. 2020, 70, 1–13. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, T.; Liu, H.; Su, T.; Wan, L. Accurate detection and localization of UAV swarms-enabled MEC system. IEEE Trans. Ind. Inform. 2020, 17, 5059–5067. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, R.; Yang, T.; Liu, X.; Liu, H.; Su, T.; Wan, L. An efficient strategy for accurate detection and localization of UAV swarms. IEEE Internet Things J. 2021. [Google Scholar] [CrossRef]
- Kong, L.; Li, X.; Cui, G.; Yi, W.; Yang, Y. Coherent integration algorithm for a maneuvering target with high-order range migration. IEEE Trans. Signal Process. 2015, 63, 4474–4486. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.-G.; Ma, J.-T.; Ma, J. Long-time coherent integration for weak maneuvering target detection and high-order motion parameter estimation based on keystone transform. IEEE Trans. Signal Process. 2016, 64, 4013–4026. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Xia, X.-G.; Wu, Y.; Bao, Z. Robust ground moving-target imaging using deramp–keystone processing. IEEE Trans. Geosci. Remote. Sens. 2012, 51, 966–982. [Google Scholar] [CrossRef]
- Kirkland, D. Imaging moving targets using the second-order keystone transform. IET Radar Sonar Navig. 2011, 5, 902–910. [Google Scholar] [CrossRef]
- Scott, K.M.; Barott, W.C.; Himed, B. The keystone transform: Practical limits and extension to second order corrections. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 1264–1269. [Google Scholar]
- Xu, J.; Zhou, X.; Qian, L.-C.; Xia, X.-G.; Long, T. Hybrid integration for highly maneuvering radar target detection based on generalized Radon-Fourier transform. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2554–2561. [Google Scholar] [CrossRef]
- Jin, K.; Lai, T.; Wang, Y.; Li, G.; Zhao, Y. Radar coherent detection for Doppler-ambiguous maneuvering target based on product scaled periodic Lv’s distribution. Signal Process. 2020, 174, 107617. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Kong, L.; Yi, W. Fast non-searching method for maneuvering target detection and motion parameters estimation. IEEE Trans. Signal Process. 2016, 64, 2232–2244. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. Radar maneuvering target detection and motion parameter estimation based on TRT-SGRFT. Signal Process. 2017, 133, 107–116. [Google Scholar] [CrossRef]
- Jin, K.; Lai, T.; Wang, Y.; Xing, X.; Zhao, Y. Parameter estimation of quadratic frequency modulated signal based on three-dimensional scaled Fourier transform. IET Radar Sonar Navig. 2019, 13, 1689–1696. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, H.; Liu, J.; Du, X.; Liu, Q.H. Radar high-speed maneuvering target detection based on three-dimensional scaled transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 2821–2833. [Google Scholar] [CrossRef]
- Yu, J.; Xu, J.; Peng, Y.-N.; Xia, X.-G. Radon-Fourier transform for radar target detection (III): Optimality and fast implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 991–1004. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.-N.; Xia, X.-G. Radon-Fourier transform for radar target detection (II): Blind speed sidelobe suppression. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2473–2489. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, H.; Liu, Q.H. Parameterized centroid frequency-chirp rate distribution for LFM signal analysis and mechanisms of constant delay introduction. IEEE Trans. Signal Process. 2017, 65, 6435–6447. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, X.; Zhang, Q. Rotation parameters estimation and cross-range scaling research for range instantaneous Doppler ISAR images. IEEE Sens. J. 2020, 20, 7010–7020. [Google Scholar] [CrossRef]
- Niu, Z.; Zheng, J.; Su, T.; Li, W.; Zhang, L. Radar High-speed Target Detection Based on Improved Minimalized Windowed RFT. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 14, 870–886. [Google Scholar] [CrossRef]
- Park, Y.; Meyer, F.; Gerstoft, P. Sparse Bayesian learning for time-varying DOA estimation. J. Acoust. Soc. Am. 2020, 148, 2543. [Google Scholar] [CrossRef]
- Jin, G.; Deng, Y.; Wang, R.; Wang, W.; Wang, P.; Long, Y.; Zhang, Z.; Zhang, Y. An advanced nonlinear frequency modulation waveform for radar imaging with low sidelobe. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 6155–6168. [Google Scholar] [CrossRef]


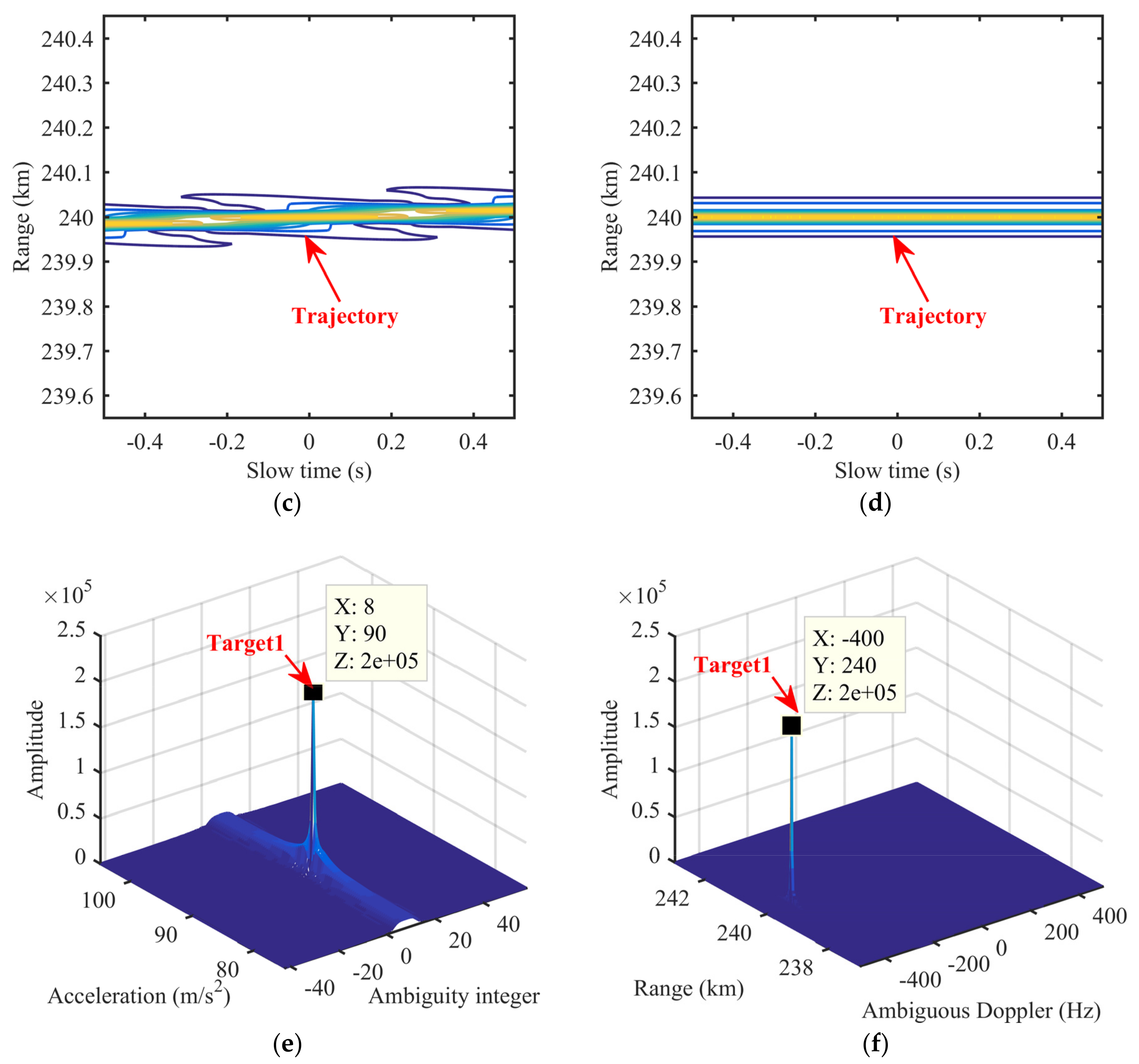
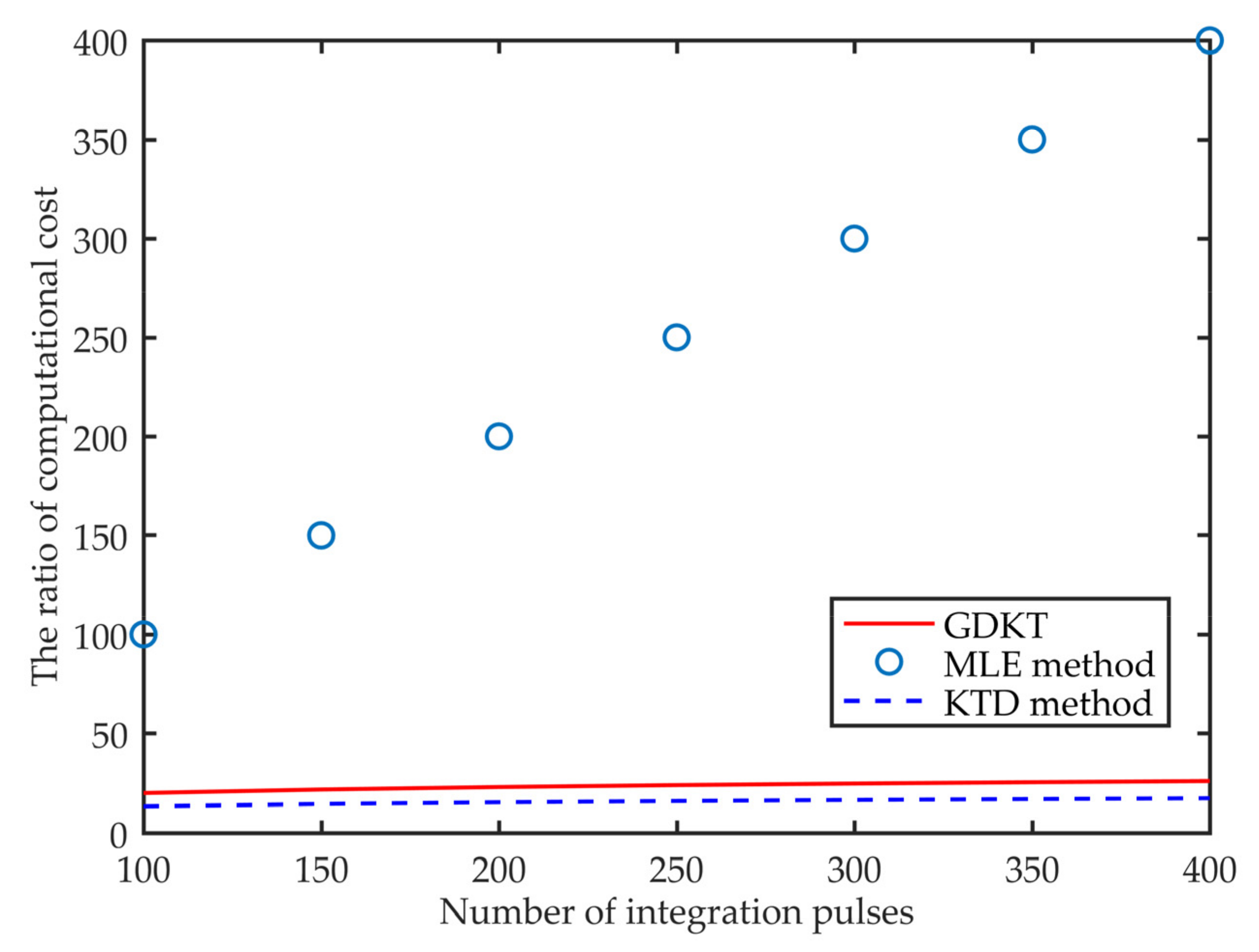
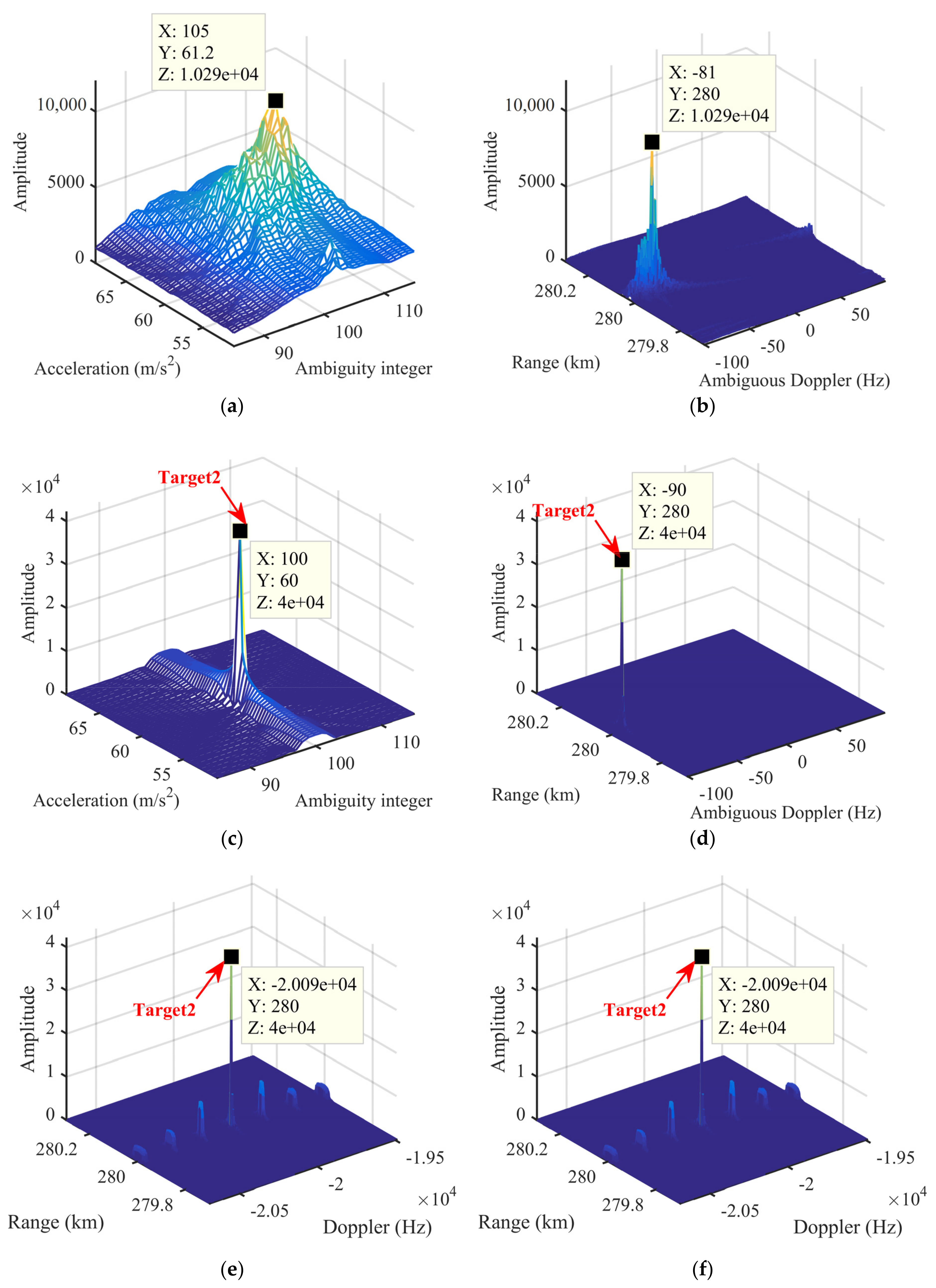
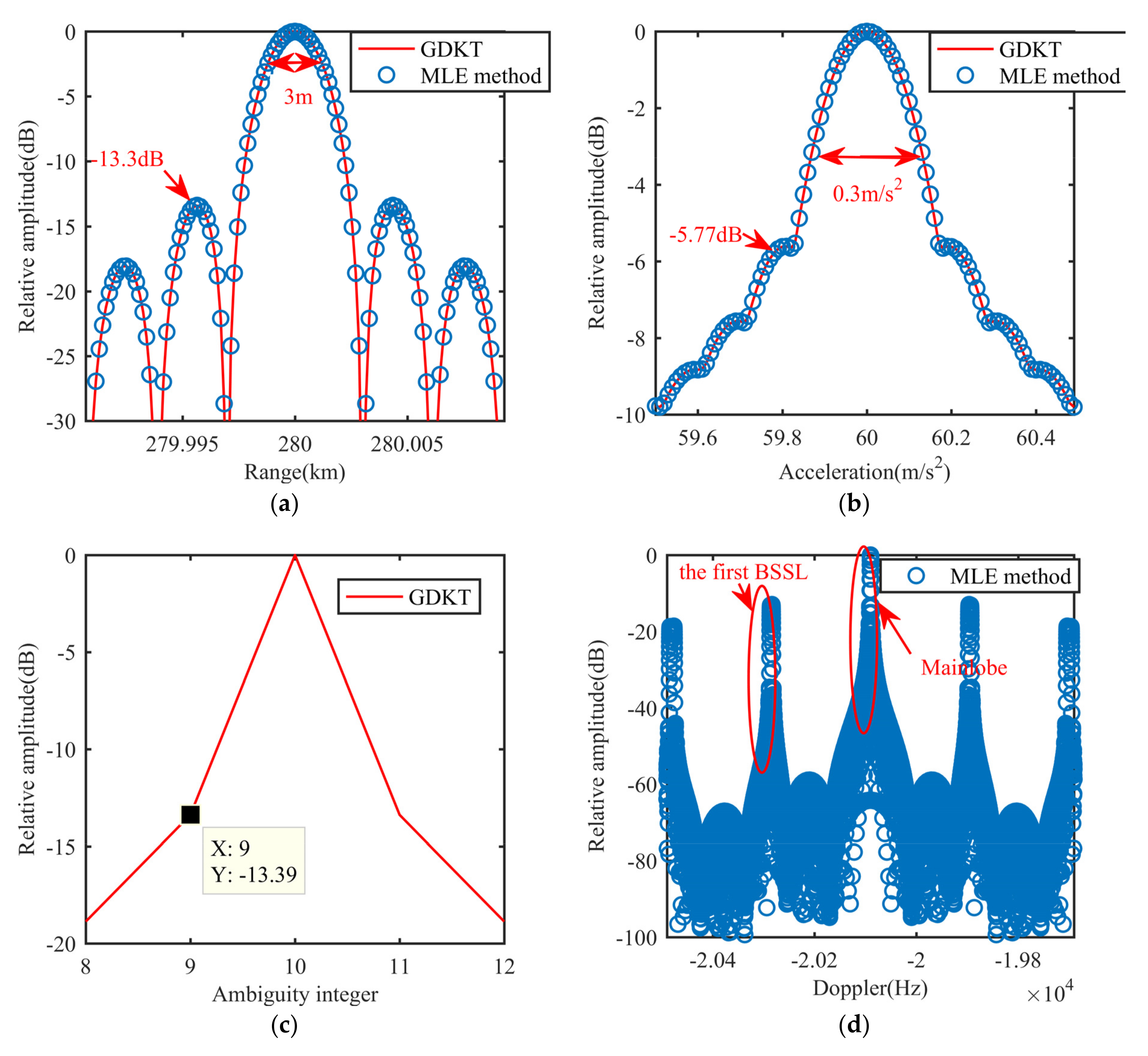





| Radar Parameters | ||||
| Carrier frequency | 4 GHz | PRF | 1000 Hz | |
| Bandwidth | 15 MHz | Sampling frequency | 20 MHz | |
| Pulse width | 10 μs | Number of pulses | 1000 | |
| Target Parameters | ||||
| Target1 | Backscattering coefficient | Range (km) | Velocity (m/s) | Acceleration (m/s2) |
| 1 | 120 | 315 | 90 | |
| Radar Parameters | |||||||
| Carrier frequency | 4 GHz | PRF | 200 Hz | ||||
| Bandwidth | 100 MHz | Sampling frequency | 200 MHz | ||||
| Pulse width | 1 μs | Number of pulses | 200 | ||||
| Target Parameters | |||||||
| Target2 | Backscattering coefficient | Range (km) | Velocity (m/s) | Acceleration (m/s2) | |||
| 1 | 140 | 753.375 | 60 | ||||
| - | Backscattering Coefficient | Range (km) | Velocity (m/s) | Acceleration (m/s2) |
|---|---|---|---|---|
| Target3 | 1 | 129.97 | 738.375 | −30 |
| Target4 | 1 | 130.015 | −738 | 48 |
| Target5 | 1 | 130.03 | 662.625 | −63 |
| - | Computational Cost | Detection and Localization Performance | Practicability |
|---|---|---|---|
| MTD | low | low | low |
| MLE | high | high | low |
| KTD | low | low | low |
| GDKT | low | high | high |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Zhu, K.; Niu, Z.; Liu, H.; Liu, Q.H. Generalized Dechirp-Keystone Transform for Radar High-Speed Maneuvering Target Detection and Localization. Remote Sens. 2021, 13, 3367. https://doi.org/10.3390/rs13173367
Zheng J, Zhu K, Niu Z, Liu H, Liu QH. Generalized Dechirp-Keystone Transform for Radar High-Speed Maneuvering Target Detection and Localization. Remote Sensing. 2021; 13(17):3367. https://doi.org/10.3390/rs13173367
Chicago/Turabian StyleZheng, Jibin, Kangle Zhu, Zhiyong Niu, Hongwei Liu, and Qing Huo Liu. 2021. "Generalized Dechirp-Keystone Transform for Radar High-Speed Maneuvering Target Detection and Localization" Remote Sensing 13, no. 17: 3367. https://doi.org/10.3390/rs13173367







