Monitoring Drought through the Lens of Landsat: Drying of Rivers during the California Droughts
Abstract
:1. Introduction
2. Study Area, Data, and Methods
2.1. Landsat Datasets and River Extent Metrics
2.2. Attrubtion of Surface River Extent Dynamics
2.2.1. Hydro-Climatic Data and Related Metrics
2.2.2. Correlation and Elasticity Analysis
3. Results
3.1. Dectectability of Landsat on River Extent Dynamics
3.2. Results of Correlation and Elasticity Analysis of FrcSA
4. Discussion
5. Conclusions
- The Landsat provides consistent observations of over 90% of the river area within bankful widths from March to October, but poor observations from November to February, making it a viable source for monitoring rivers’ seasonal drying dynamics (from spring to fall). When compared with streamflow at co-located USGS gauges, FrcSA shows fair (>0.5) correlation except for in southern dry climate divisions and high-elevation mountainous locations. The 30-m resolution causes potential underestimation of FrcSA during low flow conditions.
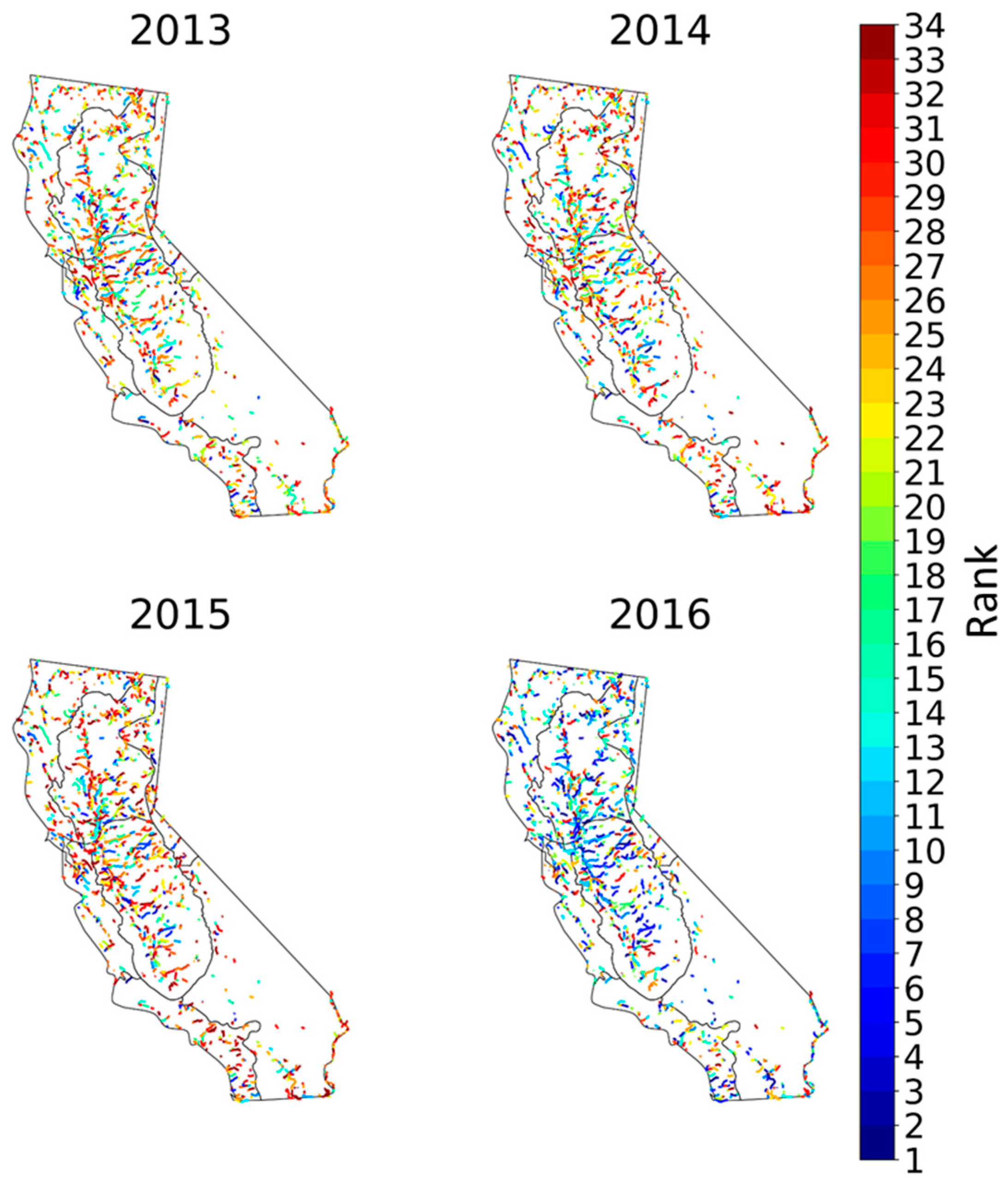
- During the 2012 to 2015 California drought and the subsequent 2016 and 2017 wet years, the rivers in California experienced the two extremes (dry and wet) of regional climatology, which is well reflected by the Landsat observation. The river extents exhibit drastic swings before and after the drought ending. River extent in water-scarce areas is more resilient to droughts because of the high degree of regulation. Rivers in northeast interior basins are significantly dried during droughts and slow to recover after drought endings due to small catchment storage.
- At a monthly scale, soil water, as a component of terrestrial water storage, shows a latitudinal gradient in the correlation with FrcSA: river extent in the humid catchments is better correlated with soil moisture than in the arid southern region. Longer lags of FrcSA following soil moisture are seen in Sierra Nevada than in coastal regions, due to the larger storage of thick soil layers. At a yearly scale, elasticity of summer-mean-FrcSA to winter precipitation (Epw) is statistically significant for over 300 low-order (1 or 2) reaches. Catchments with shallow groundwater table show high elasticity in FrcSA to Pw because their small storge favors fast draining of baseflow. Both correlation and elasticity analyses validate the hypothesis that a storage-discharge relationship controls the dynamics of river extent.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bruins, H.J.; Berliner, P.R. Bioclimatic Aridity, Climatic Variability, Drought and Desertification: Definitions and Management Options. In The Arid Frontier; Springer: Berlin/Heidelberg, Germany, 1998; pp. 97–116. [Google Scholar]
- Wilhite, D.A. Drought and Water Crises: Science, Technology, and Management Issues; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Hanel, M.; Rakovec, O.; Markonis, Y.; Máca, P.; Samaniego, L.; Kyselý, J.; Kumar, R. Revisiting the recent European droughts from a long-term perspective. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef]
- Boulton, A.J. Parallels and contrasts in the effects of drought on stream macroinvertebrate assemblages. Freshw. Biol. 2003, 48, 1173–1185. [Google Scholar] [CrossRef] [Green Version]
- Tan, M.L.; Juneng, L.; Tangang, F.T.; Samat, N.; Chan, N.W.; Yusop, Z.; Ngai, S.T. SouthEast Asia HydrO-meteorological droughT (SEA-HOT) framework: A case study in the Kelantan River Basin, Malaysia. Atmos. Res. 2020, 246, 105155. [Google Scholar] [CrossRef]
- Wieland, M.; Martinis, S. Large-scale surface water change observed by Sentinel-2 during the 2018 drought in Germany. Int. J. Remote Sens. 2020, 41, 4742–4756. [Google Scholar] [CrossRef]
- Martins, V.S.; Kaleita, A.; Barbosa, C.C.; Fassoni-Andrade, A.C.; de Lucia Lobo, F.; Novo, E.M. Remote sensing of large reservoir in the drought years: Implications on surface water change and turbidity variability of Sobradinho reservoir (Northeast Brazil). Remote Sens. Appl. Soc. Environ. 2019, 13, 275–288. [Google Scholar] [CrossRef]
- Cayan, D.R.; Das, T.; Pierce, D.W.; Barnett, T.P.; Tyree, M.; Gershunov, A. Future dryness in the southwest US and the hydrology of the early 21st century drought. Proc. Natl. Acad. Sci. USA 2010, 107, 21271–21276. [Google Scholar] [CrossRef] [Green Version]
- Deitch, M.J.; Van Docto, M.; Obedzinski, M.; Nossaman, S.P.; Bartshire, A. Impact of multi-annual drought on streamflow and habitat in coastal California salmonid streams. Hydrol. Sci. J. 2018, 63, 1219–1235. [Google Scholar] [CrossRef]
- Bhamjee, R.; Lindsay, J. Ephemeral stream sensor design using state loggers. Copernic. Publ. 2011, 15, 1009–1021. [Google Scholar] [CrossRef] [Green Version]
- Godsey, S.; Kirchner, J.W. Dynamic, discontinuous stream networks: Hydrologically driven variations in active drainage density, flowing channels and stream order. Hydrol. Process. 2014, 28, 5791–5803. [Google Scholar] [CrossRef]
- Jensen, C.K.; McGuire, K.J.; McLaughlin, D.L.; Scott, D.T. Quantifying spatiotemporal variation in headwater stream length using flow intermittency sensors. Environ. Monit. Assess. 2019, 191, 1–19. [Google Scholar] [CrossRef]
- Peirce, S.E.; Lindsay, J.B. Characterizing ephemeral streams in a southern Ontario watershed using electrical resistance sensors. Hydrol. Process. 2015, 29, 103–111. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Zhang, S.; Wu, J. Detecting, extracting, and monitoring surface water from space using optical sensors: A review. Rev. Geophys. 2018, 56, 333–360. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Wang, X.; Xie, S.; Zhang, X.; Chen, C.; Guo, H.; Du, J.; Duan, Z. A robust Multi-Band Water Index (MBWI) for automated extraction of surface water from Landsat 8 OLI imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 73–91. [Google Scholar] [CrossRef]
- Hollstein, A.; Segl, K.; Guanter, L.; Brell, M.; Enesco, M. Ready-to-use methods for the detection of clouds, cirrus, snow, shadow, water and clear sky pixels in Sentinel-2 MSI images. Remote Sens. 2016, 8, 666. [Google Scholar] [CrossRef] [Green Version]
- Isikdogan, F.; Bovik, A.C.; Passalacqua, P. Surface water mapping by deep learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4909–4918. [Google Scholar] [CrossRef]
- Li, Y.; Martinis, S.; Wieland, M. Urban flood mapping with an active self-learning convolutional neural network based on TerraSAR-X intensity and interferometric coherence. ISPRS J. Photogramm. Remote Sens. 2019, 152, 178–191. [Google Scholar] [CrossRef]
- Du, Z.; Bin, L.; Ling, F.; Li, W.; Tian, W.; Wang, H.; Gui, Y.; Sun, B.; Zhang, X. Estimating surface water area changes using time-series Landsat data in the Qingjiang River Basin, China. J. Appl. Remote Sens. 2012, 6, 063609. [Google Scholar] [CrossRef]
- Donchyts, G.; Baart, F.; Winsemius, H.; Gorelick, N.; Kwadijk, J.; Van De Giesen, N. Earth’s surface water change over the past 30 years. Nat. Clim. Chang. 2016, 6, 810–813. [Google Scholar] [CrossRef]
- Ji, L.; Gong, P.; Wang, J.; Shi, J.; Zhu, Z. Construction of the 500-m resolution daily global surface water change database (2001–2016). Water Resour. Res. 2018, 54, 10–270. [Google Scholar] [CrossRef]
- Yao, F.; Wang, J.; Wang, C.; Crétaux, J.-F. Constructing long-term high-frequency time series of global lake and reservoir areas using Landsat imagery. Remote Sens. Environ. 2019, 232, 111210. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, D.; O’Loughlin, F.; Trigg, M.A.; Miller, Z.F.; Pavelsky, T.M.; Bates, P.D. Development of the global width database for large rivers. Water Resour. Res. 2014, 50, 3467–3480. [Google Scholar] [CrossRef]
- Allen, G.H.; Pavelsky, T.M. Global extent of rivers and streams. Science 2018, 361, 585–588. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, P.; Pan, M.; Allen, G.H.; de Frasson, R.P.; Zeng, Z.; Yamazaki, D.; Wood, E.F. Global estimates of reach-level bankfull river width leveraging big data geospatial analysis. Geophys. Res. Lett. 2020, 47, e2019GL086405. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X.; Tang, Q. Satellite-derived river width and its spatiotemporal patterns in China during 1990–2015. Remote Sens. Environ. 2020, 247, 111918. [Google Scholar] [CrossRef]
- Allen, G.H.; Yang, X.; Gardner, J.; Holliman, J.; David, C.H.; Ross, M. Timing of Landsat Overpasses Effectively Captures Flow Conditions of Large Rivers. Remote Sens. 2020, 12, 1510. [Google Scholar] [CrossRef]
- Griffin, D.; Anchukaitis, K.J. How unusual is the 2012–2014 California drought? Geophys. Res. Lett. 2014, 41, 9017–9023. [Google Scholar] [CrossRef] [Green Version]
- Vose, R.S.; Applequist, S.; Squires, M.; Durre, I.; Menne, M.J.; Williams, C.N., Jr.; Fenimore, C.; Gleason, K.; Arndt, D. Improved historical temperature and precipitation time series for US climate divisions. J. Appl. Meteorol. Climatol. 2014, 53, 1232–1251. [Google Scholar] [CrossRef]
- Robeson, S.M. Revisiting the recent California drought as an extreme value. Geophys. Res. Lett. 2015, 42, 6771–6779. [Google Scholar] [CrossRef]
- Wilhite, D.A. Drought as a Natural Hazard: Concepts and Definitions. In Drought: A Global Assessment; Routledge: London, UK, 2000; pp. 3–18. [Google Scholar]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Seager, R.; Hoerling, M.; Schubert, S.; Wang, H.; Lyon, B.; Kumar, A.; Nakamura, J.; Henderson, N. Causes of the 2011–14 California drought. J. Clim. 2015, 28, 6997–7024. [Google Scholar] [CrossRef]
- Swain, D.L.; Tsiang, M.; Haugen, M.; Singh, D.; Charland, A.; Rajaratnam, B.; Diffenbaugh, N.S. The extraordinary California drought of 2013/2014: Character, context, and the role of climate change. Bull. Am. Meteorol. Soc. 2014, 95, S3–S7. [Google Scholar]
- Diffenbaugh, N.S.; Swain, D.L.; Touma, D. Anthropogenic warming has increased drought risk in California. Proc. Natl. Acad. Sci. USA 2015, 112, 3931–3936. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Williams, A.P.; Seager, R.; Abatzoglou, J.T.; Cook, B.I.; Smerdon, J.E.; Cook, E.R. Contribution of anthropogenic warming to California drought during 2012–2014. Geophys. Res. Lett. 2015, 42, 6819–6828. [Google Scholar] [CrossRef] [Green Version]
- Mao, Y.; Nijssen, B.; Lettenmaier, D.P. Is climate change implicated in the 2013–2014 California drought? A hydrologic perspective. Geophys. Res. Lett. 2015, 42, 2805–2813. [Google Scholar] [CrossRef]
- National Climatic Data Center. Palmer Drought Severity Index (PDSI) for Climate Divisions in US. Available online: https://www1.ncdc.noaa.gov/pub/data/cirs/climdiv/climdiv-pdsidv-v1.0.0-20210805 (accessed on 9 February 2020).
- Dettinger, M.D. Atmospheric rivers as drought busters on the US West Coast. J. Hydrometeorol. 2013, 14, 1721–1732. [Google Scholar] [CrossRef]
- Falcone, J.A. GAGES-II: Geospatial Attributes of Gages for Evaluating Streamflow; US Geological Survey: Reston, WA, USA, 2011.
- Falcone, J.A.; Carlisle, D.M.; Wolock, D.M.; Meador, M.R. GAGES: A stream gage database for evaluating natural and altered flow conditions in the conterminous United States: Ecological archives E091-045. Ecology 2010, 91, 621. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Pan, M. Global River Network and Unit Catchment from MERIT Hydro. Available online: http://hydrology.princeton.edu/data/mpan/MERIT_Basins/ (accessed on 10 March 2020).
- Cooper, M.; Schaperow, J.; Cooley, S.; Alam, S.; Smith, L.; Lettenmaier, D. Climate elasticity of low flows in the maritime western US mountains. Water Resour. Res. 2018, 54, 5602–5619. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M.; Limbrunner, J.F. Climate elasticity of streamflow in the United States. Water Resour. Res. 2001, 37, 1771–1781. [Google Scholar] [CrossRef]
- Milly, P.C.; Kam, J.; Dunne, K.A. On the sensitivity of annual streamflow to air temperature. Water Resour. Res. 2018, 54, 2624–2641. [Google Scholar] [CrossRef]
- Berghuijs, W.; Woods, R.; Hrachowitz, M. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat. Clim. Chang. 2014, 4, 583–586. [Google Scholar] [CrossRef] [Green Version]
- Reager, J.; Thomas, B.; Famiglietti, J. River basin flood potential inferred using GRACE gravity observations at several months lead time. Nat. Geosci. 2014, 7, 588–592. [Google Scholar] [CrossRef]
- Godsey, S.E.; Kirchner, J.W.; Tague, C.L. Effects of changes in winter snowpacks on summer low flows: Case studies in the Sierra Nevada, California, USA. Hydrol. Process. 2014, 28, 5048–5064. [Google Scholar] [CrossRef]
- Tague, C.; Grant, G.E. Groundwater dynamics mediate low-flow response to global warming in snow-dominated alpine regions. Water Resour. Res. 2009, 45, 12. [Google Scholar] [CrossRef]
- Safeeq, M.; Grant, G.E.; Lewis, S.L.; Tague, C.L. Coupling snowpack and groundwater dynamics to interpret historical streamflow trends in the western United States. Hydrol. Process. 2013, 27, 655–668. [Google Scholar] [CrossRef]
- Hodgson, D.; McDonald, J.L.; Hosken, D.J. Resilience Is Complicated, but Comparable: A Reply to Yeung and Richardson. Trends Ecol. Evol. 2015, 31, 3–4. [Google Scholar] [CrossRef]
- Fuller, I.C.; Gilvear, D.J.; Thoms, M.C.; Death, R.G. Framing resilience for river geomorphology: Reinventing the wheel? River Res. Appl. 2019, 35, 91–106. [Google Scholar] [CrossRef]
- Zimmer, M.A.; Kaiser, K.E.; Blaszczak, J.R.; Zipper, S.C.; Hammond, J.C.; Fritz, K.M.; Costigan, K.H.; Hosen, J.; Godsey, S.E.; Allen, G.H. Zero or not? Causes and consequences of zero-flow stream gage readings. Wiley Interdiscip. Rev. Water 2020, 7, e1436. [Google Scholar] [CrossRef]
- Jones, J.W. Improved automated detection of subpixel-scale inundation—Revised dynamic surface water extent (dswe) partial surface water tests. Remote Sens. 2019, 11, 374. [Google Scholar] [CrossRef] [Green Version]
- Walker, J.J.; Soulard, C.E.; Petrakis, R.E. Integrating stream gage data and Landsat imagery to complete time-series of surface water extents in Central Valley, California. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101973. [Google Scholar] [CrossRef]
- Kim, J.-W.; Lu, Z.; Jones, J.W.; Shum, C.; Lee, H.; Jia, Y. Monitoring Everglades freshwater marsh water level using L-band synthetic aperture radar backscatter. Remote Sens. Environ. 2014, 150, 66–81. [Google Scholar] [CrossRef]
- Santoro, M.; Wegmüller, U.; Lamarche, C.; Bontemps, S.; Defourny, P.; Arino, O. Strengths and weaknesses of multi-year Envisat ASAR backscatter measurements to map permanent open water bodies at global scale. Remote Sens. Environ. 2015, 171, 185–201. [Google Scholar] [CrossRef]
- Martinis, S.; Kuenzer, C.; Wendleder, A.; Huth, J.; Twele, A.; Roth, A.; Dech, S. Comparing four operational SAR-based water and flood detection approaches. Int. J. Remote Sens. 2015, 36, 3519–3543. [Google Scholar] [CrossRef]
- Huang, W.; DeVries, B.; Huang, C.; Lang, M.W.; Jones, J.W.; Creed, I.F.; Carroll, M.L. Automated extraction of surface water extent from Sentinel-1 data. Remote Sens. 2018, 10, 797. [Google Scholar] [CrossRef] [Green Version]
- Diaz-Nieto, J.; Wilby, R.L. A comparison of statistical downscaling and climate change factor methods: Impacts on low flows in the River Thames, United Kingdom. Clim. Chang. 2005, 69, 245–268. [Google Scholar] [CrossRef]
- Palmer, M.A.; Reidy Liermann, C.A.; Nilsson, C.; Flörke, M.; Alcamo, J.; Lake, P.S.; Bond, N. Climate change and the world’s river basins: Anticipating management options. Front. Ecol. Environ. 2008, 6, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Bond, N.R.; Lake, P.S.; Arthington, A.H. The impacts of drought on freshwater ecosystems: An Australian perspective. Hydrobiologia 2008, 600, 3–16. [Google Scholar] [CrossRef] [Green Version]
- Rahel, F.J.; Olden, J.D. Assessing the effects of climate change on aquatic invasive species. Conserv. Biol. 2008, 22, 521–533. [Google Scholar] [CrossRef]
- Moritz, C.; Agudo, R. The future of species under climate change: Resilience or decline? Science 2013, 341, 504–508. [Google Scholar] [CrossRef] [PubMed]
- Breshears, D.D.; López-Hoffman, L.; Graumlich, L.J. When ecosystem services crash: Preparing for big, fast, patchy climate change. Ambio 2011, 40, 256–263. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, J. Landscape sustainability science: Ecosystem services and human well-being in changing landscapes. Landsc. Ecol. 2013, 28, 999–1023. [Google Scholar] [CrossRef]
- Matthews, S.N.; Iverson, L.R.; Peters, M.P.; Prasad, A.M.; Subburayalu, S. Assessing and comparing risk to climate changes among forested locations: Implications for ecosystem services. Landsc. Ecol. 2014, 29, 213–228. [Google Scholar] [CrossRef]












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Li, Z.; Chen, M.; Allen, D.; Neeson, T.; Hong, Y. Monitoring Drought through the Lens of Landsat: Drying of Rivers during the California Droughts. Remote Sens. 2021, 13, 3423. https://doi.org/10.3390/rs13173423
Gao S, Li Z, Chen M, Allen D, Neeson T, Hong Y. Monitoring Drought through the Lens of Landsat: Drying of Rivers during the California Droughts. Remote Sensing. 2021; 13(17):3423. https://doi.org/10.3390/rs13173423
Chicago/Turabian StyleGao, Shang, Zhi Li, Mengye Chen, Daniel Allen, Thomas Neeson, and Yang Hong. 2021. "Monitoring Drought through the Lens of Landsat: Drying of Rivers during the California Droughts" Remote Sensing 13, no. 17: 3423. https://doi.org/10.3390/rs13173423
APA StyleGao, S., Li, Z., Chen, M., Allen, D., Neeson, T., & Hong, Y. (2021). Monitoring Drought through the Lens of Landsat: Drying of Rivers during the California Droughts. Remote Sensing, 13(17), 3423. https://doi.org/10.3390/rs13173423







