A Review of Voxel-Based Computerized Ionospheric Tomography with GNSS Ground Receivers
Abstract
1. Introduction
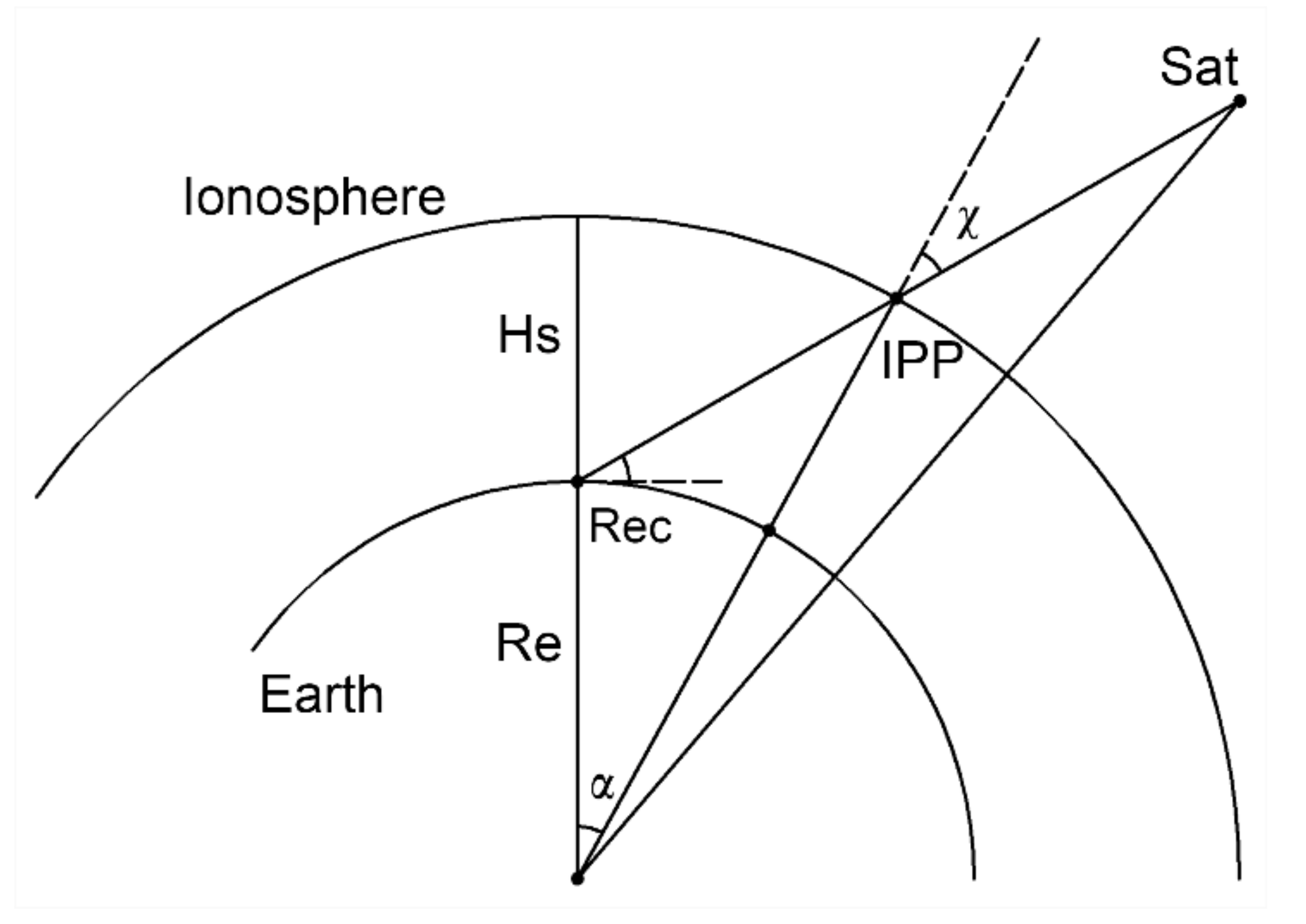
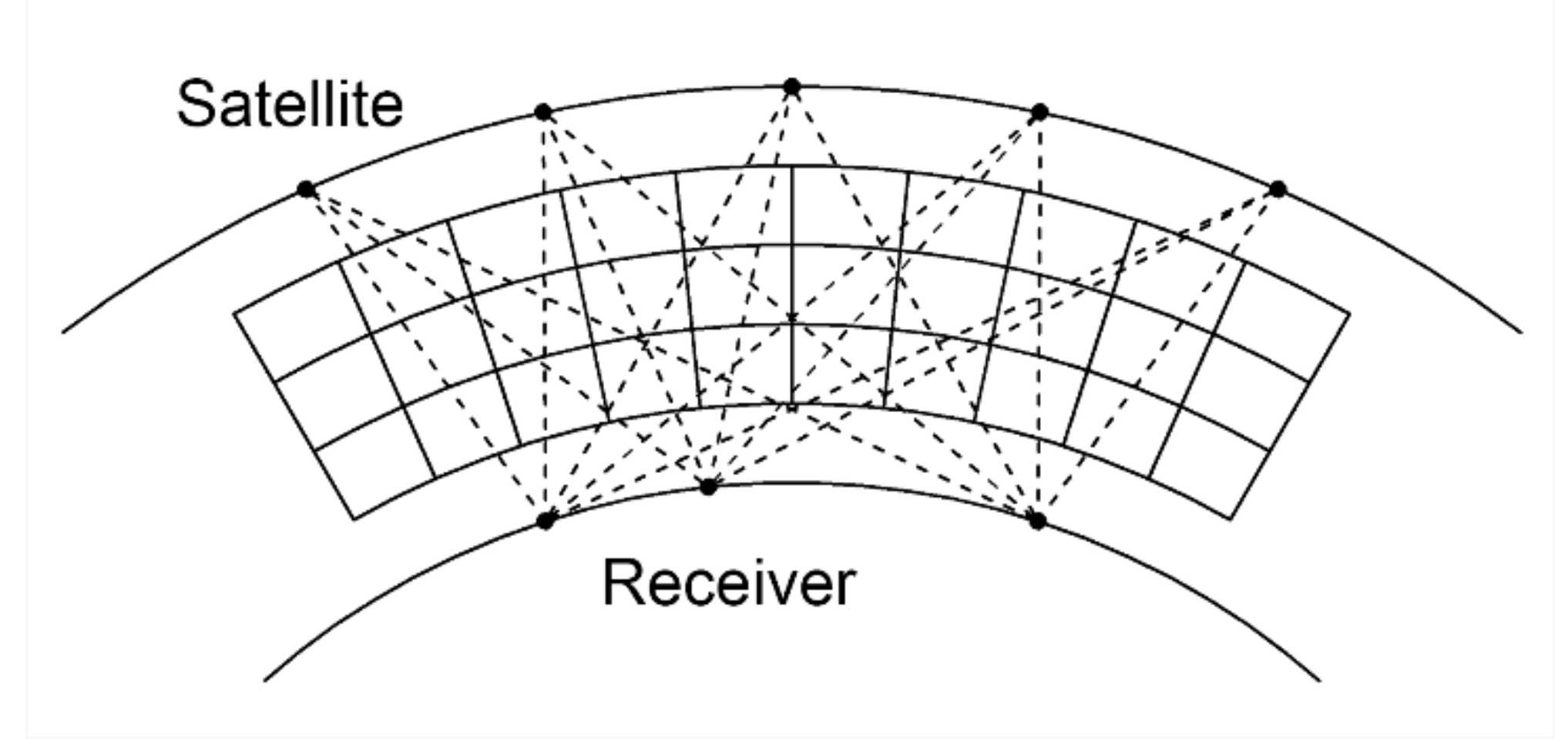
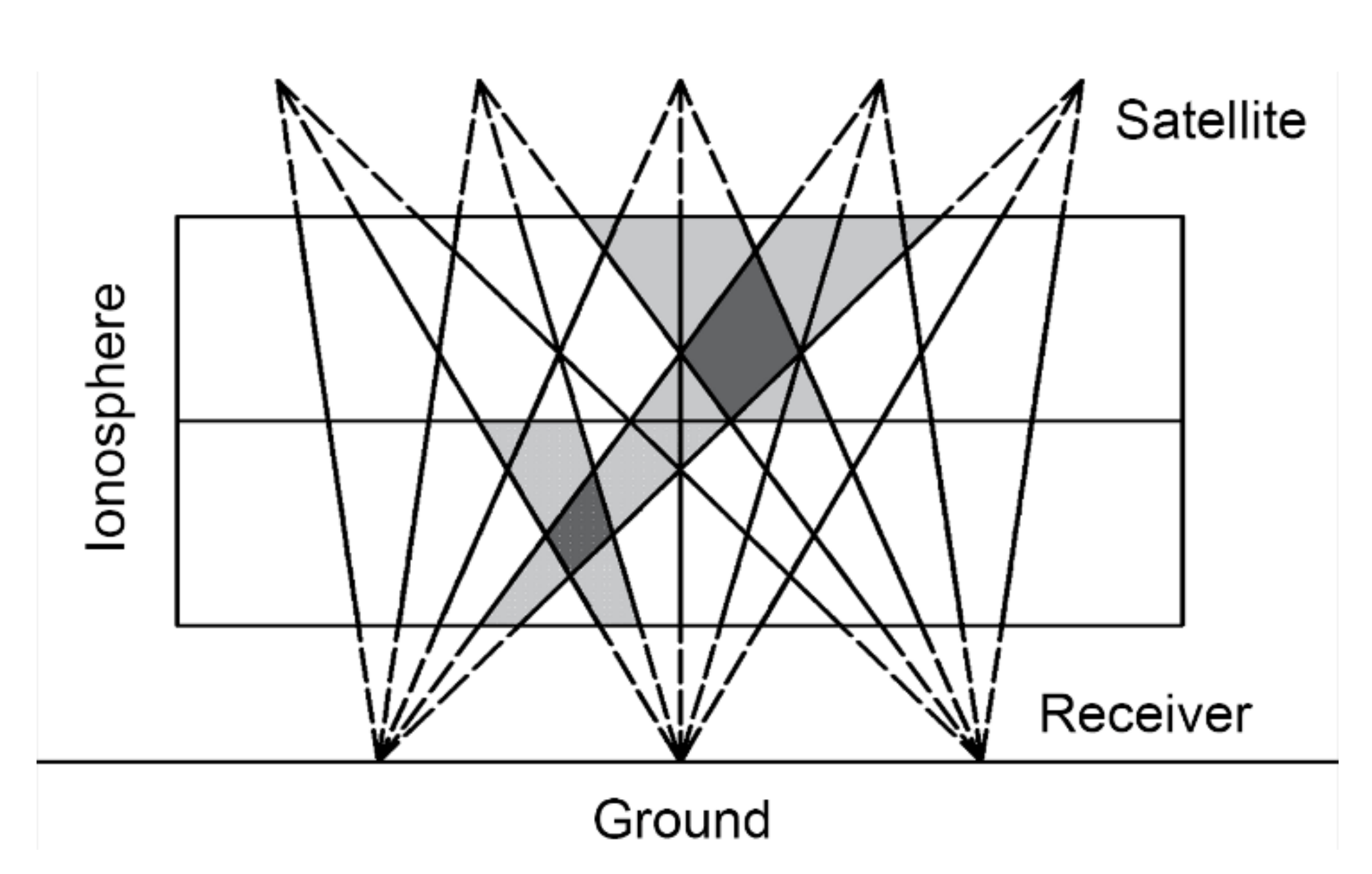
2. Statement of Tomography Problem
3. Voxel-Based Models
3.1. Variable Voxel Geometry
3.2. Variable Voxel Size
3.3. Variable Voxel Homogeneity
4. Equation Constructions
4.1. Condition Constraint
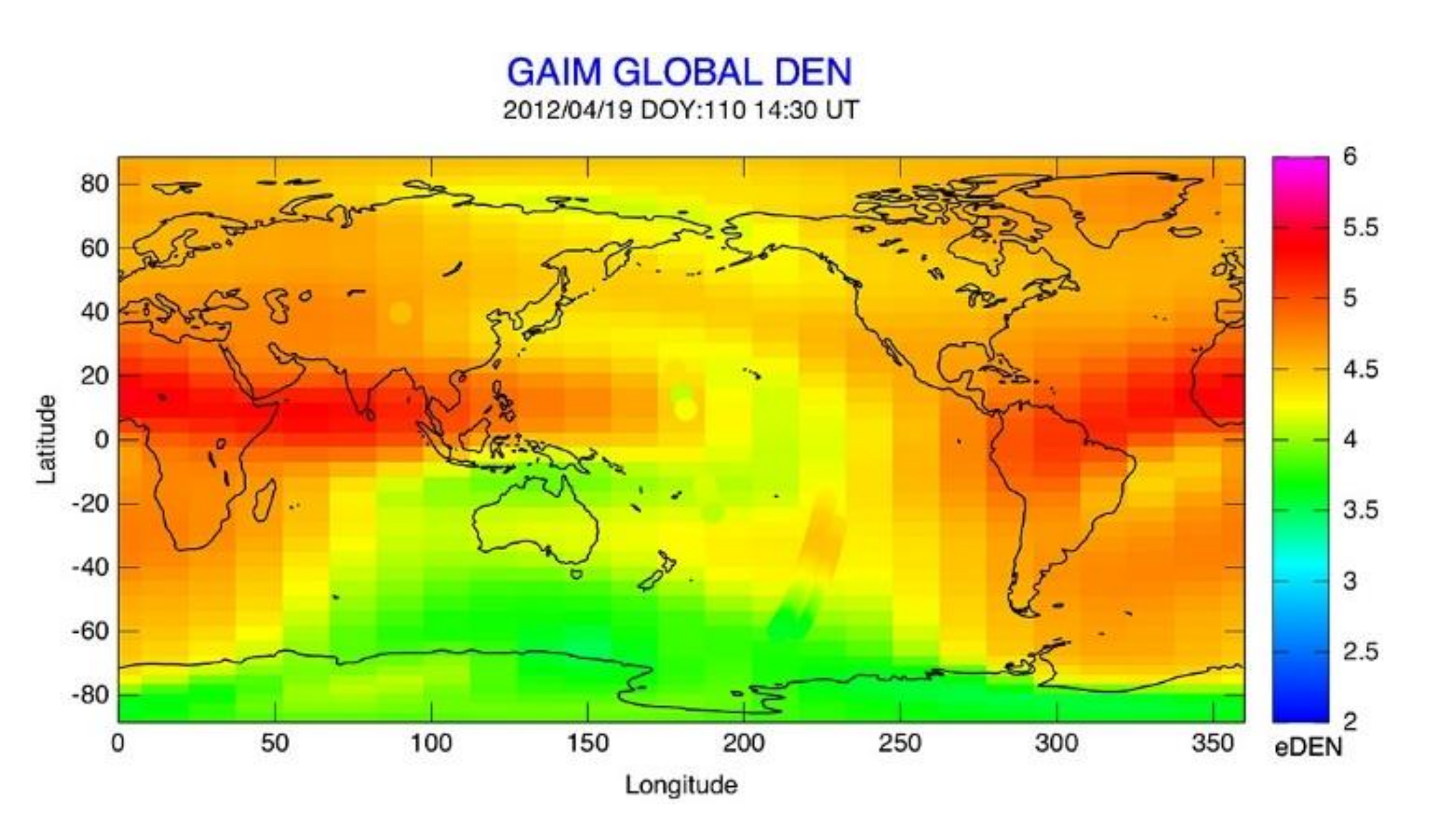
4.2. Virtual Data Assimilation
4.3. Multi-Source Observation Fusion
5. Algorithms
5.1. Iterative Reconstruction
5.2. Singular Value Decomposition
5.3. Kalman Filtering
5.4. Neural Network
5.5. Bayesian Estimation
6. CIT Results and Applications
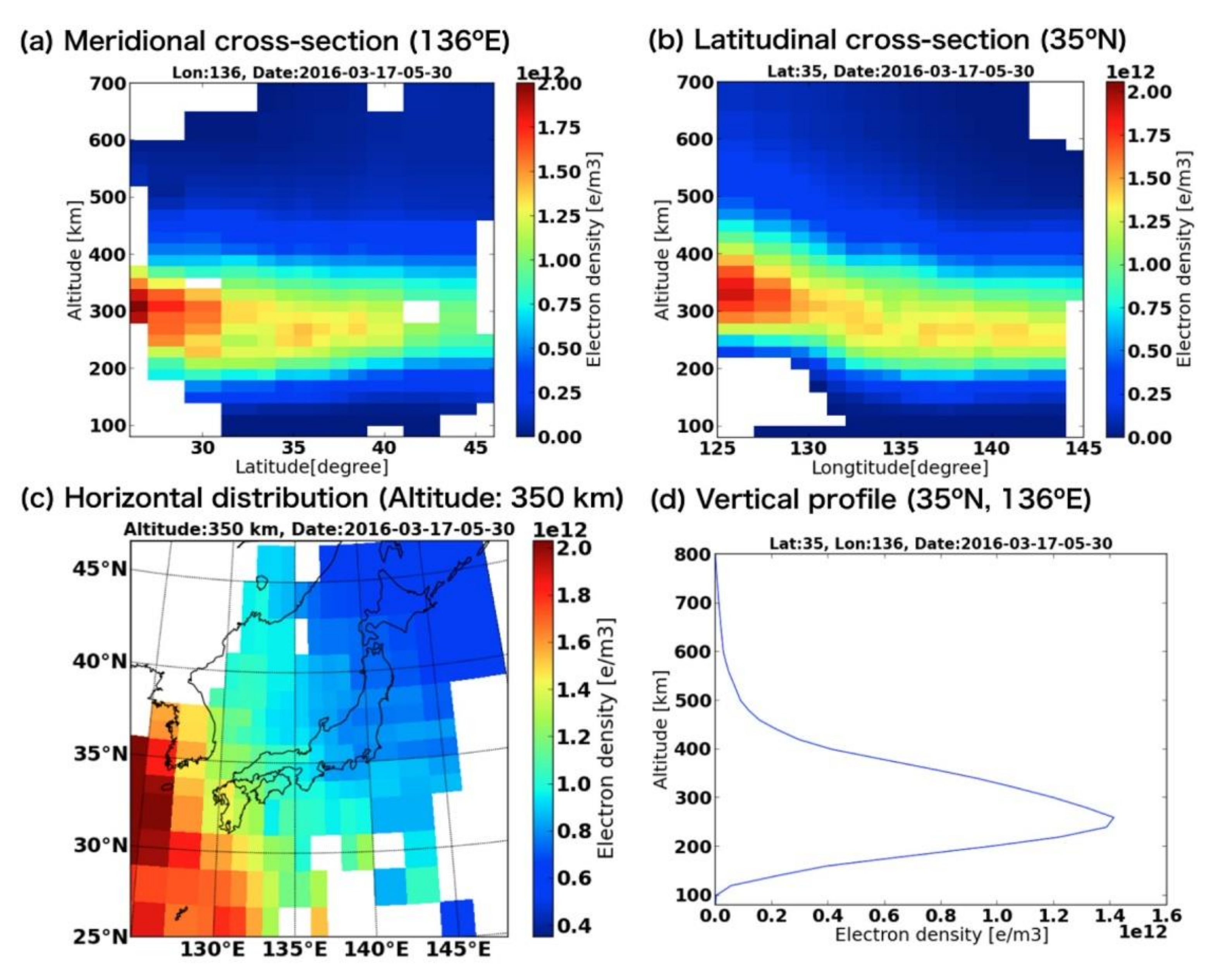
6.1. Ionospheric Height Profile and Image
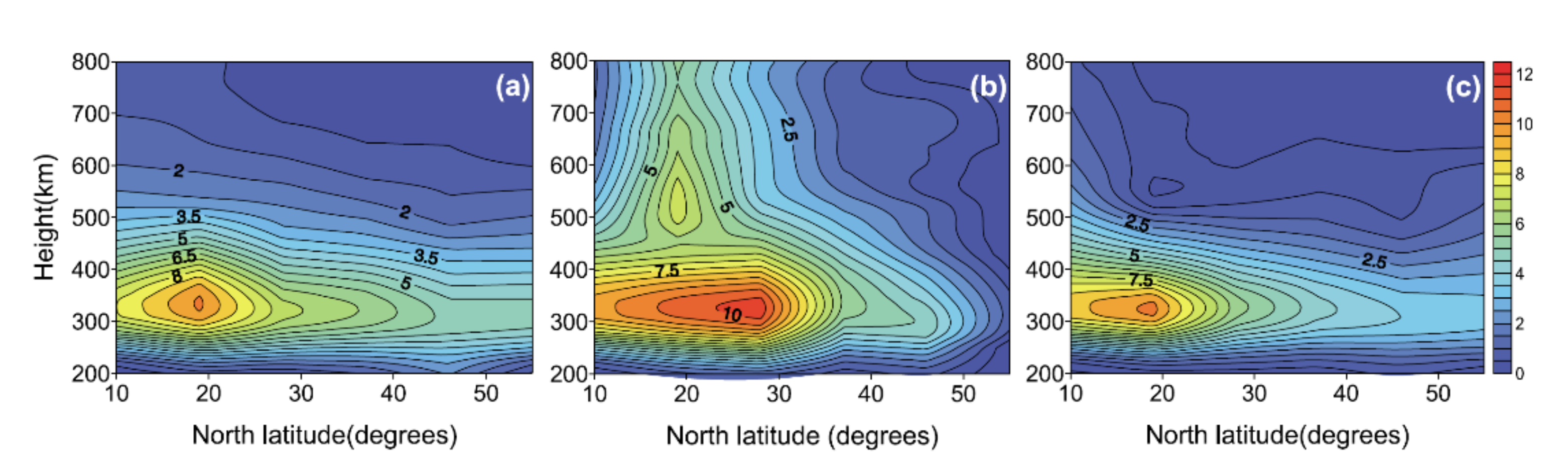
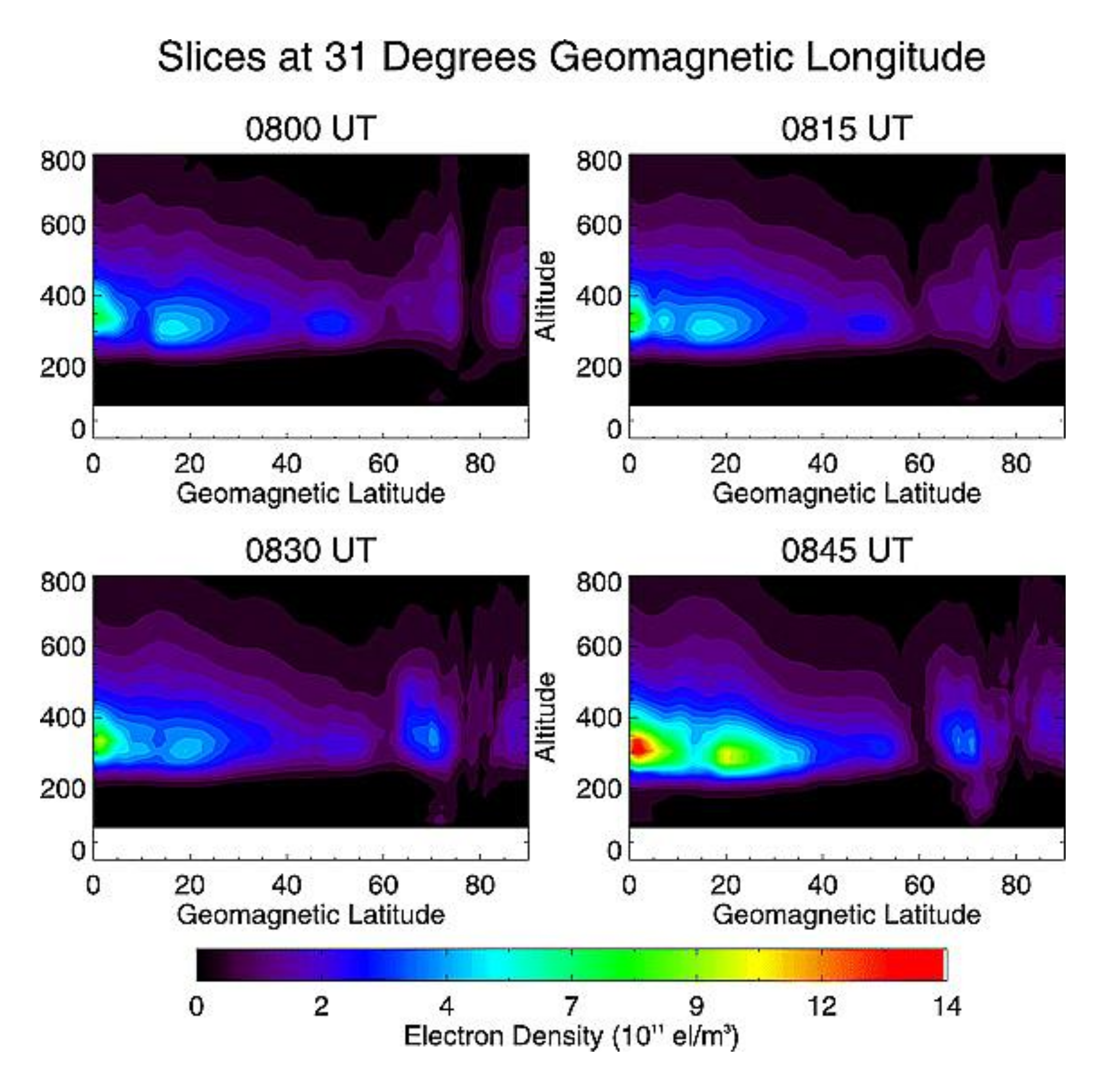
6.2. Ionospheric Disturbance Study
6.3. Ionospheric Correction
6.4. Ionospheric Monitoring
7. Future Directions
8. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement:
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite System |
| CIT | Computerized Ionospheric Tomography |
| IED | Ionospheric Electron Density |
| TEC | Total Electron Content |
| CT | Computerized Tomography |
| ART | Algebraic Reconstruction Technique |
| NNSS | Navy Navigational Satellite System |
| LEO | Low Earth Orbit |
| EIA | Equatorial Ionospheric Anomaly |
| MSTIDs | Medium-Scale Traveling Ionospheric Disturbances |
| STEC | Slant Total Electron Content |
| PPP | Precise Point Positioning |
| IPP | Ionospheric Piercing Point |
| RMSE | Root Mean Square Error |
| ROI | Region Of Interest |
| IRI | International Reference Ionosphere |
| GPS | Global Positioning System |
| EOFs | Empirical Orthogonal Functions |
| EIA | Equatorial Ionization Anomaly |
| RMS | Root Mean Square |
| ISR | Incoherent Scatter Radar |
| MART | Multiplicative Algebraic Reconstruction Technique |
| DMSP | Defense Meteorological Satellite Program |
| CART | Constrained Algebraic Reconstruction Technique |
| CMART | Constrained Multiplicative Algebraic Reconstruction Technique |
| SART | Simultaneous Algebraic Reconstruction Technique |
| SMART | Simultaneous Multiplicative Algebraic Reconstruction Technique |
| VRSs | Virtual Reference Stations |
| SVD | Singular Value Decomposition |
| GSVD | Generalized Singular Value Decomposition |
| ANN | Artificial Neural Network |
| MAP | Maximum A Posteriori |
| GAIM | Global Assimilation of Ionospheric Measurements |
| LSTIDs | Large-Scale Traveling Ionospheric Disturbances |
| EPBs | Equatorial Plasma Bubbles |
| RTK | Real-Time Kinematic |
| SBAS | Satellite-Based Augmentation System |
References
- Herman, G.T. Image Reconstruction from Projections: The Fundamentals of Computerized Tomography; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Natterer, F. The Mathematics of Computerized Tomography; Vieweg + Teubner Verlag: Wiesbaden, Germany, 1986. [Google Scholar]
- Austen, J.R.; Franke, S.J.; Liu, C.H.; Yeh, K.C. Application of computerized tomography techniques to ionospheric research. In Proceedings of the International Beacon Satellite Symposium on Radio Beacon Contribution to the Study of Ionization and Dynamics of the Ionosphere and to Corrections to Geodesy and Technical Workshop, Oulu, Finland, 9–14 June 1986; pp. 25–35, Part 1. [Google Scholar]
- Andreeva, E.S.; Galinov, A.V.; Kunitsyn, V.E.; Mel’nichenko, Y.A.; Tereschenko, E.E.; Filimonov, M.A.; Chernyakov, S.M. Radiotomographic reconstruction of ionization dip in the plasma near the earth. JETP Lett. 1990, 52, 145–148. [Google Scholar] [CrossRef]
- Fremouw, E.J.; Secan, J.A.; Howe, B.M. Application of stochastic inverse theory to ionospheric tomography. Radio Sci. 1992, 27, 721–732. [Google Scholar] [CrossRef]
- Kunitake, M.; Ohtaka, K.; Maruyama, T.; Tokumaru, M.; Morioka, A.; Watanabe, S. Tomographic imaging of the ionosphere over Japan by the modified truncated SVD method. Ann. Geophys. 1995, 13, 1303–1310. [Google Scholar]
- Kunitsyn, V.E.; Andreeva, E.S.; Razinkov, O.G. Possibilities of the nears-pace environment radio tomography. Radio Sci. 1997, 32, 1953–1963. [Google Scholar] [CrossRef]
- Rius, A.; Ruffini, G.; Cucurull, L. Improving the vertical resolution of ionospheric tomography with GPS occultations. Geophys. Res. Lett. 1997, 24, 2291–2294. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J. Global observation of the ionospheric electronic response to solar events using ground and LEO GPS data. J. Geophys. Res. Space Phys. 1998, 103, 20789–20796. [Google Scholar] [CrossRef]
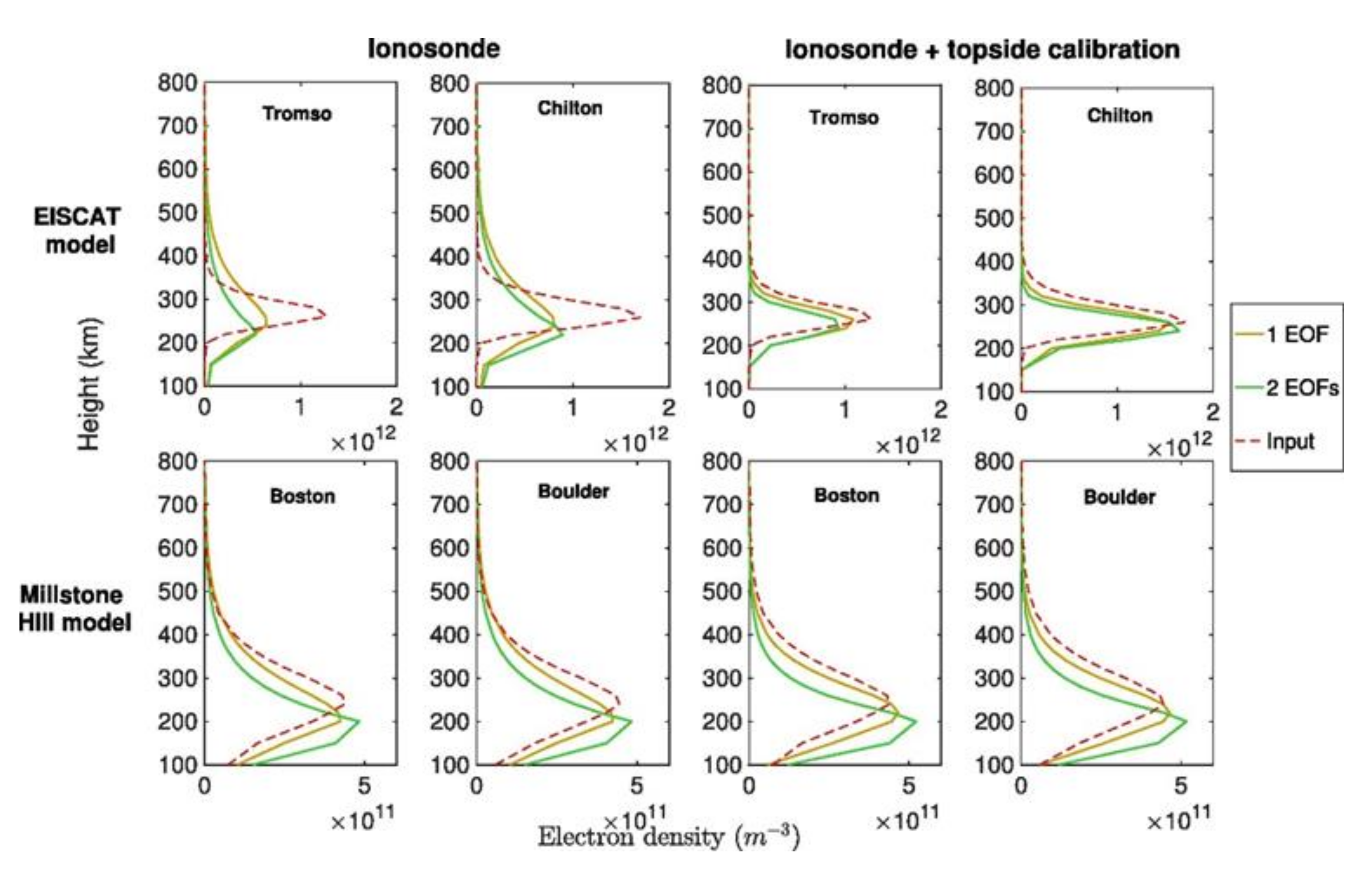
- García-Fernández, M.; Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orús, R.; Coisson, P.; Nava, B.; Radicella, S.M. Combining ionosonde with ground GPS data for electron density estimation. J. Atmos. Sol. Terr. Phys. 2003, 65, 683–691. [Google Scholar] [CrossRef]
- Ma, X.F.; Maruyama, T.; Ma, G.; Takeda, T. Three-dimensional ionospheric tomography using observation data of GPS ground receivers and ionosonde by neural network. J. Geophys. Res. Space Phys. 2005, 110, A05308. [Google Scholar] [CrossRef]
- Bust, G.S.; Mitchell, C.N. History, current state, and future directions of ionospheric imaging. Rev. Geophys. 2008, 46, RG1003. [Google Scholar] [CrossRef]
- Wen, D.; Yuan, Y.; Ou, J.; Huo, X.; Zhang, K. Ionospheric temporal and spatial variations during the 18 August 2003 storm over China. Earth Planets Space 2007, 59, 313–317. [Google Scholar] [CrossRef]
- Thampi, S.V.; Yamamoto, M.; Lin, C.; Liu, H. Comparison of FORMOSAT-3/COSMIC radio occultation measurements with radio tomography. Radio Sci. 2011, 46, RS3001. [Google Scholar] [CrossRef]
- Chen, C.H.; Saito, A.; Lin, C.H.; Yamamoto, M.; Suzuki, S.; Seemala, G.K. Medium-scale traveling ionospheric disturbances by three-dimensional ionospheric GPS tomography. Earth Planets Space 2016, 68, 32. [Google Scholar] [CrossRef]
- Nesterov, I.A.; Andreeva, E.S.; Padokhin, A.M.; Tumanova, Y.S.; Nazarenko, M.O. Ionospheric perturbation indices based on the low- and high-orbiting satellite radio tomography data. GPS Solut. 2017, 21, 1679–1694. [Google Scholar] [CrossRef]
- Andreeva, E.S.; Tereshchenko, E.D.; Nazarenko, M.O.; Nesterov, I.A.; Padokhin, A.M.; Tumanova, Y.S. Exploring the ionospheric structures by radio tomographic methods under different space weather conditions. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium-Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017; pp. 1298–1304. [Google Scholar] [CrossRef]
- Yao, Y.; Tang, J.; Chen, P.; Zhang, S.; Chen, J. An improved iterative algorithm for 3-D ionospheric tomography reconstruction. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4696–4706. [Google Scholar] [CrossRef]
- Jin, R.; Jin, S.; Feng, G. M_DCB: Matlab code for estimating GNSS satellite and receiver differential code biases. GPS Solut. 2012, 16, 541–548. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Yuan, Y.; Zhang, H.; Li, M. Joint estimation of vertical total electron content (VTEC) and satellite differential code biases (SDCBs) using low-cost receivers. J. Geod. 2018, 92, 401–413. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Colombo, O.L. Application of ionospheric tomography to real-time GPS carrier-phase ambiguities resolution, at scales of 400–1000 km and with high geomagnetic activity. Geophys. Res. Lett. 2000, 27, 2009–2012. [Google Scholar] [CrossRef]
- Ma, G.; Maruyama, T. Derivation of TEC and estimation of instrumental biases from GEONET in Japan. Ann. Geophys. 2003, 21, 2083–2093. [Google Scholar] [CrossRef]
- Liu, J.; Chen, R.; Wang, Z.; Zhang, H. Spherical cap harmonic model for mapping and predicting regional TEC. GPS Solut. 2011, 15, 109–119. [Google Scholar] [CrossRef]
- Psychas, D.; Verhagen, S.; Liu, X.; Memarzadeh, Y.; Visser, H. Assessment of ionospheric corrections for PPP-RTK using regional ionosphere modelling. Meas. Sci. Technol. 2018, 30, 014001. [Google Scholar] [CrossRef]
- Juan, J.M.; Rius, A.; Hernández-Pajares, M.; Sanz, J. A two-layer model of the ionosphere using Global Positioning System data. Geophys. Res. Lett. 1997, 24, 393–396. [Google Scholar] [CrossRef]
- Sutton, E.; Na, H. Comparison of geometries for ionospheric tomography. Radio Sci. 1995, 30, 115–125. [Google Scholar] [CrossRef]
- Semeter, J.; Kamalabadi, F. A natural pixel decomposition for tomographic imaging of the ionosphere. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, Seattle, WA, USA, 15 May 1998; Volume 5, pp. 2913–2916. [Google Scholar] [CrossRef]
- Supriadi, S.; Darmawan, D.; Septiawan, R. Checkerboard test implementation into ionospheric tomography for SuGAr data. J. Phys. Conf. Ser. 2018, 1130, 012037. [Google Scholar] [CrossRef]
- Das, S.K.; Shukla, A.K. Two-dimensional ionospheric tomography over the low-latitude Indian region: An intercomparison of ART and MART algorithms. Radio Sci. 2011, 46, RS2005. [Google Scholar] [CrossRef]
- Zheng, D.; Hu, W.; Nie, W. Multiscale ionospheric tomography. GPS Solut. 2015, 19, 579–588. [Google Scholar] [CrossRef]
- Zheng, D.; Zheng, H.; Wang, Y.; Nie, W.; Li, C.; Ao, M.; Hu, W.; Zhou, W. Variable pixel size ionospheric tomography. Adv. Space Res. 2017, 59, 2969–2986. [Google Scholar] [CrossRef]
- Saito, S.; Suzuki, S.; Yamamoto, M.; Saito, A.; Chen, C.H. Real-Time ionosphere monitoring by three-dimensional tomography over Japan. Navigation 2017, 64, 495–504. [Google Scholar] [CrossRef]
- Chen, B.; Wu, L.; Dai, W.; Luo, X.; Xu, Y. A new parameterized approach for ionospheric tomography. GPS Solut. 2019, 23, 96. [Google Scholar] [CrossRef]
- Watermann, J.; Bust, G.S.; Thayer, J.P.; Neubert, T.; Coker, C. Mapping plasma structures in the high-latitude ionosphere using beacon satellite, incoherent scatter radar and ground-based magnetometer observations. Ann. Geophys. 2002, 45, 177–189. [Google Scholar] [CrossRef]
- Mitchell, C.N.; Spencer, P.S.J. A three-dimensional time-dependent algorithm for ionospheric imaging using GPS. Ann. Geophys. 2003, 46, 687–696. [Google Scholar] [CrossRef]
- Giday, N.M.; Katamzi, Z.T.; Mckinnell, L.A. Ionospheric tomography over South Africa: Comparison of MIDAS and ionosondes measurements. Adv. Space Res. 2016, 57, 245–256. [Google Scholar] [CrossRef]
- Wen, D.; Liu, S.; Tang, P. Tomographic reconstruction of ionospheric electron density based on constrained algebraic reconstruction technique. GPS Solut. 2010, 14, 375–380. [Google Scholar] [CrossRef]
- Fehmers, G.C.; Kamp, L.P.J.; Sluijter, F.W.; Spoelstra, T.A.T. A model-independent algorithm for ionospheric tomography: 1. Theory and tests. Radio Sci. 1998, 33, 149–163. [Google Scholar] [CrossRef]
- Bruno, J.; Mitchell, C.N.; Bolmgren, K.H.A.; Witvliet, B.A. A realistic simulation framework to evaluate ionospheric tomography. Adv. Space Res. 2020, 65, 891–901. [Google Scholar] [CrossRef]
- Na, H.; Lee, H. Resolution analysis of tomographic reconstruction of electron density profiles in the ionosphere. Int. J. Imaging Syst. Technol. 1990, 2, 209–218. [Google Scholar] [CrossRef]
- Panicciari, T.; Smith, N.D.; Mitchell, C.N.; Da Dalt, F.; Spencer, P.S.J. Using sparse regularization for multi-resolution tomography of the ionosphere. Nonlinear Process. Geophys. 2015, 22, 613–624. [Google Scholar] [CrossRef]
- Wang, S.; Huang, S.; Fang, H. Dual-parameter regularization method in three-dimensional ionospheric reconstruction. Ann. Geophys. 2018, 36, 1255–1266. [Google Scholar] [CrossRef]
- Yao, Y.; Tang, J.; Kong, J.; Zhang, L.; Zhang, S. Application of hybrid regularization method for tomographic reconstruction of midlatitude ionospheric electron density. Adv. Space Res. 2013, 52, 2215–2225. [Google Scholar] [CrossRef]
- Lee, J.K.; Kamalabadi, F.; Makela, J.J. Three-dimensional tomography of ionospheric variability using a dense GPS receiver array. Radio Sci. 2008, 43, RS3001. [Google Scholar] [CrossRef]
- Panicciari, T.; Smith, N.D.; Da Dalt, F.; Mitchell, C.N. Robust ionospheric tomography using sparse regularization. In Proceedings of the 2014 XXXIth General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Ou, M.; Zhang, H.B.; Zhen, W.M. GPS-based ionospheric tomography with constrained IRI as a regularization. In Proceedings of the 10th International Symposium on Antennas, Propagation and EM Theory, Xi’an, China, 22–26 October 2012; pp. 656–659. [Google Scholar] [CrossRef]
- Ganguly, S.; Brown, A. Real-time characterization of the ionosphere using diverse data and models. Radio Sci. 2001, 36, 1181–1197. [Google Scholar] [CrossRef]
- Chen, B.; Dai, W.; Cai, C.; Kuang, C. An improved method of ionospheric tomography. Lect. Notes Electr. Eng. 2012, 159, 3–9. [Google Scholar] [CrossRef]
- Yao, Y.; Kong, J.; Tang, J. A new ionosphere tomography algorithm with two-grid virtual observations constraints and three-dimensional velocity profile. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2373–2383. [Google Scholar] [CrossRef]
- Yao, Y.; Zhai, C.; Kong, J.; Zhao, Q.; Zhao, C. A modified three-dimensional ionospheric tomography algorithm with side rays. GPS Solut. 2018, 22, 107. [Google Scholar] [CrossRef]
- Schunk, R.W.; Scherliess, L.; Sojka, J.J.; Thompson, D.C.; Anderson, D.N.; Codrescu, M.; Minter, C.; Fuller-Rowell, T.J.; Heelis, R.A.; Hairston, M.; et al. Global assimilation of ionospheric measurements (GAIM). Radio Sci. 2004, 39, RS1S02. [Google Scholar] [CrossRef]
- Angling, M.J.; Cannon, P.S. Assimilation of radio occultation measurements into background ionospheric models. Radio Sci. 2004, 39, RS1S08. [Google Scholar] [CrossRef]
- Chiang, K.Q.Z.; Psiaki, M.L. GPS and ionosonde data fusion for ionospheric tomography. In Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2014), Tampa, FL, USA, 8–12 September 2014; pp. 1163–1172. [Google Scholar]
- Chartier, A.T.; Smith, N.D.; Mitchell, C.N.; Jackson, D.R.; Patilongo, P.J.C. The use of ionosondes in GPS ionospheric tomography at low latitudes. J. Geophys. Res. Space Phys. 2012, 117, A10326. [Google Scholar] [CrossRef]
- Ssessanga, N.; Yamamoto, M.; Saito, S.; Saito, A.; Nishioka, M. Complementing regional ground GNSS-STEC computerized ionospheric tomography (CIT) with ionosonde data assimilation. GPS Solut. 2021, 25, 93. [Google Scholar] [CrossRef]
- Bust, G.S.; Coco, D.S.; Gaussiran, T.L. Computerized ionospheric tomography analysis of the combined ionospheric campaign. Radio Sci. 2001, 36, 1599–1605. [Google Scholar] [CrossRef]
- Austen, J.R.; Franke, S.J.; Liu, C.H. Ionospheric imaging using computerized tomography. Radio Sci. 1988, 23, 299–307. [Google Scholar] [CrossRef]
- Raymund, T.D.; Austen, J.R.; Franke, S.J.; Liu, C.H.; Klobuchar, J.A.; Stalker, J. Application of computerized tomography to the investigation of ionospheric structures. Radio Sci. 1990, 25, 771–789. [Google Scholar] [CrossRef]
- Prol, F.S.; Camargo, P.O. Ionospheric tomography using GNSS: Multiplicative algebraic reconstruction technique applied to the area of brazil. GPS Solut. 2016, 20, 807–814. [Google Scholar] [CrossRef]
- Yang, Z.; Song, S.; Jiao, W.; Chen, G.; Xue, J.; Zhou, W.; Zhu, W. Ionospheric tomography based on GNSS observations of the CMONOC: Performance in the topside ionosphere. GPS Solut. 2017, 21, 363–375. [Google Scholar] [CrossRef]
- Jin, S.; Li, D. 3-D ionospheric tomography from dense GNSS observations based on an improved two-step iterative algorithm. Adv. Space Res. 2018, 62, 809–820. [Google Scholar] [CrossRef]
- Li, D.; Jin, S.; Zheng, G.; Calabia, A. Evaluation of 3-D ionospheric tomography from denser GNSS observations in Japan. In Proceedings of the 2016 Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8–11 August 2016; pp. 4986–4990. [Google Scholar] [CrossRef]
- Wen, D.; Wang, Y.; Norman, R. A new two-step algorithm for ionospheric tomography solution. GPS Solut. 2012, 16, 89–94. [Google Scholar] [CrossRef]
- Prol, F.S.; Camargo, P.O.; Hernández-Pajares, M.; Muella, M.T.A.H. A new method for ionospheric tomography and its assessment by ionosonde electron density, GPS TEC, and single-frequency PPP. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2571–2582. [Google Scholar] [CrossRef]
- Ou, M.; Zhang, H.B.; Yu, X.; She, C.L.; Liu, D.; Zhen, W.M. An algorithm combined with EOFs analysis and MART for GPS-based ionospheric tomography. In Proceedings of the 9th International Symposium on Antennas, Propagation and EM Theory, Guangzhou, China, 29 November–2 December 2010; pp. 1230–1233. [Google Scholar] [CrossRef]
- Zheng, D.; Yao, Y.; Nie, W.; Yang, W.; Hu, W.; Ao, M.; Zheng, H. An improved iterative algorithm for ionospheric tomography reconstruction by using the automatic search technology of relaxation factor. Radio Sci. 2018, 53, 1051–1066. [Google Scholar] [CrossRef]
- Wen, D.; Zhang, X.; Tong, Y.; Zhang, G.; Zhang, M.; Leng, R. GPS-based ionospheric tomography with a constrained adaptive simultaneous algebraic reconstruction technique. J. Earth Syst. Sci. 2015, 124, 283–289. [Google Scholar] [CrossRef]
- Nandi, S.; Bandyopadhyay, B. Study of low-latitude ionosphere over Indian region using simultaneous algebraic reconstruction technique. Adv. Space Res. 2015, 55, 545–553. [Google Scholar] [CrossRef]
- Liu, S.; Wang, J.; Gao, J. Inversion of ionospheric electron density based on a constrained simultaneous iteration reconstruction technique. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2455–2459. [Google Scholar] [CrossRef]
- Gerzen, T.; Minkwitz, D. Simultaneous multiplicative column-normalized method (SMART) for 3-D ionosphere tomography in comparison to other algebraic methods. Ann. Geophys. 2016, 34, 97–115. [Google Scholar] [CrossRef][Green Version]
- Yao, Y.; Chen, P.; Zhang, S.; Chen, J. A new ionospheric tomography model combining pixel-based and function-based models. Adv. Space Res. 2013, 52, 614–621. [Google Scholar] [CrossRef]
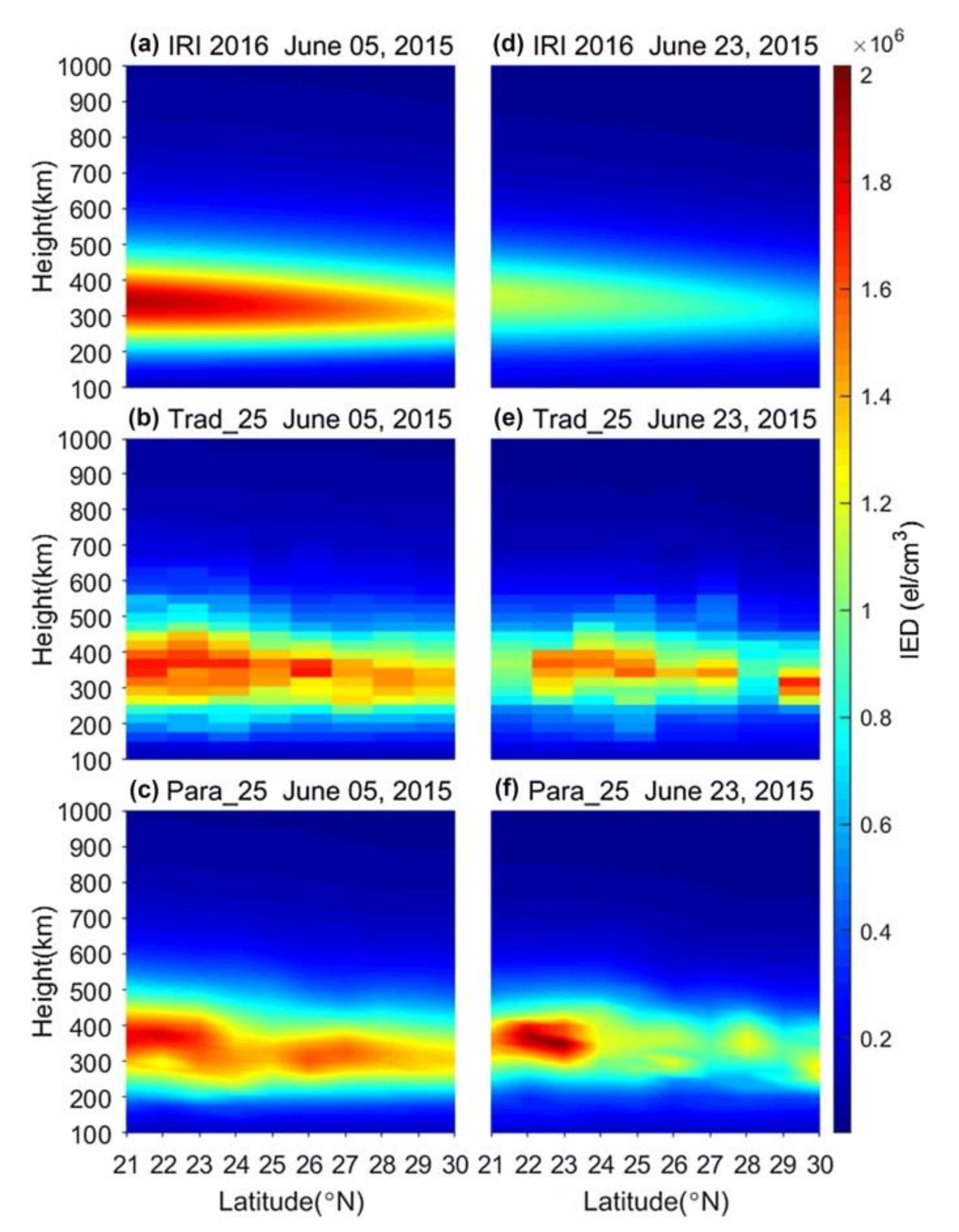
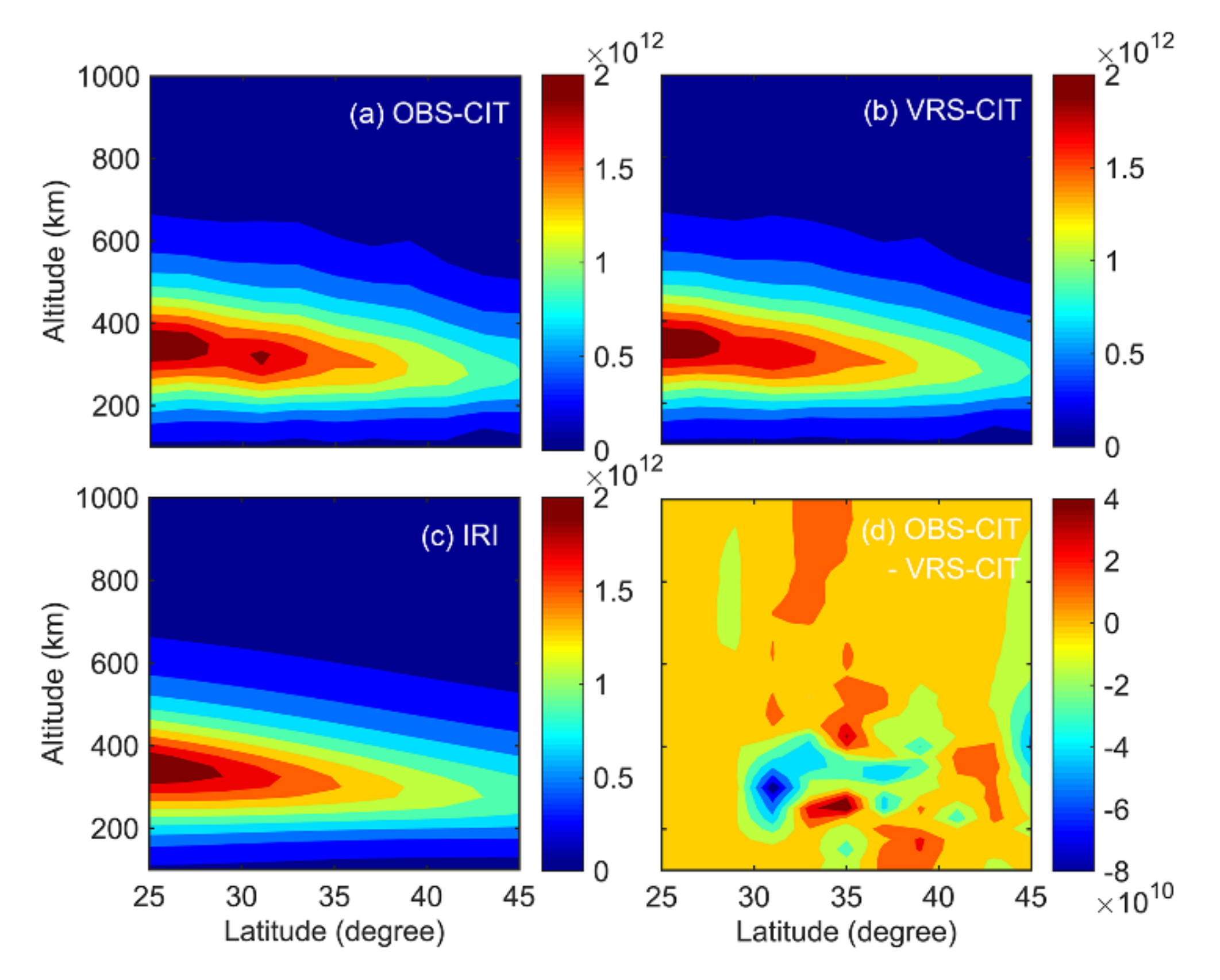
- Lu, W.; Ma, G.; Wan, Q.; Li, J.; Wang, X.; Fu, W.; Maruyama, T. Virtual reference station-based computerized ionospheric tomography. GPS Solut. 2021, 25, 8. [Google Scholar] [CrossRef]
- Fan, J.; Ma, G. Characteristics of GPS positioning error with non-uniform pseudorange error. GPS Solut. 2014, 18, 615–623. [Google Scholar] [CrossRef]
- Bhuyan, K.; Singh, S.B.; Bhuyan, P.K. Application of generalized singular value decomposition to ionospheric tomography. Ann. Geophys. 2004, 22, 3437–3444. [Google Scholar] [CrossRef]
- Wen, D.; Yuan, Y.; Ou, J.; Zhang, K.; Liu, K. A hybrid reconstruction algorithm for 3-D ionospheric tomography. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1733–1739. [Google Scholar] [CrossRef]
- Erturk, O.; Arikan, O.; Arikan, F. Tomographic reconstruction of the ionospheric electron density as a function of space and time. Adv. Space Res. 2009, 43, 1702–1710. [Google Scholar] [CrossRef]
- Howe, B.M.; Runciman, K.; Secan, J.A. Tomography of the ionosphere: Four-dimensional simulations. Radio Sci. 1998, 33, 109–128. [Google Scholar] [CrossRef]
- Scherliess, L.; Schunk, R.W.; Sojka, J.J.; Thompson, D.C. Development of a physics-based reduced state Kalman filter for the ionosphere. Radio Sci. 2004, 39, RS1S04. [Google Scholar] [CrossRef]
- Tuna, H.; Arikan, O.; Arikan, F. Model based computerized ionospheric tomography in space and time. Adv. Space Res. 2018, 61, 2057–2073. [Google Scholar] [CrossRef]
- Granat, R.A.; Na, H. Estimating dynamic ionospheric changes without a priori models. Radio Sci. 2000, 35, 341–349. [Google Scholar] [CrossRef]
- Ghaffari Razin, M.; Voosoghi, B. Ionosphere tomography using wavelet neural network and particle swarm optimization training algorithm in Iranian case study. GPS Solut. 2017, 21, 1301–1314. [Google Scholar] [CrossRef]
- Khorsheed, E.; Hurn, M.; Jennison, C. Mapping electron density in the ionosphere: A principal component MCMC algorithm. Comput. Stat. Data Anal. 2011, 55, 338–352. [Google Scholar] [CrossRef]
- Norberg, J.; Roininen, L.; Vierinen, J.; Amm, O.; Lehtinen, M. Ionospheric tomography in Bayesian framework with Gaussian Markov random field priors. Radio Sci. 2015, 50, 138–152. [Google Scholar] [CrossRef]
- Norberg, J.; Vierinen, J.; Roininen, L.; Orispää, M.; Kauristie, K.; Rideout, W.C.; Coster, A.J.; Lehtinen, M.S. Gaussian Markov random field priors in ionospheric 3-D multi-instrument tomography. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7009–7021. [Google Scholar] [CrossRef]
- Gardner, L.C.; Schunk, R.W.; Scherliess, L.; Sojka, J.J.; Zhu, L. Global assimilation of ionospheric measurements-Gauss Markov model: Improved specifications with multiple data types. Space Weather 2014, 12, 675–688. [Google Scholar] [CrossRef]
- Aa, E.; Liu, S.; Huang, W.; Shi, L.; Gong, J.; Chen, Y.; Shen, H.; Li, J. Regional 3-D ionospheric electron density specification on the basis of data assimilation of ground-based GNSS and radio occultation data. Space Weather 2016, 14, 433–448. [Google Scholar] [CrossRef]
- Ssessanga, N.; Kim, Y.H.; Kim, E. Vertical structure of medium-scale traveling ionospheric disturbances. Geophys. Res. Lett. 2015, 42, 9156–9165. [Google Scholar] [CrossRef]
- Bust, G.S.; Garner, T.W.; Gaussiran, T.L. Ionospheric data assimilation three-dimensional (IDA3D): A global, multisensor, electron density specification algorithm. J. Geophys. Res. Space Phys. 2004, 109, A11312. [Google Scholar] [CrossRef]
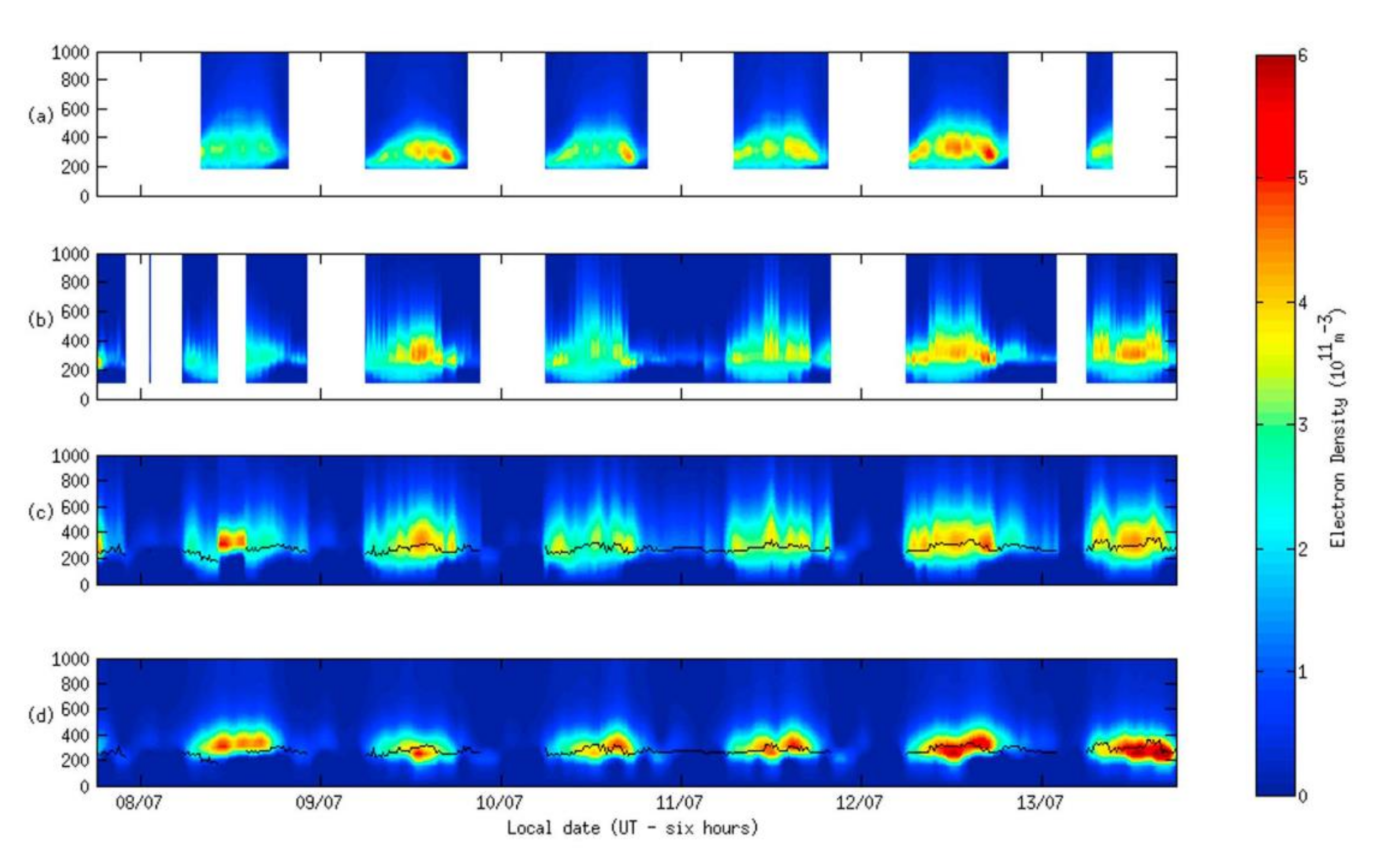
- Song, R.; Hattori, K.; Zhang, X.; Liu, J.-Y.; Yoshino, C. Detecting the ionospheric disturbances in Japan using the three-dimensional computerized tomography. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028561. [Google Scholar] [CrossRef]
- Prol, F.S.; Hernández-Pajares, M.; Muella, M.T.A.H.; Camargo, P.O. Tomographic imaging of ionospheric plasma bubbles based on GNSS and radio occultation measurements. Remote Sens. 2018, 10, 1529. [Google Scholar] [CrossRef]
- Meggs, R.W.; Mitchell, C.N. A study into the errors in vertical total electron content mapping using GPS data. Radio Sci. 2006, 41, RS1008. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P. A new ionospheric estimation algorithm for SBAS combining Kriging and tomography. In Proceedings of the 2004 National Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 26–28 January 2004; pp. 524–529. [Google Scholar]
- Olivares-Pulido, G.; Terkildsen, M.; Arsov, K.; Teunissen, P.J.G.; Khodabandeh, A.; Janssen, V. A 4D tomographic ionospheric model to support PPP-RTK. J. Geod. 2019, 93, 1673–1683. [Google Scholar] [CrossRef]
- Seemala, G.K.; Yamamoto, M.; Saito, A.; Chen, C.H. Three-dimensional GPS ionospheric tomography over japan using constrained least squares. J. Geophys. Res. Space Phys. 2014, 119, 3044–3052. [Google Scholar] [CrossRef]
- Muafiry, I.N.; Heki, K.; Maeda, J. 3D tomography of midlatitude sporadic-E in Japan from GNSS-TEC data. Earth Planets Space 2018, 70, 45. [Google Scholar] [CrossRef]
- He, L.M.; Yang, Y.; Su, C.; Yu, J.Q.; Yang, F.; Wu, L.X. Grid-based representation and dynamic visualization of ionospheric tomography. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Xuzhou, China, 11–12 November 2013; 2013; Volume XL-4/W2, pp. 71–76. [Google Scholar] [CrossRef]
- Gerzen, T.; Minkwitz, D.; Schmidt, M.; Erdogan, E. Analysis of different propagation models for the estimation of the topside ionosphere and plasmasphere with an ensemble Kalman filter. Ann. Geophys. 2020, 38, 1171–1189. [Google Scholar] [CrossRef]



| Equation | Comments | |
|---|---|---|
| (K1) | Model state forecast | |
| (K2) | Model state forecast error | |
| (K3) | Measurement equation | |
| (K4) | Kalman gain | |
| (K5) | Model state analysis | |
| (K6) | Model state analysis error |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Ma, G.; Wan, Q. A Review of Voxel-Based Computerized Ionospheric Tomography with GNSS Ground Receivers. Remote Sens. 2021, 13, 3432. https://doi.org/10.3390/rs13173432
Lu W, Ma G, Wan Q. A Review of Voxel-Based Computerized Ionospheric Tomography with GNSS Ground Receivers. Remote Sensing. 2021; 13(17):3432. https://doi.org/10.3390/rs13173432
Chicago/Turabian StyleLu, Weijun, Guanyi Ma, and Qingtao Wan. 2021. "A Review of Voxel-Based Computerized Ionospheric Tomography with GNSS Ground Receivers" Remote Sensing 13, no. 17: 3432. https://doi.org/10.3390/rs13173432
APA StyleLu, W., Ma, G., & Wan, Q. (2021). A Review of Voxel-Based Computerized Ionospheric Tomography with GNSS Ground Receivers. Remote Sensing, 13(17), 3432. https://doi.org/10.3390/rs13173432







