New Channel Errors Estimation Method for Multichannel SAR Based on Virtual Calibration Source
Abstract
:1. Introduction
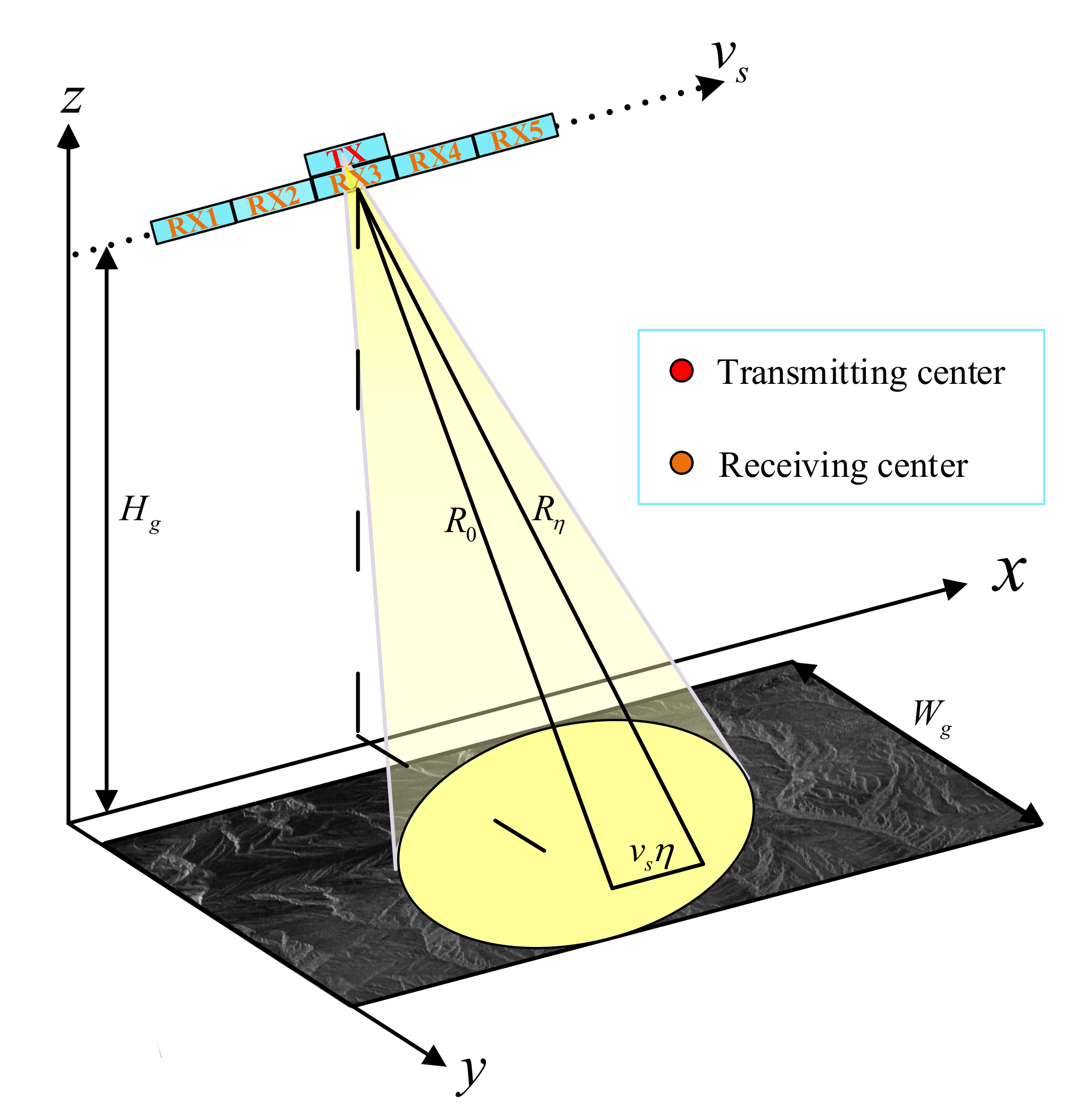
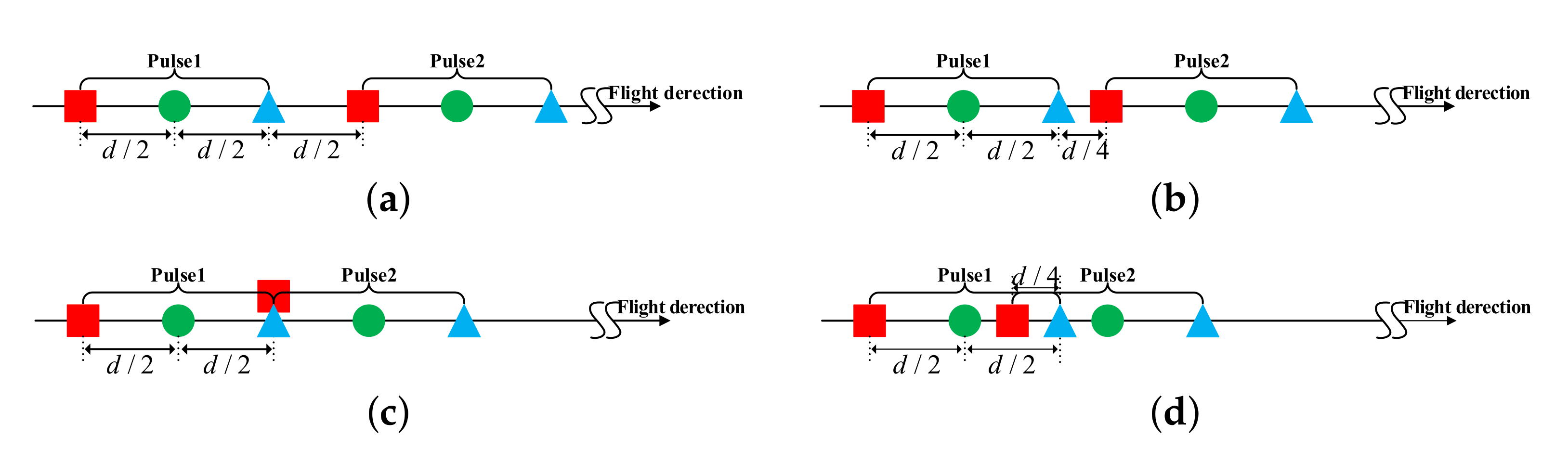
2. Error Model of Multichannel SAR Signal
3. Proposed Algorithm
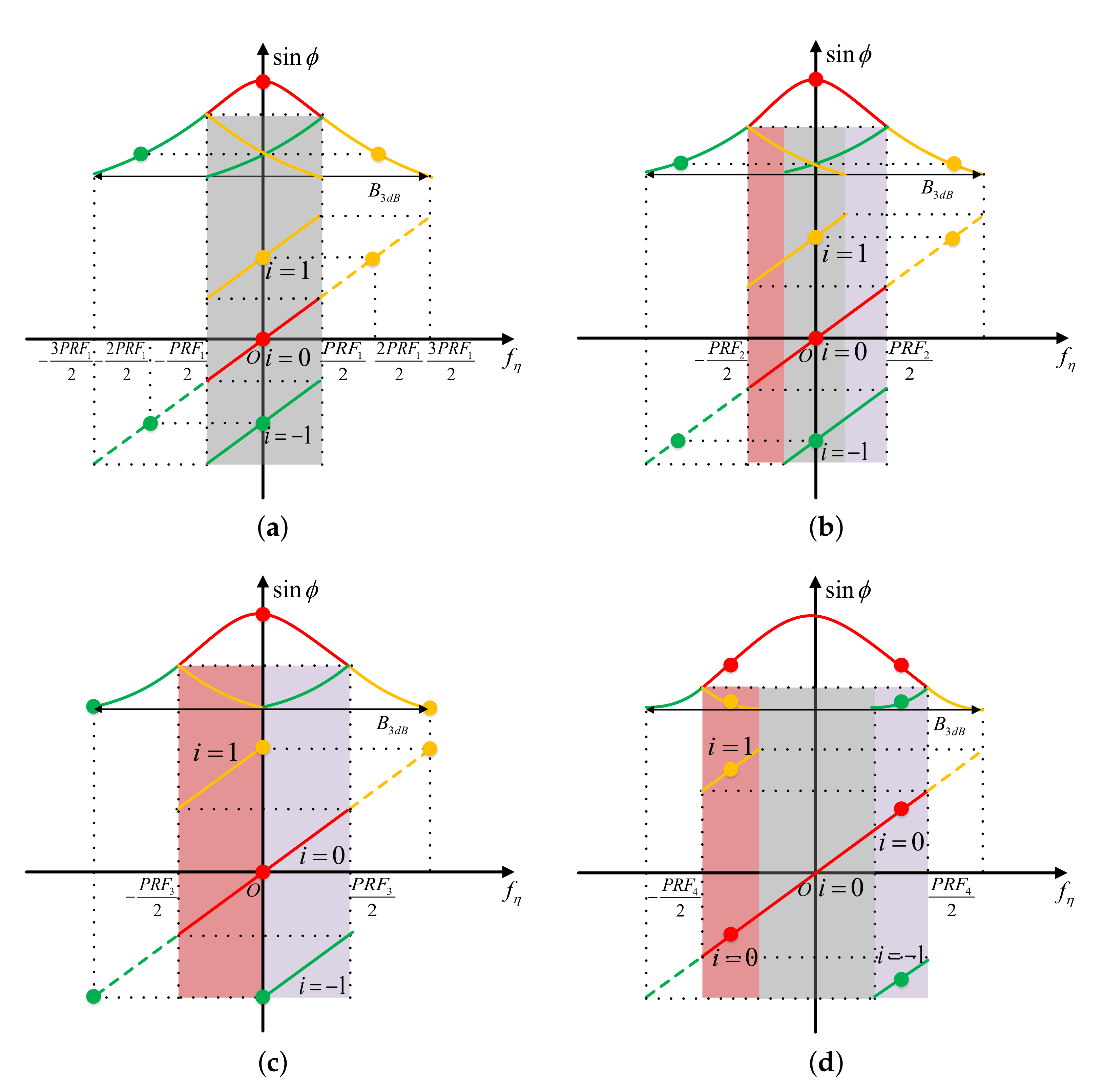
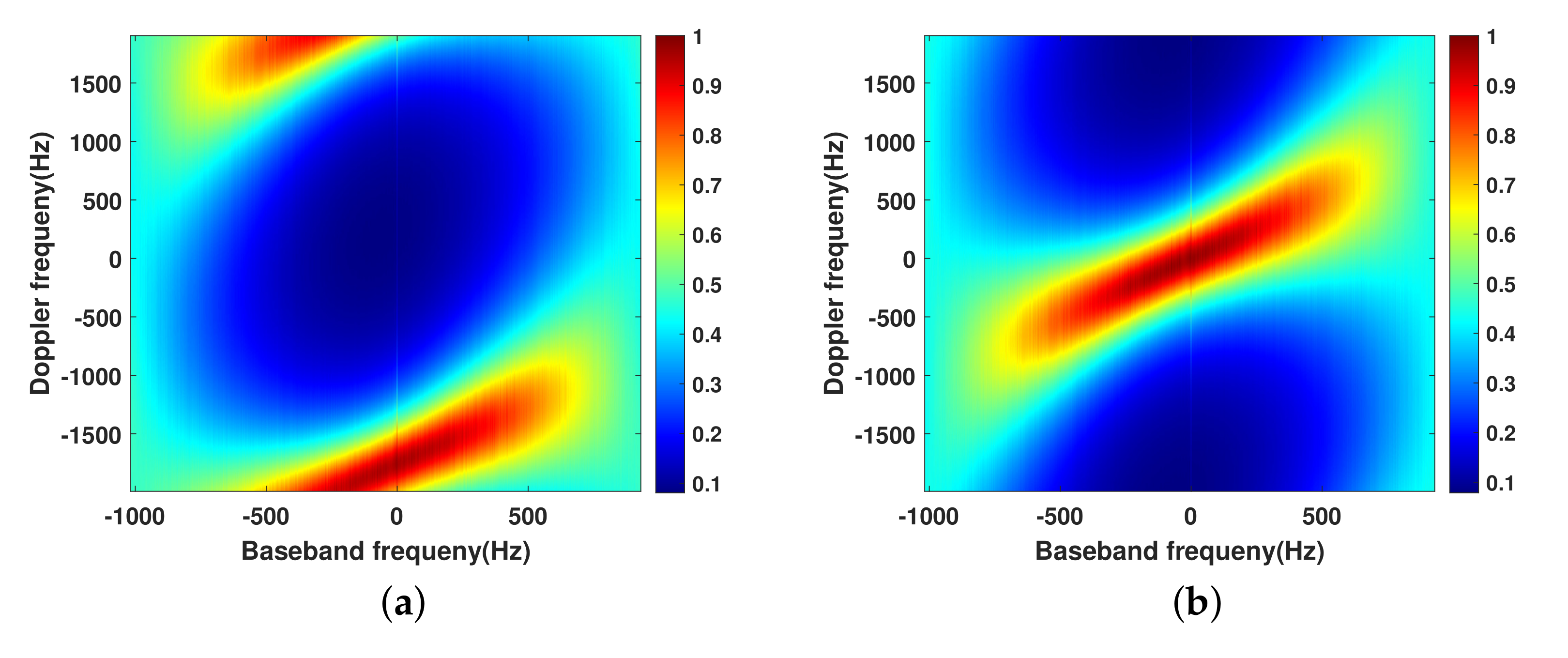
3.1. The Doppler Spectrum of Ground Echoes
3.2. Channel Errors Calibration
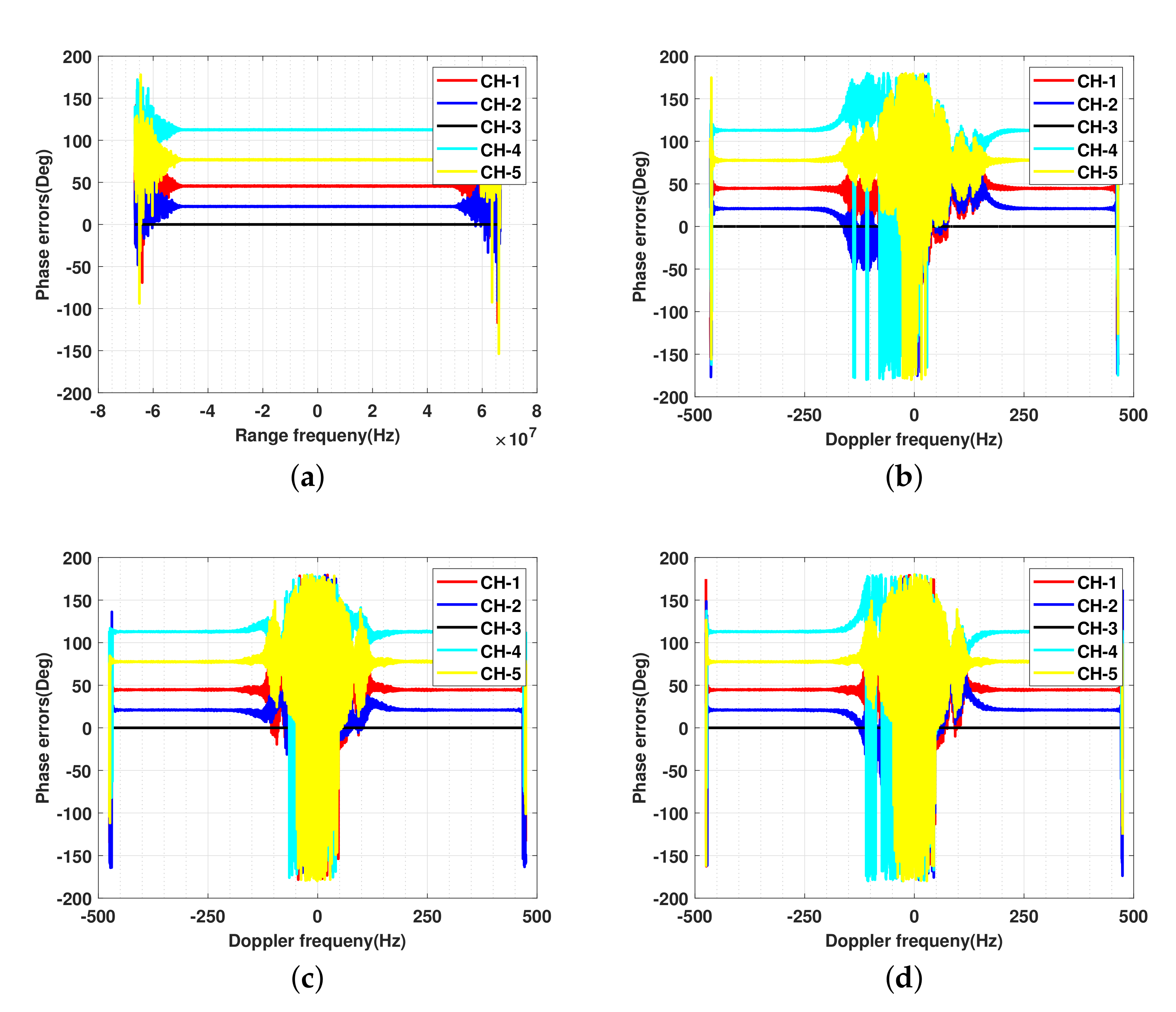
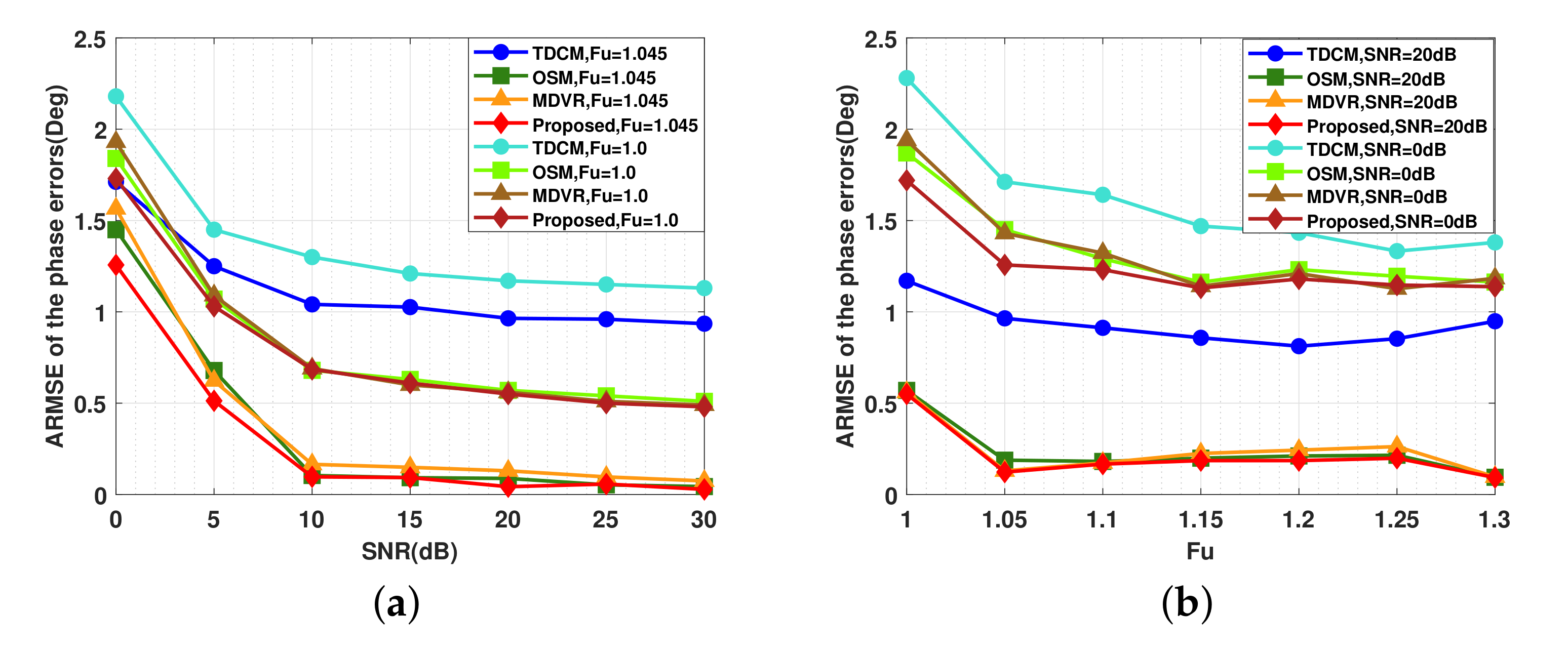
4. Experiments
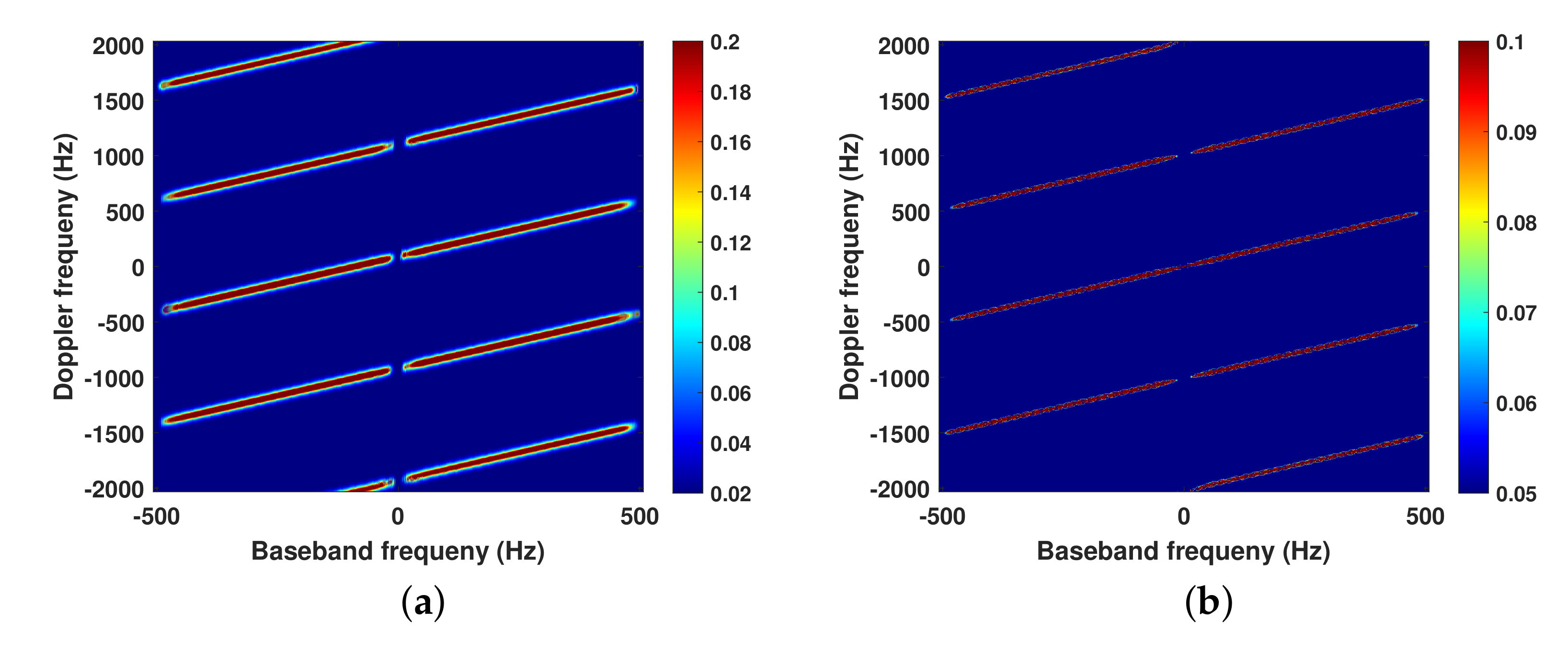
4.1. Simulated Data
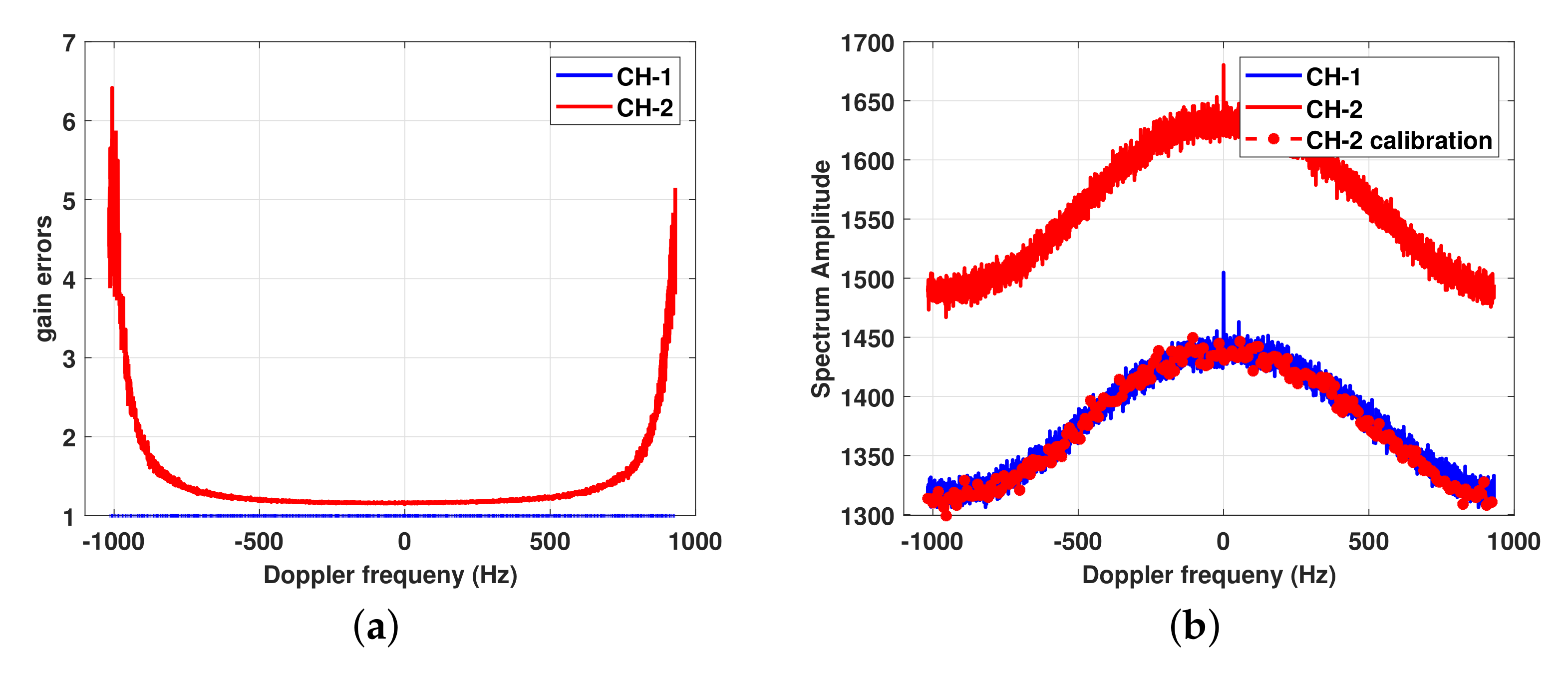
4.2. Real Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MMSE | Minimum mean square error |
| ARMSE | Average root mean square error |
| TDCM | Time-domain correlation method |
| OSM | Orthogonal subspace method |
| MVDR | minimum variance distortionless response |
Appendix A
References
- Krieger, G.; Gebert, N.; Moreira, A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling. IEEE Geosci. Remote Sens. Lett. 2004, 1, 260–264. [Google Scholar] [CrossRef] [Green Version]
- Gebert, N.; Krieger, G.; Moreira, A. Digital beamforming on receive: Techniques and optimization strategies for high-resolution wide-swath SAR imaging. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 564–592. [Google Scholar] [CrossRef] [Green Version]
- Krieger, G.; Gebert, N.; Moreira, A. SAR signal reconstruction from non-uniform displaced phase centre sampling. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2004), Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1763–1766. [Google Scholar]
- Li, Z.; Wang, H.; Su, T.; Bao, Z. Generation of wide-swath and high-resolution SAR images from multichannel small spaceborne SAR systems. IEEE Geosci. Remote Sens. Lett. 2005, 2, 82–86. [Google Scholar] [CrossRef]
- Kim, J.H.; Younis, M.; Prats-Iraola, P.; Gabele, M.; Krieger, G. First spaceborne demonstration of digital beamforming for azimuth ambiguity suppression. IEEE Trans. Geosci. Remote Sens. 2012, 51, 579–590. [Google Scholar] [CrossRef] [Green Version]
- Renyuan, C.; Kai, J.; Yanmei, Y.; Changyao, Z. High resolution dual channel receiving SAR compensation technique. In Proceedings of the 2007 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 5–9 November 2007; pp. 713–717. [Google Scholar]
- Feng, J.; Gao, C.; Zhang, Y.; Wang, R. Phase mismatch calibration of the multichannel SAR based on azimuth cross correlation. IEEE Geosci. Remote Sens. Lett. 2012, 10, 903–907. [Google Scholar] [CrossRef]
- Fang, C.; Liu, Y.; Suo, Z.; Li, Z.; Chen, J. Improved channel mismatch estimation for multi-channel HRWS SAR based on azimuth cross-correlation. Electron. Lett. 2018, 54, 235–237. [Google Scholar] [CrossRef]
- Shang, M.; Qiu, X.; Han, B.; Ding, C.; Hu, Y. Channel imbalances and along-track baseline estimation for the GF-3 azimuth multichannel mode. Remote Sens. 2019, 11, 1297. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Bao, Z.; Wang, H.; Liao, G. Performance improvement for constellation SAR using signal processing techniques. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 436–452. [Google Scholar]
- Zhang, L.; Xing, M.D.; Qiu, C.W.; Bao, Z. Adaptive two-step calibration for high-resolution and wide-swath SAR imaging. IET Radar Sonar Navig. 2010, 4, 548–559. [Google Scholar] [CrossRef]
- Guo, X.; Gao, Y.; Wang, K.; Liu, X. Improved channel error calibration algorithm for azimuth multichannel SAR systems. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1022–1026. [Google Scholar] [CrossRef]
- Yang, T.; Li, Z.; Liu, Y.; Bao, Z. Channel error estimation methods for multichannel SAR systems in azimuth. IEEE Geosci. Remote Sens. Lett. 2012, 10, 548–552. [Google Scholar] [CrossRef]
- Yang, T.; Li, Z.; Liu, Y.; Suo, Z.; Bao, Z. Channel error estimation methods for multi-channel HRWS SAR systems. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 4507–4510. [Google Scholar]
- Liu, A.; Liao, G.; Ma, L.; Xu, Q. An array error estimation method for constellation SAR systems. IEEE Geosci. Remote Sens. Lett. 2010, 7, 731–735. [Google Scholar] [CrossRef]
- Xu, Q.; Liao, G.; Liu, A.; Zhang, J. Self-calibration method without joint iteration for distributed small satellite SAR systems. EURASIP J. Adv. Signal Process. 2013, 2013, 31. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Wang, R.; Deng, Y.; Yu, W.; Fan, H.; Liang, D.; Zhao, Q. A novel approach to Doppler centroid and channel errors estimation in azimuth multi-channel SAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8430–8444. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, Y.; Liu, X. Robust channel phase error calibration algorithm for multichannel high-resolution and wide-swath SAR imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 649–653. [Google Scholar] [CrossRef]
- Huang, H.; Huang, P.; Liu, X.; Xia, X.G.; Deng, Y.; Fan, H.; Liao, G. A Novel Channel Errors Calibration Algorithm for Multichannel High-Resolution and Wide-Swath SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Zuo, S.S.; Xing, M.; Xia, X.G.; Sun, G.C. Improved signal reconstruction algorithm for multichannel SAR based on the Doppler spectrum estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 1425–1442. [Google Scholar] [CrossRef]
- Moreira, A.; Mittermayer, J.; Scheiber, R. Extended chirp scaling algorithm for air-and spaceborne SAR data processing in stripmap and ScanSAR imaging modes. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1123–1136. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR processing using chirp scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Liang, D.; Wang, R.; Deng, Y.; Fan, H.; Zhang, H.; Zhang, L.; Wang, W.; Zhou, Y. A Channel Calibration Method Based on Weighted Backprojection Algorithm for Multichannel SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1254–1258. [Google Scholar] [CrossRef]
- Gao, H.; Chen, J.; Liu, W.; Li, C.; Yang, W. Phase Inconsistency Error Compensation for Multichannel Spaceborne SAR Based on the Rotation-Invariant Property. IEEE Geosci. Remote Sens. Lett. 2020, 18, 301–305. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I.; Klare, J.; Gierull, C.H. MIMO SAR processing for multichannel high-resolution wide-swath radars. IEEE Trans. Geosci. Remote Sens. 2013, 52, 5034–5055. [Google Scholar] [CrossRef]
- Jin, T.; Qiu, X.; Hu, D.; Ding, C. An ML-based radial velocity estimation algorithm for moving targets in spaceborne high-resolution and wide-swath SAR systems. Remote Sens. 2017, 9, 404. [Google Scholar] [CrossRef] [Green Version]
- See, C.M.S.; Gershman, A.B. Direction-of-arrival estimation in partly calibrated subarray-based sensor arrays. IEEE Trans. Signal Process. 2004, 52, 329–338. [Google Scholar] [CrossRef]
- Liao, B.; Chan, S.C. Direction finding with partly calibrated uniform linear arrays. IEEE Trans. Antennas Propag. 2011, 60, 922–929. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Li, Z.F.; Yang, T.L.; Bao, Z. An adaptively weighted least square estimation method of channel mismatches in phase for multichannel SAR systems in azimuth. IEEE Geosci. Remote Sens. Lett. 2013, 11, 439–443. [Google Scholar] [CrossRef]



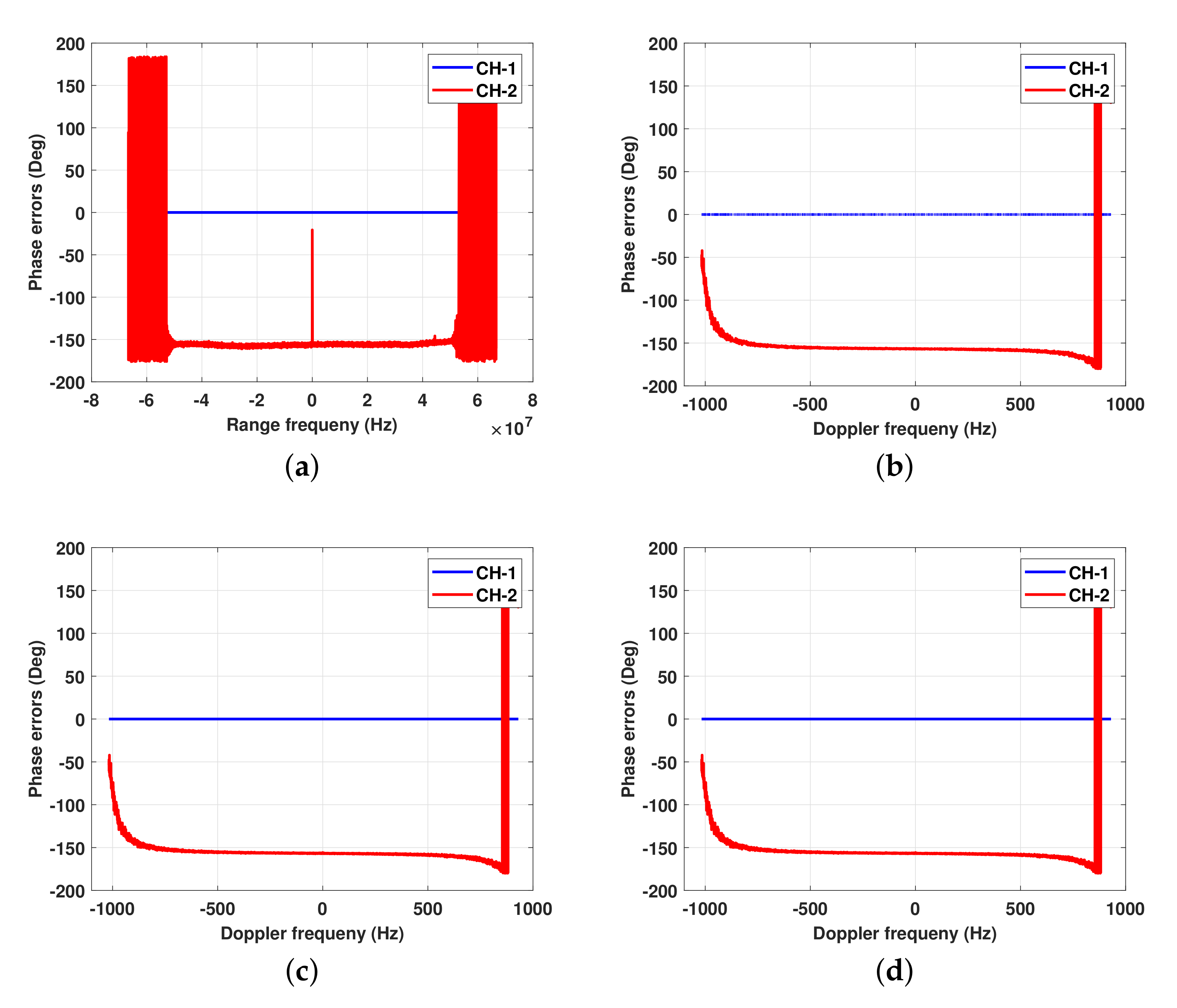
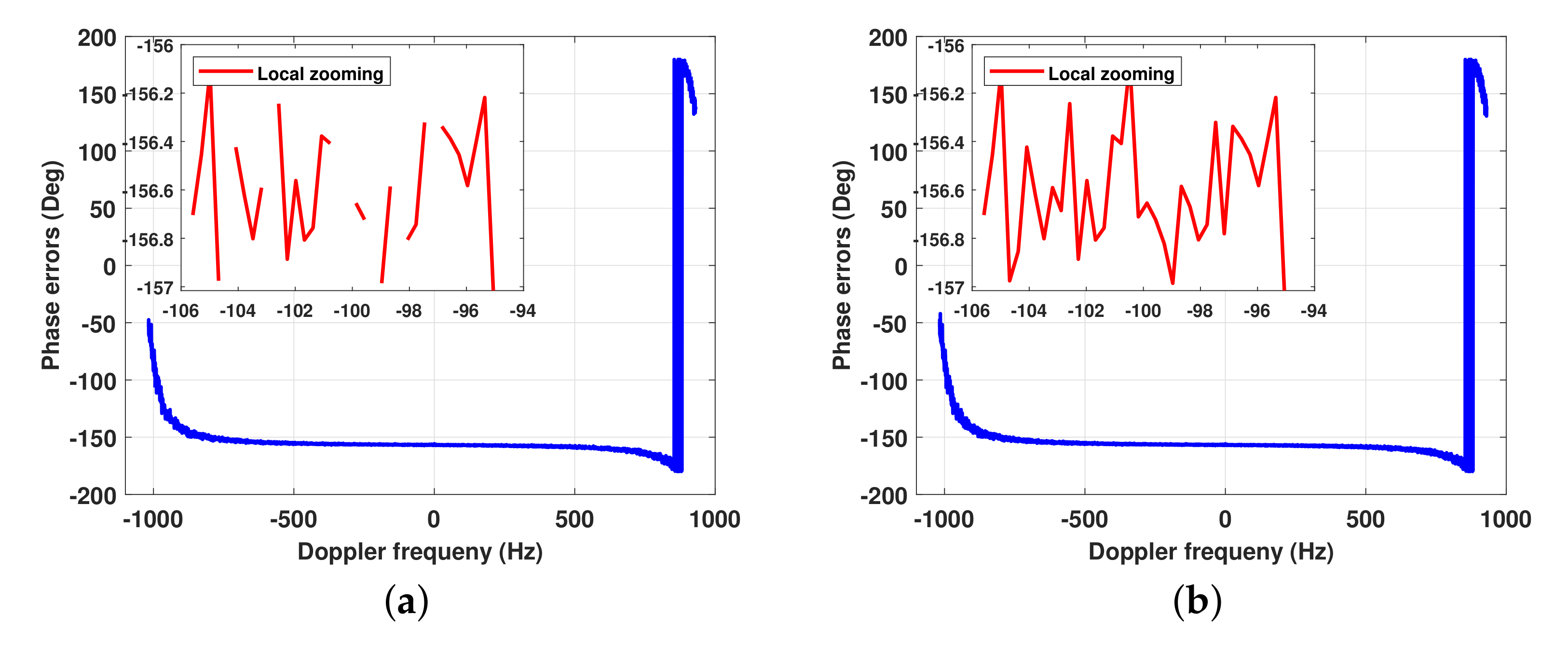

| Parameter | Symbol | Value |
|---|---|---|
| Wavelength | 0.055517 m | |
| PRF | 1015 Hz | |
| Sampling rate | 133.33 MHz | |
| Signal bandwidth | 100 MHz | |
| Pulse duration | 54.99 s | |
| Platform velocity | 7614 m/s | |
| Look-angle | 35.41 | |
| Channel number | M | 5 |
| Adjacent Channel Interval | d | 3.75 m |
| Channel Number | Real Phase Error | SNR | TDCM | OSM | SSCM | MVDR | Proposed Method |
|---|---|---|---|---|---|---|---|
| Channel 1 | 45° | 10 dB | 45.5871° | 44.4693° | 44.5184° | 44.5157° | 44.7129° |
| 20 dB | 45.6034° | 44.7021° | 44.6971° | 44.7012° | 44.7366° | ||
| 30 dB | 45.6128° | 44.7176° | 44.7036° | 44.7157° | 44.7483° | ||
| Channel 2 | 21° | 10 dB | 21.3586° | 20.6864° | 20.7473° | 21.2746° | 20.8157° |
| 20 dB | 21.3680° | 20.9492° | 20.9427° | 21.1582° | 20.9543° | ||
| 30 dB | 21.3738° | 21.0033° | 20.9802° | 20.9665° | 20.9856° | ||
| Channel 3 | 0° | 10 dB | 0.0° | 0.0° | 0.0° | 0.0° | 0.0° |
| 20 dB | 0.0° | 0.0° | 0.0° | 0.0° | 0.0° | ||
| 30 dB | 0.0° | 0.0° | 0.0° | 0.0° | 0.0° | ||
| Channel 4 | 113° | 10 dB | 112.4815° | 112.6456° | 112.7573° | 111.3848° | 112.8615° |
| 20 dB | 112.4831° | 112.9002° | 112.8991° | 112.7977° | 112.9169° | ||
| 30 dB | 112.4858° | 113.0129° | 112.9798° | 112.8825° | 112.9813° | ||
| Channel 5 | 78° | 10 dB | 76.8194° | 77.3443° | 77.4197° | 77.4258° | 77.5375° |
| 20 dB | 76.8350° | 77.6058° | 77.6123° | 77.6077° | 77.6999° | ||
| 30 dB | 76.8416° | 77.6395° | 77.6314° | 77.6425° | 77.7244° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Fu, X.; Lv, X. New Channel Errors Estimation Method for Multichannel SAR Based on Virtual Calibration Source. Remote Sens. 2021, 13, 3625. https://doi.org/10.3390/rs13183625
Liang Z, Fu X, Lv X. New Channel Errors Estimation Method for Multichannel SAR Based on Virtual Calibration Source. Remote Sensing. 2021; 13(18):3625. https://doi.org/10.3390/rs13183625
Chicago/Turabian StyleLiang, Zhen, Xikai Fu, and Xiaolei Lv. 2021. "New Channel Errors Estimation Method for Multichannel SAR Based on Virtual Calibration Source" Remote Sensing 13, no. 18: 3625. https://doi.org/10.3390/rs13183625
APA StyleLiang, Z., Fu, X., & Lv, X. (2021). New Channel Errors Estimation Method for Multichannel SAR Based on Virtual Calibration Source. Remote Sensing, 13(18), 3625. https://doi.org/10.3390/rs13183625






