Simultaneous Radio Occultation Predictions for Inter-Satellite Comparison of Bending Angle Profiles from COSMIC-2 and GeoOptics

Abstract

The Global Navigation Satellite System (GNSS) radio occultation (RO) is a remote sensing technique that uses International System of Units (SI) traceable GNSS signals for atmospheric limb soundings. The RO bending angle/sounding profiles are needed for assimilation in Numerical Weather Prediction (NWP) models, weather, climate, and space weather applications. Evaluating these RO data to ensure the high data quality for these applications is becoming more and more critical. This study presents a method for predicting radio occultation events, from which simultaneous radio occultation (SRO) for a pair of low-Earth-orbit (LEO) satellites on the limb to the same GNSS satellite can be obtained. The SRO method complements the Simultaneous Nadir Overpass (SNO) method (for nadir viewing satellite instruments), which has been widely used to inter-calibrate LEO to LEO and LEO to geosynchronous-equatorial-orbit (GEO) satellites. Unlike the SNO method, the SRO method involves three satellites: a GNSS and two LEO satellites with RO receivers. The SRO method allows for the direct comparison of bending angles when the simultaneous RO measurements for two LEO satellites receiving the same GNSS signal pass through approximately the same atmosphere within minutes in time and within less than 200 km of distance from each other. The prediction method can also be applied to radiosonde overpass prediction, and coordinate radiosonde launches for inter-comparisons between RO and radiosonde profiles. The main advantage of the SRO comparisons of bending angles is the significantly reduced uncertainties due to the much shorter time and smaller atmospheric path differences than traditional RO comparisons. To demonstrate the usefulness of this method, we present a comparison of the Constellation Observing System for Meteorology, Ionosphere, and Climate-2 (COSMIC-2) and GeoOpitcs RO profiles using SRO data for two time periods: Commercial Weather Data (CWD) data delivery order-1 (DO-1): 15 December 2020–15 January 2021 and CWD DO-2: 17 March 2021–31 August 2021. The results show good agreement in the bending angles between the COSMIC-2 RO measurements and those from GeoOptics, although systematic biases are also found in the inter-comparisons. Instrument and processing algorithm performances for the signal-to-noise ratio (SNR), penetration height, and bending angle retrieval uncertainty are also characterized. Given the efficiency of this method and the many RO measurements that are publicly and commercially available as well as the expansion of receiver capabilities to all GNSS systems, it is expected that this method can be used to validate/inter-calibrate GNSS RO measurements from different missions.

1. Introduction

The Global Navigation Satellite System (GNSS) radio occultation (RO) is a remote sensing technique that uses International System of Units (SI) traceable GNSS signals for atmospheric limb soundings. The RO receivers onboard the low-Earth-orbit (LEO) satellites receive occulted signals from GNSS satellites, which are delayed and bent due to atmospheric refraction. The observed phase delays are converted to profiles of bending angles and refractivity, which are then used to invert the temperature and water vapor in the troposphere, the temperature in the stratosphere, and the electron density in the ionosphere [1,2,3]. RO is the first technique to provide high accuracy, precision, vertical resolution, and all-weather limb-sounding measurements [4,5]. These GNSS-RO measurements are complementary to the ground and space-based nadir viewing instruments and are very important for numerical weather prediction (NWP) [6,7,8,9,10,11], meteorology, and climate applications [12,13,14,15,16,17,18,19,20].

RO measurement has been ranked as one of the top five observing systems for reducing forecast errors in NWP [10] and for complementing infrared and microwave soundings by reducing the need for bias corrections in models while providing all-weather capabilities and superior vertical resolution, particularly over data-sparse regions such as oceans, tropics, and polar regions. There are currently about 8000 non-commercial RO soundings that are available per day to provide operational input to the NWP model. The Constellation Observing System for Meteorology, Ionosphere, and Climate-2 (COSMIC-2) mission onboard Formosa Satellite Mission 7 provides about 5000 sounds per day covered within (45° S, 45° N). Other missions, including Challenging Minisatellite Payload (CHAMP), Korea Multi-Purpose Satellite-5 (KOMPSAT-5), and Meteorological Operational satellite (MetOp) series -A/-B/-C GNSS Receiver for Atmospheric Sounding (GRAS), provide the rest. A minimum of 20,000 globally distributed soundings per day is recommended for adequate coverage [10].

To mitigate the RO sounding shortage issue in NWP, through Commercial Weather Data for the RO (CWD RO) program, NOAA is buying high-quality commercial RO sounding data from private companies. NOAA recently received one month’s worth of data (from 15 December 2020 to 14 January 2021) from GeoOptics and Spire RO, receiving ~1000 occultations per day for Delivery Order-1 (DO-1) and ~1300 occultations per day for the period from March to September 2021 from GeoOptics for DO-2. Similar to COSMIC-2, these RO data are generated by the University Corporation for Atmospheric Research (UCAR) operational data processing center and are distributed by the COSMIC Data Analysis and Archive Center (CDAAC).

In the era of GNSS, the new generation of LEO RO satellites, e.g., COSMIC-2, receive navigation signals in multiple bands from multiple GNSS satellites, such as from the US Global Positioning System (GPS), the Russian GLONASS (GLObal NAvigation Satellite System), and the European Galileo system. Such design aims at enhancing RO signal quality and increasing the number of successful RO retrieval. In the coming five to ten years, it is also expected that there will be a growing number of RO sensors under the initiative of exploring the usefulness of commercial Small Satellite-based RO data in NWP by NOAA’s CWD RO program. For example, we may expect close to a hundred or more GNSS RO and GNSS Reflectometry (GNSS-R) sensors in orbit with various GNSS RO signals from Galileo, the Chinese Beidou Navigation Satellite System (BDS), GLONASS, the Indian Regional Navigation Satellite System (IRNSS), the Japanese Quazi-Satellite System (QZSS), among others. The increasing number of RO sensors paired with augmented GNSS satellites calls for the quick inter-calibration, validation, and quality assurance of Small Satellite-based multi-RO sensors to ensure that these RO data are high quality for NWP data because they are used as anchor data without bias correction.

Developing an efficient RO limb sounding prediction algorithm can help (i) RO mission planning, (ii) the pre-scheduling of radiosonde launches at a specific site with collocated RO limb sounding to support inter-calibration between RO sensors and radiosonde [21,22], and (iii) inter-calibration among multiple RO sensors using simultaneous radio occultation (SRO), which extends the work of Cao et al. [23] by introducing RO prediction capabilities for SRO. Often, such kind of predictions requires an advanced time of two weeks to a month. On the other hand, these predictions face computational challenges. Using COSMIC-2 as an example, the prediction challenge is that six small satellites belonging to the COSMIC-2 constellation may have potential RO limb sounding opportunities with any of the 32 GPS satellites or any of the 24 GLONASS satellites at a given time. Such a combination provides RO limb sounding opportunities among more than 330 RO-GNSS pairs at a given time. Therefore, an efficient algorithm to predict RO limb sounding opportunities in terms of occurrence time and location for a given RO-GNSS pair will speed up the inter-calibration and quality assurance of the RO data retrieval.

This paper presents a method for predicting radio occultation events, from which simultaneous radio occultation from a pair of LEO satellites to the same GNSS satellite can then be obtained given the time and distance criteria. The SRO method complements the simultaneous nadir overpass (SNO) method (for nadir viewing infrared (IR) and microwave (MW) sounders) [24,25,26], which has been widely used to inter-calibrate LEO to LEO and LEO to geosynchronous-equatorial-orbit (GEO) satellites. It is well accepted in the World Meteorological Organization (WMO) Global Space-based Inter-Calibration System (GSICS) community as a standard method. Without this method, it would take much longer to find the matched pairs, given the large volume of satellite observation data for IR/MW sounders. The SNO method can efficiently provide the approximately matched times and locations and thus can significantly narrow the searched dataset.

Unlike the SNO method, the SRO method involves a GNSS and two LEO satellites with RO receivers. The SRO method allows for the direct comparison of the bending angles when simultaneous RO measurements for two LEO satellites receiving the same GNSS signal pass through approximately the same atmosphere within minutes in time and less than 200 km in the distance of each other [23]. Cao et al. [23] showed that the main advantage of SRO comparisons of bending angles is the significantly reduced uncertainties due to the much shorter time and atmospheric path differences than traditional RO comparisons. Unlike Cao et al. [23], who apply the brute-force search method directly to the observed RO data, we first obtain the potential SRO pairs from the predicted RO events using the prediction method presented here and then further match the prediction and observation data. To demonstrate the usefulness of the SRO method for inter-calibration among multiple RO sensors, we also present our comparison of the COSMIC-2 and the commercial GeoOpitcs RO bending angle (BA) profiles using SRO data from two time periods: CWD DO-1: 15 December 2020–15 January 2021 and CWD DO-2: 17 March 2021–31 August 2021.

This paper is organized as follows. In Section 2, the details of the method used to predict the radio occultation opportunities is given. Section 3 uses COSMIC-2 RO observations to validate the ground track, RO events number, and RO event distribution as a function of the antenna view angle. Section 4 presents the inter-satellites simultaneous RO bending angle profile comparison results between COSMIC-2 and GeoOptics. Section 5 provides the discussion. Finally, Section 6 summarizes our studies.

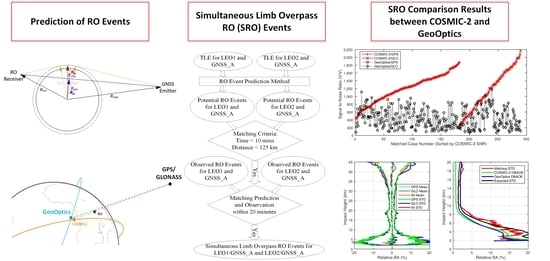
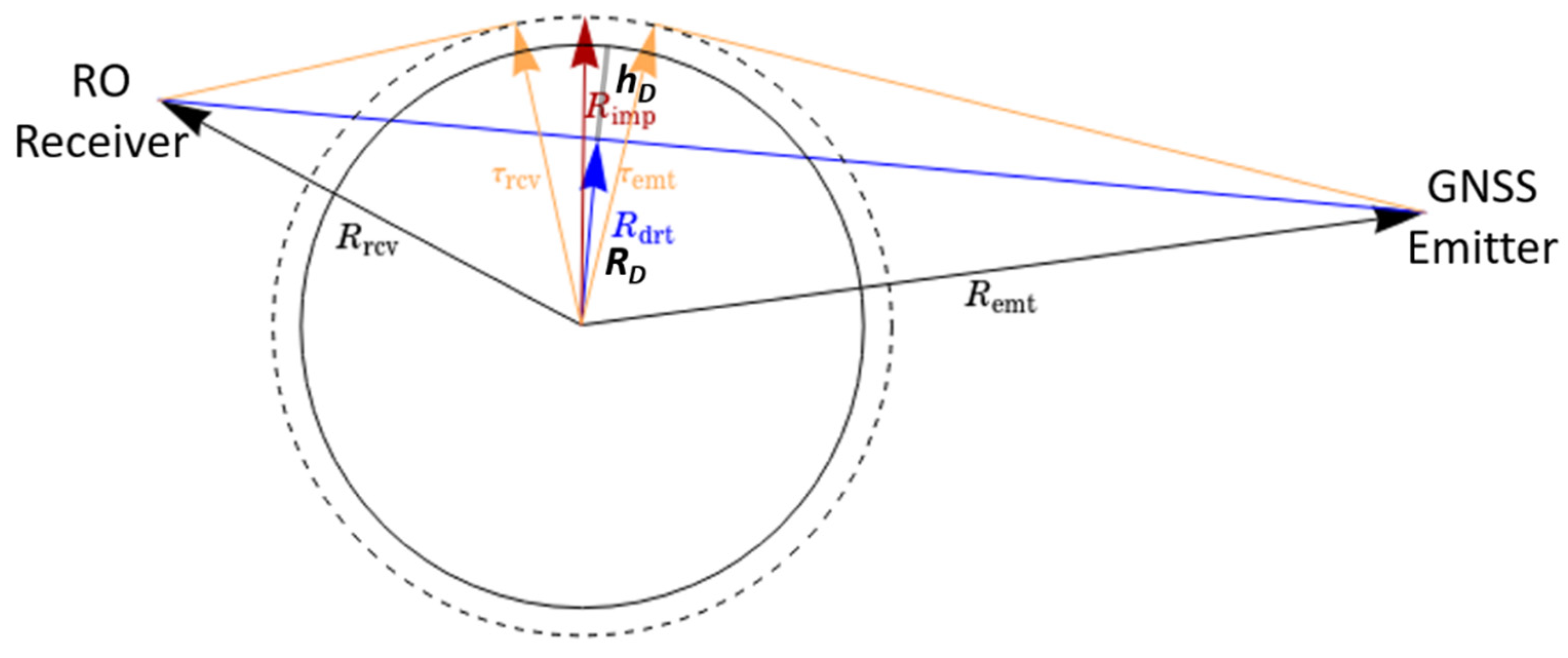
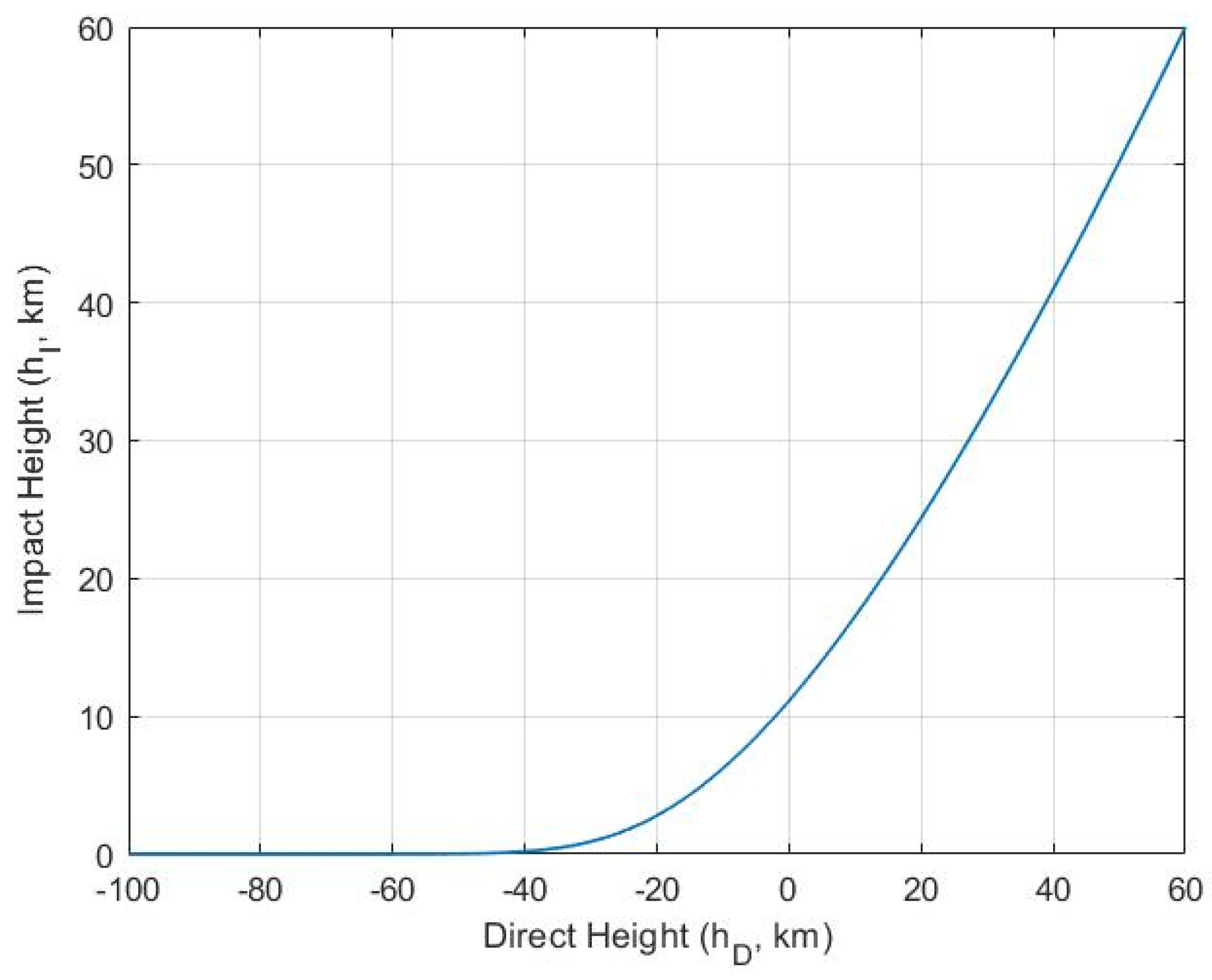
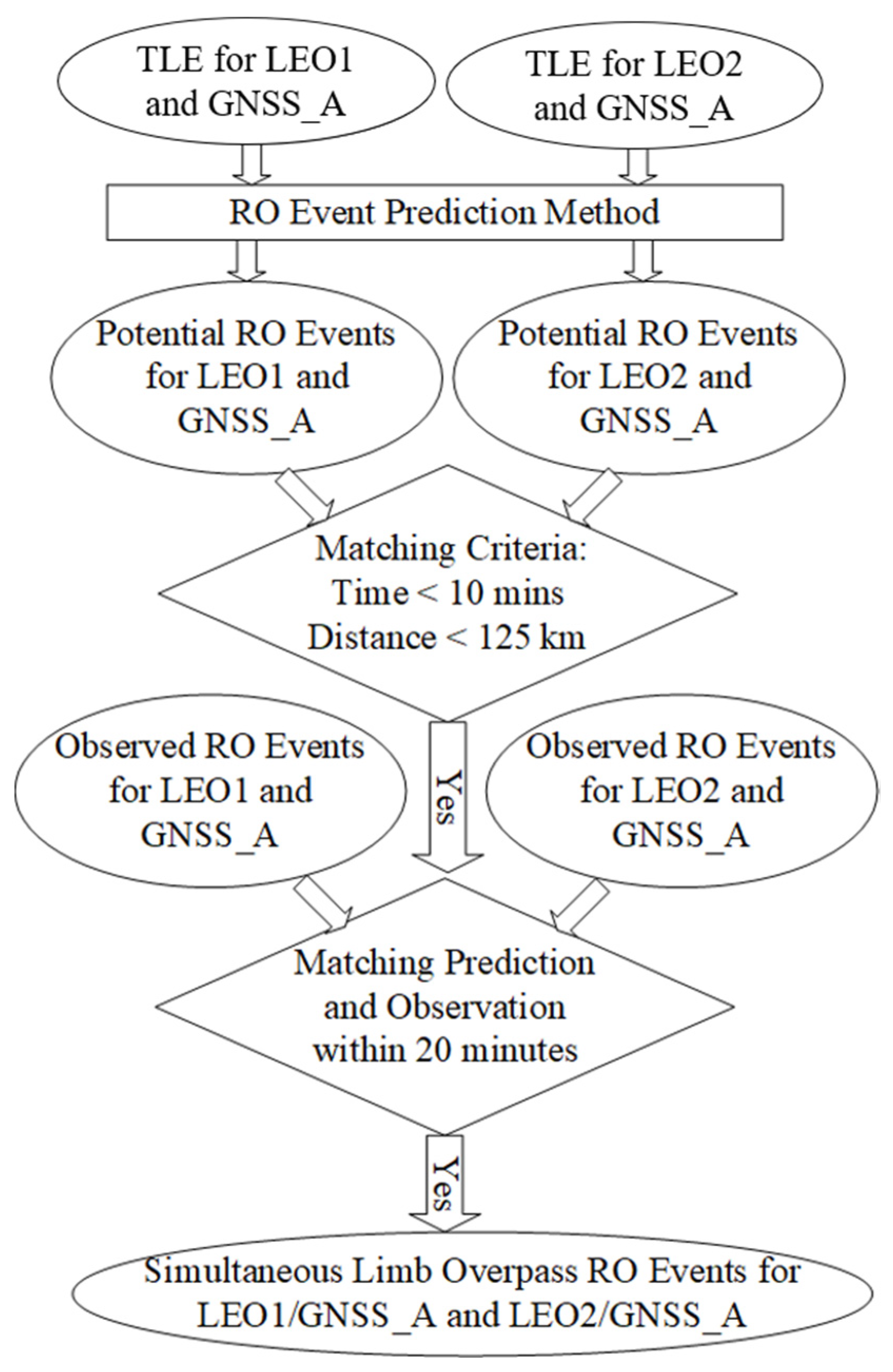
2. A Method to Predict Radio Occultation Event

This section presents an efficient method for predicting RO limb sounding events between the GNSS transmitter and LEO RO receivers. The Simplified orbital Perturbation Model (SGP4, [27]) with Two-Line Element (TLE) input from the North American Aerospace Defense Command (NORAD) (routinely available from https://celestrak.com/, accessed on 10 September 2021) have been used to predict the real-time positions of LEO or GNSS satellites. A TLE encodes a list of orbital elements of an Earth-orbiting object such as a LEO or GNSS satellite at a given time. Using SGP4, the state (position and velocity) of the satellite at any time in the past or future can be estimated. The occultation events can be expected based on the predicted locations of a given pair of LEO and GNSS satellites. It is noted that the predicted orbital velocity vector of a LEO satellite with a RO receiver (hereafter LEO/RO satellite) can help differentiate the rising or setting of RO limb sounding and can later be used the determine the forward and backward RO antenna orientation and the RO occurrence as a function of the RO antenna beam lobe angle.

Figure 1 shows an example of a RO limb sounding configuration at a given time instant t. The positions of the LEO and GNSS satellites, e.g., $R_{\mathrm{rcv}}$ and $R_{\mathrm{emt}}$, respectively, are predicted using the SGP4 model with the satellite TLE data as the inputs. Under the assumption of spherical symmetry, the ray path of the refracted GNSS signal can be approximated as bending over a circle with a radius $R_I$ in the plane formed by three points: LEO-Earth Center-GNSS. The vector connecting the inflection point of the ray path and the Earth’s center is defined as the impact height vector, i.e., $R_{\mathrm{imp}}$. Our goal is to estimate the location of the intersection point between the impact height vector $R_{\mathrm{imp}}$ and the Earth’s surface at the given time instant t for a valid RO limb sounding opportunity. Here, $\left|\right|R_{\mathrm{imp}}\left|\right|=R_I$ is the length of the impact height vector. In Figure 1, we identify the direct height vector $R_{\mathrm{drt}}$, which is perpendicular to the straight line connecting $R_{\mathrm{rcv}}$ and $R_{\mathrm{emt}}$. Its length is defined as $\left|\right|R_{\mathrm{drt}}\left|\right|=R_D$. Furthermore, we can determine $h_D$ and $h_I$ using the following equations:

$$\left|\right|R_{\mathrm{drt}}\left|\right|=R_E+h_D=R_D$$

(1)

$$\left|\right|R_{\mathrm{imp}}\left|\right|=\left|\right|{\tau }_{\mathrm{rcv}}\left|\right|=\left|\right|{\tau }_{\mathrm{emt}}\left|\right|=R_E+h_I=R_I,$$

(2)

where $R_E$ is the Earth’s radius, $h_D$ is the direct height of the straight line between the GNSS and LEO satellite pair, which can typically vary from −500 km to ~80 km, and $h_I$ is the impact height, which can vary from >0 to ~80 km. In Figure 1, we also define ${\tau }_{\mathrm{emt}}$ and ${\tau }_{\mathrm{rcv}}$, which are the vectors between the Earth’s center and the tangent points of the RO ray paths on the emitter (GNSS) and receiver (RO) side, respectively. These vectors satisfy the following geometric relations under the spherical symmetry approximation:

$${\tau }_{\mathrm{rcv}}\perp \left(R_{\mathrm{rcv}}-{\tau }_{\mathrm{rcv}}\right)$$

(3)

$${\tau }_{\mathrm{emt}}\perp \left(R_{\mathrm{emt}}-{\tau }_{\mathrm{emt}}\right)$$

(4)

$$R_{\mathrm{imp}}\left|\right|\left({\tau }_{\mathrm{emt}}+{\tau }_{\mathrm{rcv}}\right)$$

(5)

If we can establish an estimated functional relationship between $h_I$ and $h_D$, i.e., $h_I=f\left(h_D\right)$, then we can obtain $R_I$ from $R_D$, which can be calculated with the following equation.

$$R_D=\left|\right|R_{\mathrm{rcv}}\left|\right|\times \left|\right|R_{\mathrm{emt}}\left|\right|/\left|\right|R_{\mathrm{rcv}}-R_{\mathrm{emt}}\left|\right|$$

(6)

Let ${\tau }_{\mathrm{rcv}}={\alpha }_{\mathrm{rcv}}{R}_{\mathrm{rcv}}+{\beta }_{\mathrm{rcv}}{R}_{\mathrm{emt}}$. Then, we can solve ${\alpha }_{\mathrm{rcv}}$ and ${\beta }_{\mathrm{rcv}}$ (with limitations on ${\alpha }_{\mathrm{rcv}}$> 0 and ${\beta }_{\mathrm{rcv}}>0)$ by plugging ${\tau }_{\mathrm{rcv}}$ into Equations (2) and (3):

$${\alpha }_{\mathrm{rcv}}^2{R}_{\mathrm{rcv}}·R_{\mathrm{rcv}}+2{\alpha }_{\mathrm{rcv}}{\beta }_{\mathrm{rcv}}{R}_{\mathrm{rcv}}·R_{\mathrm{emt}}+{\beta }_{\mathrm{rcv}}^2{R}_{\mathrm{emt}}·R_{\mathrm{emt}}=R_I^2$$

(7)

$${\alpha }_{\mathrm{rcv}}{R}_{\mathrm{rcv}}·R_{\mathrm{rcv}}+{\beta }_{\mathrm{rcv}}{R}_{\mathrm{emt}}·R_{\mathrm{rcv}}=R_I^2$$

(8)

By solving Equations (7) and (8), we can obtain

$${\beta }_{\mathrm{rcv}}=\sqrt{\frac{\left(R_{\mathrm{rcv}}·R_{\mathrm{rcv}}\right)R_I^2-R_I^4}{\left(R_{\mathrm{rcv}}·R_{\mathrm{rcv}}\right)\left(R_{\mathrm{emt}}·R_{\mathrm{emt}}\right)-{\left(R_{\mathrm{rcv}}·R_{\mathrm{emt}}\right)}^2}}$$

(9)

where the negative root is the tangent line on the opposite side of the Earth and should be neglected. From Equations (8) and (9), we can calculate ${\alpha }_{\mathrm{rcv}}$ as

$${\alpha }_{\mathrm{rcv}}=(R_I^2-{\beta }_{\mathrm{rcv}}{R}_{\mathrm{emt}}·R_{\mathrm{rcv}})/(R_{\mathrm{rcv}}·R_{\mathrm{rcv}})$$

(10)

The calculation of ${\tau }_{\mathrm{emt}}={\alpha }_{\mathrm{emt}}{R}_{\mathrm{rcv}}+{\beta }_{\mathrm{emt}}{R}_{\mathrm{emt}}$ is similar to ${\tau }_{\mathrm{rcv}}$, and we can derive ${\alpha }_{\mathrm{emt}}$ and ${\beta }_{\mathrm{emt}}$ from Equations (1) and (4) as

$${\alpha }_{\mathrm{emt}}=\sqrt{\frac{\left(R_{\mathrm{emt}}·R_{\mathrm{emt}}\right)R_I^2-R_I^4}{\left(R_{\mathrm{emt}}·R_{\mathrm{emt}}\right)\left(R_{\mathrm{rcv}}·R_{\mathrm{rcv}}\right)-{\left(R_{\mathrm{emt}}·R_{\mathrm{rcv}}\right)}^2}}$$

(11)

$${\beta }_{\mathrm{emt}}=(R_I^2-{\alpha }_{\mathrm{emt}}{R}_{\mathrm{rcv}}·R_{\mathrm{emt}})/(R_{\mathrm{emt}}·R_{\mathrm{emt}}).$$

(12)

We can then obtain $R_{\mathrm{imp}}$ from Equation (5)

$$R_{\mathrm{imp}}=c\left({\tau }_{\mathrm{emt}}+{\tau }_{\mathrm{rcv}}\right)$$

(13)

where c is the renormalization factor for $\left|\right|R_{\mathrm{imp}}\left|\right|=R_I$ to be satisfied. The longitude and latitude of the RO limb sounding profile location (defined at the intersection point of $R_{\mathrm{imp}}$ with the Earth’s surface) can be computed using existing ECEF (Earth-Centered Earth-Fixed) to the Latitude/Longitude/Altitude coordinate conversion function. In this paper, the estimated function $h_I=f\left(h_D\right)$ is fitted with a weighted monotonically increasing spline fitting function by using ($h_I$, $h_D$) data from COSMIC-2 RO observations. An example of such a fitted function is shown in Figure 2. The output from our prediction module is the predicted time and location (longitude and latitude) of the rising or setting RO limb sounding event. In addition, the information about the RO event view angles, azimuth angles, and the paired LEO/RO satellite name and GNSS (GPS or GLONASS) satellite ID are also recorded. The view angle is the angle between the GNSS-LEO vector and the LEO orbital velocity vector, and the azimuth angle is the angle between the occultation plane and the direction to true North. The RO limb-sounding event prediction data sets are further processed to support the ground site overpass and the SRO predictions.

It is noted that this prediction method can have residual errors due to several factors, such as the assumption of spherical symmetry using an empirical relation of $h_I=f\left(h_D\right)$, which can vary with location and atmospheric conditions, and the increasing error over time due to the use of TLE in predicting satellite orbital state vectors. As shown later, the residual error from prediction varies with latitudes. Over the low-latitude region, the prediction error is to the order of ~1 km. The most significant location deviation of the RO event path from the actual observation is to the order of ~10 km at high latitudes (~40 degrees). Given that the RO’s typical inter-comparison collocation criteria with other RO sensors or radiosonde launch sites are around 150 to 250 km, such prediction accuracy is sufficient for radiosonde launch planning and SRO matching. The computational time for the prediction of RO events between COMSIC-2 (6 satellites) with GPS (32 satellites) and GLONASS (24 satellites) over one month takes about 5 h on a DELL Precision Linux server. Such computational efficiency is adequate to meet the needs required to support the planning, inter-calibration, and quality monitoring of the growing number of RO sensors, primarily to support the anticipated growth in the commercial RO satellites used in the data assimilation of NWP under the NOAA CWD program.

3. Method Validation Using RO Observations

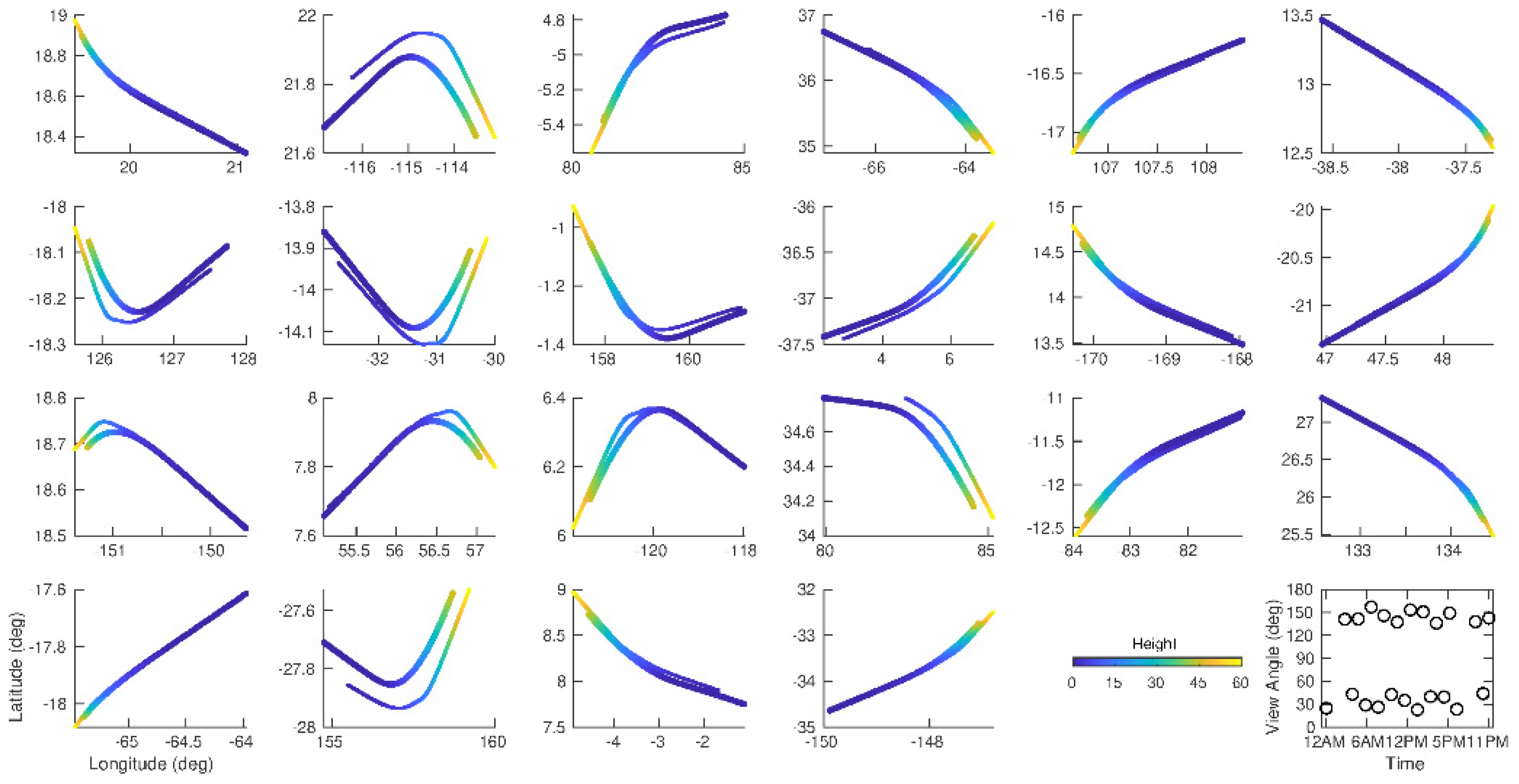
3.1. Ground Track Comparison (Latitude, Longitude, and Distance)

To validate the RO event prediction method, we use COSMIC-2 RO data as an example. All of the predicted RO pairs for each GNSS satellite and the LEO/RO receiver from COSMIC-2 flight modules 1–6 (named C2E1-6) are generated using the prediction method for 1 January 2021. There are about 23–28 potential RO pairs for each day for a GNSS satellite and COSMIC-2 receiver. Figure 3 shows the predicted (thick dashed line) and observed (thin dashed line) matched RO events with a time difference of less than 10 min ground track comparison for receiver the C2E1 and the emitter G01 for 1 January 2021. The scatter plots show the mean sea level height as a function of latitude and longitude, as indicated by the colored bar. There are 22 matched pairs between the prediction and observation, in which all of the observed RO events (from UCAR atmPrf) between C2E1 and G01 have matched pairs from the prediction. The antenna view angle, defined as the bent GNSS signal ray path and the COSMIC-2 orbital velocity vector was also plotted as a function of UTC for each RO event. The matching RO pairs are primarily consistent in latitude, longitude, and height. For a given height, the distance between the predicted and observed RO pairs are mostly within 15 km. Given the fact that typical co-located RO and radiosonde is within 150–250 km and within a 3-h time window (Sun et al., 2019; Shao et al., 2021), such a prediction accuracy is enough for SRO and coordinated radiosonde launching. One of the potential applications of this RO event prediction method is to coordinate the radiosonde launches at the WMO Global Climate Observing System (GCOS) Reference Upper-Air Network (GRUAN) sites with the predicted potential RO overpass for dedicated RO and radiosonde observation comparison.

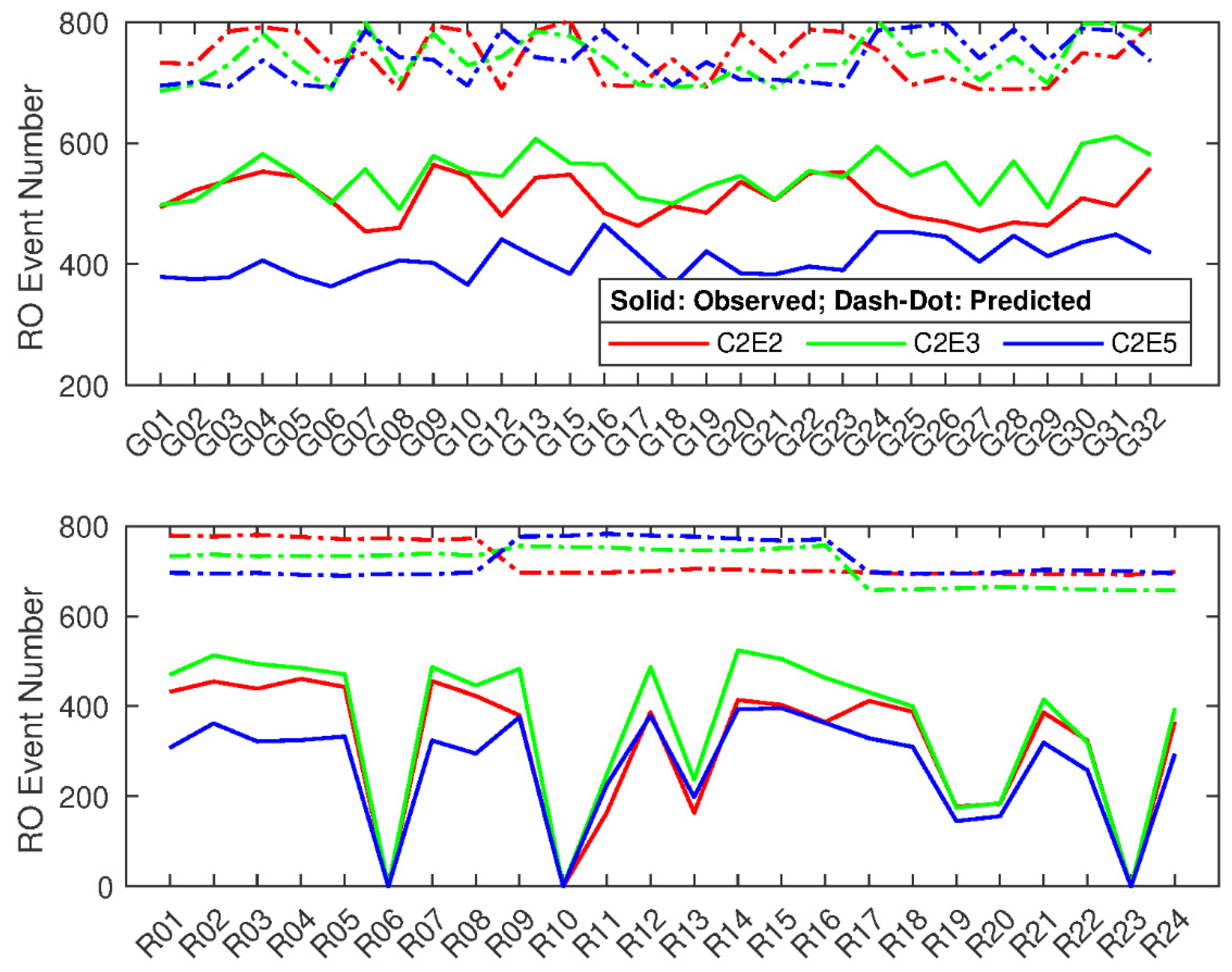
3.2. Radio Occultation Events from Prediction and Observation

We used the prediction method to predict all of the RO events for COSMIC-2 for GPS (30 satellites) and GLONASS (24 satellites) using one month’s worth of data from 15 December 2020 to 15 January 2021. The total predicted (dash-dot lines) and observed (solid lines) RO events for each GNSS satellite and C2E2, C2E3, and C2E5 are shown in Figure 4. Apparently, there are significantly more predicted RO events than observed, as shown in the figure. Note that all of the observed RO events obtained from the UCAR level 2 atmPrf product match the corresponding predicted RO events. During this month, the expected RO events were around 700–800 for each GNSS satellite, with a slightly more significant variation from the GPS than from GLONASS. The RO events (matched between observed and predicted) from C2E3 are significantly more than those from C2E2 and C2E5 for almost all of the GNSS satellites. At the same time, C2E5 has less matched RO events among these three flight modules due to the C2E5 transition from Parking Orbit (720 km) to Mission Orbit (550 km) during this period. The percentages (match rate) of the matched RO events from different GPS satellites are very stable, around 74%, 68%, and 55% for C2E3, C2E2, and C2E5, respectively. For GLONASS, three GLONASS satellites (R06, R10, and R23) do not have matched RO observation events from COSMIC-2, which suggests that these three GLONASS satellites were not healthy enough to successfully emit the GNSS signal. Although the predicted RO events are relatively stable from different GLONASS, the matched RO events have more significant variation than GPS. On average, the percentages for the matched RO events are about 58%, 50%, and 42% for C2E3, C2E2, and C2E5, respectively, without considering the R06, R10, and R23 contributions. Compared to the results for the RO events from GPS satellites, the corresponding match rate from the GLONASS satellites is about 15% lower. The lower match rate from the GLONASS satellites may indicate that the receivers from COSMIC-2 have had tracking issues when receiving signals from GLONASS satellites during this period. The large discrepancy in the RO event number between the anticipated RO events and observations may indicate the health status of the GNSS satellites or LEO/RO satellites.

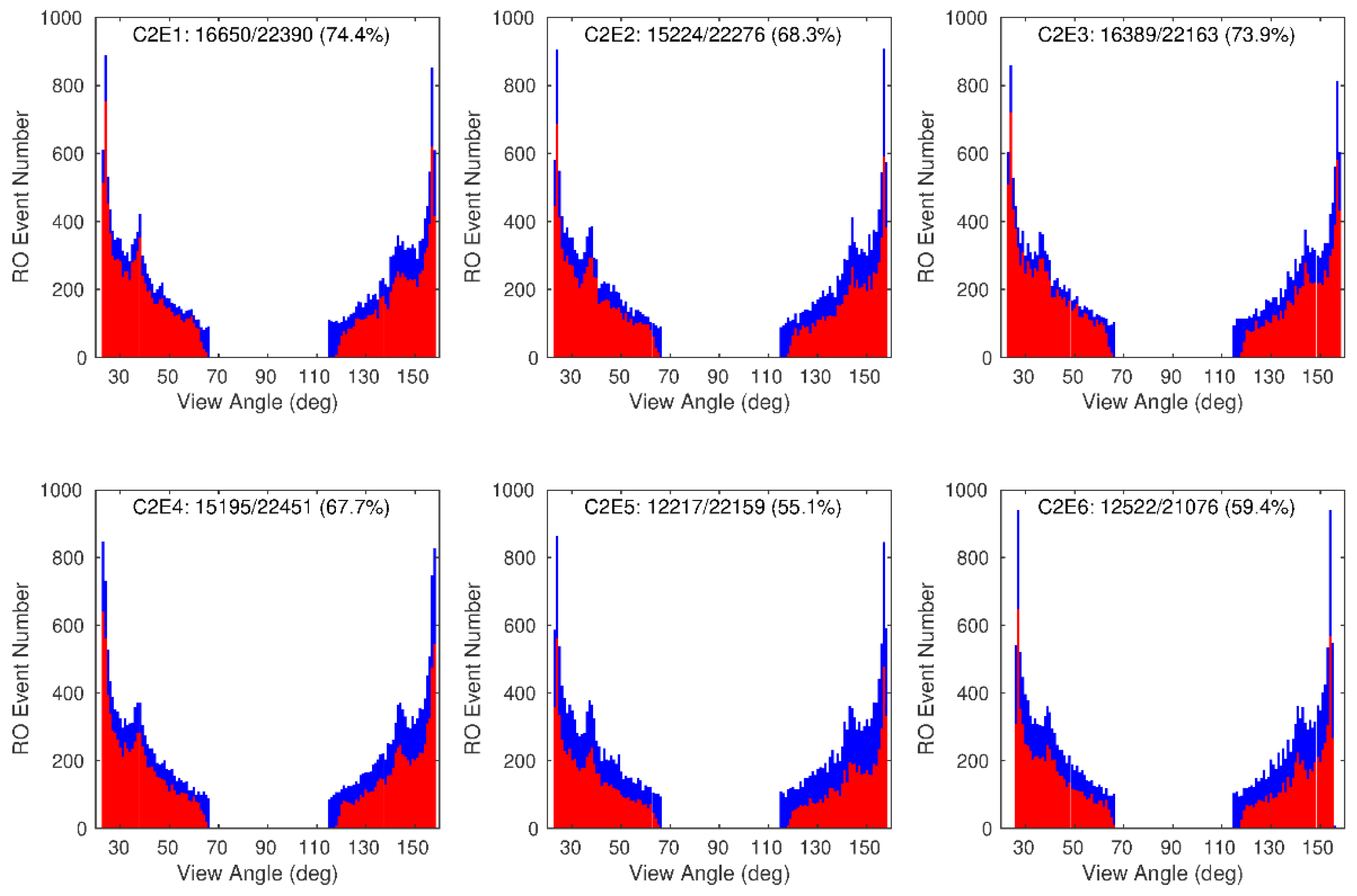
3.3. RO Event Distribution as a Function of Antenna View Angle

All COSMIC-2 flight modules include two Tri-GNSS Radio Occultation System (TGRS) RO antennas, one fore antenna (+X) and one aft antenna (−X). By design, the RO antennas have a Field of View (FOV) azimuth angle ±60 degrees, an elevation angle +20 degrees for the fore antenna, and a −70 degree for aft antenna. Considering the antenna beam lobe effects, the effective RO antenna view angles for COSMIC-2 are within (23°, 66°) and (115°, 158°) for the forward and backward antennas, respectively. Figure 5 shows the RO event distribution as a function of the antenna view angle for both predictions (blue color) and observations (red color) from COSMIC-2 flight modules 1–6 (from left to right and top to bottom) over the one month, from 15 December 2020 to 15 January 2021. The antenna view angle distributions of the predicted potential RO events for C2E1 to C2E6 are very similar, with a maximum at 24° for the forward antenna and 157° for the backward antenna, with an almost symmetrical pattern between the forward and backward directions.

The distribution patterns from the observed RO events closely follow the ones from the predicted events, with peaks at the same view angles (24° for the forward antenna and at 157° for the backward antenna), but with fewer RO events at all angles. The match rates (matched RO events divided by predicted potential events) are different among these six flight modules. C2E1 has the highest match rate with 74.4%, followed by C2E3 (73.9%), C2E2 (68.3%), C2E4 (67.7%), C2E6 (59.4%), and C2E5 (55.1%). The significant low match rates for C2E5 and C2E6 are due to the orbital maneuver during that month. (C2E6 started orbit transfer on 8 January 2021, and C2E5 was from the Parking Orbit (720 km) to the Mission Orbit (550 km)).

Figure 6 shows the RO event distribution as a function of the antenna view angle for the GLONASS satellites. The overall distribution pattern is very similar to the GPS results showed in Figure 5. However, the RO event match rates from the GLONASS satellites are significantly less than those from the GPS satellites. The highest match rate is from C2E3 with 50.3%, followed by C2E1 (46.5%), C2E4 (46.1%), C2E2 (43.9%), C2E5 (37%), and C2E6 (36.8). One of the reasons is that three GLONASS satellites (R06, R10, and R23) do not have observed RO events from each COSMIC-2 flight module, but each one has about 800 predicted potential RO events (see Figure 4). The other reason is that the receivers from COSMIC-2 may have had a problem tracking the signals from the GLONASS satellites (see Figure 4).

The prediction method can successfully predict all of the observed COSMIC-2 RO events, and the prediction accuracy compared to the observation is within 10 min and less than 15 km in distance. The performance of the prediction method indicates its broader use: (i) coordinate the radiosonde launches at GRUAN sites for field campaign; (ii) monitor the health status of GNSS satellites or LEO/RO satellites from the matched RO events, and (iii) find potential SRO events from two LEO/RO satellites using the predicted time and distance criteria.

4. Simultaneous Limb Overpass RO Matchup for Different LEO/RO Satellites

With the RO event prediction presented in the previous section, this study further applies the RO prediction method for the direct comparison of the RO bending angles from a pair of LEO satellites near the simultaneous limb overpass radio occultation, known as SRO. Similar to the SNO method for nadir-viewing sounders, the SRO approach explores the direct comparison of observations for two LEO/RO receivers when they are close to each other and when they receive the same GNSS signal through the approximated the same atmospheric path.

4.1. SRO Matchup Criteria

In this section, we discuss the SRO matchup procedures using the RO prediction method in detail. Assuming we have two different LEO/RO receivers on LEO1 and LEO2 at different orbital planes and altitudes and one GNSS transmitter on the satellite GNSS_A, the TLEs from the three satellites for a given period can then be used as inputs to the RO prediction method. The RO prediction method will generate two datasets containing all of the potential RO events for the receiver LEO1 and the transmitter GNSS_A and the receiver LEO2 and the same transmitter GNSS_A. These two datasets are used to pair the possible SRO events with the matchup criteria for a time less than 10 min and a distance less than 125 km between any tangent points along with the tracking positions of the two RO events. Figure 7 provides a summary of the matchup procedures.

Furthermore, the obtained potential paired SRO events are used to identify the observed RO events from LEO1 or LEO2 based only on the time tag in the filenames of the RO atmPrf data products. The only matchup criterion is that the time difference between the predicted and observed RO events is within ±10 min. If the observed RO events found for LEO1 and LEO2 are for a given potential paired SRO events, then the observed RO events are paired as a potential SRO. This method is very general and can be applied to any two GNSS receivers on different LEO satellites. In addition, it is also very efficient to find such events, which infrequently occur in time and space.

4.2. Data

To demonstrate the usefulness of this SRO method, we apply this method to COSMIC-2 and GeoOptics RO data during two periods: CWD data delivery order-1 (DO-1): 15 December 2020–15 January 2021 and CWD DO-2: 17 March 2021–31 August 2021. Both RO data products were generated by UCAR, which can efficiently remove the RO data processing uncertainty from different data processing centers [28,29] so that we can focus on the systematic biases from the instruments and processing algorithm performance for the signal-to-noise ratio (SNR), penetration height, and bending angle retrieval uncertainty in the SRO inter-comparisons. There are 289 SRO cases (182 for GPS and 107 for GLONASS) meeting the criteria of 10 min and less than 200 km in the distance at all impact heights from 5 km to 16 km after excluding bad-quality cases.

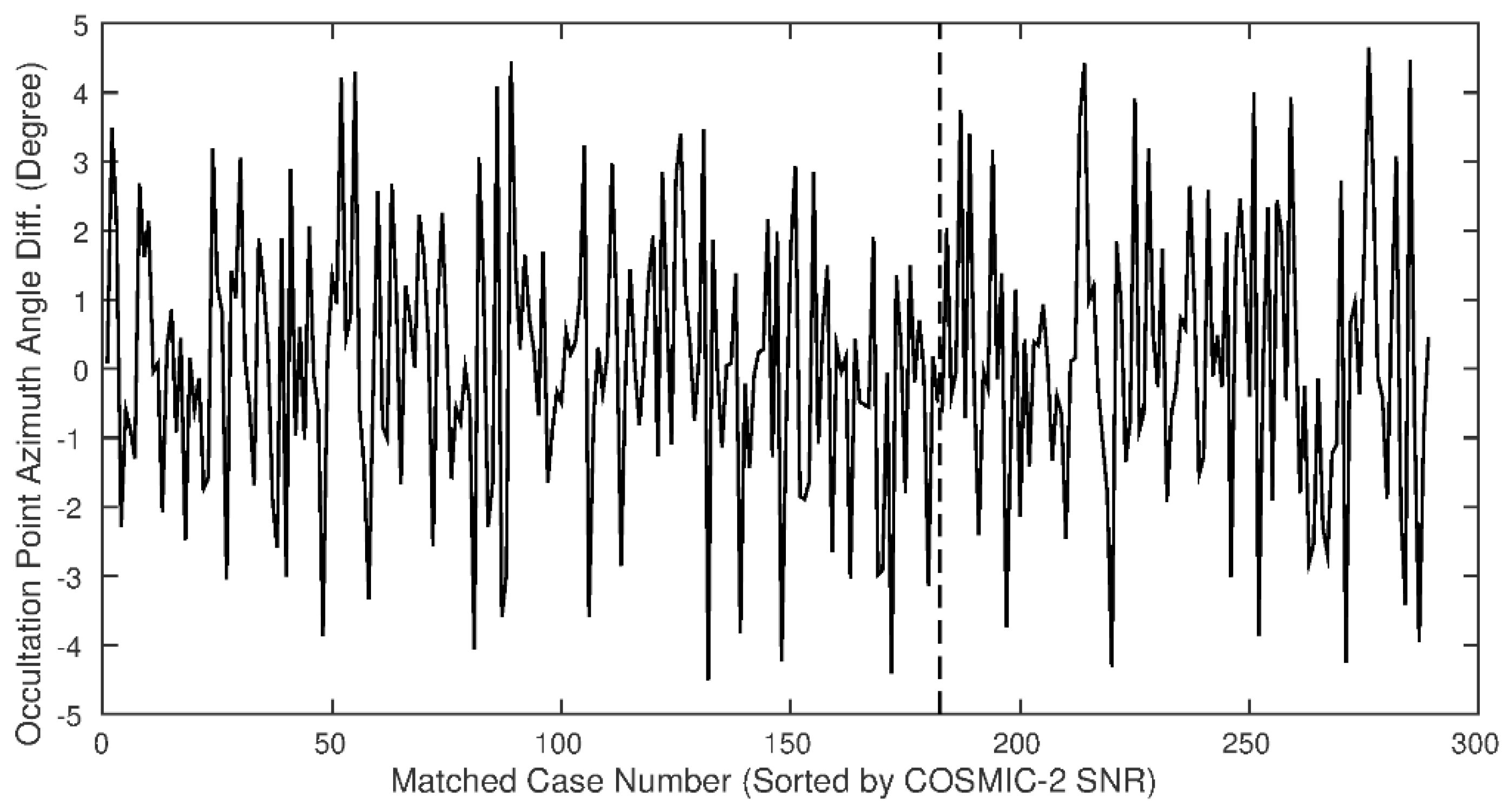
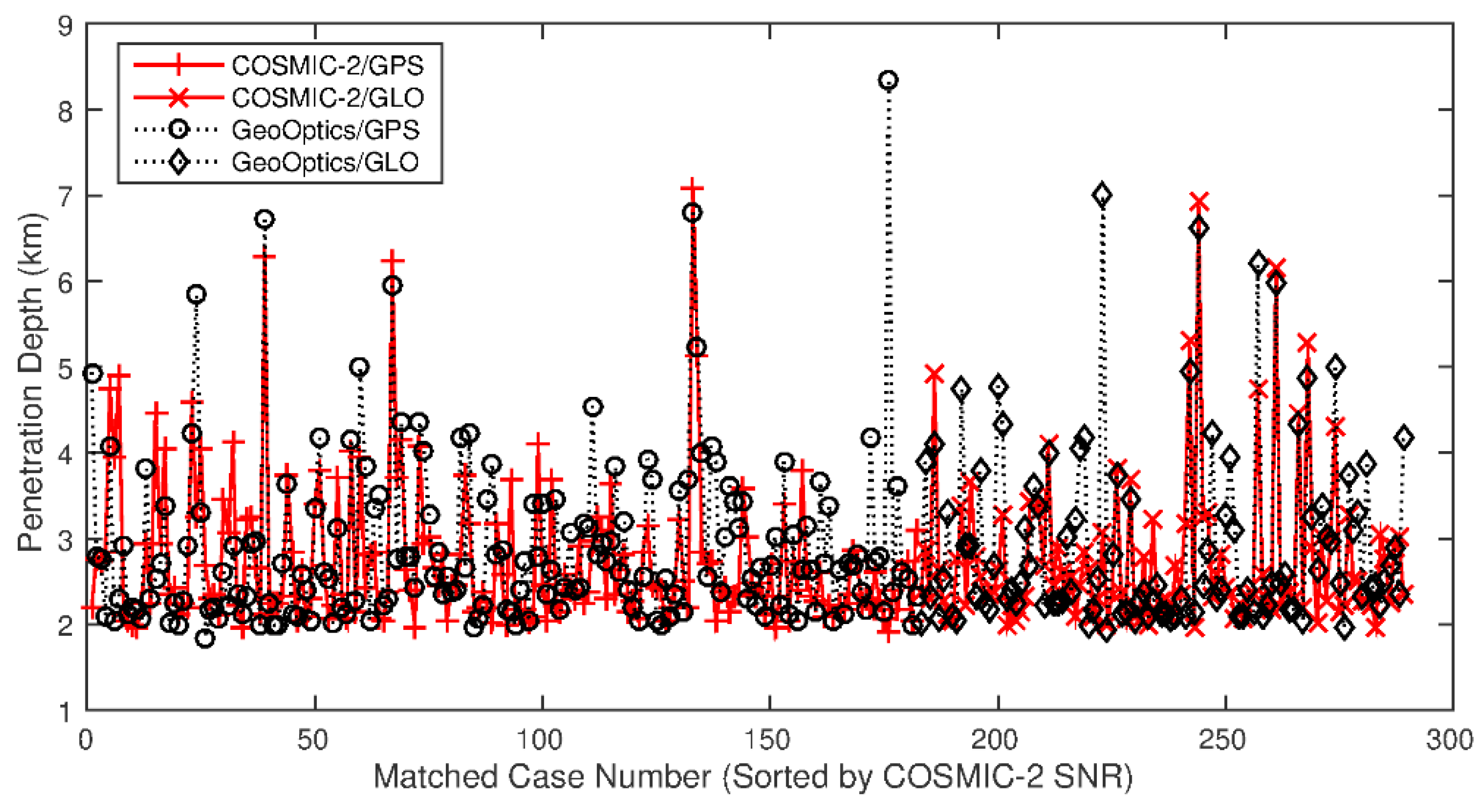
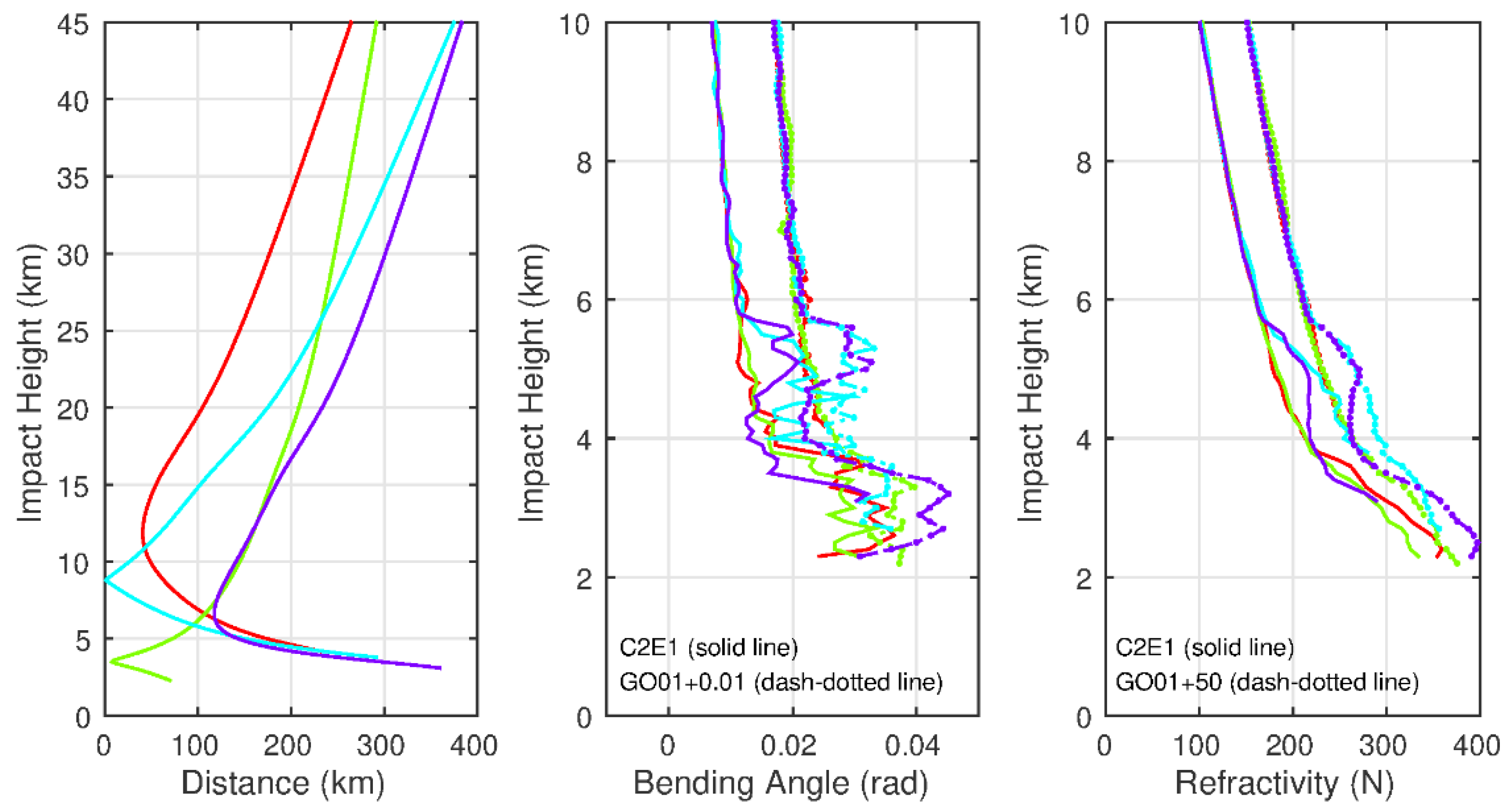
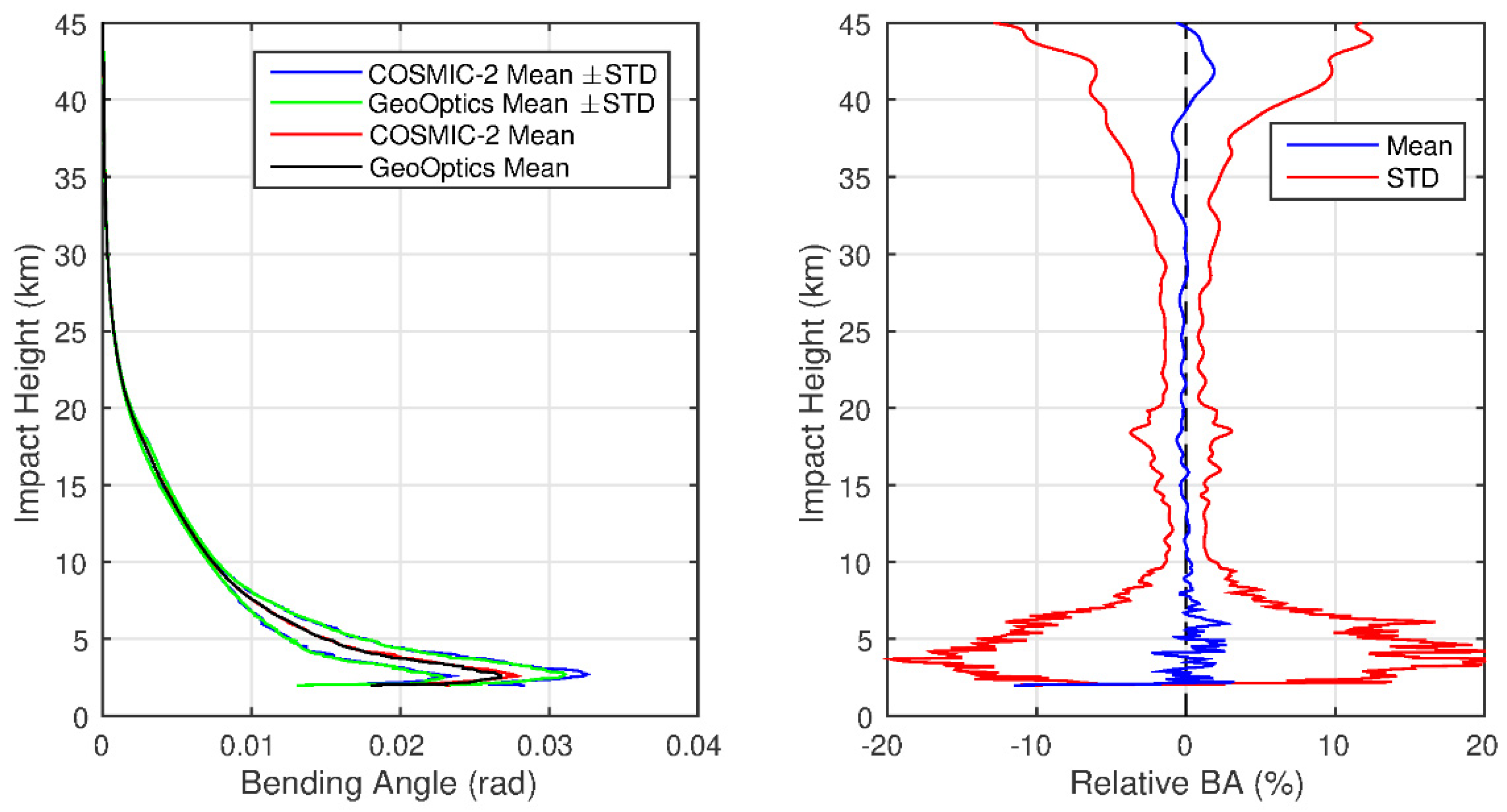
4.3. SRO Inter-Comparison Results

The occultation plane is defined by the vectors $R_{\mathrm{rcv}}$ and $R_{\mathrm{emt}}$ from the center of the reference frame to LEO and GNSS, respectively. The occultation point is defined as the lowest perigee point at the Earth’s surface. It is estimated under the tangent point of the ray connecting GNSS and LEO, for which the L1 excess phase is equal to 500 m [30]. The occultation point is defined by latitude and longitude in the Earth’s fixed reference frame. The occultation point azimuth angle is defined as the GNSS to the LEO direction concerning true North in the LEO pitch–yaw plane at the occultation point, which is in the range of (0°, 360°).

Figure 8 shows the occultation point azimuth angle differences from all of the SRO events for the COSMIC-2 and GeoOptics satellites. Note that the SRO cases are sorted by the averaged signal-to-noise ratio (SNR) between 60 to 80 km from COSMIC-2 and are separated by GPS (from index 1 to 182) and GLONASS (from index 183 to 289). For all of the SRO cases, the azimuth angle differences are very small and are within ±5 degrees.

Figure 9 shows the occultation point distance for all of the SRO pairs between COSMIC-2 and GeoOptics. Since we use less than 200 km from the impact height at 5 km to 16 km as one of the criteria, 30 SRO cases have a slightly larger distance than 200 km (but less than 240 km) at the occultation points. All of the other SRO cases are less than 200 km. Some of them are even less than 50 km.

Combining the results shown in Figure 8 and Figure 9, we can conclude that for the simultaneous limb overpass RO events in our study, all meet the SRO criteria: (1) the azimuth angle differences between these matched RO events are close to zero, (2) the distances are less than ~230 km (from occultation points up to 16 km) at the given impact heights, and (3) the observation time differences are less than 10 min. These conditions indicate that the GNSS signal passes through the same atmosphere plane and reaches the two different LEO/RO receivers within a slight temporal time difference and spatial distance.

Signal-to-noise ratio (SNR) is one of the essential characteristics of RO observation and is associated with the receivers. Different receivers have different SNRs, which directly affect the accuracy of the L1 and L2 bending angle and refractivity profiles, especially for the retrieval uncertainty and penetration height. The retrieval bending angle errors are roughly proportional to the inverse of SNR [30]. Combining a high-performance GPS + GLONASS receiver and steering beam antenna design, COSMIC-2 increases the number of successful RO retrievals per satellite and enhances the GNSS-RO measurement quality with higher SNR and improved penetration depth for the tropical troposphere [31,32]. Figure 10 shows the SNR (from L1 averaged SNR between 60 to 80 km) comparison for all SRO pairs between COSMIC-2/GPS (red solid plus line) and GeoOptics/GPS (black dotted circle line) as well as between COSMIC-2/GLONASS (red solid cross line) and GeoOptics/GLONASS (black dotted diamond line). The SNRs from COSMIC-2/GPS range from 400 V/V to 1900 V/V compared to about 100 V/V to 1100 V/V from GeoOptics/GPS, while the SNRs from COSMIC-2/GLONASS range from 300 V/V to 2200 V/V compared to about 100 V/V to 1200 V/V from GeoOptics/GLONASS. In general, the SNRs from the COSMIC-2 observations are much larger (on average about two times larger) than those from GeoOptics. For GeoOptics, the SNR distributions from the GPS and GLONASS are very close. Both SNRs can get up to 1200 V/V.

Figure 11 shows the penetration depth comparison for the SRO pairs between COSMIC-2/GPS (red solid plus line) and GeoOptics/GPS (black dotted circle line) as well as between COSMIC-2/GLONASS (red solid cross line) and GeoOptics/GLONASS (black dotted diamond line). Here, the penetration depth is defined as the minimum impact height above ground level with a valid (not a filled missing value) bending angle for a given RO event. A smaller penetration depth indicates that the RO signal reaches much closer to the Earth’s surface. With the exception of five cases with a larger penetration depth from GeoOptics (case 1: 2.20 km vs. 4.94 km; case 24: 3.24 km vs. 5.84 km; case 176: 1.92 km vs. 8.36 km; case 200: 2.62 km vs. 4.78 km; and case 223: 3.08 km vs. 7.00 km) and one case a with larger penetration depth from COSMIC-2 (case 7: 4.89 km vs. 2.30 km), the penetration depth differences are within 2 km. In general, the penetration depth from COSMIC-2 is less than that from GeoOptics and is consistent with the higher SNR having a lower penetration depth [31,32]. However, the penetration depths from COSMIC-2 and GeoOptics are very close, and the averaged penetration depth difference is just around 100 m. The trimmed mean penetration depth after removing the aforementioned outlines are 2.72 km, 2.84 km, 2.75 km, and 2.89 km from COSMIC-2/GPS, GeoOptics/GPS, COSMIC-2/GLONASS, and GeoOptics/GLONASS, respectively. It is remarkable how small the penetration depth difference is for such a large difference in the SNR between COSMIC-2 and GeoOptics. Given the limited dataset used in our comparison, the relationship between the penetration depth and the SNR should be investigated further.

Figure 12 shows the comparison results for the randomly selected SRO cases (4 out of 19 cases) between COSMIC-2-FM1 (C2E1) and GeoOptics-01 (GO01) during the comparison period. The distance profiles between the SRO as a function of impact height are shown in the right panel of Figure 12. All four cases meet the matchup distance criteria (less than 200 km from 5 km to 16 km). The middle panel of Figure 12 shows the bending angle profiles from those four SRO events below 10 km to emphasize the detailed difference below that height. The solid lines are for the bending angle profiles from C2E1, while the dashed lines are for GO01. The left panel of Figure 12 shows the corresponding refractivity profiles. The bending angles increase relatively smoothly for a single bending angle profile, increasing with a decreasing impact height above 6 km. Below 6 km, the bending angle shows more significant variation. It changes dramatically among different heights, indicating that the RO signal senses small-scale phenomena at the lower troposphere. However, the refractivity profile derived from the bending angle profile using the Abel transformation is smoother than its corresponding bending angle profile. Note that the lowest impact height in the distance profile for an SRO case is determined by the higher penetration depth between C2E1 and GO01. For example, the distance profile in red ends slightly above 4 km, which is the penetration height (slightly above 4 km) from the GO01 bending angle profile (red dashed line in middle panel), while the penetration height (slightly above 2 km) from C2E1 is well below that height. With the exception of the different penetration heights, the direct comparison of the bending angle profiles (and refractivity profiles) from the SRO events overall has a very similar structure. However, at some impact heights, the relative differences can be significant. When comparing the inter-satellite SRO observations, the difference in observation SNRs and the penetration heights from the SRO events should be considered carefully.

We have compared the bending angle profiles from all of the SRO events, and the results are presented and separated by the emitters GPS and GLONASS and all of the GNSS satellites. Note that for a given impact height, only the bending angles from both COSMIC-2 and GeoOptics have valid data that are included in the statistics in terms of mean and standard deviation. Figure 13 shows the bending angle profiles comparing GeoOptics/GPS and COSMIC-2/GPS using all of the 182 SRO cases. The left panel in Figure 13 displays the mean and standard deviation bending angle profiles from GPS, with the COSMIC-2 standard deviation profiles in blue and the GeoOptics profiles in green. The mean profiles from COSMIC-2 (red) and GeoOptics (black) are also included. The right panel in Figure 13 shows the mean (blue) and standard deviation (STD, red, mean ± standard deviation) relative bending angle (defined as (BA_GeoOptics − BA_COSMIC-2)/BA_COSMIC-2 × 100) profiles between GeoOptics and COSMIC-2. The bending angle profiles generally show good agreement from the two different LEO/RO receiver systems between 10 to 30 km, with an absolute mean less than 0.2% and a standard deviation less than 2%. Above 30 km, the mean differences are still minimal (less than 0.5%), but the standard deviations gradually increase with the impact height and can reach 10% at 45 km. Below 10 km, the mean relative bending angles increase while the impact height decreases, and there is more significant oscillation toward the surface. At the same time, the standard deviations dramatically increase toward the lower impact height and reach the maximum (~20%) at about 3 km.

Figure 14 shows the bending angle profiles comparing GeoOptics/GLONASS and COSMIC-2/GLONASS using all of the 107 SRO cases. The overall statistics characterization from GLONASS is very similar to that from GPS. However, there are some noticeable differences between GLONASS and GPS: (1) larger mean differences and oscillation occurred at impact height from 15 to 20 km; (2) larger absolute mean differences and standard deviations above 35 km; and (3) slightly smaller standard deviations below 5 km.

It is essential to understand the statistical characteristics of SRO by comparing the uncertainty from the individual instrument measurements and bending angle retrieval and the expected uncertainty (standard deviation) from the matchup SRO dataset. Based on Poe et al. [33], if X and Y are independent datasets, the variance of the difference between the two datasets X − Y is Var(X) + Var(Y). Therefore, the variance of the difference of means is the sum of the variances of each mean. Since the two observations from the SRO pair are independent, the expected standard deviation from the two matchup RO events would be $\sqrt{{\sigma }_{GO}^2+{\sigma }_{C2}^2}$, where ${\sigma }_{GO}$ and ${\sigma }_{C2}$ are the bending angle retrieval standard deviation from the GeoOptics and COSMIC-2 excess phases, respectively.

The bending angle retrieval uncertainty is available from the CDAAC standard RO data product level 2 atmProf below 20 km. A proxy for the BA error is calculated from half of the local spectral width (LSW) of the L1 RO signal transformed to the impact parameter by least-squares fitting to the power spectrum [34]. The LSW represents the uncertainty of BA related to the effect of non-spherically symmetric irregularities in the lower troposphere. The relative dynamic bending angle observation error (DBAOE) is defined as the ratio of the bending angle uncertainty to the bending angle itself. The overall statistics comparison is summarized in Figure 15. The left panel in Figure 15 shows the overall relative BA statistics (mean and standard deviation) comparison from the GPS (green lines), as shown in the right panel in Figure 13; GLONASS (blue lines), as shown in the right panel in Figure 14; and all GNSS satellites (red lines). Overall, the relative bending angle profile statistics from the GPS and GLONASS are in good agreement (mean difference is less than 0.5%, and STD less than 5%), with the exception of these two impact height intervals (above 35 km and below 5 km). The right panel in Figure 15 shows the standard deviation comparison among the overall SRO cases between GeoOptics and COSMIC-2 (red line), the COSMIC-2 mean relative dynamic bending angle observation error (DBAOE) (green line), the GeoOpitcs DBAOE (blue line) calculated from the bending angle retrieval process, and the expected standard deviation from the SRO difference between the COSMIC-2 and GeoOptics datasets (black line). Only impact heights below 20 km are shown here because the retrieval standard deviation is only available below that height in the level 2 atmPrf product. One interesting observation is that below 5 km, the COSMIC-2 DBAOE is larger than that from GeoOptics, while above 5 km, the pattern changes, with COSMIC-2 being less than GeoOptics for the DBAOE. One possible reason for this feature is that below 5 km, the effect of non-spherically symmetric irregularities dramatically increases due to the larger water vapor horizontal gradient in the atmosphere, and perhaps the COSMIC-2 signals with a larger SNR (see Figure 10) could more easily detect these irregularities.

The standard deviations from the SRO events are more significant than either DBAOE from COSMIC-2 or GeoOptics (except those over 10–14 km, whivh is very close to the DBAOE from GeoOptics). Unlike the relatively smooth DBAOE profiles, the STD profile from the SRO events has vertical oscillation, which gradually increases as the impact height decreases below 10 km. However, this STD profile follows (within 1–2% at most impact heights) the expected standard deviations derived from these two matchup RO datasets closely. This indicates that the bending angle uncertainty from the SRO events is expected and can be fully explained by the retrieval uncertainty from the retrieval process. The large oscillation in the bending angle differences at the lower levels can be attributed to several factors, including the small-scale atmospheric phenomena with nonuniformity in the vertical and horizontal directions, different penetration depths from the SRO events (see Figure 11), large horizontal distances near the surface (see Figure 12), and the smaller sample size. However, the larger differences and oscillations in the bending angle profiles can be significantly reduced by increasing the vertical thickness. We have binned the results at eight heights based on the pattern similarity from the relative bending angle difference profiles: 2–4 km, 4–6 km, 6–10 km, 10–20 km, 20–30 km, 30–35 km, 35–40 km, and 40–45 km. The statistical results are summarized in

Table 1. Bending angle comparison (relative difference %) between GeoOptics and COSMIC-2 for GPS, GLONASS, and GNSS satellites. Only the bending angles from both COSMIC-2 and GeoOptics with valid data at the given impact height interval are included in the statistics.

Impact Height (km)	GPS			GLONASS			All (GPS and GLONASS)
	Mean	STD	Cases	Mean	STD	Cases	Mean	STD	STD Exp.	Cases
40–45	0.06	7.16	182	1.10	9.25	107	0.44	8.01	N/A	289
35–40	−0.13	3.44	182	−0.48	4.31	107	−0.26	3.78	N/A	289
30–35	−0.11	2.02	182	−0.41	2.36	107	−0.22	2.16	N/A	289
20–30	−0.24	1.54	182	−0.18	1.33	107	−0.22	1.47	N/A	289
10–20	−0.08	1.78	182	−0.13	1.85	107	−0.10	1.81	1.98	289
6–10	0.24	5.85	181	0.38	5.85	106	0.29	5.85	4.60	287
4–6	−0.02	12.93	173	0.96	13.65	100	0.34	13.20	13.97	273
2–4	−0.20	16.10	97	0.13	14.60	59	−0.17	15.54	20.18	156

. The mean difference at all levels is less than 1.1%. For example, the most significant difference (1.1%) occurred at 40–45 km for GeoOptics/GLONASS and COSMIC-2/GLONASS, and the second-largest difference (0.96%) happened at 4–6 km, also for GLONASS. From 6–35 km, the standard deviations from GPS and GLONASS are comparable for a given impact height. However, the standard deviation from GLONASS is significantly larger than that from GPS above 35 km, which is consistent with previous findings [23]. For example, at 40–45 km, the STD from GLONASS can reach 9.25%, whereas GPS can only reach s 7.16%.

The SRO inter-satellite comparison results clearly show that the SRO bending angle profiles from the GLONASS satellites have a larger standard deviation above 35 km than those from the GPS satellites. However, we do not know whether the RO bending angles from COSMIC-2 or GeoOptics have potential quality issues based on the comparison results. We further used the fifth-generation European Center for Medium-Range Weather Forecasts (ECMWF) Reanalysis (ERA5) data [35] as an independent data source to evaluate the RO data quality. Using a forward model, the bending angle profile can be simulated using the ERA5 profile, with temporal/spatial interpolation being integrated into the time/location from the corresponding RO observation as input. The statistics compare the observed bending angle profiles and the simulated BA profiles using ERA5 for all 289 SRO cases, which are separated by the GNSS satellites (GPS, GLONASS, and all) and the LEO satellites (COSMIC-2 and GeoOptics), as summarized in Figure 16. In general, the statistical results from comparing the observations and simulations from the ERA5 in terms of the mean difference (Figure 16 left panel) and standard deviation (Figure 16 right panel) are very similar to the results from the direct SRO comparison between COSMIC-2 and GeoOptics. The relative bending angle biases are less than 1% from 6 km to 40 km. However, the bias becomes significantly negative below ~6 km and above ~40 km, and the standard deviation also increases dramatically at the same time, compared to the simulation from ERA5. These statistical features are well-known issues for RO bending angle profiles, which depend on certain assumptions, approximations, and tunable processing strategy parameters in the RO retrieval process [36]. The RO bending angle standard deviations from GLONASS are larger than those from the GPS above 35 km for COSMIC-2 and GeoOptics. For the SRO cases from the GLONASS satellites, the standard deviations from GeoOptics are substantially larger than those from COSMIC-2 above 35 km.

The independent statistical analysis and validation from ERA5 and the direct bending angle profile comparison from these SRO cases above 35 km suggest that (1) in general, the RO bending angle profiles retrieved from GPS satellites are better than those from GLONASS satellites and that (2) significant uncertainty exists for the RO bending angle profiles from GeoOptics/GLONASS, which indicates potential RO phase issues related to the residual ionospheric effects, receiver noise, and orbit determination errors for GLONASS.

5. Discussion

The prediction method presented in this study can efficiently predict all of the observed RO events from COSMIC-2. Compared to the observations, the prediction accuracy is within 10 min and with a distance less than 15 km, which is sufficient for many applications. The performance of the prediction method and computational efficiency indicate its broader use to support the planning, inter-calibration, and quality monitoring of the growing number of RO sensors, primarily to support the anticipated growth in the commercial RO satellites used in the data assimilation of NWP under the NOAA CWD program. Specifically, the method can be used to coordinate the radiosonde launches at GRUAN sites for field campaigns, to monitor the health status of GNSS satellites or LEO satellites from the matched RO events, and to find potential simultaneous RO events from two LEO/RO satellites using the predicted time and distance criteria. The SRO method presented in this study extends that of Cao et al. [23] by introducing the RO prediction capabilities for SRO. While both used brute-force search to obtain the SRO pairs, the method presented in this paper is first based on predicted RO events and is then validated with observations. The predicting capabilities of our approach are novel and have distinct advantages with a variety of applications, as discussed in this paper.

The main advantage of bending angle SRO comparisons is the significantly reduced uncertainties due to the much shorter time and minor atmospheric path differences than traditional RO comparisons (150–250 km and within a 3 h time window). These SRO cases also characterize the instrument and processing algorithm performances for SNR, penetration height, and bending angle retrieval uncertainty from different RO missions. In this study, we used COSMIC-2 and GeoOptics as examples. It is generally assumed that RO events with a higher SNR correspond to lower penetration depths [31,32]. The SRO comparison results showed that the penetration depth from COSMIC-2 is slightly less than that from GeoOptics and that the averaged penetration depth difference is about 100 m. Given the large difference in SNR between COSMIC-2 and GeoOptics, it is remarkable how small the penetration depth difference is. Considering the limited dataset used in our comparison, the relationship between the penetration depth and SNR requires further investigation.

6. Conclusions

This paper presents a method that predicts all of the potential RO events using the SGP4 orbital perturbation model with the TLEs from a GNSS satellite and a LEO satellite. COSMIC-2 RO observations are used to validate the method in terms of ground track, RO events number, and RO event distribution as a function of the antenna view angle.

The SRO from a pair of LEO satellites to the same GNSS satellite can be obtained from the predicted RO events. To demonstrate the usefulness of this method, we present the comparison of the COSMIC-2 and GeoOpitcs RO profiles using SRO data for two time periods: CWD DO-1: 15 December 2020–15 January 2021 and CWD DO-2: 17 March 2021–31 August 2021. There is a total of 289 matched cases (182 for GPS and 107 for GLONASS) meeting the SRO criteria: (i) the azimuth angle differences between these matched RO events are very close to zero, (ii) the distances are less than ~200 km (from 5 km to 16 km) at the any given impact heights, and (iii) the observation time differences are less than 10 min. These conditions indicate that the GNSS signal passes through the same atmosphere plane and reaches the two different LEO/RO receivers within a slight temporal time difference and spatial distance.

The results show very good agreement in the bending angles between the COSMIC-2 RO measurements and those from GeoOptics, although systematic biases are also found in the inter-comparisons. Overall, the relative bending angle profile statistics from the GPS and GLONASS are in good agreement, with the exception of two impact height intervals (above 35 km and below 5 km). The mean difference of the SRO cases at all levels is less than 1.1%. The most significant difference (1.1%) occurred at 40–45 km for GeoOptics/GLONASS and COSMIC-2/GLONASS, and the second-largest difference (0.96%) happened at 4–6 km for GLONASS. From 6–35 km, the standard deviations from the GPS and GLONASS are very comparable for a given impact height. However, the standard deviation from GLONASS is significantly larger than that from GPS above 35 km. At 40–45 km, the STD from GLONASS can reach 9.25%, where the GPS only has 7.16%. The independent statistical analysis and validation using simulation from the ERA5 and the direct bending angle profile comparison from these SRO cases above 35 km suggest that (1) in general, the RO bending angle profiles retrieved from the GPS satellites are better than those from the GLONASS satellites and that (2) significant large uncertainty exists for the RO bending angle profiles from GeoOptics/GLONASS.

Given the efficiency of this method and the many RO measurements made available publicly and commercially and the expansion of receiver capabilities of all GNSS systems, it is expected that this method can be used to validate/inter-calibrate GNSS RO measurements from different missions.