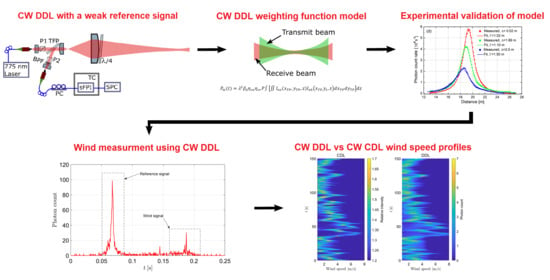
CW Direct Detection Lidar with a Large Dynamic Range of Wind Speed Sensing in a Remote and Spatially Confined Volume
Abstract
:1. Introduction
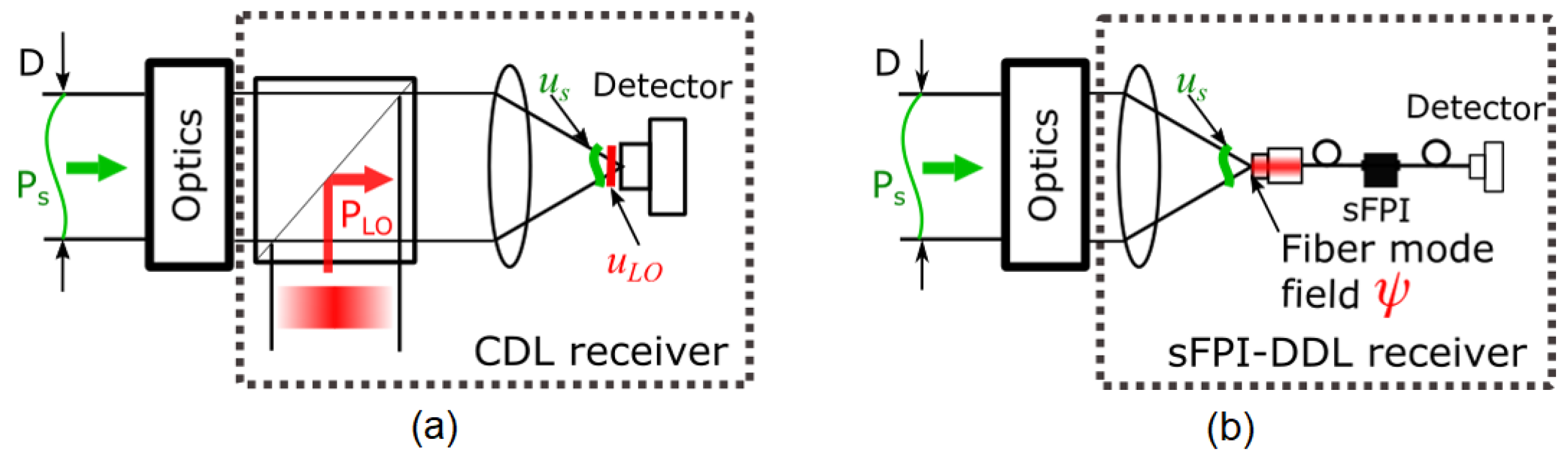
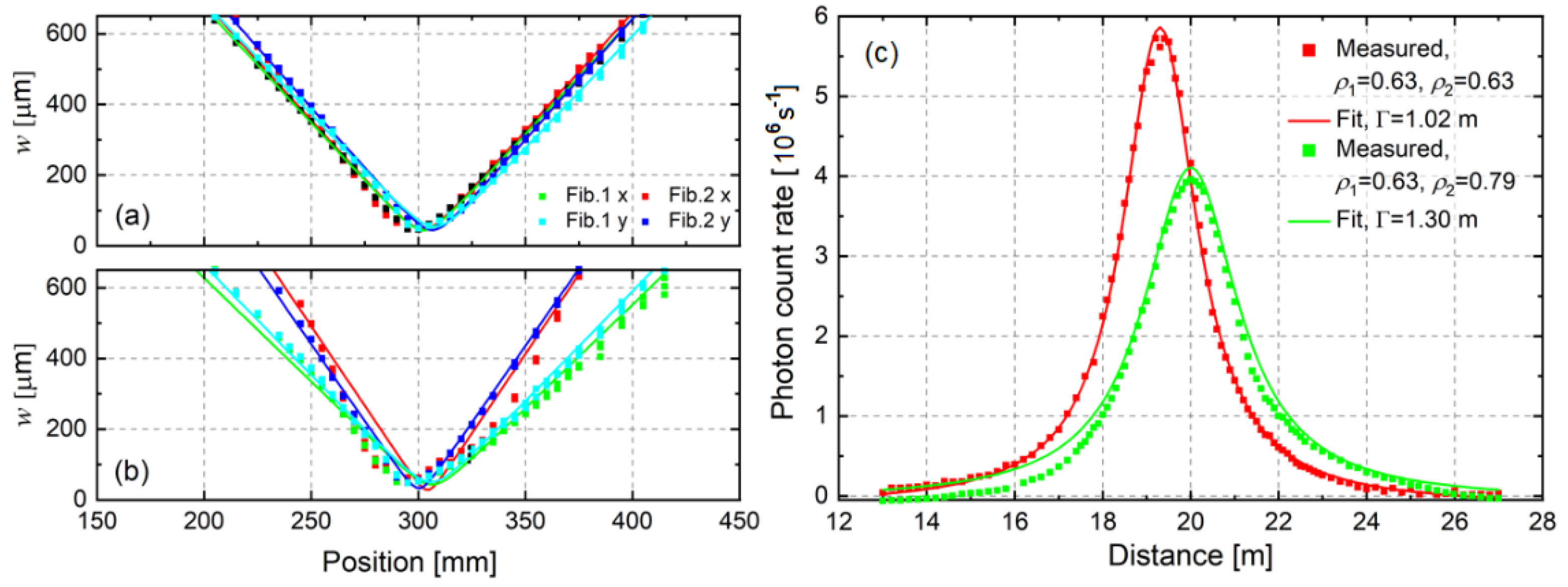
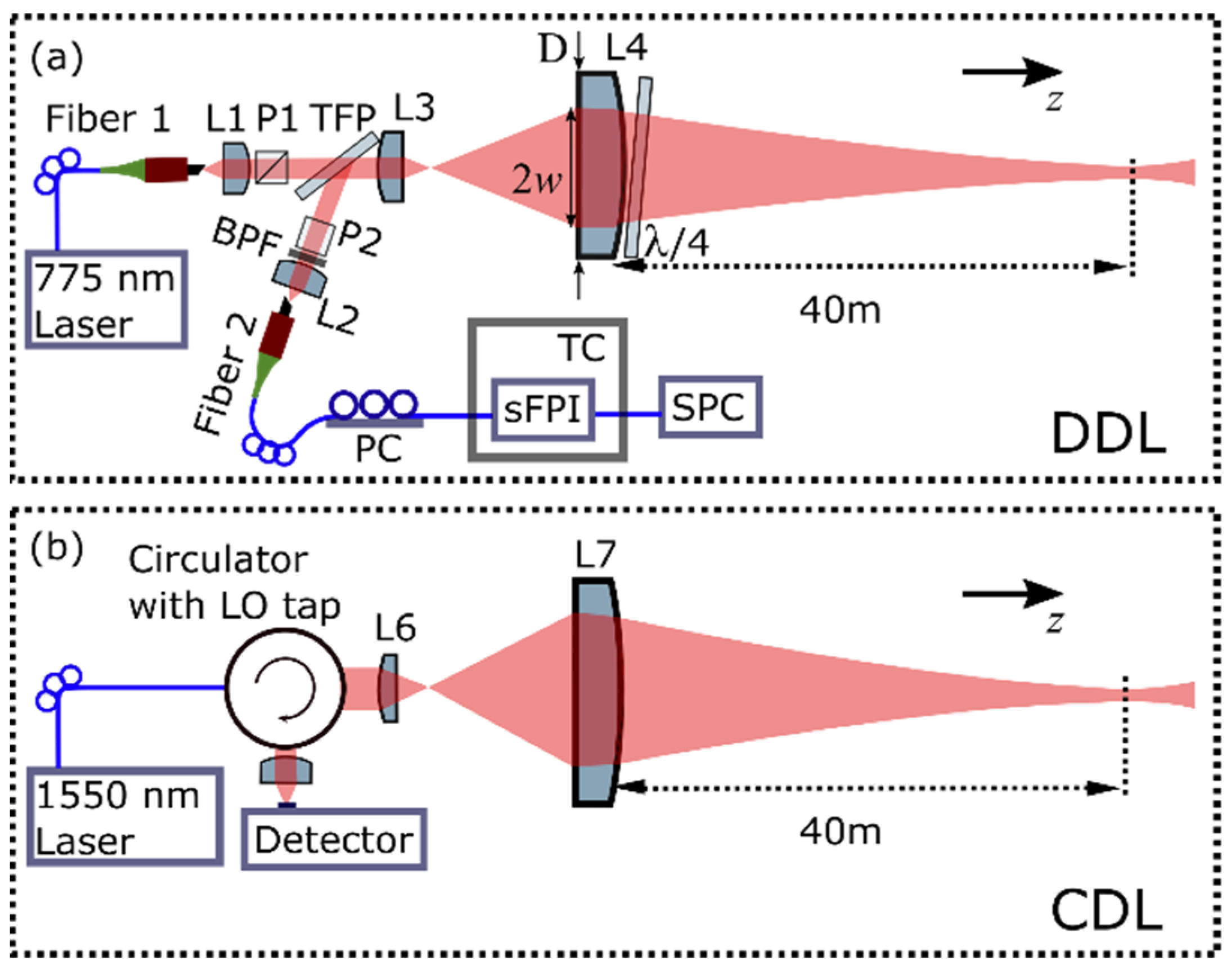
2. Spatial Confinement of the sFPI-DDL
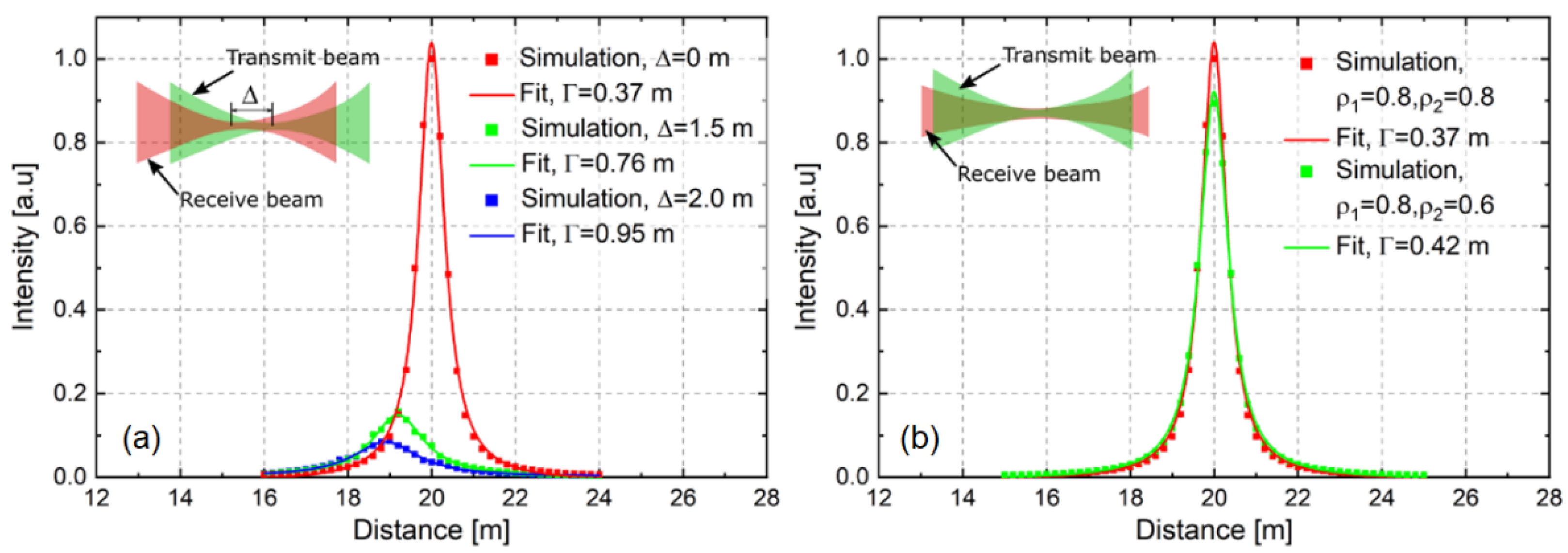
2.1. Theory
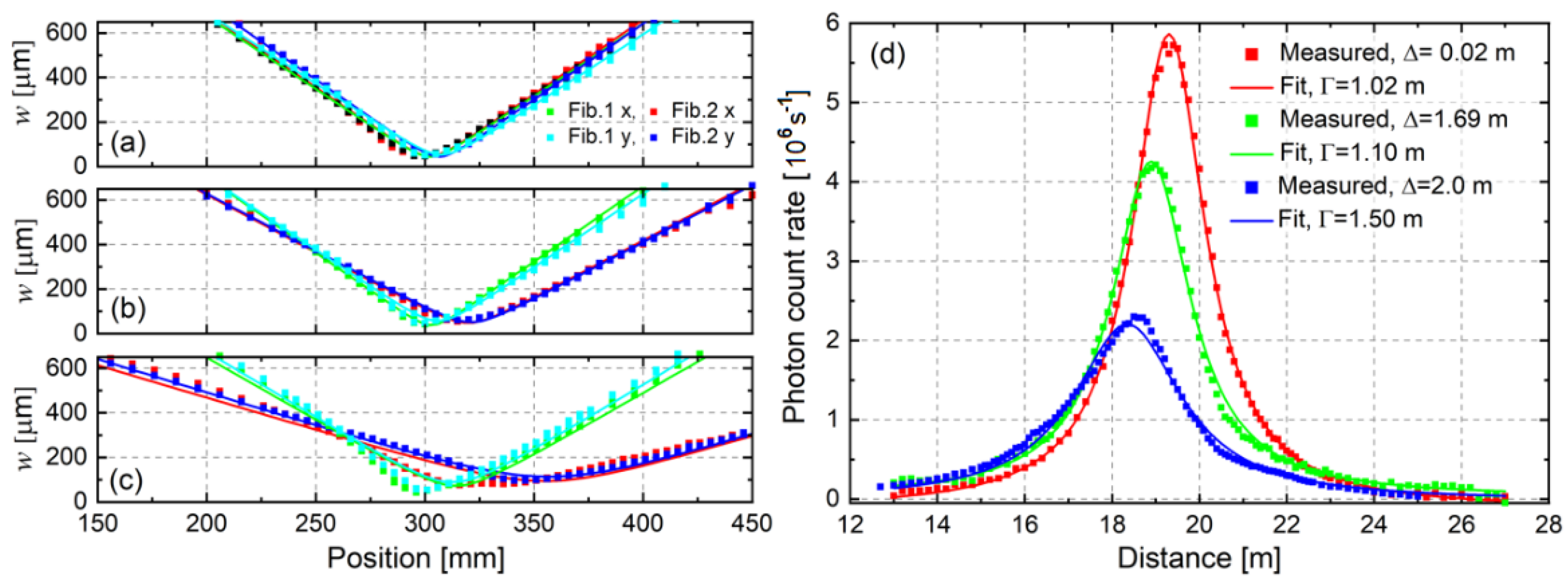
2.2. Experiments and Results
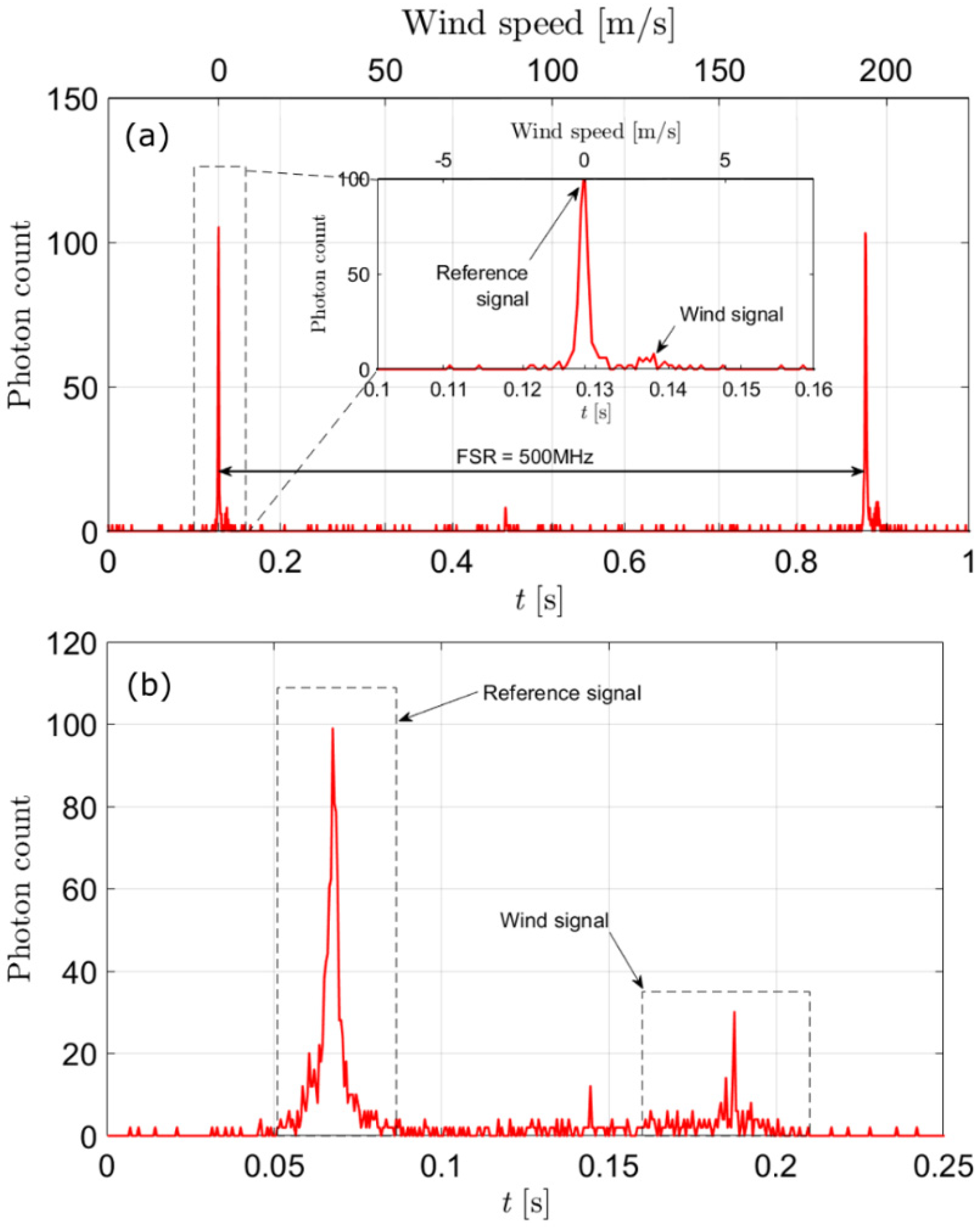
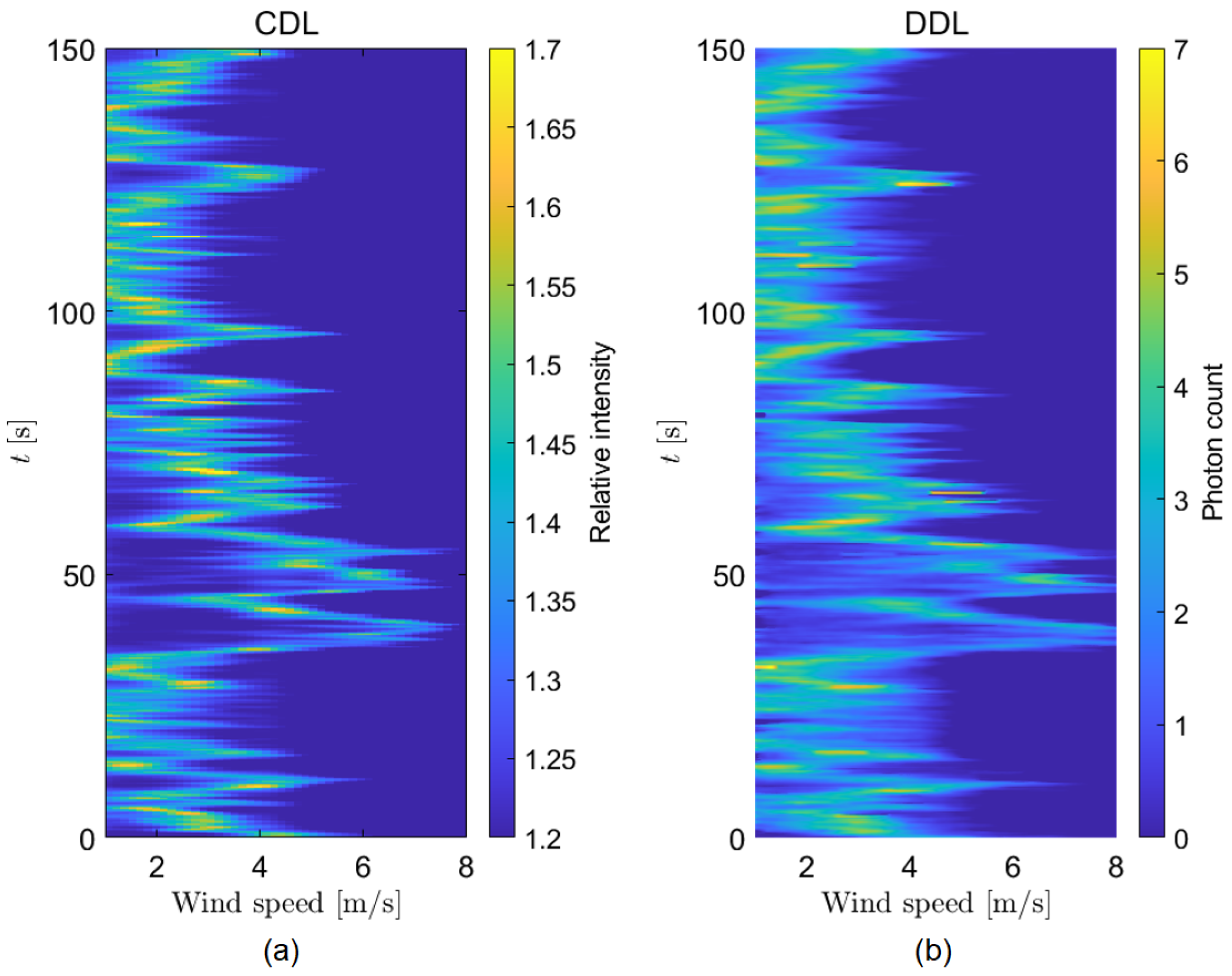
3. Wind Measurement Using sFPI-DDL
4. Discussion
- Truncation ratio
- 2.
- Aperture of lens L4
- 3.
- Transmission of the fiber-based sFPI
- 4.
- Laser wavelength tuning
- 5.
- Ranging capability
5. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Manninen, A.J.; Marke, T.; Tuononen, M.J.; O’Connor, E.J. Atmospheric boundary layer classification with Doppler lidar. J. Geophys. Res. Atmos. 2018, 123, 8172–8189. [Google Scholar] [CrossRef]
- Prasad, N.S.; Tracy, A.; Vetorino, S.; Higgins, R.; Sibell, R. Innovative fiber-laser architecture-based compact wind lidar. In Photonic Instrumentation Engineering III; International Society for Optics and Photonics: Bellingham, WA, USA, 2016; Volume 9754, p. 97540J. [Google Scholar]
- Wu, S.; Zhai, X.; Liu, B. Aircraft wake vortex and turbulence measurement under near-ground effect using coherent Doppler lidar. Opt. Express 2019, 27, 1142–1163. [Google Scholar] [CrossRef] [PubMed]
- Smalikho, I.N.; Köpp, F.; Rahm, S. Measurement of atmospheric turbulence by 2-μm Doppler lidar. J. Atmos. Ocean. Technol. 2019, 22, 1733–1747. [Google Scholar] [CrossRef]
- Peña, A.; Mann, J. Turbulence measurements with dual-Doppler scanning lidars. Remote Sens. 2019, 11, 2444. [Google Scholar] [CrossRef] [Green Version]
- Shimada, S.; Goit, J.P.; Ohsawa, T.; Kogaki, T.; Nakamura, S. Coastal wind measurements using a single scanning LiDAR. Remote Sens. 2020, 12, 1347. [Google Scholar] [CrossRef] [Green Version]
- Shun, C.M.; Chan, P.W. Applications of an infrared Doppler lidar in detection of wind shear. J. Atmos. Ocean. Technol. 2008, 25, 637–655. [Google Scholar] [CrossRef]
- Beuth, T.; Fox, M.; Stork, W. Parameterization of a geometrical reaction time model for two beam nacelle lidars. In Lidar Remote Sensing for Environmental Monitoring XV; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9612, p. 96120J. [Google Scholar]
- van Dooren, M.F.; Campagnolo, F.; Sjöholm, M.; Angelou, N.; Mikkelsen, T.; Kühn, M. Demonstration and uncertainty analysis of synchronised scanning lidar measurements of 2-D velocity fields in a boundary-layer wind tunnel. Wind Energy Sci. 2017, 2, 329–341. [Google Scholar] [CrossRef] [Green Version]
- Iungo, G.V. Experimental characterization of wind turbine wakes: Wind tunnel tests and wind LiDAR measurements. J. Wind Eng. Ind. Aerod. 2016, 149, 35–39. [Google Scholar] [CrossRef]
- Rye, B.J. Primary aberration contribution to incoherent backscatter heterodyne lidar returns. Appl. Opt. 1982, 21, 839–844. [Google Scholar] [CrossRef] [PubMed]
- Frehlich, R.G.; Kavaya, M.J. Coherent laser radar performance for general atmospheric refractive turbulence. Appl. Opt. 1991, 30, 5325–5352. [Google Scholar] [CrossRef]
- Sonnenschein, C.M.; Horrigan, F.A. Signal-to-noise relationships for coaxial systems that heterodyne backscatter from the atmosphere. Appl. Opt. 1971, 10, 1600–1604. [Google Scholar] [CrossRef] [PubMed]
- Hill, C. Coherent Focused Lidars for Doppler Sensing of Aerosols and Wind. Remote Sens. 2018, 10, 466. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.Y. Optimal truncation of a lidar transmitted beam. Appl. Opt. 1988, 27, 4470–4474. [Google Scholar] [CrossRef]
- Rye, B.J.; Frehlich, R.G. Optimal truncation and optical efficiency of an apertured coherent lidar focused on an incoherent backscatter target. Appl. Opt. 1992, 31, 2891–2899. [Google Scholar] [CrossRef]
- Zhao, Y.; Post, M.J.; Hardesty, R.M. Receiving efficiency of pulsed coherent lidars. 1: Theory. Appl. Opt. 1990, 29, 4111–4119. [Google Scholar] [CrossRef]
- Fujii, T.; Fukuchi, T. Laser Remote Sensing, 1st ed.; CRC Press Taylor: Boca Raton, FL, USA; Francis Group: Abingdon, UK, 2005; pp. 469–722. [Google Scholar]
- Xia, H.Y.; Sun, D.S.; Yang, Y.H.; Shen, F.H.; Dong, J.J.; Kobayashi, T. Fabry-Perot interferometer based Mie Doppler lidar for low tropospheric wind observation. Appl. Opt. 2007, 46, 7120–7131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Z.; Liu, B.; Li, Z. Wind measurements with incoherent Doppler lidar based on iodine filters at night and day. Appl. Phys. B 2007, 88, 327–335. [Google Scholar] [CrossRef]
- McKay, J.A. Assessment of a multibeam Fizeau wedge interferometer for Doppler wind lidar. Appl. Opt. 2002, 41, 1760–1767. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, P.J.; Pedersen, C. Monostatic coaxial 1.5 μm laser Doppler velocimeter using a scanning Fabry-Perot interferometer. Opt. Express 2013, 21, 21105–21112. [Google Scholar] [CrossRef] [Green Version]
- Rodrigo, P.J.; Pedersen, C. Direct detection Doppler lidar using a scanning Fabry-Perot interferometer and a single-photon counting module. In Proceedings of the European Conference on Lasers and Electro-Optics-European Quantum Electronics Conference, Munich, Germany, 21–25 June 2015; p. CH_P_15. [Google Scholar]
- Shangguan, M.; Xia, H.; Wang, C.; Qiu, J.; Shentu, G.; Zhang, Q.; Dou, X.; Pan, J.W. All-fiber upconversion high spectral resolution wind lidar using a Fabry-Perot interferometer. Opt. Express 2016, 24, 19322–19336. [Google Scholar] [CrossRef]
- Xia, H.; Shangguan, M.; Wang, C.; Shentu, G.; Qiu, J.; Zhang, Q.; Dou, X.; Pan, J. Micro-pulse upconversion Doppler lidar for wind and visibility detection in the atmospheric boundary layer. Opt. Lett. 2016, 41, 5218–5221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pedersen, A.T.; Montes, B.F.; Pedersen, J.E.; Harris, M.; Mikkelsen, T. Demonstration of short-range wind lidar in a high- performance wind tunnel. In Proceedings of the EWEA 2012, Copenhagen, Denmark, 16–19 April 2012. [Google Scholar]
- Siegman, A.E. The antenna properties of optical heterodyne receivers. Appl. Opt. 1966, 5, 1588–1594. [Google Scholar] [CrossRef] [PubMed]
- Winzer, P.J.; Leeb, W.R. Fiber coupling efficiency for random light and its applications to lidar. Opt. Lett. 1998, 23, 986–988. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Rodrigo, P.J.; Iversen, T.F.Q.; Pedersen, C. Investigation of spherical aberration effects on coherent lidar performance. Opt. Express 2013, 21, 25670–25676. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, L.; Pedersen, C.; Rodrigo, P.J. CW Direct Detection Lidar with a Large Dynamic Range of Wind Speed Sensing in a Remote and Spatially Confined Volume. Remote Sens. 2021, 13, 3716. https://doi.org/10.3390/rs13183716
Meng L, Pedersen C, Rodrigo PJ. CW Direct Detection Lidar with a Large Dynamic Range of Wind Speed Sensing in a Remote and Spatially Confined Volume. Remote Sensing. 2021; 13(18):3716. https://doi.org/10.3390/rs13183716
Chicago/Turabian StyleMeng, Lichun, Christian Pedersen, and Peter John Rodrigo. 2021. "CW Direct Detection Lidar with a Large Dynamic Range of Wind Speed Sensing in a Remote and Spatially Confined Volume" Remote Sensing 13, no. 18: 3716. https://doi.org/10.3390/rs13183716
APA StyleMeng, L., Pedersen, C., & Rodrigo, P. J. (2021). CW Direct Detection Lidar with a Large Dynamic Range of Wind Speed Sensing in a Remote and Spatially Confined Volume. Remote Sensing, 13(18), 3716. https://doi.org/10.3390/rs13183716