Mid-Latitude Mesospheric Zonal Wave 1 and Wave 2 in Recent Boreal Winters
Abstract
:1. Introduction
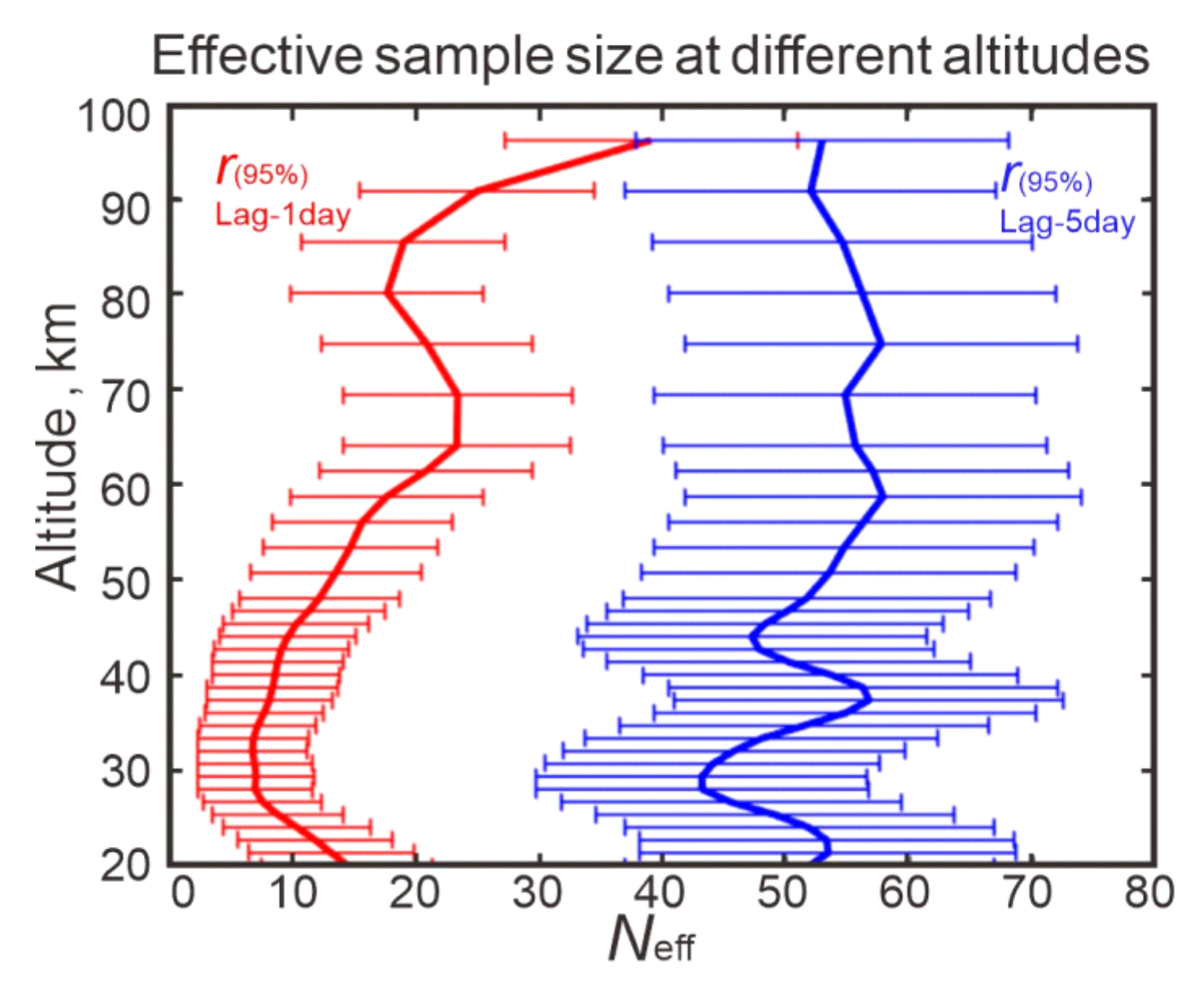
2. Materials and Methods
3. Results
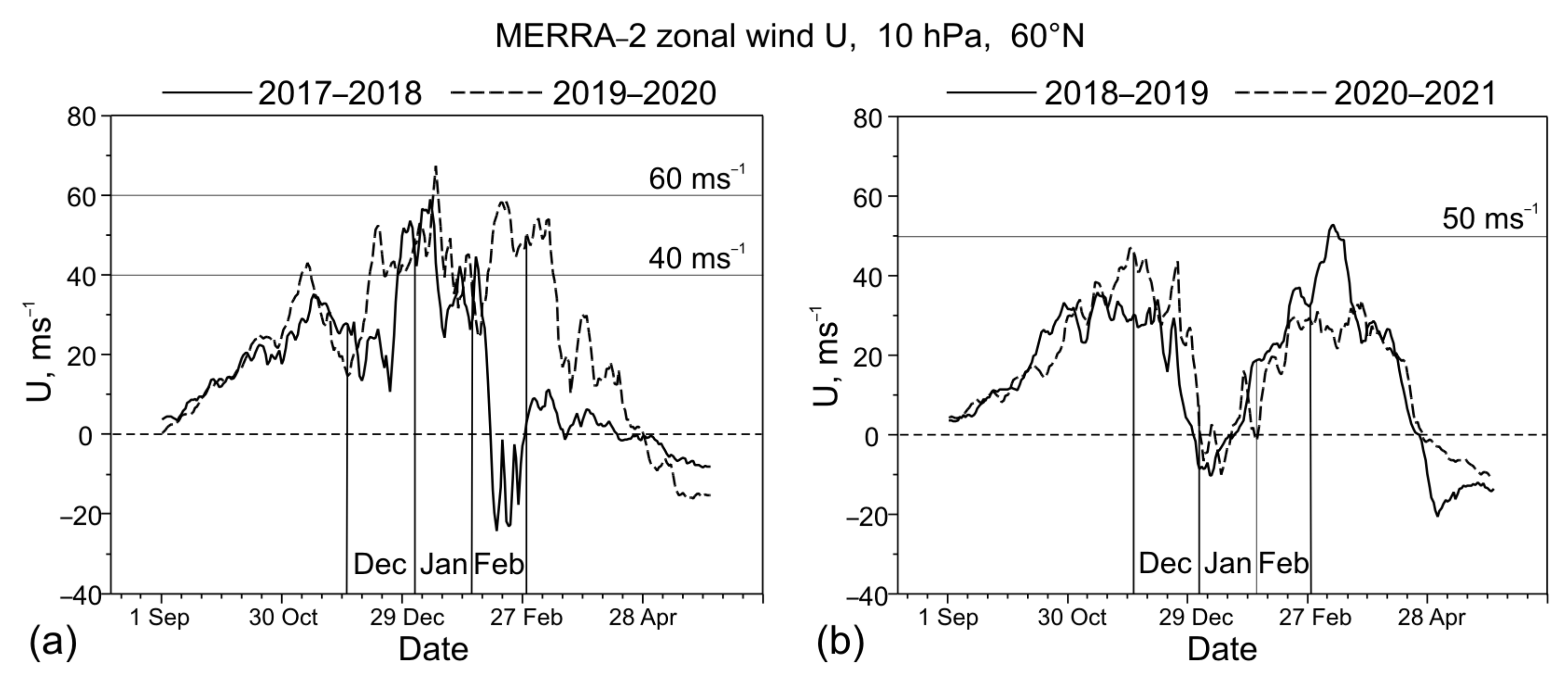
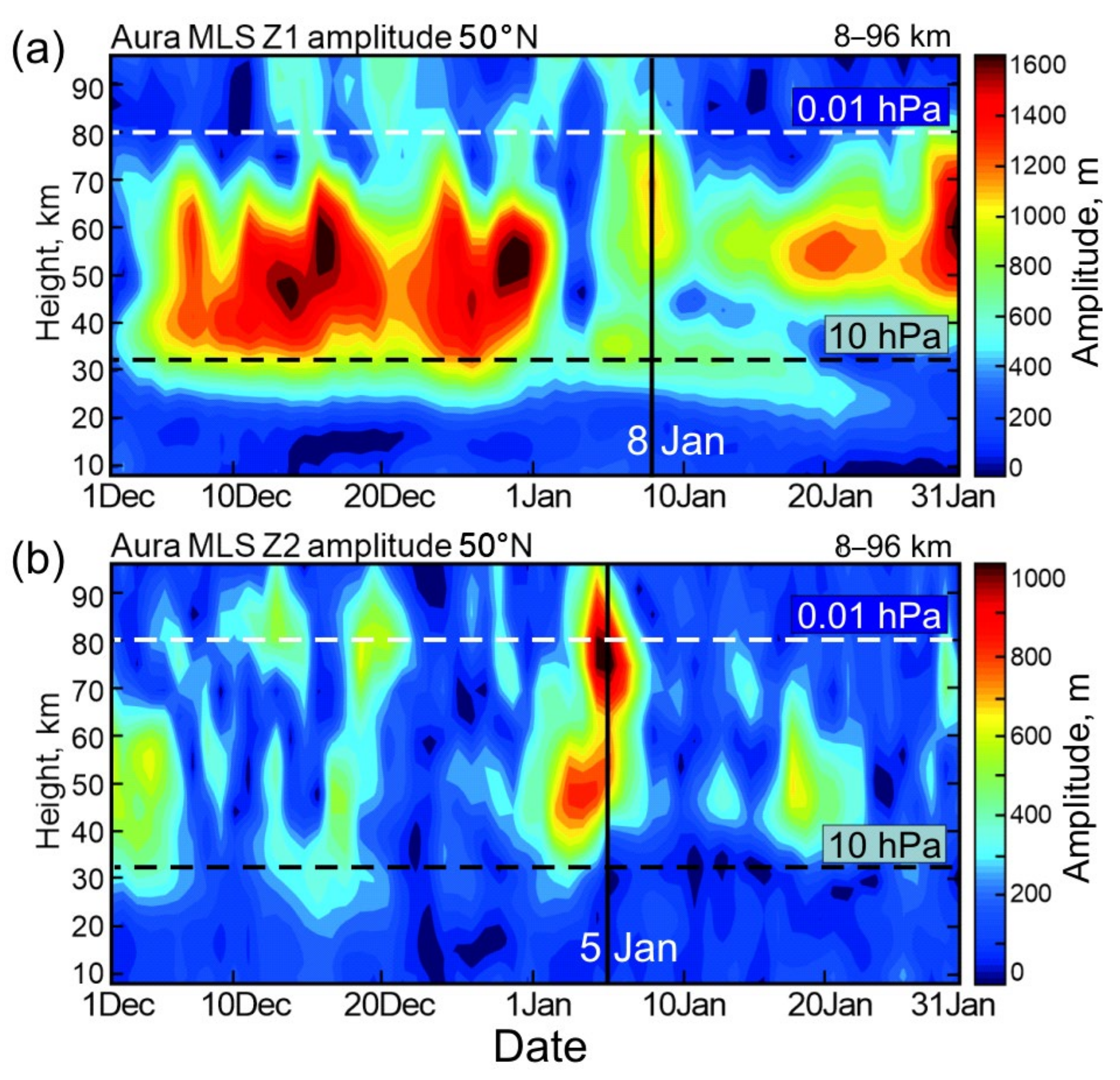
3.1. Mid-Latitude Manifestations of the Major SSW 2021
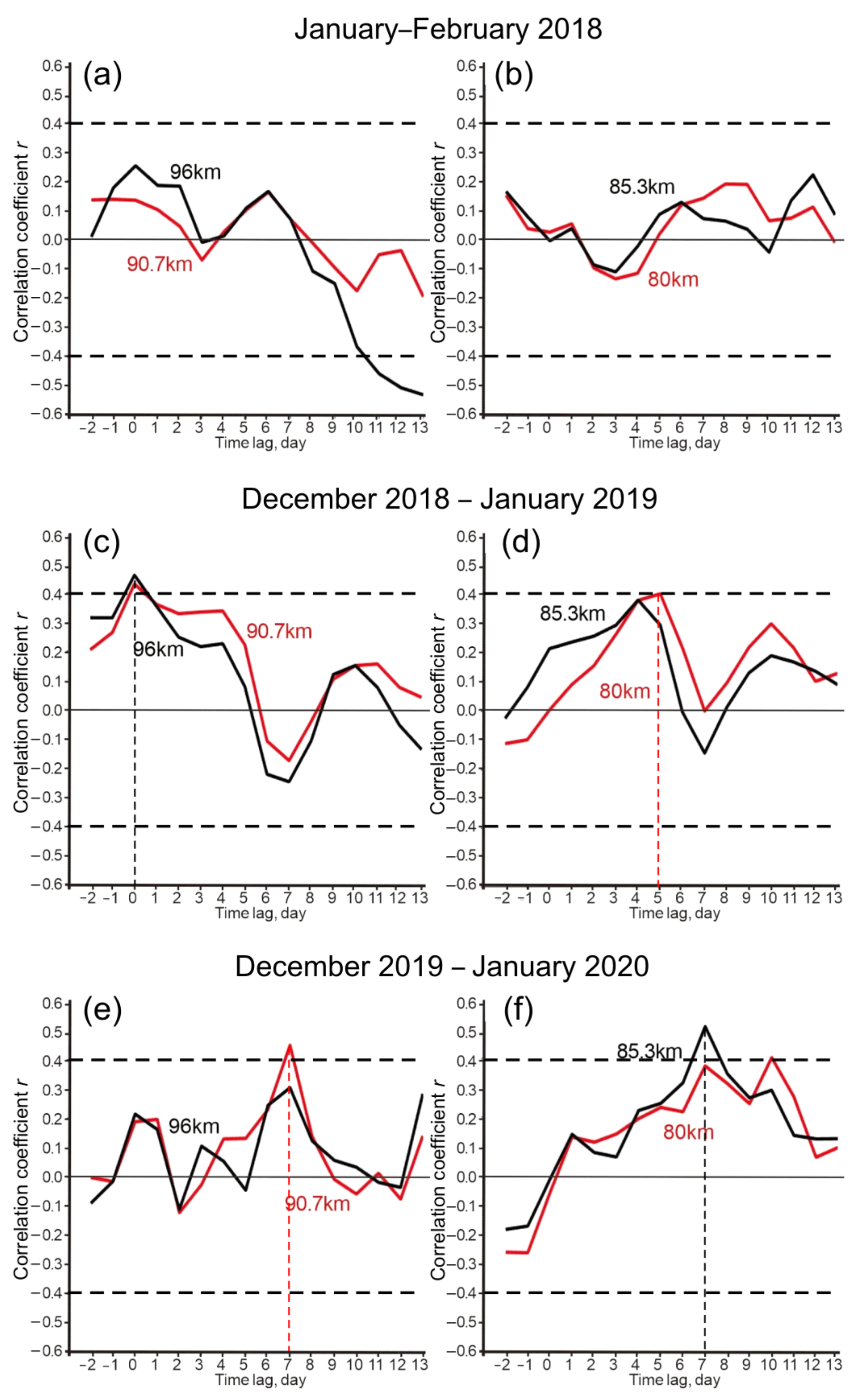
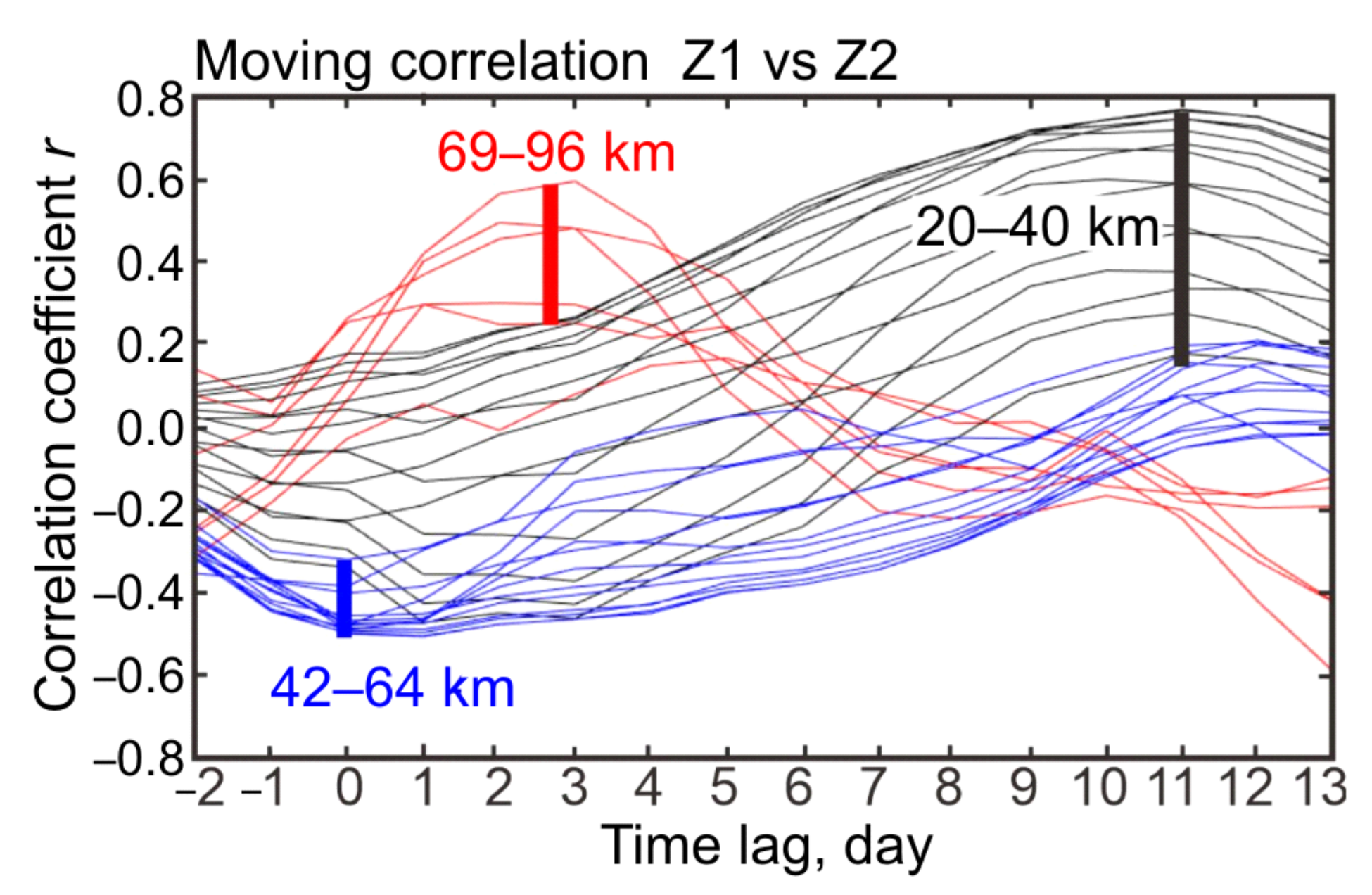
3.2. Moving Correlations between Wave 1 and Wave 2
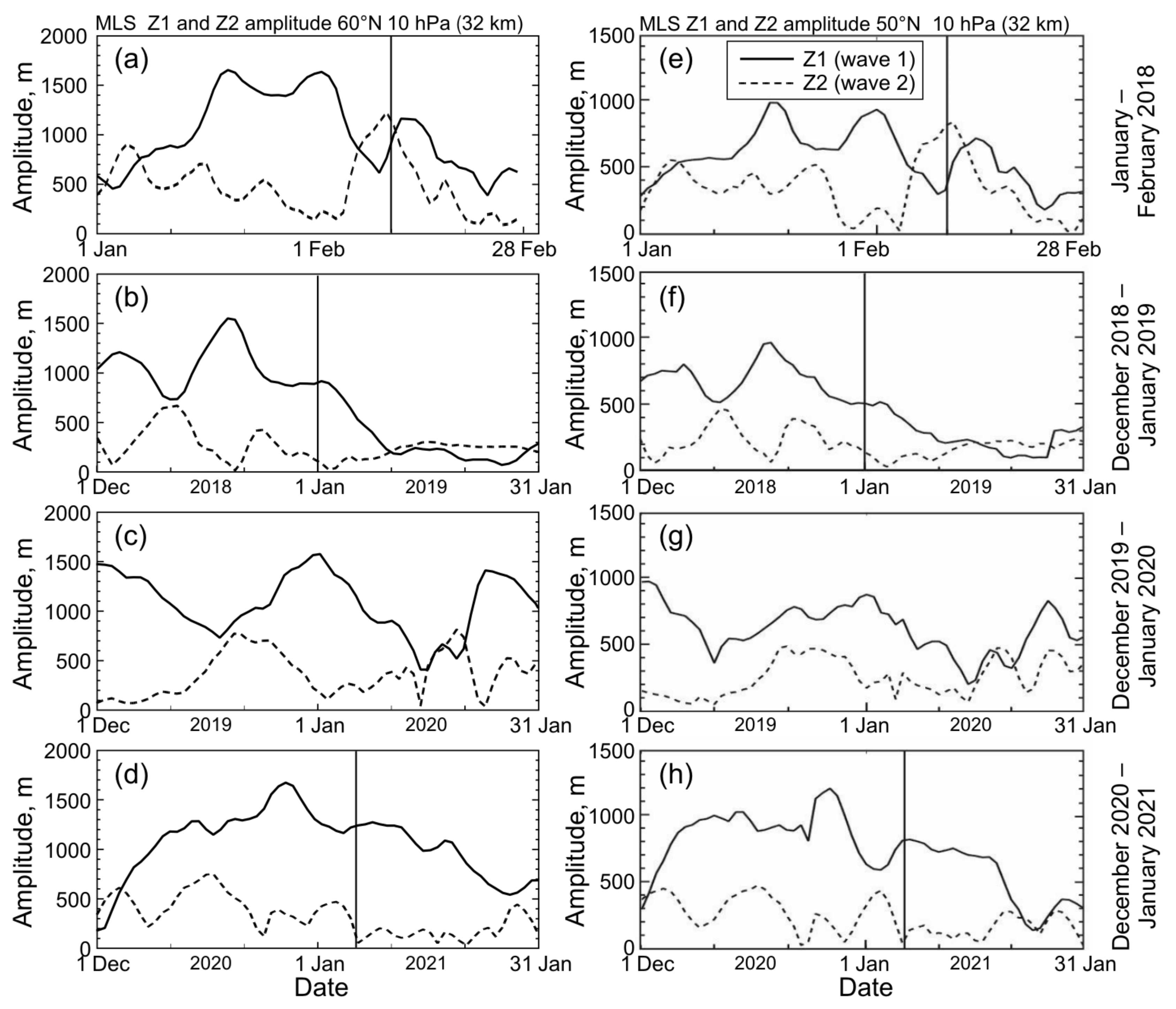
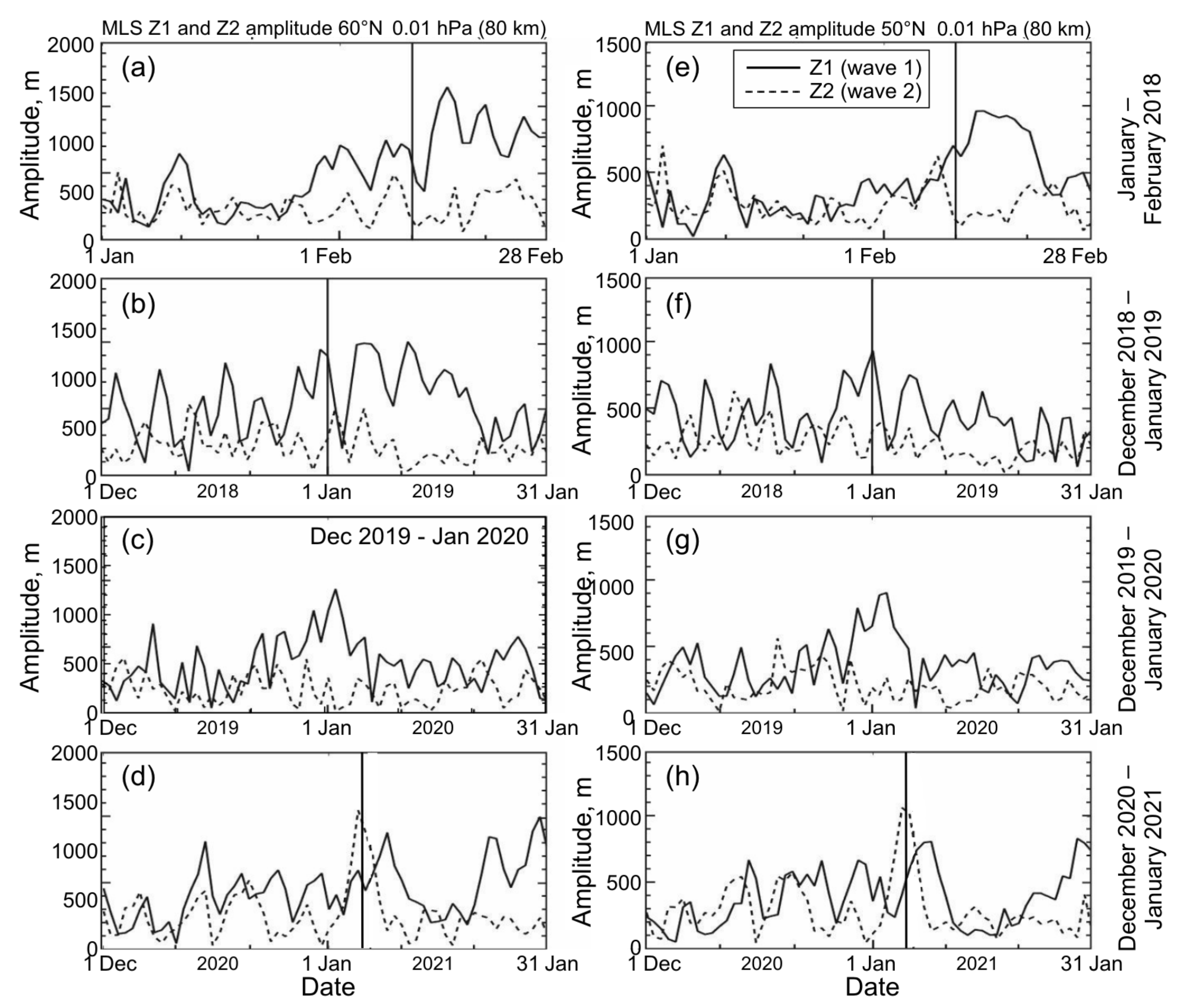
3.3. Periodicity of Z1 and Z2 Variations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Jan–Feb 2018 | Dec 2018–Jan 2019 | Dec 2019–Jan 2020 | Dec 2020–Jan 2021 | |
|---|---|---|---|---|
| Mesosphere (0.01 hPa, 80 km, 50°N) MLS | ||||
| Z1 | 428 | 436 | 361 | 381 |
| Z2 | 260 | 240 | 212 | 293 |
| Z1/Z2 | 1.6 | 1.8 | 1.7 | 1.3 |
| Mesosphere (0.01 hPa, 80 km, 60°N) MLS | ||||
| Z1 | 512 | 546 | 377 | 446 |
| Z2 | 240 | 218 | 191 | 258 |
| Z1/Z2 | 2.1 | 2.5 | 2.0 | 1.7 |
| Stratosphere (10 hPa, 32 km, 50°N) MLS | ||||
| Z1 | 586 | 470 | 623 | 726 |
| Z2 | 355 | 193 | 255 | 238 |
| Z1/Z2 | 1.6 | 2.4 | 2.4 | 3.1 |
| Stratosphere (10 hPa, 32 km, 60°N) MLS | ||||
| Z1 | 985 | 711 | 1076 | 1054 |
| Z2 | 490 | 267 | 361 | 330 |
| Z1/Z2 | 2.0 | 2.7 | 3.0 | 3.2 |
| Stratosphere (10 hPa, 32 km, 60°N) MERRA | ||||
| Z1 | 1003 | 691 | 1081 | 1055 |
| Z2 | 482 | 261 | 358 | 326 |
| Z1/Z2 | 2.1 | 2.6 | 3.0 | 3.2 |
References
- Matsuno, T. A dynamical model of the stratospheric sudden warming. J. Atmos. Sci. 1971, 28, 1479–1494. [Google Scholar] [CrossRef]
- Butler, A.H.; Gerber, E.P. Optimizing the definition of a sudden stratospheric warming. J. Clim. 2018, 31, 2337–2344. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Ayarzagüena, B.; Birner, T.; Butchart, N.; Butler, A.H.; Charlton-Perez, A.J.; Domeisen, D.I.V.; Garfinkel, C.I.; Garny, H.; Gerber, E.P.; et al. Sudden stratospheric warmings. Rev. Geophys. 2021, 59, e2020RG000708. [Google Scholar] [CrossRef]
- Manney, G.L.; Schwartz, M.J.; Krüger, K.; Santee, M.L.; Pawson, S.; Lee, J.N.; Daffer, W.H.; Fuller, R.A.; Livesey, N.J. Aura Microwave Limb Sounder observations of dynamics and transport during the record-breaking 2009 Arctic stratospheric major warming. Geophys. Res. Lett. 2009, 36, L12815. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Milinevsky, G.; Evtushevsky, O.; Klekociuk, A.; Han, W.; Grytsai, A.; Antyufeyev, O.; Shi, Y.; Ivaniha, O.; Shulga, V. Planetary wave spectrum in the stratosphere–mesosphere during sudden stratospheric warming 2018. Remote Sens. 2021, 13, 1190. [Google Scholar] [CrossRef]
- Baldwin, M.; Birner, T.; Brasseur, G.; Burrows, J.; Butchart, N.; Garcia, R.; Geller, M.; Gray, L.; Hamilton, K.; Harnik, N.; et al. 100 years of progress in understanding the stratosphere and mesosphere. Meteorol. Monogr. 2019, 59, 27. [Google Scholar] [CrossRef]
- Matsuno, T. Vertical propagation of stationary planetary waves in the winter Northern Hemisphere. J. Atmos. Sci. 1970, 27, 871–883. [Google Scholar] [CrossRef] [Green Version]
- Plumb, R.A. Planetary waves and the extratropical winter stratosphere. In The Stratosphere: Dynamics, Transport, and Chemistry; Geophysical Monograph Series; Wiley: Hoboken, NJ, USA, 2010; Volume 190, pp. 23–41. [Google Scholar]
- Smith, A.K.; Gille, J.C.; Lyjak, L.V. Wave–wave interactions in the stratosphere: Observations during quiet and active wintertime periods. J. Atmos. Sci. 1984, 41, 363–373. [Google Scholar] [CrossRef] [Green Version]
- Lindgren, E.A.; Sheshadri, A. The role of wave–wave interactions in sudden stratospheric warming formation. Weather Clim. Dynam. 2020, 1, 93–109. [Google Scholar] [CrossRef] [Green Version]
- Labitzke, K. Interannual variability of the winter stratosphere in the Northern Hemisphere. Mon. Wea. Rev. 1977, 105, 762–770. [Google Scholar] [CrossRef]
- McIntyre, M.E. How well do we understand the dynamics of stratospheric warmings? J. Meteor. Soc. Japan 1982, 60, 37–65. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.K. Observation of wave–wave interaction in the stratosphere. J. Atmos. Sci. 1983, 40, 2484–2496. [Google Scholar] [CrossRef] [Green Version]
- Robinson, W.A. A model of the wave 1–wave 2 vacillation in the winter stratosphere. J. Atmos. Sci. 1985, 42, 2289–2304. [Google Scholar] [CrossRef] [Green Version]
- Watt-Meyer, O.; Kushner, P.J. Decomposition of atmospheric disturbances into standing and traveling components, with application to Northern Hemisphere planetary waves and stratosphere–troposphere coupling. J. Atmos. Sci. 2015, 72, 787–802. [Google Scholar] [CrossRef] [Green Version]
- Charney, J.; Drazin, P. Propagation of planetary-scale disturbances from the lower into the upper atmosphere. J. Geophys. Res. 1961, 66, 83–109. [Google Scholar] [CrossRef]
- Stray, N.H.; Orsolini, Y.J.; Espy, P.J.; Limpasuvan, V.; Hibbins, R.E. Observations of planetary waves in the mesosphere–lower thermosphere during stratospheric warming events. Atmos. Chem. Phys. 2015, 15, 4997–5005. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.K. The origin of stationary planetary waves in the upper mesosphere. J. Atmos. Sci. 2003, 60, 3033–3041. [Google Scholar] [CrossRef]
- Chandran, A.; Garcia, R.R.; Collins, R.L.; Chang, L.C. Secondary planetary waves in the middle and upper atmosphere following the stratospheric sudden warming event of January 2012. Geophys. Res. Lett. 2013, 40, 1861–1867. [Google Scholar] [CrossRef]
- Matthias, V.; Ern, M. On the origin of the mesospheric quasi-stationary planetary waves in the unusual Arctic winter 2015/2016. Atmos. Chem. Phys. 2018, 18, 4803–4815. [Google Scholar] [CrossRef] [Green Version]
- Pancheva, D.; Mukhtarov, P.; Mitchell, N.J.; Andonov, B.; Merzlyakov, E.; Singer, W.; Murayama, Y.; Kawamura, S.; Xiong, J.; Wan, W.; et al. Latitudinal wave coupling of the stratosphere and mesosphere during the major stratospheric warming in 2003/2004. Ann. Geophys. 2008, 26, 467–483. [Google Scholar] [CrossRef]
- Garcia, R.R.; Lieberman, R.; Russell, J.M., III; Mlynczak, M.G. Large-scale waves in the mesosphere and lower thermosphere observed by SABER. J. Atmos. Sci. 2005, 62, 4384–4399. [Google Scholar] [CrossRef]
- Gu, S.-Y.; Dou, X.; Pancheva, D.; Yi, W.; Chen, T. Investigation of the abnormal quasi 2-day wave activities during the sudden stratospheric warming period of January 2006. J. Geophys. Res. Space Phys. 2018, 123, 6031–6041. [Google Scholar] [CrossRef]
- Wang, Y.; Shulga, V.; Milinevsky, G.; Patoka, A.; Evtushevsky, O.; Klekociuk, A.; Han, W.; Grytsai, A.; Shulga, D.; Myshenko, V.; et al. Winter 2018 major sudden stratospheric warming impact on midlatitude mesosphere from microwave radiometer measurements. Atmos. Chem. Phys. 2019, 19, 10303–10317. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Shulga, V.; Ivaniha, O.; Wang, Y.; Evtushevsky, O.; Milinevsky, G.; Klekociuk, A.; Patoka, A.; Han, W.; Shulga, D. Comparison of major sudden stratospheric warming Impacts on the mid-latitude mesosphere based on local microwave radiometer CO observations in 2018 and 2019. Remote Sens. 2020, 2, 3950. [Google Scholar] [CrossRef]
- Lee, S.H. The January 2021 sudden stratospheric warming. Weather 2021, 76, 135–136. [Google Scholar] [CrossRef]
- Wright, C.J.; Hall, R.J.; Banyard, T.P.; Hindley, N.P.; Mitchell, D.M.; Seviour, W.J.M. Dynamical and surface impacts of the January 2021 sudden stratospheric warming in Novel Aeolus Wind observations, MLS and ERA5. Weather Clim. Dynam. Discuss. 2021. preprint, under review. [Google Scholar] [CrossRef]
- Lu, Q.; Rao, J.; Liang, Z.; Guo, D.; Luo, J.; Liu, S.; Wang, C.; Wang, T. The sudden stratospheric warming in January 2021. Environ. Res. Lett. 2021, 16, 084029. [Google Scholar] [CrossRef]
- Schwartz, M.; Livesey, N.; Read, W. MLS/Aura Level 2 Geopotential Height V004, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), 2015. Available online: https://disc.gsfc.nasa.gov/datasets/ML2GPH_004/summary/ (accessed on 15 July 2021).
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- MERRA-2: The Goddard Earth Sciences Data and Information Services Center. Available online: https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/ (accessed on 15 July 2021).
- Brigham, E.O. The Fast Fourier Transform; Prentice Hall: Englewood Cliffs, NJ, USA, 1974; 252p. [Google Scholar]
- Livezey, R.E.; Chen, W.Y. Statistical field significance and its determination by Monte Carlo Techniques. Mon. Wea. Rev. 1983, 111, 46–59. [Google Scholar] [CrossRef] [Green Version]
- Ciasto, L.M.; Thompson, D.W.J. Observations of large-scale ocean-atmosphere interaction in the Southern Hemisphere. J. Clim. 2008, 21, 1244–1259. [Google Scholar] [CrossRef]
- Wang, Y.; Evtushevsky, O.; Milinevsky, G.; Shulga, V.; Yukhymchuk, Y.; Han, W.; Shulga, D.; Grytsai, A. The major sudden stratospheric warming impact on mid-latitude surface weather. Europ. Phys. J. Web Conf. 2020, 237, 04007. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Widmann, M.; Dymnikov, V.P.; Wallace, J.M.; Bladé, I. The effective number of spatial degrees of freedom of a time-varying field. J. Clim. 1999, 12, 1990–2009. [Google Scholar] [CrossRef]
- Domeisen, D.I.V.; Martius, O.; Jiménez-Esteve, B. Rossby wave propagation into the Northern Hemisphere stratosphere: The role of zonal phase speed. Geophys. Res. Lett. 2018, 45, 2064–2071. [Google Scholar] [CrossRef] [Green Version]
- Salby, M.L. Fundamentals of Atmospheric Physics; Academic Press: San Diego, CA, USA, 1996; 627p, ISBN -13: 978-0-12-615160-2. [Google Scholar]

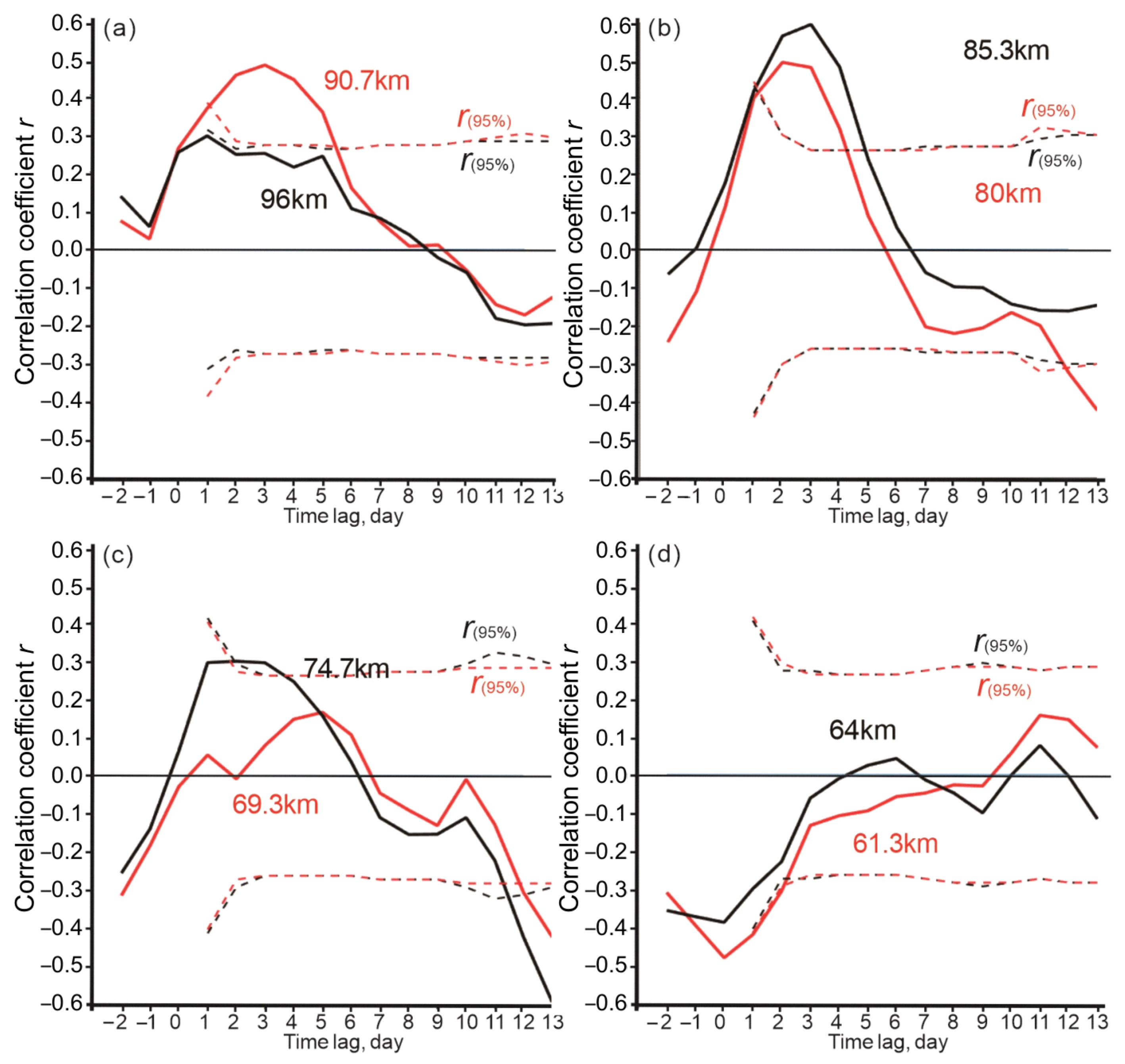

| Altitude | 75 km | 80 km | 85 km | 90 km |
|---|---|---|---|---|
| Wave1 | 0.70 | 0.77 | 0.78 | 0.75 |
| Wave2 | 0.70 | 0.72 | 0.67 | 0.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Evtushevsky, O.; Shulga, V.; Milinevsky, G.; Klekociuk, A.; Andrienko, Y.; Han, W. Mid-Latitude Mesospheric Zonal Wave 1 and Wave 2 in Recent Boreal Winters. Remote Sens. 2021, 13, 3749. https://doi.org/10.3390/rs13183749
Shi Y, Evtushevsky O, Shulga V, Milinevsky G, Klekociuk A, Andrienko Y, Han W. Mid-Latitude Mesospheric Zonal Wave 1 and Wave 2 in Recent Boreal Winters. Remote Sensing. 2021; 13(18):3749. https://doi.org/10.3390/rs13183749
Chicago/Turabian StyleShi, Yu, Oleksandr Evtushevsky, Valerii Shulga, Gennadi Milinevsky, Andrew Klekociuk, Yulia Andrienko, and Wei Han. 2021. "Mid-Latitude Mesospheric Zonal Wave 1 and Wave 2 in Recent Boreal Winters" Remote Sensing 13, no. 18: 3749. https://doi.org/10.3390/rs13183749
APA StyleShi, Y., Evtushevsky, O., Shulga, V., Milinevsky, G., Klekociuk, A., Andrienko, Y., & Han, W. (2021). Mid-Latitude Mesospheric Zonal Wave 1 and Wave 2 in Recent Boreal Winters. Remote Sensing, 13(18), 3749. https://doi.org/10.3390/rs13183749








