Optimizing the Sowing Date to Improve Water Management and Wheat Yield in a Large Irrigation Scheme, through a Remote Sensing and an Evolution Strategy-Based Approach
Abstract
:1. Introduction
1.1. Background and Context
1.2. State of the Art
2. Materials and Methods
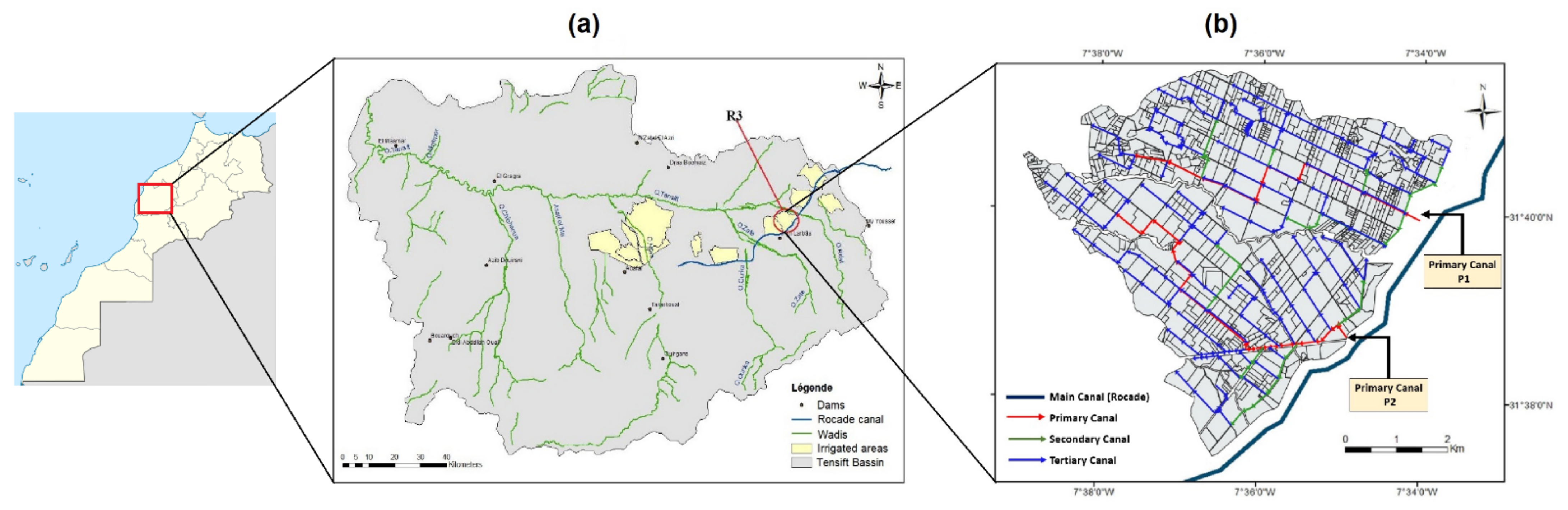
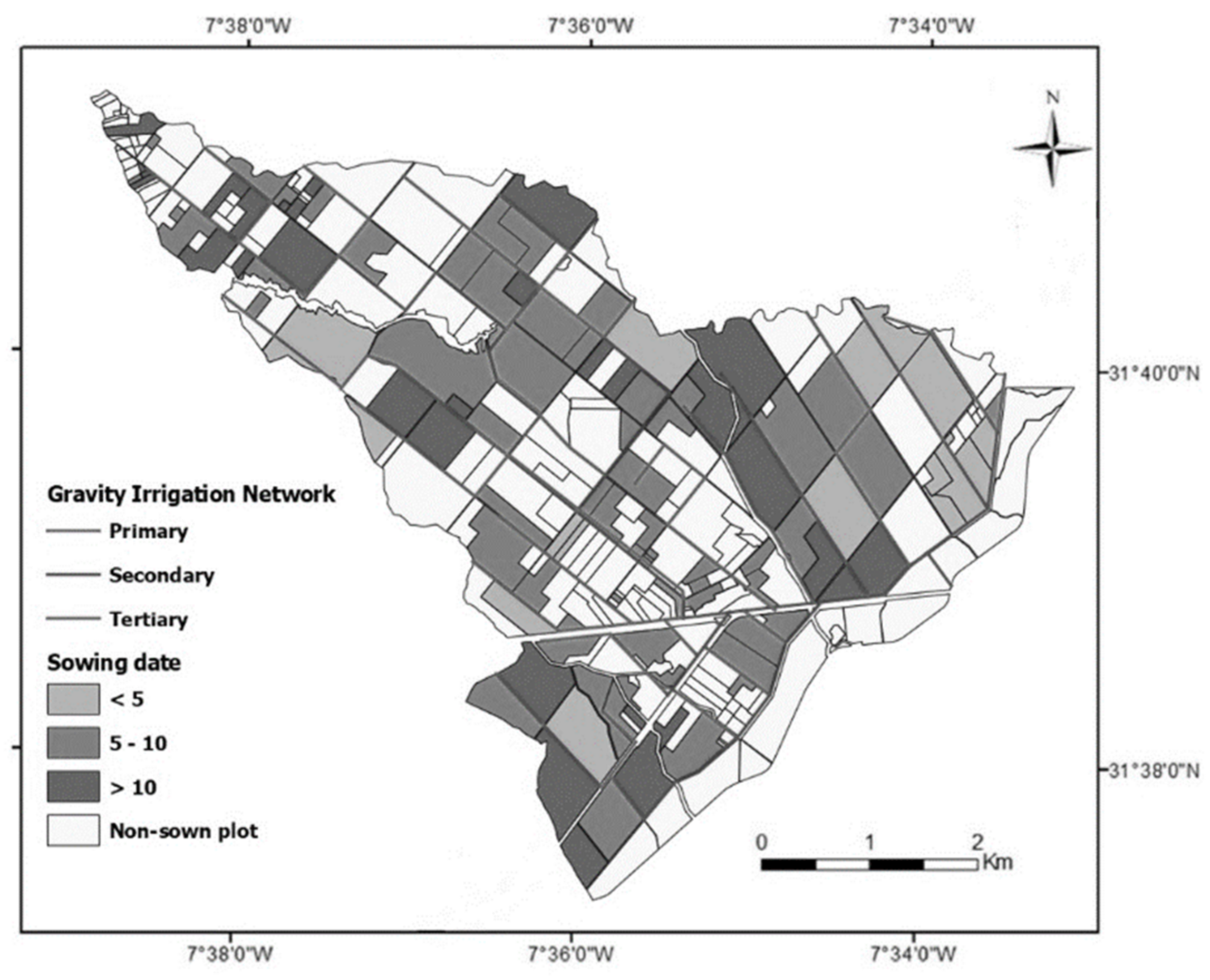
2.1. Study Area
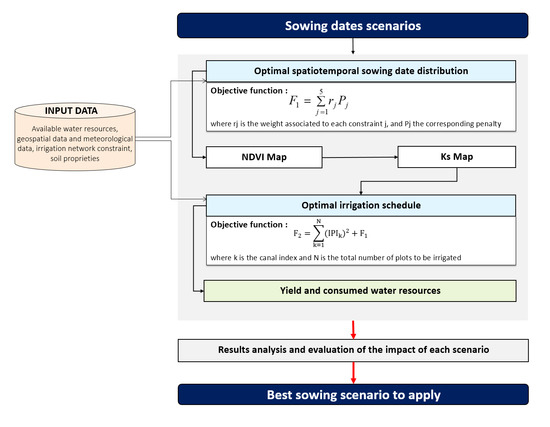
2.2. The Proposed Approach
- At the beginning of the agricultural season, the spatiotemporal distribution of the sowing dates over the irrigation scheme is optimized, considering the irrigation network constraints and the adopted sowing scenario. The number of plots to be sown in a same day is defined based mainly on the capacity of the irrigation network, i.e., the maximum volume of water that can be delivered to the plots irrigated by the same canal, according to its maximum discharge and location (tertiary, secondary or primary). Thus, the total area that will be sown in a given day is determined such that it can be completely irrigated in one single day during an irrigation round;
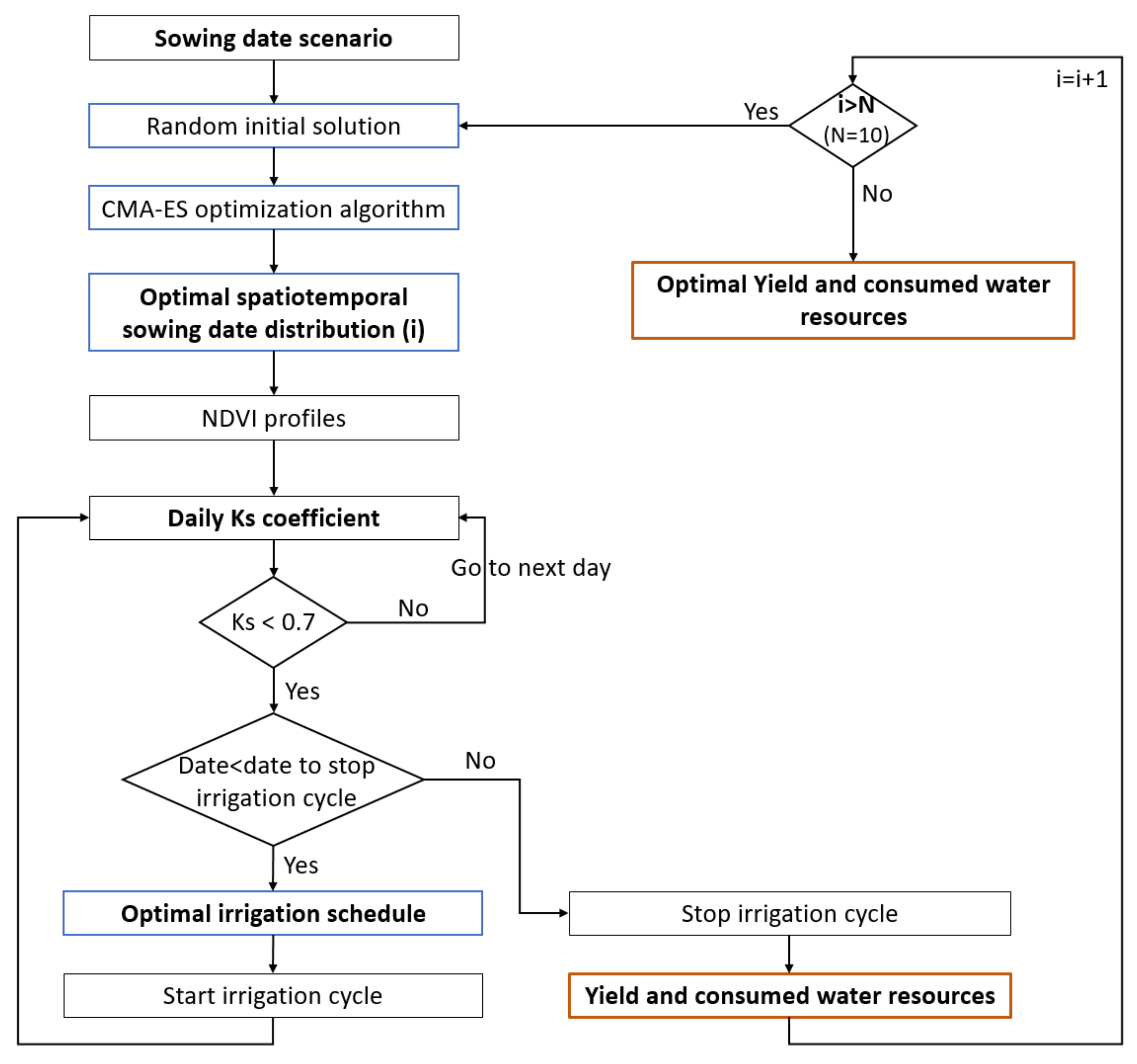
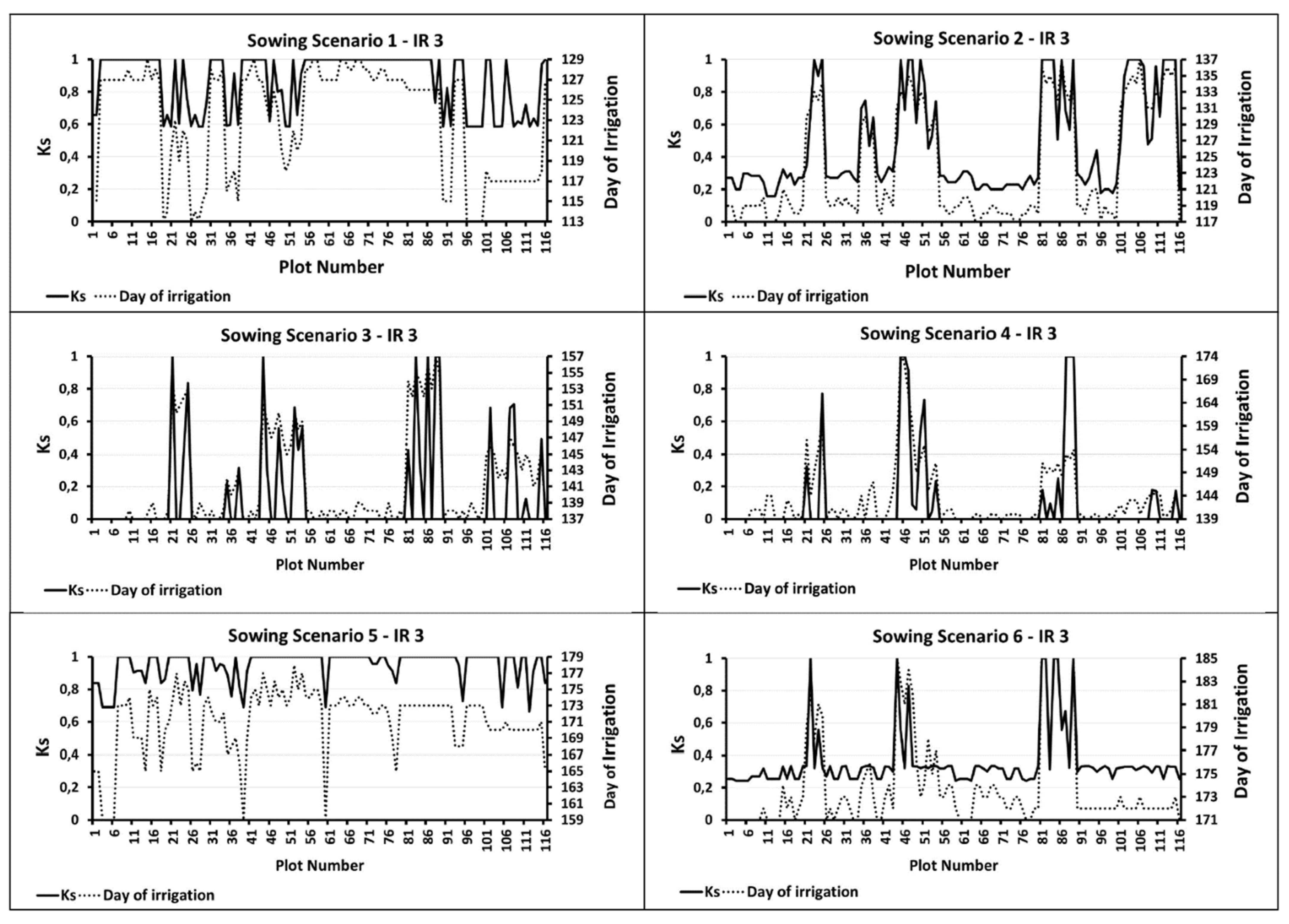
- During the agricultural season, before starting each irrigation round, we elaborate an optimal irrigation planning (irrigation date and irrigation water requirement for each plot) over the irrigation scheme according to the sowing calendar scenario and the crop water stress levels in each field. The starting date of each irrigation round is calculated based on the water stress coefficient (Ks), which is used to measure the soil water deficit levels for the crop, as defined in the FAO56 model [61], based on the Normalized Difference Vegetation Index (NDVI), which is a common and widely used remote sensing index to assess the green biomass and the state and health of crops by measuring the difference between near-infrared and red light. Thus, the Ks is equal to 1 at the day of sowing (because the farmers sow after a heavy rainfall event or a pre-irrigation at the beginning of the season). Then, Ks is calculated using the daily soil water balance at the root zone (see Section 2.3). An irrigation round is decided when the Ks reaches a value less than 0.7 at most for 5% of the total cultivated area. This threshold of Ks has been identified as the value above which the water stress does not affect significantly wheat yield [36,62,63]. Then, for each irrigation round, the spatiotemporal irrigation planning is optimized based on the Irrigation Priority Index (IPI) [56] (see Section 2.4 and Section 2.6). When a plot is irrigated, the Ks coefficient becomes equal to 1 and the process continues to define the starting of the next irrigation round. Additionally, no more irrigation is decided for wheat crop at the end of the season when the canopy cover reaches the half of the maximum canopy cover during the senescence stage (see Section 2.2);
- At the end of the agricultural season, an evaluation of the irrigation water consumed and the final yield expected is conducted in order to decide on the most optimal spatiotemporal sowing date calendar to be adopted, i.e., the best recommendations concerning the cultivation schedule which will allow to increase incomes and reduce the use of water resources during the agricultural season.
2.3. Dataset
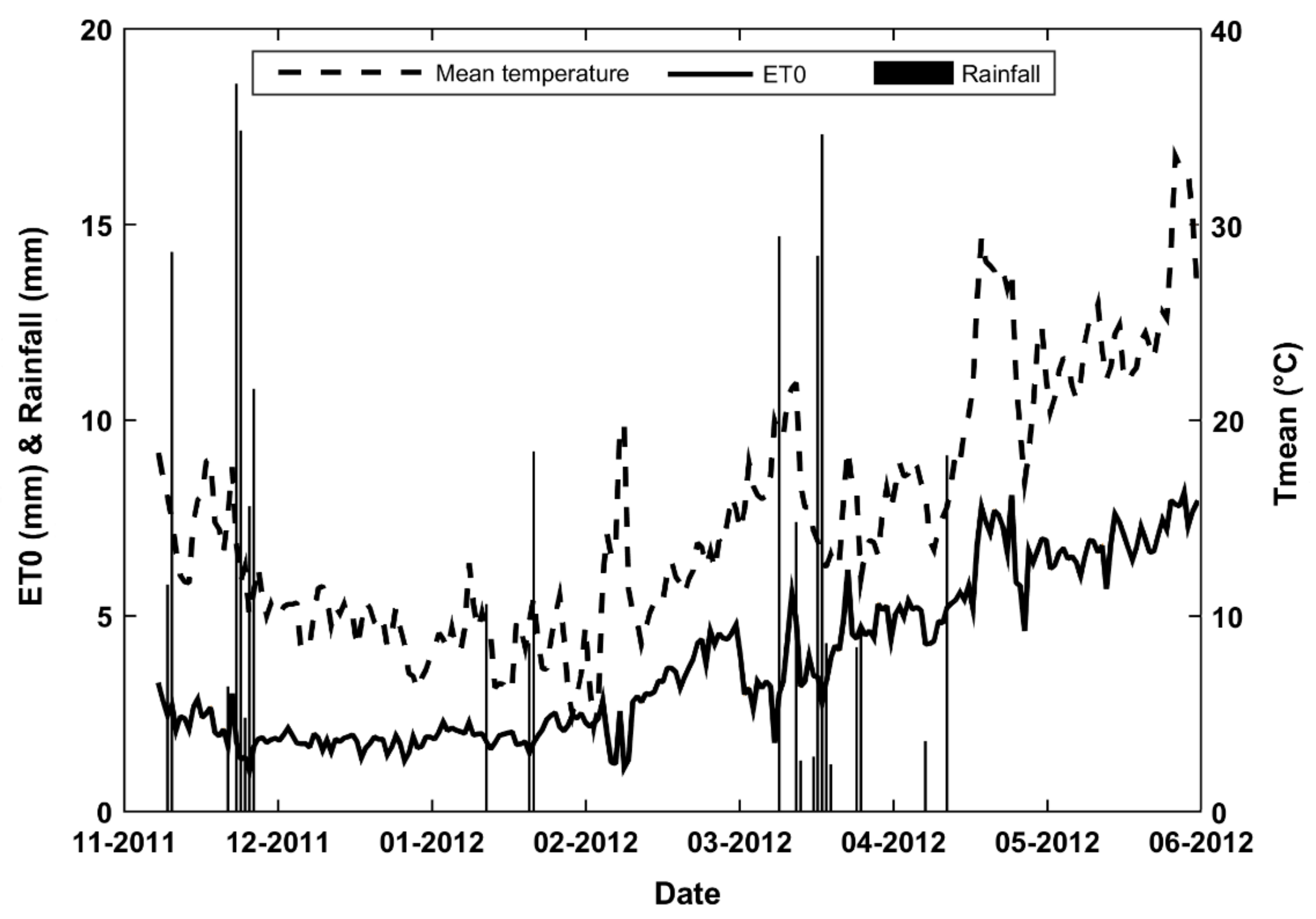
2.3.1. Meteorological Data
2.3.2. Irrigation Water Supply
2.3.3. Wheat Fields Identification
2.3.4. Applied Sowing Dates Identification
2.3.5. Irrigation Network Identification
- Canals: line type, characterized by an id number, maximum discharge, the flow direction, the geographic coordinates, the category (primary, secondary or tertiary) and plots that are fed;
- Water intakes: point type, representing the devices that supply a plot or a set of plots. Each intake is characterized by an id number, the geographical coordinates, the maximum discharge, the number of plots it supply, the opening and closing times and the id number of the canal to which it is linked;
- Plots: polygon type, characterized by an id number, the farmer’s name, the type of crop, the id number of the canal and the water intake, the date of sowing, the overall area, the irrigated area and the effective irrigation water applied in 2011–2012 season (in terms of time and quantity).
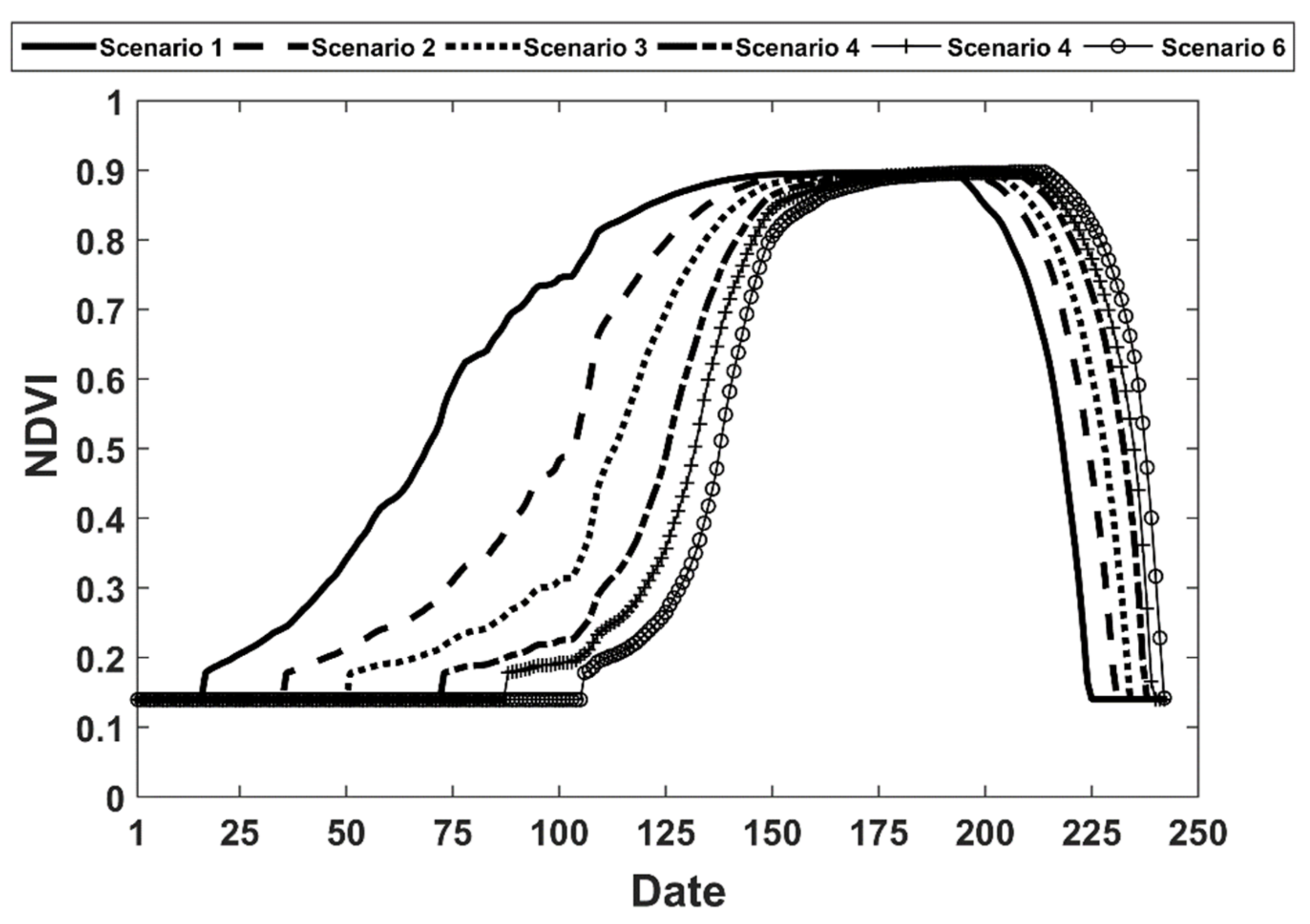
2.4. NDVI Profiles Simulation
- Exponential growth (CC <= CCx/2):
- Exponential decay (CC > CCx/2):
- The decline in green crop canopy is described by:where CC is the canopy cover at time t (%), CC0 is the initial canopy cover at t = 0 (%), CCx is the maximum canopy cover at the start of senescence (t = 0), CGC is the canopy growth coefficient (% or cumulative growing degree days), CDC is the canopy decline coefficient (% or cumulative growing degree days), and t is time (days or cumulative growing degree days).
2.5. Spatialized Estimates of Crop Water Needs and Water Stress Level
2.6. Grain Yield Estimation
2.6.1. NDVI-Based Approach
2.6.2. AquaCrop-Based Approach
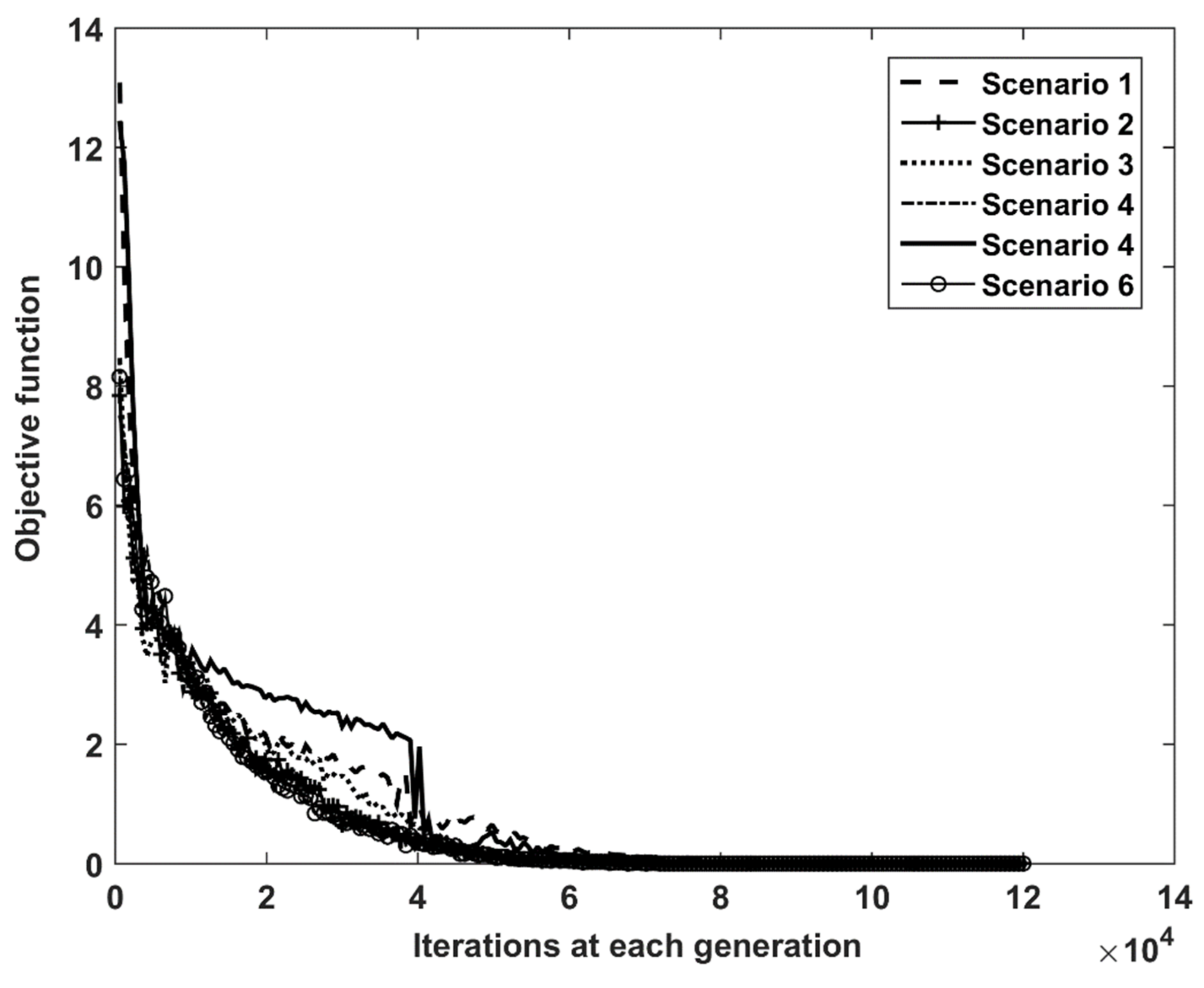
2.7. The Optimization Methodology
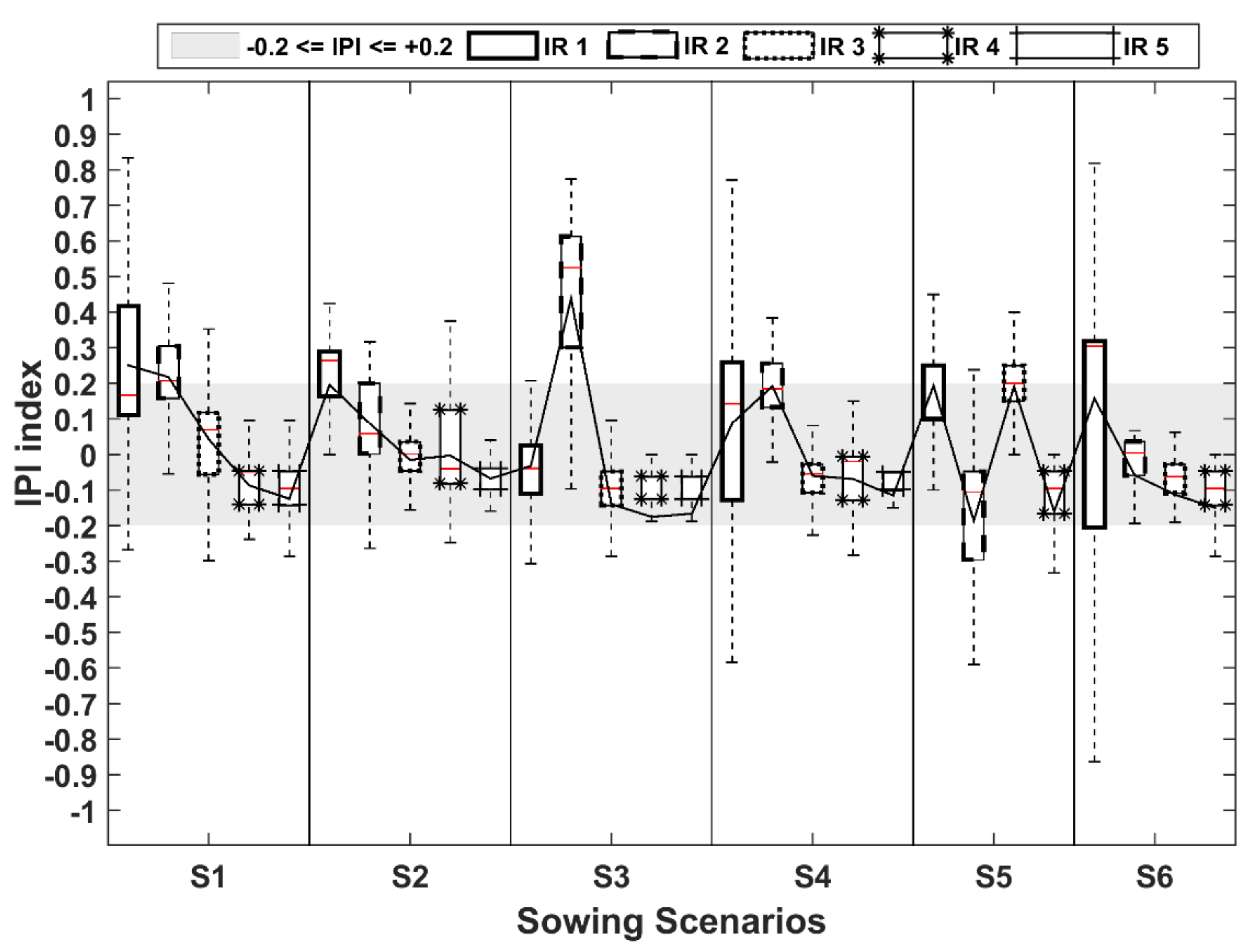
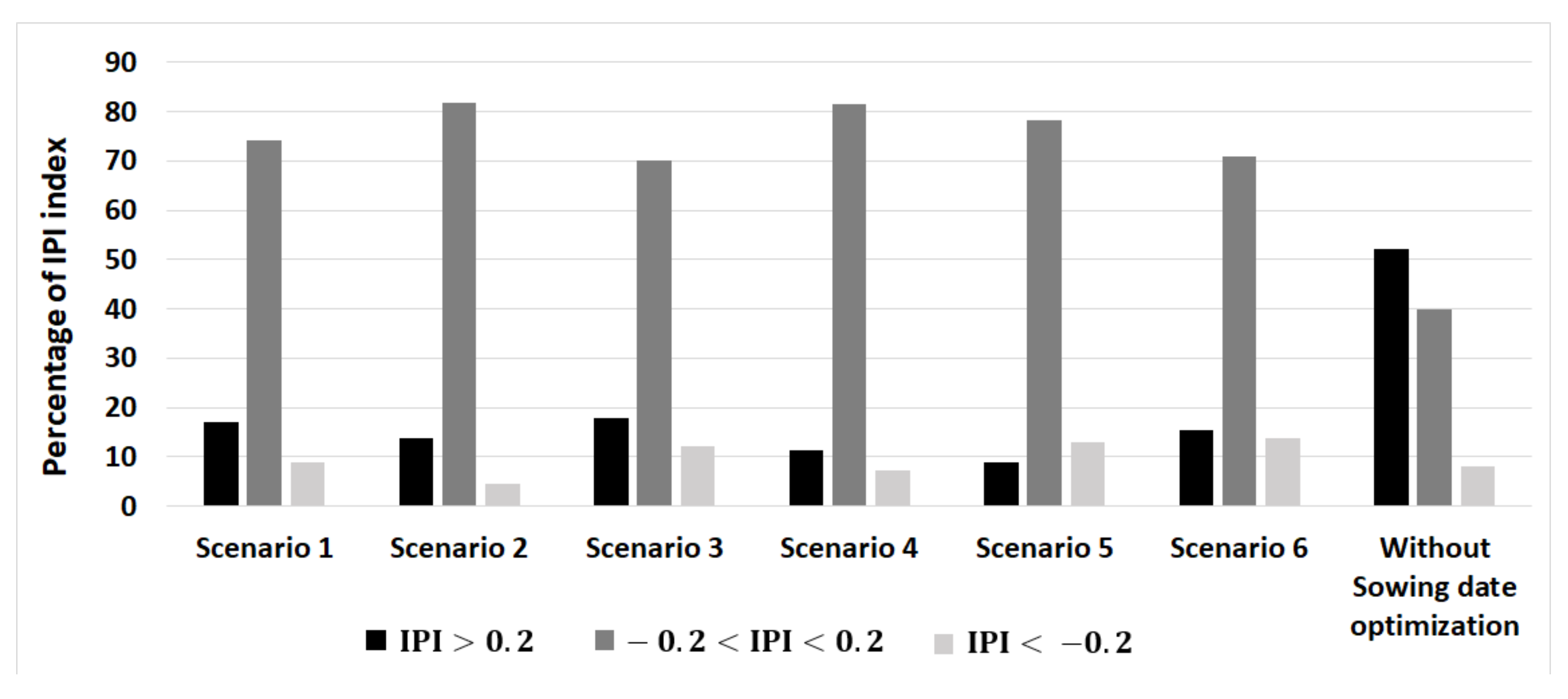
2.7.1. Irrigation Priority Index (IPI)
2.7.2. Sowing Date Optimization
- (a)
- Inputs: available water resources, geospatial data and meteorological data;
- (b)
- Decision variables: the sowing date of each plot. We have 116 plots to be sown, which means 116 decision variables are considered;
- (c)
- Optimization constraints: we identified five constraints which we present by a decreasing level of priority.
- The capacity constraint: supplies must never exceed the total capacity of the canal. This constraint is expressed by Equations (16) and (17):where , and are respectively the discharge of the primary, secondary and tertiary canals (in m3/s), i and j are respectively the tertiary and secondary canals’ number, opened at the same time;
- The interval constraint: all the irrigation tasks must be scheduled within the specified irrigation round interval, expressed by Equations (18) and (19):where is the starting date of the irrigation round; the opening time scheduled for canal i; E the allowed duration of the irrigation round, and Di the irrigation duration scheduled for the canal I;
- The overlap constraint: all the practical actions must be applied dependably (not simultaneously), considering the geographical distance between water intakes and the irrigation time span required for each plot supplied by the same canal;
- The traveling time: the time required for the operator to travel from one canal gate to another to start/stop an irrigation which depends on the distance between canals that can be significant. This time is calculated linearly based on the spatial distance between two intakes and assuming a moving speed of 30 km/h;
- The daily working time of operators: each scheduled task (start/stop an irrigation) must be scheduled within the specified working time that is between 8:00 h and 18:00 h;
- (d)
- The objective function: the first objective function aims to propose the best spatiotemporal sowing distribution which minimize the gravity irrigation network constraints by exploring the space of decision variables in an efficient manner. In case the constraints are not met, we adopt the penalty method by adding penalty function. Thus, the first objective function is defined by Equation (20):where rj is the weight associated to each constraint j, and Pj the corresponding penalty expressed by Equation (21):where N is the total number of plots to be irrigated and if the task is satisfying the constraints, otherwise.
2.7.3. Irrigation Scheduling Optimization
- (a)
- Inputs: available water resources, geospatial data, meteorological data, soil proprieties, NDVI profiles, and Ks;
- (b)
- Decision variables: During each irrigation round, two types of decisions must be made: when to irrigate the plots and in what order (i.e., the sequence and scheduling of the irrigations). The answer to these two questions is integrated into a single decision variable that consists of defining the start date to irrigate each plot (the stopping date is calculated based on the water amount to be supplied to a plot given the calculated irrigation duration and the constant flow rate of the tertiary canal). The stating date to irrigate the plots can therefore be considered as the only decision variables in the optimization process. In this work, 116 plots are scheduled, which means that 116 decision variables are considered during the optimization process while considering the constraints related to the irrigation network;
- (c)
- Optimization constraints: the same as the first optimization (i.e., irrigation network constraints);
- (d)
- The objective function: the second objective function aims to propose the best spatiotemporal irrigation distribution, which minimize the IPI index and the gravity irrigation network constraints. Thus, the second objective function is defined by Equation (22):where k is the canal index and N is the total number of plots to be irrigated.
- if capacity = 30 L/s: flow = 0.03 × 3600 = 108 m3/h;
- if capacity = 60 L/s: flow = 0.06 × 3600 = 216 m3/h;
- if capacity = 90 L/s: flow = 0.09 × 3600 = 324 m3/h.
3. Results
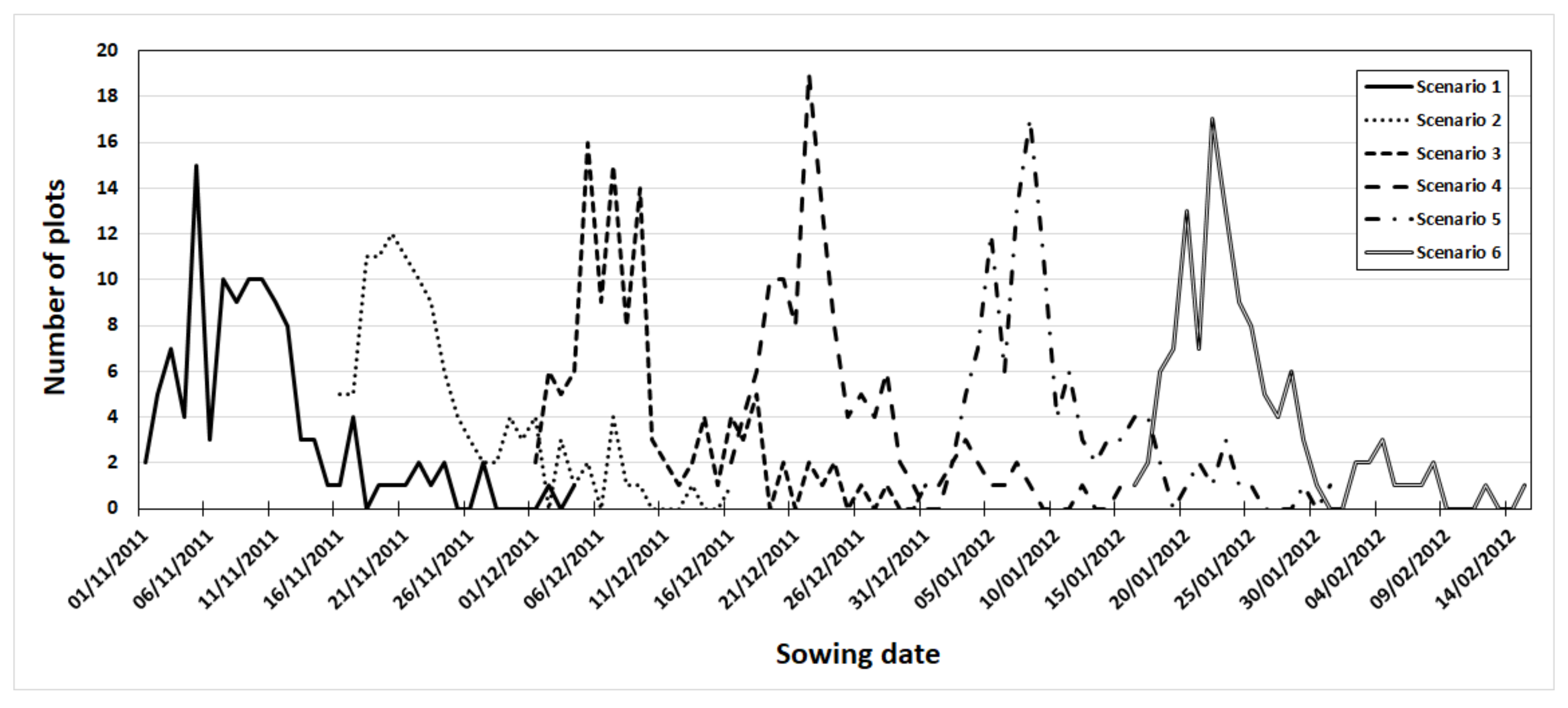
3.1. Optimization of the Spatiotemporal Sowing Date Distribution
3.2. Effect of Sowing Date Optimization on Wheat Growth and Irrigation Schedules
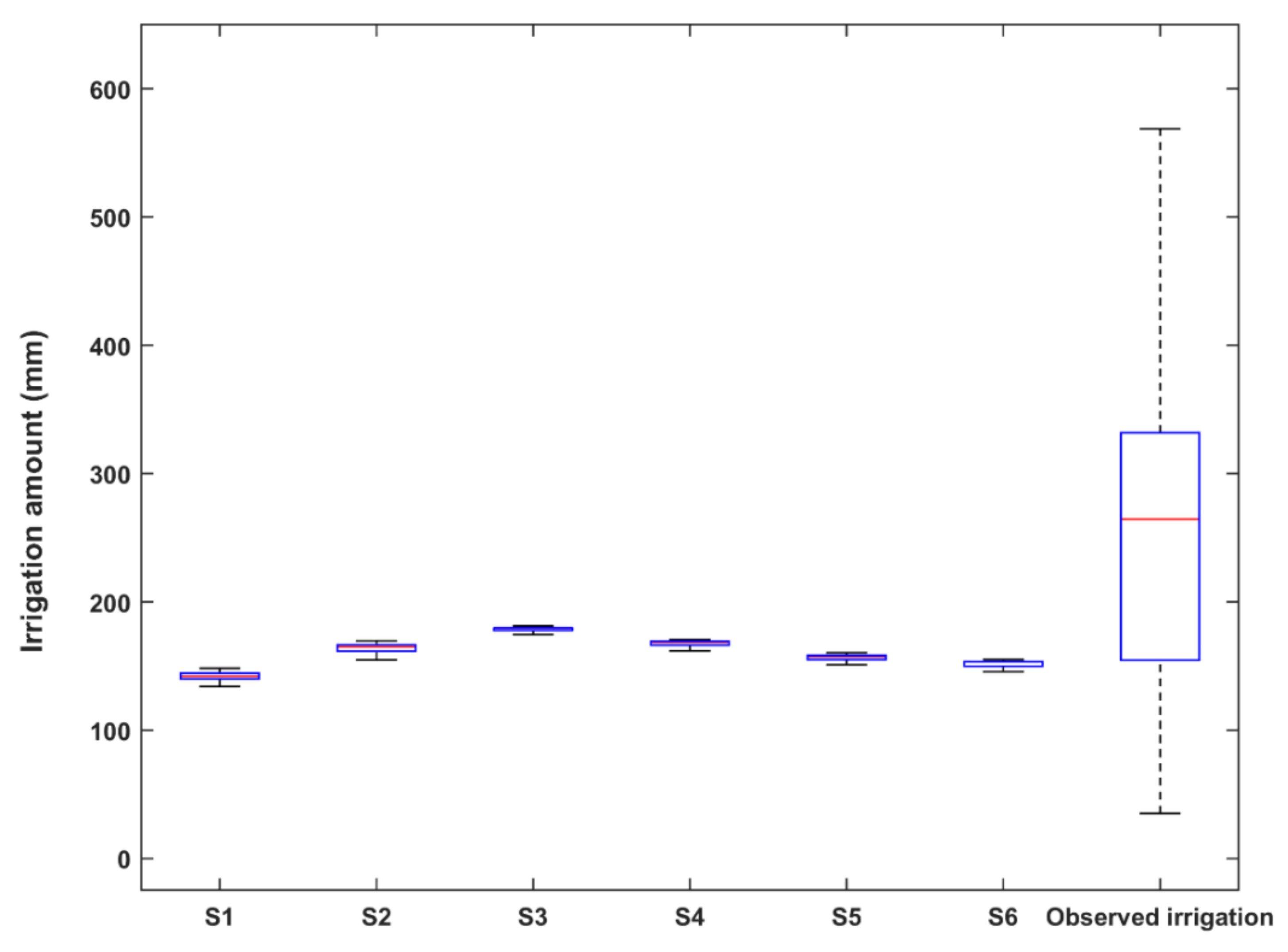
3.3. Effect of Sowing Date Optimization on Water Requirements
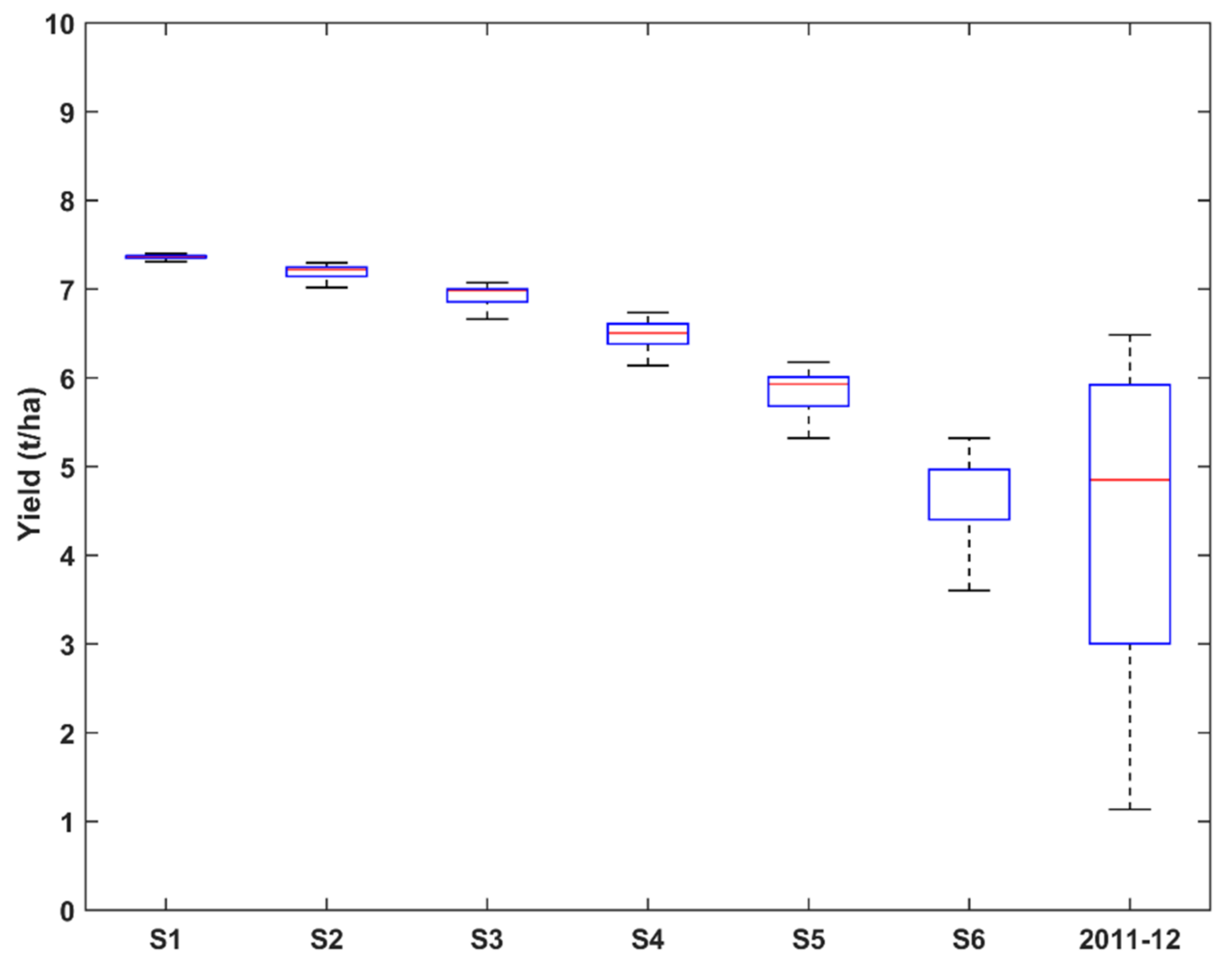
3.4. Effect of Sowing Date Optimization on Wheat Yield
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harbouze, R.; Pellissier, J.-P.; Rolland, J.-P.; Khechimi, W. Rapport de synthèse sur l’agriculture au Maroc. [Research Report] CIHEAM-IAMM. 2019, pp. 104, hal-02137637v2. Available online: https://hal.archives-ouvertes.fr/hal-02137637v2 (accessed on 20 July 2021).
- Verner, D.; Treguer, D.; Redwood, J.; Christensen, J.; McDonnell, R.; Elbert, C.; Konishi, Y.; Belghazi, S. Climate Variability, Drought, and Drought Management in Morocco’s Agricultural Sector. World Bank, Washington, DC. © World Bank. 2018. Available online: https://openknowledge.worldbank.org/handle/10986/30603 (accessed on 20 July 2021). License: CC BY 3.0 IGO.
- Trnka, M.; Feng, S.; Semenov, M.A.; Olesen, J.E.; Kersebaum, K.C.; Rötter, R.P.; Semerádová, D.; Klem, K.; Huang, W.; Ruiz-Ramos, M.; et al. Mitigation efforts will not fully alleviate the increase in water scarcity occurrence probability in wheat-producing areas. Sci. Adv. 2019, 5, eaau2406. [Google Scholar] [CrossRef] [Green Version]
- Le Page, M.; Zribi, M. Analysis and Predictability of Drought In Northwest Africa Using Optical and Microwave Satellite Remote Sensing Products. Sci. Rep. 2019, 9, 1466. [Google Scholar] [CrossRef] [Green Version]
- IPCC. Annex II: Glossary. In Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Core Writing Team; Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; pp. 117–130. [Google Scholar]
- Tian, Y.; Zheng, C.; Chen, J.; Chen, C.; Deng, A.; Song, Z.; Zhang, B.; Zhang, W. Climatic Warming Increases Winter Wheat Yield but Reduces Grain Nitrogen Concentration in East China. PLoS ONE 2014, 9, e95108. [Google Scholar] [CrossRef] [Green Version]
- Porter, J.R.; Semenov, M. Crop responses to climatic variation. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 2021–2035. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B.; Tebaldi, C.; Mastrandrea, M.D.; Falcon, W.P.; Naylor, R.L. Prioritizing Climate Change Adaptation Needs for Food Security in 2030. Science 2008, 319, 607–610. [Google Scholar] [CrossRef]
- Schlenker, W.; Roberts, M.J. Nonlinear temperature effects indicate severe damages to U.S. crop yields under climate change. Proc. Natl. Acad. Sci. USA 2009, 106, 15594–15598. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fedoroff, N.V.; Battisti, D.; Beachy, R.N.; Cooper, P.J.M.; Fischhoff, D.A.; Hodges, C.N.; Knauf, V.C.; Lobell, D.; Mazur, B.J.; Molden, D.; et al. Radically Rethinking Agriculture for the 21st Century. Science 2010, 327, 833–834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farooq, M.; Bramley, H.; Palta, J.; Siddique, K. Heat Stress in Wheat during Reproductive and Grain-Filling Phases. Crit. Rev. Plant Sci. 2011, 30, 491–507. [Google Scholar] [CrossRef]
- Alghabari, F.; Lukac, M.; Jones, H.; Gooding, M. Effect of Rht Alleles on the Tolerance of Wheat Grain Set to High Temperature and Drought Stress During Booting and Anthesis. J. Agron. Crop. Sci. 2013, 200, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Cuculeanu, V.; Tuinea, P.; Balteanu, D. Climate change impacts in Romania: Vulnerability and adaptation options. Geojournal 2002, 57, 203–209. [Google Scholar] [CrossRef]
- Kang, Y.; Khan, S.; Ma, X. Climate change impacts on crop yield, crop water productivity and food security—A review. Prog. Nat. Sci. 2009, 19, 1665–1674. [Google Scholar] [CrossRef]
- El Houssaine, B.; Jarlan, L.; Khabba, S.; Er-Raki, S.; Dezetter, A.; Sghir, F.; Tramblay, Y. Assessing the impact of global climate changes on irrigated wheat yields and water requirements in a semi-arid environment of Morocco. Sci. Rep. 2019, 9, 19142. [Google Scholar] [CrossRef]
- Ren, A.-X.; Sun, M.; Wang, P.-R.; Xue, L.-Z.; Lei, M.-M.; Xue, J.-F.; Gao, Z.-Q.; Yang, Z.-P. Optimization of sowing date and seeding rate for high winter wheat yield based on pre-winter plant development and soil water usage in the Loess Plateau, China. J. Integr. Agric. 2019, 18, 33–42. [Google Scholar] [CrossRef]
- Ferrise, R.; Triossi, A.; Stratonovitch, P.; Bindi, M.; Martre, P. Sowing date and nitrogen fertilisation effects on dry matter and nitrogen dynamics for durum wheat: An experimental and simulation study. Field Crop. Res. 2010, 117, 245–257. [Google Scholar] [CrossRef]
- Bassu, S.; Asseng, S.; Motzo, R.; Giunta, F. Optimising sowing date of durum wheat in a variable Mediterranean environment. Field Crop. Res. 2009, 111, 109–118. [Google Scholar] [CrossRef]
- Tapley, M.; Ortiz, B.V.; Van Santen, E.; Balkcom, K.S.; Mask, P.; Weaver, D.B. Location, Seeding Date, and Variety Interactions on Winter Wheat Yield in Southeastern United States. Agron. J. 2013, 105, 509–518. [Google Scholar] [CrossRef] [Green Version]
- Waha, K.; Van Bussel, L.G.J.; Müller, C.; Bondeau, A. Climate-driven simulation of global crop sowing dates. Glob. Ecol. Biogeogr. 2011, 21, 247–259. [Google Scholar] [CrossRef]
- Bondeau, A.; Smith, P.C.; Zaehle, S.; Schaphoff, S.; Lucht, W.; Cramer, W.; Gerten, D.; Lotze-Campen, H.; Müller, C.; Reichstein, M.; et al. Modelling the role of agriculture for the 20th century global terrestrial carbon balance. Glob. Chang. Biol. 2006, 13, 679–706. [Google Scholar] [CrossRef]
- Soltani, A.; Hoogenboom, G. Assessing crop management options with crop simulation models based on generated weather data. Field Crop. Res. 2007, 103, 198–207. [Google Scholar] [CrossRef]
- Rozbicki, J.; Ceglińska, A.; Gozdowski, D.; Jakubczak, M.; Cacak-Pietrzak, G.; Mądry, W.; Golba, J.; Piechociński, M.; Sobczyński, G.; Studnicki, M.; et al. Influence of the cultivar, environment and management on the grain yield and bread-making quality in winter wheat. J. Cereal Sci. 2015, 61, 126–132. [Google Scholar] [CrossRef]
- Moriondo, M.; Bindi, M.; Kundzewicz, Z.W.; Szwed, M.; Choryński, A.; Matczak, P.; Radziejewski, M.; McEvoy, D.; Wreford, A. Impact and adaptation opportunities for European agriculture in response to climatic change and variability. Mitig. Adapt. Strat. Glob. Chang. 2010, 15, 657–679. [Google Scholar] [CrossRef]
- Dettori, M.; Cesaraccio, C.; Duce, P. Simulation of climate change impacts on production and phenology of durum wheat in Mediterranean environments using CERES-Wheat model. Field Crop. Res. 2017, 206, 43–53. [Google Scholar] [CrossRef]
- Nouri, M.; Homaee, M.; Bannayan, M.; Hoogenboom, G. Towards shifting planting date as an adaptation practice for rainfed wheat response to climate change. Agric. Water Manag. 2017, 186, 108–119. [Google Scholar] [CrossRef]
- Ruiz-Ramos, M.; Ferrise, R.; Rodríguez, A.; Lorite, I.; Bindi, M.; Carter, T.; Fronzek, S.; Palosuo, T.; Pirttioja, N.; Baranowski, P.; et al. Adaptation response surfaces for managing wheat under perturbed climate and CO2 in a Mediterranean environment. Agric. Syst. 2018, 159, 260–274. [Google Scholar] [CrossRef]
- Giuliani, M.M.; Gatta, G.; Cappelli, G.A.; Gagliardi, A.; Donatelli, M.; Fanchini, D.; De Nart, D.; Mongiano, G.; Bregaglio, S. Identifying the most promising agronomic adaptation strategies for the tomato growing systems in Southern Italy via simulation modeling. Eur. J. Agron. 2019, 111, 125937. [Google Scholar] [CrossRef]
- Salado-Navarro, L.R.; Sinclair, T.R. Crop rotations in Argentina: Analysis of water balance and yield using crop models. Agric. Syst. 2009, 102, 11–16. [Google Scholar] [CrossRef]
- Soltani, A.; Maddah, V.; Sinclair, T.R. SSM-wheat: A simulation model for wheat development, growth and yield. Int. J. Plant Prod. 2013, 7, 4. [Google Scholar]
- Chmielewski, F.-M.; Müller, A.; Bruns, E. Climate changes and trends in phenology of fruit trees and field crops in Germany. Agric. For. Meteorol. 2004, 121, 69–78. [Google Scholar] [CrossRef]
- Harrison, P.A.; Porter, J.R.; Downing, T.E. Scaling-up the AFRCWHEAT2 model to assess phenological development for wheat in Europe. Agric. For. Meteorol. 2000, 101, 167–186. [Google Scholar] [CrossRef]
- Rauniyar, G.P.; Goode, F.M. Technology adoption on small farms. World Dev. 1992, 20, 275–282. [Google Scholar] [CrossRef]
- Chehbouni, A.; Escadafal, R.; Duchemin, B.; Boulet, G.; Simonneaux, V.; Dedieu, G.; Mougenot, B.; Khabba, S.; Kharrou, H.; Maisongrande, P.; et al. An integrated modelling and remote sensing approach for hydrological study in arid and semi-arid regions: The SUDMED Programme. Int. J. Remote Sens. 2008, 29, 5161–5181. [Google Scholar] [CrossRef] [Green Version]
- Driouech, F.; Déqué, M.; Sánchez-Gómez, E. Weather regimes—Moroccan precipitation link in a regional climate change simulation. Glob. Planet. Chang. 2010, 72, 1–10. [Google Scholar] [CrossRef]
- Toumi, J.; Er-Raki, S.; Ezzahar, J.; Khabba, S.; Jarlan, L.; Chehbouni, A. Performance assessment of AquaCrop model for estimating evapotranspiration, soil water content and grain yield of winter wheat in Tensift Al Haouz (Morocco): Application to irrigation management. Agric. Water Manag. 2016, 163, 219–235. [Google Scholar] [CrossRef]
- Mailhol, J.C. Contribution à l’Amélioration des Pratiques d’Irrigation à la Raie par Une Modélisation Simplifiée à l’Échelle de la Parcelle et de la Saison. Ph.D. Thesis, University Montpellier II, Montpellier, France, 2001; 276p. [Google Scholar]
- Kharrou, M.H.; Er-Raki, S.; Chehbouni, A.; Duchemin, B.; Simonneaux, V.; LePage, M.; Ouzine, L.; Jarlan, L. Water use efficiency and yield of winter wheat under different irrigation regimes in a semi-arid region. Agric. Sci. 2011, 2, 273–282. [Google Scholar] [CrossRef] [Green Version]
- Kharrou, M.; Simonneaux, V.; Er-Raki, S.; Le Page, M.; Khabba, S.; Chehbouni, A. Assessing Irrigation Water Use with Remote Sensing-Based Soil Water Balance at an Irrigation Scheme Level in a Semi-Arid Region of Morocco. Remote Sens. 2021, 13, 1133. [Google Scholar] [CrossRef]
- Reddy, F.; Wilamowski, J.M.; Sharmasarakar, B. Optimal scheduling of irrigation for lateral canals. ICID J. 1999, 48, 1–12. [Google Scholar]
- Anwar, A.A.; Clarke, D. Irrigation Scheduling Using Mixed-Integer Linear Programming. J. Irrig. Drain. Eng. 2001, 127, 63–69. [Google Scholar] [CrossRef]
- Alaya, K.; Sammoud, I.; Hammami, O.; Ghédira, M. Ant Colony Optimization for the k-Graph Partitioning Problem. In Proceedings of the 3rd Tunisia-Japan Symposium on Science and Technology, TJASST2003, Sousse, Tunisia, 29 November–2 December 2003. [Google Scholar]
- Tzimopoulos, S.T.; Balioti, C.; Evangelides, V.; Yannopoulos, C. Irrigation network planning using linear programming. In Proceedings of the 12th International Conference on Environmental Science and Technology, Rhodes, Greece, 8–10 September 2011; pp. 8–10. [Google Scholar]
- Georgakakos, K.P. Water Supply and Demand Sensitivities of Linear Programming Solutions to a Water Allocation Problem. Appl. Math. 2012, 3, 1285–1297. [Google Scholar] [CrossRef] [Green Version]
- Mayer, D.; Kinghorn, B.; Archer, A. Differential evolution—An easy and efficient evolutionary algorithm for model optimisation. Agric. Syst. 2005, 83, 315–328. [Google Scholar] [CrossRef]
- De Paly, M.; Zell, A. Optimal Irrigation Scheduling with Evolutionary Algorithms. In Workshops on Applications of Evolutionary Computation; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5484, pp. 142–151. [Google Scholar] [CrossRef]
- Raju, K.S.; Kumar, D.N. Irrigation Planning using Genetic Algorithms. Water Resour. Manag. 2004, 18, 163–176. [Google Scholar] [CrossRef] [Green Version]
- Mathur, A.W.; Sharma, Y.P.; Pawde, G. Optimal Operation Scheduling of Irrigation Canals Using Genetic Algorithm. Int. J. Recent Trends Eng. 2009, 6, 11–15. [Google Scholar]
- Elferchichi, A.; Gharsallah, O.; Nouiri, I.; Lebdi, F.; Lamaddalena, N. The genetic algorithm approach for identifying the optimal operation of a multi-reservoirs on-demand irrigation system. Biosyst. Eng. 2009, 102, 334–344. [Google Scholar] [CrossRef]
- Sharif, M.; Wardlaw, R. Multireservoir Systems Optimization Using Genetic Algorithms: Case Study. J. Comput. Civ. Eng. 2000, 14, 255–263. [Google Scholar] [CrossRef]
- Kuo, S.-F.; Merkley, G.P.; Liu, C.-W. Decision support for irrigation project planning using a genetic algorithm. Agric. Water Manag. 2000, 45, 243–266. [Google Scholar] [CrossRef]
- Tayebiyan, A.; Ali, T.A.M.; Ghazali, A.H.; Malek, M.A. Optimization of Exclusive Release Policies for Hydropower Reservoir Operation by Using Genetic Algorithm. Water Resour. Manag. 2016, 30, 1203–1216. [Google Scholar] [CrossRef]
- Hansen, N.; Auger, A.; Ros, R.; Finck, S.; Pošík, P. Comparing results of 31 algorithms from the black-box optimization benchmarking BBOB. In Proceedings of the 12th Annual Conference Comp on Genetic and Evolutionary Computation—GECCO ’10, Portland, OR, USA, 7–11 July 2010; pp. 1689–1696. [Google Scholar]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the Time Complexity of the Derandomized Evolution Strategy with Covariance Matrix Adaptation (CMA-ES). Evol. Comput. 2003, 11, 159–195. [Google Scholar] [CrossRef] [PubMed]
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: A case study on the CEC’2005 Special Session on Real Parameter Optimization. J. Heuristics 2009, 15, 617–644. [Google Scholar] [CrossRef]
- Belaqziz, S.; Mangiarotti, S.; Le Page, M.; Khabba, S.; Er-Raki, S.; Agouti, T.; Drapeau, L.; Kharrou, M.; El Adnani, M.; Jarlan, L. Irrigation scheduling of a classical gravity network based on the Covariance Matrix Adaptation—Evolutionary Strategy algorithm. Comput. Electron. Agric. 2014, 102, 64–72. [Google Scholar] [CrossRef] [Green Version]
- Er-Raki, S.; Chehbouni, A.; Duchemin, B. Combining Satellite Remote Sensing Data with the FAO-56 Dual Approach for Water Use Mapping In Irrigated Wheat Fields of a Semi-Arid Region. Remote Sens. 2010, 2, 375–387. [Google Scholar] [CrossRef] [Green Version]
- Duchemin, B.; Hadria, R.; Er-Raki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, A.; Escadafal, R.; Ezzahar, J.; Hoedjes, J.C.B.; Kharrou, M.H.; et al. Monitoring wheat phenology and irrigation in Central Morocco: On the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Le Page, M.; Toumi, J.; Khabba, S.; Hagolle, O.; Tavernier, A.; Kharrou, M.H.; Er-Raki, S.; Huc, M.; Kasbani, M.; El Moutamanni, A.; et al. A Life-Size and Near Real-Time Test of Irrigation Scheduling with a Sentinel-2 Like Time Series (SPOT4-Take5) in Morocco. Remote Sens. 2014, 6, 11182–11203. [Google Scholar] [CrossRef] [Green Version]
- Gosse, G.; Varlet-Grancher, C.; Bonhomme, R.; Chartier, M.; Allirand, J.-M.; Lemaire, G. Maximum dry matter production and solar radiation intercepted by a canopy. Agronomie 1986, 6, 47–56. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration—Guidelines for computing crop water requirements—FAO Irrigation and drainage paper. Irrig. Drain. 1998, 300, D05109. [Google Scholar] [CrossRef]
- Hadria, R.; Khabba, S.; Lahrouni, A.; Duchemin, B.; Chehbouni, A.; Carriou, J.; Ouzine, L. Calibration and validation of the STICS crop model for managing wheat irrigation in the semi-arid Marra-kech/al Haouz plain. Arab. J. Sci. Eng. 2007, 32, 87–101. [Google Scholar]
- Khabba, S.; Er-Raki, S.; Toumi, J.; Ezzahar, J.; Hssaine, B.A.; Le Page, M.; Chehbouni, A. A Simple Light-Use-Efficiency Model to Estimate Wheat Yield in the Semi-Arid Areas. Agronomy 2020, 10, 1524. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Khabba, S.; Simonneaux, V.; Jarlan, L.; Ouldbba, A.; Rodriguez, J.; Allen, R. Assessment of reference evapotranspiration methods in semi-arid regions: Can weather forecast data be used as alternate of ground meteorological parameters? J. Arid. Environ. 2010, 74, 1587–1596. [Google Scholar] [CrossRef] [Green Version]
- Simonneaux, V.; Duchemin, B.; Helson, D.; Er-Raki, S.; Olioso, A.; Chehbouni, A.G. The use of high-resolution image time series for crop classification and evapotranspiration estimate over an irrigated area in central Morocco. Int. J. Remote Sens. 2008, 29, 95–116. [Google Scholar] [CrossRef] [Green Version]
- Hagolle, O.; Dedieu, G.; Mougenot, B.; Debaecker, V.; Duchemin, B.; Meygret, A. Correction of aerosol effects on multi-temporal images acquired with constant viewing angles: Application to Formosat-2 images. Remote Sens. Environ. 2008, 112, 1689–1701. [Google Scholar] [CrossRef] [Green Version]
- Karrou, M. Conduite du Blé au Maroc; INRA Editions: Paris, France, 2003; pp. 1–57.
- Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E. AquaCrop- The FAO Crop Model to Simulate Yield Response to Water: II. Main Algorithms and Software Description. Agron. J. 2009, 101, 438–447. [Google Scholar] [CrossRef] [Green Version]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop-The FAO Crop Model to Simulate Yield Response to Water: I. Concepts and Underlying Principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef] [Green Version]
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining FAO-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef] [Green Version]
- Tucker, J.C. Red and photographie infrared linear combinaitions for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Lin, W. Winter wheat yield estimation based on MODIS EVI. Nongye Gongcheng Xuebao Trans. Chin. Soc. Agric. Eng. 2005, 21, 10. [Google Scholar]
- Ren, J.; Chen, Z.; Zhou, Q.; Tang, H. Regional yield estimation for winter wheat with MODIS-NDVI data in Shandong, China. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 403–413. [Google Scholar] [CrossRef]
- Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
- Balaghi, R.; Tychon, B.; Eerens, H.; Jlibene, M. Empirical regression models using NDVI, rainfall and temperature data for the early prediction of wheat grain yields in Morocco. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 438–452. [Google Scholar] [CrossRef] [Green Version]
- Hadria, R.; Duchemin, B.; Lahrouni, A.; Khabba, S.; Er-Raki, S.; Dedieu, G.; Chehbouni, A.G.; Olioso§, A. Monitoring of irrigated wheat in a semi-arid climate using crop modelling and remote sensing data: Impact of satellite revisit time frequency. Int. J. Remote Sens. 2006, 27, 1093–1117. [Google Scholar] [CrossRef] [Green Version]
- Belaqziz, S.; Khabba, S.; Er-Raki, S.; Jarlan, L.; Le Page, M.; Kharrou, M.H.; El Adnani, M.; Chehbouni, A. A new irrigation priority index based on remote sensing data for assessing the networks irrigation scheduling. Agric. Water Manag. 2013, 119, 1–9. [Google Scholar] [CrossRef]
- Ouattar, T.E.; Ameziane, S. Les Céréales au Maroc, de la Recherche à L’amélioration des Techniques de Production; Les Éditions Toubkal: Rabat, Morocco, 1989. [Google Scholar]
- Hsiao, T.C.; Heng, L.; Steduto, P.; Rojas-Lara, B.; Raes, D.; Fereres, E. AquaCrop-The FAO Crop Model to Simulate Yield Response to Water: III. Parameterization and Testing for Maize. Agron. J. 2009, 101, 448–459. [Google Scholar] [CrossRef]
- Tanenbaum, A.S.; Bos, H. Modern Operating Systems; Pearson: Boston, MA, USA, 2014; Volume 2, ISBN 978-0-13-359162-0. [Google Scholar]
- Rousson, V. Statistique Appliquée aux Sciences de la Vie; Éditions Lavoisier: Lausanne, Switzerland, 2013; p. 318. [Google Scholar]
- Er-Raki, S.; Chehbouni, A.; Ezzahar, J.; Khabba, S.; Lakhal, E.K.; Duchemin, B. Derived crop coefficients for winter wheat using different reference evpotranspiration estimates methods. J. Agric. Sci. Technol. 2011, 13, 209–221. [Google Scholar]
- Sinclair, R.C.; Muchow, T.R. Radiation use Efficiency. Adv. Agron. 1999, 65, 215–265. [Google Scholar]
- John, R.P.; Megan, G. Temperatures and the growth and development of wheat: A review. Eur. J. Agron. 1999, 10, 23–36. [Google Scholar]



| Irrigation Round | Start Date | End Date | Duration (Day) | Applied Water Amounts (mm) |
|---|---|---|---|---|
| 1 | 3 December 2011 | 24 December 2011 | 21 | 46 |
| 2 | 1 January 2012 | 21 January 2012 | 20 | 52 |
| 3 | 9 February 2012 | 29 February 2012 | 20 | 52 |
| 4 | 1 March 2012 | 23 March 2012 | 22 | 100 |
| 5 | 22 April 2012 | 4 May 2012 | 12 | 24 |
| Early Sowing | Late Sowing | |
|---|---|---|
| CC0 | 4.5 | 3.83 |
| CCX | 89.33 | 81.33 |
| CGC | 0.0089 | 0.0089 |
| CDC | 0.145 | 0.145 |
| Scenario | Gap between IR (Day) | Mean IR Duration (Day) | Number of IR | All Irrigations Window | Stopping Irrigation Window | Sowing Window |
|---|---|---|---|---|---|---|
| 1 | 16 | 18 | 5 | [14 December 2011–19 May 2012] | [30 May 2012– 12 June 2012] | [1 November 2011– 4 December 2011] |
| 2 | 14 | 21 | 5 | [15 December 2011–29 May 2012] | [7 June 2012– 17 June 2012] | [16 November 2011– 16 December 2011] |
| 3 | 18 | 18 | 5 | [30 December 2011–9 June 2012] | [13 June 2012– 25 June 2012] | [1 December 2011–31 December 2011] |
| 4 | 14 | 19 | 5 | [14 January 2012– 13 June 2012] | [17 June 2012– 29 June 2012] | [16 December 2011–15 January 2012] |
| 5 | 13 | 19 | 4 | [7 February 2012–4 June 2012] | [20 June 2012– 3 July 2012] | [1 January 2012– 31 January 2012] |
| 6 | 16 | 19 | 4 | [14 February 2012–17 June 2012] | [23 June 2012– 7 July 2012] | [16 January 2012– 15 February 2012] |
| Observed irrigation | 15 | 19 | 5 | [3 December 2011–4 May 2012] | [7 June 2012– 25 June 2012] | [16 November 2011–31 January 2012] |
| IR 1 (mm) | IR 2 (mm) | IR 3 (mm) | IR 4 (mm) | IR 5 (mm) | Total (mm) | |
|---|---|---|---|---|---|---|
| 1st Sowing Scenario | 10 | 19 | 30 | 35 | 47 | 141 |
| 2nd Sowing Scenario | 7 | 10 | 33 | 53 | 61 | 164 |
| 3rd Sowing Scenario | 6 | 11 | 32 | 54 | 75 | 178 |
| 4th Sowing Scenario | 6 | 11 | 27 | 48 | 75 | 168 |
| 5th Sowing Scenario | 8 | 24 | 45 | 79 | 156 | |
| 6th Sowing Scenario | 4 | 29 | 48 | 72 | 152 | |
| Observed Irrigation | 46 | 52 | 52 | 100 | 24 | 274 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belaqziz, S.; Khabba, S.; Kharrou, M.H.; Bouras, E.H.; Er-Raki, S.; Chehbouni, A. Optimizing the Sowing Date to Improve Water Management and Wheat Yield in a Large Irrigation Scheme, through a Remote Sensing and an Evolution Strategy-Based Approach. Remote Sens. 2021, 13, 3789. https://doi.org/10.3390/rs13183789
Belaqziz S, Khabba S, Kharrou MH, Bouras EH, Er-Raki S, Chehbouni A. Optimizing the Sowing Date to Improve Water Management and Wheat Yield in a Large Irrigation Scheme, through a Remote Sensing and an Evolution Strategy-Based Approach. Remote Sensing. 2021; 13(18):3789. https://doi.org/10.3390/rs13183789
Chicago/Turabian StyleBelaqziz, Salwa, Saïd Khabba, Mohamed Hakim Kharrou, El Houssaine Bouras, Salah Er-Raki, and Abdelghani Chehbouni. 2021. "Optimizing the Sowing Date to Improve Water Management and Wheat Yield in a Large Irrigation Scheme, through a Remote Sensing and an Evolution Strategy-Based Approach" Remote Sensing 13, no. 18: 3789. https://doi.org/10.3390/rs13183789
APA StyleBelaqziz, S., Khabba, S., Kharrou, M. H., Bouras, E. H., Er-Raki, S., & Chehbouni, A. (2021). Optimizing the Sowing Date to Improve Water Management and Wheat Yield in a Large Irrigation Scheme, through a Remote Sensing and an Evolution Strategy-Based Approach. Remote Sensing, 13(18), 3789. https://doi.org/10.3390/rs13183789