Parameter Estimation Based on a Local Ensemble Transform Kalman Filter Applied to El Niño–Southern Oscillation Ensemble Prediction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Zebiak–Cane Model
2.2. LETKF-Based Parameter Estimation
2.3. Covariance Inflation Scheme
2.4. Model Parameters
2.5. Experimental Designs
2.5.1. Experimental Designs in OSSE Framework
2.5.2. Experimental Designs in the Real World
3. Results
3.1. Results of the OSSE Framework
3.2. Results in Real-World Experiments
3.3. Validation of Optimized Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Chen, D.K.; Cane, M.A.; Kaplan, A.; Zebiak, S.; Huang, D. Predictability of El Niño over the past 148 years. Nature 2004, 428, 733–736. [Google Scholar] [CrossRef]
- O’Kane, T.J.; Sandery, P.A.; Monselesan, D.P.; Sakov, P.; Stevens, L. Coupled Data Assimilation and Ensemble Initialization with Application to Multiyear ENSO Prediction. J. Clim. 2019, 32, 997–1024. [Google Scholar] [CrossRef]
- Gao, Y.Q.; Liu, T.; Song, X.S.; Shen, Z.Q.; Tang, Y.M.; Chen, D.K. An extension of LDEO5 model for ENSO ensemble predictions. Clim. Dyn. 2020, 55, 2979–2991. [Google Scholar] [CrossRef]
- Latif, M.; Sperber, K.; Arblaster, J.; Braconnot, P.; Chen, D.; Colman, A.; Cubasch, U.; Cooper, C.; Delecluse, P.; DeWitt, D.; et al. ENSIP: The El Niño simulation intercomparison project. Clim. Dyn. 2001, 18, 255–276. [Google Scholar] [CrossRef] [Green Version]
- Stainforth, D.A.; Aina, T.; Christensen, C.; Collins, M.; Faull, N.; Frame, D.J.; Kettleborough, J.A.; Knight, S.; Martin, A.; Murphy, J.M. Uncertainty in predictions of the climate response to rising levels of greenhouse gases. Nature 2005, 433, 403–406. [Google Scholar] [CrossRef] [PubMed]
- Zheng, F.; Wang, H.; Zhu, J. ENSO ensemble prediction: Initial error perturbations vs. model error perturbations. Chin. Sci. Bull. 2009, 54, 2516–2523. [Google Scholar] [CrossRef]
- Tao, L.J.; Gao, C.; Zhang, R.H. Model parameter-related optimal perturbations and their contributions to El Niño prediction errors. Clim. Dyn. 2019, 52, 1425–1441. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Liu, Z.Y.; Rosati, A.; Delworth, T. A study of enhancive parameter correction with coupled data assimilation for climate estimation and prediction using a simple coupled model. Tellus A 2012, 64, 10963. [Google Scholar] [CrossRef] [Green Version]
- Qi, Q.Q.; Duan, W.S.; Zheng, F.; Tang, Y.M. On the “spring predictability barrier’’ for strong El Niño events as derived from an intermediate coupled model ensemble prediction system. Sci. China Earth Sci. 2017, 60, 1614–1631. [Google Scholar] [CrossRef]
- Song, J.Q.; Cao, X.Q.; Zhang, W.M.; Zhu, X.Q. Estimating parameters for coupled air-sea model with variational method. Acta Phys. Sin. 2012, 61, 110401. (In Chinese) [Google Scholar] [CrossRef]
- Wu, X.; Zhang, S.; Liu, Z.; Rosati, A.; Delworth, T.L.; Liu, Y. Impact of geographic-dependent parameter optimization on climate estimation and prediction: Simulation with an intermediate coupled model. Mon. Weather Rev. 2012, 140, 3956–3971. [Google Scholar] [CrossRef]
- Wu, X.; Han, G.; Zhang, S.; Liu, Z. A study of the impact of parameter optimization on ENSO predictability with an intermediate coupled model. Clim. Dyn. 2016, 46, 711–727. [Google Scholar] [CrossRef]
- Navon, I.M. Practical and theoretical aspects of adjoint parameter estimation and identifiability in meteorology and oceanography. Dyn. Atmos. Ocean. 1998, 27, 55–79. [Google Scholar] [CrossRef] [Green Version]
- Annan, J.D.; Hargreaves, J.C.; Edwards, N.R.; Marsh, R. Parameter estimation in an intermediate complexity Earth System Model using an ensemble Kalman filter. Ocean Model. 2004, 8, 135–154. [Google Scholar] [CrossRef]
- Annan, J.D. Parameter estimation using chaotic time series. Tellus A 2005, 57, 709–714. [Google Scholar] [CrossRef]
- Du, H.; Huang, S.; Cai, Q.; Cheng, L. Studies of variational assimilation for the inversion of the coupled air-sea model. Mar. Sci. Bull. 2009, 11, 13–22. [Google Scholar]
- Hu, X.M.; Zhang, F.; Nielsen-Gammon, J.W. Ensemble based simultaneous state and parameter estimation for treatment of mesoscale model error: A real-data study. Geophys. Res. Lett. 2010, 37, L08802. [Google Scholar] [CrossRef] [Green Version]
- Ito, K.; Ishikawa, Y.; Awaji, T. Specifying air-sea exchange coefficients in the high-wind regime of a mature tropical cyclone by an adjoint data assimilation method. Sola 2010, 6, 13–16. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.Q.; Cao, A.Z.; Chen, H.B.; Lv, X.Q. Estimation of bottom friction coefficients based on an isopycnic-coordinate internal tidal model with adjoint method. Math. Probl. Eng. 2013, 2013, 532814. [Google Scholar] [CrossRef]
- Peng, S.Q.; Li, Y.N.; Xie, L. Adjusting the wind stress drag coefficient in storm surge forecasting using an adjoint technique. J. Atmos. Ocean. Technol. 2013, 30, 590–608. [Google Scholar] [CrossRef]
- Han, G.; Wu, X.; Zhang, S.; Liu, Z.; Navon, I.M.; Li, W. A study of coupling parameter estimation implemented by 4D-Var and EnKF with a simple coupled system. Adv. Meteorol. 2015, 2015, 530764. [Google Scholar] [CrossRef] [Green Version]
- Gao, C.; Zhang, R.H.; Wu, X.R.; Sun, J.C. Idealized experiments for optimizing model parameters using a 4D-variational method in an intermediate coupled model of ENSO. Adv. Atmos. Sci. 2018, 35, 410–422. [Google Scholar] [CrossRef]
- Zhang, J.C.; Li, G.Q.; Yi, J.C.; Gao, Y.Q.; Cao, A.Z. A method on estimating time-varying vertical eddy viscosity for an Ekman layer model with data assimilation. J. Atmos. Ocean. Technol. 2019, 36, 1789–1812. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.; Kalnay, E.; Liu, J.; Fung, I.; Miyoshi, T.; Ide, K. Estimation of surface carbon fluxes with an advanced data assimilation methodology. J. Geophys. Res. 2012, 117, D24101. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Z.; Zheng, F.; Jin, Y. Parameter optimization for real-world ENSO forecast in an intermediate coupled model. Mon. Weather Rev. 2019, 147, 1429–1445. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Liu, Z.; Lu, L.; Zhu, J.; Zhang, X.; Wu, X.; Zhao, M.; Vecchi, G.A.; Zhang, R.; et al. Estimating convection parameters in the GFDL CM2.1 model using ensemble data assimilation. J. Adv. Model. Earth Syst. 2018, 10, 989–1010. [Google Scholar] [CrossRef]
- Shen, Z.Q.; Tang, Y.M.; Gao, Y.Q. The theoretical framework of the ensemble-based data assimilation method and its prospect in oceanic data assimilation. Haiyang Xuebao 2016, 38, 1–14. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, S.; Liu, Z.; Wu, X.; Han, G. Correction of biased climate simulated by biased physics through parameter estimation in an intermediate coupled model. Clim. Dyn. 2015, 47, 1899–1912. [Google Scholar] [CrossRef]
- Anderson, J.L. An ensemble adjustment Kalman filter for data assimilation. Mon. Weather Rev. 2001, 129, 2884–2903. [Google Scholar] [CrossRef] [Green Version]
- Hansen, J.; Penland, C. On stochastic parameter estimation using data assimilation. Phys. D 2007, 230, 88–98. [Google Scholar] [CrossRef]
- Han, G.; Wu, X.; Zhang, S.; Liu, Z.; Li, W. Error covariance estimation for coupled data assimilation using a Lorenz atmosphere and a simple pycnocline ocean model. J. Clim. 2013, 26, 10218–10231. [Google Scholar] [CrossRef]
- Anderson, J.L.; Anderson, S.L. A Monte Carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts. Mon. Weather Rev. 1999, 127, 2741–2758. [Google Scholar] [CrossRef]
- Aksoy, A.; Zhang, F.Q.; Nielsen-Gammon, J.W. Ensemble-based simultaneous state and parameter estimation in a two-dimensional sea-breeze model. Mon. Weather Rev. 2006, 134, 2951–2970. [Google Scholar] [CrossRef] [Green Version]
- Hunt, B.R.; Kostelich, E.J.; Szunyogh, I. Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter. Phys. D 2007, 230, 112–126. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S. Coupled data assimilation and parameter estimation in coupled ocean–atmosphere models: A review. Clim. Dyn. 2020, 54, 5127–5144. [Google Scholar] [CrossRef]
- Zhang, F.; Snyder, Q.; Sun, J. Impacts of initial estimate and observation availability on convective-scale data assimilation with an ensemble Kalman filter. Mon. Weather Rev. 2004, 132, 1238–1253. [Google Scholar] [CrossRef]
- Whitaker, J.; Hamill, M. Evaluating methods to account for system errors in ensemble data assimilation. Mon. Weather Rev. 2012, 140, 3078–3089. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, S.; Liu, Z.; Rosati, A.; Delworth, T. A study of impact of the geographic dependent of observing system on parameter estimation with intermediate coupled model. Clim. Dyn. 2013, 40, 1789–1798. [Google Scholar] [CrossRef]
- Ruiz, J.J.; Pulido, M.; Miyoshi, T. Estimating model parameters with ensemble-based data assimilation: A review. J. Meteorol. Soc. Jpn. Ser. II 2013, 91, 79–99. [Google Scholar] [CrossRef] [Green Version]
- Gill, A.E. Some simple solutions for heat-induced tropical circulation. Q. J. R. Meteorol. Soc. 1980, 106, 447–462. [Google Scholar] [CrossRef]
- Zebiak, S.E.; Cane, M.A. A model El Niño-Southern oscillation. Mon. Weather Rev. 1987, 115, 2262–2278. [Google Scholar] [CrossRef] [Green Version]
- Sluka, T.C.; Penny, S.G.; Kalnay, E.; Miyoshi, T. Assimilating atmospheric observations into the ocean using strongly coupled ensemble data assimilation. Geophys. Res. Lett. 2016, 43, 752–759. [Google Scholar] [CrossRef] [Green Version]
- Duc, L.; Saito, K.; Hotta, D. Analysis and design of covariance inflation methods using inflation functions. Part 1: Theoretical framework. Q. J. R. Meteorol. Soc. 2020, 146, 3638–3660. [Google Scholar] [CrossRef]
- Kleeman, R.; Moore, A.M. A theory for the limitation of ENSO predictability due to stochastic atmospheric transients. J. Atmos. Sci. 1997, 54, 753–767. [Google Scholar] [CrossRef]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Latif, M.; Barnett, T.P.; Cane, M.A.; Flugel, M.; Graham, N.E.; Storch, H.; Xu, J.S.; Zebiak, S.E. A review of ENSO prediction studies. Clim. Dyn. 1994, 9, 167–179. [Google Scholar] [CrossRef]
- Webster, P.J.; Yang, S. Monsoon and ENSO: Selectively interactive systems. Q. J. R. Meteorol. Soc. 1992, 118, 877–926. [Google Scholar] [CrossRef]
- Samelson, R.G.; Tziperman, E. Instability of the chaotic ENSO: The growth-phase predictability barrier. J. Atmos. Sci. 2001, 58, 3613–3625. [Google Scholar] [CrossRef] [Green Version]
- Mu, M.; Duan, W.; Wang, B. Season-dependent dynamics of nonlinear optimal error growth and El Niño-Southern Oscillation predictability in a theoretical model. J. Geophys. Res. 2007, 112, D10113. [Google Scholar] [CrossRef] [Green Version]
- Jin, E.K.; Kinter, J.L.; Wang, B.; Park, C.K.; Kang, I.S.; Kirtman, B.P.; Kug, J.S.; Kumar, A.; Luo, J.J.; Schemm, J.; et al. Current status of ENSO prediction skill in coupled ocean-atmosphere models. Clim. Dyn. 2008, 31, 647–664. [Google Scholar] [CrossRef]
- Barnston, A.G.; Tippett, M.K.; L’Heureux, M.L.; Li, S.H.; DeWitt, D.G. Skill of real-time seasonal ENSO model predictions during 2002–11: Is our capability increasing? Bull. Am. Meteorol. Soc. 2012, 93, 631–651. [Google Scholar] [CrossRef]
- Lian, T.; Chen, D. An evaluation of rotated EOF analysis and its application to tropical Pacific SST variability. J. Clim. 2012, 25, 5361–5373. [Google Scholar] [CrossRef]
- Zheng, F.; Fang, X.H.; Zhu, J.; Yu, J.Y.; Li, X.C. Modulation of Bjerknes feedback on the decadal variations in ENSO predictability. Geophys. Res. Lett. 2016, 43, 12560–12568. [Google Scholar] [CrossRef]

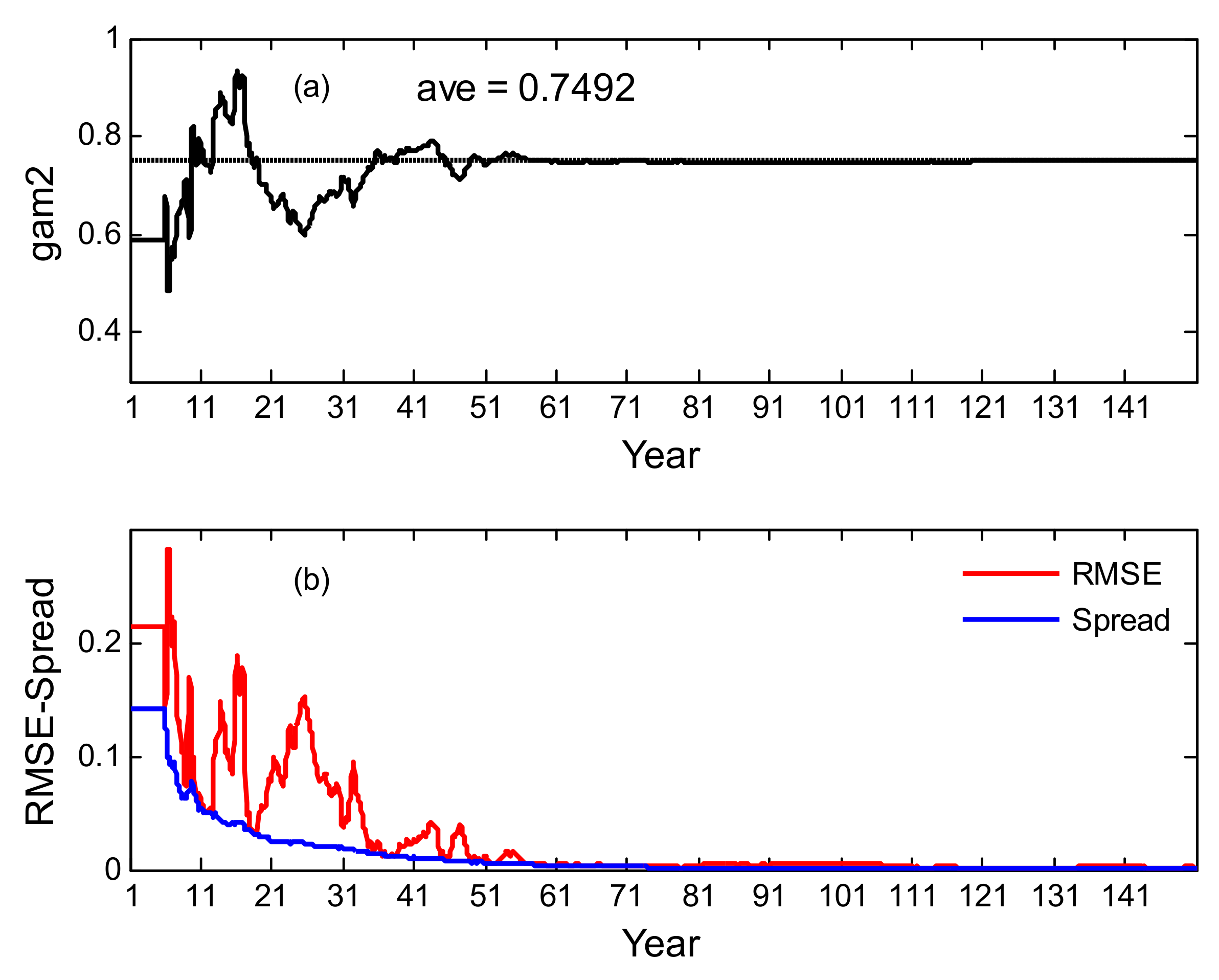







| Schemes | FI | CCI | EPES | RTPS | RTPP | New |
|---|---|---|---|---|---|---|
| Convergence times | 296 | 323 | 27 | 312 | 365 | 288 |
| Estimated values | 0.7631 | 0.7793 | 0.8006 | 0.7318 | 0.7249 | 0.7492 |
| Relative errors(%) | 1.75 | 3.91 | 6.75 | 2.42 | 3.35 | 0.11 |
| Pars. | Physical Meanings | Units | Truths | Initial Guesses |
|---|---|---|---|---|
| gam1 | Strength of mean upwelling advection term | - | 0.75 | 0.6 |
| gam2 | Strength of anomalous upwelling advection term | - | 0.75 | 0.6 |
| tda1 | Amplitude of subsurface temperature anomaly +h perturbations | °C | 28 | 22.4 |
| tda2 | Amplitude of subsurface temperature anomaly for −h perturbations | °C | −40 | −48 |
| tdb1 | Affect the nonlinearity of subsurface temperature anomaly for +h perturbations | m−1 | 1.25 | 1.0 |
| tdb2 | Affect the nonlinearity of subsurface temperature anomaly for −h perturbations | m−1 | 3.0 | 2.4 |
| Experiments | Assimilated | Estimated | (a,b) |
|---|---|---|---|
| onlySE | SSTA | SSTA | (-,-) |
| SPE | SSTA | gam2\SSTA | (0.15,0.08) |
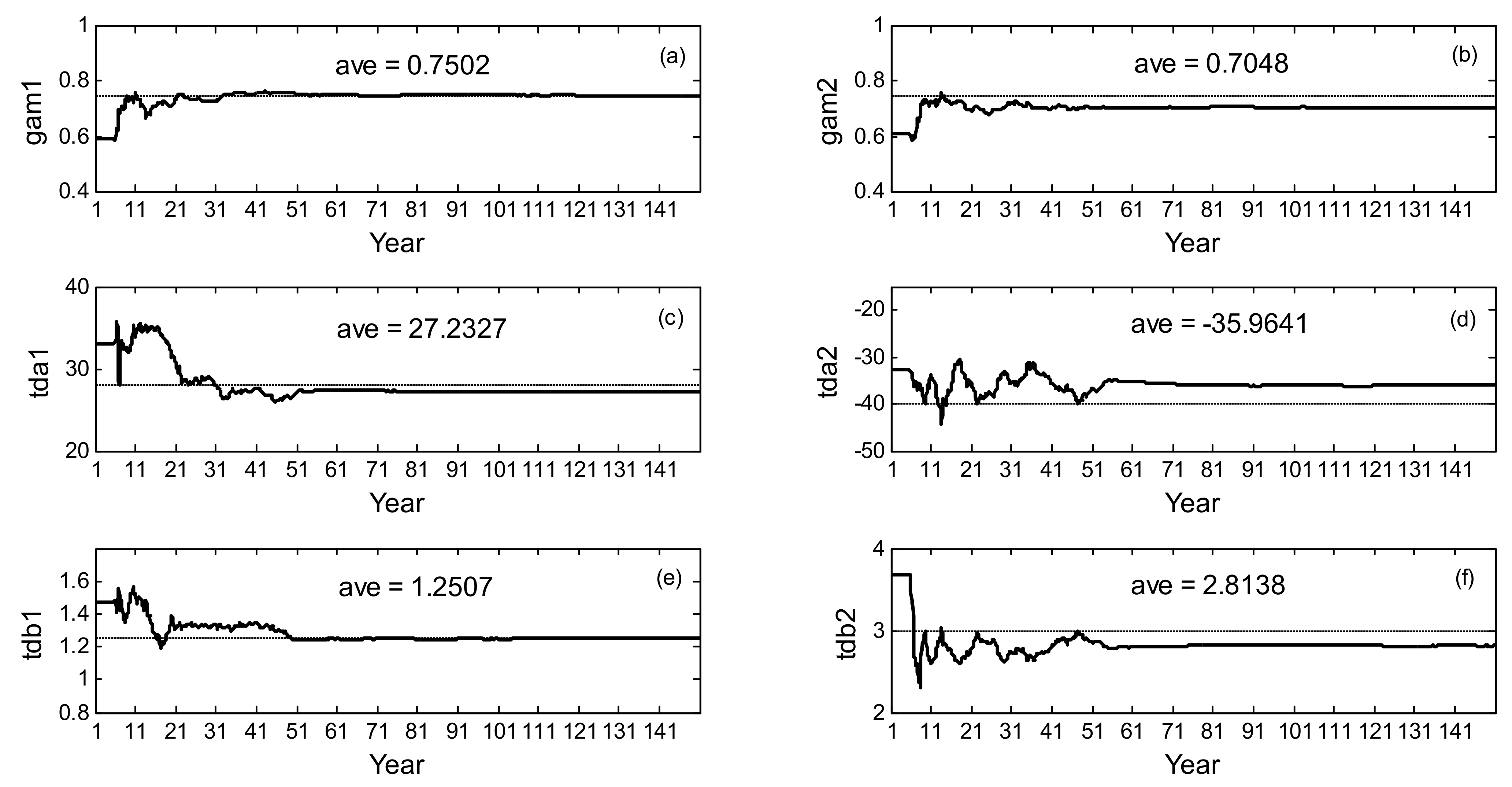
| MPE | SSTA | gam1\gam2\tda1\tda2\ tdb1\tdb2\SSTA | (0.31,0.016)\(0.30,0.015)\(4.12,1.69)\ (6.58,3.44)\(0.09,0.05)\(0.45,0.20) |
| Experiments | Assimilated | Estimated | (a,b) |
|---|---|---|---|
| OnlySE | SSTA | SSTA | (-,-) |
| MPE | SSTA | gam1\gam2\tda1\ tda2\tdb1\tdb2\SSTA | (0.02,0.01)\(0.02,0.01)\ (0.80,0.38)\(1.14,0.54)\ (0.04,0.02)\(0.08,0.04) |
| Relative Errors | gam1 | gam2 | tda1 | tda2 | tdb1 | tdb2 |
|---|---|---|---|---|---|---|
| Initial | −20% | −20% | 20% | 20% | 20% | 20% |
| Estimated | 0.03% | −6% | −2.7% | 10.1% | 0.05% | −6.2% |
| State Variables | SSTA | ZWA | ULDA | TeA | ||||
|---|---|---|---|---|---|---|---|---|
| Exps. | onlySE | MPE | onlySE | MPE | onlySE | MPE | onlySE | MPE |
| Correlation coefficients | 0.9256 | 0.9594 | 0.8248 | 0.8356 | 0.7172 | 0.8205 | 0.7605 | 0.7893 |
| RMSEs | 0.3071 | 0.2818 | 0.2318 | 0.2271 | 6.6496 | 6.5208 | 0.9197 | 0.9092 |
| Experiments | Parameter Values (Truncated to Two Decimal Places) |
|---|---|
| Optimized Pars | gam1 = 0.73, gam2 = 0.70, tda1 = 26.24, tda2 = −37.48, tdb1 = 1.17, tdb2 = 2.81 |
| Default Pars | gam1 = 0.75, gam2 = 0.75, tda1 = 28.00, tda2 = −40.00, tdb1 = 1.25, tdb2 = 3.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Tang, Y.; Song, X.; Shen, Z. Parameter Estimation Based on a Local Ensemble Transform Kalman Filter Applied to El Niño–Southern Oscillation Ensemble Prediction. Remote Sens. 2021, 13, 3923. https://doi.org/10.3390/rs13193923
Gao Y, Tang Y, Song X, Shen Z. Parameter Estimation Based on a Local Ensemble Transform Kalman Filter Applied to El Niño–Southern Oscillation Ensemble Prediction. Remote Sensing. 2021; 13(19):3923. https://doi.org/10.3390/rs13193923
Chicago/Turabian StyleGao, Yanqiu, Youmin Tang, Xunshu Song, and Zheqi Shen. 2021. "Parameter Estimation Based on a Local Ensemble Transform Kalman Filter Applied to El Niño–Southern Oscillation Ensemble Prediction" Remote Sensing 13, no. 19: 3923. https://doi.org/10.3390/rs13193923
APA StyleGao, Y., Tang, Y., Song, X., & Shen, Z. (2021). Parameter Estimation Based on a Local Ensemble Transform Kalman Filter Applied to El Niño–Southern Oscillation Ensemble Prediction. Remote Sensing, 13(19), 3923. https://doi.org/10.3390/rs13193923






