Assessment of Near-Real-Time Satellite Precipitation Products from GSMaP in Monitoring Rainfall Variations over Taiwan
Abstract
:1. Introduction
2. Data and Methodology
2.1. Data
2.2. Statistical Methods Applied for Evaluations
3. Results
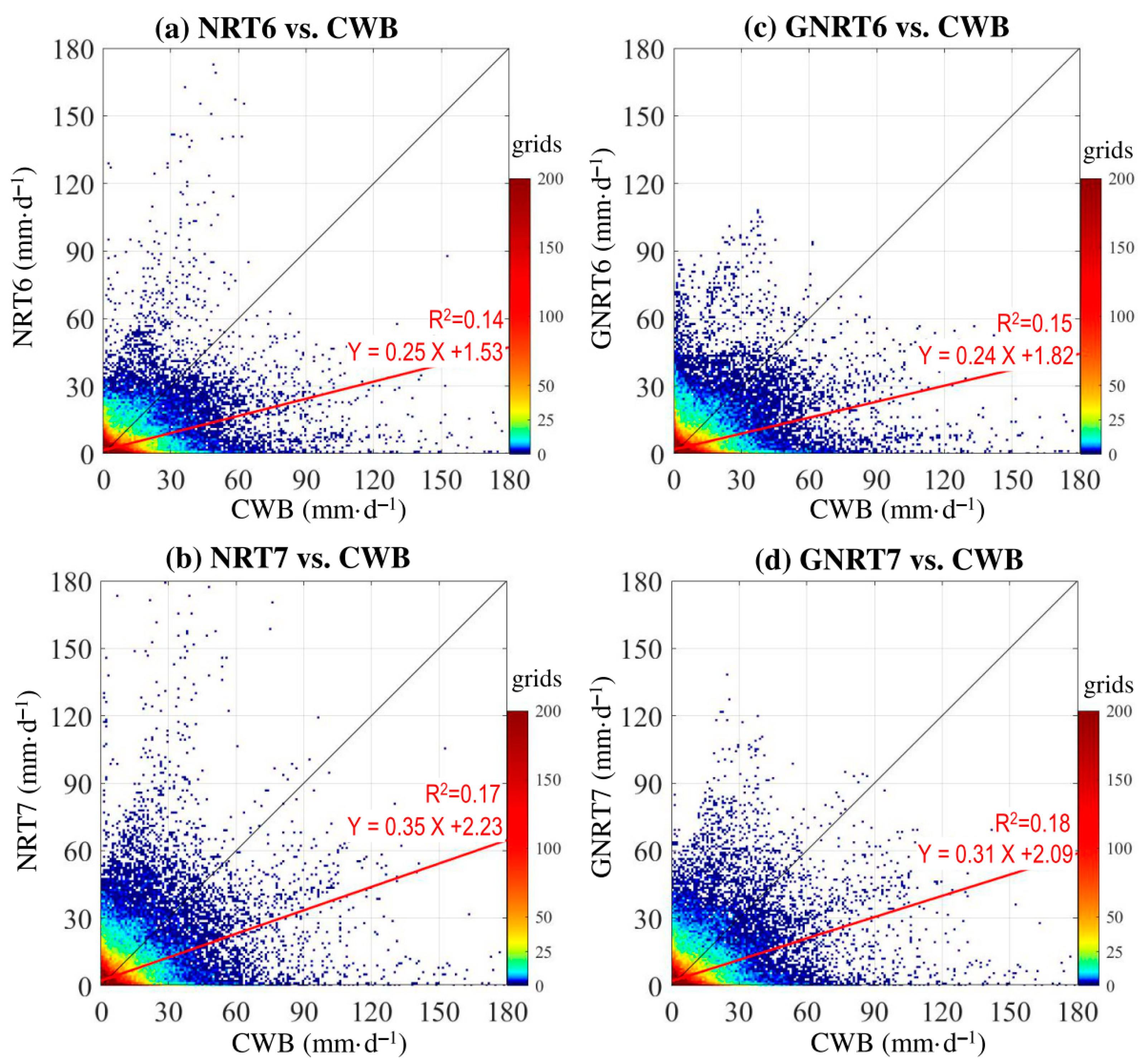
3.1. Case Study and Annual Rainfall Pattern
3.2. Rainfall Evaluation for Warm Months
3.3. Rainfall Evaluation for Cold Months
3.4. More Discussions and Explanations for the Difference Between SPPs
4. Conclusions
- (1)
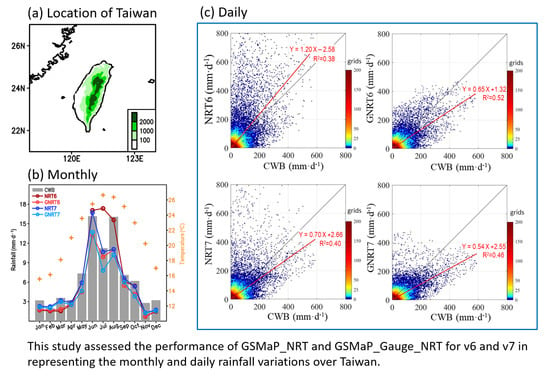
- For the annual cycle of monthly rainfall, NRT7 is superior in quantitative rainfall estimation (Figure 2). Among SPPs, most of them underestimated the monthly rainfall throughout the year (except NRT6, which overestimated July rainfall), and the observed errors were larger in the GNRTs than the NRTs. The differences between NRT and GNRT in depicting monthly rainfall are larger during warm months than during cold months. For monthly rainfall during the cold months, v7 performed better than v6, although this was not always true for the warm months. The differences between SPPs in depicting the monthly rainfall variations are mainly controlled by the stronger rainfall events (Figure 3).
- (2)
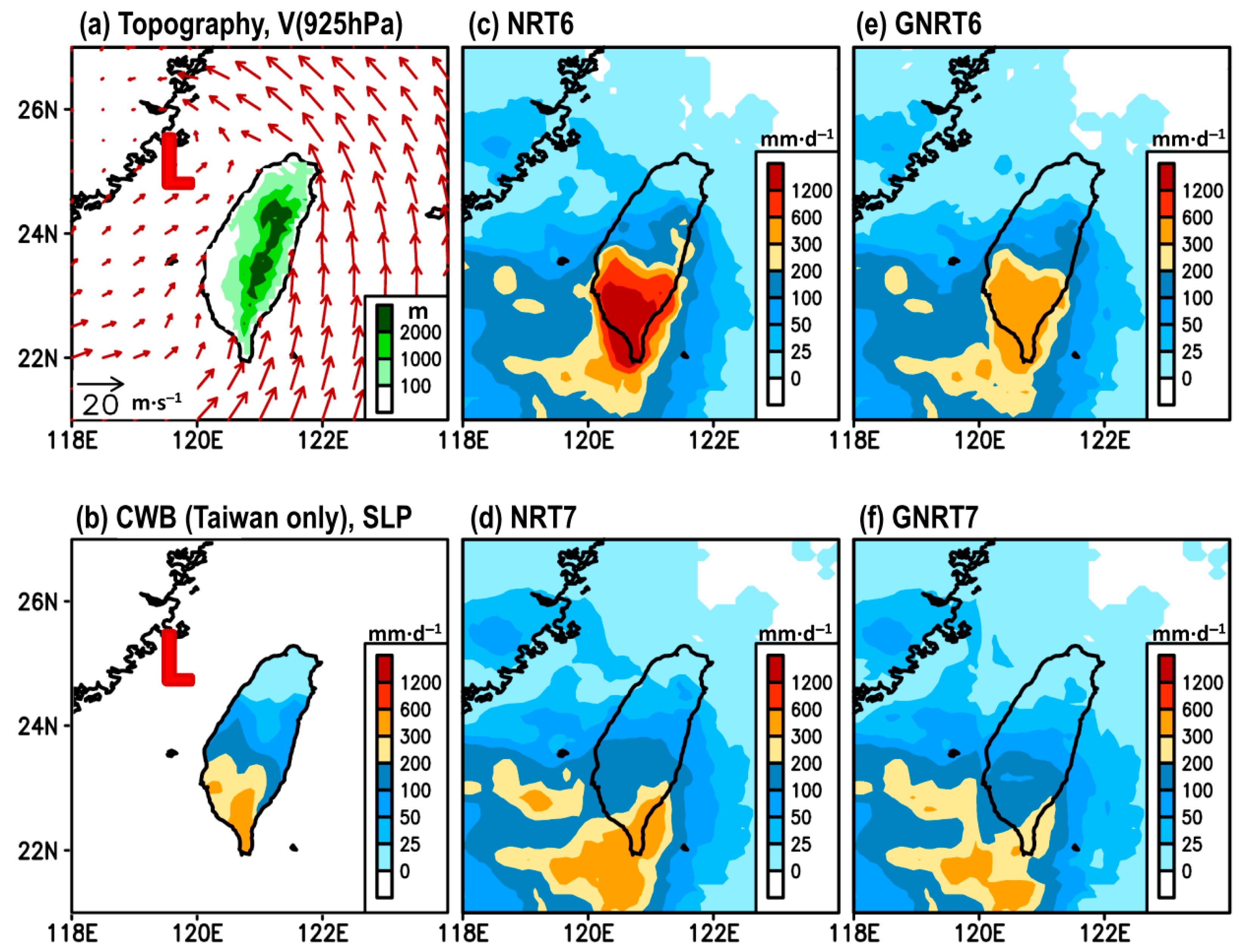
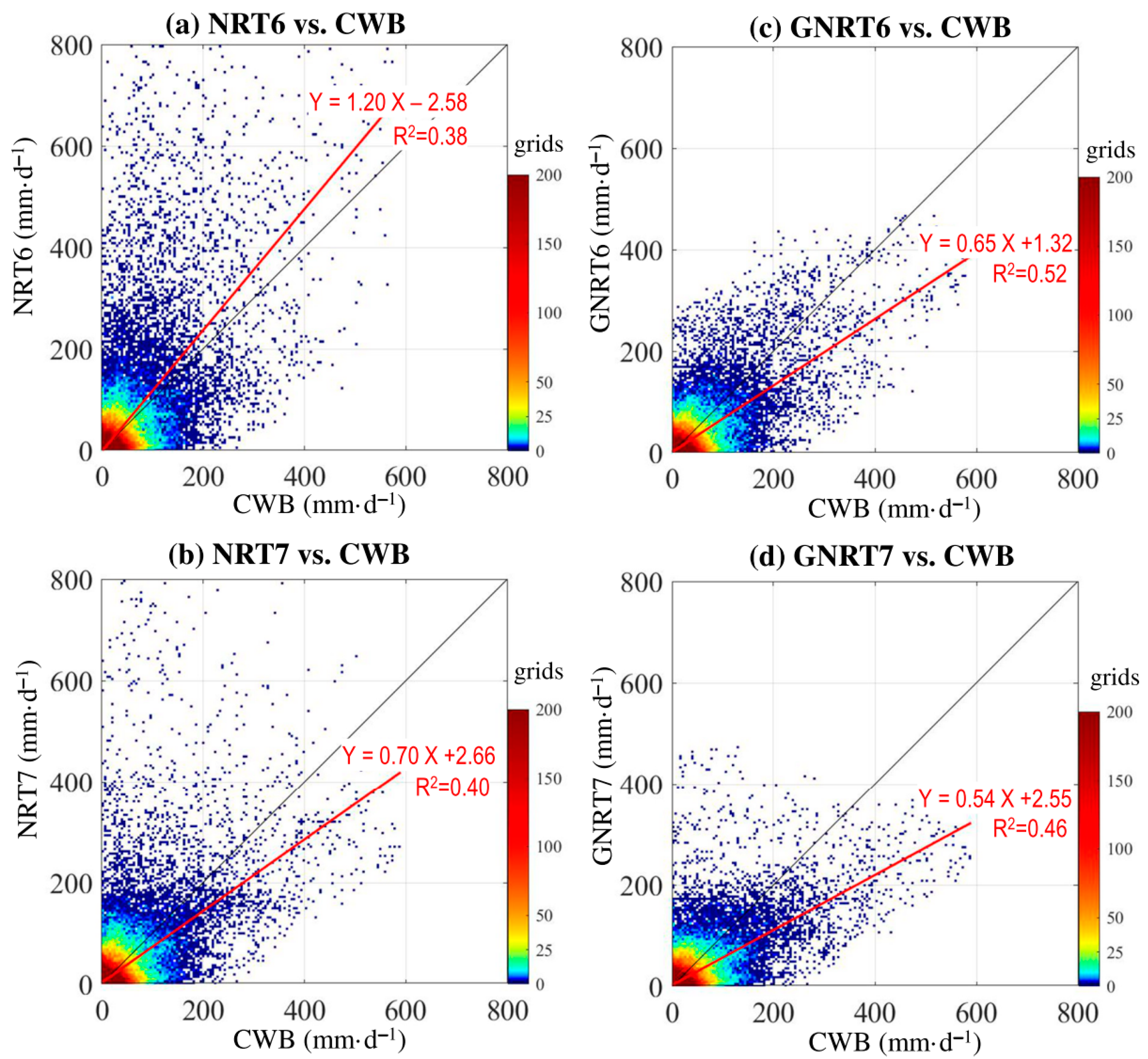
- Among the four SPPs, GNRT6 and GNRT7 were the best in capturing the daily rainfall variations, including stronger rainfall events during warm (Figure 4 and Figure 5) and cold months (Figure 6 and Figure 7), respectively. Spatially, the major improvements from NRT6 to GNRT6 and NRT7 to GNRT7 in monitoring the stronger rainfall events over southwestern Taiwan can be seen during warm and cold months, respectively. Between NRT6 and NRT7, NRT7 was better at monitoring larger daily rainfall over southwestern Taiwan during both warm and cold months.
- (3)
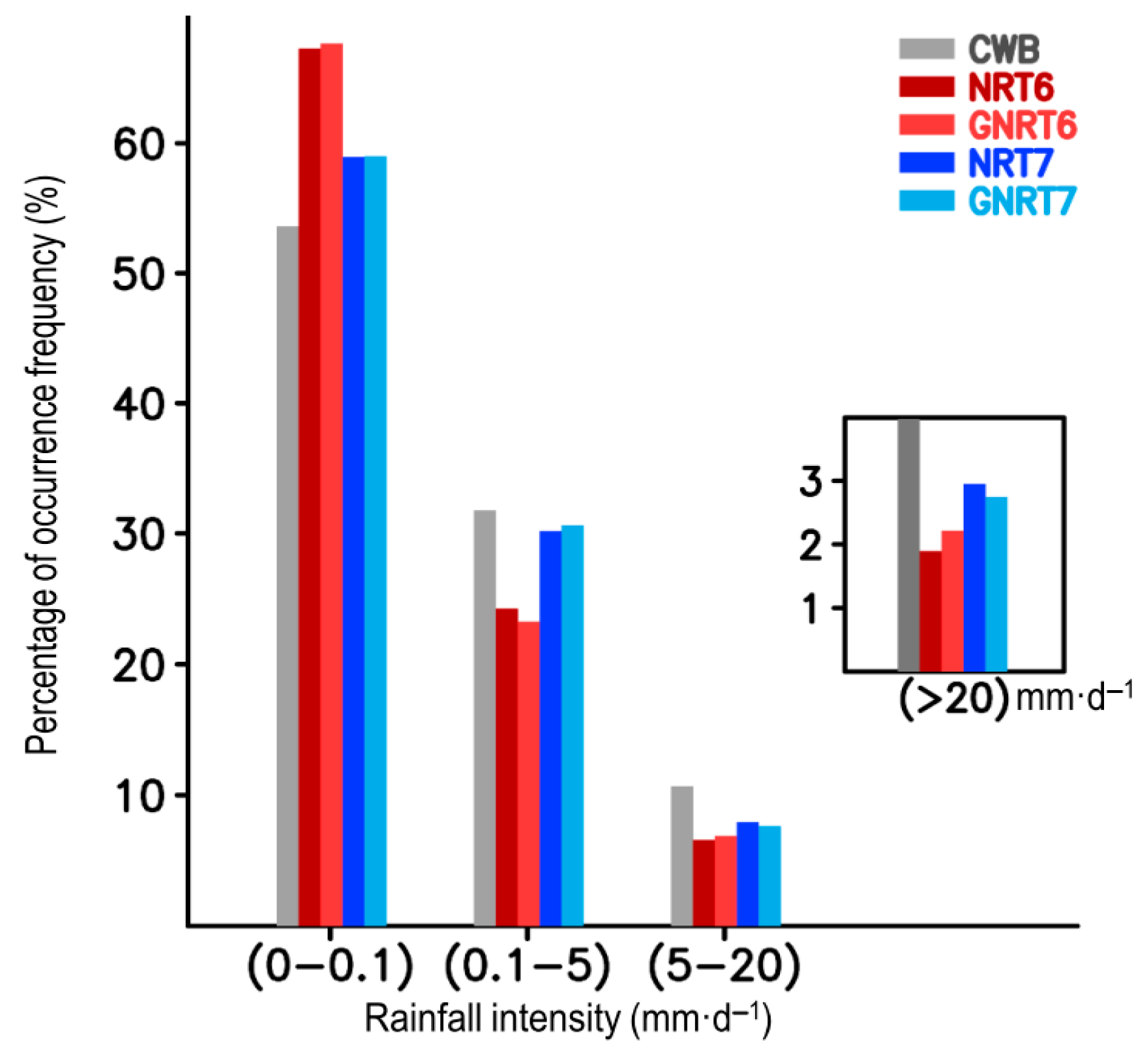
- GNRT helped reduce the error seen in NRT’s overestimation of stronger rainfall events for both warm and cold months in v6 and v7 (Figure 9 and Figure 10). NRT7 is better than NRT6 in both the warm and cold months. Possible explanations for the differences between the ability of SPPs are attributed to the algorithms used in SPPs.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mao, J.; Wu, G. Diurnal variations of summer precipitation over the Asian monsoon region as revealed by TRMM satellite data. Sci. China Earth Sci. 2012, 55, 554–566. [Google Scholar] [CrossRef]
- Xu, W. Precipitation and Convective Characteristics of Summer Deep Convection over East Asia Observed by TRMM. Mon. Weather Rev. 2013, 141, 1577–1592. [Google Scholar] [CrossRef]
- Hsu, H.H.; Zhou, T.; Matsumoto, J. East Asian, Indochina and Western North Pacific Summer Monsoon—An update. Asia Pac. J. Atmos. Sci. 2014, 50, 45–68. [Google Scholar] [CrossRef]
- Huang, W.R.; Wang, S.Y. Impact of land-sea breezes at different scales on the diurnal rainfall in Taiwan. Clim. Dyn. 2014, 43, 1951–1963. [Google Scholar] [CrossRef]
- Chen, G.; Sha, W.; Iwasaki, T.; Wen, Z. Diurnal Cycle of a Heavy Rainfall Corridor over East Asia. Mon. Weather Rev. 2017, 145, 3365–3389. [Google Scholar] [CrossRef]
- Fu, Y.F.; Pan, X.; Yang, Y.J.; Chen, F.J.; Liu, P. Climatological characteristics of summer precipitation over East Asia measured by TRMM PR: A review. J. Meteorol. Res. 2017, 31, 142–159. [Google Scholar] [CrossRef]
- Huang, W.R.; Chang, Y.H. Impact of Boreal Summer Intraseasonal Oscillations on Warm Season Diurnal Convection Activity in Taiwan. Int. J. Climatol. 2018, 38, 2187–2200. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K. Global precipitation map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Stocker, E.F.; Tan, J. V06 IMERG Release Notes; NASA/GSFC: Greenbelt, MD, USA, 2019. [Google Scholar]
- Kubota, T.; Aonashi, K.; Ushio, T.; Shige, S.; Takayabu, Y.N.; Kachi, M.; Arai, Y.; Tashima, T.; Masaki, T.; Kawamoto, N.; et al. Global Satellite Mapping of Precipitation (GSMaP) Products in the GPM Era. In Satellite Precipitation Measurement. Advances in Global Change Research, 1st ed.; Levizzani, V., Kidd, C., Kirschbaum, D., Kummerow, C., Nakamura, K., Turk, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 67. [Google Scholar]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.-H.; Chen, H.; Delrieu, G.; Hsu, Y.C.; et al. Evaluation of GPM-era Global Satellite Precipitation Products over Multiple Complex Terrain Regions. Remote Sens. 2019, 11, 2936. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.Y.; Aryastana, P.; Liu, G.R.; Huang, W.R. Assessment of satellite precipitation product estimates over Bali Island. Atmos. Res. 2020, 244, 105032. [Google Scholar] [CrossRef]
- Lu, D.; Yong, B. Evaluation and Hydrological Utility of the Latest GPM IMERG V5 and GSMaP V7 Precipitation Products over the Tibetan Plateau. Remote Sens. 2018, 10, 2022. [Google Scholar] [CrossRef] [Green Version]
- Tan, M.L.; Duan, Z. Assessment of GPM and TRMM Precipitation Products over Singapore. Remote Sens. 2017, 9, 720. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.; Zhang, L.; Soe, K.M.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Applications of TRMM- and GPM-Era Multiple- Satellite Precipitation Products for Flood Simulations at Sub-Daily Scales in a Sparsely Gauged Watershed in Myanmar. Remote Sens. 2019, 11, 140. [Google Scholar] [CrossRef] [Green Version]
- Ning, S.; Song, F.; Udmale, P.; Jin, J.; Thapa, B.R.; Ishidaira, H. Error Analysis and Evaluation of the Latest GSMap and IMERG Precipitation Products over Eastern China. Adv. Meteorol. 2017, 2017, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Tan, X.; Yong, B.; Ren, L. Error features of the hourly GSMaP multi-satellite precipitation estimates over nine major basins of China. Hydrol. Res. 2018, 49, 761–779. [Google Scholar] [CrossRef]
- Shi, J.; Yuan, F.; Shi, C.; Zhao, C.; Zhang, L.; Ren, L.; Zhu, Y.; Jiang, S.; Liu, Y. Statistical Evaluation of the Latest GPM-Era IMERG and GSMaP Satellite Precipitation Products in the Yellow River Source Region. Water 2020, 12, 1006. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.Q.; Zeng, Z.; Ma, M.; Liu, R.; Wen, Y.; Hon, Y. Can near–real–time satellite precipitation products capture rainstorms and guide flood warning for the 2016 summer in south China? IEEE Geosci. Remote Sens. 2017, 14, 1208–1212. [Google Scholar] [CrossRef]
- Chen, T.C.; Huang, W.R.; Yen, M.C. Interannual variation of the late spring–early summer monsoon rainfall in the northern part of the South China Sea. J. Clim. 2011, 24, 4295–4313. [Google Scholar] [CrossRef]
- Kerns, B.W.J.; Chen, Y.L.; Chang, M.Y. The diurnal cycle of winds, rain, and clouds over Taiwan during the Mei-yu, summer, and autumn rainfall regimes. Mon. Weather Rev. 2010, 138, 497–516. [Google Scholar] [CrossRef]
- Wu, Y.C.; Wang, S.Y.; Yu, Y.C.; Kung, C.Y.; Wang, A.H.; Los, S.A.; Huang, W.R. Climatology and Change of Extreme Precipitation Events in Taiwan Based on Weather Types. Int. J. Climatol. 2019, 39, 5351–5366. [Google Scholar] [CrossRef] [Green Version]
- Yen, M.C.; Chen, T.C. Seasonal variation of the rainfall over Taiwan. Int. J. Climatol. 2000, 20, 803–809. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Y. The Rainfall Characteristics of Taiwan. Mon. Weather Rev. 2003, 131, 1323–1341. [Google Scholar] [CrossRef]
- Huang, W.R.; Chang, Y.H. Characteristics and Mechanisms of the Diurnal Variation of Winter Precipitation in Taiwan. Int. J. Climatol. 2018, 38, 3058–3068. [Google Scholar] [CrossRef]
- Huang, W.R.; Chang, Y.H.; Liu, P.Y. Assessment of IMERG precipitation over Taiwan at multiple timescales. Atmos. Res. 2018, 214, 239–249. [Google Scholar] [CrossRef]
- Huang, W.R.; Liu, P.Y.; Chang, Y.H.; Liu, C.Y. Evaluation and Application of Satellite Precipitation Products in Studying the Summer Precipitation Variations over Taiwan. Remote Sens. 2020, 12, 347. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.Y.; Huang, W.R. Comparison of the warm season rainfall estimations in Taiwan during 2014–2017 from IMERG version 5 Early, Late and Final run satellite products. J. Geogr. Sci. 2020, 96, 1–26. (In Chinese) [Google Scholar]
- Lu, D.; Yong, B. A Preliminary Assessment of the Gauge-Adjusted Near-Real-Time GSMaP Precipitation Estimate over Mainland China. Remote Sens. 2020, 12, 141. [Google Scholar] [CrossRef] [Green Version]
- Mastrantonas, N.; Bhattacharya, B.; Shibuo, Y.; Rasmy, M.; Espinoza-Dávalos, G.; Solomatine, D. Evaluating the Benefits of Merging Near-Real-Time Satellite Precipitation Products: A Case Study in the Kinu Basin Region, Japan. J. Hydrometeorol. 2019, 20, 1213–1233. [Google Scholar] [CrossRef]
- Tam, T.H.; Abd Rahman, M.Z.; Harun, S.; Hanapi, M.N.; Kaoje, I.U. Application of Satellite Rainfall Products for Flood Inundation Modelling in Kelantan River Basin, Malaysia. Hydrology 2019, 6, 95. [Google Scholar] [CrossRef] [Green Version]
- Palharini, R.S.A.; Vila, D.A.; Rodrigues, D.T.; Quispe, D.P.; Palharini, R.C.; de Siqueira, R.A.; de Sousa Afonso, J.M. Assessment of the Extreme Precipitation by Satellite Estimates over South America. Remote Sens. 2020, 12, 2085. [Google Scholar] [CrossRef]
- Kubota, T.; Liu, G.; Tashima, T.; Oki, R. Development of snowfall estimation method in Global Satellite Mapping of Precipitation (GSMaP) product. In Proceedings of the Japan Geoscience Union Meeting 2018, Chiba, Japan, 20–24 May 2018. [Google Scholar]
- Mega, T.; Ushio, T.; Matsuda, M.T.; Kubota, T.; Kachi, M.; Oki, R. Gauge-adjusted global satellite mapping of precipitation. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1928–1935. [Google Scholar] [CrossRef]
- Tashima, T.; Kubota, T.; Mega, T.; Ushio, T.; Oki, R. Precipitation Extremes Monitoring Using the Near-Real-Time GSMaP Product. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 5640–5651. [Google Scholar] [CrossRef]
- Chen, H.; Yong, B.; Shen, Y.; Liu, J.; Hong, Y.; Zhang, J. Comparison analysis of six purely satellite-derived global precipitation estimates. J. Hydrol. 2020, 581, 124376. [Google Scholar] [CrossRef]
- Kachi, M.; Kubota, T.; Ushio, T.; Shige, S.; Kida, S.; Aonashi, K.; Okamoto, K. Development and utilization of “JAXA Global Rainfall Watch” system. IEEJ Trans. Fundam. Mater. 2011, 131, 729–737, (In Japanese with English abstract). [Google Scholar] [CrossRef]
- Ushio, T.; Kubota, T.; Shige, S.; Okamoto, K.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M.; Oki, R.; et al. A Kalman filter approach to the Global Satellite Mapping of Precipitation (GSMaP) from combined passive microwave and infrared radiometric data. J. Meteorol. Soc. Jpn. 2009, 87A, 137–151. [Google Scholar] [CrossRef] [Green Version]
- Storch, H.V.; Zwiers, F.W. Statistical Analysis in Climate Research, 1st ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Huang, W.R.; Chang, Y.H.; Hsu, H.H.; Cheng, C.T.; Tu, C.Y. Dynamical Downscaling Simulation and Future Projection of Summer Rainfall in Taiwan: Contributions from Different Types of Rain Events. J. Geophys. Res. Atmos. 2016, 121, 13973–13988. [Google Scholar] [CrossRef]






| Diagnostic Statistics | NRT6 | GNRT6 | NRT7 | GNRT7 |
|---|---|---|---|---|
| SCC | 0.89 | 0.91 * | 0.83 | 0.85 |
| RMSE | 581.3 | 69.2 | 67.5 * | 89.9 |
| Diagnostic Statistics | NRT6 | GNRT6 | NRT7 | GNRT7 |
|---|---|---|---|---|
| TCC | 0.95 | 0.98 * | 0.96 | 0.97 |
| RMSE | 2.2 | 2.3 | 1.7 * | 2.5 |
| Diagnostic Statistics | NRT6 | GNRT6 | NRT7 | GNRT7 | |
|---|---|---|---|---|---|
| All rainfall events CWB > 0.1 mm· | CC | 0.62 | 0.72 * | 0.63 | 0.68 |
| RMSE | 50.9 | 25.1* | 32.4 | 26.3 | |
| Stronger rainfall events CWB > 80 mm· | CC | 0.49 | 0.62 * | 0.53 | 0.58 |
| RMSE | 209.7 | 88.8 * | 104.9 | 94.8 | |
| Weaker rainfall events CWB~0.1–80 mm· | CC | 0.40 | 0.48 * | 0.41 | 0.45 |
| RMSE | 29.1 | 17.9 * | 25.1 | 18.5 |
| Diagnostic Statistics | NRT6 | GNRT6 | NRT7 | GNRT7 | |
|---|---|---|---|---|---|
| All rainfall events CWB > 0.1 mm· | CC | 0.37 | 0.39 | 0.41 | 0.43 * |
| RMSE | 12.8 | 12.4 | 12.3 | 12.1 * | |
| Stronger rainfall events CWB > 20 mm· | CC | 0.08 | 0.10 | 0.10 | 0.12 * |
| RMSE | 37.6 | 36.3 | 36.1 | 34.7 * | |
| Weaker rainfall events CWB~0.1–20 mm· | CC | 0.28 | 0.35 | 0.36 | 0.37 * |
| RMSE | 7.4 | 6.8 | 6.7 | 5.9 * |
| Diagnostic Statistics | NRT6 > 80 mm·day−1 | NRT7 > 80 mm·day−1 | ||
|---|---|---|---|---|
| NRT6 | GNRT6 | NRT7 | GNRT7 | |
| CC | 0.33 | 0.62 * | 0.46 | 0.48 |
| RMSE | 226.4 | 80.1 * | 128.8 | 89.6 |
| Diagnostic Statistics | NRT6 > 20 mm·day−1 | NRT7 > 20 mm·day−1 | ||
|---|---|---|---|---|
| NRT6 | GNRT6 | NRT7 | GNRT7 | |
| CC | 0.18 | 0.21 | 0.19 | 0.23 * |
| RMSE | 31.5 | 27.1 | 28.6 | 25.1 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.-R.; Liu, P.-Y.; Hsu, J.; Li, X.; Deng, L. Assessment of Near-Real-Time Satellite Precipitation Products from GSMaP in Monitoring Rainfall Variations over Taiwan. Remote Sens. 2021, 13, 202. https://doi.org/10.3390/rs13020202
Huang W-R, Liu P-Y, Hsu J, Li X, Deng L. Assessment of Near-Real-Time Satellite Precipitation Products from GSMaP in Monitoring Rainfall Variations over Taiwan. Remote Sensing. 2021; 13(2):202. https://doi.org/10.3390/rs13020202
Chicago/Turabian StyleHuang, Wan-Ru, Pin-Yi Liu, Jie Hsu, Xiuzhen Li, and Liping Deng. 2021. "Assessment of Near-Real-Time Satellite Precipitation Products from GSMaP in Monitoring Rainfall Variations over Taiwan" Remote Sensing 13, no. 2: 202. https://doi.org/10.3390/rs13020202
APA StyleHuang, W.-R., Liu, P.-Y., Hsu, J., Li, X., & Deng, L. (2021). Assessment of Near-Real-Time Satellite Precipitation Products from GSMaP in Monitoring Rainfall Variations over Taiwan. Remote Sensing, 13(2), 202. https://doi.org/10.3390/rs13020202