Validation of CHIRPS Precipitation Estimates over Taiwan at Multiple Timescales
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
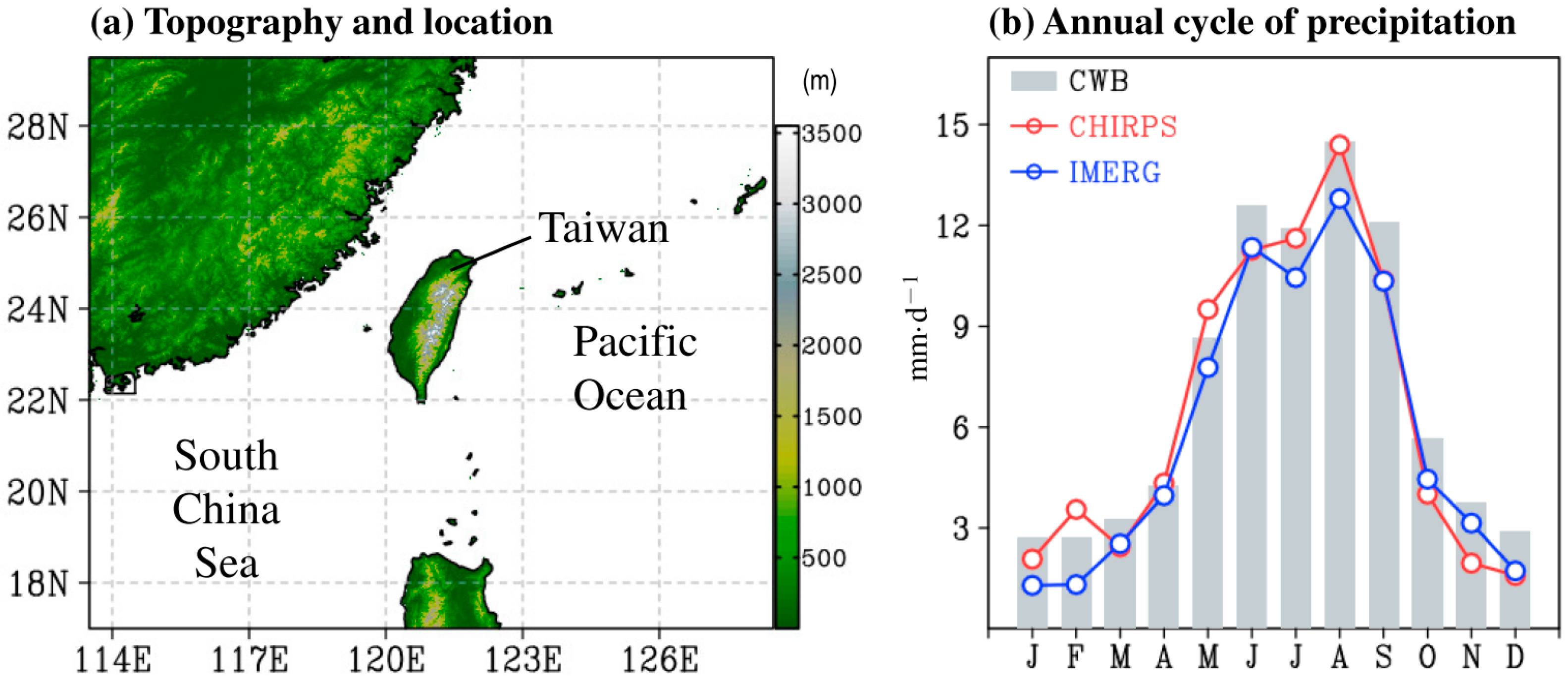
3. Results
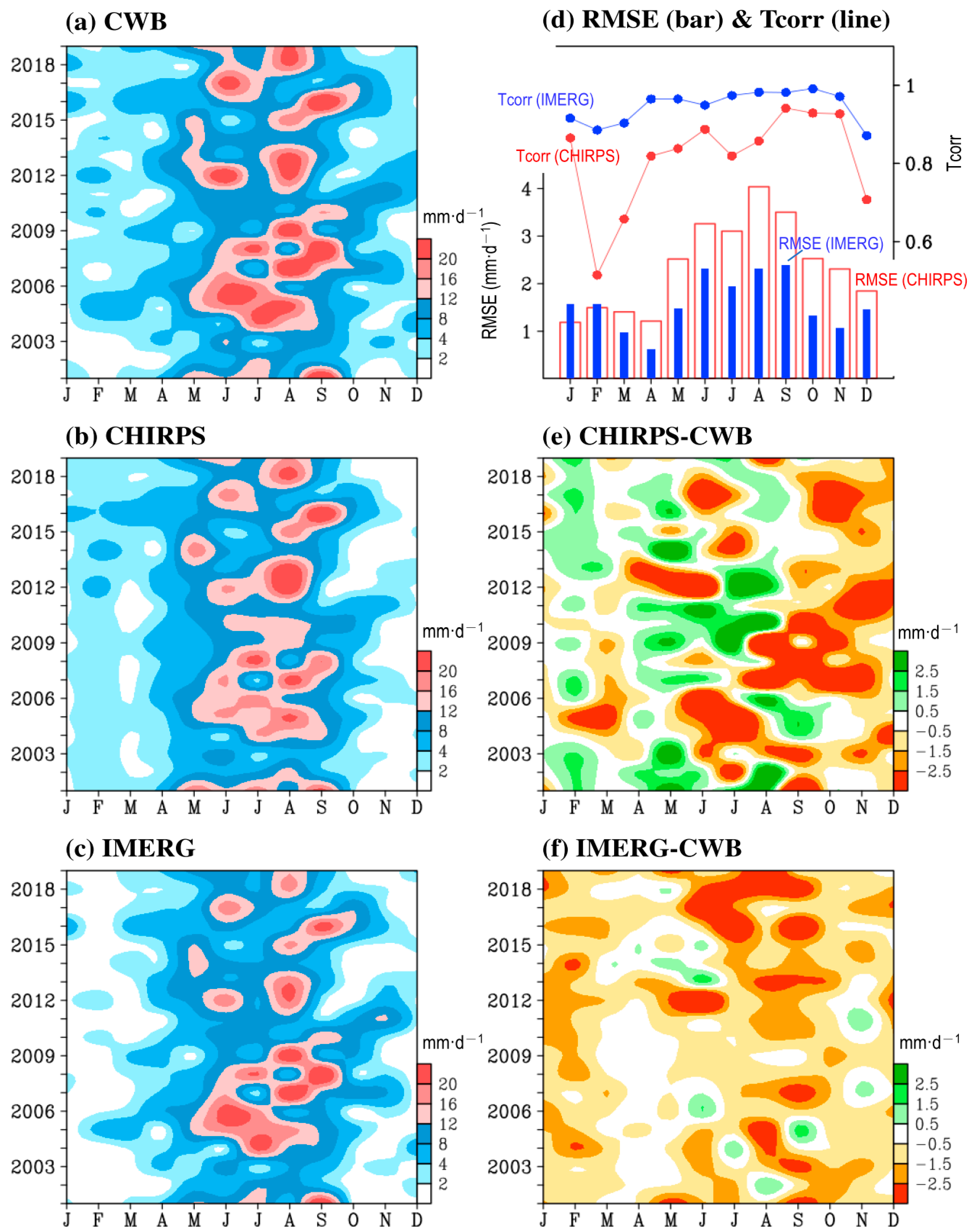
3.1. Temporal Variations of Monthly and Seasonal Precipitation
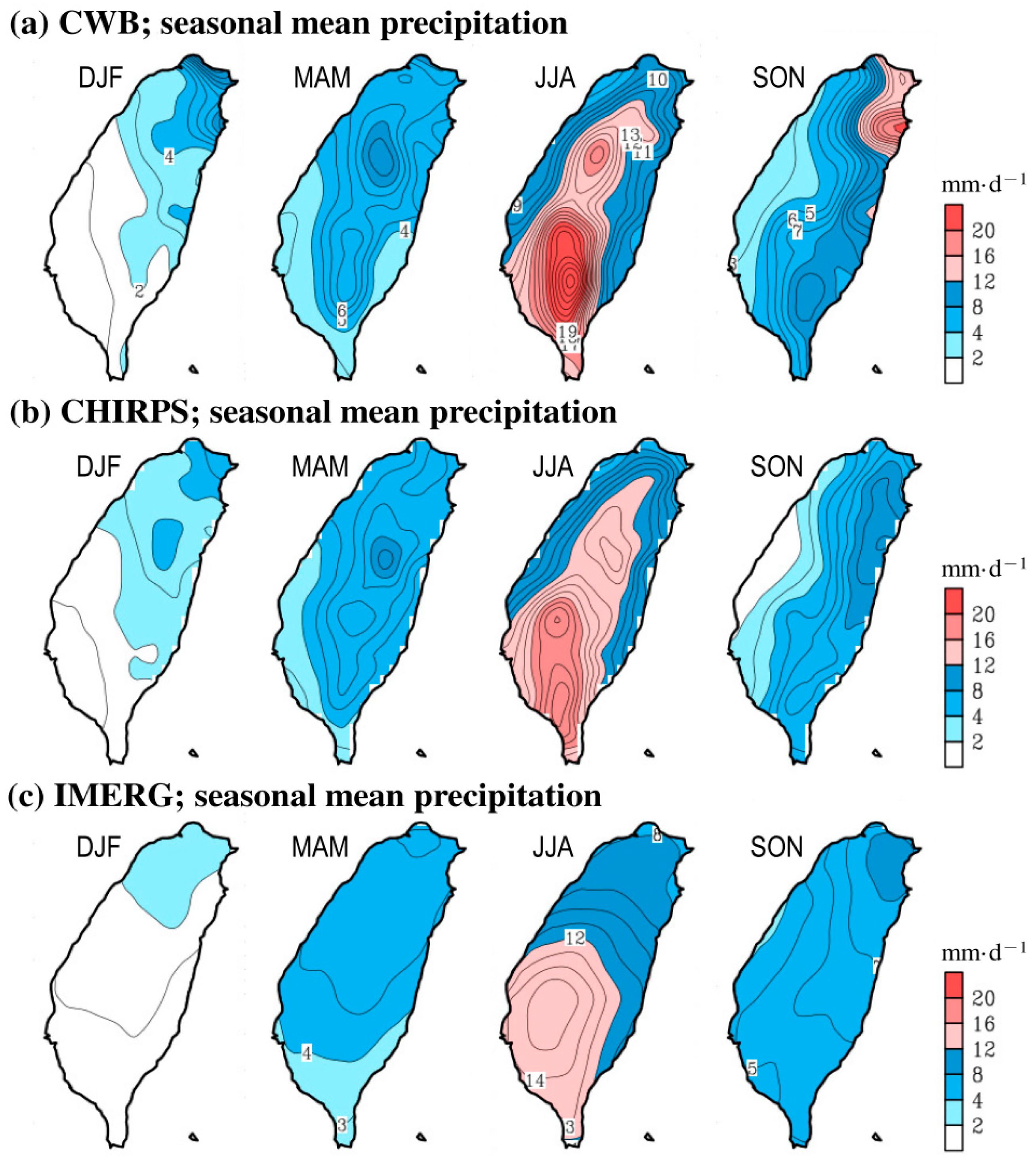
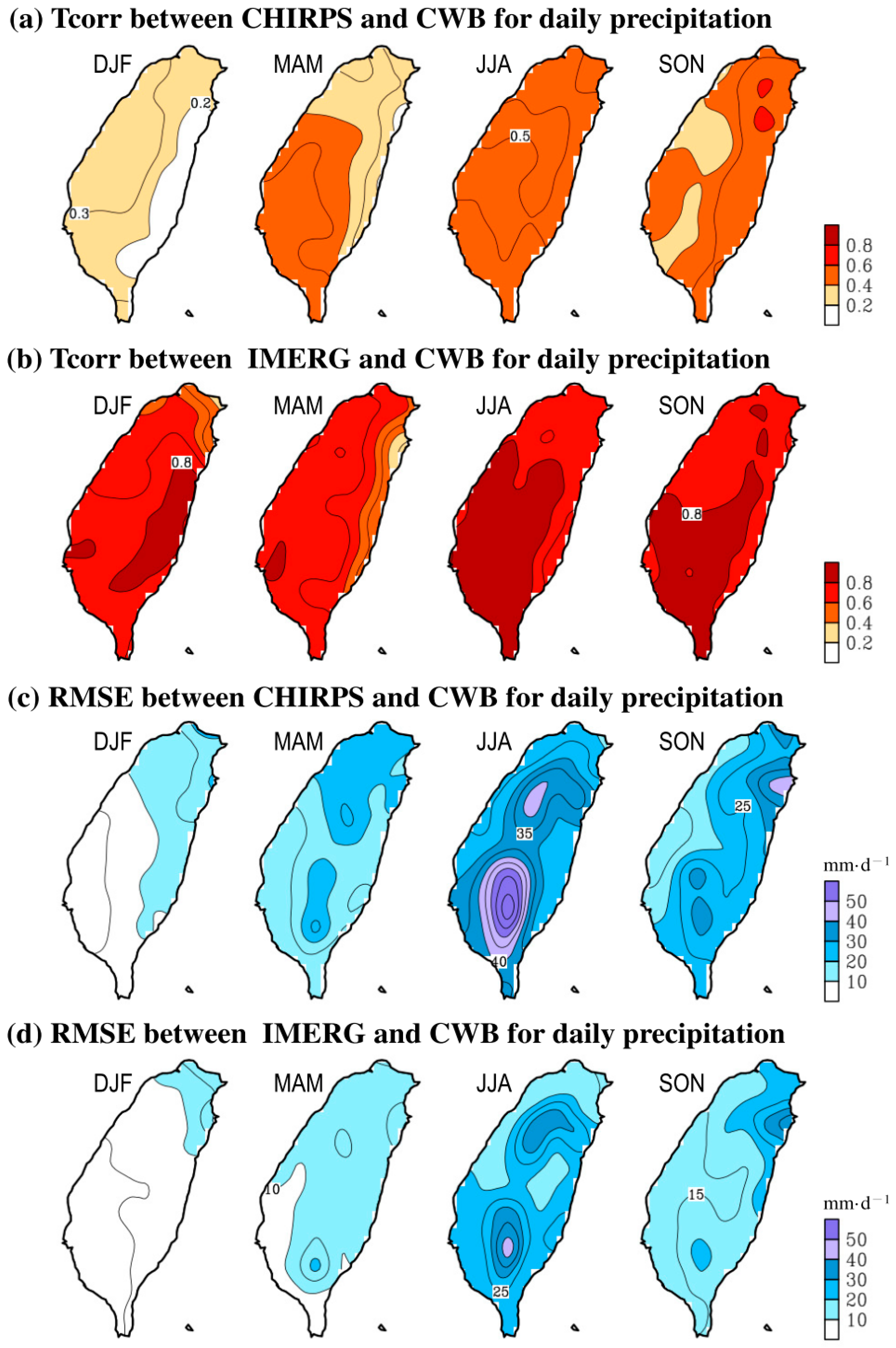
3.2. Sptatial Distribution of Seasonal Mean Precipitation
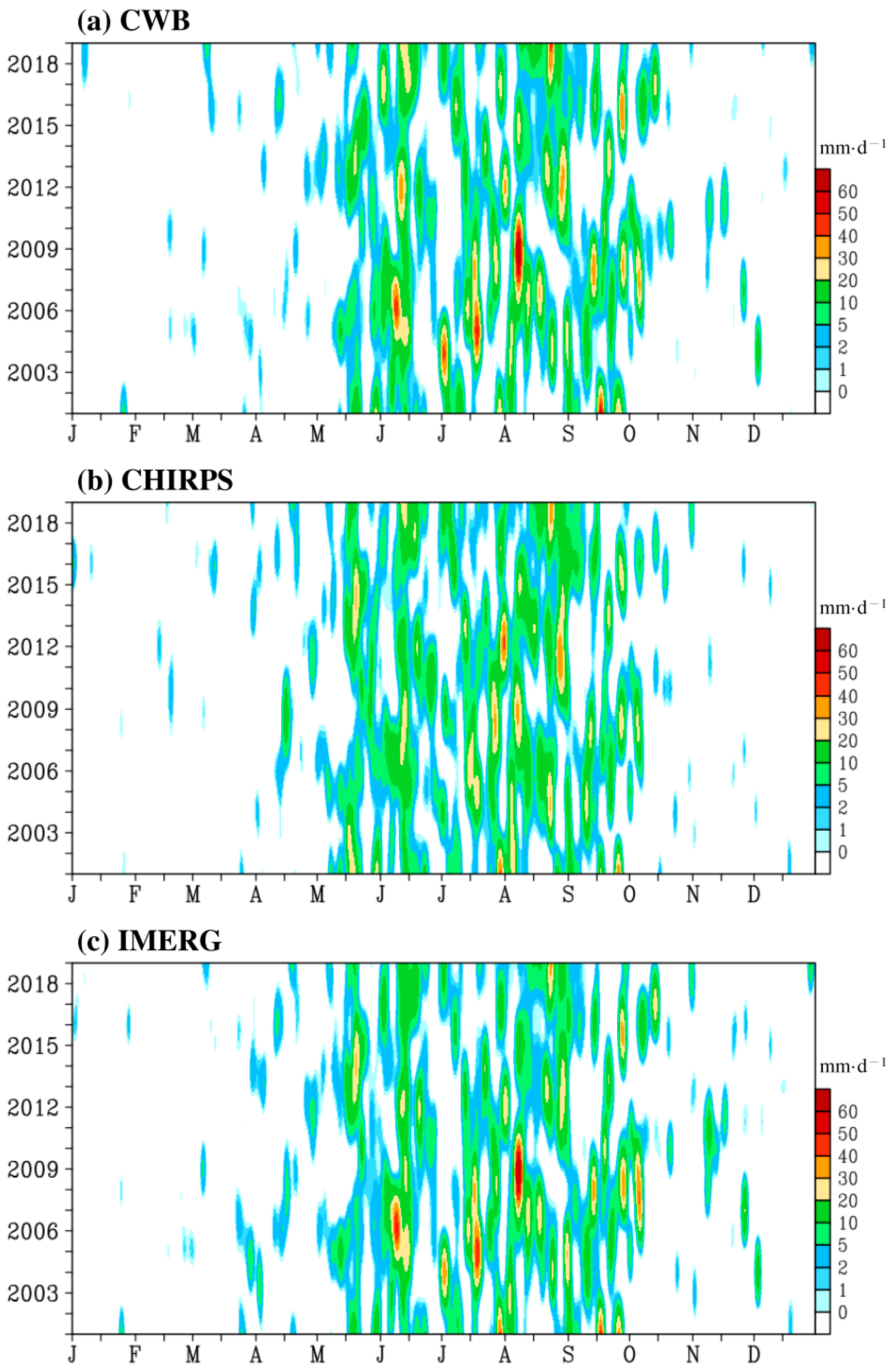
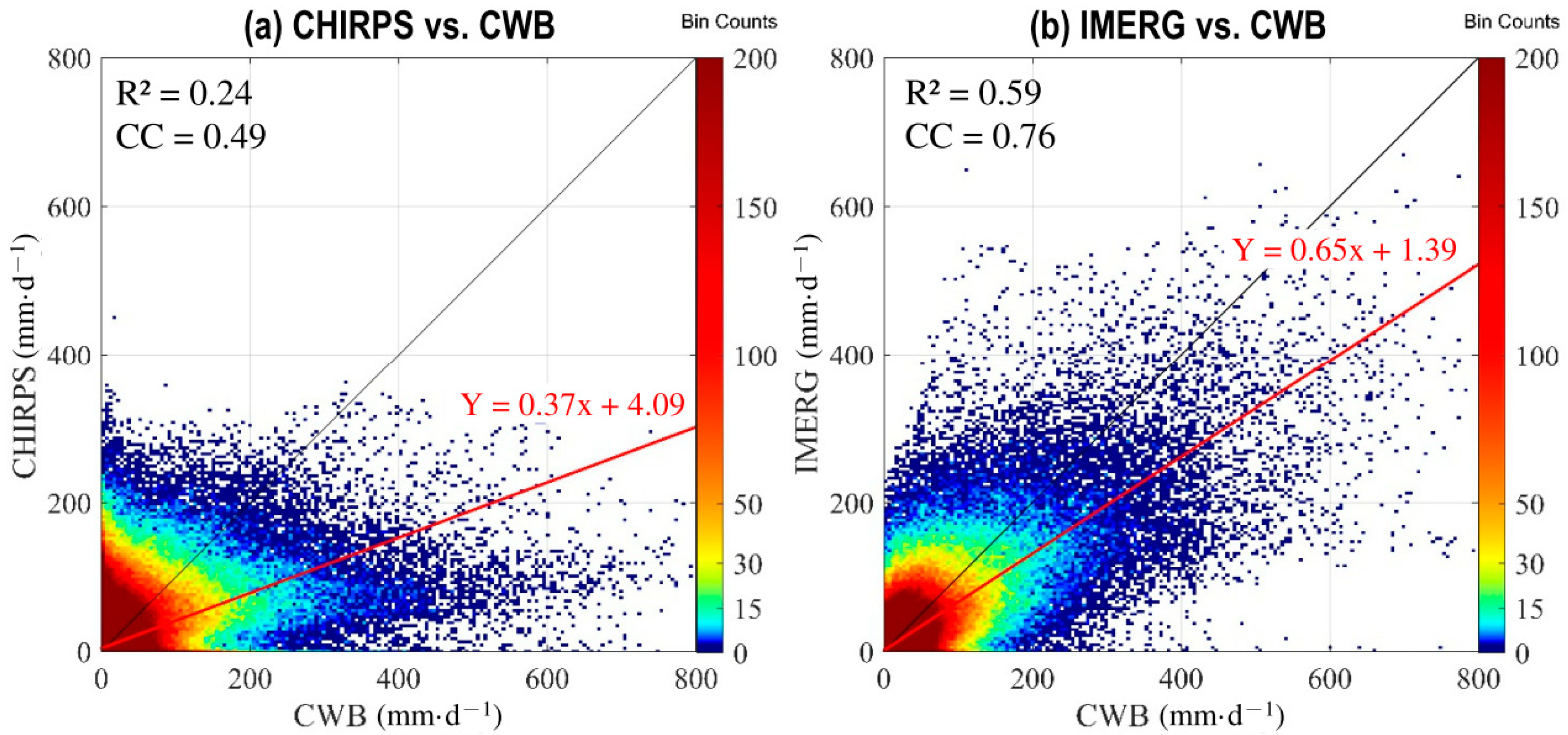
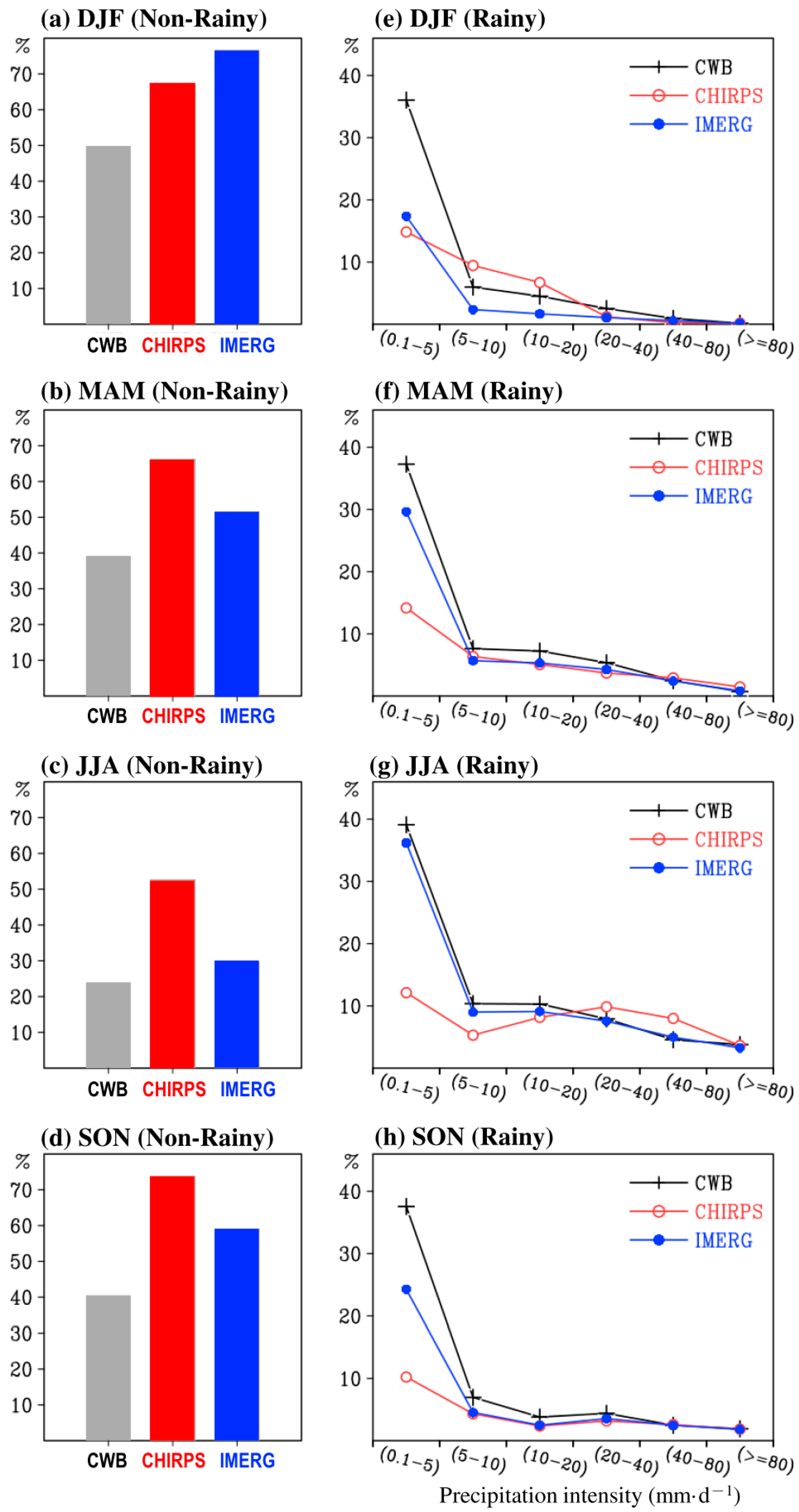
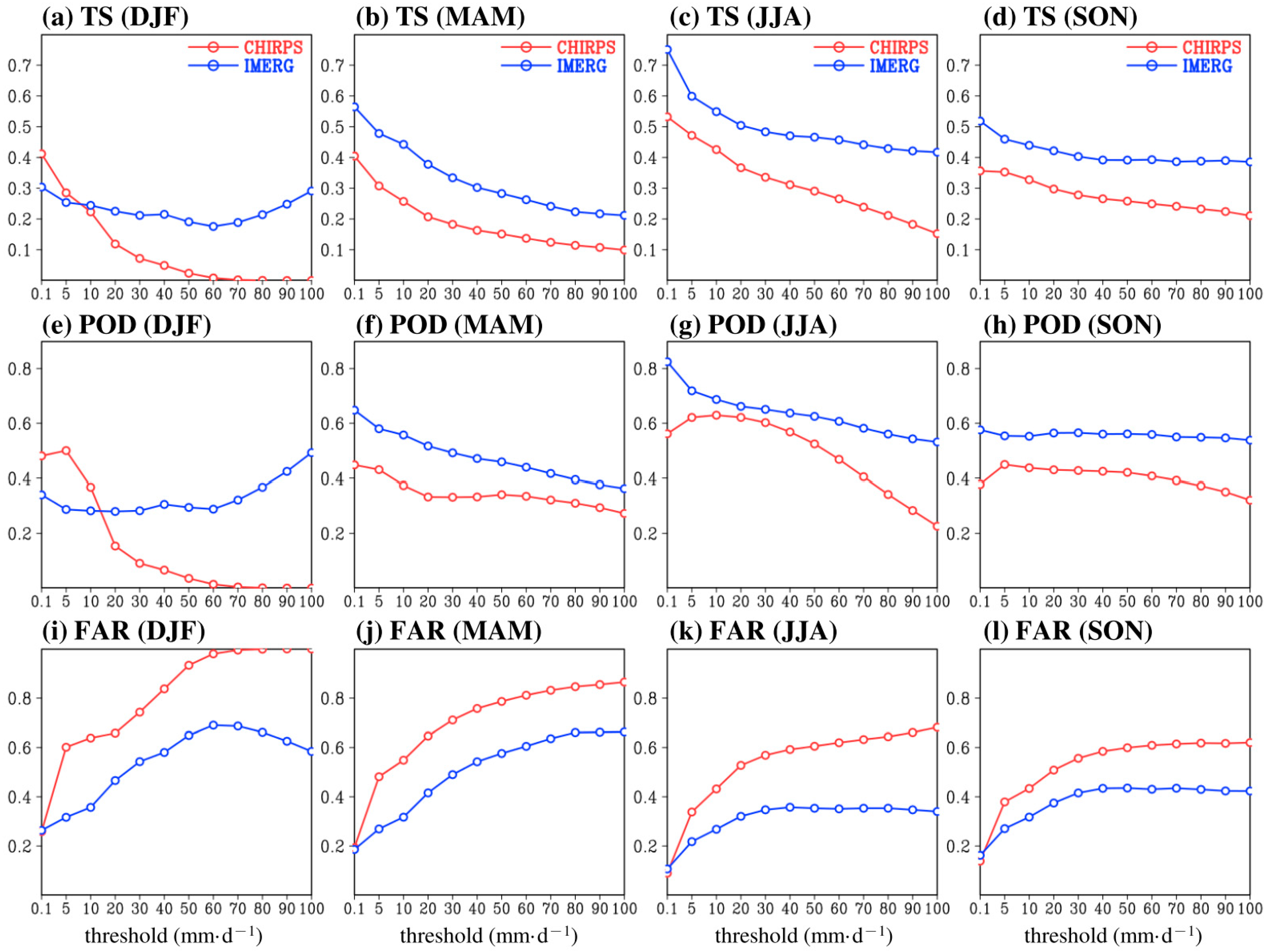
3.3. Daily Variation
3.4. More Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, T.C.; Yen, M.C.; Hsieh, J.C.; Arritt, R.W. Diurnal and seasonal variations of the rainfall measured by the automatic rainfall and meteorological telemetry system in Taiwan. Bull. Am. Meteor. Soc. 1999, 80, 2299–2312. [Google Scholar] [CrossRef] [Green Version]
- Dinku, T.; Ceccato, P.; Grover-Kopec, E.; Lemma, M.; Connor, S.J.; Ropelewski, C.F. Validation of satellite rainfall products over East Africa’s complex topography. Int. J. Remote Sens. 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzambwa, S.; Ceccato, P.; Connor, S.J.; Ropelewski, C.F. Validation of high-resolution satellite rainfall products over complex terrain in Africa. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- Dinku, T.; Ruiz, F.; Connor, S.; Ceccato, P. Validation and intercomparison of satellite rainfall estimates over Colombia. J. Appl. Meteor. Climatol. 2009, 49, 1004–1014. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Adler, R.F.; Kubota, T.; Ushio, T. Evaluation of GSMaP Precipitation Estimates over the Contiguous United States. J. Hydrometeorol. 2010, 11, 566–574. [Google Scholar] [CrossRef]
- Stampoulis, D.; Anagnostou, E.N. Evaluation of Global Satellite Rainfall Products over Continental Europe. J. Hydrometeorol. 2012, 13, 588–603. [Google Scholar] [CrossRef]
- Derin, Y.; Yilmaz, K.K. Evaluation of multiple satellite-based precipitation products over complex topography. J. Hydrometeorol. 2014, 15, 1498–1516. [Google Scholar] [CrossRef] [Green Version]
- Prakash, S.; Mitra, A.K.; Rajagopal, E.N.; Pai, D.S. Assessment of TRMM-based TMPA-3B42 and GSMaP precipitation products over India for the peak southwest monsoon season. Int. J. Climatol. 2015, 36, 1614–1631. [Google Scholar] [CrossRef]
- Huang, W.R.; Chang, Y.H.; Liu, P.Y. Assessment of IMERG precipitation over Taiwan at multiple timescales. Atmos. Res. 2018, 214, 239–249. [Google Scholar] [CrossRef]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.; Delrieu, G.; Hong, Y.; Hsu, Y.C.; et al. Multiregional Satellite Precipitation Products Evaluation over Complex Terrain. J. Hydrometeorol. 2016, 17, 1817–1836. [Google Scholar] [CrossRef]
- Huang, W.R.; Liu, P.Y.; Chang, Y.H.; Liu, C.Y. Evaluation and Application of Satellite Precipitation Products in Studying the Summer Precipitation Variations over Taiwan. Remote Sens. 2020, 12, 347. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.Y.; Aryastana, P.; Liu, G.R.; Huang, W.R. Assessment of satellite precipitation product estimates over Bali Island. Atmos. Res. 2020, 244, 105032. [Google Scholar] [CrossRef]
- Zhao, C.; Ren, L.; Yuan, F.; Zhang, L.; Jiang, S.; Shi, J.; Chen, T.; Liu, S.; Yang, X.; Liu, Y.; et al. Statistical and Hydrological Evaluations of Multiple Satellite Precipitation Products in the Yellow River Source Region of China. Water 2020, 12, 3082. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Ushio, T.; Aonashi, K.; Kachi, M.; Okamoto, K. Global Precipitation Map Using Satellite-Borne Microwave Radiometers by the GSMaP Project: Production and Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. Algorithm Theoretical Basis Document (ATBD) Version 06: NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); NASA/GSFC: Greenbelt, MD, USA, 2019.
- Ashouri, H.; Hsu, K.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Bolvin, D.T.; Neklin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.J.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A review of merged high-resolution satellite precipitation product accuracy during the Tropical Rainfall Measuring Mission (TRMM) era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.-H.; Chen, H.; Delrieu, G.; Hsu, Y.C.; et al. Evaluation of GPM-era Global Satellite Precipitation Products over Multiple Complex Terrain Regions. Remote Sens. 2019, 11, 2936. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Hanati, G.; Danierhan, S.; Liu, Q.; Xu, Z. Evaluation and comparison of daily GPM/TRMM precipitation products over the Tianshan Mountains in China. Water 2020, 12, 3088. [Google Scholar] [CrossRef]
- Chen, C.S.; Chen, Y.L. The rainfall characteristics of Taiwan. Mon. Weather Rev. 2003, 131, 1323–1341. [Google Scholar] [CrossRef]
- Yen, M.C.; Chen, T.C. Seasonal variation of the rainfall over Taiwan. Int. J. Climatol. 2000, 20, 803–809. [Google Scholar] [CrossRef]
- Kerns, B.W.J.; Chen, Y.L.; Chang, M.Y. The diurnal cycle of winds, rain, and clouds over Taiwan during the mei-yu, summer, and autumn rainfall regimes. Mon. Weather Rev. 2010, 138, 497–516. [Google Scholar] [CrossRef]
- Kishtawal, C.M.; Krishnamurti, T.N. Diurnal variation of summer rainfall over Taiwan and its detection using TRMM observations. J. Appl. Meteorol. 2001, 40, 331–344. [Google Scholar] [CrossRef]
- Huang, W.R.; Wang, S.Y. Impact of Land-Sea breezes at different scales on the diurnal rainfall in Taiwan. Clim. Dyn. 2014, 43, 1951–1963. [Google Scholar] [CrossRef]
- Chen, S.Y.; Huang, W.R. Evaluation on the performance of TRMM, CMORPH, and PERSIANN in depicting the diurnal precipitation variation in Taiwan. Atmos. Sci. 2017, 45, 167–191, (In Chinese with an English Abstract). [Google Scholar]
- Bichet, A.; Diedhiou, A. West African Sahel has become wetter during the last 30 years, but dry spells are shorter and more frequent. Clim. Res. 2018, 75, 155–162. [Google Scholar] [CrossRef] [Green Version]
- Bichet, A.; Diedhiou, A. Less frequent and more intense rainfall along the coast of the Gulf of Guinea in West and Central Africa (1981–2014). Clim. Res. 2018, 76, 191–201. [Google Scholar] [CrossRef] [Green Version]
- Sacré Regis, M.D.; Mouhamed, L.; Kouakou, K.; Adeline, B.; Arona, D.; Houebagnon Saint, J.C.; Koffi Claude, A.K.; Talnan Jean, H.C.; Salomon, O.; Issiaka, S. Using the CHIRPS dataset to investigate historical changes in precipitation extremes in West Africa. Climate 2020, 8, 84. [Google Scholar] [CrossRef]
- Paredes, F.; Barbosa, H.A.; Lakshmi-Kumar, T. Validating CHIRPS-based satellite precipitation estimates in Northeast Brazil. J. Arid Environ. 2016, 139, 26–40. [Google Scholar] [CrossRef]
- Ogbu, K.N.; Hounguè, N.R.; Gbode, I.E.; Tischbein, B. Performance evaluation of satellite-based rainfall products over Nigeria. Climate 2020, 8, 103. [Google Scholar] [CrossRef]
- Atiah, W.A.; Amekudzi, L.K.; Aryee, J.N.A.; Preko, K.; Danuor, S.K. Validation of satellite and merged rainfall data over Ghana, West Africa. Atmosphere 2020, 11, 859. [Google Scholar] [CrossRef]
- AL-Falahi, A.H.; Saddique, N.; Spank, U.; Gebrechorkos, S.H.; Bernhofer, C. Evaluation the performance of several gridded precipitation products over the highland region of yemen for water resources management. Remote Sens. 2020, 12, 2984. [Google Scholar] [CrossRef]
- Bai, L.; Shi, C.; Li, L.; Yang, Y.; Wu, J. Accuracy of CHIRPS satellite-rainfall products over Mainland China. Remote Sens. 2018, 10, 362. [Google Scholar] [CrossRef] [Green Version]
- An, Y.; Zhao, W.; Li, C.; Liu, Y. Evaluation of six satellite and reanalysis precipitation products using gauge observations over the Yellow River Basin, China. Atmosphere 2020, 11, 1223. [Google Scholar] [CrossRef]
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Funk, C.; Michaelsen, J.; Marshall, M. Mapping recent decadal climate variations in Eastern Africa and the Sahel. In Remote Sensing of Drought: Innovative Monitoring Approaches; Wardlow, B., Anderson, M., Verdin, J., Eds.; CRC Press: Lincoln, NE, USA, 2012. [Google Scholar]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Reynolds, R.W. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Sorooshian, S.; Gao, X. Precipitation estimation from remotely sensed imagery using an artificial neural network cloud classification system. J. Appl. Meteorol. 2004, 43, 1834–1852. [Google Scholar] [CrossRef] [Green Version]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 1st ed.; Academic Press: Cambridge, MA, USA, 1995; p. 467. [Google Scholar]
- Ebert, E. Methods for verifying satellite precipitation estimates. In Measuring Precipitation from Space; Levizzani, V., Bauer, P., Turk, F.J., Eds.; Springer: Dordrecht, The Netherlands, 2007; Volume 28, pp. 345–356. [Google Scholar]
- Hou, A.; Kakar, R.; Neeck, S.; Azarbarzin, A.; Kummerow, C.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Kolluru, V.; Kolluru, S.; Wagle, N.; Acharya, T.D. Secondary precipitation estimate merging using machine learning: Development and evaluation over Krishna River Basin, India. Remote Sens. 2020, 12, 3013. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, Y.; Ren, X.; Yao, Y.; Hao, Z.; Cai, W. Evaluation of CHIRPS and its application for drought monitoring over the Haihe River Basin, China. Nat. Hazards 2018, 92, 155–172. [Google Scholar] [CrossRef]
- Abebe, S.A.; Qin, T.; Yan, D.; Gelaw, E.B.; Workneh, H.T.; Kun, W.; Liu, S.; Dong, B. Spatial and Temporal Evaluation of the latest high-resolution precipitation products over the Upper Blue Nile River Basin, Ethiopia. Water 2020, 12, 3072. [Google Scholar] [CrossRef]


| SPP Estimates | |||
|---|---|---|---|
| Yes | No | ||
| CWB estimates | Yes | Hits | Misses |
| No | False alarms | Correct rejections | |
| Tcorr | RMSE | |
|---|---|---|
| CHIRPS | 0.97 | 1.13 |
| IMERG | 0.99 | 1.25 |
| DJF | MAM | JJA | SON | |
|---|---|---|---|---|
| Tcorr for CHIRPS | 0.74 | 0.83 | 0.86 | 0.92 |
| Tcorr for IMERG | 0.90 * | 0.95 * | 0.96 * | 0.98 * |
| RMSE for CHIRPS | 0.82 * | 0.99 | 1.76 | 2.21 |
| RMSE for IMERG | 1.45 | 0.86* | 1.74 * | 1.35 * |
| DJF | MAM | JJA | SON | |
|---|---|---|---|---|
| Mean for CWB | 2.75 | 5.41 | 13.02 | 7.19 |
| Mean for CHIRPS | 2.42 | 5.43 | 12.43 | 5.44 |
| Mean for IMERG | 1.38 | 4.76 | 11.53 | 5.98 |
| DJF | MAM | JJA | SON | |
|---|---|---|---|---|
| Scorr for CHIRPS | 0.83 * | 0.86 * | 0.89 * | 0.82 * |
| Scorr for IMERG | 0.55 | 0.60 | 0.69 | 0.72 |
| RMSE for CHIRPS | 1.46 * | 0.96 * | 2.40 * | 2.96 * |
| RMSE for IMERG | 2.92 | 1.70 | 3.72 | 3.72 |
| DJF | MAM | JJA | SON | |
|---|---|---|---|---|
| Tcorr for CHIRPS | 0.66 | 0.74 | 0.75 | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, J.; Huang, W.-R.; Liu, P.-Y.; Li, X. Validation of CHIRPS Precipitation Estimates over Taiwan at Multiple Timescales. Remote Sens. 2021, 13, 254. https://doi.org/10.3390/rs13020254
Hsu J, Huang W-R, Liu P-Y, Li X. Validation of CHIRPS Precipitation Estimates over Taiwan at Multiple Timescales. Remote Sensing. 2021; 13(2):254. https://doi.org/10.3390/rs13020254
Chicago/Turabian StyleHsu, Jie, Wan-Ru Huang, Pin-Yi Liu, and Xiuzhen Li. 2021. "Validation of CHIRPS Precipitation Estimates over Taiwan at Multiple Timescales" Remote Sensing 13, no. 2: 254. https://doi.org/10.3390/rs13020254
APA StyleHsu, J., Huang, W.-R., Liu, P.-Y., & Li, X. (2021). Validation of CHIRPS Precipitation Estimates over Taiwan at Multiple Timescales. Remote Sensing, 13(2), 254. https://doi.org/10.3390/rs13020254








