Abstract
Marginal seas are a dynamic and still to large extent uncertain component of the global carbon cycle. The large temporal and spatial variations of sea-surface partial pressure of carbon dioxide (pCO2) in these areas are driven by multiple complex mechanisms. In this study, we analyzed the variable importance for the sea surface pCO2 estimation in the Baltic Sea and derived monthly pCO2 maps for the marginal sea during the period of July 2002–October 2011. We used variables obtained from remote sensing images and numerical models. The random forest algorithm was employed to construct regression models for pCO2 estimation and produce the importance of different input variables. The study found that photosynthetically available radiation (PAR) was the most important variable for the pCO2 estimation across the entire Baltic Sea, followed by sea surface temperature (SST), absorption of colored dissolved organic matter (aCDOM), and mixed layer depth (MLD). Interestingly, Chlorophyll-a concentration (Chl-a) and the diffuse attenuation coefficient for downwelling irradiance at 490 nm (Kd_490nm) showed relatively low importance for the pCO2 estimation. This was mainly attributed to the high correlation of Chl-a and Kd_490nm to other pCO2-relevant variables (e.g., aCDOM), particularly in the summer months. In addition, the variables’ importance for pCO2 estimation varied between seasons and sub-basins. For example, the importance of aCDOM were large in the Gulf of Finland but marginal in other sub-basins. The model for pCO2 estimate in the entire Baltic Sea explained 63% of the variation and had a root of mean squared error (RMSE) of 47.8 µatm. The pCO2 maps derived with this model displayed realistic seasonal variations and spatial features of sea surface pCO2 in the Baltic Sea. The spatially and seasonally varying variables’ importance for the pCO2 estimation shed light on the heterogeneities in the biogeochemical and physical processes driving the carbon cycling in the Baltic Sea and can serve as an important basis for future pCO2 estimation in marginal seas using remote sensing techniques. The pCO2 maps derived in this study provided a robust benchmark for understanding the spatiotemporal patterns of CO2 air-sea exchange in the Baltic Sea.
1. Introduction
Global oceans are an important sink of atmospheric CO2 and uptake approximately 30% of the global anthropogenic CO2 emissions [1]. As the global ocean uptake of CO2 increases by a rate proportional to the atmospheric CO2, substantial differences exist between oceans and marginal seas [1,2]. The changing air-sea exchange of CO2 in marginal seas, particularly those at high-latitude, is found to be the major source of uncertainties in the estimate of ocean CO2 uptake [3,4]. As the atmospheric CO2 is as rather globally homogenous, sea surface partial pressure of carbon dioxide (pCO2) in the marginal sea is the key component for precisely determining the direction of the air-sea exchange of CO2. Therefore, deriving maps of the changing pCO2 for marginal seas over time is critical for precise estimate of global air-sea exchange and ocean uptake of CO2 [2,3,5].
Generally, sea surface pCO2 is jointly determined by biogeochemical processes, vertical and horizontal mixing of sea water, and the air-sea exchange of CO2 [6,7]. Many sea surface variables related to these processes are can be retrieved from remote sensing images. Given their vast spatial coverages, remotely sensed sea surface variables have increasingly been used in sea surface pCO2 estimation. Remotely sensed Chlorophyll-a concentration (Chl-a) is commonly used as an indicator of biological activities in water [8]. Sea surface temperature (SST) largely determines the solubility of CO2 in sea water and has been frequently used to estimate pCO2 from remote sensing [9,10,11,12,13]. In addition, bacteria respiration produces CO2 by decomposing dissolved organic matter (DOM) [14,15]. Therefore, absorption of colored dissolved organic matter (aCDOM) retrieved from remote sensing images was used in sea surface pCO2 estimation [16,17]. Furthermore, after [18] found from in-situ measurements that sea surface salinity (SSS) was highly related to sea surface pCO2, SSS derived directly from remote sensing images or remotely sensed aCDOM were adopted to support sea surface pCO2 estimate [16,19]. Kd_490nm, a proxy of water transparency, was derived from remote sensing and included in sea surface pCO2 estimation to indicate the effect of biological activities [16]. Mixed layer depth (MLD) determines thermal stratification between different water masses and, however, is not retrievable with remote sensing approaches. Therefore, some studies used the MLD obtained from ocean models to support the derivation of sea surface pCO2 maps [9,12]. Similarly, model-yield gross primary production (GPP) and net primary production (NPP) were also included to support pCO2 estimation by approximating the biological control on pCO2 in sea water [9,12].
Sea surface pCO2 in many global marginal seas have been estimated with various remote sensing supported approaches [9,12,16,17,20,21,22,23]. Most of the studies chose the variables based on empirical knowledge and focused on deriving pCO2 maps with small estimate errors (e.g., RMSE). However, few studies have investigated the spatiotemporal variabilities of the variable’s relevance to sea surface pCO2 in marginal seas. Considering the high spatial variabilities in the controlling forces of sea surface pCO2 in marginal seas, some studies divided the targeted seas into sub-basins/subsets and separately constructed models for pCO2 retrieval in each of the sub-basins/subset [12,22,24]. Though this strategy produced maps of good quality in the sub-basins/subsets, it provided little knowledge on the variables’ relevance to pCO2 distribution. Furthermore, Reference [25] regarded the sea surface pCO2 in the targeted area as a mixture of the pCO2 controlled by different processes (e.g., vertical mixing and biological uptake) and determined each of the processes separately from different sets of variables. Despite the successfully applications in multiple marginal seas [10,25,26], their method was often limited to pCO2 estimation in summer time and thus fails to provide information for other seasons. Overall, large space remains for investigation on variables’ relevance (importance) in sea surface pCO2 estimate across different time and space.
The Baltic Sea is a semi-enclosed marginal sea located in northern Europe. The carbon budget of the Baltic Sea displays considerable seasonal and interannual variabilities. To date, the few studies attempting to estimate sea surface pCO2 in the Baltic Sea using remote sensing approaches, e.g., [12]., have barely provided information on the variables’ relevance/importance to the pCO2 estimate for this marginal sea. In this study, we aimed to analyze the importance of different variables for pCO2 estimation and derive improved monthly pCO2 maps for the Baltic Sea from 2002 to 2011. We conducted the following: (1) filtering the in-situ pCO2 data for the model training and validation; (2) assessing the relative importance of the input variables for the pCO2 estimation on different spatial and seasonal scales; and (3) deriving pCO2 maps for the Baltic Sea.
2. Study Area
The Baltic Sea is located at high latitudes (55–60° N) in Europe. As the sun illumination and temperature there exhibit significant seasonal changes, the Baltic Sea and adjacent terrestrial ecosystems also undergo high seasonality. In addition, the wide span of the Baltic Sea in latitude forms a large spatial gradient in sun illumination and the corresponding environment condition, like SST. The Baltic Sea has restricted water exchange with the open North Atlantic Ocean via the Danish straits and is a semi-enclosed marginal sea. More than 600 rivers drain the catchment of total 1.7 million km2 and export to the Baltic Sea substantial freshwater and terrigenous substances, including organic carbon [27,28,29,30]. Therefore, the Baltic Sea is characterized with a high concentration of CDOM, and most part of the sea presents as “brown water”. With varying inputs from different rivers, the sub-basins of the Baltic Sea create highly heterogeneous biogeochemical conditions in this marginal sea. Consequently, the pCO2 distribution in the Baltic Sea displays evident seasonality and spatial heterogeneity [31]. Upwelling characterized with evident seasonality and spatiality occurs frequently in the Baltic Sea and brings up deep water of high pCO2 up to 2000 µatm to the sea surface [32,33]. The high concentration of nutrients brought up together with the deep water leads to cyanobacteria and phytoplankton blooms after the upwelling event, which further complicates the pCO2 distribution in the Baltic Sea [34].
Till now, nearly all the pCO2 related studies in the Baltic Sea were based on in-situ measurements from ship and/or buoys, and the findings are often valid for limited sites of the sea. Therefore, analyzing variables’ relevance and obtaining reliable pCO2 maps is critical for better understanding the carbon cycle and the air-sea exchange in the Baltic Sea [35].
3. Data
We chose the variables for pCO2 estimation based on previous studies and the characteristic of the Baltic Sea. The variables SST, photosynthetically available radiation (PAR), Chl-a, Kd_490 nm, and aCDOM were remotely sensed. SSS and MLD were produced by the numerical model NEMO-NORDIC together with data assimilation. In-situ pCO2 measurements from three different sources were used to train and validate the model for pCO2 estimation.
3.1. Remote Sensing Products
The Moderate Resolution Imaging Spectroradiometer (MODIS) on board Aqua satellite was designed for ocean surface investigations. The sensor maps the earth every two days from July 2002 on. A MODIS image consists of 36 spectral bands covering the spectrum of wavelength from 0.63 to 14.38 µm. Images from MODIS Aqua have been successfully used to detect coastal water clarity [36], survey red tides [37], map lake suspended matter [38], and retrieve coastal dissolved organic carbon [39]. Variables, like Chl-a and SST retrieved from MODIS-Aqua images with already mature algorithms, have been widely used to estimate sea surface pCO2 or simulate sea surface CO2 flux in different oceans and marginal seas [11,16,17,40,41]. From the National Aeronautics and Space Administration (NASA) Goddard Space Flight Center (https://oceancolor.gsfc.nasa.gov/), we obtained the level-3 monthly mean MODIS products of PAR, Kd_490 nm and SST covering the period of August 2002–October 2020. All data have a spatial resolution equivalent to 4×4 km at the equator (Table 1).

Table 1.
Variables used to estimate partial pressure of carbon dioxide (pCO2) in the study.
The Medium Resolution Imaging Spectrometer (MERIS) on board Envisat satellite was designed for ocean color observation. During its life span from 2002 to 2011, MERIS mapped the earth every 1–3 days and measured water surface radiances in 15 spectral bands from visible to infrared spectrum. Up to now, MERIS data have been frequently used to investigate water related issues in global ocean and marginal seas, including mapping sea algae coverage [42], detecting phytoplankton bloom [43] and cyanobacterial bloom [44], and estimating Chl-a, aCDOM, and suspended matter [45,46,47,48,49]. Most of these studies targeted at European lakes and seas and demonstrated the great potential of MERIS data for investigating these waters. Specifically, [45] found that Chl-a retrieved from MERIS for the Baltic Sea had similar distributions to that of in-situ measurements.
The MERIS data from the MERCI data base (https://merisrr-merci-ds.eo.esa.int/merci) were used to retrieve Chl-a and aCDOM for the Baltic Sea with the Free University of Berlin (FUB) processor which were especially developed for European coastal waters. Invalid pixels (i.e., land, mixture of land and water, various cloud types, and cloud shadow) were masked out from MERIS images before the Chl-a and aCDOM retrieval. The performance of Chl-a and aCDOM retrieved from MERIS with FUB processor in the Baltic Sea were assessed to be excellent [49,50]. In this study, the daily Chl-a and aCDOM derived from MERIS images were aggregated monthly and resampled to 4×4 km. The Chl-a and aCDOM derived from the full MERIS archive spans from July 2002 to December 2011. Comparison of the contributions of the Chl-a products from MODIS and MERIS to pCO2 estimation in the method employed here did not show significant differences (Figure S2).
3.2. Modeled Data
MLD and SSS are important variables for pCO2 estimates. However, remotely sensed SSS have much coarser resolutions than other variables, such as Chl-a, and MLD is not yet obtainable from remote sensing. Alternatively, modeled MLD and SSS have been applied in many studies on sea surface pCO2 estimation [9,12,20,51,52]. Therefore, we employed the monthly MLD and SSS produced by the NEMO-NORDIC model which is a a Baltic and North Sea model based on the NEMO ocean engine and a local singular evolutive interpolated Kalman (LSEIK)filter data assimilation with a spatial resolution of 4 × 4 km [53] (Table 1). Validation of the modeled SSS against the station observation demonstrated a bias smaller than 0.5 ppt and a RMSE of 0.5 ppt [53].
3.3. In-Situ Data
We used all the in-situ sea surface pCO2 measurements available in the Baltic sea during August 2002–November 2011 (Table 2 and Figure 1). They included the data from the Surface Ocean CO₂ Atlas (SOCAT) (2nd Version) [54], the measurements from a moored buoy at Östergarnsholm site [55], and data from [56].

Table 2.
The in-situ measurements used in this study.
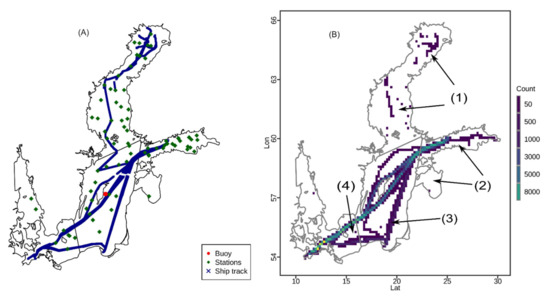
Figure 1.
The location where the in-situ pCO2 were measured in the Baltic Sea from August 2002 to November 2011 (A) and the density distribution of the in-situ pCO2 measurements (B). The numbers in parentheses indicate the sub-basins where the variables’ importance was analyzed. (1) Gulf of Bothnia, including Bothnia Bay (north) and Bothnia Sea (south); (2) Gulf of Finland (north) and Gulf of Riga (south); (3) Baltic Proper; (4) Arkona Basin.
All the data in SOCAT have undergone quality control and were of error < 10 µatm [54,57]. We used pCO2 measurements acquired from 2002 to 2011 to match the remotely sensed variables. The data from SOCAT for this period were obtained from the Finnpartner vessels which travelled between Lübeck and Helsinki every second day [58]. The pCO2 measurements are available every 1–2 min and appear as a series of points distributed along the ship tracks (Figure 1A).
At the Östergarnsholm site, the sea surface pCO2 is measured by a submersible autonomous moored instrument (SAMI) mounted on a buoy mooring one kilometer east off the island Östergarnsholm in the central Baltic Sea (Figure 1A). The SAMI sensor was installed four meters below the water surface and has recorded the pCO2 there every 30 or 60 min from 2005 May to the present [55]. The pCO2 measurement from Östergarnsholm site also fulfills the accuracy criterion of <10 µatm.
The pCO2 data used by [56] filled the data gap left by the previous two data sources in the Gulf of Bothnia. The data set consisted of both manual bottle measurements from discrete stations and continuous ferry box measurements obtained with the same method as the vessel data in SOCAT (Figure 1A). The measurements were mainly from the year of 2006, 2009, and 2010. More details about the data are available from [56]).
4. Methods
4.1. Random Forest
Random forest is a tree-assembled model where the trees are constructed based on a set training samples [59]. Random forest has shown excellent performance in classification and regression [60,61]. Therefore, it has been used in various fields. For example, it has been used to estimate gross primary production of vegetation from remote sensing images [62], downscaling the soil moisture data and chlorophyll fluorescence of coarse resolutions etc. [63,64]. With respect to pCO2 estimation from remote sensing data [17] derived pCO2 maps for the Gulf of Mexico with an RMSE of 31.7 µatm using a similar tree-based algorithm. In addition, [16] compared random forest with other commonly used approaches (e.g., multiple linear regression) and proved that random forest was a robust algorithm for sea surface pCO2 estimation from remote sensing data in the Gulf of Mexico [16].
In this study, random forest models were trained to express the relationship between the in-situ pCO2 measurements and spatially and temporally co-located variables (i.e., Chl-a, aCDOM, SST, PAR, Kd490nm, SSS, and MLD). Each random forest model contained a number of tree (known as Ntree) with each node splitting to a number of leaves (known as Mtry). At each node, a bootstrapped subset of randomly selected training samples was used to construct the relationship between the Mtry variables (e.g., Chl- and SST) and the dependent variable (i.e., pCO2) in the form of split leaves [65]. The tree grew as the nodes were produced and connected in a cascade manner. Each decision tree was independently produced. The forest construction was finished as the trees grew to Ntree, a user-defined number of trees [59]. The final random forest is a set of trees with best performance in expressing the relationship between variables in the training samples. Further details on the random forest model are to be found in Breiman (2001). Each random forest model contained 500 trees (N tree = 500) of the leaf size of three (Mtry = 3). We used the random forest algorithm implemented in the package randomForest [66] for the open access software R [67].
Subsequently, the importance of each variable in the random forest model was also extracted and analyzed. The importance of a variable was determined by the mean decrease accuracy (MDA) of the random forest model when the variable is randomly permuted in the training samples [59]. Therefore, the importance of variable in a random forest model indicates its contributions/relevance to the model and the response of corresponding variable to the pCO2 variation in the training data set. For each variable, the importance was derived independently. The variables are not complementary to each other in pCO2 estimate, Therefore, the sum of the variables’ importance cannot stay as constant value, like 100%, across different time and spatial scale.
4.2. Filtering In-Situ Data
The diurnal differences of sea surface pCO2 in the Baltic Sea can reach up to 40 µatm [68], and using only the data from day time or night time would introduce 8% to 36% error on monthly air–sea CO2 fluxes [69]. Pre-analysis also found that using in-situ pCO2 measurements from 24 h for sea surface pCO2 estimation would increase the uncertainty of results by 30–60 µatm (Supplementary Materials Figure S2). Therefore, we only used the in-situ pCO2 measurements obtained during the exact period of the two satellites (i.e., MODIS Aqua and MERIS) passes over the Baltic Sea, i.e., 9:00–14:00 UTC 00. Subsequently, the in-situ data were aggregated monthly to match the frequency of the remotely sensed and modelled variables. The variables exactly co-located to the in-situ pCO2 measurements were extracted and used for random forest model construction and validation.
Using the variables (e.g., SST) derived for the months characterized with frequent upwelling occurrences can significantly affect the monthly pCO2 estimates by introducing large biases (Figure S3). Therefore, the upwelling effect should be eliminated to the largest possible extent. To achieve this, we constructed a random forest model using in-situ data from each month as validation data and the rest as training data. All the models with the alternative absence of in-situ data from each month were constructed with identical settings. Inspection on the mean absolute errors (MAE) and RMSE of these models showed that the following monthly data were dominated by upwelling (i.e., large bias): 2003–09, 2006–09, 2006–08, 2009–07, 2009–09, 2009–10, 2011–04, 2011–08, 2011–09, 2011–10 (Figure S4). Nearly all of them were in fall when upwelling prevails in the Baltic Sea [32]. In-situ pCO2 measurements from these months were eliminated from training and validating the model. Sea surface pCO2 maps in these months were not predicted as it would produce misestimation for these months.
After narrowing the time window of in-situ pCO2 measurements down to 9:00–14:00, aggregating these in-situ pCO2 measurements monthly, and filtering out the data from the upwelling dominated months, 10,769 in-situ pCO2 measurements with matching variables remained, as shown in Figure S1.
4.3. Analyzing Variables’ Importance for pCO2 Estimation
We derived the variables’ importance to the pCO2 estimation on two scales: spatially and temporally. On the spatial scale, the random forest models were constructed both for the overall Baltic Sea and its sub-basins indicated in Figure 1B. In each sub-basin, a random forest model was trained with the in-situ in the sub-basin from 2/3 of the months from random selection. Each model was then validated with the in-situ data in the sub-basin from the rest 1/3 months. We constructed 50 random forest models in each sub-basin with the training and validation data selected in such way. In the temporal analysis of the variables’ importance to the pCO2 estimates, the in-situ measurements were divided into different seasons. Specifically, February–April was spring, May–July was summer, and August–October was fall. The limited availability of satellite data due to frequent and extensive cloud coverage in November, December, and January did not allow for such analysis during these months. Like the spatial analysis, in-situ data from 2/3 of the months from random selection were used for training and the rest 1/3 for validation. Fifty random forest models were constructed in each season with the training data selected in the same manner and validated with the corresponding complementary data.
4.4. Constructing the Fnal Model for pCO2 Estimation in the Baltic Sea
We constructed a final random forest model for pCO2 estimation in the entire Baltic Sea. This model was trained with the in-situ pCO2 measurements in odd months of even years (e.g., March 2002) and even months of odd years (e.g., April 2003) and validated with the remaining data. By doing this, both the training and validation data covered each of the 12 months in a year and the pCO2 relevant processes from each month. Exchanging the training data and validation data yielded models with nearly the same performance (Figure S7). The monthly mean pCO2 distribution in the entire Baltic Sea were predicted with this model.
The Pearson correlations of the pCO2 estimated with above model to each of the variables were analyzed. In order to speed up the processing, the correlation was analyzed on a 0.5° × 0.5° grid form. In each month, the mean of pCO2 and the means of each targeted variables (e.g., Chl-a) in the same grid cell was derived. The Pearson correlations between pCO2 and each of the variables in each grid cell were obtained across the study period of 2002–2011.
4.5. Comparing the Random Forest to Self-Organized Map (SOM) and Multiple Linear Regression (MLR) for pCO2 Estimation in the Baltic Sea
SOM is an artificial neuronal network algorithm which classifies the input samples into a number of classes, based on their Euclidian distance from each other in the space determined by the variables of the input data [20,70]. Often, the number of classes (neuron) are given a priori in a grid format (e.g., 2 × 5). Each class corresponds to a neuron which contains the coefficients determining the relationship between the variables and the dependent variable in the same class, which is also called labelling the class with the dependent variable (output). In the case of sea surface pCO2 estimation with SOM, the remotely sensed variables, like Chl-a and SST, in the training data, are used to calculate the distance between the input samples for classification. In the pCO2 prediction with such a SOM model, the samples will be attributed with the pCO2 of a class to whom the sample show the closest distance to. Detailed description of a SOM application for sea surface pCO2 estimation by remote sensing data is available in Telszewski et al. (2009). SOM and its variants have been widely used to estimate sea surface pCO2 with support of remote sensing products [11,12,20,71,72,73,74]. In this study, we used the SOM algorithm implemented in the R packages of kohonen [75]. We set the size neurons (class) grid to be 25 × 20, in order to have the total number of classes same to the number of trees in the random forest models constructed in this study.
Furthermore, multiple linear regression (MLR) has been used in many studies for estimating sea surface pCO2 in marginal seas and performed good results [9,16]. Therefore, we compared the performance of SOM, MLR, and random forest in the sea surface pCO2 estimation in the Baltic Sea. During the comparison, the same variables were used in the three algorithms without any preselection. Random forest, SOM, and MLR models were trained with the identical data and validated likewise.
Two schemes of training data selection were adopted, one with in-situ pCO2 measurements from 2/3 of the months from random selection (scheme Number 1, same as in Section 4.3) and the other one using 2/3 of in-situ pCO2 measurements from random selection as training data (scheme Number 2). Scheme Number 2 was similar to the training data selection by [12]. In both schemes, the validation data were the complementary of the training data.
5. Results
5.1. Spatiotemporal Characteristics of Variable Importance to pCO2 Estimation
On the entire Baltic Sea scale, PAR was the most important variable (mean importance of 66%) for the sea surface pCO2 estimate during 2002–2011. It meant that the errors of the random forest model constructed without PAR would be by 66% higher than that constructed with PAR. PAR was followed by SST, MLD, aCDOM, and SSS with mean importance of 21%, 20%, 15%, and 14%, respectively. Chl-a and Kd_490nm showed the lowest importance of 12% and 10% (Figure 2A).
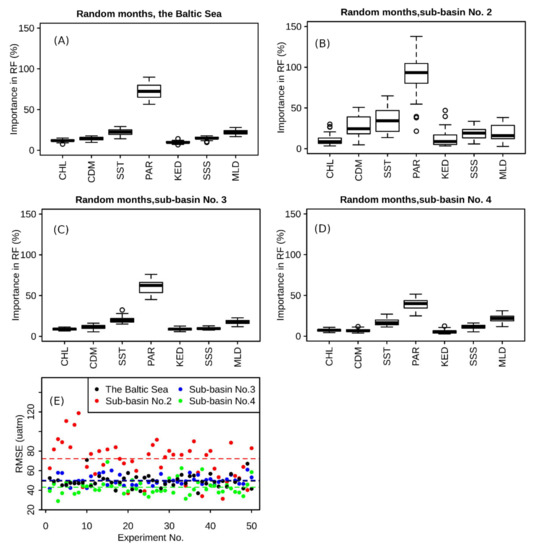
Figure 2.
Variables’ importance for pCO2 estimate in the Baltic Sea and its sub-basins. (A) Variables’ importance in the 50 models trained with in-situ data in the entire Baltic Sea from 2/3 months of random selection; (B–D) Variables’ importance in the 50 models trained with in-situ data from each sub-basin from 2/3 months of random selection. (E) The RMSEs of the 50 models trained with in-situ data from the four regions, respectively. CDM in the sub-figures donates the aCDOM derived from Medium Resolution Imaging Spectrometer (MERIS) images, KED stands for Kd_490nm.
The variables importance differed among the sub-basins of the Baltic Sea. Compare to the pCO2 estimate in the entire Baltic Sea (Figure 2A), the importance of PAR, SST, aCDOM, SSS, and MLD for pCO2 estimation in the Gulf of Finland (i.e., sub-basin No.2) increased by 26%, 13 %, 15%, 5%, and 1% (Figure 2B). For pCO2 estimation in this sub-basin, PAR was still the most importance variable. With the mean importance of 25%, aCDOM and SST are the next most importance variables, followed by SSS and MLD with respective importance of 18% and 16% (Figure 2B). The importance of Chl-a and aCDOM to the pCO2 estimation in the southern Baltic Sea (i.e., sub-basins No.3–4) were similar to that for the overall Baltic Sea, with slightly lower importance of SSS in sub-basin No.3 (Figure 2A). The filtering and time window narrowing down left the Gulf of Bothnia (i.e., sub-basin No.1, Figure 1) with the in-situ data from March 2006 and September 2009. It hampered the construction of random forest model for pCO2 estimate in this sub-basin, due to the strategy of data from 2/3 months for model training. The 50 random forest models constructed in the Baltic Sea, sub-basin No.2, sub-basin No.3, and sub-basin No.4 had the means of 49 µatm, 72 µatm, 50 µatm, and 43 µatm, respectively.
The variables’ importance for pCO2 estimation also varied on seasonal scales. For the sea surface pCO2 estimate in the entire Baltic Sea during February–April, PAR was the most important variable with mean importance of 56%, followed by MLD (20%), SSS (15%), SST (15%), and aCDOM (10%). Chl-a and Kd_490nm showed mean importance of 8% (Figure 3B). From May to July, all the variables displayed a similar importance (12–14%), with Kd_490nm (7%) and MLD (5%) (Figure 3C). The low importance of all the variables in May-July means that during this period the alternative absence of the variables in the models constructed did not significantly change the accuracies of the respective models. In another word, during May-July, the combination of any six out of the seven variables used in the study can well cover the variations of pCO2 in the Baltic Sea. For pCO2 estimation in the entire Baltic Sea in the period of August-October, PAR and SST were the first two most important variables with respective importance of 38% and 31% (Figure 3D), followed by MLD (16%) and SSS (12%) and the rest variables with importance of 10%. Chl-a and Kd_490nm showed overall low importance for the pCO2 estimate across Baltic Sea, regardless of the season. From November to the following January, the dense cloud cover over the Baltic Sea region barely allowed any optical images qualified for the retrieval of remote sensed variables. The RMSEs of the 50 models were in the range of 30–80 µatm. The models trained with data from May–July showed the smaller RMSEs (41 µatm) than those trained with in-situ data from February–April and August–October (52 µatm and 55 µatm) (Figure 3D).
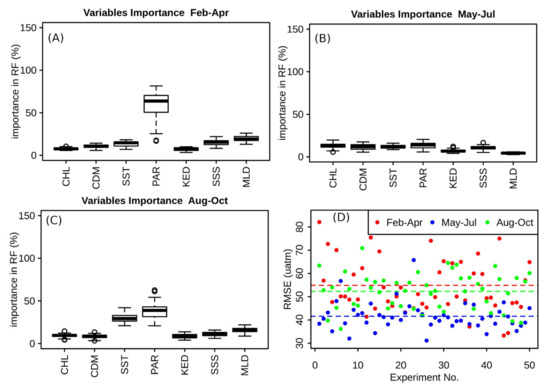
Figure 3.
Variables’ importance for pCO2 estimate in the entire Baltic Sea in different seasons (A–C) and the RMSEs of the corresponding 50 models (D).
Overall, PAR showed the highest importance for pCO2 estimate in the Baltic Sea across different seasons and locations. SST was the second most important variable. aCDOM is important for pCO2 estimate in the Gulf of Finland. MLD is important for pCO2 estimate in all the sub-basins of the Baltic Sea but varied seasonally. SSS is important for pCO2 estimation in the Baltic Sea both spatially and temporally. Chl-a, which has been commonly considered as the determining variable for pCO2, showed low importance to the pCO2 estimate over the entire Baltic Sea and its sub-basins. Kd_490nm showed low importance for pCO2 estimation in the Baltic Sea across different seasons and sub-basins.
5.2. pCO2 Maps from Final Random Forest Model
The final random forest model for sea surface pCO2 estimation for the entire Baltic Sea engaged all the variables, namely, PAR, Chl-a, aCDOM, SST, Kd_490nm, SSS, and MLD. Its RMSE was 47.8 µatm and its coefficient of determination (i.e., R2) was 0.63 (Figure 4A). The mean absolute error (MAE) of the model was -3.26 µatm, implying a slight overall underestimate of pCO2. The pCO2 predicted with this model exhibited minor overestimates for pCO2 larger than 450 µatm and slight overestimates for pCO2 around 200 µatm (Figure 4A). Both the estimated and observed pCO2 values were mainly in the range of 100–500 µatm, with a few pCO2 observations between 500 µatm and 600 µatm (Figure 4A).
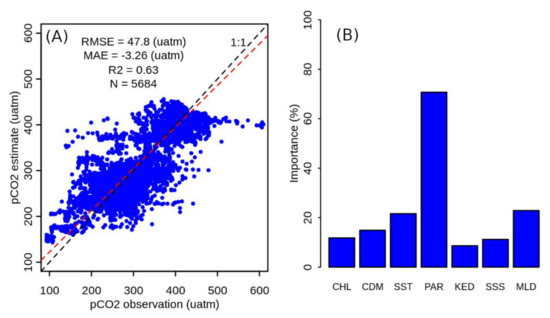
Figure 4.
The final random forest model for the pCO2 estimate. (A) Quality performance of the model, where the red dashed line is the regression line between the pCO2 observation and the estimate and black dashed line is 1:1 line; (B) the variables’ importance in the model.
The variable importance in the final model was similar to that in Figure 2A. Specifically, PAR was the most important variable, followed by SST, MLD, and aCDOM. Ch-a and Kd_490nm showed the lowest importance (Figure 4B).
For the period of August 2002–October 2011, pCO2 maps covering the entire Baltic Sea were retrieved for each month except November, December, January, and February, when the remotely sensed variables were not available due to frequent cloud coverage. Taking the year of 2005 as example (Figure 5), the sea surface pCO2 in the Baltic Sea were in the range of 100–500 µatm. On the spatial scale, the pCO2 maps exhibited reasonable transitions in the Baltic Sea (Figure 5). In addition, detailed features of the pCO2 variation were also displayed in those maps. For example, in April 2005, much lower pCO2 was present at the river mouths in the southern Baltic Sea compared to other areas. In May 2005, a strip of low pCO2 was present in the central Baltic Proper. In September 2005, an area of pCO2 higher than both August and October was displayed in the southern Baltic Sea (Figure 5).
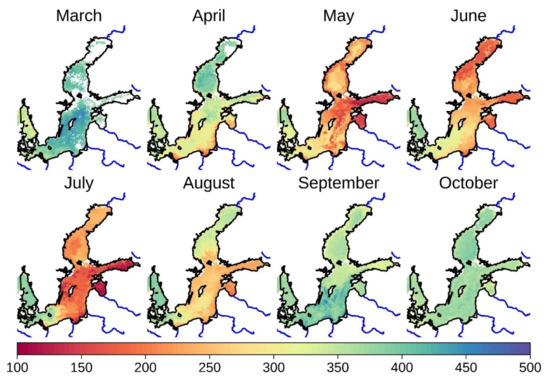
Figure 5.
Seasonal distribution of pCO2 in the Baltic Sea in the year of 2005 and the large rivers draining to the Baltic Sea.
The sea surface pCO2 in the Baltic Sea exhibited significant seasonal variations (Figure 5). Generally, low (undersaturated) pCO2 conditions of 100–300 µatm prevailed during summer months (e.g., July) and the winter months (e.g., October) were characterized by oversaturated pCO2 conditions of up to 500 µatm (Figure 5). The pCO2 variation at different sites in the Baltic Sea also exhibited these characteristics (Figure 6).
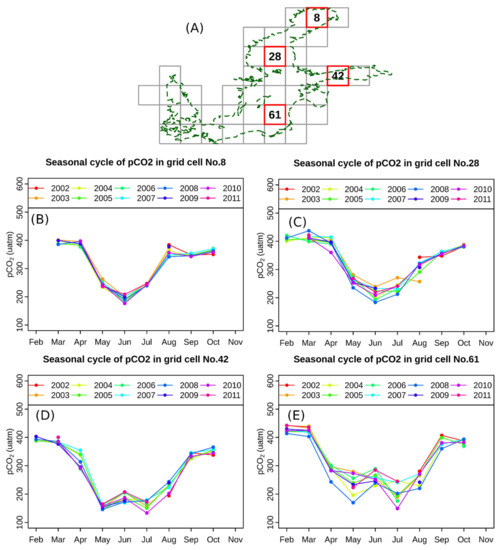
Figure 6.
Seasonal cycle of monthly pCO2 at different sites in the Baltic Sea. The pCO2 estimate for the months determined with significant upwelling effect in Section 4.2 were excluded from this analysis. (A): the location of the sites, (B–E): the seasonal cycle of monthly pCO2 at sites in sub-figure A.
The sea surface pCO2 in the Baltic Sea also showed significant spatial gradient and variation along the months, particularly between April and September (Figure 5). In April, July, and August, the southern central Baltic Sea (excluding the sub-basin No.4 in Figure 1B) often displayed pCO2 approximately 100–150 µatm lower than the northern sub-basins (Figure 5). In May, the Gulf of Finland and the Gulf of Riga (Sub-basin No.2 in Figure 1B) showed the lowest pCO2 of 100 µatm in the Baltic Sea. In June, sea surface pCO2 in the two narrow gulfs increased slightly, while the Gulf of Bothnia exhibits its lowest seas surface pCO2 in a year. In September, the sea surface pCO2 in the southern Baltic Sea increased rapidly and displayed a reversed the gradient to that in August. In October, the pCO2 in the entire Baltic Sea was in the range of 380–420 µatm, rather homogenous in comparison to other months (Figure 5 and Figure 6). On the other hand, different areas in the Baltic Sea showed their minimum pCO2 at different time. While the Gulf of Finland (No.42 in Figure 6A) and the Baltic Proper (i.e., No.61 in Figure 6A) had two seasonal minima in May and July, respectively, the Bothnia Sea (i.e., No.8 in Figure 6A) and the Bothnia Bay (No.28 in Figure 6A) showed their only seasonal minima of 180–250 µatm in June. Thirdly, the seasonal change points of pCO2 int the Baltic Sea varied spatially. The pCO2 in the Bothnia Bay and Bothnia Sea started decreasing in May (Figure 6B,C), but the pCO2 in the Baltic Proper and Gulf of Finland in the south showed this change already in April, one month earlier (Figure 6D,E). The pCO2 in the Gulf of Bothnia (i.e., No.8 and 28 in Figure 6A) increased already in July, but such changes in the pCO2 in the southern Baltic Sea were delayed by one month to August. Consequently, in August, when pCO2 in the northern Baltic displayed are almost equal to the values in winter months (Figure 6B,C), pCO2 in the Baltic Proper and Gulf of Finland remained on the level of its summer value (Figure 6D,E). Furthermore, in the Gulf of Finland (i.e., No.42 in Figure 6A), significant inter-annual pCO2 differences were present in April and August (Figure 6D), but, in the Baltic Proper (i.e., No.62, Figure 6A), this occurred in May, July, and August (Figure 6E).
Across the period of 2002–2011, the estimated pCO2 were correlated to the variables in the Baltic Sea to different degrees in different directions, varying spatially (Figure 7). The Chl-a-pCO2 correlation varied between −0.5 and 0.5, with general positive correlation in the northern Baltic Sea and negative correlation in the south. The estimated pCO2 were generally negatively correlated to the co-located aCDOM in the Baltic Sea with correlation coefficients ranging from −1 to 0, and the correlation exhibited larger absolute coefficients than Chl-a-pCO2 correlation, particularly in the southern Baltic Sea. SST-pCO2 correlation mostly exhibited negative coefficients (i.e., from −0.5 to 0) in the Baltic Sea, with larger absolute values in the south than in the north. Exceptionally high positive SST-pCO2 correlation, up to 0.8, was present in the very west part of the Baltic Sea. The PAR-pCO2 correlation in the Baltic presented the largest absolute coefficients and pCO2 was mostly negatively correlated to PAR in the entire Baltic Sea (i.e., from −1 to −0.6), showing the same pattern to the SST-pCO2 correlation. Kd_490nm-pCO2 correlation showed the similar pattern as Chl-a-pCO2, with slightly higher absolute coefficients in the southeastern coasts. SSS exhibited high positive correlation to the co-located pCO2 at the coastal waters with values ranging from 0 to 0.8, mostly at 0. MLD was positively correlated to pCO2 in the entire Baltic Sea with large absolute coefficients (0.5–1), except in the very north and west part of the sea.
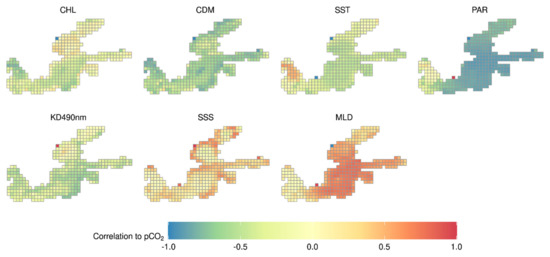
Figure 7.
The spatial correlation between the estimate pCO2 and the variables the study period of 2002–2011. The size of grid cells is 0.5° × 0.5°. Minus value the variable was negatively correlated to the pCO2 there and the positive values mean positive correlations.
5.3. Comparison of Random Forest and SOM
In the both schemes of training and validation data selection described in Section 4.5, majority of validation data were in the range of 100–500 µatm. The pCO2 estimated with random forest were in the same range as the validation data (Figure 8A,C). In contrast, the SOM model constrained the pCO2 estimate into the range of 230–430 µatm (Figure 8A,C), particularly in the scheme No.2 where the training data were the randomly selected pCO2 measurements (Figure 8C). In addition, often one pCO2 value estimated from SOM responded to a large range of observed pCO2, forming evident horizontal features in the cross-validation (Figure 8A,D), particularly when the prediction covers multiple months. However, such patterns were not notable in the pCO2 estimated with random forest or MLR (Figure 8B,E).
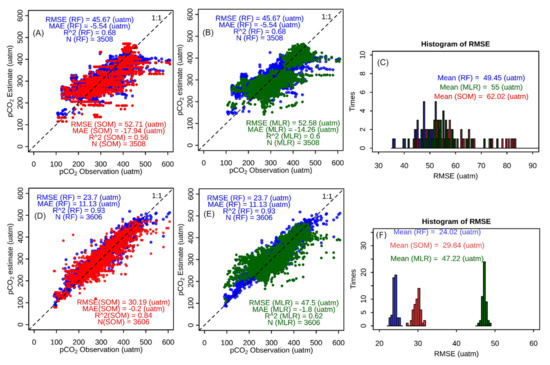
Figure 8.
Comparison of random forest, SOM, and multiple linear regression (MLR) in pCO2 estimation in the Baltic Sea. (A,B) Comparison of a random forest model (i.e., RF in the figures) to the SOM model and MLR model trained with exactly the same in-situ data from 2/3 of months selected randomly; (C) Histograms of RMSE of 50 models trained in the same manner as in A and B; (D,E) Comparison of a random forest model to the SOM model and MLR model trained with exactly the same 2/3 of the in-situ data selected randomly; (F) Histograms of RMSE of 50 models constructed the same manner as in (D,E).
In an example of 50 experiments where the training data were selected with scheme No.1 (Figure 8A,B), the coefficient of determination of the random forest model prediction was 0.68, much larger than 0.58 and 0.6, the coefficient of determination of the prediction with the SOM and MLR trained with the identical pCO2 measurements. The mean RMSE of the 50 random forest models trained with training data selected with scheme No.1 was 49 µatm, while the mean RMSE of their SOM and MLR counterparts were 55 and 62 µatm (Figure 8C). In the case of training data selected with scheme No.2, the mean RMSE of the 50 random forest models was 24 µatm, significantly lower than 30 and 48 µatm, the respective means of RMSEs of the 50 SOM models and MLR models trained with the same sets of training data (Figure 8F). This indicated random forest outperformed SOM in the pCO2 estimation in the Baltic Sea.
6. Discussion
6.1. Characteristics of Variable Contribution to the pCO2 Estimate
We analyzed the importance of different variables to the pCO2 estimation in the Baltic Sea using random forest on different spatial and temporal scales. It was evident that the spatiotemporal variability in the variable’s importance was high, but some general patterns were visible.
Chl-a displayed overall low importance (small contribution) to the pCO2 estimate across different spatial and temporal scales in the Baltic Sea (Figure 2 and Figure 3). The Chl-a-pCO2 correlation in the Baltic Sea was also relatively low, compared to the other variables’ correlation to pCO2 (Figure 7). This was in contrast to previous findings that Chl-a was closely related to pCO2 in global oceans [13] and marginal seas, like the Gulf of Mexico [10]. The limited importance of Chl-a is probably due to: (1) In addition to Chl-a, PAR, and SST are also fundamental factors for the photosynthesis induced biological fixation of carbon; (2) The studies that established or confirmed correlations between Chl-a and pCO2 did not include aCDOM [13,76]. But high correlation (r > 0.9) was found between remotely sensed Chl-a and aCDOM in the Gulf of Mexico [17] and West Florida Shelf [41]. Chl-a and aCDOM also displayed similar spatiotemporal patterns in the Baltic Sea (Figure S8). In the analysis of variables’ importance, aCDOM exhibited a more pronounced response to pCO2 variation than Chl-a (Figure 2A), as it showed higher correlation to pCO2 than Chl-a did (Figure 7). Similarly, sea surface pCO2 in the Gulf of Mexico is more closely related to aCDOM than to Chl-a [41]. However, despite its low importance for sea sur face pCO2 estimate in the Baltic Sea at all the spatial and temporal scales and its general low correlation to pCO2 (Figure 2, Figure 3 and Figure 7), we still regarded Chl-a as an important variable for the pCO2 estimation in the Baltic Sea. This is particularly the case during summer (i.e., May–July), when the cyanobacteria and phytoplankton blooms takes place often, uptakes CO2 and reduces the sea surface pCO2 in the Baltic Sea [58]. The low importance of Chl-a in May–Jul (summer in this study) (Figure 3B) is very likely that, during this time, the effect of absent Chl-a in the model was compensated by variables highly correlated to Chl- a during in this time (e.g., CDOM and SST). Likewise, the other variables also exhibited low importance for pCO2 estimate in May–July (Figure 3B). Yet, this was the case for the Baltic Sea, as for its applicability in other marginal seas, and the situation should be treated carefully.
Overall, PAR exhibited the highest importance for the pCO2 estimation in the Baltic Sea across different sub-basin and nearly in every season, except summer. In addition, the PAR-pCO2 correlation coefficients were of the largest absolute values among all the variable-pCO2 correlations (Figure 7). The high importance of PAR for pCO2 in the Baltic Sea and its sub-basins and the high correlation of this variable to sea surface pCO2 are attributed to the high seasonality of the sun illumination. Located at the high latitude of the Baltic Sea 54–66°N (Figure 1), the sun illumination in the central Baltic Sea, for example, varies from 6 h in winter to 18 h in summer. As phytoplankton photosynthesis is largely determined by the available sun illumination, it is reasonable that seasonality of pCO2 aligns with that of PAR. In addition, river discharge loaded with CDOM, etc. is also characterized with high seasonality and, to large extent, synchronized to PAR [30], so is the bacteria respiration dependent on the available organic matter. Therefore, it is reasonable that PAR exhibited high importance for sea surface pCO2 estimation in the Baltic Sea and its sub-basins. The importance of PAR in the pCO2 estimate in the Baltic Sea in different seasons can be attributed to the wide span of the Baltic Sea (12°) in latitude (Figure 1) and the resultant large gradient in sun illumination. On a day in spring, the sun illumination in the southern Baltic Sea is 2–3 h longer than that in the north, same for fall. The gradients in PAR largely impose differences in the intensities of phytoplankton photosynthesis, SST distribution, and ultimately to CO2 uptake of sea water via primary production. As for in summer when PAR and other variables displayed similar but low importance, sun illumination in the northern Baltic Sea is up to 6 h longer than in the southern Baltic Sea, displaying an even larger spatial gradient across the Baltic Sea than in other seasons. However, owing to snowmelt, the co-current freshwater discharge and the nutrients it loads are all very high in the Baltic Sea in late spring and early summer [30], create a high spatiality in the nutrient and DOM etc. Yet, the spatial pattern of cDOM etc. are likely different from that of PAR, depending on the sizes of catchment and land cover types. When all the processes determining pCO2 take place with similarly high intensities, none of the variables exhibit prominent importance, but all of them jointly determined the pCO2 in the Baltic Sea in summertime with similar degree (importance).
Concerning the determination of the seasonality in sea surface pCO2, the Julian day of the year (DOY) has been frequently in previous studies [12,16]. However, in this study, PAR holds two advantages over DOY. Firstly, PAR is a direct measure of sun radiation available for photosynthesis, and it has physical meaning, while DOY is a proxy of the seasonality. Secondly, a trigonometric conversion is often applied on DOY to correctly proximate the seasonality. Specifically, the minus cosine of DOY was used for pCO2 estimate in waters in the northern hemisphere and cosine of DOY for waters in the southern hemisphere [16,18]. Consequently, a trigonometric conversion of DOY attributes a spatially constant value in the entire hemisphere and overlook the effect spatial gradient of sun illumination. In contrast, PAR captures well the spatial gradient of sun illumination along the longitude and express its effect on photosynthesis in the water. Therefore, we suggest that future sea surface pCO2 estimation consider the participation of PAR instead of DOY (Figure 1).
The SST holds the same position in the pattern of variables’ importance for pCO2 estimate in the Baltic Sea and its sub-basin (Figure 2). This was probably because the seasonality magnitudes of SST in each sub-basin are on the same order, particularly when the sub-basins are relatively small and well mixed horizontally. In many cases, despite its correlation to pCO2 being on the same order as the Chl-a-pCO2 and Kd_490nm-pCO2 correlations, SST showed a larger importance than Chl-a, which aligned with the prediction error produced by alternatively omitting the variables by [17]. In the pCO2 estimates for the Baltic Sea in different seasons, SST was more important in August–October than in other seasons (Figure 3). This was probably because, in fall, the large spatial gradient in SST in the Baltic Sea responded more to the pCO2 distribution at a similar degree as the PAR does, but more than other variables. For example, the sea surface in the Gulf of Bothnia starts freezing already in October and lower down the primary production, whereas the southern Baltic Sea remains open water at time and allow the biological CO2 uptake [77].
Despite its low importance for the pCO2 estimate for the entire Baltic Sea, aCDOM exhibited more important for the pCO2 estimate in the Gulf of Finland than in other sub-basins (Figure 2B). The aCDOM -pCO2 correlation in the Baltic Sea is also relatively large, particularly at the coast and in the Gulf of Finland (Figure 7). As mentioned previously, bacteria respiration produces CO2 by decomposing organic carbons, like DOM [14,15]. The relatively narrow waters of the Gulf of Finland receive a large terrestrial input of DOM from the rivers, including the Neva, which drains the largest sub-catchment of the Baltic Sea, approximately 1/6 of the total Baltic Sea catchment [30]. The changes of sea surface pCO2 in the Gulf of Finland largely responded to the changes in CDOM there. Therefore, aCDOM is important for pCO2 estimation in the Gulf of Finland (Figure 2B) and thus in the Baltic Sea, as well. Similar mechanism very likely applies at coastal waters receiving river discharges. Moreover, this study used the aCDOM derived from MERIS images. The MERIS sensor was succeeded by the Ocean and Land Color Instrument (OLCI) sensors on Sentinel-3 satellites in 2016. Therefore, aCDOM derived from OLCI images will likely play an equivalent role in the pCO2 estimate in the Baltic Sea and other similar waters.
Though less than PAR and sometimes slightly less than SST, MLD was important for the pCO2 estimation in the Baltic Sea and all its sub-basins (Figure 2B). pCO2 in the Baltic Sea is largely and positively correlated to MLD (Figure 7). This is probably resulted from the seasonally varying amount of fresh water discharged by the many rivers and lay above the relatively saline and heavy water [78]. In addition, seasonal winds in the Baltic Sea might have jointly determined the high variation of MLD [32] and, consequently, the vertical mixing of sea water and pCO2, as well.
In this study, Kd_490 nm showed low importance to the pCO2 estimation in the Baltic Sea, regardless of season or sub-basin (Figure 2 and Figure 3) and a relatively weaker correlations to pCO2 (i.e., from −0.7 to 0), compared to variables, like PAR and aCDOM. This aligns with the previously found negatively correlation between Kd_490 nm and pCO2 in the Gulf of Mexico [16]. Here, we argue that the reasons behind the low contribution of Chl-a to pCO2 estimation very likely also applied to Kd_490nm. This argument is well supported by previous studies. It is found that Kd_490nm in the Baltic Sea was a function of inherent optical properties, i.e., absorption and scattering of phytoplankton, and effects of illumination and viewing angle [79,80]. Furthermore, [81] observed a strong positive correlation between Kd_490nm and river discharge into the Baltic Sea and the latter is rich of CDOM. In addition, a positive correlation of Kd_490nm to Chl-a and aCDOM were noticed in the Baltic Sea (S9), and the Kd_490nm-pCO2 and aCDOM-pCO2 correlations also exhibited similar patterns (Figure 7).
6.2. Impact of Unbalanced In-Situ Measurements Distribution on the Model for pCO2 Estimate
The in-situ pCO2 measurements available in the Baltic Sea during 2002–2011 were unevenly distributed, namely, relatively sparse measurements in the north and dense measurements in the south (Figure 1). In order to ensure the participation of the in-situ data from the northern Baltic Sea, we selected in-situ data month-wise to train and validate the model for pCO2 estimation, instead of randomly selecting from the in-situ measurements. However, this measure led to the missing determination of variables’ importance for the Gulf of Bothnia due to the few months of in-situ measurements in this basin (i.e., March 2006 and September 2009). In the future, including additional in-situ pCO2 measurements from the Gulf of Bothnia can help analyze the variables’ importance for the pCO2 estimate in that region and understand the processes controlling pCO2 there. These additional in-situ pCO2 measurements are also expected to improve the RMSE of pCO2 estimate for the entire Baltic Sea.
Despite the unbalanced distribution of in-situ data in the Baltic Sea, the monthly pCO2 maps were retrieved for the Baltic Sea for the period of August–October 2011 (Figure 5). The RMSE of the model for pCO2 estimation was 47.8 µatm (Figure 4), slightly larger than 25 µatm and 31.7 µatm, the RMSEs of the models constructed by [16] and [17], respectively, for pCO2 estimation in the Gulf of Mexico using similar tree-based regression algorithms. Still, the RMSE of 47.8 µatm is relatively small for pCO2 estimation in the Baltic Sea, considering the following factors: (1) the pCO2 estimation was undertaken on the monthly frequency, where the in-situ data from entire month was integrated to the few days with remote sensing images; (2) The magnitudes of the seasonal changes in pCO2 in the Baltic Sea are much larger than that in middle or low latitude marginal seas. For example, the pCO2 in the Baltic Sea was in the range of 100–600 µatm (Figure 8), while, in the Gulf of Mexico, it was 200–450 µatm [16], and, in the South China Sea, it was 250–450 µatm [11]; (3). The processes controlling pCO2 across the Baltic sea (e.g., phytoplankton photosynthesis, bacteria respiration and runoff) vary spatially and temporally [30,82] and thus increase the difficulties in mapping pCO2 in the Baltic Sea with high accuracy; (4) Upwelling take places in the Baltic Sea with varying frequencies among years and months [83] and complicates the pCO2 process in multiple manners [34,84]. Even though we eliminated the months dominated by upwelling, few upwelling might have remained in the rest of the months and increased the RMSE of the model; (5) Most importantly, the random forest model covered the processes that took places in the entire Baltic Sea in all the seasons in the period of 2002–2011. This task itself is a challenging one due to the above factors. All these factors rendered deriving sea surface pCO2 in the Baltic Sea more challenging than in other marginal seas.
The random forest algorithm outperformed SOM and MLR in the sea surface pCO2 estimation (Figure 8). We attributed this to how the three algorithms treated the variables. In random forest, a series of forests were constructed, and the most effective one was chosen for prediction [59,65]. While the variables and training samples were randomly selected for the tree construction, the best model was the one with little participation of the unimportant variables. In contrast, when the mode was constructed with SOM, all the input variables had the same weights [70]. This very likely amplified the contribution of the unimportant or correlated variables and suppresses the important ones at the corresponding temporal and spatial scale, thus caused misestimates (Figure 8A,C). The variants of SOM, such as SOMLO, probably also inherit such effects. MLR attributed weights to the input variables by determining their correlation coefficients to the dependent variables. The effect of the coefficients is very evident in the case when the training samples were chosen across months and cover a large variation. For example, in the experiments in Figure 8A–C, the samples covered 2/3 of the months and performed RMSE similar to that of random forest and better than SOM. In contrast, in the experiment where the samples were 2/3 of the entire in-situ data set from random selection, samples from the same season/months of high similarity were likely used. Given that the time window of in-situ data was narrowed down to 9:00–14:00, and the in-situ data from the months dominated by upwelling were also removed, we did not consider the effect of outlier on the modeling and the errors produced by the models were regarded to be from the misestimate of the models. Overall, random forest performs better than MLR and SOM regardless of the variation range of the training data. MLR performs better than SOM when the training data cover a large variation, and SOM performs better than MLR when the training data cover a relatively small variation.
6.3. pCO2 Maps for the Baltic Sea and Its Spatiotemporal Characteristics
In this study, we produced the monthly pCO2 maps for the entire Baltic Sea over the period of August 2002–October 2020. These maps showed that pCO2 across the Baltic Sea was characterized by strong seasonality, generally, high pCO2 in winter and low pCO2 in summer (Figure 5 and Figure 6). The trend aligned well with that derived from in-situ data in the Baltic Sea [85]. The seasonality of pCO2 in the Baltic Sea was similar to that in the marginal sea of Gulf of Maine but different from the one observed in Gulf of Mexico by [16]. In addition, the range of seasonal pCO2 variation in the Baltic Sea (i.e., 100–500 µatm) was larger than that observed for the two marginal seas (i.e., 300–500 µatm) (Figure 5 and Figure 6) [16]. These different seasonal variations trends and variables’ importance (e.g., Kd_490nm) suggest that the processes determining the pCO2 in the Baltic Sea are likely different from that observed in other seas, or same processes work on different intensity, for example, the gradient in PAR.
In addition to the similar seasonal trend, minor differences exist in the seasonal trends of pCO2 in the Baltic Sea. For example, Baltic Proper and the Gulf of Finland showed pCO2 minima both in May and July, while, in the Bothnia Bay and Bothnia Sea, it was only shown on minima in June (Figure 6). May is the time when most rivers pass their annual peak of water levels [30], and, in July, the daytime is the longest in a year in Baltic Sea, with the most sunny days. In addition, different areas in the Baltic Sea showed interannual variations in different months (Figure 6). For example, the waters in the Gulf of Finland exhibited large interannual variation in April (Figure 6D), when the large river input take place in the sub-basin [27]. The Baltic Proper showed such variations during May–July (Figure 6E), when the primary production is high in this sub-basin and upwelling also occurs very often there [58,68]. This indicates that the dominantly driver of pCO2 are spatially variable across the Baltic Sea. The pCO2 maps derived from this model exhibited continuous transitions between the sub-basins of the Baltic Sea (Figure 5). Therefore, these maps are a significant improvement from those produced in previous studied by dividing the Baltic sea into different sub-basins [12].
7. Conclusions
This study analyzed the variables’ importance in the pCO2 estimation for the Baltic Sea across different time and sub-basins with the support of remote sensing and derived pCO2 maps for the Baltic Sea from August 2002 to October 2011. We found that the contributions of the variables to pCO2 retrieval for the Baltic Sea vary both spatially and temporally and likely replicated the spatiotemporal characteristics of the driving forces. Among all the variables, PAR was the most important, followed by SST and MLD. Chl-a contributed surprisingly little to the pCO2 estimate. aCDOM was important for the pCO2 estimation for the Gulf of Finland and the Gulf of Riga. The random forest model used for the pCO2 estimate for the entire Baltic Sea had the RMSE of 47.8 µatm, MAE of −3.26 µatm, and coefficient of determination of 0.63. These pCO2 maps derived in this study are one of the most reliable pCO2 fields in the Baltic Sea and can potentially support determining the role of the Baltic Sea as sink/source of the atmospheric CO2. Moreover, the variables importance/relevance from this study can provide a benchmark for understanding the different drivers of pCO2 in the Baltic Sea and how they vary in different time and space.
In the Baltic Sea region, frequent clouds in November, December, and January lead to the absence of pCO2 maps during those three months. This is an inevitable situation considering the high-latitude location of the Baltic Sea. Derivation of sea surface pCO2 for the Baltic Sea in the wintertime needs to be achieved by combining the remote sensing supported results with additional sources information, e.g., modeling.
Supplementary Materials
The following are available online at https://www.mdpi.com/2072-4292/13/2/259/s1, Figure S1: Spatial and temporal distributions of the in-situ data used for training and validating the pCO2 estimate. Figure S2: Diurnal effect on the pCO2 estimate. Figure S3: Scenarios where the upwelling affects the pCO2 estimate from remote sensing images. Figure S4: The effect of upwelling in the pCO2 estimate with remote sensing image. Figure S5: The monthly mean product of Chl-a derived from MODIS and MERIS images in May, July and September 2011 mapping the Baltic Sea. Figure S6: aCDOM from MODIS and MERIS in the Baltic Sea. Figure S7: The performance differences between of Chl-a from MODIS and Chl-a from MERIS in the pCO2 estimate. Figure S8: Alternative of the final model for pCO2 estimate in the entire Baltic Sea. Figure S9: Relationship between variables in the Baltic Sea.
Author Contributions
S.Z., A.R. and P.P. designed the study. S.Z. did the data collection, analysis and manuscript preparation. Writing—review & editing, S.Z., A.R., P.P. and M.B.W. Investigation, S.Z., P.P. and M.B.W. All authors have read and agreed to the published version of the manuscript.
Funding
Swedish National Space Board (Project No: 174/17) and the BONUS Blue Baltic (Call No. 2015-101: Integrated carboN and TracE Gas monitoRing for the bALtic sea) funded this study.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Acknowledgments
The computations were performed on Swedish National Infrastructure for Computing (SNIC) through Uppsala Multidisciplinary Center for Advanced Computational Science (UPPMAX) (Project No. SNIC 2019-8-223 & SNIC2019-30-7). The MODIS data were provided by Physical Oceanography Distributed Active Archive Center (PODAAC: https://podaac.jpl.nasa.gov/). Copernicus Marine Environment Monitoring Service (CMEMS: https://marine.copernicus.eu/) provided SSS and MLD data. The ICOS (Integrated Carbon Observation System) station Östergarnsholm is funded by Swedish Research Council and Uppsala University. Bernd Schneider and Matti Perttilä coordinated in the provision of original data used by Löffler et al. (2012). We are thankful to the constructive comments from three anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gruber, N.; Clement, D.; Carter, B.R.; Feely, R.A.; Van Heuven, S.; Hoppema, M.; Ishii, M.; Key, R.M.; Kozyr, A.; Lauvset, S.K.; et al. The oceanic sink for anthropogenic CO2 from 1994 to 2007. Science 2019, 363, 1193–1199. [Google Scholar] [CrossRef]
- Laruelle, G.G.; Cai, W.; Hu, X.; Gruber, N.; MacKenzie, F.T.; Regnier, P. Continental shelves as a variable but increasing global sink for atmospheric carbon dioxide. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Gruber, N. Carbon at the coastal interface. Nat. Cell Biol. 2015, 517, 148–149. [Google Scholar] [CrossRef]
- Laruelle, G.G.; Lauerwald, R.; Pfeil, B.; Regnier, P. Regionalized global budget of the CO2exchangeat the air-water interface in continental shelf seas. Glob. Biogeochem. Cycles 2014, 28, 1199–1214. [Google Scholar] [CrossRef]
- Hofmann, E.E.; Cahill, B.; Fennel, K.; Friedrichs, M.A.; Hyde, K.; Lee, C.; Mannino, A.; Najjar, R.G.; O’Reilly, J.E.; Wilkin, J.; et al. Modeling the Dynamics of Continental Shelf Carbon. Annu. Rev. Mar. Sci. 2011, 3, 93–122. [Google Scholar] [CrossRef]
- Fennel, K.; Wilkin, J.; Previdi, M.; Najjar, R. Denitrification effects on air-sea CO2 flux in the coastal ocean.pdf. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Xue, L.; Cai, W.-J.; Hu, X.; Sabine, C.L.; Jones, S.M.; Sutton, A.J.; Jiang, L.-Q.; Reimer, J.J. Sea surface carbon dioxide at the Georgia time series site (2006–2007): Air–sea flux and controlling processes. Prog. Oceanogr. 2016, 140, 14–26. [Google Scholar] [CrossRef]
- Schneider, B.; Müller, J.D. Biogeochemical Transformations in the Baltic Sea–Observations through Carbon Dioxide Glasses; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 978-3-319-61698-8. [Google Scholar]
- Chierici, M.; Signorini, S.R.; Mattsdotter-Björk, M.; Fransson, A.; Olsen, A. Surface water fCO2 algorithms for the high-latitude Pacific sector of the Southern Ocean. Remote Sens. Environ. 2012, 119, 184–196. [Google Scholar] [CrossRef]
- Chen, S.; Hu, C.; Cai, W.; Yang, B. Estimating surface pCO2 in the northern Gulf of Mexico: Which remote sensing model to use? Cont. Shelf Res. 2017, 151, 94–110. [Google Scholar] [CrossRef]
- Jo, Y.-H.; Dai, M.; Zhai, W.; Yan, X.-H.; Shang, S. On the variations of sea surfacepCO2in the northern South China Sea: A remote sensing based neural network approach. J. Geophys. Res. Space Phys. 2012, 117, 1–13. [Google Scholar] [CrossRef]
- Parard, G.; Charantonis, A.A.; Rutgersson, A. Remote sensing the sea surface CO2 of the Baltic Sea using the SOMLO methodology. Biogeosciences 2015, 12, 3369–3384. [Google Scholar] [CrossRef]
- Fay, A.R.; McKinley, G. Correlations of surface ocean pCO2 to satellite chlorophyll on monthly to interannual timescales. Glob. Biogeochem. Cycles 2017, 31, 436–455. [Google Scholar] [CrossRef]
- Gustafsson, E.; Omstedt, A.; Gustafsson, B.G. The air-water CO2 exchange of a coastal sea—A sensitivity study on factors that influence the absorption and outgassing of CO2 in the Baltic Sea. J. Geophys. Res. Oceans 2015, 120, 5342–5357. [Google Scholar] [CrossRef]
- Gustafsson, E.; Deutsch, B.; Gustafsson, B.; Humborg, C.; Mörth, C.-M. Carbon cycling in the Baltic Sea—The fate of allochthonous organic carbon and its impact on air–sea CO2 exchange. J. Mar. Syst. 2014, 129, 289–302. [Google Scholar] [CrossRef]
- Chen, S.; Hu, C.; Barnes, B.B.; Wanninkhof, R.; Cai, W.-J.; Barbero, L.; Pierrot, D. A machine learning approach to estimate surface ocean pCO2 from satellite measurements. Remote Sens. Environ. 2019, 228, 203–226. [Google Scholar] [CrossRef]
- Lohrenz, S.E.; Cai, W.; Chakraborty, S.; Huang, W.-J.; Guo, X.; He, R.; Xue, Z.G.; Fennel, K.; Howden, S.; Tian, H. Satellite estimation of coastal pCO2 and air-sea flux of carbon dioxide in the northern Gulf of Mexico. Remote Sens. Environ. 2018, 207, 71–83. [Google Scholar] [CrossRef]
- Ikawa, H.; Faloona, I.; Kochendorfer, J.; Paw, K.T.; Oechel, W. Air–sea exchange of CO2 at a Northern California coastal site along the California Current upwelling system. Biogeosciences 2013, 10, 4419–4432. [Google Scholar] [CrossRef]
- Joshi, I.D.; Ward, N.D.; D’Sa, E.J.; Osburn, C.L.; Bianchi, T.S.; Oviedo-Vargas, D. Seasonal Trends in Surface pCO2 and Air-Sea CO2 Fluxes in Apalachicola Bay, Florida, From VIIRS Ocean Color. J. Geophys. Res. Biogeosci. 2018, 123, 2466–2484. [Google Scholar] [CrossRef]
- Telszewski, M.; Chazottes, A.; Schuster, U.; Watson, A.J.; Moulin, C.; Bakker, D.C.E.; González-Dávila, M.; Johannessen, T.; Körtzinger, A.; Lüger, H.; et al. Estimating the monthly pCO2 distribution in the North Atlantic using a self-organizing neural network. Biogeosciences 2009, 6, 1405–1421. [Google Scholar] [CrossRef]
- Friedrich, T.; Oschlies, A. Neural network-based estimates of North Atlantic surface pCO2 from satellite data: A methodological study. J. Geophys. Res. Space Phys. 2009, 114, 1–12. [Google Scholar] [CrossRef]
- Hales, B.; Strutton, P.G.; Saraceno, M.; Letelier, R.; Takahashi, T.; Feely, R.; Sabine, C.; Chavez, F. Satellite-based prediction of pCO2 in coastal waters of the eastern North Pacific. Prog. Oceanogr. 2012, 103, 1–15. [Google Scholar] [CrossRef]
- Salisbury, J.; VanDeMark, D.; Hunt, C.W.; Campbell, J.W.; McGillis, W.R.; McDowell, W.H. Seasonal observations of surface waters in two Gulf of Maine estuary-plume systems: Relationships between watershed attributes, optical measurements and surface pCO2. Estuar. Coast. Shelf Sci. 2008, 77, 245–252. [Google Scholar] [CrossRef]
- Signorini, S.R.; Mannino, A.; Najjar, R.G., Jr.; Friedrichs, M.A.M.; Cai, W.-J.; Salisbury, J.; Wang, Z.A.; Thomas, H.; Shadwick, E.H. Surface ocean p CO2 seasonality and sea-air CO2 flux estimates for the North American east coast. J. Geophys. Res. Oceans 2013, 118, 5439–5460. [Google Scholar] [CrossRef]
- Bai, Y.; Cai, W.-J.; He, X.; Zhai, W.; Pan, D.; Dai, M.; Yu, P. A mechanistic semi-analytical method for remotely sensing sea surfacepCO2 in river-dominated coastal oceans: A case study from the East China Sea. J. Geophys. Res. Oceans 2015, 120, 2331–2349. [Google Scholar] [CrossRef]
- Song, X.; Bai, Y.; Cai, W.; Chen, C.-T.A.; Pan, D.; He, X.; Zhu, Q. Remote Sensing of Sea Surface pCO2 in the Bering Sea in Summer Based on a Mechanistic Semi-Analytical Algorithm (MeSAA). Remote Sens. 2016, 8, 558. [Google Scholar] [CrossRef]
- Bergström, S.; Carlsson, B. River runoff to the Baltic Sea. Ambio 1994, 23, 280–287. [Google Scholar]
- Omstedt, A.; Elken, J.; Lehmann, A.D.; Piechura, J. Knowledge of the Baltic Sea physics gained during the BALTEX and related programmes. Prog. Oceanogr. 2004, 63, 1–28. [Google Scholar] [CrossRef]
- Meier, H.E.M.; Rutgersson, A.; Reckermann, M. An Earth System Science Program for the Baltic Sea Region. Eos 2014, 95, 109–110. [Google Scholar] [CrossRef]
- Käyhkö, J.; Apsite, E.; Bolek, A.; Filatov, N.; Kondratyev, S.; Korhonen, J.; Kriaučiūnienė, J.; Lindström, G.; Nazarova, L.; Pyrh, A.; et al. Recent Change—River Run-off and Ice Cover. In Second Assessment of Climate Change for the Baltic Sea Basin; Regional Climate Studies Series; Springer: Berlin/Heidelberg, Germany, 2015; pp. 99–115. ISBN 9783319160054. [Google Scholar]
- Schneider, B.; Dellwig, O.; Kuliński, K.; Omstedt, A.; Pollehne, F.; Rehder, G.; Savchuk, O. Ecological processes in the Baltic Sea. In Biological Oceanography of the Baltic Sea; Snoeijs-Leijonmalm, P., Schubert, H., Radziejewska, T., Eds.; Springer Nature: Berlin/Heidelberg, Germany, 2017; Volume 30, pp. 87–278. ISBN 9789400706675. [Google Scholar]
- Lehmann, A.; Myrberg, K. Upwelling in the Baltic Sea—A review. J. Mar. Syst. 2008, 74, S3–S12. [Google Scholar] [CrossRef]
- Norman, M.; Parampil, S.R.; Rutgersson, A.; Sahlée, E. Influence of coastal upwelling on the air–sea gas exchange of CO2 in a Baltic Sea Basin. Tellus B Chem. Phys. Meteorol. 2013, 65, 1–16. [Google Scholar] [CrossRef]
- Wasmund, N.; Nausch, G.; Voss, M. Upwelling events may cause cyanobacteria blooms in the Baltic Sea. J. Mar. Syst. 2012, 90, 67–76. [Google Scholar] [CrossRef]
- Wesslander, K.; Hall, P.; Hjalmarsson, S.; Lefèvre, M.; Omstedt, A.; Rutgersson, A.; Sahlée, E.; Tengberg, A. Observed carbon dioxide and oxygen dynamics in a Baltic Sea coastal region. J. Mar. Syst. 2011, 86, 1–9. [Google Scholar] [CrossRef]
- Barnes, B.B.; Hu, C.; Schaeffer, B.A.; Lee, Z.; Palandro, D.; Lehrter, J.C. MODIS-derived spatiotemporal water clarity patterns in optically shallow Florida Keys waters: A new approach to remove bottom contamination. Remote Sens. Environ. 2013, 134, 377–391. [Google Scholar] [CrossRef]
- Hu, C.; Muller-Karger, F.E.; Taylor, C.J.; Carder, K.L.; Kelble, C.; Johns, E.; Heil, C.A. Red tide detection and tracing using MODIS fluorescence data: A regional example in SW Florida coastal waters. Remote Sens. Environ. 2005, 97, 311–321. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Zhu, G.; Liu, X.; Zhou, Y.; Xu, H.; Qin, B.; Liu, G.; Li, Y. Long-term remote monitoring of total suspended matter concentration in Lake Taihu using 250 m MODIS-Aqua data. Remote Sens. Environ. 2015, 164, 43–56. [Google Scholar] [CrossRef]
- Liu, B.; D’Sa, E.J.; Joshi, I.D. Multi-decadal trends and influences on dissolved organic carbon distribution in the Barataria Basin, Louisiana from in-situ and Landsat/MODIS observations. Remote Sens. Environ. 2019, 228, 183–202. [Google Scholar] [CrossRef]
- Parard, G.; Charantonis, A.; Rutgersson, A. Using satellite data to estimate partial pressure of CO2 in the Baltic Sea. J. Geophys. Res. Biogeosci. 2016, 121, 1002–1015. [Google Scholar] [CrossRef]
- Chen, S.; Hu, C.; Byrne, R.H.; Robbins, L.L.; Yang, B. Remote estimation of surface pCO2 on the West Florida Shelf. Cont. Shelf Res. 2016, 128, 10–25. [Google Scholar] [CrossRef]
- Gower, J.; King, S. Satellite Images Show the Movement of Floating Sargassum in the Gulf of Mexico and Atlantic Ocean. Nat. Preced. 2008, 1–13. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Borstad, G.; Brown, L. Detection of intense plankton blooms using the 709 nm band of the MERIS imaging spectrometer. Int. J. Remote Sens. 2005, 26, 2005–2012. [Google Scholar] [CrossRef]
- Matthews, M.W. Eutrophication and cyanobacterial blooms in South African inland waters: 10 years of MERIS observations. Remote Sens. Environ. 2014, 155, 161–177. [Google Scholar] [CrossRef]
- Attila, J.; Kauppila, P.; Kallio, K.Y.; Alasalmi, H.; Keto, V.; Bruun, E.; Koponen, S. Applicability of Earth Observation chlorophyll-a data in assessment of water status via MERIS—With implications for the use of OLCI sensors. Remote Sens. Environ. 2018, 212, 273–287. [Google Scholar] [CrossRef]
- Vilas, L.G.; Spyrakos, E.; Palenzuela, J.M.T. Neural network estimation of chlorophyll a from MERIS full resolution data for the coastal waters of Galician rias (NW Spain). Remote Sens. Environ. 2011, 115, 524–535. [Google Scholar] [CrossRef]
- Loisel, H.; Mangin, A.; Vantrepotte, V.; Dessailly, D.; Dinh, D.N.; Garnesson, P.; Ouillon, S.; Lefebvre, J.-P.; Mériaux, X.; Phan, T.M. Variability of suspended particulate matter concentration in coastal waters under the Mekong’s influence from ocean color (MERIS) remote sensing over the last decade. Remote Sens. Environ. 2014, 150, 218–230. [Google Scholar] [CrossRef]
- Kutser, T.; Verpoorter, C.; Paavel, B.; Tranvik, L.J. Estimating lake carbon fractions from remote sensing data. Remote Sens. Environ. 2015, 157, 138–146. [Google Scholar] [CrossRef]
- Kratzer, S.; Brockmann, C.; Moore, G. Using MERIS full resolution data to monitor coastal waters—A case study from Himmerfjärden, a fjord-like bay in the northwestern Baltic Sea. Remote Sens. Environ. 2008, 112, 2284–2300. [Google Scholar] [CrossRef]
- Schroeder, T.; Schaale, M.; Fischer, J. Retrieval of atmospheric and oceanic properties from MERIS measurements: A new Case-2 water processor for BEAM. Int. J. Remote Sens. 2007, 28, 5627–5632. [Google Scholar] [CrossRef]
- Olsen, A.; Brown, K.R.; Chierici, M.; Johannessen, T.; Neill, C.J. Sea-surface CO2 fugacity in the subpolar North Atlantic. Biogeosciences 2008, 5, 535–547. [Google Scholar] [CrossRef]
- Chierici, M.; Olsen, A.; Johannesen, T.; Trinañes, J.; Wanninkhof, R. Algorithms to estimate the carbon dioxide uptake in the northern North Atlantic using shipboard observations, satellite and ocean analysis data. Deep Sea Res. Part II Top. Stud. Oceanogr. 2009, 56, 630–639. [Google Scholar] [CrossRef]
- Axell, L. CMEMS Baltic Sea Physical Reanalysis Product BALTICSEA_REANALYSIS_PHY_003_011; EU Copernicus Marine Service: Toulouse, France, 2019. [Google Scholar]
- Bakker, D.C.E.; Pfeil, B.; Landa, C.S.; Metzl, N.; O’Brien, K.M.; Olsen, A.; Smith, K.; Cosca, C.; Harasawa, S.; Jones, S.D.; et al. A multi-decade record of high-quality fCO2 data in version 3 of the Surface Ocean CO2 Atlas (SOCAT). Earth Syst. Sci. Data 2016, 8, 383–413. [Google Scholar] [CrossRef]
- Rutgersson, A.; Pettersson, H.; Nilsson, E.; Bergström, H.; Wallin, M.B.; Sahlée, E.; Wu, L.E.; Mårtensson, E.M. Using land-based stations for air–sea interaction studies. Tellus A Dyn. Meteorol. Oceanogr. 2019, 72, 1–23. [Google Scholar] [CrossRef]
- Löffler, A.; Schneider, B.; Perttilä, M.; Rehder, G. Air–sea CO2 exchange in the Gulf of Bothnia, Baltic Sea. Cont. Shelf Res. 2012, 37, 46–56. [Google Scholar] [CrossRef]
- Pfeil, B.; Olsen, A.; Bakker, D.C.E.; Hankin, S.; Koyuk, H.; Kozyr, A.; Malczyk, J.; Manke, A.; Metzl, N.; Sabine, C.L.; et al. A uniform, quality controlled Surface Ocean CO2 Atlas (SOCAT). Earth Syst. Sci. Data 2013, 5, 125–143. [Google Scholar] [CrossRef]
- Schneider, B.; Kaitala, S.; Maunula, P. Identification and quantification of plankton bloom events in the Baltic Sea by continuous pCO2 and chlorophyll a measurements on a cargo ship. J. Mar. Syst. 2006, 59, 238–248. [Google Scholar] [CrossRef]
- Breiman, L. Random Forest; University of California Berkeley: Berkeley, CA, USA, 2001. [Google Scholar]
- Belgiu, M.; Drăgut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Waske, B.; Member, A.; Van Der Linden, S. Classifying Multilevel Imagery from SAR and Optical Sensors by Decision Fusion. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1457–1466. [Google Scholar] [CrossRef]
- Wolanin, A.; Camps-Valls, G.; Gómez-Chova, L.; Mateo-García, G.; Van Der Tol, C.; Zhang, Y.; Guanter, L. Estimating crop primary productivity with Sentinel-2 and Landsat 8 using machine learning methods trained with radiative transfer simulations. Remote Sens. Environ. 2019, 225, 441–457. [Google Scholar] [CrossRef]
- Wei, Z.; Meng, Y.; Zhang, W.; Peng, J.; Meng, L. Downscaling SMAP soil moisture estimation with gradient boosting decision tree regression over the Tibetan Plateau. Remote Sens. Environ. 2019, 225, 30–44. [Google Scholar] [CrossRef]
- Liu, X.; Guanter, L.; Liu, L.; Damm, A.; Malenovský, Z.; Rascher, U.; Peng, D.; Du, S.; Gastellu-Etchegorry, J.-P. Downscaling of solar-induced chlorophyll fluorescence from canopy level to photosystem level using a random forest model. Remote Sens. Environ. 2019, 231, 110772. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictions. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Breiman and Cutler’s Random Forests for Classification and Regression; R Package Version: 4.6–14. 2018. Available online: https://www.stat.berkeley.edu/~breiman/RandomForests/ (accessed on 10 November 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 10 November 2020).
- Wesslander, K. The Carbon Dioxide System in the Baltic Sea Surface Waters; University of Gotenburg: Gothenburg, Sweden, 2011. [Google Scholar]
- Bozec, Y.; Merlivat, L.; Baudoux, A.-C.; De Beaumont, L.; Blain, S.; Bucciarelli, E.; Danguy, T.; Grossteffan, E.; Guillot, A.; Guillou, J.; et al. Diurnal to inter-annual dynamics of pCO2 recorded by a CARIOCA sensor in a temperate coastal ecosystem (2003–2009). Mar. Chem. 2011, 126, 13–26. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organization and Associative Memory, 3rd ed.; Huang, T.S., Kohonen, T., Schroeder, M.R., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; London, UK; Paris, France; Tokyo, Japan; Hong Kong, China, 2001; ISBN 9783540513872. [Google Scholar]
- Landschützer, P.; Gruber, N.; Bakker, D.C.E.; Schuster, U.; Nakaoka, S.; Payne, M.R.; Sasse, T.P.; Zeng, J. A neural network-based estimate of the seasonal to inter-annual variability of the Atlantic Ocean carbon sink. Biogeosciences 2013, 10, 7793–7815. [Google Scholar] [CrossRef]
- Le Quéré, C.; Moriarty, R.; Andrew, R.M.; Canadell, J.G.; Sitch, S.; Korsbakken, J.I.; Friedlingstein, P.; Peters, G.P.; Andres, R.J.; Boden, T.A.; et al. Global Carbon Budget. Earth Syst. Sci. Data 2015, 7, 349–396. [Google Scholar] [CrossRef]
- Landschützer, P.; Laruelle, G.G.; Roobaert, A.; Regnier, P. A uniform pCO2 climatology combining open and coastal oceans. Earth Syst. Sci. Data 2020, 12, 2537–2553. [Google Scholar] [CrossRef]
- Yasunaka, S.; Siswanto, E.; Olsen, A.; Hoppema, M.; Watanabe, E.; Fransson, A.; Chierici, M.; Murata, A.; Lauvset, S.K.; Wanninkhof, R.; et al. Arctic Ocean CO2 uptake: An improved multiyear estimate of the air–sea CO2 flux incorporating chlorophyll a concentrations. Biogeosciences 2018, 15, 1643–1661. [Google Scholar] [CrossRef]
- Wehrens, R.; Kruisselbrink, J. Flexible Self-Organizing Maps in kohonen 3.0. J. Stat. Softw. 2018, 87, 1–18. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.; Wang, R.; Mo, G.; Luo, S.; Luo, X.; He, L.; Gonsamo, A.; Arabian, J.; Zhang, Y.; et al. The global distribution of leaf chlorophyll content. Remote Sens. Environ. 2020, 236, 111479. [Google Scholar] [CrossRef]
- Haapala, J.J.; Ronkainen, I.; Schmelzer, N.; Sztobryn, M. Recent Change—Sea Ice. In Second Assessment of Climate Change for the Baltic Sea Basin; Springer: Berlin/Heidelberg, Germany, 2015; pp. 145–153. [Google Scholar]
- Myrberg, K.; Andrejev, O. Main upwelling regions in the Baltic Sea—A statistical analysis based on three-dimensional modelling. Boreal Environ. Res. 2003, 8, 97–112. [Google Scholar]
- Pierson, D.C.; Kratzer, S.; Strömbeck, N.; Håkansson, B. Relationship between the attenuation of downwelling irradiance at 490 nm with the attenuation of PAR (400–700 nm) in the Baltic Sea. Remote Sens. Environ. 2008, 112, 668–680. [Google Scholar] [CrossRef]
- Stramska, M.; Stramski, D.; Mitchell, B.G.; Mobley, C.D. Estimation of the absorption and backscattering coefficients from inߚwater radiometric measurements. Limnol. Oceanogr. 2000, 45, 628–641. [Google Scholar] [CrossRef]
- Stramska, M.; Świrgoń, M. Influence of atmospheric forcing and freshwater discharge on interannual variability of the vertical diffuse attenuation coefficient at 490 nm in the Baltic Sea. Remote Sens. Environ. 2014, 140, 155–164. [Google Scholar] [CrossRef]
- Algesten, G.; Wikner, J.; Sobek, S.; Tranvik, L.J.; Jansson, M. Seasonal variation of CO2 saturation in the Gulf of Bothnia: Indications of marine net heterotrophy. Glob. Biogeochem. Cycles 2004, 18, 1–7. [Google Scholar] [CrossRef]
- Lehmann, A.D.; Myrberg, K.; Höflich, K. A statistical approach to coastal upwelling in the Baltic Sea based on the analysis of satellite data for 1990–2009. Oceanologia 2012, 54, 369–393. [Google Scholar] [CrossRef]
- Lips, I.; Lips, U.; Liblik, T. Consequences of coastal upwelling events on physical and chemical patterns in the central Gulf of Finland (Baltic Sea). Cont. Shelf Res. 2009, 29, 1836–1847. [Google Scholar] [CrossRef]
- Wesslander, K.; Omstedt, A.; Schneider, B. Inter-annual and seasonal variations in the air–sea CO2 balance in the central Baltic Sea and the Kattegat. Cont. Shelf Res. 2010, 30, 1511–1521. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).