Assessment of BRDF Impact on VIIRS DNB from Observed Top-of-Atmosphere Reflectance over Dome C in Nighttime
Abstract
:1. Introduction
2. Data and Models
2.1. VIIRS DNB
2.2. Ground Measured Surface Reflectance
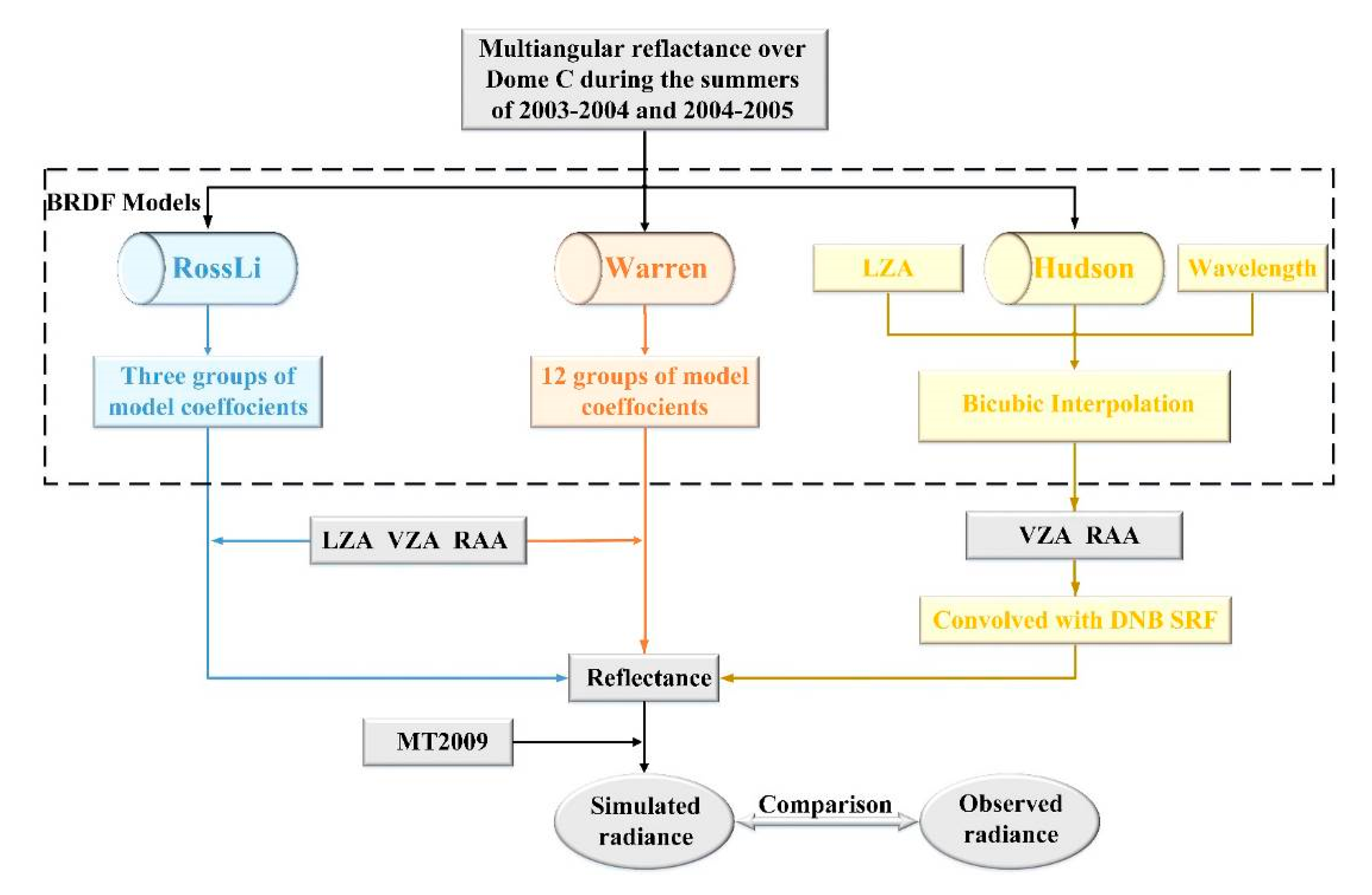
2.3. BRDF Models
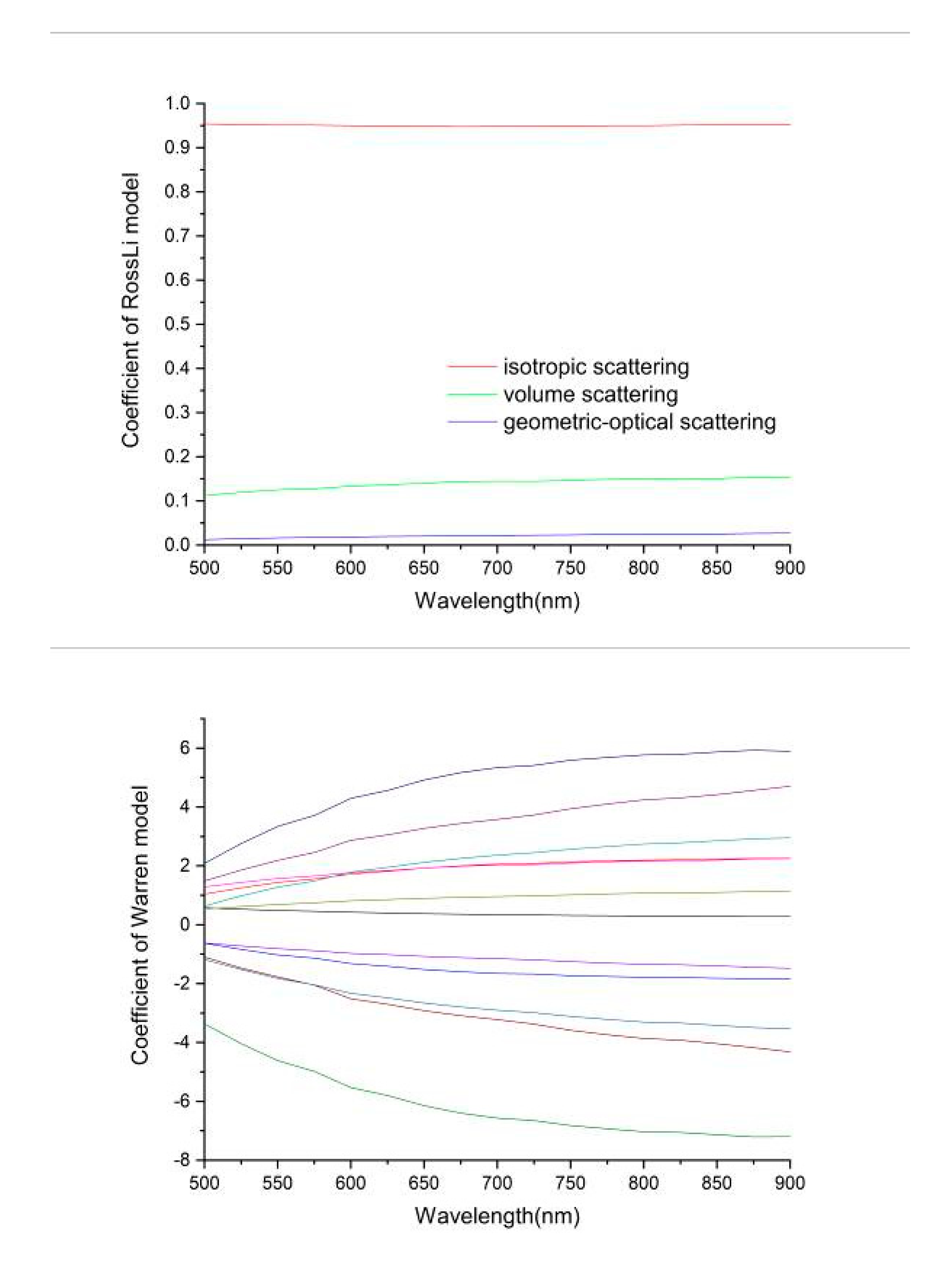
2.3.1. RossLi BRDF Model
2.3.2. Warren Model
2.3.3. Hudson Model
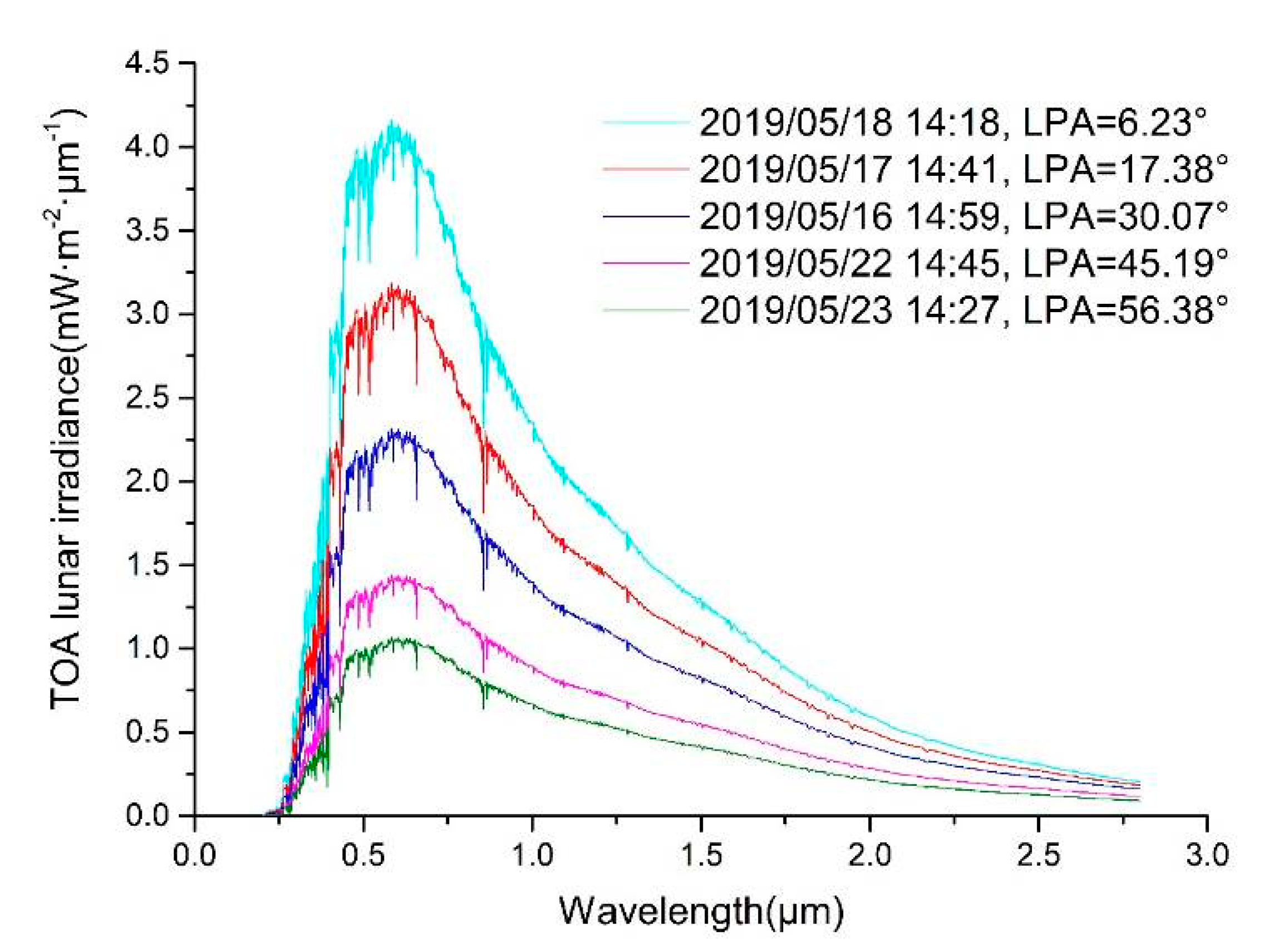
2.4. Lunar Irradiance Model
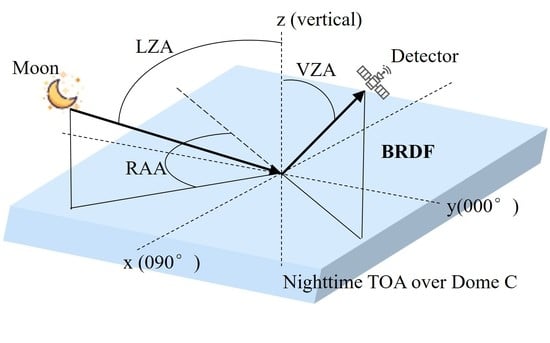
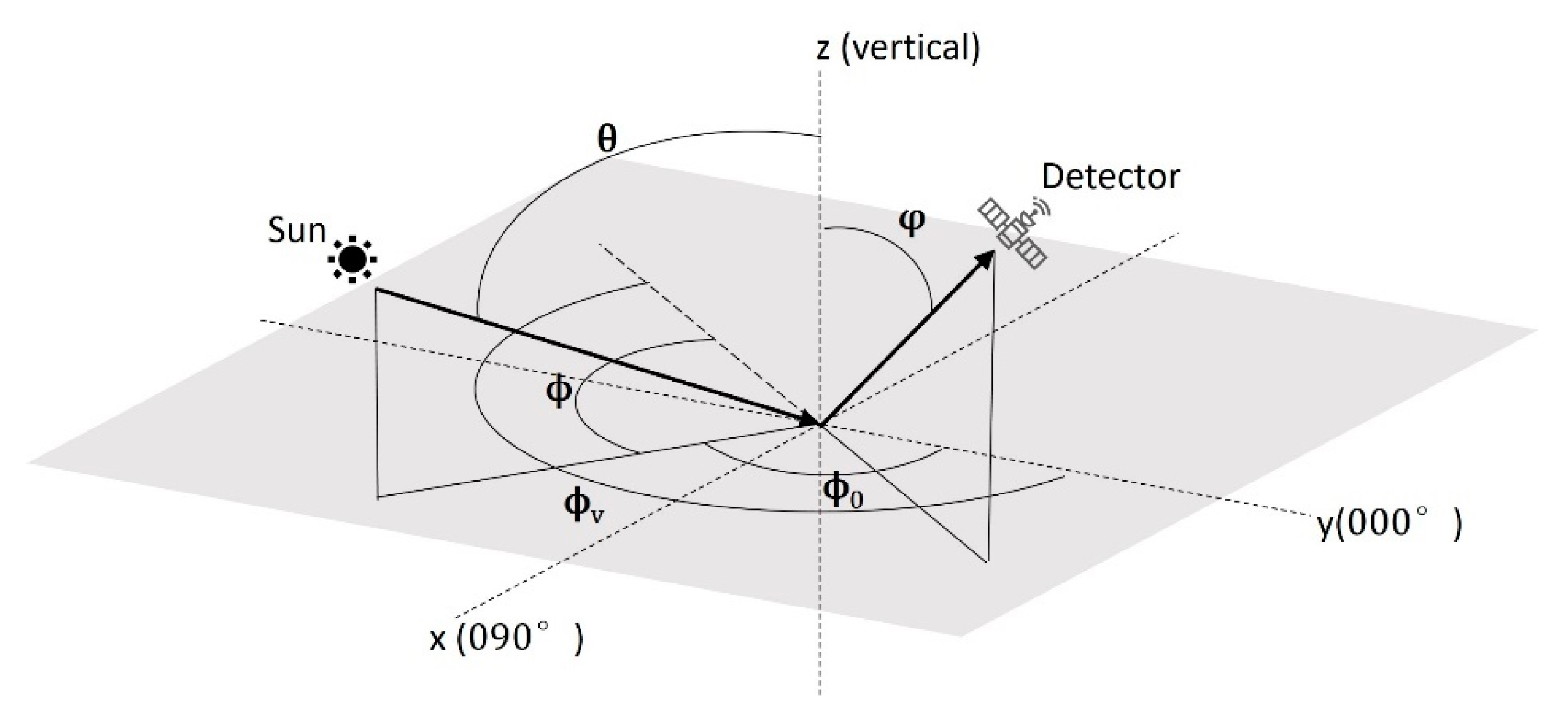
3. Methodology and Study Area
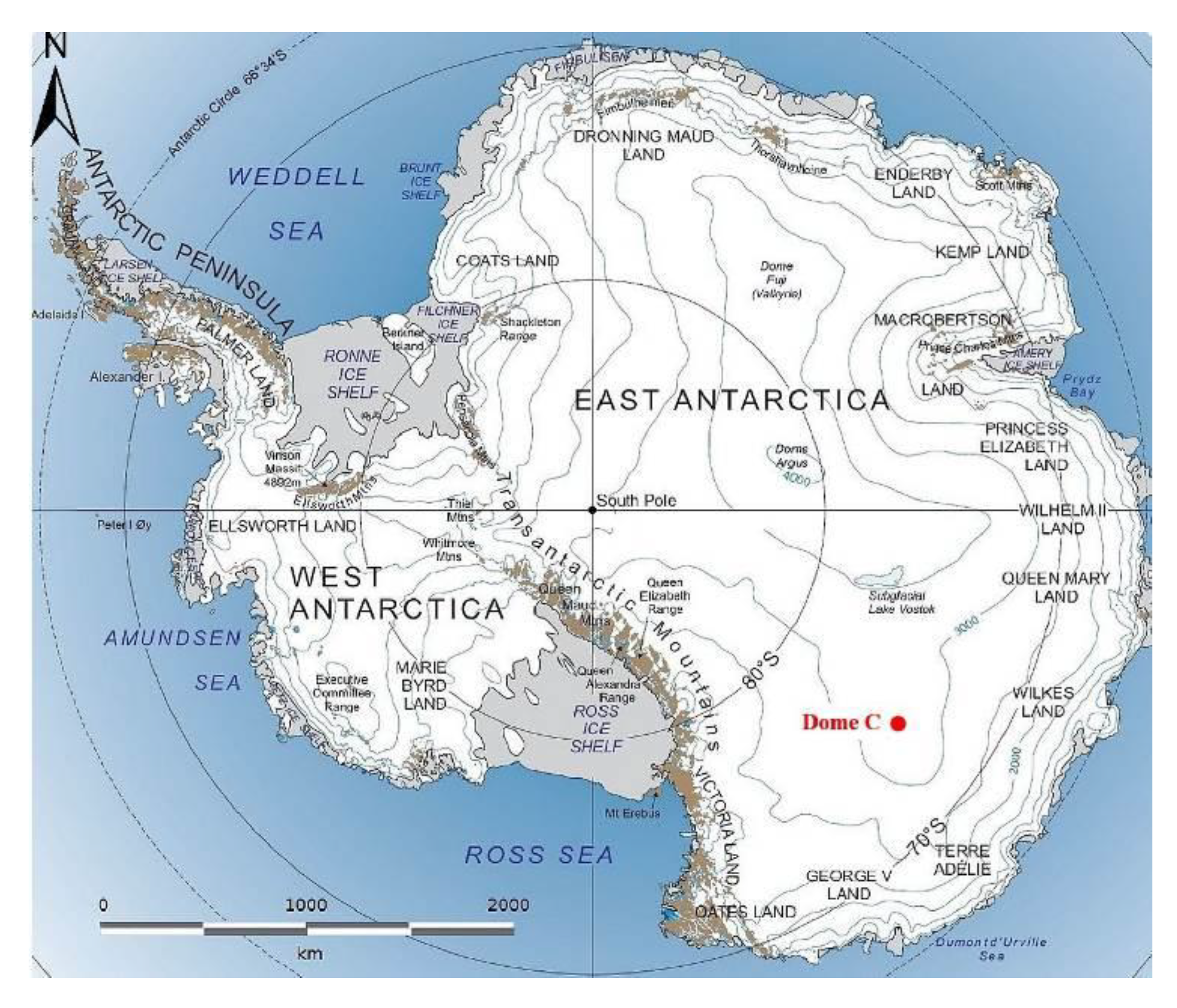
3.1. Study Area
3.2. Selection of Observations
- (1)
- (2)
- LPA is less than 90° to ensure sufficient moonlight.
- (3)
- LZA is less than 75° to ensure sufficient moonlight, too.
- (4)
- SZA is greater than 118.4°, to remove the influences of stray-light effects present at Dome C, during the observations [21].
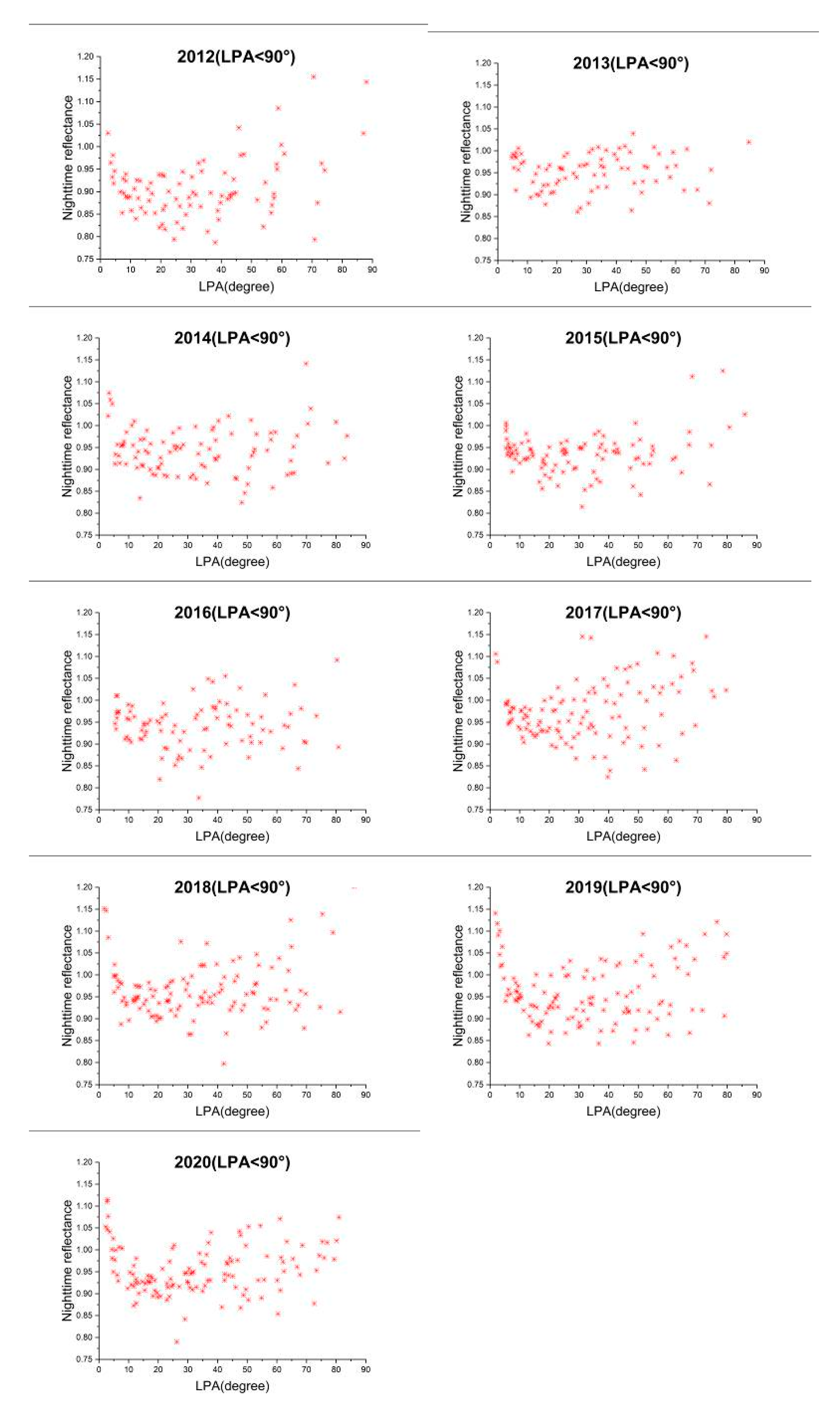
3.3. Further Data Filtering According to LPA
3.4. Data Processing
4. Results and Discussion
4.1. The Impact of Multiple Angles on Nighttime TOA Reflectance
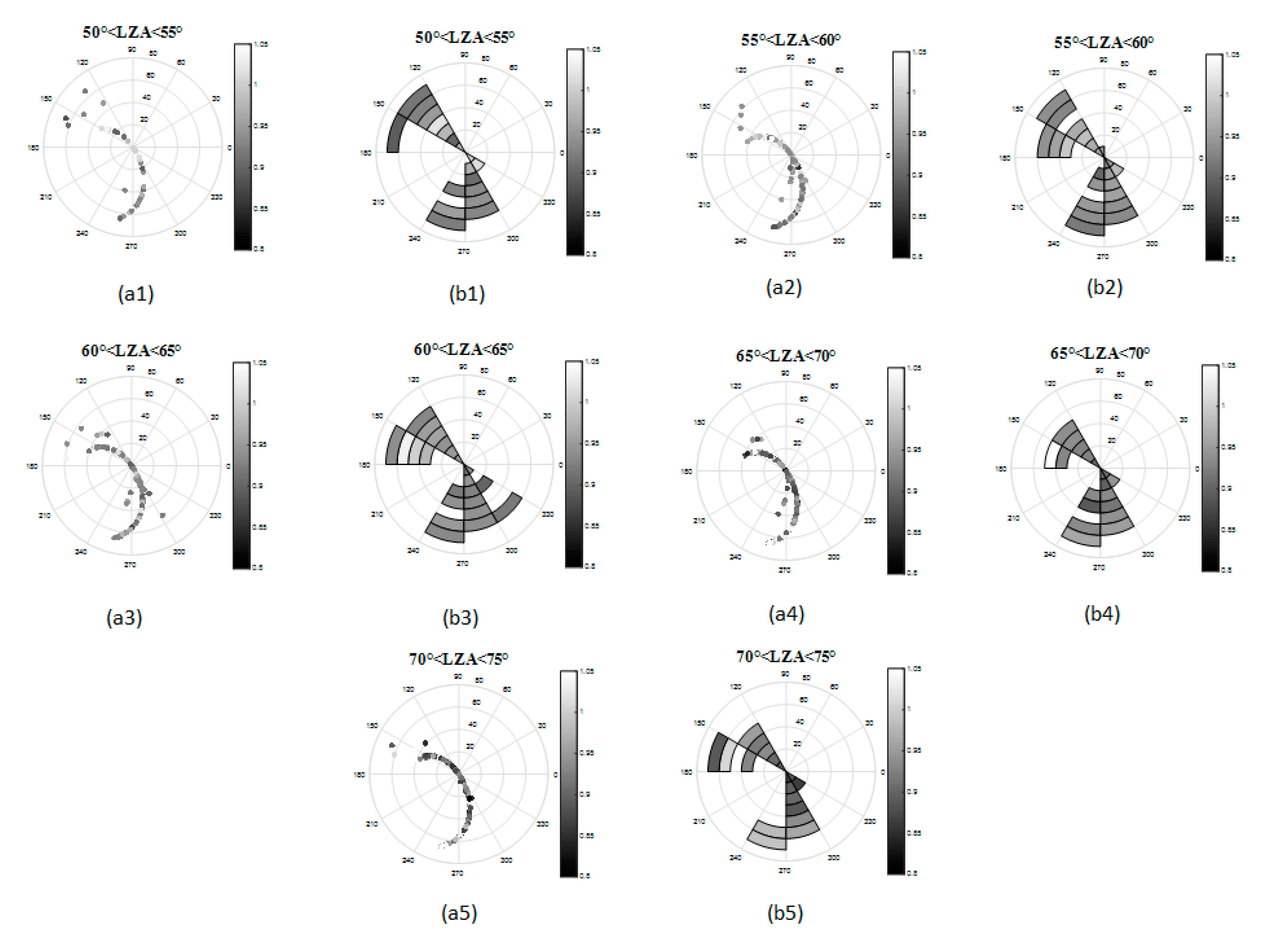
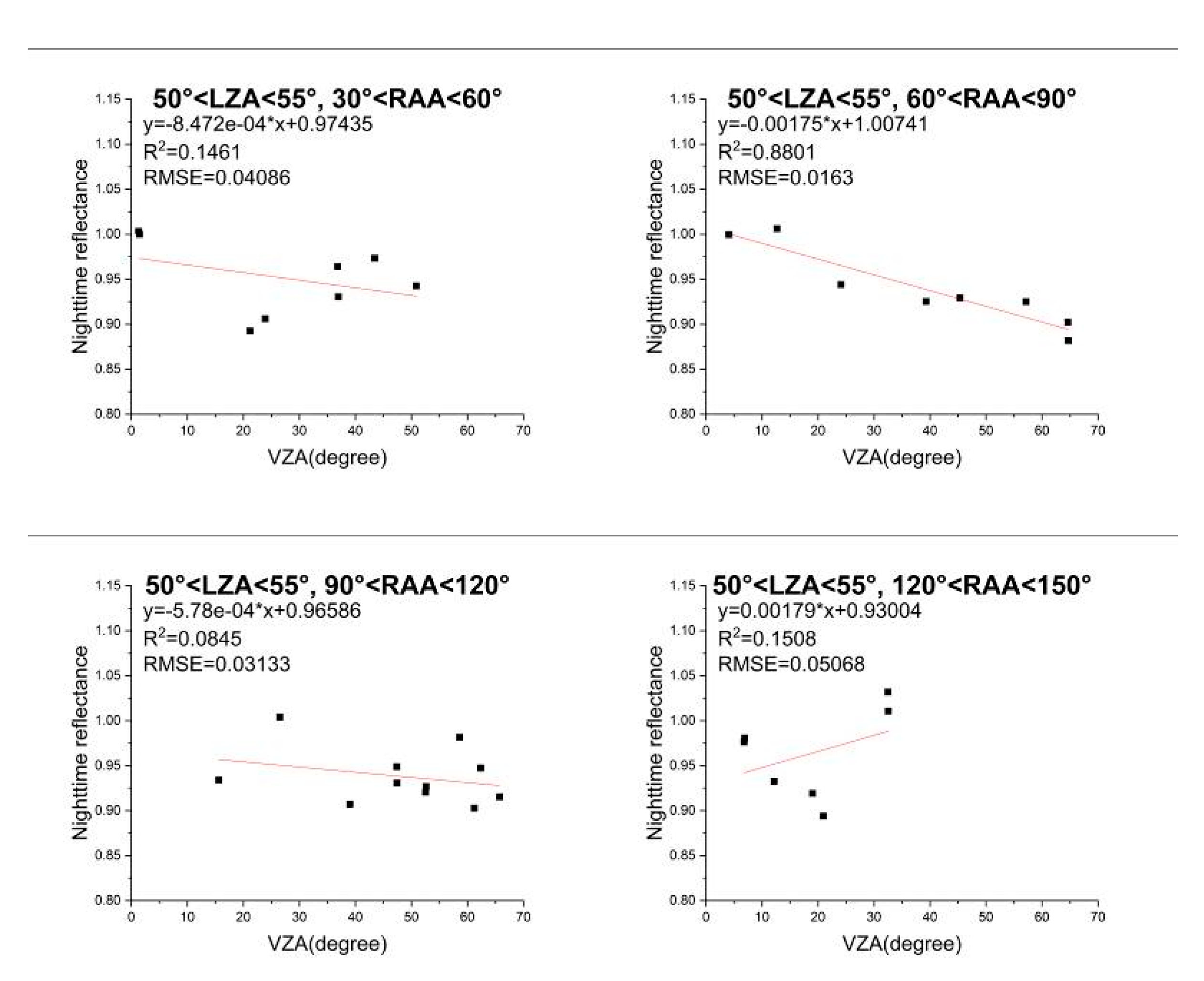
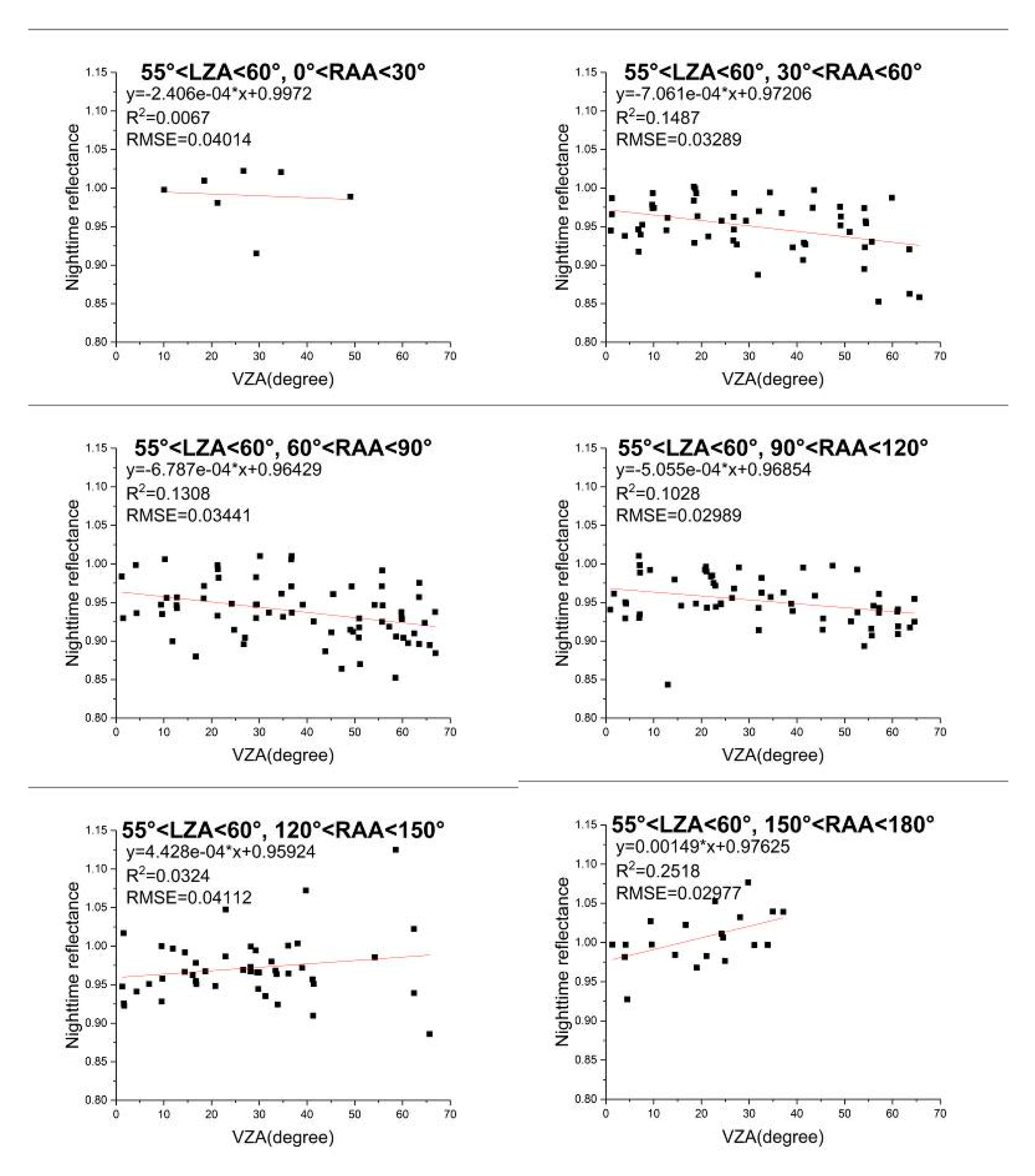
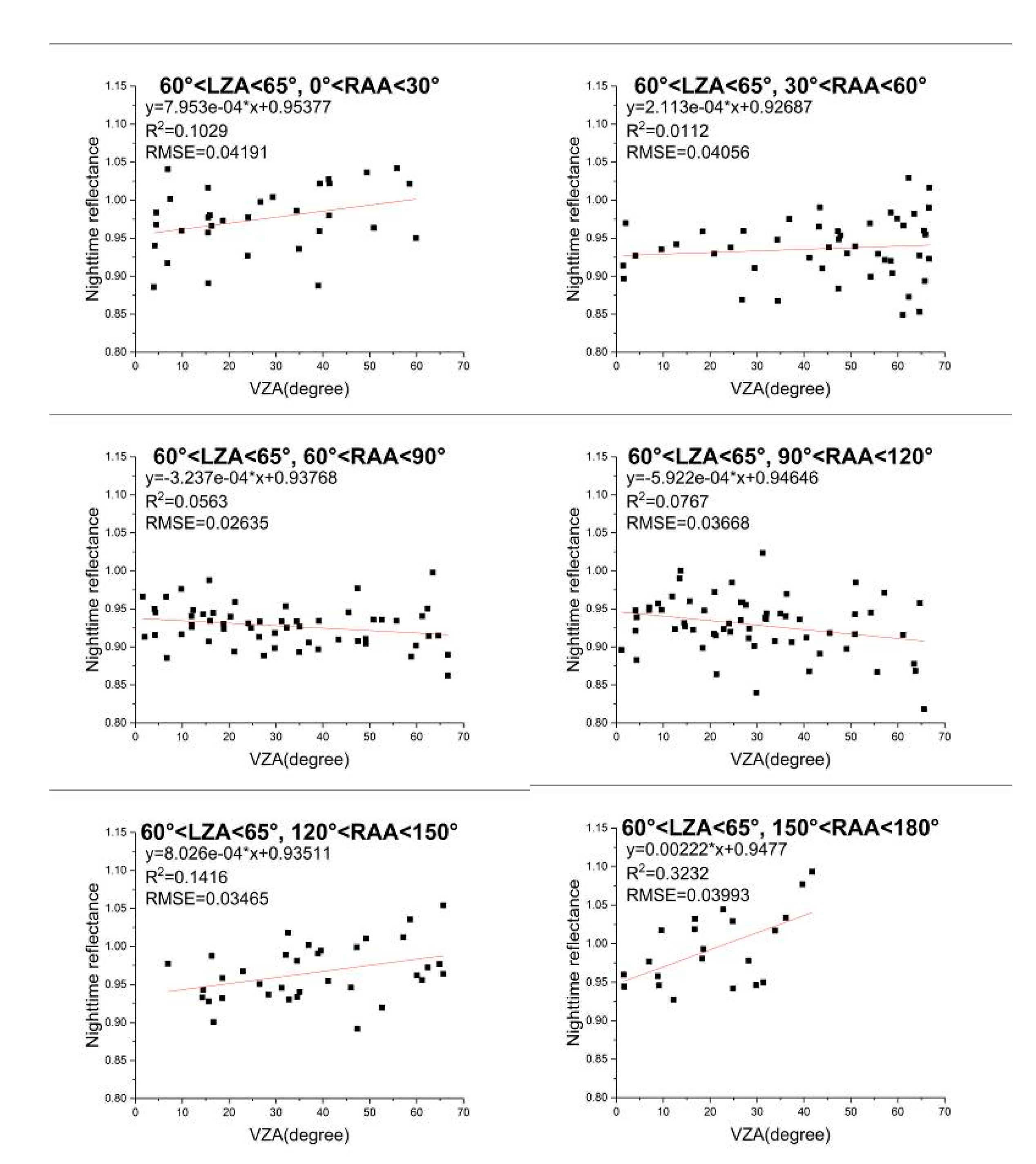
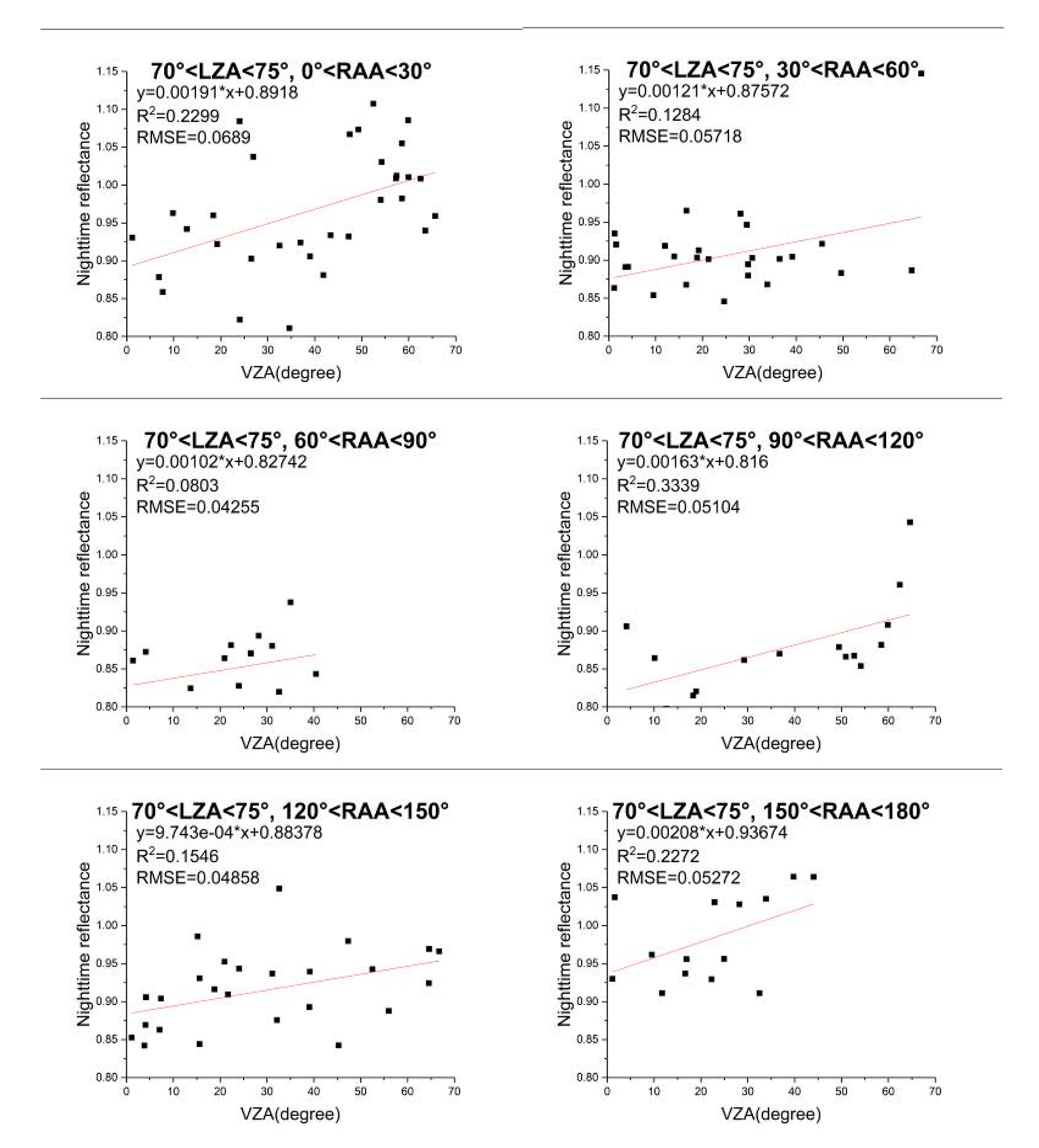
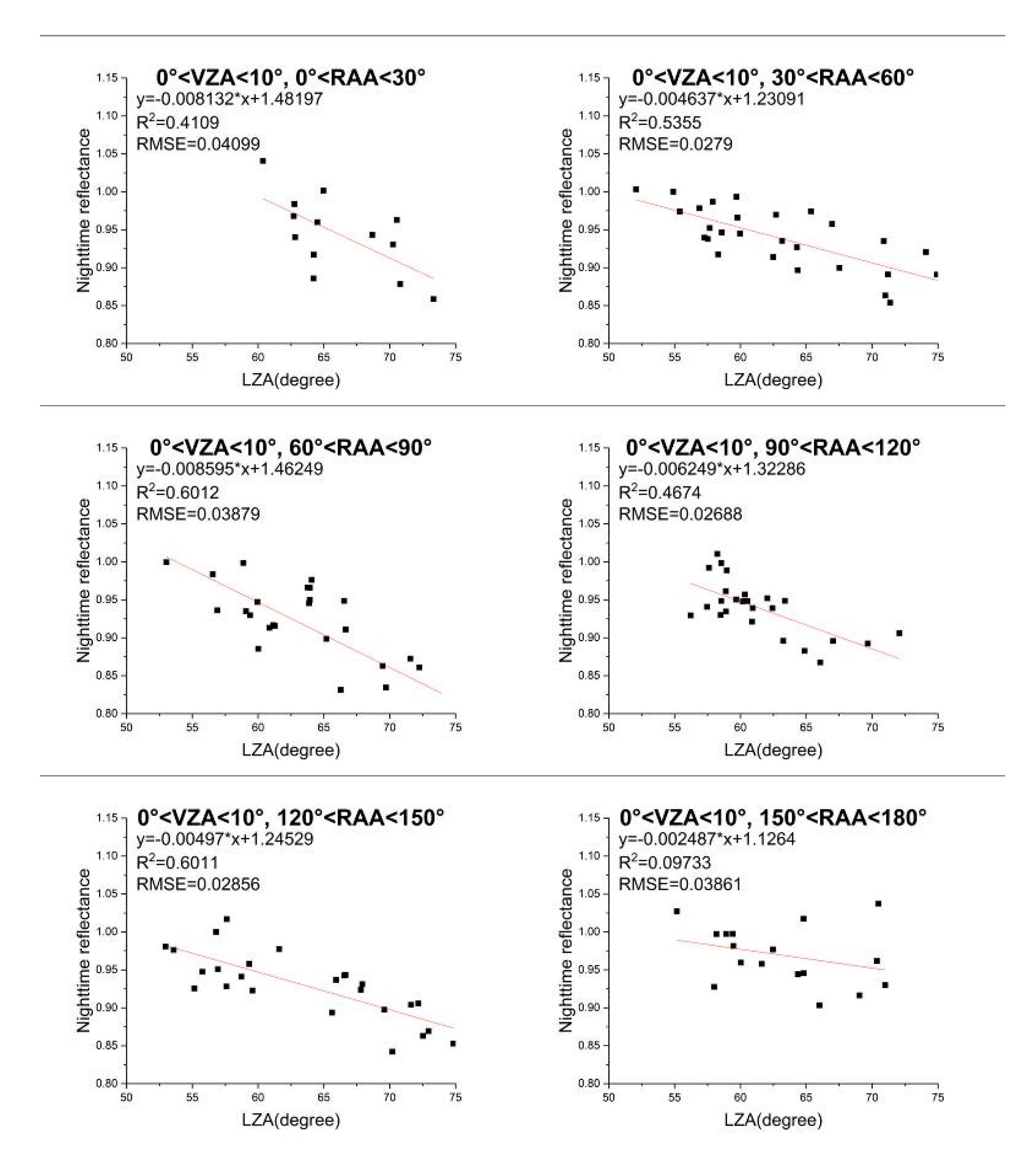
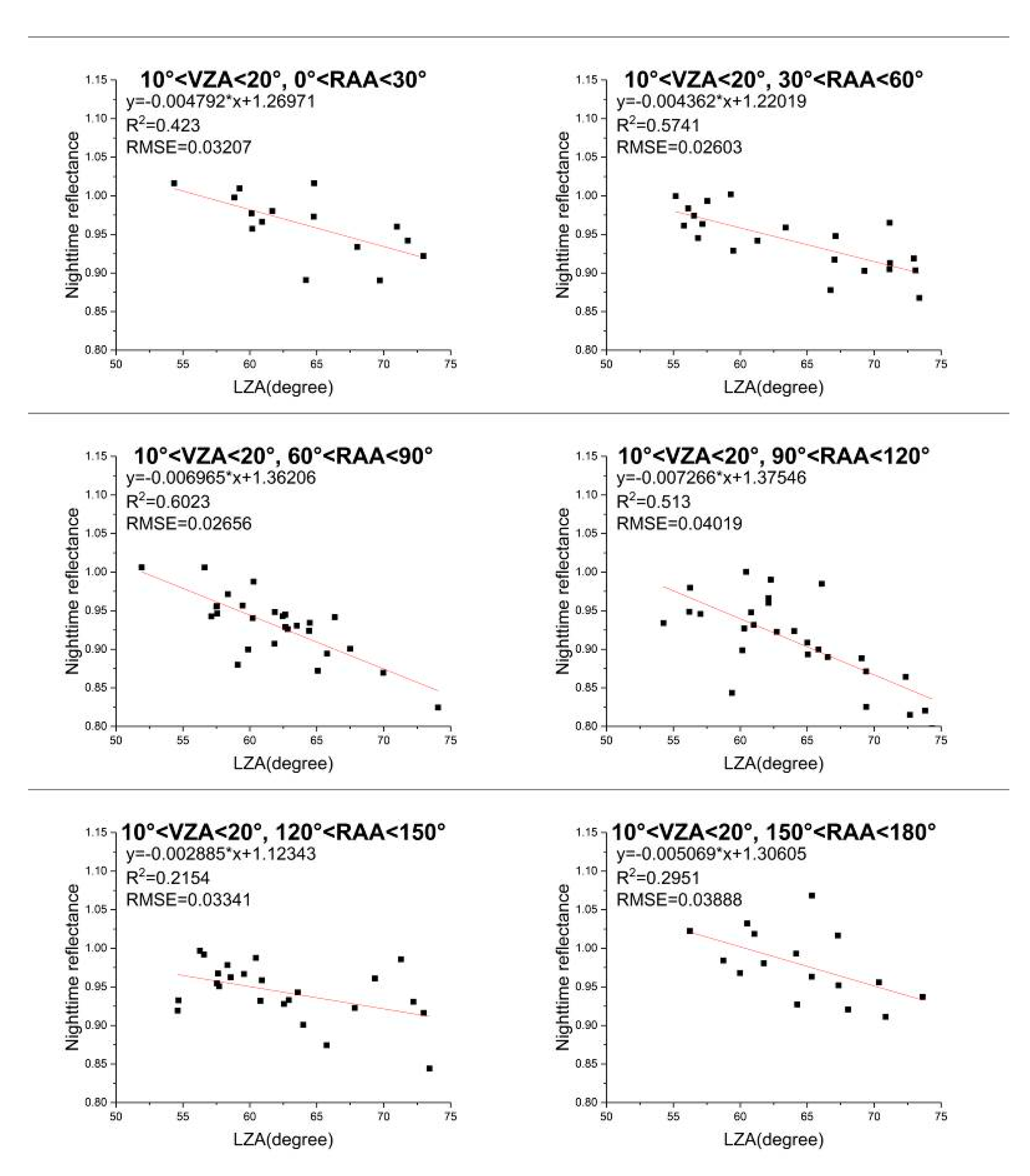
4.1.1. Impact of VZA on Nighttime TOA Reflectance
- (1)
- When LZA is less than 65°, especially when the RAA approaches 90°, the reflectance tends to decrease with the increase of VZA, which is consistent with the finding in Shao et al. [47] and Qiu et al. [49]. At 55°–60° of the LZA, the average of the slopes of linear fitting is the smallest, which means that the reflectance is relatively the most stable and little affected by the VZA.
- (2)
- When LZA is higher than 65°, the reflectance increases with the increase of VZA. Generally, the variation is more sharply at 70°–75°, so the effect of VZA reaches the most.
- (3)
- In each group divided by LZA, the value of the slope tends to decrease at first and drops to the minimum when the RAA approaches 90°. It then increases with the increase of RAA. Besides, the maximum slope in each group always corresponds to the maximum RAA.
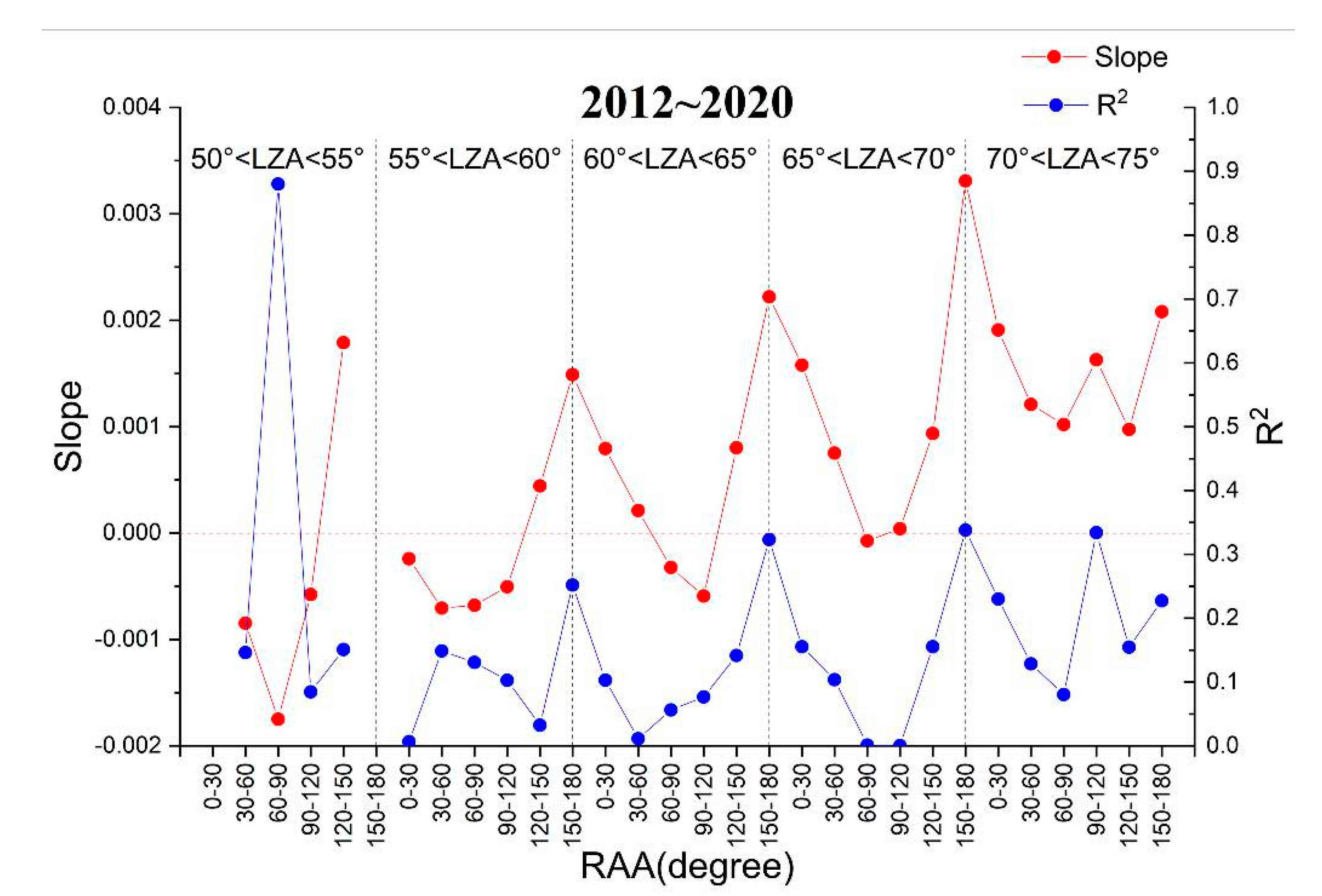
4.1.2. Impact of LZA on Nighttime TOA Reflectance
- (1)
- Only when the VZA is in 50°–60° and RAA is less than 30°, and VZA is in 60°–70° and RAA is in 30°–120°, the nighttime TOA reflectance is positively correlated with the LZA. In other cases, the reflectance is negatively correlated with the LZA.
- (2)
- On the whole, as the absolute value of the slope decreases, the correlation coefficient tends to decrease.
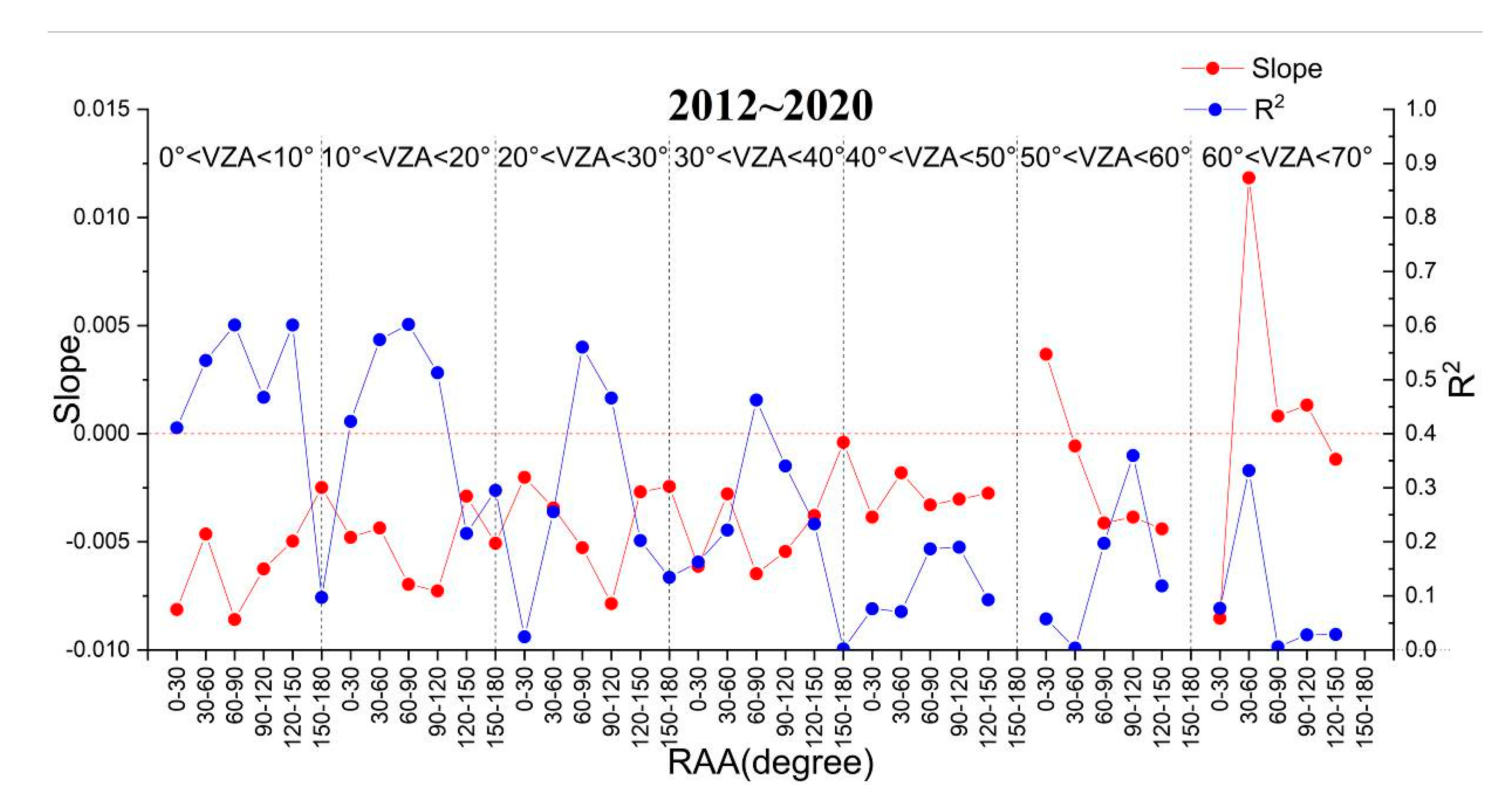
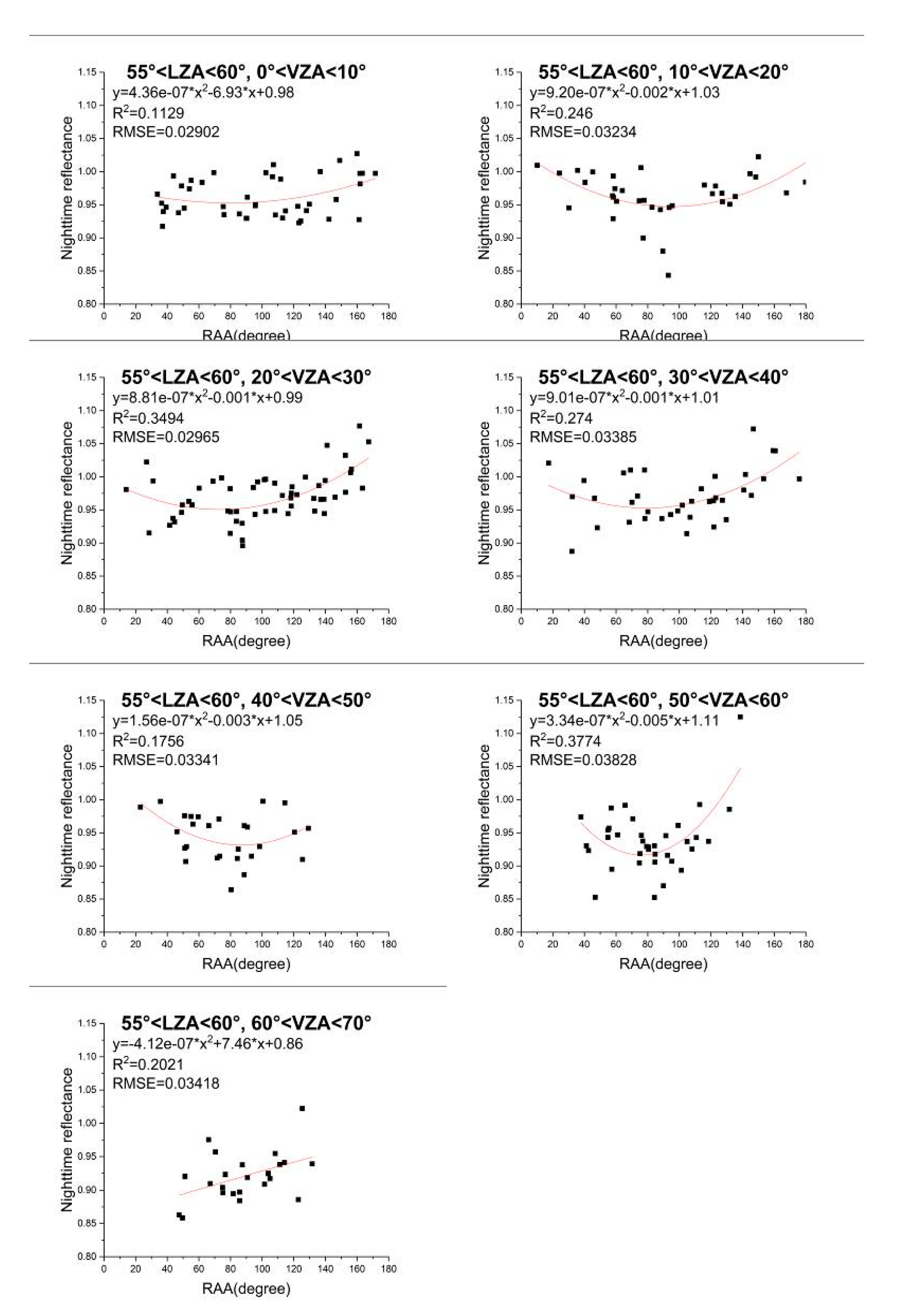
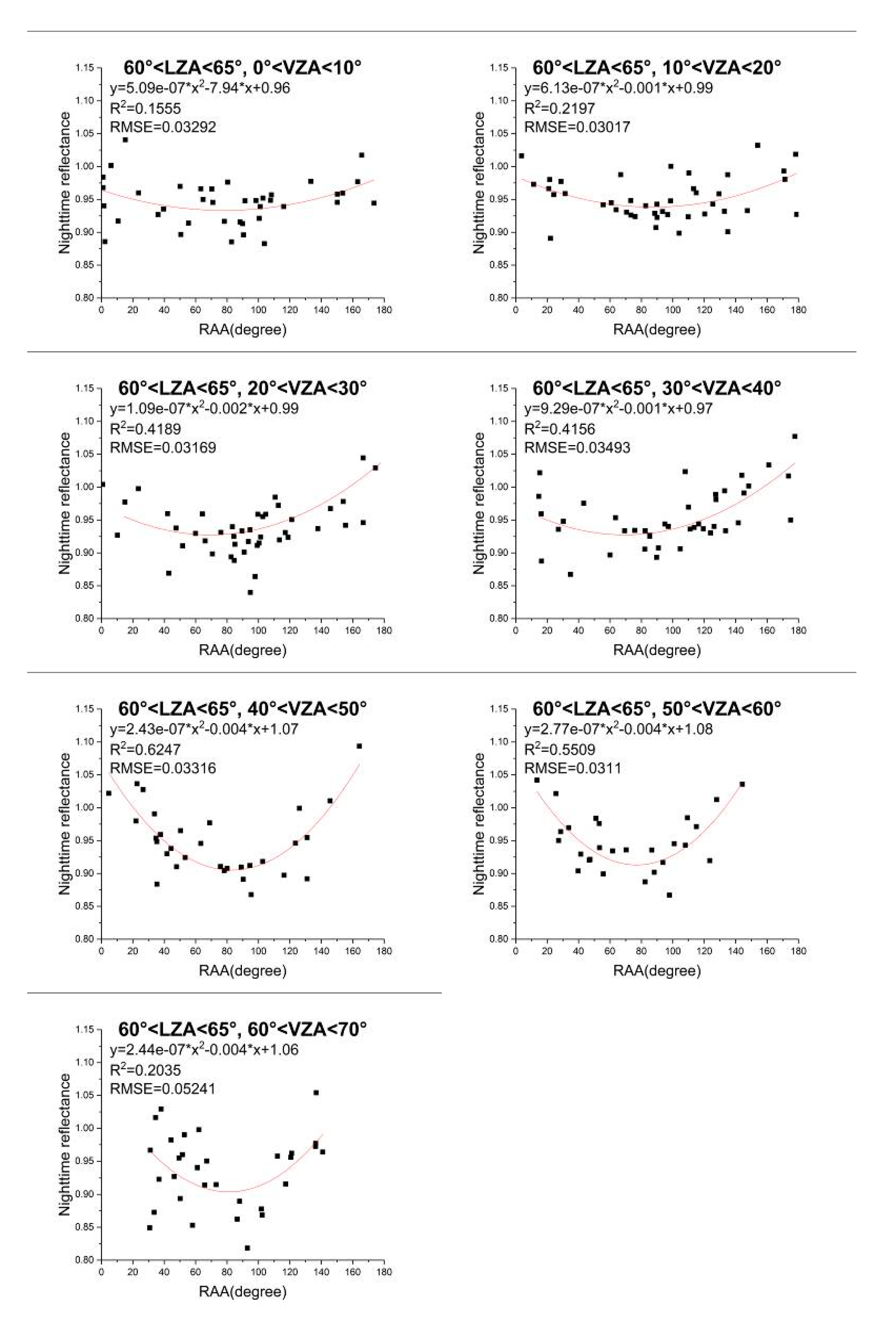
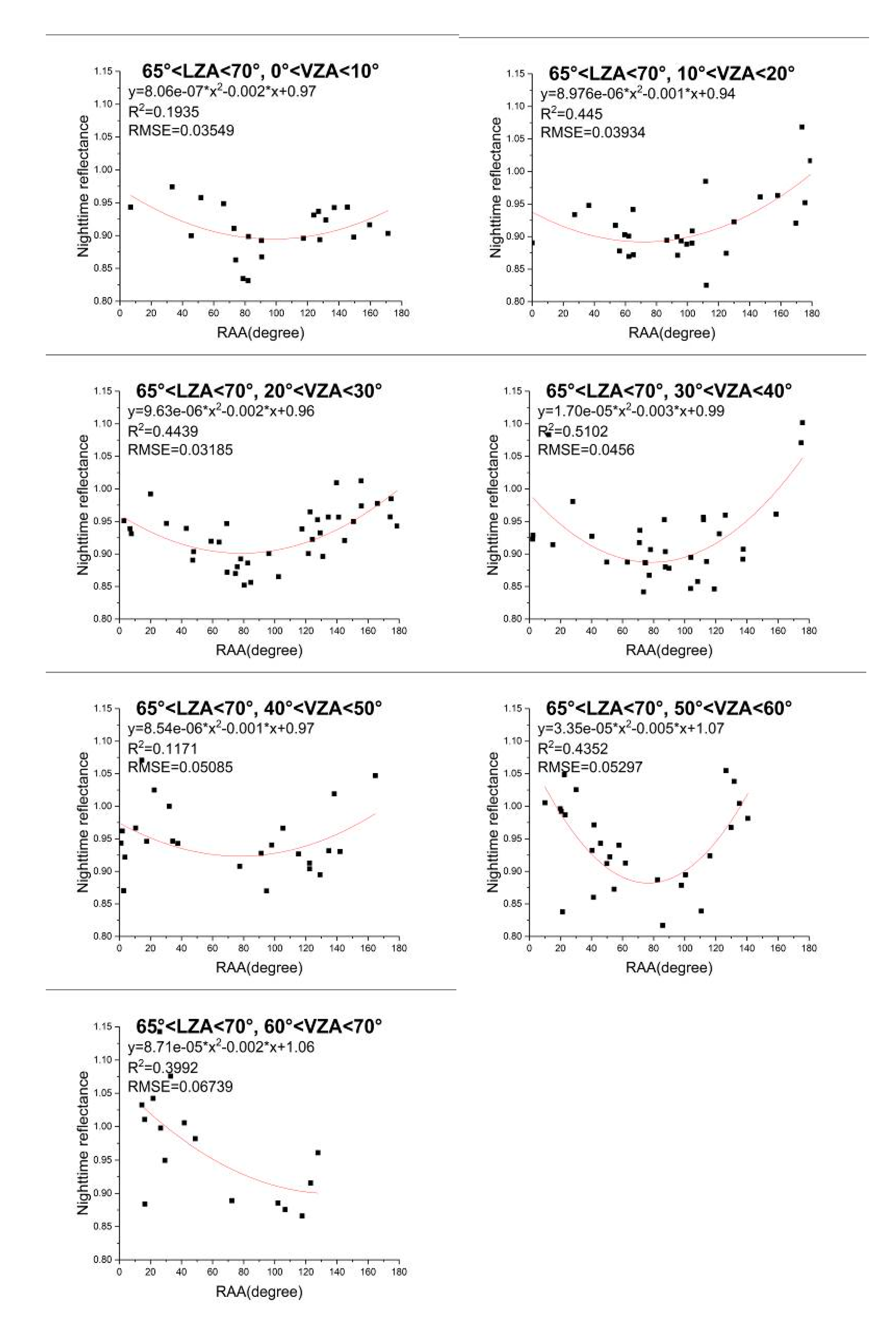
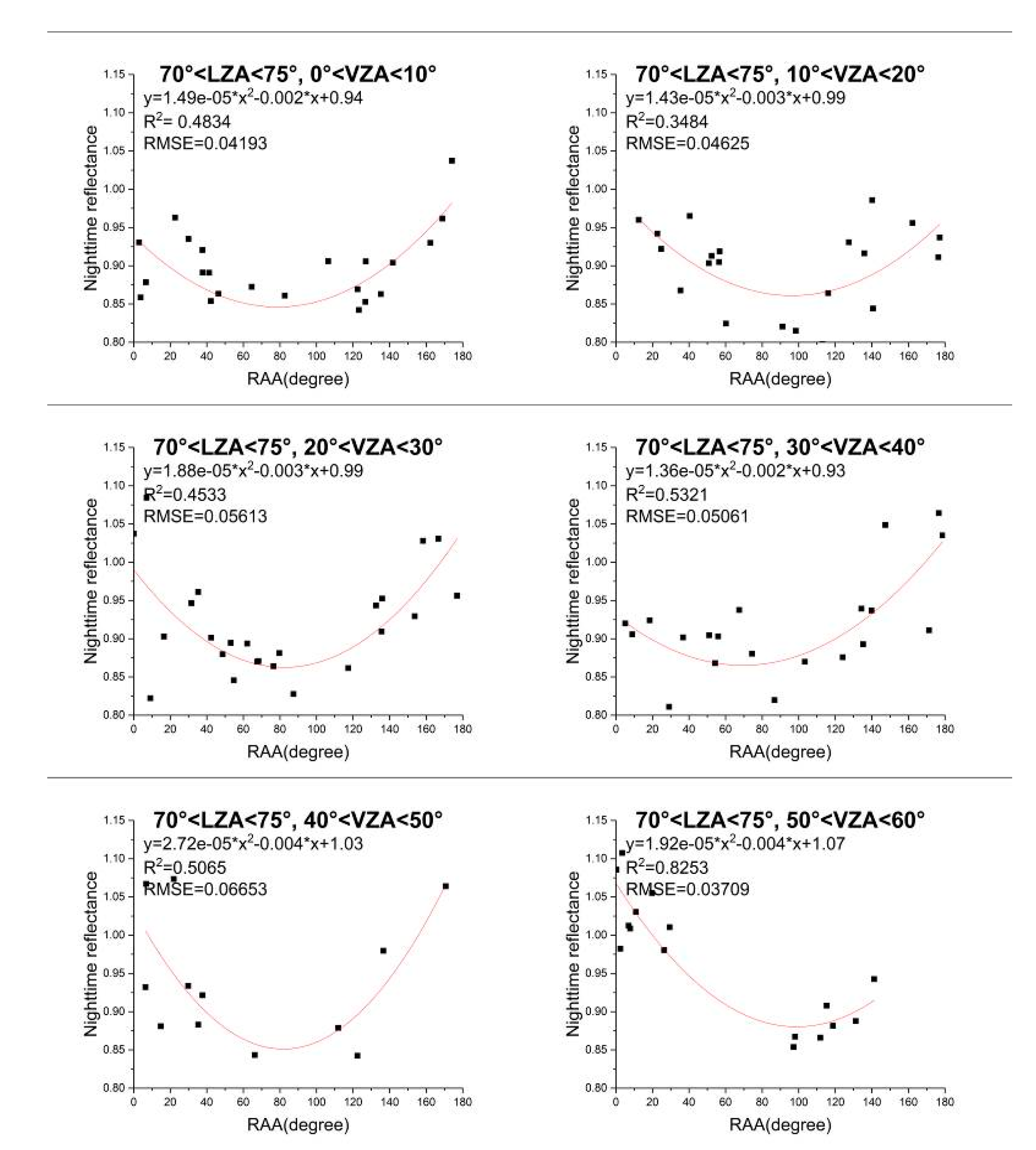
4.1.3. Impact of RAA on Nighttime TOA Reflectance
- (1)
- (2)
- The forward scattering (RAA = 180°) and backward scattering (RAA = 0°) are not symmetric at night, according to the distribution of reflectance with RAA.
- (3)
- The fitting effect of quadratic polynomial on the relation between reflectance and RAA is relatively better. The correlation coefficient of the polynomial fitting is between 0.1129 and 0.8263.
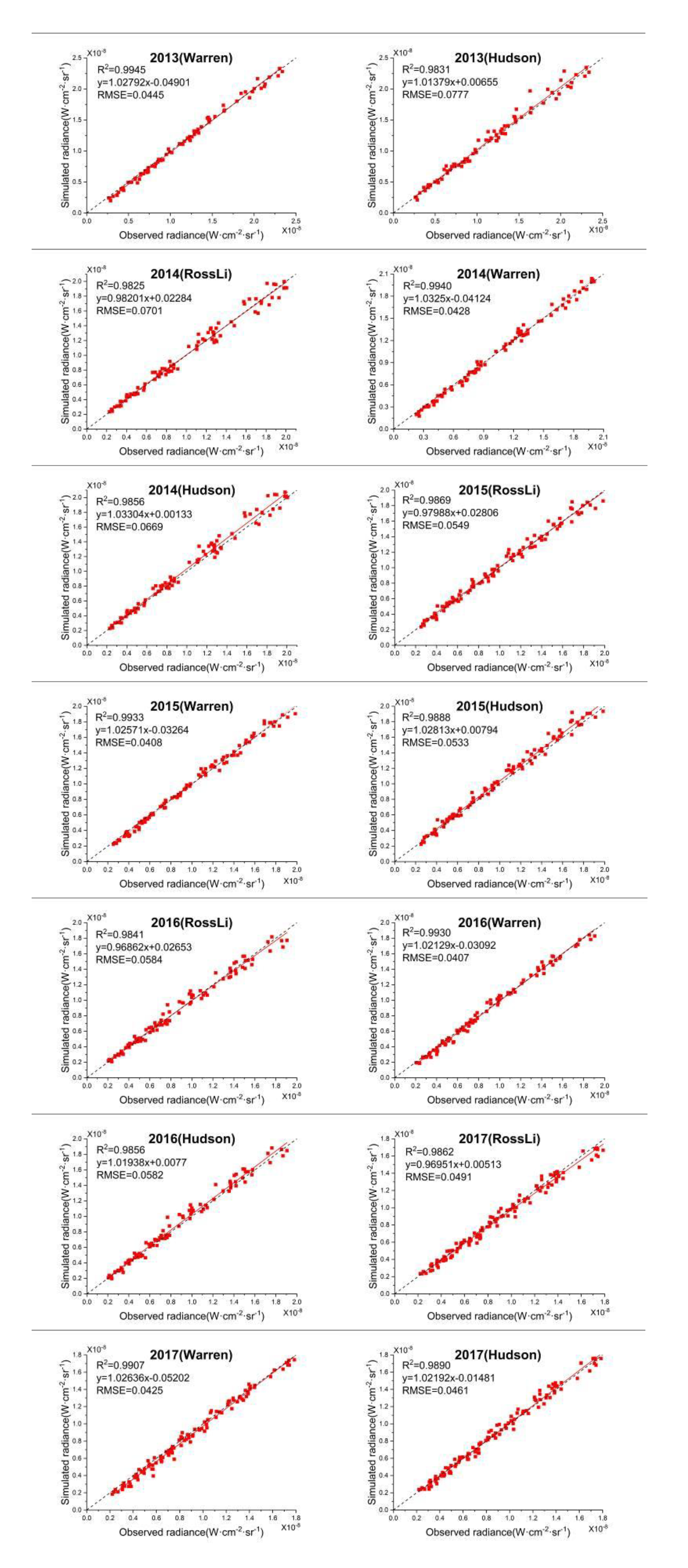
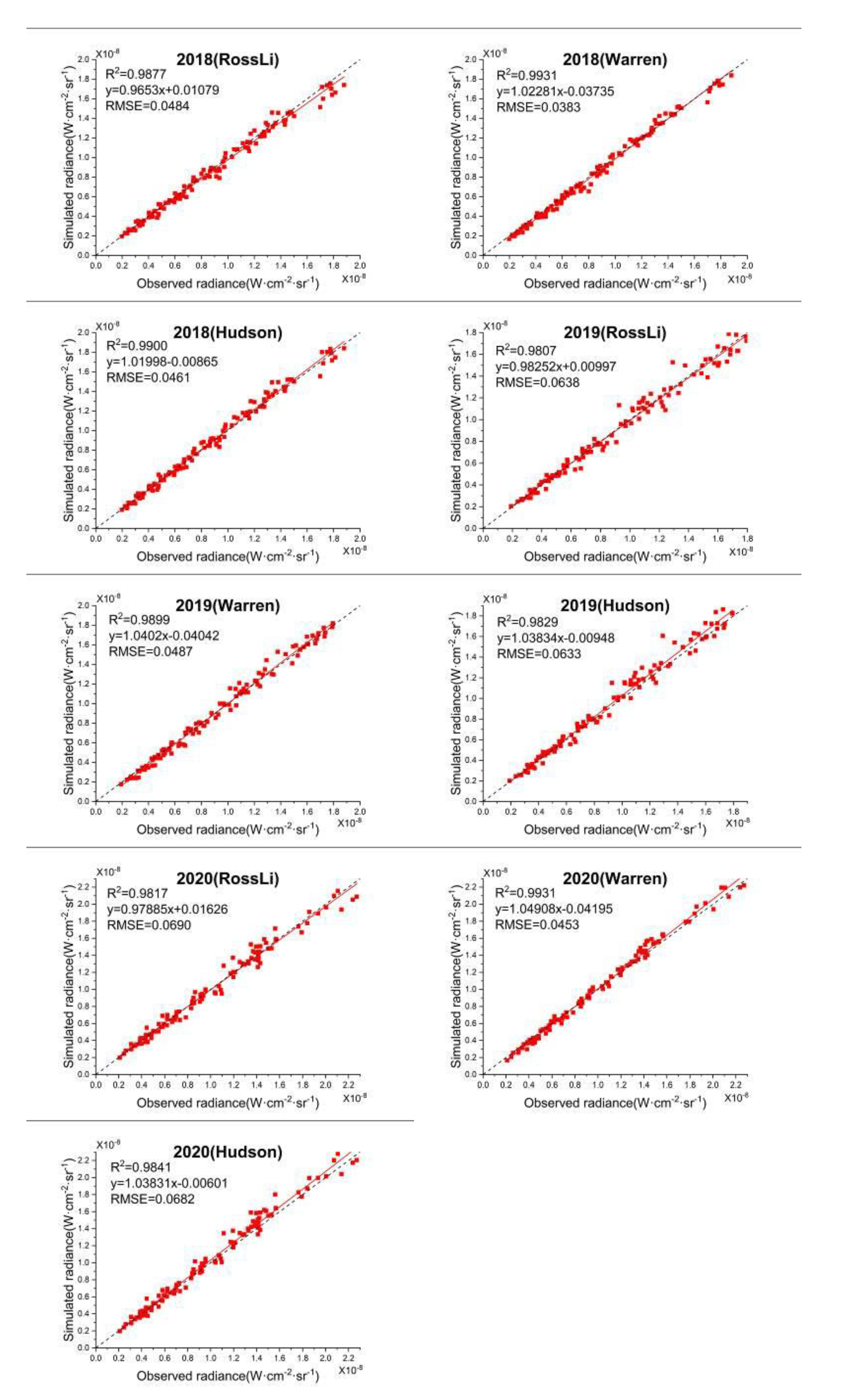
4.2. Application of Three BRDF Model at Nighttime TOA
- (1)
- In Figure 23, the simulated nighttime radiance at satellite using BRDF models and the observed radiance agrees well. Almost all the results are located along the 1:1 line and show high consistency with a correlation coefficient of greater than 0.9723 and an RMSE of less than 0.0799 W⋅cm−2⋅sr−1.
- (2)
- In Figure 23, the correlation of the simulated radiance and the observed has a decreasing tendency with the increase of radiance value, especially in the results of the RossLi BRDF model and Hudson model.
- (3)
- The correlation coefficients, in descending order, each year, are Warren>Hudson>RossLi. The RMSEs, in ascending order, each year, are Warren<Hudson<RossLi. The reason why the applicability of RossLi BRDF model is lower than the other two models may be that the accuracy of RossLi BRDF model is reduced under a large zenith angle [23].
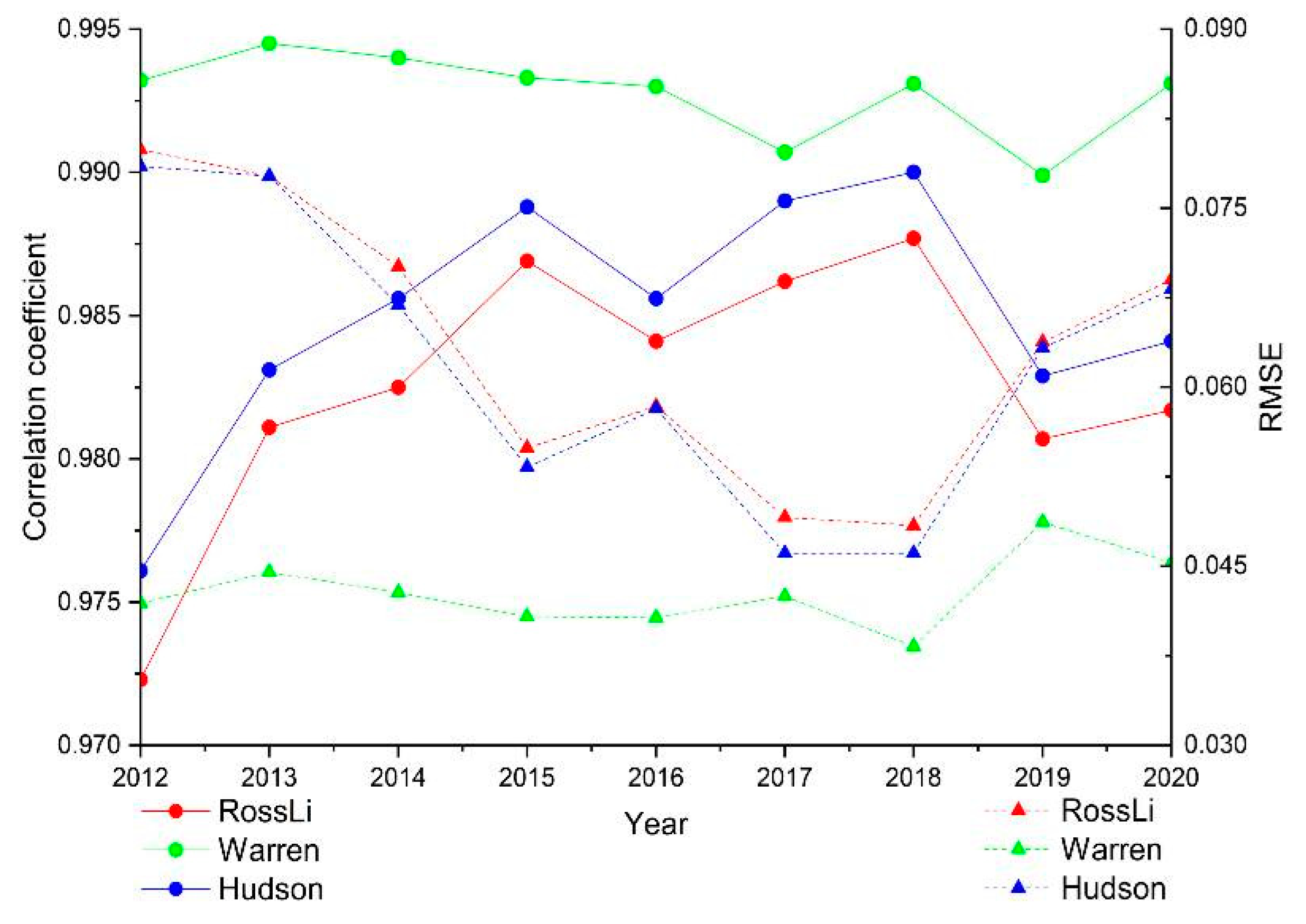
- (4)
- During the nine years, as shown in Figure 24, the RossLi BRDF model and Hudson model have kept a good consistency. Thus, these two models may have similar effects in the description of the nighttime TOA over Dome C.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liao, L.; Weiss, S.; Mills, S.; Hauss, B. Suomi NPP VIIRS day-night band on-orbit performance. J. Geophys. Res. Atmos. 2013, 118, 12705–12718. [Google Scholar] [CrossRef]
- Lee, S.; McIntire, J.; Oudrari, H.; Schwarting, T.; Xiong, X. A New Method for Suomi-NPP VIIRS Day–Night Band on-Orbit Radiometric Calibration. IEEE Trans. Geosci. Remote Sens. 2015, 53, 324–334. [Google Scholar] [CrossRef]
- Lee, S.; Chiang, K.; Xiong, X.; Sun, C.; Anderson, S. The S-NPP VIIRS Day-Night Band On-Orbit Calibration/Characterization and Current State of SDR Products. Remote Sens. 2014, 6, 12427–12446. [Google Scholar] [CrossRef] [Green Version]
- Mills, S.; Weiss, S.; Liang, C. VIIRS day/night band (DNB) stray light characterization and correction. Proc. SPIE 2013, 8866, 1–18. [Google Scholar] [CrossRef]
- Ma, S.; Yan, W.; Huang, Y.; Ai, W.; Zhao, X. Vicarious calibration of S-NPP/VIIRS day–night band using deep convective clouds. Remote Sens. Environ. 2014, 158, 42–55. [Google Scholar] [CrossRef]
- Cao, C.; Bai, Y.; Wang, W.; Choi, T. Radiometric Inter-Consistency of VIIRS DNB on Suomi NPP and NOAA-20 from Observations of Reflected Lunar Lights over Deep Convective Clouds. Remote Sens. 2019, 11, 934. [Google Scholar] [CrossRef] [Green Version]
- Román, M.O.; Wang, Z.; Sun, Q.; Kalb, V.; Miller, S.D.; Molthan, A.; Schultz, L.; Bell, J.; Stokes, E.C.; Pandey, B.; et al. NASA’s Black Marble nighttime lights product suite. Remote Sens. Environ. 2018, 210, 113–143. [Google Scholar] [CrossRef]
- Roujean, J.; Leroy, M.; Deschamps, P. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Ni, W.; Li, X. A Coupled Vegetation–Soil Bidirectional Reflectance Model for a Semiarid Landscape. Remote Sens. Environ. 2000, 74, 113–124. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Bréon, F. Towards a Generalized Approach for Correction of the BRDF Effect in MODIS Directional Reflectances. IEEE Trans. Geosci. Remote Sens. 2009, 47, 898–980. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Henebry, J.; Gao, F. Development and evaluation of a new algorithm for detecting 30 m land surface phenology from VIIRS and HLS time series. ISPRS J. Photogramm. 2020, 161, 37–51. [Google Scholar] [CrossRef]
- Li, C.; Xue, Y.; Liu, Q.; Ouazzane, K.; Zhang, J. Using SeaWiFS Measurements to Evaluate Radiometric Stability of Pseudo-Invariant Calibration Sites at Top of Atmosphere. IEEE Geosci. Remote. Sens. Lett. 2015, 12, 125–129. [Google Scholar] [CrossRef]
- Doherty, S.; Warren, S. The Antarctic and Greenland snow surfaces as calibration targets for the visible channel of the Advanced Very High Resolution Radiometer. Proc. IEEE Int. Geosci. Remote Sens. Symp. 1998, 4, 2267–2269. [Google Scholar] [CrossRef]
- Jiao, Z.; Ding, A.; Kokhanovsky, A.; Schaaf, C.; Bréon, F.; Dong, Y.; Wang, Z.; Liu, Y.; Zhang, X.; Yin, S.; et al. Development of a snow kernel to better model the anisotropic reflectance of pure snow in a kernel-driven BRDF model framework. Remote Sens. Environ. 2019, 221, 189–209. [Google Scholar] [CrossRef]
- Walther, A.; Heidinger, A.; Miller, S. The expected performance of cloud optical and microphysical properties derived from Suomi NPP VIIRS day/night band lunar reflectance. J. Geophys. Res. Atmos. 2013, 118, 13230–13240. [Google Scholar] [CrossRef]
- Cao, C.; Uprety, S.; Xiong, J.; Wu, A.; Jing, P.; Smith, D.; Chander, G.; Fox, N.; Ungar, S. Establishing the Antarctic Dome C community reference standard site towards consistent measurements from Earth observation satellites. Can. J. Remote Sens. 2014, 36, 498–513. [Google Scholar] [CrossRef]
- Chen, X.; Wu, A.; Xiong, X.; Lei, N.; Wang, Z.; Chiang, K. Using Ground Targets to Validate S-NPP VIIRS Day-Night Band Calibration. Remote Sens. 2016, 8, 984. [Google Scholar] [CrossRef] [Green Version]
- Warren, S.; Brandt, R.; Hinton, P. Effect of surface roughness on bidirectional reflectance of Antarctic snow. J. Geophys. Res. 1998, 103, 25789–25807. [Google Scholar] [CrossRef]
- Hudson, S.; Warren, S.; Brandt, R.; Grenfell, T.; Six, D. Spectral bidirectional reflectance of Antarctic snow: Measurements and parameterization. J. Geophys. Res. 2006, 111, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Baker, N. Joint Polar Satellite System (JPSS) VIIRS Radiometric Calibration Algorithm Theoretical Basis Document (ATBD), Revision C; Goddard Space Flight Center: Greenbelt, MD, USA, 2013. [Google Scholar]
- Qiu, S.; Shao, X.; Cao, C.; Uprety, S.; Wang, W. Assessment of straylight correction performance for the VIIRS Day/Night Band using Dome-C and Greenland under lunar illumination. Int. J. Remote Sens. 2017, 38, 5880–5898. [Google Scholar] [CrossRef]
- Chen, H.; Sun, C.; Chen, X.; Chiang, K.; Xiong, X. On-orbit calibration and performance of S-NPP VIIRS DNB. Proc. SPIE 2016, 9881, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Lucht, W.; Schaaf, C.; Strahler, A. An algorithm for the retrieval of albedo from space using semi-empirical BRDF models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 977–998. [Google Scholar] [CrossRef] [Green Version]
- Lucht, W.; Roujean, J. Considerations in the parametric modeling of BRDF and albedo from multiangular satellite sensor observations. Remote Sens. Rev. 2000, 18, 343–379. [Google Scholar] [CrossRef]
- Schaaf, C.; Gao, F.; Strahler, A.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.; Zhang, X.; Jin, Y.; Muller, J. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef] [Green Version]
- Román, M.; Schaaf, C.; Lewis, P.; Gao, F.; Anderson, G.; Privette, J.; Strahler, A.; Woodcock, C.; Barnsley, M. Assessing the coupling between surface albedo derived from MODIS and the fraction of diffuse skylight over spatially-characterized landscapes. Remote Sens. Environ. 2010, 114, 738–760. [Google Scholar] [CrossRef]
- Ross, J.K. The Radiation Regime and Architecture of Plant Stands; Junk, W., Ed.; Dr W. Junk Publishers: Norwell, MA, USA, 1981; 392p. [Google Scholar]
- Li, X.; Strahler, A.H. Geometric–optical bidirectional reflectance modeling of the discrete crown vegetation canopy: Effect of crown shape and mutual shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Wu, A.; Xiong, X.; Cao, C.; Angal, A. Monitoring MODIS calibration stability of visible and near-IR bands from observed top-of-atmosphere BRDF-normalized reflectances over Libyan Desert and Antarctic surfaces. Proc. SPIE 2008, 7081, 1–9. [Google Scholar] [CrossRef]
- Wu, A.; Xiong, X.; Cao, C. Assessment of stability of the response versus scan angle for the S-NPP VIIRS reflective solar bands using pseudo-invariant desert and Dome C sites. Proc. SPIE 2017, 10423, 1–9. [Google Scholar] [CrossRef]
- Lucht, W. Expected retrieval accuracies of bidirectional reflectance and albedo from EOS-MODIS and MISR angular sampling. J. Geophys. Res. 1998, 103, 8763–8778. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Jiao, Z.; Dong, Y.; Zhang, H.; Li, X. Analysis of BRDF and Albedo Retrieved by Kernel-Driven Models Using Field Measurements. IEEE J. Stars. 2013, 6, 149–161. [Google Scholar] [CrossRef]
- Strahler, A.; Muller, J.; Lucht, W.; Schaaf, C.; Tsang, T.; Gao, F.; Li, X.; Lewis, P.; Barnsley, M. MODIS BRDF/Albedo Product: Algorithm Theoretical Basis Document Version 5.0. MODIS Doc. 1999, 23, 42–47. [Google Scholar]
- Miller, S.; Turner, R. A Dynamic Lunar Spectral Irradiance Data Set for NPOESS/VIIRS Day/Night Band Nighttime Environmental Applications. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2316–2329. [Google Scholar] [CrossRef]
- Wu, A.; Xiong, X.; Cao, C. Examination of Calibration Performance of NOAA KLM AVHRR Using Measurements over the Dome C Site in Antarctica. Proc. SPIE 2008, 7106, 1–10. [Google Scholar] [CrossRef]
- Helder, D.; Thome, K.; Mishra, N.; Chander, G.; Xiong, X.; Angal, A.; Choi, T. Absolute Radiometric Calibration of Landsat Using a Pseudo Invariant Calibration Site. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1360–1369. [Google Scholar] [CrossRef]
- Loeb, N. In-flight calibration of NOAA AVHRR visible and near-IR bands over Greenland and Antarctica. Int. J. Remote Sens. 1997, 18, 477–490. [Google Scholar] [CrossRef]
- Masonis, S.; Warren, S. Gain of the AVHRR visible channel as tracked using bidirectional reflectance of Antarctic and Greenland snow. Int. J. Remote Sens. 2001, 22, 1495–1520. [Google Scholar] [CrossRef]
- Six, D.; Fily, M.; Alvain, S.; Henry, P.; Benoist, J. Surface characterisation of the Dome Concordia area (Antarctica) as a potential satellite calibration site, using Spot 4/Vegetation instrument. Remote Sens. Environ. 2004, 89, 83–94. [Google Scholar] [CrossRef]
- Walden, V.; Roth, W.; Stone, R.; Halter, B. Radiometric validation of the Atmospheric Infrared Sounder over the Antarctic Plateau. J. Geophys. Res. 2006, 111, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Jaross, G.; Warner, J. Use of Antarctica for validating reflected solar radiation measured by satellite sensors. J. Geophys. Res. 2008, 113, 1–13. [Google Scholar] [CrossRef]
- Wenny, B.; Xiong, X. Using a Cold Earth Surface Target to Characterize Long-Term Stability of the MODIS Thermal Emissive Bands. IEEE Geosci. Remote. Sens. Lett. 2008, 5, 162–165. [Google Scholar] [CrossRef]
- Uprety, S.; Cao, C. A comparison of the Antarctic Dome C and Sonoran Desert sites for the cal/val of visible and near infrared radiometers. Proc. SPIE 2010, 7811, 1–10. [Google Scholar] [CrossRef]
- Uprety, S.; Cao, C. Radiometric and spectral characterization and comparison of the Antarctic Dome C and Sonoran Desert sites for the calibration and validation of visible and near-infrared radiometers. J. Appl. Remote Sens. 2012, 6, 063541. [Google Scholar] [CrossRef]
- Uprety, S.; Cao, C. Suomi NPP VIIRS reflective solar band on-orbit radiometric stability and accuracy assessment using desert and Antarctica Dome C sites. Remote Sens. Environ. 2015, 166, 106–115. [Google Scholar] [CrossRef]
- Zeng, X.; Shao, X.; Qiu, S.; Ma, L.; Gao, C.; Li, C. Stability Monitoring of the VIIRS Day/Night Band over Dome C with a Lunar Irradiance Model and BRDF Correction. Remote Sens. 2018, 10, 189. [Google Scholar] [CrossRef] [Green Version]
- Shao, X.; Cao, C.; Uprety, S. Vicarious Calibration of S-NPP/VIIRS Day-Night Band. Proc. SPIE 2013, 8866, 88661S. [Google Scholar] [CrossRef]
- Hapke, B.; Nelson, R.; Smythe, W. The Opposition Effect of the Moon: The Contribution of Coherent Backscatter. Science 1993, 260, 509–511. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Shao, X.; Cao, C.; Uprety, S. Feasibility demonstration for calibrating Suomi-National Polar-Orbiting Partnership Visible Infrared Imaging Radiometer Suite day/night band using Dome C and Greenland under moon light. J. Appl. Remote Sens. 2016, 10, 016024. [Google Scholar] [CrossRef]




| Characteristics | Specification | |
|---|---|---|
| VIIRS | Orbital altitude (km) * | 824 |
| Scanning swath (km) * | 3044 | |
| Revisit time (h) | 12 | |
| Wavelength range (nm) | 410–12,500 | |
| Bands | 5 I-bands, 16 M-bands, and 1 DNB | |
| 14 RSBs, 7 TEBs, and 1 DNB | ||
| DNB | Spatial resolution | ~750 m |
| Wavelength range (nm) | 500–900 | |
| Dynamic range (W∙cm−2∙sr−1) * | 3 × 10−9 to 0.02 | |
| Gains | LGS, MGS, and HGS | |
| Quantization * | 14 bits for HGS, 13 bits for others | |
| Time Delay Integration (TDI) ** | 1, 3, and 250 pixels for LGS, MGS, and HGS, respectively |
| Characteristics | Specification |
|---|---|
| Location | The top of a 32 m tower over Dome C |
| Date | Summers of 2003–2004 and 2004–2005 |
| Instrument | Analytical Spectral Devices (ASD) |
| wavelength | 350–2400 nm, 25 nm resolution |
| SZA | 51.57°–87° |
| VZA | 7.5°–82.5°, 15° resolution |
| Relative solar azimuth | 0°–180° |
| Day of Year of 2019 | Universal Time Coordinated | LPA (°) | SZA (°) | LZA (°) | VZA (°) | |
|---|---|---|---|---|---|---|
| 1 | 167 | 13:37 | 10.07 | 125.59 | 57.26 | 26.43 |
| 2 | 140 | 13:43 | 21.21 | 122.66 | 61.64 | 24.69 |
| 3 | 136 | 14:59 | 30.07 | 123.72 | 71.21 | 4.14 |
| 4 | 143 | 14:27 | 56.38 | 124.57 | 67.52 | 9.48 |
| VZA (°) | RAA (°) | Linear Fitting Equations | R2 | RMSE | Number of Cases |
|---|---|---|---|---|---|
| 20–30 | 0–30 | y = −0.002018x + 1.09869 | 0.02447 | 0.06524 | 15 |
| 30–60 | y = −0.003435x + 1.14072 | 0.2556 | 0.0372 | 27 | |
| 60–90 | y = −0.005272x + 1.24841 | 0.5602 | 0.02763 | 38 | |
| 90–120 | y = −0.007858x + 1.42437 | 0.4661 | 0.03127 | 35 | |
| 120–150 | y = −0.00269x + 1.12341 | 0.2023 | 0.03174 | 28 | |
| 150–180 | y = −0.002437x + 1.14849 | 0.1342 | 0.03913 | 24 | |
| 30–40 | 0–30 | y = −0.006134x + 1.35817 | 0.1625 | 0.06192 | 15 |
| 30–60 | y = −0.002781x + 1.1022 | 0.2217 | 0.03659 | 16 | |
| 60–90 | y = −0.006477x + 1.3295 | 0.4624 | 0.03554 | 35 | |
| 90–120 | y = −0.005443x + 1.2702 | 0.3403 | 0.03479 | 27 | |
| 120–150 | y = −0.003783x + 1.20248 | 0.2332 | 0.0414 | 31 | |
| 150–180 | y = −0.0003982x + 1.04648 | 0.001884 | 0.05543 | 14 | |
| 40–50 | 0–30 | y = −0.003853x + 1.24236 | 0.07624 | 0.06199 | 18 |
| 30–60 | y = −0.001811x + 1.05826 | 0.07089 | 0.03142 | 25 | |
| 60–90 | y = −0.003297x + 1.11836 | 0.1869 | 0.03261 | 18 | |
| 90–120 | y = −0.003026x + 1.1147 | 0.1899 | 0.03529 | 18 | |
| 120–150 | y = −0.002753x + 1.1167 | 0.09274 | 0.04692 | 16 | |
| 50–60 | 0–30 | y = −0.003675x + 0.75391 | 0.05745 | 0.05679 | 19 |
| 30–60 | y = −0.0005718x + 0.97066 | 0.003635 | 0.0399 | 28 | |
| 60–90 | y = −0.004129x + 1.16262 | 0.1973 | 0.03362 | 24 | |
| 90–120 | y = −0.003857x + 1.15772 | 0.3597 | 0.03325 | 28 | |
| 120–150 | y = −0.004404x + 1.2833 | 0.1185 | 0.06326 | 12 | |
| 60–70 | 0–30 | y = −0.008533x + 1.5922 | 0.07706 | 0.07173 | 10 |
| 30–60 | y = 0.01183x + 0.19632 | 0.3319 | 0.0657 | 21 | |
| 60–90 | y = 0.0008173x + 0.86726 | 0.005966 | 0.03506 | 20 | |
| 90–120 | y = 0.001327x + 0.83565 | 0.0281 | 0.04762 | 20 | |
| 120–150 | y = −0.001188x + 1.03823 | 0.02873 | 0.04263 | 14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Qiu, S.; Zhang, Y.; Yang, B.; Gao, C.; Qian, Y.; Liu, Y.; Zhao, Y. Assessment of BRDF Impact on VIIRS DNB from Observed Top-of-Atmosphere Reflectance over Dome C in Nighttime. Remote Sens. 2021, 13, 301. https://doi.org/10.3390/rs13020301
Li J, Qiu S, Zhang Y, Yang B, Gao C, Qian Y, Liu Y, Zhao Y. Assessment of BRDF Impact on VIIRS DNB from Observed Top-of-Atmosphere Reflectance over Dome C in Nighttime. Remote Sensing. 2021; 13(2):301. https://doi.org/10.3390/rs13020301
Chicago/Turabian StyleLi, Jinjin, Shi Qiu, Yu Zhang, Benyong Yang, Caixia Gao, Yonggang Qian, Yaokai Liu, and Yongguang Zhao. 2021. "Assessment of BRDF Impact on VIIRS DNB from Observed Top-of-Atmosphere Reflectance over Dome C in Nighttime" Remote Sensing 13, no. 2: 301. https://doi.org/10.3390/rs13020301
APA StyleLi, J., Qiu, S., Zhang, Y., Yang, B., Gao, C., Qian, Y., Liu, Y., & Zhao, Y. (2021). Assessment of BRDF Impact on VIIRS DNB from Observed Top-of-Atmosphere Reflectance over Dome C in Nighttime. Remote Sensing, 13(2), 301. https://doi.org/10.3390/rs13020301