A New Empirical Estimation Scheme for Daily Net Radiation at the Ocean Surface
Abstract
:1. Introduction
2. Data and Preprocessing
2.1. Measurements from Moored Buoy Sites
2.1.1. Introduction to the Moored Buoy Sites
2.1.2. Radiative Measurements
2.1.3. Meteorological and Other Ancillary Information
2.1.4. Uncertainty Analysis
2.2. CERES SYN1deg_Ed4A Product
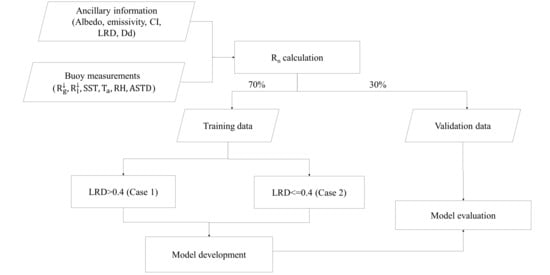
3. A New Ocean Surface Rn Empirical Estimation Scheme
3.1. Relationships between the Ocean Surface Rn and
3.2. Conditional Model Development
3.2.1. Case 1 Model
3.2.2. Case 2 model
4. Results and Discussions
4.1. Validation Results
4.2. Model Sensitivity Analysis
4.3. Error Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, B.; Zhang, Y.; Liang, S.; Wohlfahrt, G.; Arain, A.; Cescatti, A.; Georgiadis, T.; Jia, K.; Kiely, G.; Lund, M.; et al. Empirical estimation of daytime net radiation from shortwave radiation and ancillary information. Agric. For. Meteorol. 2015, 211–212, 23–36. [Google Scholar] [CrossRef] [Green Version]
- Tomita, H.; Hihara, T.; Kako, S.I.; Kubota, M.; Kutsuwada, K. An introduction to J-OFURO3, a third-generation Japanese ocean flux data set using remote-sensing observations. J. Oceanogr. 2019, 75, 171–194. [Google Scholar] [CrossRef] [Green Version]
- Trenberth, K.E.; Fasullo, J.T.; Balmaseda, M.A. Earth’s energy imbalance. J. Clim. 2014, 27, 3129–3144. [Google Scholar] [CrossRef] [Green Version]
- Fujii, Y.; Tsujino, H.; Toyoda, T.; Nakano, H. Enhancement of the southward return flow of the Atlantic Meridional Overturning Circulation by data assimilation and its influence in an assimilative ocean simulation forced by CORE-II atmospheric forcing. Clim. Dyn. 2015, 49, 869–889. [Google Scholar] [CrossRef]
- Wunsch, C. The total meridional heat flux and its oceanic and atmospheric partition. J. Clim. 2005, 18, 4374–4380. [Google Scholar] [CrossRef] [Green Version]
- Stephens, G.L.; Li, J.; Wild, M.; Clayson, C.A.; Loeb, N.; Kato, S.; L’Ecuyer, T.; Stackhouse, P.W., Jr.; Lebsock, M.; Andrews, T. An update on Earth’s energy balance in light of the latest global observations. Nat. Geosci. 2012, 5, 691–696. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Schar, C.; Loeb, N.; Dutton, E.G.; Konig-Langlo, G. The global energy balance from a surface perspective. Clim. Dyn. 2013, 40, 3107–3134. [Google Scholar] [CrossRef] [Green Version]
- Trenberth, K.E.; Caron, J.M. Estimates of meridional atmosphere and ocean heat transports. J. Clim. 2001, 14, 3433–3443. [Google Scholar] [CrossRef]
- Baggenstos, D.; Haberli, M.; Schmitt, J.; Shackleton, S.A.; Birner, B.; Severinghaus, J.P.; Kellerhals, T.; Fischer, H. Earth’s radiative imbalance from the Last Glacial Maximum to the present. Proc. Natl. Acad. Sci. USA 2019, 116, 14881–14886. [Google Scholar] [CrossRef] [Green Version]
- Hansen, J.; Sato, M.; Kharecha, P.; Schuckmann, K.V. Earth’s energy imbalance and implications. Atmos. Chem. Phys. 2011, 11, 13421–13449. [Google Scholar] [CrossRef] [Green Version]
- von Schuckmann, K.; Palmer, M.D.; Trenberth, K.E.; Cazenave, A.; Chambers, D.; Champollion, N.; Hansen, J.; Josey, S.A.; Loeb, N.; Mathieu, P.P.; et al. An imperative to monitor Earth’s energy imbalance. Nat. Clim. Chang. 2016, 6, 138–144. [Google Scholar] [CrossRef] [Green Version]
- Cronin, M.F.; Gentemann, C.L.; Edson, J.; Ueki, I.; Bourassa, M.; Brown, S.; Clayson, C.A.; Fairall, C.W.; Farrar, J.T.; Gille, S.T.; et al. Air-sea fluxes with a focus on heat and momentum. Front. Mar. Sci. 2019, 6, 430. [Google Scholar] [CrossRef] [Green Version]
- Pinker, R.T.; Bentamy, A.; Katsaros, K.B.; Ma, Y.; Li, C. Estimates of net heat fluxes over the Atlantic Ocean. J. Geophys. Res.-Oceans 2014, 119, 410–427. [Google Scholar] [CrossRef] [Green Version]
- Wielicki, B.A.; Barkstrom, B.R.; Baum, B.A.; Charlock, T.P.; Green, R.N.; Kratz, D.P.; Lee, R.B.; Minnis, P.; Smith, G.L.; Takmeng, W.; et al. Clouds and the Earth’s radiant energy system (CERES): Algorithm overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1127–1141. [Google Scholar] [CrossRef] [Green Version]
- Rossow, W.B.; Zhang, Y.C. Calculation of surface and top of atmosphere radiative fluxes from physical quantities based on ISCCP data sets: 2. Validation and first results. J. Geophys. Res.-Atmos. 1995, 100, 1167–1197. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Berry, D.I.; Kent, E.C. Air-sea fluxes from ICOADS: The construction of a new gridded dataset with uncertainty estimates. Int. J. Climatol. 2011, 31, 987–1001. [Google Scholar] [CrossRef]
- Jin, X.; Weller, R.A. Multidecade Global Flux Datasets from the Objectively Analyzed Air-Sea Fluxes (Oaflux) Project: Latent and Sensible Heat Fluxes, Ocean Evaporation, and Related Surface Meteorological Variables Lisan Yu; OAFlux Project Technical Report (OA-2008-01); NOAA: Washington, DC, USA, 2008; Volume 74, pp. 1–64. [Google Scholar]
- Kaminsky, K.Z.; Dubayah, R. Estimation of surface net radiation in the boreal forest and northern prairie from shortwave flux measurements. J. Geophys. Res.-Atmos 1997, 102, 29707–29716. [Google Scholar] [CrossRef]
- Iziomon, M.G.; Mayer, H.; Matzarakis, A. Empirical models for estimating net radiative flux: A case study for three mid-latitude sites with orographic variability. Astrophys. Space Sci. 2000, 273, 313–330. [Google Scholar] [CrossRef]
- Jiang, B.; Liang, S.; Jia, A.; Xu, J.; Zhang, X.; Xiao, Z.; Zhao, X.; Jia, K.; Yao, Y. Validation of the surface daytime net radiation product from version 4.0 GLASS product suite. IEEE Geosci. Remote Sens. Lett. 2019, 16, 509–513. [Google Scholar] [CrossRef]
- Polavarapu, R.J. Estimation of net radiation at sea. Atmos.-Ocean 1979, 17, 24–35. [Google Scholar] [CrossRef] [Green Version]
- McPhaden, M.J.; Meyers, G.; Ando, K.; Masumoto, Y.; Murty, V.S.N.; Ravichandran, M.; Syamsudin, F.; Vialard, J.; Yu, L.; Yu, W. RAMA: The research moored array for African–Asian–Australian monsoon analysis and prediction. Bull. Am. Meteorol. Soc. 2009, 90, 459–480. [Google Scholar] [CrossRef] [Green Version]
- McPhaden, M.J.; Busalacchi, A.J.; Cheney, R.; Donguy, J.R.; Gage, K.S.; Halpern, D.; Ji, M.; Julian, P.; Meyers, G.; Mitchum, G.T.; et al. The Tropical Ocean-Global Atmosphere observing system: A decade of progress. J. Geophys. Res.-Oceans 1998, 103, 14169–14240. [Google Scholar] [CrossRef]
- Lumb, F.E. The influence of cloud on hourly amounts of total solar radiation at the sea surface. Q. J. R. Meteorol. Soc. 1964, 90, 43–56. [Google Scholar] [CrossRef]
- Dobson, F.W.; Smith, S.D. A comparison of incoming solar radiation at marine and continental stations. Q. J. R. Meteorol. Soc. 1989, 115, 353–364. [Google Scholar] [CrossRef]
- Kalisch, J.; Macke, A. Estimation of the total cloud cover with high temporal resolution and parametrization of short-term fluctuations of sea surface insolation. Meteorol. Z. 2008, 17, 603–611. [Google Scholar] [CrossRef] [Green Version]
- Bignami, F.; Marullo, S.; Santoleri, R.; Schiano, M.E. Longwave radiation budget in the Mediterranean Sea. J. Geophys. Res.-Oceans 1995, 100, 2501–2514. [Google Scholar] [CrossRef]
- Josey, S.A.; Oakley, D.; Pascal, R.W. On estimating the atmospheric longwave flux at the ocean surface from ship meteorological reports. J. Geophys. Res.-Oceans 1997, 102, 27961–27972. [Google Scholar] [CrossRef]
- Josey, S.A.; Gulev, S.; Yu, L. Exchanges through the ocean surface. Int. Geophys. 2013, 103, 115–140. [Google Scholar] [CrossRef]
- Yang, H.; Lohmann, G.; Wei, W.; Dima, M.; Ionita, M.; Liu, J. Intensification and poleward shift of subtropical western boundary currents in a warming climate. J. Geophys. Res.-Oceans 2016, 121, 4928–4945. [Google Scholar] [CrossRef] [Green Version]
- Franz, G.; Garcia, C.A.E.; Pereira, J.; de Freitas Assad, L.P.; Rollnic, M.; Garbossa, L.H.P.; da Cunha, L.C.; Lentini, C.A.D.; Nobre, P.; Turra, A.; et al. Coastal Ocean Observing and Modeling Systems in Brazil: Initiatives and Future Perspectives. Front. Mar. Sci. 2021, 8, 1038. [Google Scholar] [CrossRef]
- Roughan, M.; Morris, B.D.; Suthers, I.M. NSW-IMOS: An integrated marine observing system for southeastern Australia. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2010; p. 012030. [Google Scholar]
- Schulz, E.W.; Josey, S.A.; Verein, R. First air-sea flux mooring measurements in the Southern Ocean. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Bourlès, B.; Lumpkin, R.; McPhaden, M.J.; Hernandez, F.; Nobre, P.; Campos, E.; Yu, L.; Planton, S.; Busalacchi, A.; Moura, A.D. The PIRATA program: History, accomplishments, and future directions. Bull. Am. Meteorol. Soc. 2008, 89, 1111–1126. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Ando, K.; Bourlès, B.; Freitag, H.P.; Lumpkin, R.; Masumoto, Y.; Murty, V.S.N.; Nobre, P.; Ravichandran, M.; Vialard, J.; et al. The global tropical moored buoy array. Proc. OceanObs 2010, 9, 668–682. [Google Scholar] [CrossRef] [Green Version]
- Medovaya, M.; Waliser, D.E.; Weller, R.A.; McPhaden, M.J. Assessing ocean buoy shortwave observations using clear-sky model calculations. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef] [Green Version]
- Lake, B.J. Calibration Procedures and Instrumental Accuracy Estimates of ATLAS Air Temperature and Relative Humidity Measurements; NOAA Tech Memo. OAR PMEL-123; NOAA/Pacific Marine Environmental Laboratory: Seattle, WA, USA, 2003; p. 23. [Google Scholar]
- May, J.C.; Rowley, C.; Barron, C.N. NFLUX satellite-based surface radiative heat fluxes. part II: Gridded products. J. Appl. Meteorol. Climatol. 2017, 56, 1043–1057. [Google Scholar] [CrossRef] [Green Version]
- Cronin, M.F.; Fairall, C.W.; McPhaden, M.J. An assessment of buoy-derived and numerical weather prediction surface heat fluxes in the tropical Pacific. J. Geophys. Res.-Oceans 2006, 111, 6. [Google Scholar] [CrossRef]
- Cronin, M.F.; McPhaden, M.J. The upper ocean heat balance in the western equatorial Pacific warm pool during September–December 1992. J. Geophys. Res.-Oceans 1997, 102, 8533–8553. [Google Scholar] [CrossRef]
- Petrova, D.; Ballester, J.; Koopman, S.J.; Rodó, X. Multiyear statistical prediction of ENSO enhanced by the tropical Pacific observing system. J. Clim. 2020, 33, 163–174. [Google Scholar] [CrossRef] [Green Version]
- Praveen Kumar, B.; Vialard, J.; Lengaigne, M.; Murty, V.S.N.; McPhaden, M.J. TropFlux: Air-sea fluxes for the global tropical oceans—description and evaluation. Clim. Dyn. 2011, 38, 1521–1543. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, B.; Liang, S.; Li, X.; Wang, Y.; Peng, J.; Chen, H.; Liang, H.; Li, S. Generating a High-Resolution Time-Series Ocean Surface Net Radiation Product by Downscaling J-OFURO3. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2794–2809. [Google Scholar] [CrossRef]
- Clark, N.E.; Eber, L.; Laurs, R.M.; Renner, J.A.; Saur, J.F.T. Heat Exchange between Ocean and Atmosphere in the Eastern North Pacific for 1961–1971; Technical Report NMFS SSRF-682; NOAA, U.S. Department of Commerce: Washington, DC, USA, 1974. [Google Scholar]
- Cheng, J.; Cheng, X.; Liang, S.; Niclòs, R.; Nie, A.; Liu, Q. A lookup table-based method for estimating sea surface hemispherical broadband emissivity values (8–13.5 μm). Remote Sens. 2017, 9, 245. [Google Scholar] [CrossRef] [Green Version]
- Hogikyan, A.; Cronin, M.F.; Zhang, D.; Kato, S. Uncertainty in net surface heat flux due to differences in commonly used albedo products. J. Clim. 2020, 33, 303–315. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, Q.; Qu, Y.; Liang, S. Estimation of the ocean water albedo from remote sensing and meteorological reanalysis data. IEEE Trans. Geosci. Remote Sens. 2015, 54, 850–868. [Google Scholar] [CrossRef]
- Jin, Z.; Charlock, T.P.; Smith, W.L.; Rutledge, K. A parameterization of ocean surface albedo. Geophys. Res. Lett 2004, 31. [Google Scholar] [CrossRef]
- Donlon, C.J.; Minnett, P.J.; Gentemann, C.; Nightingale, T.J.; Barton, I.J.; Ward, B.; Murray, M.J. Toward improved validation of satellite sea surface skin temperature measurements for climate research. J. Clim. 2002, 15, 353–369. [Google Scholar] [CrossRef] [Green Version]
- Alappattu, D.P.; Wang, Q.; Yamaguchi, R.; Lind, R.J.; Reynolds, M.; Christman, A.J. Warm layer and cool skin corrections for bulk water temperature measurements for air-sea interaction studies. J. Geophys. Res.-Oceans 2017, 122, 6470–6481. [Google Scholar] [CrossRef]
- Vanhellemont, Q. Automated water surface temperature retrieval from Landsat 8/TIRS. Remote Sens. Environ. 2020, 237, 111518. [Google Scholar] [CrossRef]
- Fung, I.Y.; Harrison, D.; Lacis, A.A. On the variability of the net longwave radiation at the ocean surface. Rev. Geophys. 1984, 22, 177–193. [Google Scholar] [CrossRef]
- Bunker, A.F. Computations of surface energy flux and annual air–sea interaction cycles of the North Atlantic Ocean. Mon. Weather Rev. 1976, 104, 1122–1140. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.K.; Kratz, D.P.; Stackhouse, P.W.; Wilber, A.C.; Zhang, T.; Sothcott, V.E. Improvement of surface longwave flux algorithms used in CERES processing. J. Appl. Meteorol. Climatol. 2010, 49, 1579–1589. [Google Scholar] [CrossRef]
- Swinbank, W.C. Longwave radiation from clear skies. Q. J. R. Meteorol. Soc. 1963, 89, 339–348. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D. Thermal radiation from the atmosphere. J. Geophys. Res. 1969, 74, 5397–5403. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S.; Wang, W.; Guo, Y. An efficient hybrid method for estimating clear-sky surface downward longwave radiation from MODIS data. J. Geophys. Res.-Atmos. 2017, 122, 2616–2630. [Google Scholar] [CrossRef]
- Boilley, A.; Wald, L. Comparison between meteorological re-analyses from ERA-Interim and MERRA and measurements of daily solar irradiation at surface. Renew. Energy 2015, 75, 135–143. [Google Scholar] [CrossRef]
- Jiang, B.; Liang, S.; Ma, H.; Zhang, X.; Xiao, Z.; Zhao, X.; Jia, K.; Yao, Y.; Jia, A. GLASS daytime all-wave net radiation product: Algorithm development and preliminary validation. Remote Sens. 2016, 8, 222. [Google Scholar] [CrossRef] [Green Version]
- Payne, R.E. Albedo of the sea surface. J. Atmos. Sci. 1972, 29, 959–970. [Google Scholar] [CrossRef]
- Iziomon, M.G.; Mayer, H.; Matzarakis, A. Downward atmospheric longwave irradiance under clear and cloudy skies: Measurement and parameterization. J. Atmos. Sol.-Terr. Phys. 2003, 65, 1107–1116. [Google Scholar] [CrossRef]
- Foltz, G.R.; Evan, A.T.; Freitag, H.P.; Brown, S.; McPhaden, M.J. Dust accumulation biases in PIRATA shortwave radiation records. J. Atmos. Ocean. Technol. 2013, 30, 1414–1432. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J.R. Error Analysis; Univ. Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Chen, J.; He, T.; Jiang, B.; Liang, S. Estimation of all-sky all-wave daily net radiation at high latitudes from MODIS data. Remote Sens. Environ. 2020, 245, 111842. [Google Scholar] [CrossRef]
- Wang, K.C.; Liang, S.L. Estimation of daytime net radiation from shortwave radiation measurements and meteorological observations. J. Appl. Meteorol. Climatol. 2009, 48, 634–643. [Google Scholar] [CrossRef]
- Wang, C.; Enfield, D.B. The tropical Western Hemisphere warm pool. Geophys. Res. Lett. 2001, 28, 1635–1638. [Google Scholar] [CrossRef]
- Meloni, D. Tropospheric aerosols in the Mediterranean: 2. Radiative effects through model simulations and measurements. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Nair, V.S.; Babu, S.S.; Satheesh, S.K.; Moorthy, K.K. Effects of sea surface winds on marine aerosols characteristics and impacts on longwave radiative forcing over the Arabian Sea. Atmos. Chem. Phys. 2008, 8, 15855–15899. [Google Scholar] [CrossRef]
- Tarantola, S.; Chan, K.P.S.; Saltelli, A.; Chan, K.P.S. A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Thandlam, V.; Rahaman, H. Evaluation of surface shortwave and longwave downwelling radiations over the global tropical oceans. SN Appl. Sci. 2019, 1, 1171. [Google Scholar] [CrossRef] [Green Version]
- Colbo, K.; Weller, R.A. Accuracy of the IMET sensor package in the subtropics. J. Atmos. Ocean. Technol. 2009, 26, 1867–1890. [Google Scholar] [CrossRef] [Green Version]
- Macwhorter, M.A.; Weller, R.A. Error in measurements of incoming shortwave radiation made from ships and buoys. J. Atmos. Ocean. Technol. 1991, 8, 108–117. [Google Scholar] [CrossRef]
















| Abbreviation | Variable | Unit | Source | |
|---|---|---|---|---|
| Independent variables | Daily downward longwave radiation | Wm−2 | In situ | |
| Daily surface incoming solar radiation | Wm−2 | In situ/CERES | ||
| RH | Daily mean relative humidity | % | In situ | |
| SST 1 | Daily mean sea surface temperature | K | In situ | |
| Ta | Daily air temperature | K | In situ | |
| ASTD | Air–sea temperature difference | K | Calculated | |
| CI | Clearness index | Calculated | ||
| Dd | Daytime duration | Hour | Calculated | |
| Dependent variable | Rn | Daily ocean-surface net radiation | Wm−2 | Calculated |
| Network/Program | Number of Sites | Period | Observation Frequency | URL |
|---|---|---|---|---|
| UOP | 23 | 1988–2017 | 1 h | http://uop.whoi.edu/index.html (accessed on 15 October 2021) |
| TAO/TRITON | 21 | 2000–2019 | 10 min | https://www.pmel.noaa.gov/tao/drupal/disdel/ (accessed on 15 October 2021) |
| RAMA | 7 | 2004–2018 | 10 min | https://www.pmel.noaa.gov/tao/drupal/disdel/ (accessed on 15 October 2021) |
| PIRATA | 7 | 2006–2017 | 10 min | https://www.pmel.noaa.gov/tao/drupal/disdel/ (accessed on 15 October 2021) |
| OceanSITES | 8 | 2000–2019 | 1 h | http://www.oceansites.org/ (accessed on 15 October 2021) |
| Conditional Model | Classification Criteria | Training Samples | Validation Samples |
|---|---|---|---|
| Case 1 | LRD > 0.4 | 37,054 | 15,952 |
| Case 2 | LRD <= 0.4 | 324 | 130 |
| Model | RH | CI | ASTD | Dd | SST | ||
|---|---|---|---|---|---|---|---|
| Case 1 | 0.869 | \ | 0.031 | 0.055 | 0.003 | \ | \ |
| Case 2 | \ | 0.643 | \ | 0.177 | \ | 0.053 | 0.052 |
| Abbreviation | Stands for |
|---|---|
| P | Ocean surface Rn estimations |
| O | In situ ocean surface Rn calculations |
| Ocean surface Rn estimations with “true” inputs | |
| In situ ocean surface Rn without measurement errors (true values) | |
| Uncertainty of the ocean surface Rn estimations | |
| Uncertainty of the in situ ocean surface Rn calculations | |
| Uncertainty of the model |
| Parameters | Case 1 Standard Error\Average | Case 2 Standard Error\Average | Source |
|---|---|---|---|
| (Wm−2) | 6\225.40 | 0.90\33.90 | [72] |
| (Wm−2) | 2.5\397.0 | 2.5\310.99 | [72] |
| RH (%) | 0.027\- | -\- | [38] |
| CI | 0.015\0.57 | 0.06\0.31 | Calculated |
| ASTD (K) | 0.20\- | -\- | [72] |
| Dd (Hour) | -\- | 0\- | Calculated |
| SST (K) | 0.07\298.20 | 0.07\280.63 | [50] |
| 0.0049\0.06 | 0.0049\0.06 | [48] | |
| 0.002\0.95 | 0.002\0.95 | [46] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Jiang, B.; Chen, H.; Liang, S.; Liang, H.; Li, S.; Han, J.; Liu, Q.; Cheng, J.; Yao, Y.; et al. A New Empirical Estimation Scheme for Daily Net Radiation at the Ocean Surface. Remote Sens. 2021, 13, 4170. https://doi.org/10.3390/rs13204170
Peng J, Jiang B, Chen H, Liang S, Liang H, Li S, Han J, Liu Q, Cheng J, Yao Y, et al. A New Empirical Estimation Scheme for Daily Net Radiation at the Ocean Surface. Remote Sensing. 2021; 13(20):4170. https://doi.org/10.3390/rs13204170
Chicago/Turabian StylePeng, Jianghai, Bo Jiang, Hongkai Chen, Shunlin Liang, Hui Liang, Shaopeng Li, Jiakun Han, Qiang Liu, Jie Cheng, Yunjun Yao, and et al. 2021. "A New Empirical Estimation Scheme for Daily Net Radiation at the Ocean Surface" Remote Sensing 13, no. 20: 4170. https://doi.org/10.3390/rs13204170
APA StylePeng, J., Jiang, B., Chen, H., Liang, S., Liang, H., Li, S., Han, J., Liu, Q., Cheng, J., Yao, Y., Jia, K., & Zhang, X. (2021). A New Empirical Estimation Scheme for Daily Net Radiation at the Ocean Surface. Remote Sensing, 13(20), 4170. https://doi.org/10.3390/rs13204170