Quasi Geoid and Geoid Modeling with the Use of Terrestrial and Airborne Gravity Data by the GGI Method—A Case Study in the Mountainous Area of Colorado
Abstract
:1. Introduction
2. Materials and Methods
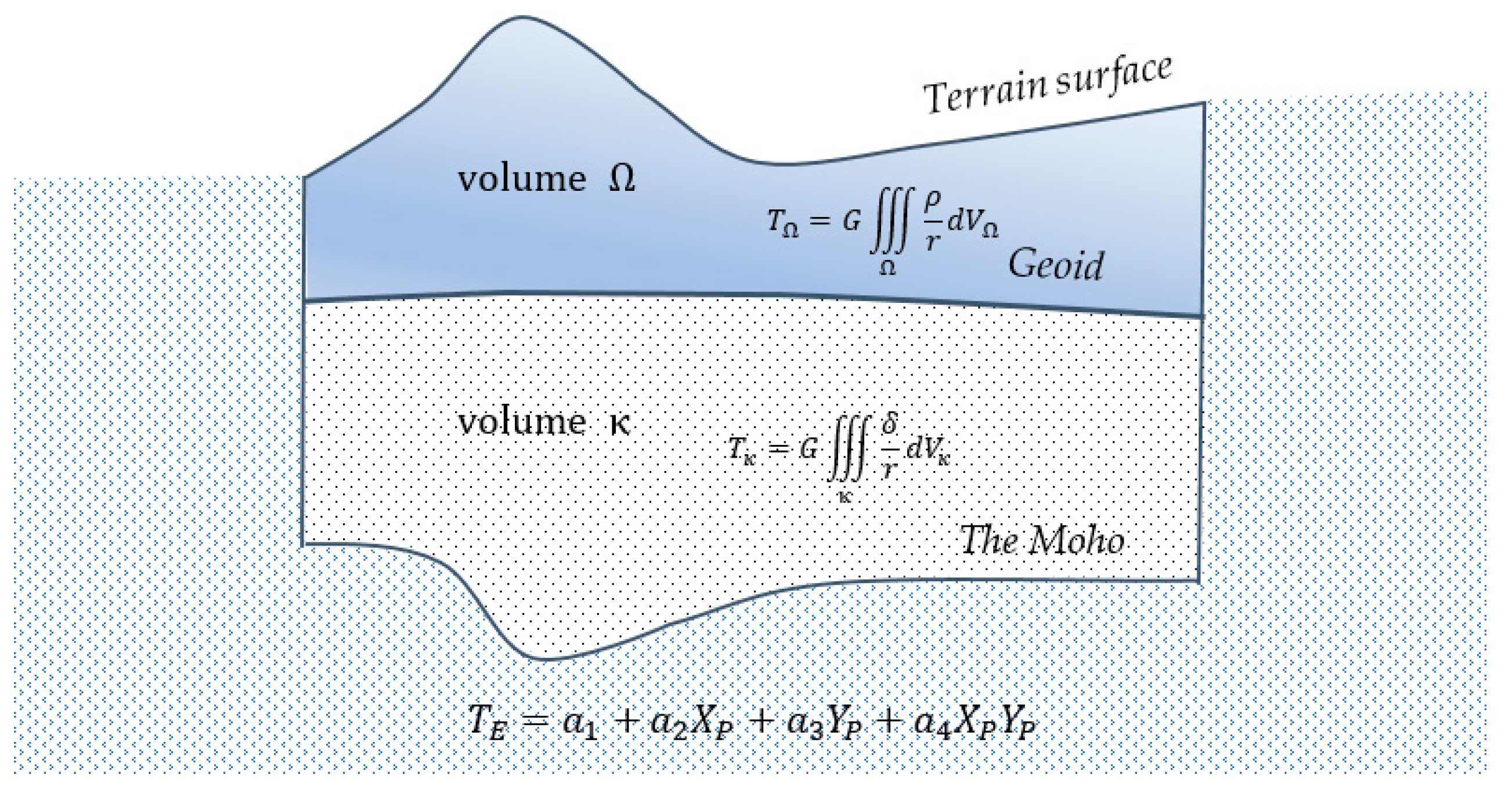
2.1. The Utilized Solution: Overview
- 1.
- Removal from the original data of a global model part (long-wavelength part) and determination of the residual disturbing potential values and the residual gravity .where , and are the disturbing potential, gravity potential, and gravity from the global model, while is the measured gravity.
- 2.
- On the basis of the residual data, the residual model of the disturbing gravity potential is built using the GGI method.where the components , and are residual parts of the componenets , and (after removing from them parts contained in the global geopotential model).
- 3.
- For new points, the residual disturbing potential values from the GGI model and the gravity potential values from the global model are determined. Consequently, the values of gravity potential and gravity can be determined.where is the residual gravity from the GGI model.
- 1.
- The determined quasigeoid model should be consistent with the IHRS reference level [48], which is different from the normal potential on the reference ellipsoid surface GRS80, . Hence, determining the height anomaly based on the gravity potential value (24), the difference has been taken into account.
- 2.
- Since the GM used is in the zero-tide system and the models developed in the Colorado geoid experiment were developed in the non-tidal system, for the determined height anomalies, a small correction was added [49].where is the point latitude, is the Love number, and the result is in meters.Finally, the height anomalies were determined by the following equation:
- 3.
- It should be added that the mean gravity (used in Equation (27)) should be consistent with the orthometric height type used. As in the analyzed area, Helmert orthometric heights are used, the mean gravity in our analyses were calculated in accordance with these heights, according to the following equation [2]:which assumes a density of the topography .
2.2. The Used Data
- Terrestrial gravity data (59,303 points)
- De-biased GRAV-D airborne data of the survey block MS05 (283,717 measured values)
- SRTM v4.1 digital elevation model at grid spacing
- Historical GPS/levelling data (509 points)
- GSVS17 GPS/levelling data set (223 points)
- A detailed description of these datasets can be found in [28].
3. Results
3.1. Preliminary Phase Analyses
- terrestrial-only,
- airborne-only and
- combined (with the use of terrestrial and airborne gravity data).
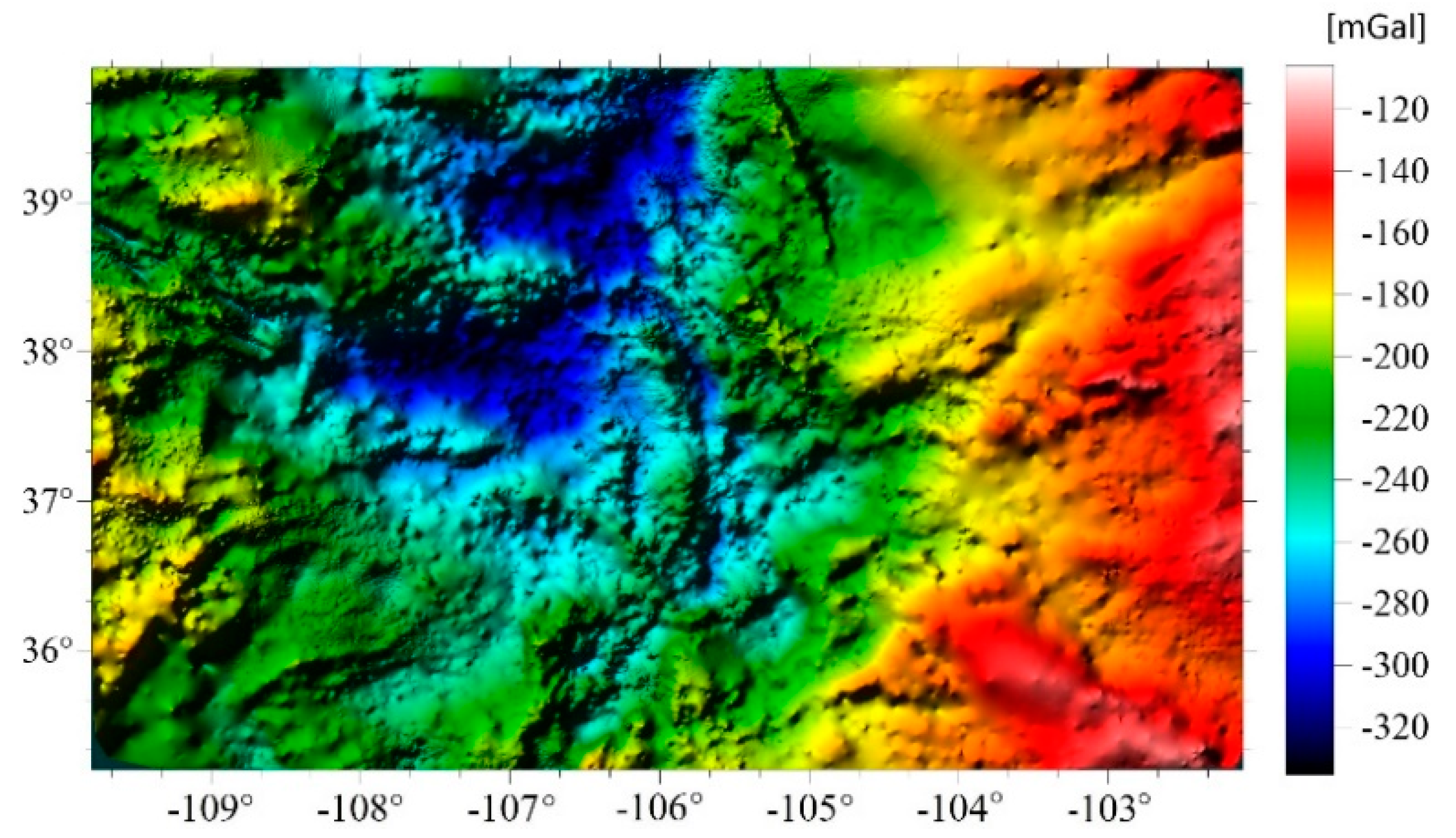
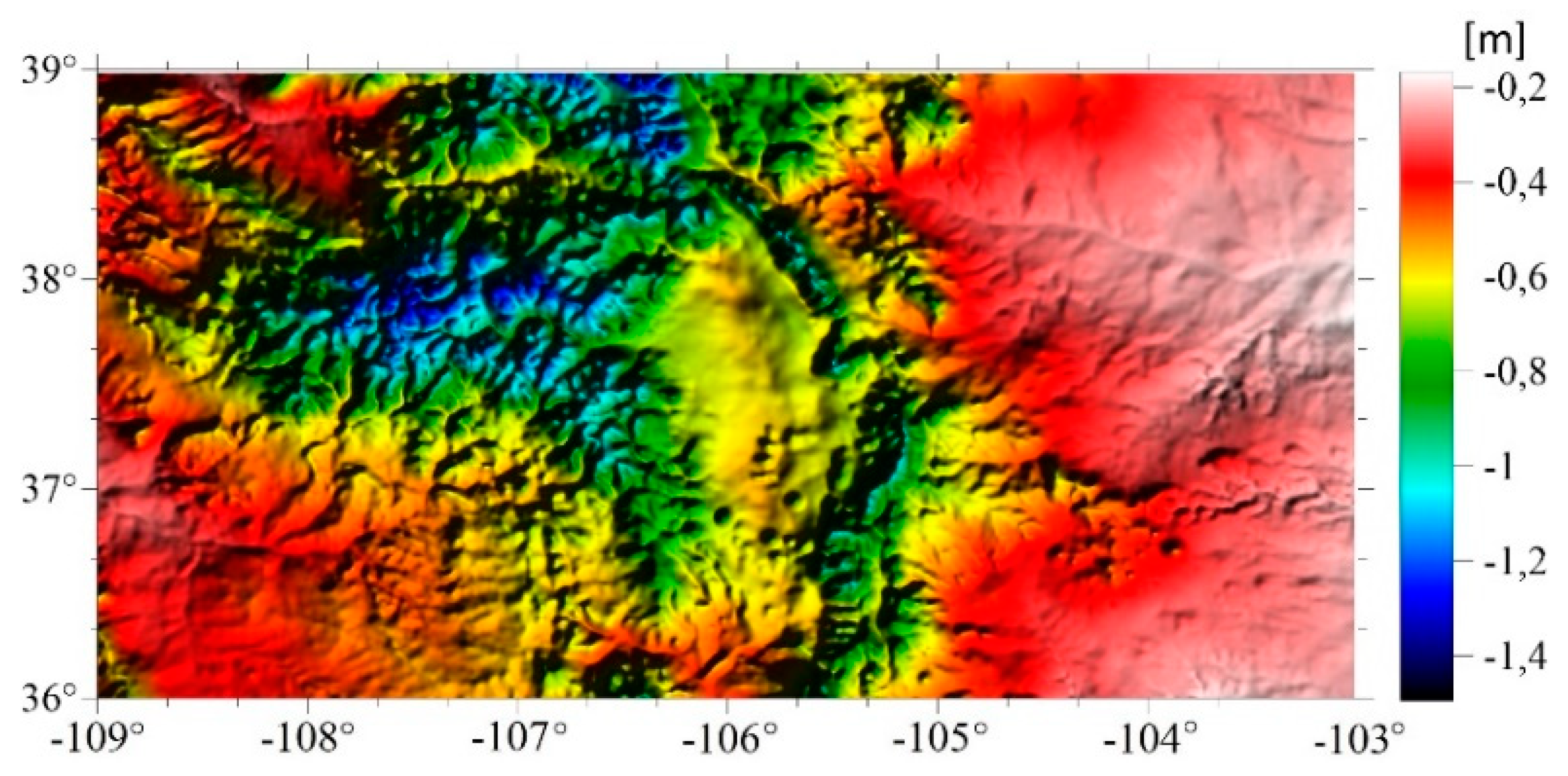
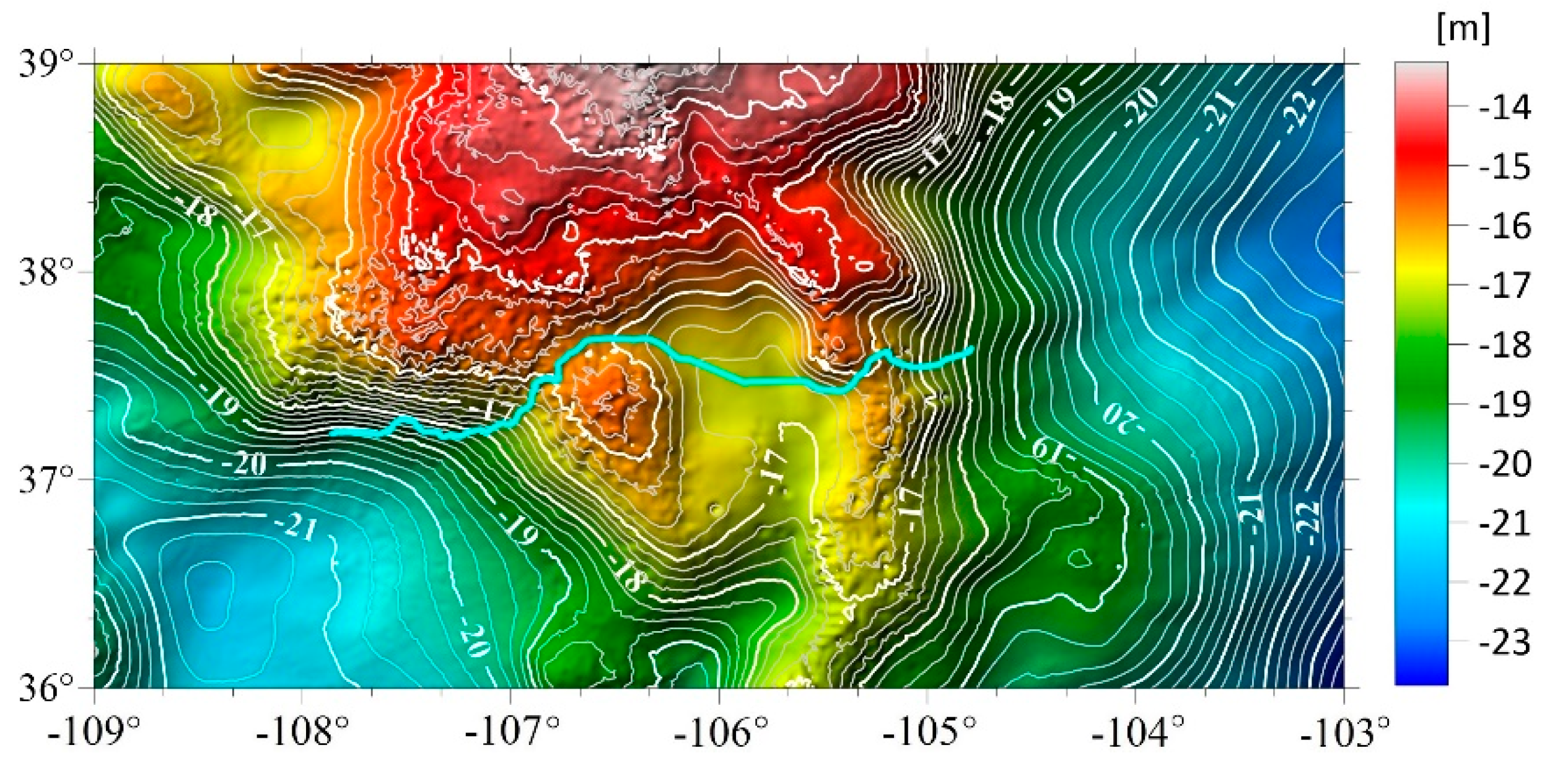
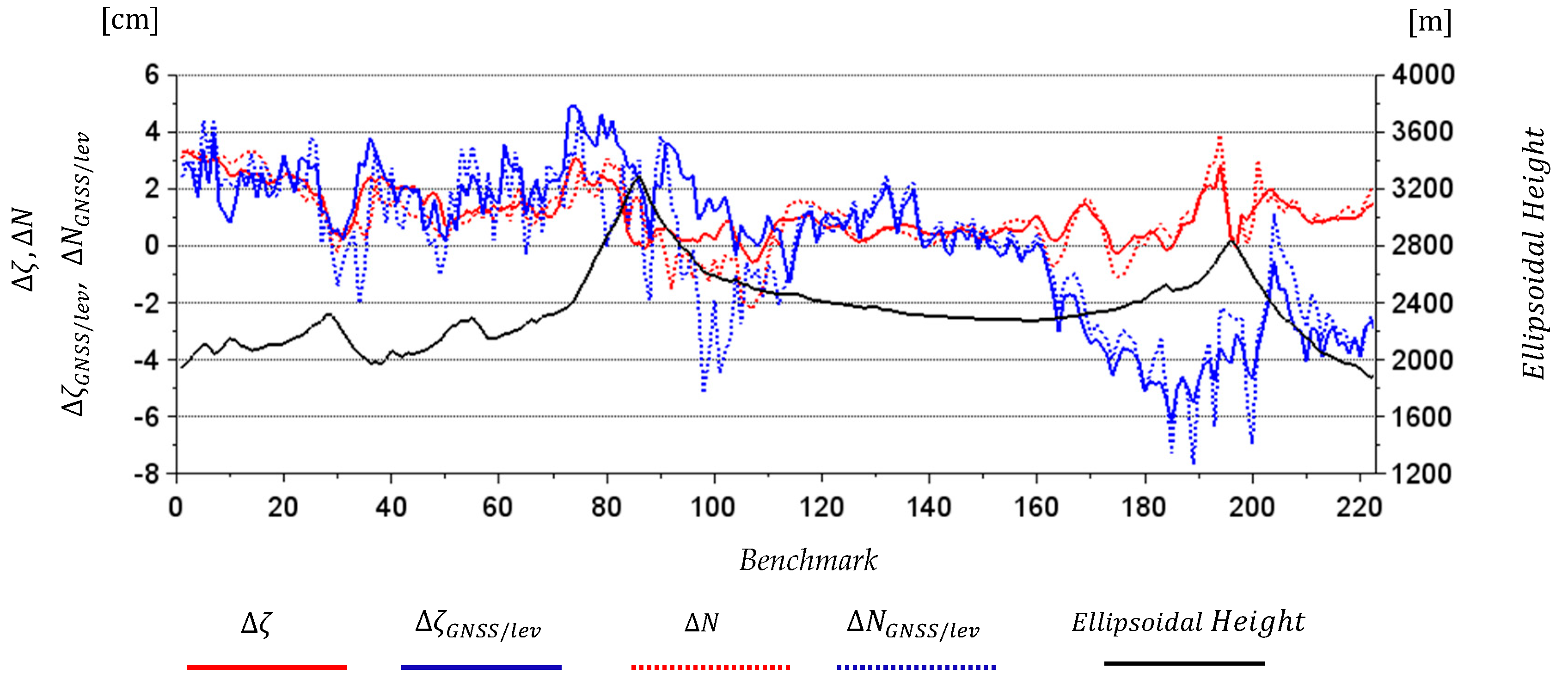
3.2. Determination of GGI Geoid and Quasi Geoid Models for Colorado Geoid Experiment Area
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W. H. Freeman and Company: New York, NY, USA, 1967. [Google Scholar]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Torge, W. Geodesy, 3rd ed.; Walter de Gruyter: Berlin/Heidelberg, Germany; New York, NY, USA, 2001. [Google Scholar]
- Vanicek, P.; Kleusberg, A. The Canadian geoid-stokesian approach. Manuscr. Geod. 1987, 12, 86–98. [Google Scholar]
- Sjöberg, L.E. On the topographic effects by the Stokes-Helmert method of geoid and quasigeoid determination. J. Geod. 2000, 74, 255–268. [Google Scholar]
- Heck, B. On Helmert’s methods of condensation. J. Geod. 2003, 77, 155–170. [Google Scholar] [CrossRef]
- Huang, J.; Véronneau, M. Canadian gravimetric geoid model 2010. J. Geod. 2013, 87, 771–790. [Google Scholar] [CrossRef]
- Forsberg, R. A Study of Terrain Reductions, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modelling; Report 355; Department of Geodetic Science, The Ohio State University: Columbus, OH, USA, 1984. [Google Scholar]
- Forsberg, R. Terrain effects in geoid computation. In Lecture Notes, International School for the Determination and Use of the Geoid; International Geoid Service, DIIAR—Politecnico di Milano: Milano, Italy, 1994; pp. 101–134. [Google Scholar]
- Forsberg, R.; Tscherning, C.C. Topographic effects in gravity field modelling for BVP. In Geodetic Boundary Value Problems in View of the One Centimeter Geoid; Lecture Notes in Earth Sciences, 65, Sansó, F., Rummel, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 121–160. [Google Scholar]
- Omang, O.C.D.; Forsberg, R. How to handle the topography in geoid determination: Three examples. J. Geod. 2003, 74, 458–466. [Google Scholar] [CrossRef]
- Abd-Elmotaal, H.; Kühtreiber, N. Geoid Determination Using Adapted Reference Field, Seismic Moho Depths and Variable Density Contrast. J. Geod. 2003, 77, 77–85. [Google Scholar] [CrossRef]
- Forsberg, R. Gravity field terrain effect computations by FFT. Bull. Géod. 1985, 59, 342–360. [Google Scholar] [CrossRef]
- Schwarz, K.P.; Sideris, M.G.; Forsberg, R. Use of FFT methods in physical geodesy. Geophys. J. Int. 1990, 100, 485–514. [Google Scholar] [CrossRef] [Green Version]
- Forsberg, R.; Sideris, M.G. Geoid computation by the multi-band spherical FFT approach. Manuscr. Geod. 1993, 18, 82–90. [Google Scholar]
- Sideris, M.G. Geoid determination by FFT techniques. In Lecture Notes, International School for the Determination and Use of the Geoid; International Geoid Service, DIIAR—Politecnico di Milano: Milano, Italy, 1994. [Google Scholar]
- Haagmans, R.; de Min, E.; Van Gelderen, M. Fast evaluation of convolution integrals on the sphere using 1D FFT and a comparison with existing methods for Stokes’ integral. Manuscr. Geod. 1993, 18, 227–241. [Google Scholar]
- Sjöberg, L.E. Refined least squares modification of Stokes’ formula. Manuscr. Geod. 1991, 16, 367–375. [Google Scholar]
- Sjöberg, L.E. A general model for modifying Stokes’ formula and its least squares solution. J. Geod. 2003, 77, 459–464. [Google Scholar] [CrossRef]
- Sjöberg, L.E. A computational scheme to model the geoid by the modified Stokes formula without gravity reductions. J. Geod. 2003, 77, 423–432. [Google Scholar] [CrossRef]
- Sjöberg, L.E. A local least-squares modification of Stokes’ formula. Stud. Geoph. Geod. 2005, 49, 23–30. [Google Scholar] [CrossRef]
- Freeden, W.; Gervens, T.; Schreiner, M. Constructive Approximation on the Sphere with Applications to Geomathematics; Oxford University Press on Demand: Oxford, UK, 1998. [Google Scholar]
- Freeden, W.; Michel, V. Multiscale Potential Theory: With Applications to Geoscience; Birkhäuser: Basel, Switzerland, 2004. [Google Scholar]
- Schmidt, M.; Han, S.C.; Kusche, J.; Sanchez, L.; Shum, C. Regional high-resolution spatiotemporal gravity modeling from GRACE data using spherical wavelets. Geophys. Res. Lett. 2006, 33, L08403. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, M.; Fengler, M.; Mayer-Gürr, T.; Eicker, A.; Kusche, J.; Sánchez, L.; Han, S.C. Regional gravity modeling in terms of spherical base functions. J. Geod. 2007, 81, 17–38. [Google Scholar] [CrossRef] [Green Version]
- Klees, R.; Tenzer, R.; Prutkin, I.; Wittwer, T. A data-driven approach to local gravity field modelling using spherical radial basis functions. J. Geod. 2008, 82, 457–471. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Schmidt, M.; Sánchez, L.; Willberg, M. Regional gravity field refinement for (quasi-) geoid determination based on spherical radial basis functions in Colorado. J. Geod. 2020, 94, 99. [Google Scholar] [CrossRef]
- Wang, Y.M.; Sánchez, L.; Agren, J.; Huang, J.; Forsberg, R.; Abd-Elmotaal, H.; Barzaghi, R.; Bašić, T.; Carrion, D.; Claessens, S.; et al. Colorado geoid computation experiment—Overview and summary. J. Geod. Special Issue on Reference Systems in Physical Geodesy (under review). 2021. [Google Scholar]
- Ligas, M.; Kulczycki, M. Kriging and moving window kriging on a sphere in geometric (GNSS/levelling) geoid modelling. Surv. Rev. 2018, 50, 155–162. [Google Scholar] [CrossRef]
- Zhong, D. Robust estimation and optimal selection of polynomial parameters for the interpolation of GPS geoid heights. J. Geod. 1997, 71, 552–561. [Google Scholar] [CrossRef]
- Das, R.K.; Samanta, S.; Jana, S.K.; Rosa, R. Polynomial interpolation methods in development of local geoid model. Egypt. J. Remote Sens. Space Sci. 2017, 21, 265–271. [Google Scholar] [CrossRef]
- Lin, L. Application of a back-propagation artificial neural network to regional grid-based geoid model generation using GPS and leveling data. J. Surv. Eng. 2007, 133, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Cakir, L.; Yilmaz, N. Polynomials, radial basis functions and multilayer perceptron neural network methods in local geoid determination with GPS/levelling. Measurement 2014, 57, 148–153. [Google Scholar] [CrossRef]
- Trojanowicz, M. Local modelling of quasigeoid heights with the use of the gravity inverse method—Case study for the area of Poland. Acta Geodyn. Geomater. 2012, 9, 5–18. [Google Scholar]
- Trojanowicz, M.; Osada, E.; Karsznia, K. Precise local quasigeoid modelling using GNSS/levelling height anomalies and gravity data. Surv. Rev. 2020, 52, 76–83. [Google Scholar] [CrossRef]
- Banasik, P.; Bujakowski, K.; Kudrys, J.; Ligas, M. Development of a precise local quasigeoid model for the city of Krakow—QuasigeoidKR2019. Rep. Geod. Geoinform. 2020, 109, 25–31. [Google Scholar] [CrossRef]
- Trojanowicz, M. Assessment of the accuracy of local quasigeoid modelling using the GGI method: Case study for the area of Poland. Studia Geophys. Geod. 2015, 59, 505–523. [Google Scholar] [CrossRef]
- Łyszkowicz, A. Quasigeoid for the area of Poland computed by least squares collocation. Tech. Sci. 2010, 13, 147–163. [Google Scholar] [CrossRef]
- Szelachowska, M.; Kryński, J. GDQM-PL13—the new gravimetric quasigeoid model for Poland. Geoinf. Issues 2014, 6, 5–19. [Google Scholar]
- Trojanowicz, M. Local disturbing potential model with the use of geophysical gravity data inversion—case study in the area of Poland. Acta Geodyn. Geomater. 2019, 16, 293–299. [Google Scholar] [CrossRef]
- Trojanowicz, M.; Owczarek-Wesołowska, M.; Pospíšil, L.; Jamroz, O. Determination of the Selected Gravity Field Functionals by the GGI Method: A Case Study of the Western Carpathians Area. Appl. Sci. 2020, 10, 7892. [Google Scholar] [CrossRef]
- Trojanowicz, M.; Owczarek-Wesołowska, M.; Wang, Y.M.; Jamroz, O. Gravimetric quasigeoid modelling by the GGI method in the Colorado mountains area. In Proceedings of the Scientific Assembly of the International Association of Geodesy, Beijing, China, 28 June–2 July 2021. [Google Scholar]
- Trojanowicz, M. Local quasigeoid modelling using gravity data inversion technique—Analysis of fixed coefficients of density model weighting matrix. Acta Geodyn. Geomater. 2012, 9, 269–281. [Google Scholar]
- Blakely, R.J. Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Nagy, D. The gravitational attraction of right angular prism. Geophysics 1966, 31, 362–371. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geod. 2001, 74, 552–560. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Sánchez, L.; Agren, J.; Huang, J.; Wang, Y.; Forsberg, R. Basic Agreements for the Computation of Station Potential Values as IHRS Coordinates, Geoid Undulations and Height Anomalies within the Colorado 1 cm Geoid Experiment. Available online: https://ihrs.dgfi.tum.de/fileadmin/JWG_2015/Colorado_Experiment_Basic_req_V0.5_Oct30_2018.pdf (accessed on 21 October 2021).
- Mäkinen, J.; Ihde, J. The Permanent Tide in Height Systems. In Observing Our Changing Earth; Internation Association of Geodesy Symposia 133; Sideris, M.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Pail, R.; Fecher, T.; Barnes, D.; Factor, J.; Holmes, S.; Gruber, T.; Zingerle, P. The experimental gravity field model XGM2016. GFZ Data Serv. 2017. [Google Scholar] [CrossRef]
- Wang, Y.M.; Saleh, J.; Li, X.; Roman, D.R. The US Gravimetric Geoid of 2009 (USGG2009): Model development and evaluation. J. Geod. 2012, 86, 165–180. [Google Scholar] [CrossRef]




| Version | The Optimal Range of | Minimal Accuracy in the Optimal Range | The Best Accuracy in the Optimal Range |
|---|---|---|---|
| Unit | cm | cm | |
| Terrestrial only | 2000–2300 | 1.5 | 1.3 |
| Airborne only | 1200–2670 | 1.9 | 1.7 |
| Combined | 1700–2670 | 1.1 | 0.9 |
| Min | Max | Mean | RMS | Stdev | Range | |
|---|---|---|---|---|---|---|
| −0.5 | 3.3 | 1.1 | 1.4 (1.0 3.4) | 0.9 (0.7 2.4) | 3.9 (3.4 13.9) | |
| −2.3 | 3.9 | 1.0 | 1.5 (1.3 3.6) | 1.2 (1.1 2.9) | 6.2 (6.8 16.6) | |
| 83.8 | 94.9 | 90.2 | 90.2 | 2.6 (1.8 3.6) | 11.2 (10.7 17.1) | |
| 82.3 | 94.7 | 89.4 | 89.9 | 2.5 (2.0 4.1) | 12.4 (10.0 25.1) |
| Min | Max | Mean | RMS | Stdev | Range | |
|---|---|---|---|---|---|---|
| −10.5 | 14.2 | 1.4 | 2.7 (1.6 5.2) | 2.3 (1.5 5.2) | 24.6 (18.0 70.0) | |
| −17.5 | 17.0 | 1.4 | 3.0 (2.3 5.6) | 2.6 (2.1 5.6) | 34.4 (25.5 68.7) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trojanowicz, M.; Owczarek-Wesołowska, M.; Wang, Y.M.; Jamroz, O. Quasi Geoid and Geoid Modeling with the Use of Terrestrial and Airborne Gravity Data by the GGI Method—A Case Study in the Mountainous Area of Colorado. Remote Sens. 2021, 13, 4217. https://doi.org/10.3390/rs13214217
Trojanowicz M, Owczarek-Wesołowska M, Wang YM, Jamroz O. Quasi Geoid and Geoid Modeling with the Use of Terrestrial and Airborne Gravity Data by the GGI Method—A Case Study in the Mountainous Area of Colorado. Remote Sensing. 2021; 13(21):4217. https://doi.org/10.3390/rs13214217
Chicago/Turabian StyleTrojanowicz, Marek, Magdalena Owczarek-Wesołowska, Yan Ming Wang, and Olgierd Jamroz. 2021. "Quasi Geoid and Geoid Modeling with the Use of Terrestrial and Airborne Gravity Data by the GGI Method—A Case Study in the Mountainous Area of Colorado" Remote Sensing 13, no. 21: 4217. https://doi.org/10.3390/rs13214217
APA StyleTrojanowicz, M., Owczarek-Wesołowska, M., Wang, Y. M., & Jamroz, O. (2021). Quasi Geoid and Geoid Modeling with the Use of Terrestrial and Airborne Gravity Data by the GGI Method—A Case Study in the Mountainous Area of Colorado. Remote Sensing, 13(21), 4217. https://doi.org/10.3390/rs13214217






