Quantifying Soil Moisture Impacts on Water Use Efficiency in Terrestrial Ecosystems of China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.3. Methods
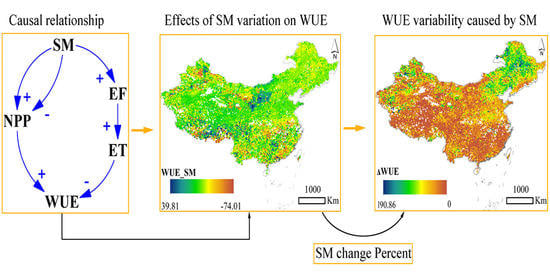
2.3.1. Mathematical Expression between SM and EF
2.3.2. The Response of WUE to SM Variation
3. Results
3.1. Data Verification
3.2. Spatiotemporal Variation of WUE
3.3. Elasticity of WUE to SM
3.4. WUE Variability Caused by SM
4. Discussion
4.1. The Reliability of Evaluation Results
4.2. The Coupling Relationship between Soil Moisture and WUE
4.3. Plausible Changing Trend and Adjustment of WUE
5. Conclusions
- (1)
- SM had an overall negative effect on the WUE in the terrestrial ecosystems during the last 30 years. In the NPP pathway, SM significantly affected WUE, and the sensitivity coefficient ranged from −68.66 to 43.19. However, in the ET pathway, SM completely negatively affected WUE. Under the dual effects of ET and NPP pathways, SM negatively affected WUE in 84.62% of the area, whereas it showed a positive influence on WUE in the remaining 15.38% of the area. Thus, although SM had a positive effect on the WUE of individual regions, it still had an overall negative effect on the WUE of each climatic zone.
- (2)
- The variation in SM could lead to a significant WUE variability, especially in Northeast and Northwest China. During the growing season in the past 30 years, the average and maximum variability of WUE caused by variation in SM were 28.02% and 109.29%, respectively. Regarding different climatic zones, SM in CTMP had the greatest effect on WUE, whereas it had the least impact on WUE in PTMP. In addition, the lower the forest covers, the higher the variability of WUE caused by changes in SM. The WUE of forest ecosystems is more resistant to changes in SM, whereas the WUE of non-forest vegetation is more sensitive to changes in SM.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, G.; Song, X.; Wang, Q.; Liu, Y.; Guan, D.; Yan, J.; Sun, X.; Zhang, L.; Wen, X. Water-use efficiency of forest ecosystems in eastern China and its relations to climatic variables. New Phytol. 2008, 177, 927–937. [Google Scholar] [CrossRef]
- Aguilos, M.; Stahl, C.; Burban, B.; Hérault, B.; Bonal, D. Interannual and Seasonal Variations in Ecosystem Transpiration and Water Use Efficiency in a Tropical Rainforest. Forests 2018, 10, 14. [Google Scholar] [CrossRef] [Green Version]
- Malone, S.L.; Tulbure, M.G.; Pérez Luque, A.J.; Assal, T.J.; Bremer, L.L.; Drucker, D.P.; Hillis, V.; Varela, S.; Goulden, M.L. Drought resistance across California ecosystems: Evaluating changes in carbon dynamics using satellite imagery. Ecosphere 2016, 7, e01561. [Google Scholar] [CrossRef]
- Wang, L.; Li, M.; Wang, J.; Li, X. An analytical reductionist framework to separate the effects of climate change and human activities on variation in water use efficiency. Sci. Total Environ. 2020, 727, 138306. [Google Scholar] [CrossRef]
- Lavergne, A.; Graven, H.; De Kauwe, M.G.; Keenan, T.F.; Medlyn, B.E.; Prentice, I.C. Observed and modelled historical trends in the water-use efficiency of plants and ecosystems. Glob. Chang. Biol. 2019, 25, 2242–2257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, J.X.; Feng, H.Z.; Xu, T.R.; Xiao, J.F.; Gueerieri, R.; Liu, S.M.; Wu, X.C.; He, X.L.; He, X.P. Physiological and environmental control on ecosystem water use efficiency in response to drought across the northern hemisphere. Sci. Total Environ. 2020, 758, 143599. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; Han, J.; Wang, J.; Ron, Y. Evaluating global ecosystem water use efficiency response to drought based on multi-model analysis. Sci. Total Environ. 2021, 778, 146356. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Sun, F.; Liu, W.; Zhang, Y.; Wang, H.; Cui, H.; Wang, H.; Zhang, J.; Du, B. Response of Ecosystem Water Use Efficiency to Drought over China during 1982 2015: Spatiotemporal Variability and Resilience. Forests 2019, 10, 598. [Google Scholar] [CrossRef] [Green Version]
- Hao, X.; Hao, H.; Zhang, J. Soil moisture influenced the variability of air temperature and oasis effect in a large inland basin of an arid region. Hydrol. Process. 2021, 35, e14246. [Google Scholar] [CrossRef]
- Yin, D.; Roderick, M.L.; Leech, G.; Sun, F.; Huang, Y. The contribution of reduction in evaporative cooling to higher surface air temperatures during drought. Geophys. Res. Lett. 2014, 41, 7891–7897. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.; Lin, H.; Zhou, W.; Bao, H.; Zhu, X.; Jin, Z.; Song, Y.; Wang, Y.; Liu, W.; Tang, Y. Revegetation has increased ecosystem water-use efficiency during 2000–2014 in the Chinese Loess Plateau: Evidence from satellite data. Ecol. Indic. 2019, 102, 507–518. [Google Scholar] [CrossRef]
- Liu, W.; Sun, F.; Sun, S.; Guo, L.; Wang, H.; Cui, H. Multi-scale assessment of eco-hydrological resilience to drought in China over the last three decades. Sci. Total Environ. 2019, 672, 201–211. [Google Scholar] [CrossRef]
- Zou, J.; Ding, J.L.; Welp, M.; Huang, S.; Liu, B.H. Assessing the Response of Ecosystem Water Use Efficiency to Drought During and after Drought Events across Central Asia. Sensors 2020, 20, 581. [Google Scholar] [CrossRef] [Green Version]
- Mokhtar, A.; He, H.; Alsafadi, K.; Mohammed, S.; He, W.; Li, Y.; Zhao, H.; Abdullahi, N.M.; Gyasi-Agyei, Y. Ecosystem Water Use Efficiency Response to Drought over Southwest China. Ecohydrology 2021, e2317. [Google Scholar] [CrossRef]
- He, B.; Wang, H.; Huang, L.; Liu, J.; Chen, Z. A new indicator of ecosystem water use efficiency based on surface soil moisture retrieved from remote sensing. Ecol. Indic. 2017, 75, 10–16. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Zha, T.; Bourque, C.P.A.; Jia, X.; Ma, J.; Liu, P.; Yang, R.; Li, C.; Du, T.; Wu, Y. Variation in ecosystem water use efficiency along a southwest-to-northeast aridity gradient in China. Ecol. Indic. 2020, 110, 105932. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, T.; Xiao, J.; Liu, S.; Mao, K.; Song, L.; Yao, Y.; He, X.; Feng, H. Responses of Water Use Efficiency to Drought in Southwest China. Remote Sens. 2020, 12, 199. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; He, B.; Han, L.; Liu, J.; Wang, H.; Chen, Z. A global examination of the response of ecosystem water-use efficiency to drought based on MODIS data. Sci. Total Environ. 2017, 601–602, 1097–1107. [Google Scholar] [CrossRef] [PubMed]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- van der Molen, M.K.; Dolman, A.J.; Ciais, P.; Eglin, T.; Gobron, N.; Law, B.E.; Meir, P.; Peters, W.; Phillips, O.L.; Reichstein, M.; et al. Drought and ecosystem carbon cycling. Agric. For. Meteorol. 2011, 151, 765–773. [Google Scholar] [CrossRef]
- Liu, X.; Feng, X.; Fu, B. Changes in global terrestrial ecosystem water use efficiency are closely related to soil moisture. Sci. Total Environ. 2020, 698, 134165. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Fu, B.; Zhang, L.; Xu, Z. Soil moisture plant interactions: An ecohydrological review. J. Soils Sediments 2019, 19, 1–9. [Google Scholar] [CrossRef]
- Stocker, B.D.; Zscheischler, J.; Keenan, T.F.; Prentice, I.C.; Pe Uelas, J.; Seneviratne, S.I. Quantifying soil moisture impacts on light use efficiency across biomes. New Phytol. 2018, 218, 1430–1449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Granier, A.; Reichstein, M.; Bréda, N.; Janssens, I.A.; Falge, E.; Ciais, P.; Grünwald, T.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; et al. Evidence for soil water control on carbon and water dynamics in European forests during the extremely dry year: 2003. Agric. For. Meteorol. 2007, 143, 123–145. [Google Scholar] [CrossRef]
- Tong, X.; Mu, Y.; Zhang, J.; Meng, P.; Li, J. Water stress controls on carbon flux and water use efficiency in a warm-temperate mixed plantation. J. Hydrol. 2019, 571, 669–678. [Google Scholar] [CrossRef]
- Nie, C.; Huang, Y.; Zhang, S.; Yang, Y.; Zhou, S.; Lin, C.; Wang, G. Effects of soil water content on forest ecosystem water use efficiency through changes in transpiration/evapotranspiration ratio. Agric. For. Meteorol. 2021, 308–309, 108605. [Google Scholar] [CrossRef]
- Boese, S.; Jung, M.; Carvalhais, N.; Reichstein, M. The importance of radiation for semiempirical water-use efficiency models. Biogeosciences 2017, 14, 3015–3026. [Google Scholar] [CrossRef] [Green Version]
- Aguilos, M.; Hérault, B.; Burban, B.; Wagner, F.; Bonal, D. What drives long-term variations in carbon flux and balance in a tropical rainforest in French Guiana? Agric. For. Meteorol. 2018, 253, 114–123. [Google Scholar] [CrossRef]
- Qi, H.; Huang, F.; Zhai, H. Monitoring Spatio-Temporal Changes of Terrestrial Ecosystem Soil Water Use Efficiency in Northeast China Using Time Series Remote Sensing Data. Sensors 2019, 19, 1481. [Google Scholar] [CrossRef] [Green Version]
- Begum, F.A.; Paul, N.K. Influence of Soil Moisture on Growth, Water Use and Yield of Mustard. J. Agron. Crop Sci. 2010, 170, 136–141. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ahmadalipour, A.; Tootle, G.; Moradkhani, H. Remote Sensing of Water Use Efficiency and Terrestrial Drought Recovery across the Contiguous United States. Remote Sens. 2019, 11, 731. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Gudmundsson, L.; Hauser, M.; Qin, D.; Seneviratne, S.I. Soil moisture dominates dryness stress on ecosystem production globally. Nat. Commun. 2020, 11, 1234567890. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Anderson, M.; Holmes, T.; Hain, C.; Reichle, R.; Koster, R.; Middleton, E.; Zeng, F.-W. Global relationships among traditional reflectance vegetation indices (NDVI and NDII), evapotranspiration (ET), and soil moisture variability on weekly timescales. Remote Sens. Environ. 2018, 219, 339–352. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Talsma, C.J.; Good, S.P.; Jimenez, C.; Martens, B.; Fisher, J.B.; Miralles, D.G.; McCabe, M.F.; Purdy, A.J. Partitioning of evapotranspiration in remote sensing-based models. Agric. For. Meteorol. 2018, 260–261, 131–143. [Google Scholar] [CrossRef]
- Li, X.D.; Shao, M.A.; Zhao, C.L.; Liu, T.; Ma, C.K. Regional spatial variability of root-zone soil moisture in arid regions and the driving factors—A case study of Xinjiang, China. Can. J. Soil Sci. 2019, 99, 277–291. [Google Scholar] [CrossRef]
- Peterson, A.M.; Helgason, W.H.; Ireson, A.M. How spatial patterns of soil moisture dynamics can explain field-scale soil moisture variability: Observations from a sodic landscape. Water Resour. Res. 2019, 55, 4410–4426. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Klooster, S.A. Terrestrial Ecosystem Production: A Process Model Based on Global Satellite and Surface Data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Guo, Q.H. Application of casa model to the estimation of Chinese terrestrial net primary productivity. Chin. J. Plant Ecol. 2001, 025, 603–608. [Google Scholar]
- Fang, J.Y.; Piao, S.L.; Field, C.B.; Pan, Y.D.; Guo, Q.H.; Zhou, L.M.; Peng, C.H.; Tao, S. Increasing net primary production in China from 1982 to 1999. Ecol. Environ. 2003, 1, 293–297. [Google Scholar] [CrossRef]
- Feng, X.; Liu, G.; Chen, J.M.; Chen, M.; Liu, J.; Ju, W.M.; Sun, R.; Zhou, W. Net primary productivity of China’s terrestrial ecosystems from a process model driven by remote sensing. J. Environ. Manag. 2007, 85, 563–573. [Google Scholar] [CrossRef]
- Pei, F.; Li, X.; Liu, X.; Lao, C. Assessing the impacts of droughts on net primary productivity in China. J. Environ. Manag. 2013, 114, 362–371. [Google Scholar] [CrossRef]
- Liang, W.; Yang, Y.; Fan, D.; Guan, H.; Zhang, T.; Long, D.; Zhou, Y.; Bai, D. Analysis of spatial and temporal patterns of net primary production and their climate controls in China from 1982 to 2010. Agric. For. Meteorol. 2015, 204, 22–36. [Google Scholar] [CrossRef]
- Chen, P.F. Monthly NPP Dataset Covering China’s Terrestrial Ecosystems at North of 18°N (1985–2015). J. Glob. Chang. Data Discov. 2019, 3, 34–41. [Google Scholar]
- Yang, K.; Watanabe, T.; Koike, T.; Li, X.; Fuji, H.; Tamagawa, K.; Ma, Y.M.; Ishikawa, H. Auto-calibration system developed to assimilate AMSR-E data into a land surface model for estimating soil moisture and the surface energy budget. J. Meteorol. Soc. Jpn. 2007, 85A, 229–242. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Chen, Y.; He, J.; Zhao, L.; Lu, H.; Qin, J.; Zheng, D.; Li, X. Development of a daily soil moisture product for the period of 2002–2011 in Chinese mainland. Sci. China Earth Sci. 2020, 63, 1113–1125. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, L.; Chen, Y.; Zhao, L.; Qin, J.; Lu, H.; Tang, W.; Han, M.; Ding, B.; Fang, N. Land surface model calibration through microwave data assimilation for improving soil moisture simulations. J. Hydrol. 2016, 533, 266–276. [Google Scholar] [CrossRef]
- Liu, B.; Henderson, M.; Zhang, Y.; Ming, X. Spatiotemporal change in China’s climatic growing season: 1955–2000. Clim. Chang. 2010, 99, 93–118. [Google Scholar] [CrossRef]
- Li, P.; Hu, Z.; Liu, Y. Shift in the trend of browning in Southwestern Tibetan Plateau in the past two decades. Agric. For. Meteorol. 2020, 287, 107950. [Google Scholar] [CrossRef]
- Wang, J.F.; Wang, G.X.; Wang, Y.B.; Li, Y.S. Influences of the degradation of swamp and alpine meadows on CO2 emission during growing season on the Qinghai-Tibet Plateau. Chin. Sci. Bull. 2007, 52, 2565–2574. [Google Scholar] [CrossRef]
- Schwingshackl, C.; Hirschi, M.; Seneviratne, S.I. Quantifying Spatiotemporal Variations of Soil Moisture Control on Surface Energy Balance and Near-Surface Air Temperature. J. Clim. 2017, 30, 7105–7124. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Nishat, S.; Guo, Y.; Baetz, B.W. Development of a simplified continuous simulation model for investigating long-term soil moisture fluctuations. Agric. Water Manag. 2007, 92, 53–63. [Google Scholar] [CrossRef]
- Wang, B.; Huang, J.; Gong, X. Grid Soil Moisture Constants Estimation based on HWSD over Basin. J. China Hydrol. 2015, 35, 8–11. [Google Scholar]
- Purdy, A.J.; Fisher, J.B.; Goulden, M.L.; Colliander, A.; Halverson, G.; Tu, K.; Famiglietti, J.S. SMAP soil moisture improves global evapotranspiration. Remote Sens. Environ. 2018, 219, 1–14. [Google Scholar] [CrossRef]
- Walker, E.; García, G.A.; Venturini, V.; Carrasco, A. Regional evapotranspiration estimates using the relative soil moisture ratio derived from SMAP products. Agric. Water Manag. 2019, 216, 254–263. [Google Scholar] [CrossRef]
- Brandes, D.; Wilcox, B.P. Evapotranspiration and soil moisture dynamics on a semiarid ponderosa pine hillslope. Jawra J. Am. Water Resour. Assoc. 2000, 36, 965–974. [Google Scholar] [CrossRef]
- Xue, B.L.; Wang, L.; Li, X.P.; Yang, K.; Chen, D.L.; Sun, L.T. Evaluation of evapotranspiration estimates for two river basins on the Tibetan Plateau by a water balance method. J. Hydrol. 2013, 492, 290–297. [Google Scholar] [CrossRef]
- Syed, T.H.; Fa Miglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44, W02433. [Google Scholar] [CrossRef]
- Hao, X.; Ma, H.; Hua, D.; Qin, J.; Zhang, Y. Response of ecosystem water use efficiency to climate change in the Tianshan Mountains, Central Asia. Environ. Monit. Assess. 2019, 191, 561. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Piao, S.; Zeng, Z.; Peng, S.; Ciais, P.; Cheng, L.; Mao, J.; Poulter, B.; Shi, X.; Yao, Y. Seasonal responses of terrestrial ecosystem water-use efficiency to climate change. Glob. Chang. Biol. 2016, 22, 2165–2177. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Yu, G.; Fu, Y.; Sun, X.; Li, Y.; Shi, P.; Wangw, Y.; Zheng, Z. Effects of vegetation control on ecosystem water use efficiency within and among four grassland ecosystems in China. Glob. Chang. Biol. 2010, 14, 1609–1619. [Google Scholar] [CrossRef]
- Li, B.; Huang, F.; Chang, S.; Sun, N. The Variations of Satellite-Based Ecosystem Water Use and Carbon Use Efficiency and Their Linkages with Climate and Human Drivers in the Songnen Plain, China. Adv. Meteorol. 2019, 2019, 8659138. [Google Scholar] [CrossRef] [Green Version]
- Garcia, A.; Guerra, L.C.; Hoogenboom, G. Water use and water use efficiency of sweet corn under different weather conditions and soil moisture regimes. Agric. Water Manag. 2009, 96, 1369–1376. [Google Scholar] [CrossRef]
- Su, B.; Shangguan, Z. Decline in soil moisture due to vegetation restoration on the Loess Plateau of China. Land Degrad. Dev. 2018, 30, 290–299. [Google Scholar] [CrossRef]
- Chen, F.; Shen, Y.; Qian, L.; Ying, G.; Xu, L. Spatio-temporal variation analysis of Ecological system NPP in China In past 30 years. Sci. Geogr. Sin. 2011, 31, 1409–1414. [Google Scholar]
- Yu, M.; Wang, G.; Parr, D.; Ahmed, K.F. Future changes of the terrestrial ecosystem based on a dynamic vegetation model driven with RCP8.5 climate projections from 19 GCMs. Clim. Chang. 2014, 127, 257–271. [Google Scholar] [CrossRef]
- Yu, L.; Gu, F.; Huang, M.; Tao, B.; Hao, M.; Wang, Z. Impacts of 1.5 °C and 2 °C Global Warming on Net Primary Productivity and Carbon Balance in China’s Terrestrial Ecosystems. Sustainability 2020, 12, 2849. [Google Scholar] [CrossRef] [Green Version]
- Lüdeke, M.K.B.; Dönges, S.; Otto, R.D.; Kindermann, J.; Badeck, F.W.; Ramge, P.; Jäkel, U.; Kohlmaier, G.H. Responses in NPP and carbon stores of the northern biomes to a CO2-induced climatic change, as evaluated by the Frankfurt biosphere model (FBM). Tellus 2010, 47, 191–205. [Google Scholar] [CrossRef] [Green Version]
- Pei, Y.; Huang, J.; Wang, L.; Chi, H.; Zhao, Y. An improved phenology-based CASA model for estimating net primary production of forest in central China based on Landsat images. Int. J. Remote Sens. 2018, 39, 7664–7692. [Google Scholar] [CrossRef]
- Sun, C.X.; Huang, G.H.; Fan, Y.; Zhou, X.; Lu, C.; Wang, X.Q. Drought Occurring with Hot Extremes: Changes under Future Climate Change on Loess Plateau, China. Earth’s Future 2019, 7, 587–604. [Google Scholar] [CrossRef] [Green Version]
- Waseem, M.; Ajmal, M.; Ahmad, I.; Khan, N.M.; Azam, M.; Sarwar, M.K. Projected drought pattern under climate change scenario using multivariate analysis. Arab. J. Geosci. 2021, 14, 1–13. [Google Scholar] [CrossRef]
- Fan, X.; Hao, X.; Hao, H.; Zhang, J.; Li, Y. Comprehensive Assessment Indicator of Ecosystem Resilience in Central Asia. Water 2021, 13, 124. [Google Scholar] [CrossRef]
- Zhang, D.S.; Li, A.L.; Lam, S.K.; Li, P.; Zong, Y.Z.; Gao, Z.Q.; Hao, X.Y. Increased carbon uptake under elevated CO2 concentration enhances water-use efficiency of C4 broomcorn millet under drought. Agric. Water Manag. 2021, 245, 106631. [Google Scholar] [CrossRef]





| Soil Diameter (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|
| >3 | 3~2 | 2~1 | 1~0.5 | 0.5~0.25 | 0.25~0.1 | 0.1~0.05 | 0.05~0.002 | <0.002 |
| rock | gravel | sand | silt | clay | ||||
| very coarse sand | coarse sand | medium sand | fine sand | very fine sand | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, X.; Zhang, J.; Fan, X.; Hao, H.; Li, Y. Quantifying Soil Moisture Impacts on Water Use Efficiency in Terrestrial Ecosystems of China. Remote Sens. 2021, 13, 4257. https://doi.org/10.3390/rs13214257
Hao X, Zhang J, Fan X, Hao H, Li Y. Quantifying Soil Moisture Impacts on Water Use Efficiency in Terrestrial Ecosystems of China. Remote Sensing. 2021; 13(21):4257. https://doi.org/10.3390/rs13214257
Chicago/Turabian StyleHao, Xingming, Jingjing Zhang, Xue Fan, Haichao Hao, and Yuanhang Li. 2021. "Quantifying Soil Moisture Impacts on Water Use Efficiency in Terrestrial Ecosystems of China" Remote Sensing 13, no. 21: 4257. https://doi.org/10.3390/rs13214257
APA StyleHao, X., Zhang, J., Fan, X., Hao, H., & Li, Y. (2021). Quantifying Soil Moisture Impacts on Water Use Efficiency in Terrestrial Ecosystems of China. Remote Sensing, 13(21), 4257. https://doi.org/10.3390/rs13214257