MIMO-SAR Interferometric Measurements for Structural Monitoring: Accuracy and Limitations
Abstract
:1. Introduction
MIMO-SAR in Structural Health Monitoring
2. MIMO-SAR Principles
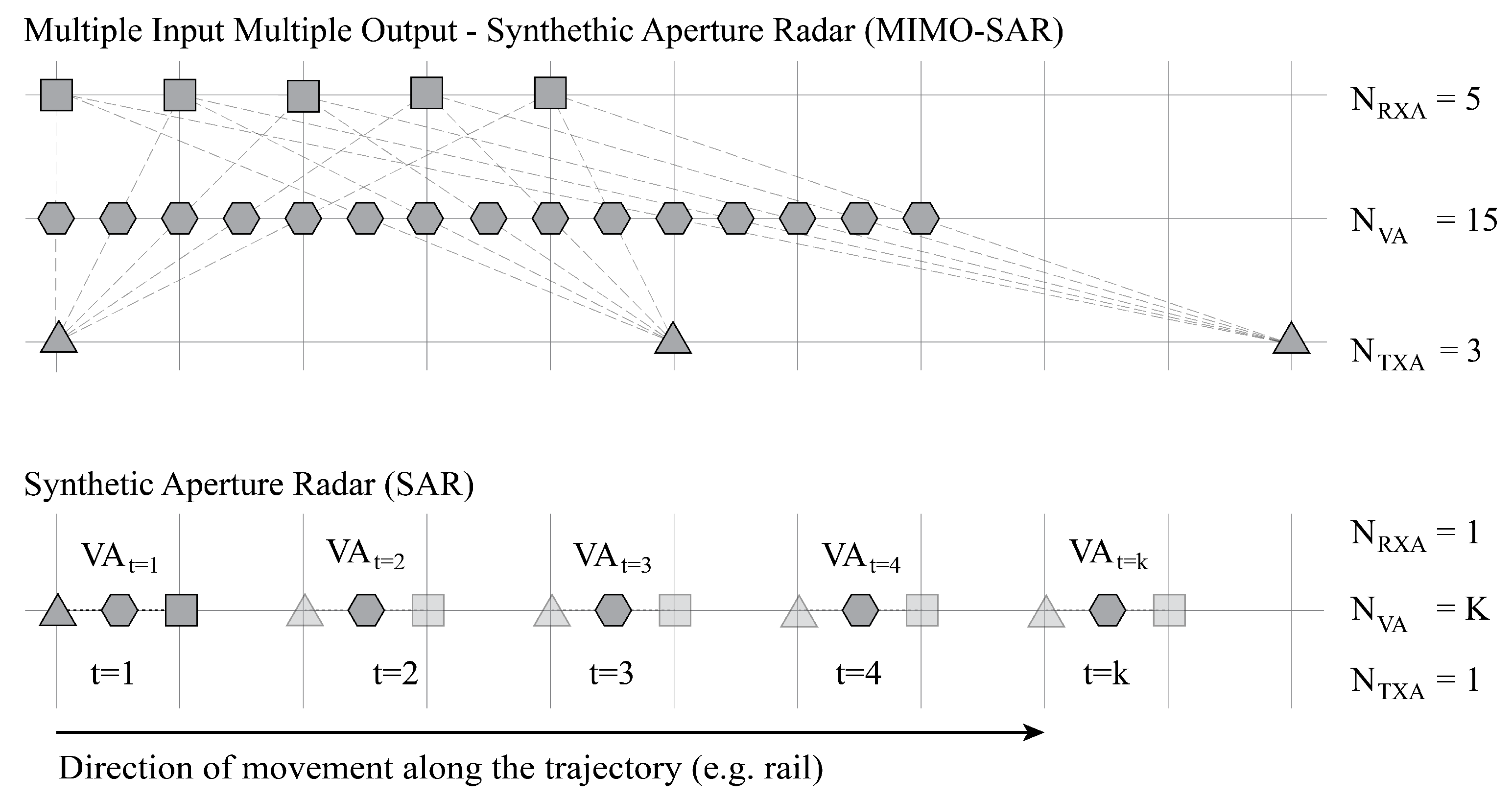
2.1. Antenna Configuration
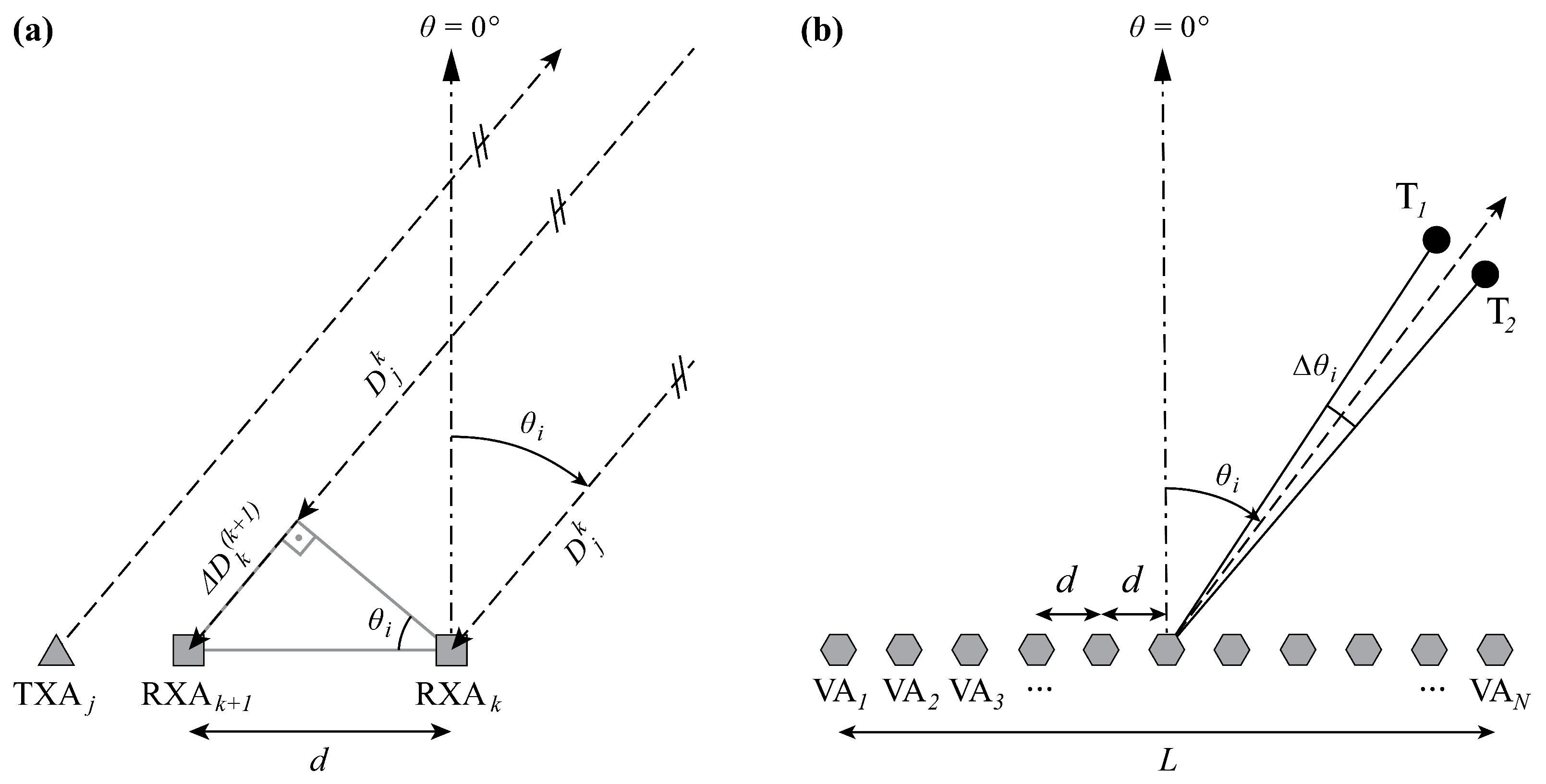
2.2. Angle Estimation and Field of View
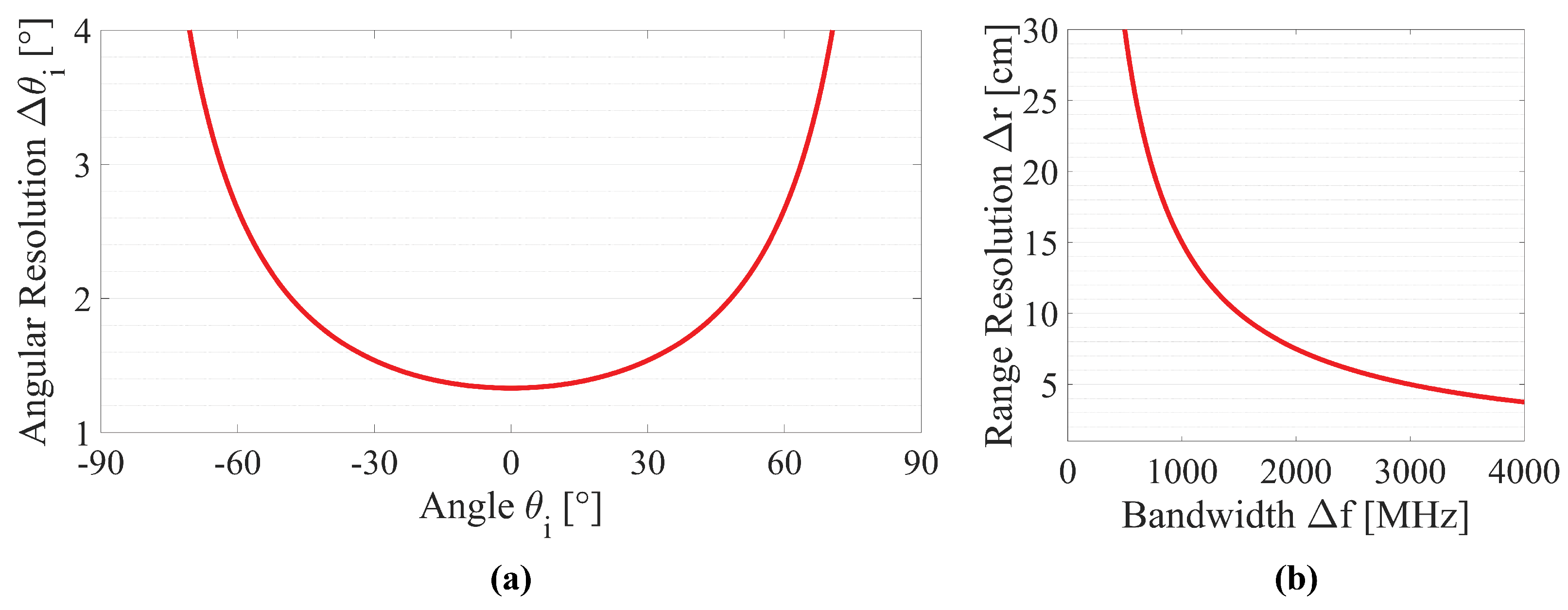
2.3. Angular and Range Resolution
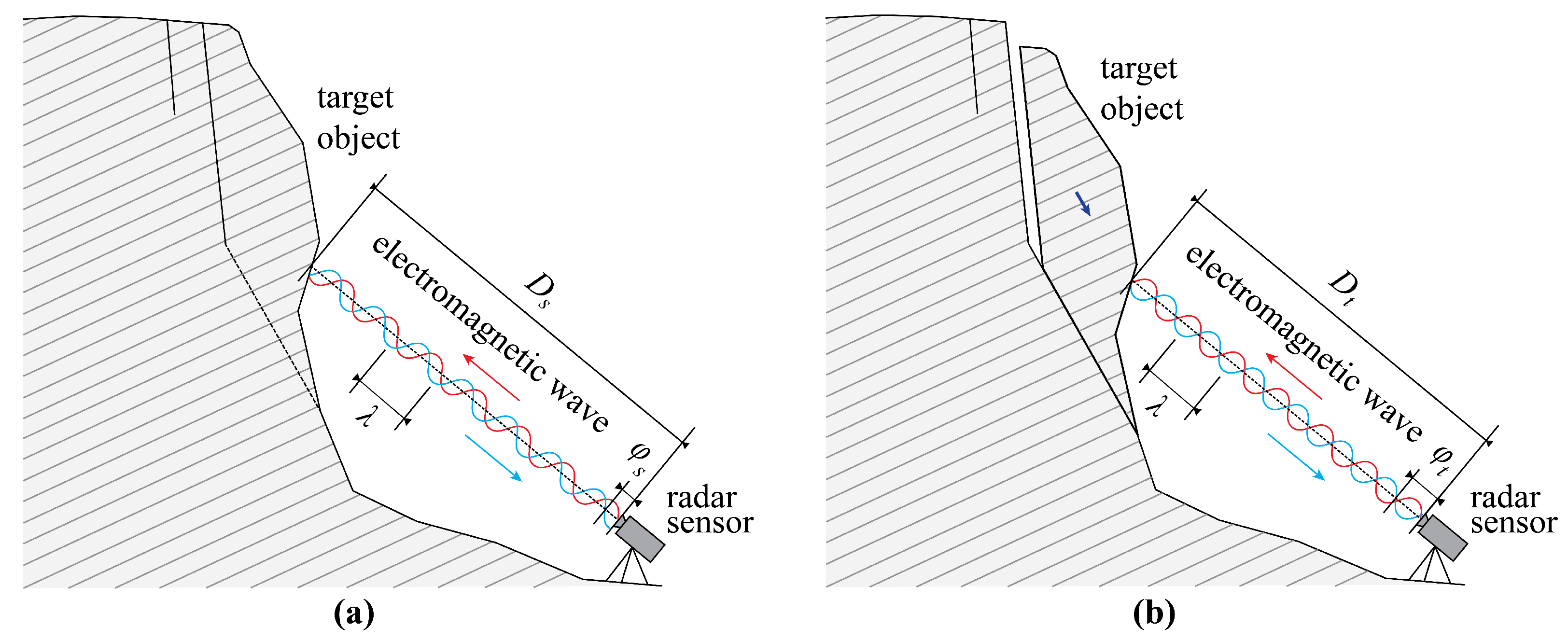
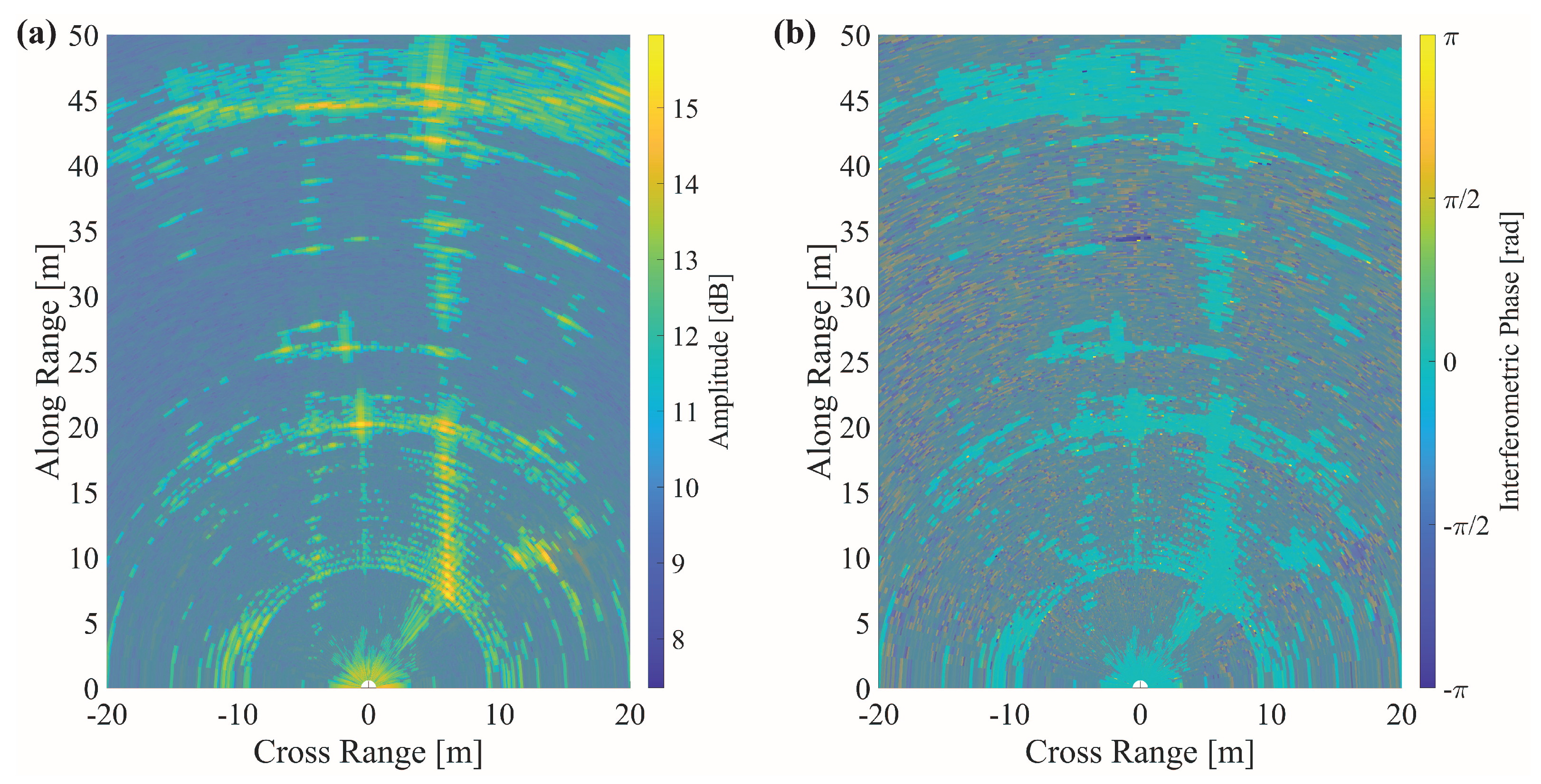
2.4. Radar Interferometry
3. Experiments
3.1. Experimental Device
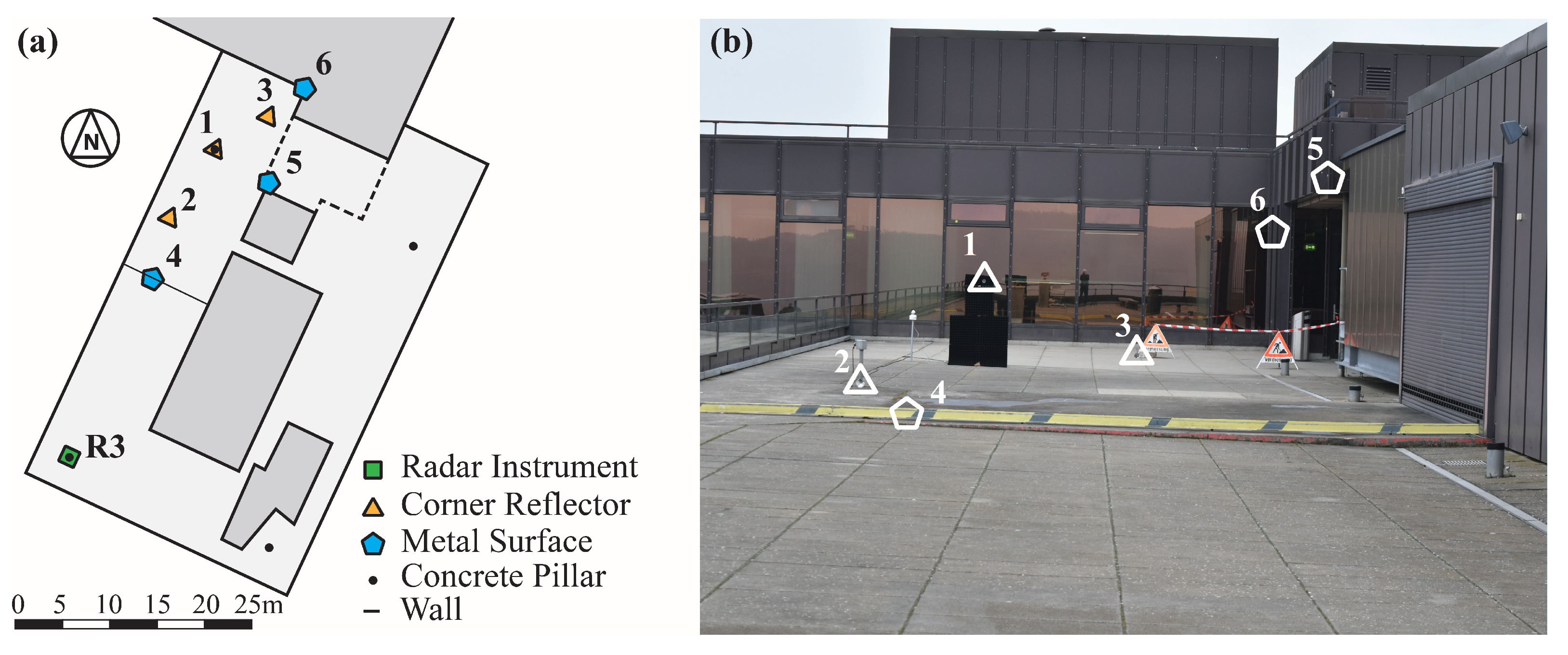
3.2. General Experimental Setup
3.3. Indoor Experiments
3.4. Outdoor Experiments
4. Results and Discussion
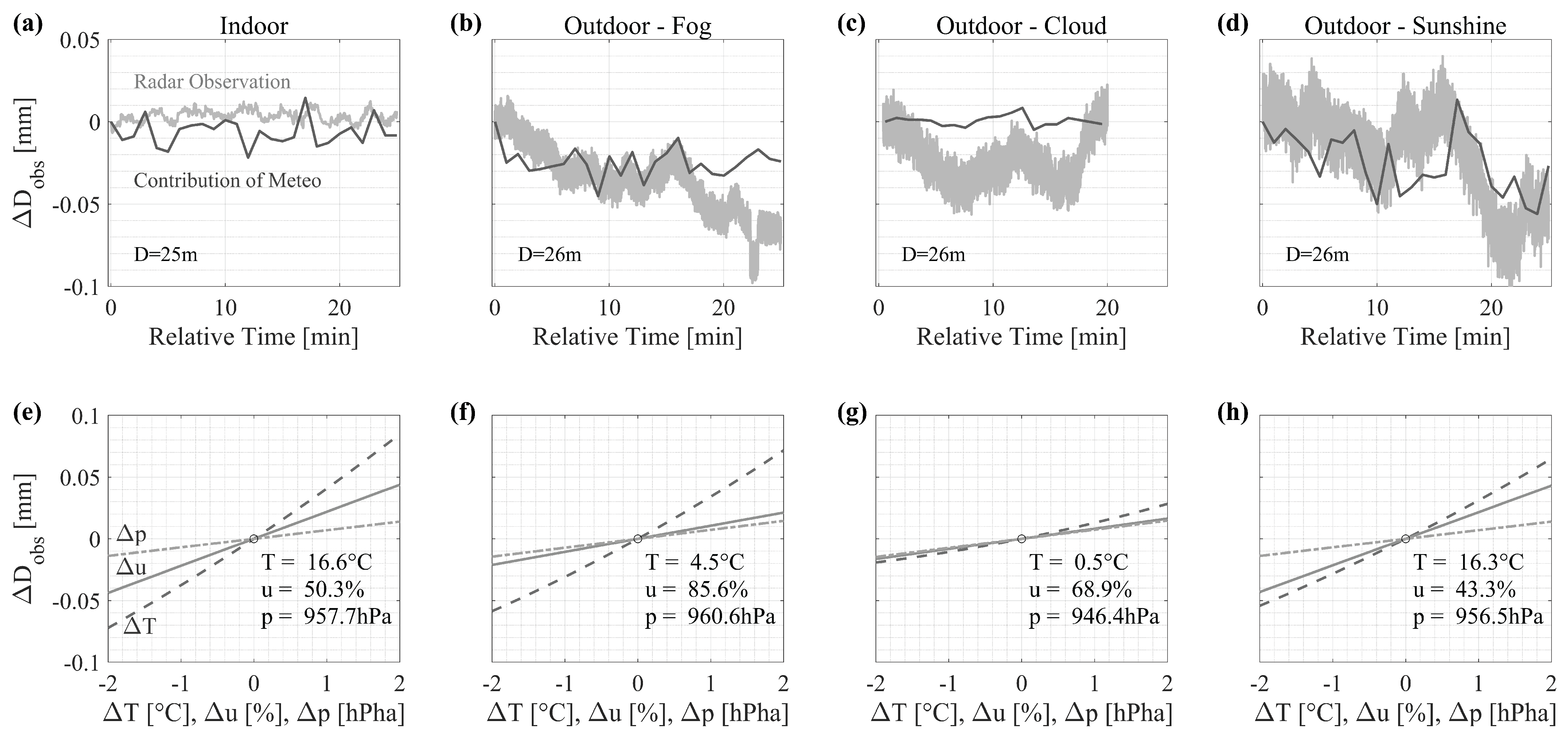
4.1. Meteorological Impacts
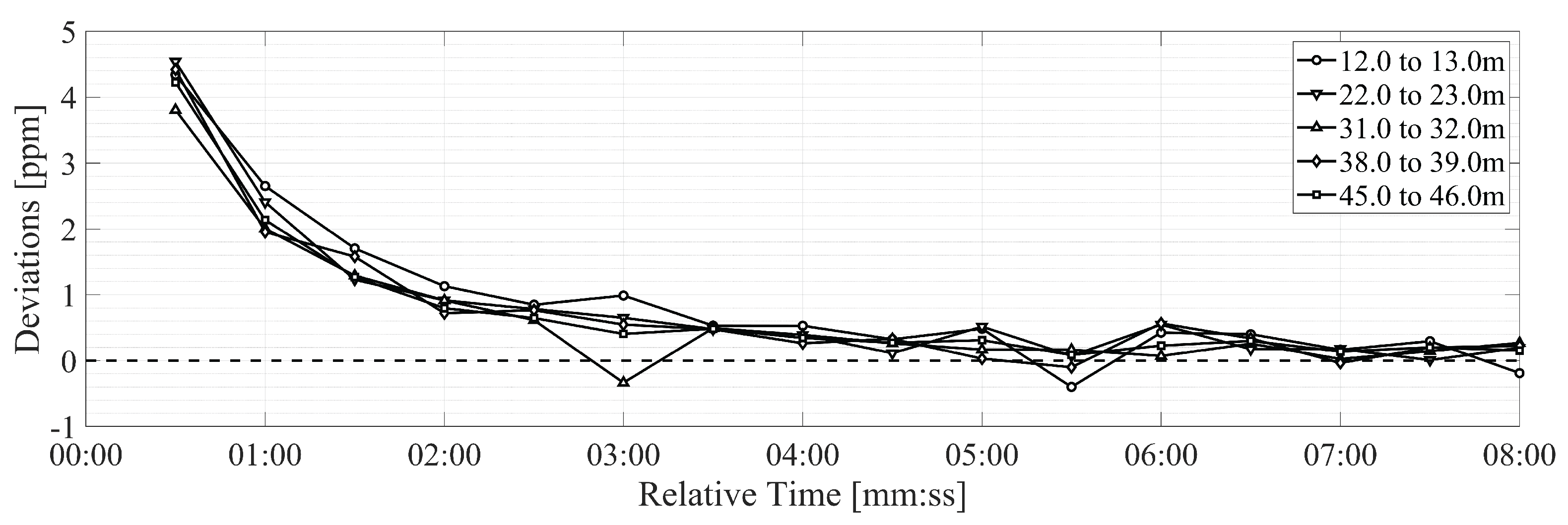
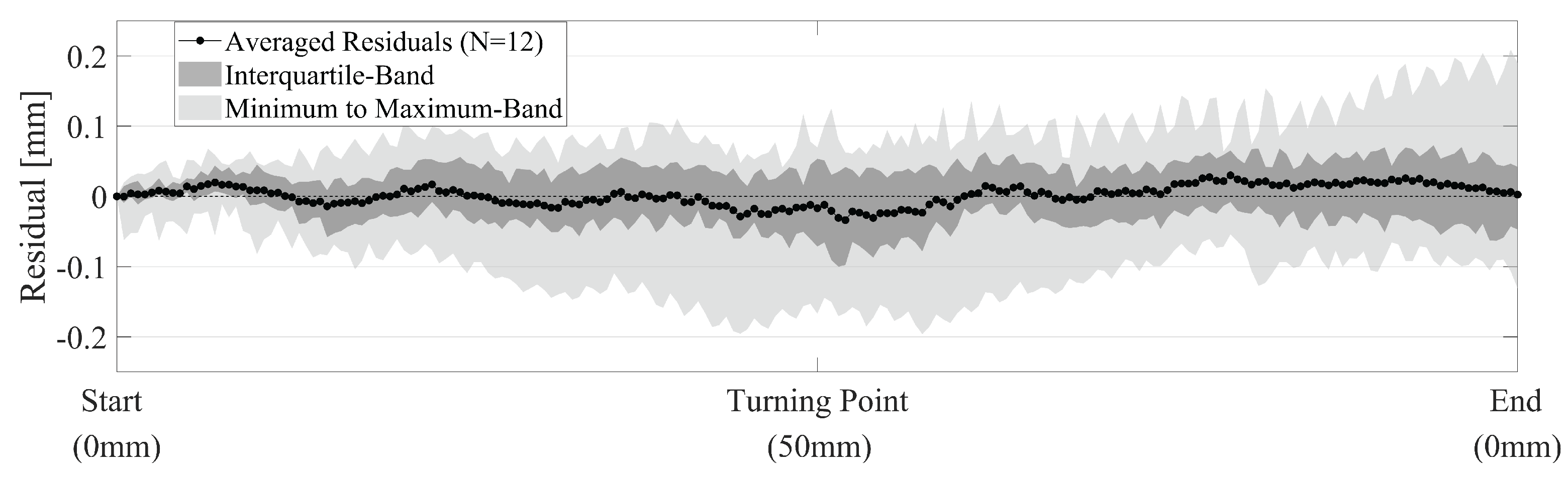
4.2. Quantification of Systematic, Instrument-Induced Effects
- •
- Mounting the radar in a protective box with active heating to stabilize the operating temperature.
- •
- Estimating the relative frequency drift based on known stable points and removing it from all observations.
- •
- Ignoring the first three minutes of acquisitions.
4.3. Quantification of Phase Stability
4.4. Detection Limits and Relative Accuracy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADC | Analog-to-Digital Converter |
| FMCW | Frequency Modulated Continous Wave |
| FOV | Field Of View |
| GNSS | Global Navigation Satellite System |
| LOS | Line Of Sight |
| MDD | Minimum Detectable Displacement |
| MIMO | Multiple Input Multiple Output |
| Radar | RAdio Detection And Ranging |
| RAR | Real Aperture Radar |
| RXA | Receiving Antenna |
| SAR | Synthetic Aperture Radar |
| SHM | Structural Health Monitoring |
| SLC | Single Look Complex |
| TRI | Terrestrial Radar Interferometry |
| TXA | Transmitting Antenna |
| VA | Virtual Antenna |
References
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef] [Green Version]
- Monserrat, G.; Crosetto, M.; Luzi, G. A review of ground-based SAR interferometry for deformation measurement. ISPRS J. Photogramm. Remote Sens. 2014, 93, 40–48. [Google Scholar] [CrossRef] [Green Version]
- Pepe, A.; Calò, F. A Review of Interferometric Synthetic Aperture RADAR (InSAR) Multi-Track Approaches for the Retrieval of Earth’s Surface Displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef] [Green Version]
- Solari, L.; Del Soldato, M.; Bianchini, S.; Ciampalini, A.; Ezquerro, P.; Montalti, R.; Raspini, F.; Moretti, S. From ERS 1/2 to Sentinel-1: Subsidence Monitoring in Italy in the Last Two Decades. Front. Earth Sci. 2018, 6, 149. [Google Scholar] [CrossRef]
- Caduff, R.; Schlunegger, F.; Kos, A.; Wiesmann, A. A review of terrestrial radar interferometry for measuring surface change in the geosciences. Earth Surf. Process. Landforms 2015, 40, 208–228. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L. Ground-Based Radar Interferometry: A Bibliographic Review. Remote Sens. 2019, 11, 1029. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Petropulu, A.P.; Poor, H.V. MIMO Radar for Advanced Driver-Assistance Systems and Autonomous Driving: Advantages and Challenges. IEEE Signal Process. Mag. 2020, 37, 98–117. [Google Scholar] [CrossRef]
- Casas, J.R.; Cruz, P.J.S. Fiber Optic Sensors for Bridge Monitoring. J. Bridge Eng. 2003, 8, 362–373. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Xue, X. Advances in the Structural Health Monitoring of Bridges Using Piezoelectric Transducers. Sensors 2018, 18, 4312. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, J.; Meng, X.; Shao, X.; Yan, B.; Yang, L. Identification of dynamic displacements and modal frequencies of a medium-span suspension bridge using multimode GNSS processing. Eng. Struct. 2014, 81, 432–443. [Google Scholar] [CrossRef]
- Sabato, A.; Niezrecki, C.; Fortino, G. Wireless MEMS-Based Accelerometer Sensor Boards for Structural Vibration Monitoring: A Review. IEEE Sens. J. 2017, 17, 226–235. [Google Scholar] [CrossRef]
- Ha, D.; Park, H.; Choi, S.; Kim, Y. A Wireless MEMS-Based Inclinometer Sensor Node for Structural Health Monitoring. Sensors 2013, 13, 16090–16104. [Google Scholar] [CrossRef] [Green Version]
- Lienhart, W.; Ehrhart, M.; Grick, M. High frequent total station measurements for the monitoring of bridge vibrations. J. Appl. Geod. 2017, 11, 1–8. [Google Scholar] [CrossRef]
- Gordon, S.; Lichti, D.; Stewart, M. Application of a high-resolution ground-based laser scanner for deformation measurements. In Proceedings of the 10th FIG International Symposium on Deformation Measurements, Orange, CA, USA, 19–22 March 2001. [Google Scholar]
- Pieraccini, M.; Fratini, M.; Parrini, F.; Atzeni, C. Dynamic Monitoring of Bridges Using a High-Speed Coherent Radar. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3284–3288. [Google Scholar] [CrossRef]
- Jung, J.; Kim, D.-J.; Palanisamy Vadivel, S.K.; Yun, S.-H. Long-Term Deflection Monitoring for Bridges Using X and C-Band Time-Series SAR Interferometry. Remote Sens. 2019, 11, 1258. [Google Scholar] [CrossRef] [Green Version]
- D’Amico, F.; Gagliardi, V.; Bianchini Ciampoli, L.; Tosti, F. Integration of InSAR and GPR techniques for monitoring transition areas in railway bridges. NDT E Int. 2020, 115, 102291. [Google Scholar] [CrossRef]
- Xiong, S.; Wang, C.; Qin, X.; Zhang, B.; Li, Q. Time-Series Analysis on Persistent Scatter-Interferometric Synthetic Aperture Radar (PS-InSAR) Derived Displacements of the Hong Kong–Zhuhai–Macao Bridge (HZMB) from Sentinel-1A Observations. Remote Sens. 2021, 13, 546. [Google Scholar] [CrossRef]
- Montalvao, D.; Maia, N.M.M.; Ribeiro, A.M.R. A review of vibration-based structural health monitoring with special emphasis on composite materials. Shock Vib. Dig. 2006, 38, 295–324. [Google Scholar] [CrossRef]
- Catieni, R. Dynamic Load Tests on Highway Bridges in Switzerland; EMPA Report No. 211; EMPA: Dübendorf, Switzerland, 1983. [Google Scholar]
- Meng, X.; Roberts, G.; Dodson, A.; Andreotti, M.; Cosser, E.; Meo, M. Development of a Prototype Remote Structural Health Monitoring System (RSHMS). In Proceedings of the 1st FIG International Symposium on Engineering Surveys for Construction Works and Structural Engineering, Nottingham, UK, 28 June–1 July 2004. [Google Scholar]
- Gaunt, J.T.; Sutton, C.D. Highway Bridge Vibration Studies. In Publication FHWA/IN/JHRP-81/11; Joint Highway Research Project; Indiana Department of Transportation: Indianapolis, IN, USA; Purdue University: West Lafayette, IN, USA, 1981. [Google Scholar]
- Shannon, C.E. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Gambi, E.; Ciattaglia, G.; De Santis, A. Automotive Radar Applications for Structural Health Monitoring. WIT Trans. Build. Environ. 2019, 189, 79–89. [Google Scholar]
- D’Aria, D.; Falcone, P.; Maggi, L.; Cero, A.; Amoroso, G. MIMO Radar-Based System for Structural Health Monitoring and Geophysical Applications. Int. J. Struct. Constr. Eng. 2019, 13, 258–265. [Google Scholar]
- Pieraccini, M.; Miccinesi, L. An Interferometric MIMO Radar for Bridge Monitoring. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1383–1387. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L.; Rojhani, N. Monitoring of Vespucci bridge in Florence, Italy using a fast real aperture radar and a MIMO radar. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1982–1985. [Google Scholar]
- Hu, C.; Wang, J.; Tian, W.; Zeng, T.; Wang, R. Design and Imaging of Ground-Based Multiple-Input Multiple-Output Synthetic Aperture Radar (MIMO SAR) with Non-Collinear Arrays. Sensors 2017, 17, 598. [Google Scholar] [CrossRef]
- Jiao, A.; Han, C.; Huo, R.; Tian, W.; Zeng, T.; Dong, X. A Method of Acquiring Vibration Mode of Bridge Based on MIMO Radar. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–6. [Google Scholar]
- Hu, C.; Deng, Y.; Tian, W.; Wang, J. A PS processing framework for long-term and real-time GB-SAR monitoring. Int. J. Remote Sens. 2019, 40, 6298–6314. [Google Scholar] [CrossRef]
- Tian, W.; Li, Y.; Hu, C.; Li, Y.; Wang, J.; Zeng, T. Vibration Measurement Method for Artificial Structure Based on MIMO Imaging Radar. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 748–760. [Google Scholar] [CrossRef]
- Tarchi, D.; Oliveri, F.; Sammartino, P.F. MIMO Radar and Ground-Based SAR Imaging Systems: Equivalent Approaches for Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 425–435. [Google Scholar] [CrossRef]
- Broussolle, J.; Kyovtorov, V.; Basso, M.; Di Silvi, E.F.; Castiglione, G.; Figueiredo Morgado, J.; Giuliani, R.; Oliveri, F.; Sammartino, P.F.; Tarchi, D. MELISSA, a new class of ground based InSAR system. An example of application in support to the Costa Concordia emergency. ISPRS J. Photogramm. Remote Sens. 2014, 91, 50–58. [Google Scholar] [CrossRef]
- Abdullah, H.; Mabrouk, M.; Abd-Elnaby Kabeel, A.; Hussein, A. High-Resolution and Large-Detection-Range Virtual Antenna Array for Automotive Radar Applications. Sensors 2021, 21, 1702. [Google Scholar] [CrossRef]
- Rao, S. MIMO Radar. In Application Report SWRA554A; Texas Instruments Inc.: Dallas, TX, USA, 2018. [Google Scholar]
- Stutzman, W.L.; Thiele, G.A. Antenna Theory and Design; Wiley: Hoboken, NJ, USA, 2012; ISBN 9780470576649. [Google Scholar]
- Brooker, G.M. Understanding Millimetre Wave FMCW Radars. In Proceedings of the 1st International Conference on Sensing Technology, Palmerston North, New Zealand, 21–23 November 2005; pp. 152–157. [Google Scholar]
- Yu, H.; Lan, Y.; Yuan, Z.; Xu, J.; Lee, H. Phase Unwrapping in InSAR: A Review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 40–58. [Google Scholar] [CrossRef]
- Thorlabs Inc. MTS25-Z8 and MTS50-Z8 Brushed DC Motorized Translation Stages. In Original Instructions HA0210T Rev K; Thorlabs Inc.: Newton, NJ, USA, 2021. [Google Scholar]
- Texas Instruments Inc. mmWave Studio Cascade. In Users Guide; Texas Instruments Inc.: Dallas, TX, USA, 2019. [Google Scholar]
- Manual Sensors with Datalogger; Reinhardt System- und Messelectronic GmbH: Obermühlhausen, Germany, 30 May 2012.
- Butt, J.; Wieser, A.; Conzett, S. Intrinsic random functions for mitigation of atmospheric effects in terrestrial radar interferometry. J. Appl. Geod. 2017, 11, 89–98. [Google Scholar] [CrossRef] [Green Version]
- Izumi, Y.; Frey, O.; Baffelli, S.; Hajnsek, I.; Sato, M. Efficient Approach for Atmospheric Phase Screen Mitigation in Time Series of Terrestrial Radar Interferometry Data Applied to Measure Glacier Velocity. JIEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7734–7750. [Google Scholar] [CrossRef]
- Rüeger, J.M. Refractive Index Formulae for Radio Waves. In Proceedings of the FIG XXII International Congress, Washington, DC, USA, 19–26 April 2002. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Quartz Crystal CX3225SA-Factsheet; CX3225SA40000D0PTWCC. Rev. 1; Kyocera Corporation: Kyoto, Japan, 8 November 2018.
- IEEE std 952. In IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Interferometric Fiber Optic Gyros; 1997 (R2008); Annex C; 1997; pp. 62–73. ISBN 1-55937-961-8.





| System Name or First Publication | Year | Angular Res. [°] | Range Res. [m] | Acquisition Rate [Hz] | Accuracy Def. [µm] | Reference |
|---|---|---|---|---|---|---|
| TI AWR1642 | 2019 | 14.3 | 4 | 16.7 | - | [24] |
| ScanBrick | 2019 | few deg. | >5 | <1000 | 10 | [25] |
| Pieraccini et al. | 2019 | 2.865 | 47 | 1/30 | 100 | [26,27] |
| Hu et al. | 2017 | 0.466 | 37.5 | 37 | sub-mm | [28,29,30,31] |
| Melissa | 2013 | 1.2 | 89 | 1.4 | 10 | [32,33] |
| Parameter | Indoor Static | Indoor Dynamic | Outdoor Dynamic |
|---|---|---|---|
| Center Frequency [GHz] | 77.72 | 77.72 | 77.72 |
| Frequency Slope [MHz/μs] | 40 | 40 | 40 |
| Idle Time [μs] | 2 | 2 | 2 |
| ADC Start Time [μs] | 2 | 2 | 2 |
| ADC Samples [-] | 512 | 512 | 512 |
| Sample Frequency [kHz] | 16,000 | 16,000 | 16,000 |
| Ramp End Time [μs] | 35 | 99 | 99 |
| Acquisition Rate [Hz] | 400 | 20 | 10 |
| Day | Location | Weather | Temperature [°C] | Humidity [%] | Pressure [hPa] |
|---|---|---|---|---|---|
| 17 October 2020 | Indoor | - | 16.0–16.8 | 49.9–50.7 | |
| 14 November 2020 | Outdoor | Sunshine | 15.8–16.6 | 40.7–44.8 | |
| 14 December 2020 | Outdoor | Fog | 3.4–4.6 | 80.3–84.9 | |
| 18 December 2020 | Outdoor | Fog | 3.8–4.8 | 82.3–90.9 | |
| 5 January 2021 | Outdoor | Cloud | 0.3–0.6 | 67.8–69.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baumann-Ouyang, A.; Butt, J.A.; Salido-Monzú, D.; Wieser, A. MIMO-SAR Interferometric Measurements for Structural Monitoring: Accuracy and Limitations. Remote Sens. 2021, 13, 4290. https://doi.org/10.3390/rs13214290
Baumann-Ouyang A, Butt JA, Salido-Monzú D, Wieser A. MIMO-SAR Interferometric Measurements for Structural Monitoring: Accuracy and Limitations. Remote Sensing. 2021; 13(21):4290. https://doi.org/10.3390/rs13214290
Chicago/Turabian StyleBaumann-Ouyang, Andreas, Jemil Avers Butt, David Salido-Monzú, and Andreas Wieser. 2021. "MIMO-SAR Interferometric Measurements for Structural Monitoring: Accuracy and Limitations" Remote Sensing 13, no. 21: 4290. https://doi.org/10.3390/rs13214290
APA StyleBaumann-Ouyang, A., Butt, J. A., Salido-Monzú, D., & Wieser, A. (2021). MIMO-SAR Interferometric Measurements for Structural Monitoring: Accuracy and Limitations. Remote Sensing, 13(21), 4290. https://doi.org/10.3390/rs13214290








