Geographic Graph Network for Robust Inversion of Particulate Matters
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. PM Measurement Data
2.2.2. Remotely Sensed Data
2.2.3. Geographic Zone
2.2.4. Reanalysis Data
2.2.5. High-Resolution Meteorology and the Other Data
2.3. Methods
2.3.1. Preprocessing
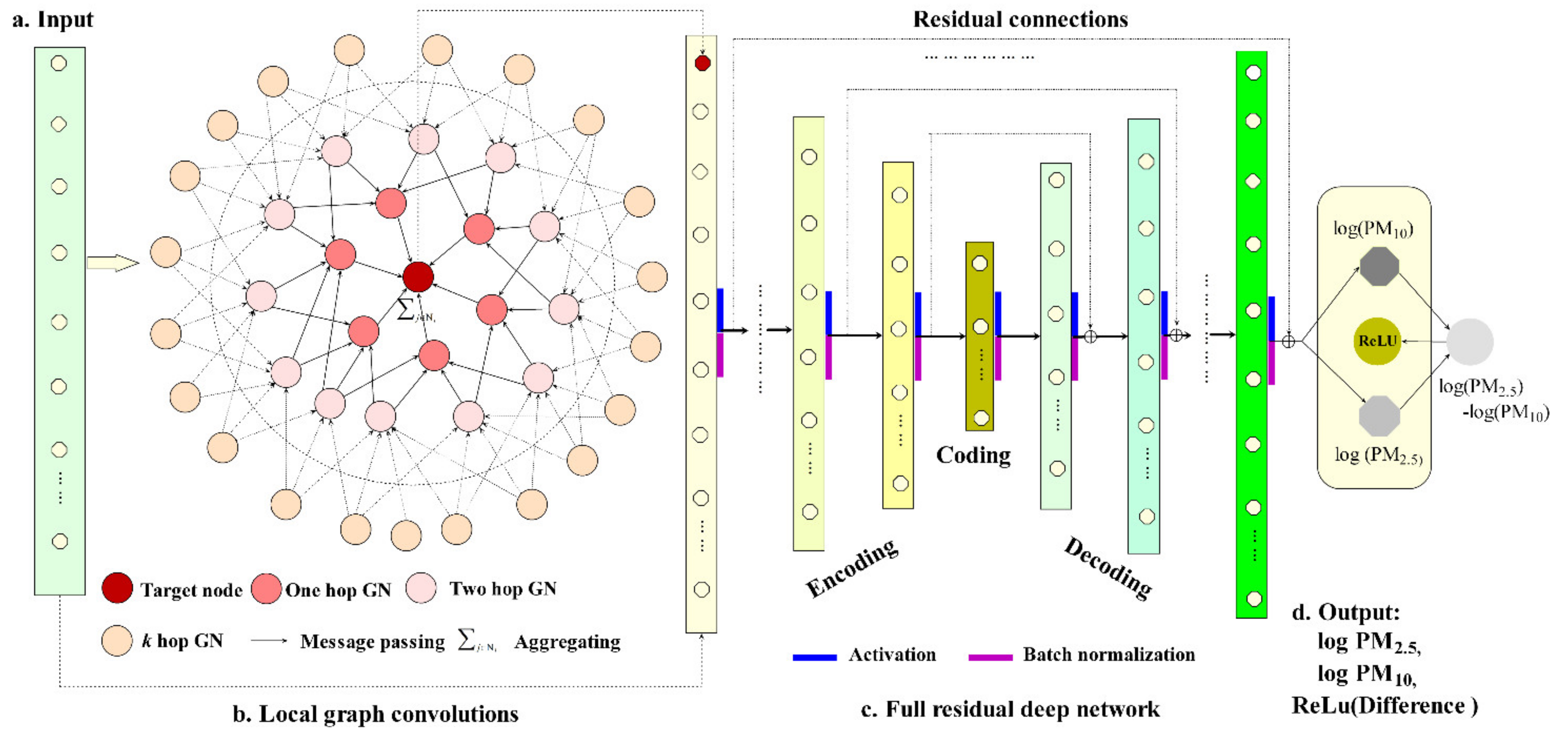
2.3.2. Geographic Graph Network
| Algorithm 1: Geographic graph convolution forward algorithm |
| Input: Set of minibatch sample indices: ; Input features: (: the set of all the nodes); Depth for convolutions: Output: Geographic graph convolution feature vector: Function: k-NN nearest function: Parameter: Matrix of reciprocal distances: ; Weight matrix for neighborhood feature: ; Weight matrix for last convolution output: 1: Calculate the matrix of reciprocal distances: ; 2: ; 3: for do 4: ; 5: for do 6: ; 7: end for 8: end for 9: ; 10: for do 11: for do 12: ; 13: ; 14: ; 15: end for 16: end for 17: Return |
2.3.3. Concatenating with Full Residual Layers
2.3.4. Parameter Sharing Output Subject to the Relationship Constraint
2.4. Evaluation
3. Results
3.1. Descriptive Statstics of PM2.5 and PM10 and Critical Covariates
3.1.1. Summary of Daily PM2.5 and PM10
3.1.2. Selection of Significant Covariates
3.2. Modeling Performance
3.3. Findings
3.3.1. Surfaces of Predicted PM2.5 and PM10 Concentration for Mainland China
3.3.2. Seasonal and Yearly Variation of the Predicted Surfaces
3.3.3. Local Variation in the Predicted Surfaces
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Class | Variable | Unit | Description and Source |
|---|---|---|---|
| PBLH | Planetary boundary layer height (PBLH) | m | From NASA GMI. |
| MERRA2-GMI | Carbon monoxide | mol mol−1 | Bottom layer diagnostics (50–60 m above the ground): hourly values for a variety of surface-level values, including PM, PM2.5, NO and NO2. These will likely provide the most valuable model inputs. |
| Dust mass mixing ratio PM2.5 | kg kg−1 | ||
| Nitrate mass mixing ratio | kg/kg | ||
| Nitrogen dioxide | mol mol−1 | ||
| Ozone | mol mol−1 | ||
| Organic carbon mass mixing ratio | kg kg−1 | ||
| Total reconstructed PM2.5 | kg m−3 | ||
| Sea salt mass mixing ratio PM2.5 | kg kg−1 | ||
| Black carbon surface mass concentration | kg m−3 | Aerosol diagnostics: total aerosol extinction on an hourly basis, which may be used for model input (and estimates of surface mass concentrations for black carbon, dust, etc.). | |
| DMS surface mass concentration | kg m−3 | ||
| Dust surface mass concentration—PM2.5 | kg m−3 | ||
| Nitric acid surface mass concentration | kg m−3 | ||
| Nitrate surface mass concentration | kg m−3 | ||
| Organic carbon surface mass concentration | kg m−3 | ||
| Total reconstructed PM2.5 | kg m−3 | ||
| SO2 surface mass concentration | kg m−3 | ||
| Sea salt surface mass concentration PM 2.5 | kg m−3 | ||
| Total aerosol extinction AOT [550 nm] | - | ||
| Sulfur dioxide local | mol mol−1 | Daily satellite overpass fields: instantaneous measurements at 10 AM and 2 PM local time. | |
| Nitrogen dioxide local | mol mol−1 | ||
| 50 m eastward wind; 10 m eastward wind; 2 m eastward wind; 50 m northward wind; 10 m northward wind; 2 m northward wind | m s−1 | Single-level diagnostics: basic meteorological information such as temperature and humidity at 2 m and 10 m. These may be useful model inputs. | |
| total tropospheric ozone | Dobsons | ||
| Derived wind variables | Stagnation of wind speed, derived from wind speeds of single-level diagnostics. | m/s | |
| Wind mechanical mixing, derived from wind speeds of single-level diagnostics. | m/s |
References
- WHO. Health Effects of Particulate Matter: Policy Implications for Countries in Eastern Europe, Caucasus and Central Asia; WHO: Geneva, Switzerland, 2013. [Google Scholar]
- Dawson, J.P.; Adams, P.J.; Pandis, S.N. Sensitivity of PM2.5 to climate in the Eastern US: A modeling case study. Atmos. Chem. Phys. Discuss. 2007, 7, 4295–4309. [Google Scholar] [CrossRef]
- Hong, C.; Zhang, Q.; Zhang, Y.; Davis, S.J.; Tong, D.; Zheng, Y.; Liu, Z.; Guan, D.; He, K.; Schellnhuber, H.J. Impacts of climate change on future air quality and human health in China. Proc. Natl. Acad. Sci. USA 2019, 116, 17193–17200. [Google Scholar] [CrossRef] [PubMed]
- IASS. Air Pollution and Climate Change. Available online: https://www.iass-potsdam.de/en/output/dossiers/air-pollution-and-climate-change (accessed on 1 March 2021).
- Kloog, I.; Ridgway, B.; Koutrakis, P.; Coull, B.A.; Schwartz, J.D. Long- and short-term exposure to PM2.5 and mortality. Epidemiology 2013, 24, 555–561. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ruan, Z.; Wang, X.; Yang, Y.; Mason, T.G.; Lin, H.; Tian, L. Short-term and long-term exposures to fine particulate matter constituents and health: A systematic review and meta-analysis. Environ. Pollut. 2019, 247, 874–882. [Google Scholar] [CrossRef] [PubMed]
- Benaissa, F.; Maesano, C.N.; Alkama, R.; Annesi-Maesano, I. Short-term health impact assessment of urban PM10 in Bejaia City (Algeria). Can. Respir. J. 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Maciejewska, K. Short-term impact of PM2.5, PM10, and PMc on mortality and morbidity in the agglomeration of Warsaw, Poland. Air Qual. Atmos. Health 2020, 13, 659–672. [Google Scholar] [CrossRef]
- Zeka, A.; Zanobetti, A.; Schwartz, J. Short term effects of particulate matter on cause specific mortality: Effects of lags and modification by city characteristics. Occup. Environ. Med. 2005, 62, 718–725. [Google Scholar] [CrossRef]
- Hoek, G.; Krishnan, R.M.; Beelen, R.; Peters, A.; Ostro, B.; Brunekreef, B.; Kaufman, J.D. Long-term air pollution exposure and cardio- respiratory mortality: A review. Environ. Health 2013, 12, 43. [Google Scholar] [CrossRef]
- EPA. Air Quality and Climate Change Research. Available online: https://www.epa.gov/air-research/air-quality-and-climate-change-research (accessed on 2 July 2021).
- Zhang, G.; Rui, X.; Fan, Y. Critical review of methods to estimate PM2.5 concentrations within specified research region. ISPRS Int. J. Geo-Inform. 2018, 7, 368. [Google Scholar] [CrossRef]
- Borghi, F.; Spinazzè, A.; Campagnolo, D.; Rovelli, S.; Cattaneo, A.; Cavallo, D.M. Precision and accuracy of a direct-reading miniaturized monitor in PM2.5 exposure assessment. Sensors 2018, 18, 3089. [Google Scholar] [CrossRef]
- NASA. MODIS Atmosphere. Available online: https://modis-images.gsfc.nasa.gov/products.html (accessed on 3 September 2020).
- NASA. MODIS Grids. Available online: https://modis-land.gsfc.nasa.gov/MODLAND_grid.html (accessed on 1 June 2021).
- Lyapustin, A.; Martonchik, J.; Wang, Y.; Laszlo, I.; Korkin, S. Multiangle implementation of atmospheric correction (MAIAC): 1. Radiative transfer basis and look-up tables. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y. MODIS Multi-Angle Implementation of Atmospheric Correction (MAIAC) Data User’s Guide; NASA. 2016. Available online: https://lpdaac.usgs.gov/documents/110/MCD19_User_Guide_V6.pdf (accessed on 1 April 2019).
- Lyapustin, A.; Wang, Y.; Laszlo, I.; Kahn, R.; Korkin, S.; Remer, L.; Levy, R.; Reid, J.S. Multiangle implementation of atmospheric correction (MAIAC): 2. Aerosol algorithm. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Korkin, S.; Huang, D. MODIS Collection 6 MAIAC algorithm. Atmos. Meas. Tech. 2018, 11, 5741–5765. [Google Scholar] [CrossRef]
- Mhawish, A.; Banerjee, T.; Sorek-Hamer, M.; Lyapustin, A.; Broday, D.M.; Chatfield, R. Comparison and evaluation of MODIS Multi-angle Implementation of Atmospheric Correction (MAIAC) aerosol product over South Asia. Remote. Sens. Environ. 2019, 224, 12–28. [Google Scholar] [CrossRef]
- Tao, M.; Wang, J.; Li, R.; Wang, L.; Wang, L.; Wang, Z.; Tao, J.; Che, H.; Chen, L. Performance of MODIS high-resolution MAIAC aerosol algorithm in China: Characterization and limitation. Atmos. Environ. 2019, 213, 159–169. [Google Scholar] [CrossRef]
- Chiliński, M.T.; Markowicz, K.; Kubicki, M. UAS as a support for atmospheric aerosols research: Case study. Pure Appl. Geophys. PAGEOPH 2018, 175, 3325–3342. [Google Scholar] [CrossRef]
- Mamali, D.; Marinou, E.; Sciare, J.; Pikridas, M.; Kokkalis, P.; Kottas, M.; Binietoglou, I.; Tsekeri, A.; Keleshis, C.; Engelmann, R.; et al. Vertical profiles of aerosol mass concentration derived by unmanned airborne in situ and remote sensing instruments during dust events. Atmos. Meas. Tech. 2018, 11, 2897–2910. [Google Scholar] [CrossRef]
- Pikridas, M.; Bezantakos, S.; Močnik, G.; Keleshis, C.; Brechtel, F.; Stavroulas, I.; Demetriades, G.; Antoniou, P.; Vouterakos, P.; Argyrides, M.; et al. On-flight intercomparison of three miniature aerosol absorption sensors using unmanned aerial systems (UASs). Atmos. Meas. Tech. 2019, 12, 6425–6447. [Google Scholar] [CrossRef]
- NASA. Modern-Era Retrospective Analysis for Research and Applications, Version 2. Available online: https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/ (accessed on 1 April 2020).
- Nielsen, J.E.; Pawson, S.; Molod, A.; Auer, B.; da Silva, A.M.; Douglass, A.R.; Duncan, B.; Liang, Q.; Manyin, M.; Oman, L.D.; et al. Chemical mechanisms and their applications in the Goddard Earth Observing System (GEOS) earth system model. J. Adv. Model. Earth Syst. 2017, 9, 3019–3044. [Google Scholar] [CrossRef]
- Akyurtlu, A.; Akyurtlu, J. Investitation of Fine Particulate Matter, NOx and Tropospheric Ozone Transport Around a Major Roadway; Hampton University: Hampton, VI, USA, 2013. [Google Scholar]
- Frontera, A.; Martin, C.; Vlachos, K.; Sgubin, G. Regional air pollution persistence links to COVID-19 infection zoning. J. Infect. 2020, 81, 318–356. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Liu, J.; Gao, W.; Song, T.; Sun, Y.; Li, L.; Li, X.; Wang, Y.; Liu, L.; et al. Exploring the regional pollution characteristics and meteorological formation mechanism of PM2.5 in North China during 2013–2017. Environ. Int. 2020, 134, 105283. [Google Scholar] [CrossRef]
- Benson, P. CALINE4—A Dispersion Model for Predicting Air Pollutant Concentrations Near Roadways; California Department of Transportation: Sacramento CA, USA, 1989.
- Bey, I.; Jacob, D.J.; Yantosca, R.; Logan, J.A.; Field, B.D.; Fiore, A.M.; Li, Q.; Liu, H.Y.; Mickley, L.J.; Schultz, M. Global modeling of tropospheric chemistry with assimilated meteorology: Model description and evaluation. J. Geophys. Res. Space Phys. 2001, 106, 23073–23095. [Google Scholar] [CrossRef]
- Byun, D.W.; Ching, J. Science Algorithms of the EPA Models-3 Community Multiscale Air Quality (CMAQ) Modeling System; United States Environmental Protection Agency: Washington, DC, USA, 1999.
- EPA. CMAQ v5.2 Operational Guidance Document. Available online: https://github.com/USEPA/CMAQ/blob/5.2/DOCS/User_Manual/README.md (accessed on 2 July 2020).
- Quennehen, B.; Raut, J.-C.; Law, K.S.; Daskalakis, N.; Ancellet, G.; Clerbaux, C.; Kim, S.-W.; Lund, M.T.; Myhre, G.; Olivié, D.J.L.; et al. Multi-model evaluation of short-lived pollutant distributions over east Asia during summer 2008. Atmos. Chem. Phys. Discuss. 2016, 16, 10765–10792. [Google Scholar] [CrossRef]
- Appel, K.W.; Chemel, C.; Roselle, S.; Francis, X.V.; Hu, R.-M.; Sokhi, R.S.; Rao, S.; Galmarini, S. Examination of the Community Multiscale Air Quality (CMAQ) model performance over the North American and European domains. Atmos. Environ. 2012, 53, 142–155. [Google Scholar] [CrossRef]
- Butland, B.K.; Armstrong, B.; Atkinson, R.W.; Wilkinson, P.; Heal, M.R.; Doherty, R.M.; Vieno, M. Measurement error in time-series analysis: A simulation study comparing modelled and monitored data. BMC Med. Res. Methodol. 2013, 13, 136. [Google Scholar] [CrossRef]
- Strickland, M.J.; Gass, K.; Goldman, G.T.; Mulholland, J.A. Effects of ambient air pollution measurement error on health effect estimates in time-series studies: A simulation-based analysis. J. Expo. Sci. Environ. Epidemiol. 2015, 25, 160–166. [Google Scholar] [CrossRef]
- Strickland, M.J.; Hao, H.; Hu, X.; Chang, H.H.; Darrow, L.A.; Liu, Y. Pediatric emergency visits and short-term changes in pm concentrations in the U.S. State of Georgia. Environ. Health Perspect. 2016, 124, 690–696. [Google Scholar] [CrossRef]
- Cressie, N. The origins of kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Gribov, A.; Krivoruchko, K. Empirical Bayesian kriging implementation and usage. Sci. Total Environ. 2020, 722, 137290. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Goovaerts, P. Ordinary cokriging revisited. Math. Geol. 1998, 30, 21–42. [Google Scholar] [CrossRef]
- Chu, Y.; Liu, Y.; Li, X.; Liu, Z.; Lu, H.; Lu, Y.; Mao, Z.; Chen, X.; Li, N.; Ren, M.; et al. A review on predicting ground PM2.5 concentration using satellite aerosol optical depth. Atmosphere 2016, 7, 129. [Google Scholar] [CrossRef]
- Hoek, G.; Beelen, R.; de Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]
- Lin, Y.; Zou, J.; Yang, W.; Li, C.-Q. A review of recent advances in research on PM2.5 in China. Int. J. Environ. Res. Public Health 2018, 15, 438. [Google Scholar] [CrossRef]
- Pebesma, E.; Graler, B. Introduction to Spatio-Temporal Variography; University of Münster: Münster, Germany, 2021. [Google Scholar]
- Song, Y.-Z.; Yang, H.-L.; Peng, J.-H.; Song, Y.-R.; Sun, Q.; Li, Y. Estimating PM2.5 concentrations in Xi’an City using a generalized additive model with multi-source monitoring data. PLoS ONE 2015, 10, e0142149. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Jia, H.; Huang, J.; Zhang, Y. A satellite-based geographically weighted regression model for regional PM2.5 estimation over the Pearl River Delta region in China. Remote. Sens. Environ. 2014, 154, 1–7. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Spurr, R.J.D.; Burnett, R.T. High-resolution satellite-derived PM2.5 from optimal estimation and geographically weighted regression over North America. Environ. Sci. Technol. 2015, 49, 10482–10491. [Google Scholar] [CrossRef]
- Mirzaei, M.; Bertazzon, S.; Couloigner, I.; Farjad, B.; Ngom, R. Estimation of local daily PM2.5 concentration during wildfire episodes: Integrating MODIS AOD with multivariate linear mixed effect (LME) models. Air Qual. Atmos. Health 2019, 13, 173–185. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, Y.; Zhang, K.; Dong, W.; Lv, B.; Bai, Y. Daily estimation of ground-Level PM2.5 concentrations over Beijing using 3 km resolution MODIS AOD. Environ. Sci. Technol. 2015, 49, 12280–12288. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Yu, Z.; Qu, Y.; Xu, J.; Cao, Y. Application of the XGBoost machine learning method in PM2.5 prediction: A case study of Shanghai. Aerosol Air Qual. Res. 2020, 20, 128–138. [Google Scholar] [CrossRef]
- Pan, B. Application of XGBoost algorithm in hourly PM2.5 concentration prediction. IOP Conf. Ser. Earth Environ. Sci. 2018, 113, 012127. [Google Scholar] [CrossRef]
- Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 concentrations in the conterminous United States using the random forest approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef]
- Li, L.; Fang, Y.; Wu, J.; Wang, J.; Ge, Y. Encoder–decoder full residual deep networks for robust regression and spatiotemporal estimation. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 4217–4230. [Google Scholar] [CrossRef] [PubMed]
- Spielman, D. Spectral Graph Theory. In Combinatorial Scientific Computing; Routledge: London, UK, 2012; pp. 495–524. [Google Scholar]
- Jain, A.; Liu, I.; Sarda, A.; Monino, P. Food Discovery with Uber Eats: Using Graph Learning to Power Recommendations. Available online: https://eng.uber.com/uber-eats-graph-learning/ (accessed on 1 March 2021).
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph Convolutional Neural Networks for Web-Scale Recommender Systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- Watters, N.; Tacchetti, A.; Weber, B.; Pascanu, R.; Zoran, D. Visual Interaction Networks: Learning a Physics Simulator from Video. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Mirhoseini, A.; Goldie, A.; Yazgan, M.; Jiang, J. Chip placement with deep reinforcement learning. arXiv 2020, arXiv:2004.10746. [Google Scholar]
- Sarlin, P.-E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperGlue: Learning Feature Matching with Graph Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Chanussot, L.; Das, A.; Goyal, S.; Lavril, T.; Shuaibi, M.; Riviere, M.; Tran, K.; Heras-Domingo, J.; Ho, C.; Hu, W.; et al. Open catalyst 2020 (OC20) dataset and community challenges. ACS Catal. 2021, 11, 6059–6072. [Google Scholar] [CrossRef]
- Stokes, J.M.; Yang, K.; Swanson, K.; Jin, W.; Cubillos-Ruiz, A.; Donghia, N.M.; Macnair, C.R.; French, S.; Carfrae, L.A.; Bloom-Ackermann, Z.; et al. A deep learning approach to antibiotic discovery. Cell 2020, 180, 688–702. [Google Scholar] [CrossRef] [PubMed]
- Gaudelet, T.; Day, B.; Jamasb, A.; Soman, J.; Regep, C.; Liu, G.; Hayter, J.; Vickers, R.; Roberts, C.; Tang, J.; et al. Utilizing graph machine learning within drug discovery and development. arXiv 2021, arXiv:2012.05716. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems 2017 (Nips 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 1025–1035. [Google Scholar]
- Ge, L.; Wu, K.; Zeng, Y.; Chang, F.; Wang, Y.; Li, S. Multi-scale spatiotemporal graph convolution network for air quality prediction. Appl. Intell. 2021, 51, 3491–3505. [Google Scholar] [CrossRef]
- Qi, Y.; Li, Q.; Karimian, H.; Liu, D. A hybrid model for spatiotemporal forecasting of PM2.5 based on graph convolutional neural network and long short-term memory. Sci. Total Environ. 2019, 664, 1–10. [Google Scholar] [CrossRef]
- Abadal, S.; Jain, A.; Guirado, R.; López-Alonso, J.; Alarcón, E. Computing graph neural networks: A survey from algorithms to accelerators. ACM Comput. Surv. 2021, 54, 1–38. [Google Scholar] [CrossRef]
- China Meteorological Administration. China Climate Bulletin 2020; China Meteorological Administration: Beijing, China, 2020. (In Chinese)
- Tang, W.-J.; Yang, K.; Qin, J.; Cheng, C.C.K.; He, J. Solar radiation trend across China in recent decades: A revisit with quality-controlled data. Atmos. Chem. Phys. Discuss. 2011, 11, 393–406. [Google Scholar] [CrossRef]
- Wikipedia. China Climate. Available online: https://zh.wikipedia.org/zh-cn/%E4%B8%AD%E5%9B%BD%E6%B0%94%E5%80%99 (accessed on 10 July 2021). (In Chinese).
- Ding, Y. China Climate; Science Press: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Chen, B. Driving forces of particulate matter emissions in China. Energy Procedia 2017, 105, 4601–4606. [Google Scholar] [CrossRef]
- Yan, B.; Liu, S.; Zhao, B.; Li, X.; Fu, Q.; Jiang, G. China’s fight for clean air and human health. Environ. Sci. Technol. 2018, 52, 8063–8064. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Luo, L.; Wang, S.; Wang, Y.; Sharma, S.; Shimadera, H.; Wang, X.; Bressi, M.; de Miranda, R.M.; Jiang, J.; et al. Status and characteristics of ambient PM2.5 pollution in global megacities. Environ. Int. 2016, 89–90, 212–221. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Zhao, S.; Jiao, L.; Taylor, M.; Zhang, B.; Xu, G.; Hou, H. Estimation of PM2.5 concentrations in China using a spatial back propagation neural network. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Nosratabadi, A.R.; Graff, P.; Karlsson, H.; Ljungman, A.G.; Leanderson, P. Use of TEOM monitors for continuous long-term sampling of ambient particles for analysis of constituents and biological effects. Air Qual. Atmos. Health 2019, 12, 161–171. [Google Scholar] [CrossRef]
- Guo, J.-P.; Zhang, X.-Y.; Che, H.; Gong, S.-L.; An, X.; Cao, C.-X.; Guang, J.; Zhang, H.; Wang, Y.-Q.; Xue, M.; et al. Correlation between PM concentrations and aerosol optical depth in eastern China. Atmos. Environ. 2009, 43, 5876–5886. [Google Scholar] [CrossRef]
- Li, L. High-resolution mapping of aerosol optical depth and ground aerosol coefficients for mainland China. Remote. Sens. 2021, 13, 2324. [Google Scholar] [CrossRef]
- Li, L.; Franklin, M.; Girguis, M.; Lurmann, F.; Wu, J.; Pavlovic, N.; Breton, C.; Gilliland, F.; Habre, R. Spatiotemporal imputation of MAIAC AOD using deep learning with downscaling. Remote. Sens. Environ. 2020, 237, 111584. [Google Scholar] [CrossRef] [PubMed]
- Seger, C. An Investigation of Categorical Variable Encoding Techniques in Machine Learning: Binary Versus One-Hot and Feature Hashing; KTH Royal Institute of Technology: Stockholm, Sweden, 2018. [Google Scholar]
- NASA. MERRA-2 GMI. Available online: https://acd-ext.gsfc.nasa.gov/Projects/GEOSCCM/MERRA2GMI/ (accessed on 1 June 2020).
- Press, H.W.; Teukolsky, A.S.; Vetterling, T.W.; Flannery, P.B. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992; pp. 123–128. [Google Scholar]
- Fang, Y.; Li, L. Estimation of high-precision high-resolution meteorological factors based on machine learning. J. Geo-Inform. Sci. 2019, 21, 799–813. [Google Scholar]
- Li, L. Geographically weighted machine learning and downscaling for high-resolution spatiotemporal estimations of wind speed. Remote. Sens. 2019, 11, 1378. [Google Scholar] [CrossRef]
- Iglewicz, B.; Hoaglin, C.D. How to detect and handle outliers. In The ASQ Basic References in Quality Control: Statistical Techniques; Mykytka, F.E., Ed.; American Society for Quality: Milwaukee, WI, USA, 1993. [Google Scholar]
- Wang, X.; Dickinson, R.E.; Su, L.; Zhou, C.; Wang, K. PM2.5 pollution in China and how it has been exacerbated by terrain and meteorological conditions. Bull. Am. Meteorol. Soc. 2018, 99, 105–119. [Google Scholar] [CrossRef]
- Zhai, S.; Jacob, D.J.; Wang, X.; Shen, L.; Li, K.; Zhang, Y.; Gui, K.; Zhao, T.; Liao, H. Fine particulate matter (PM2.5) trends in China, 2013–2018: Separating contributions from anthropogenic emissions and meteorology. Atmos. Chem. Phys. Discuss. 2019, 19, 11031–11041. [Google Scholar] [CrossRef]
- Dyatmika, H.; Sambodo, K.; Budiono, M.; Hendayani, B. Noise removal using thresholding and segmentation for random noise Sentinel-1 data. IOP Conf. Ser. Earth Environ. Sci. 2017, 54, 012105. [Google Scholar] [CrossRef]
- Freedman, D.; Pisani, R.; Purves, R. Statistics: Fourth International Student Edition; W.W. Norton & Company: New York, NY, USA, 2007. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Tobler, W. On the First Law of Geography: A Reply. Ann. Assoc. Am. Geogr. 2004, 94, 304–310. [Google Scholar] [CrossRef]
- Kipf, T.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Chen, D.; Lin, Y.; Li, W.; Li, P.; Zhou, J.; Sun, X. Measuring and Relieving the Over-Smoothing Problem for Graph Neural Networks from the Topological View. In Proceedings of the AAAI Conference on Artificial Intelligence 2020, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3438–3445. [Google Scholar]
- Li, L.; Girguis, M.; Lurmann, F.; Pavlovic, N.; McClure, C.; Franklin, M.; Wu, J.; Oman, L.D.; Breton, C.; Gilliland, F.; et al. Ensemble-based deep learning for estimating PM2.5 over California with multisource big data including wildfire smoke. Environ. Int. 2020, 145, 106143. [Google Scholar] [CrossRef] [PubMed]
- Gong, P.; Li, X.; Zhang, W. 40-Year (1978–2017) human settlement changes in China reflected by impervious surfaces from satellite remote sensing. Sci. Bull. 2019, 64, 756–763. [Google Scholar] [CrossRef]
- Bishop, M.C. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Lundberg, S.M. Welcome to the SHAP Documentation. Available online: https://shap.readthedocs.io/en/latest/index.html (accessed on 5 January 2021).
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems (Nips 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Baidu. 4.15 Sandstorm in Beijing. Available online: https://baike.baidu.com/item/4%C2%B715%E5%8C%97%E4%BA%AC%E6%B2%99%E5%B0%98%E6%9A%B4 (accessed on 12 April 2021).
- Li, X.; Jin, L.; Kan, H. Air pollution: A global problem needs local fixes. Nature 2019, 570, 437–439. [Google Scholar] [CrossRef]
- Baidu. Beijing Clean Air Action Plan for 2013–2017. Available online: https://baike.baidu.com/item/%E5%8C%97%E4%BA%AC%E5%B8%822013-2017%E5%B9%B4%E6%B8%85%E6%B4%81%E7%A9%BA%E6%B0%94%E8%A1%8C%E5%8A%A8%E8%AE%A1%E5%88%92/10348277?fr=aladdin (accessed on 2 January 2021). (In Chinese).
- Pang, N.; Gao, J.; Zhu, G.; Hui, L.; Zhao, P.; Xu, Z.; Tang, W.; Chai, F. Impact of clean air action on the PM2.5 pollution in Beijing, China: Insights gained from two heating seasons measurements. Chemosphere 2021, 263, 127991. [Google Scholar] [CrossRef] [PubMed]
- Saunders, A.; Oldenburg, I.A.; Berezovskii, V.; Johnson, C.A.; Kingery, N.D.; Elliott, H.L.; Xie, T.; Gerfen, C.R.; Sabatini, B.L. A direct GABAergic output from the basal ganglia to frontal cortex. Nat. Cell Biol. 2015, 521, 85–89. [Google Scholar] [CrossRef] [PubMed]
- Montero, J.; Fernandez-Aviles, G.; Mateu, J. Spatial and Spatio-Temporl Geostatistical Modeling and Kriging; Wiler & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Zhang, Z.; Luo, P.; Loy, C.C.; Tang, X. Learning deep representation for face alignment with auxiliary attributes. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 918–930. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Zhao, C.; Yang, Y.; Yang, X. Spatiotemporal variations of the PM2.5/PM10 ratios and its application to air pollution type classification in China. Front. Environ. Sci. 2021, 9, 218. [Google Scholar] [CrossRef]
- Abatzoglou, T.J. Development of gridded surface meteorological data for ecological applications and modelling. Int. J. Climatol. 2011, 33, 121–131. [Google Scholar] [CrossRef]














| Pollutant | Statistics (μg/m3) | Mainland China | Northeast China | North China | East China | Central China | South China | Northwest China | Southwest China |
|---|---|---|---|---|---|---|---|---|---|
| PM2.5 | Mean | 46.8 | 41.9 | 58.8 | 47.9 | 57.2 | 33.7 | 48.7 | 36.9 |
| Median | 36.0 | 31.0 | 45.0 | 39.0 | 46.0 | 28.0 | 35.0 | 29.0 | |
| Standard deviation | 39.6 | 38.6 | 50.0 | 34.9 | 43.2 | 22.0 | 50.2 | 20.2 | |
| IQR | 36.0 | 33.0 | 46.0 | 35.0 | 41.0 | 25.0 | 35.0 | 30.0 | |
| PM10 | Mean | 83.0 | 72.5 | 110.5 | 81.2 | 95.6 | 53.3 | 109.3 | 52.0 |
| Median | 66.0 | 58.0 | 91.0 | 68.0 | 80.0 | 46.0 | 80.0 | 42.5 | |
| Standard deviation | 74.8 | 56.0 | 78.6 | 68.5 | 63.4 | 30.0 | 134.6 | 42.5 | |
| IQR | 36.0 | 52.0 | 78.0 | 58.0 | 67.0 | 33.0 | 75.0 | 46.0 | |
| Ratio (PM2.5/PM10) | Mean | 0.57 | 0.57 | 0.53 | 0.60 | 0.60 | 0.62 | 0.47 | 0.58 |
| IQR | 0.24 | 0.26 | 0.25 | 0.22 | 022 | 0.19 | 0.25 | 0.23 |
| Method | Type | PM2.5 | PM10 | ||
|---|---|---|---|---|---|
| R2 | RMSE (μg/m3) | R2 | RMSE (μg/m3) | ||
| Geographic graph hybrid network (GGHN) | Training | 0.91 | 9.82 | 0.91 | 17.02 |
| Testing | 0.85 | 13.87 | 0.84 | 23.54 | |
| Site-based independent testing | 0.83 | 14.51 | 0.82 | 24.34 | |
| Full residual deep network | Training | 0.92 | 9.71 | 0.92 | 16.23 |
| Testing | 0.81 | 15.51 | 0.81 | 24.98 | |
| Site-based independent testing | 0.72 | 17.63 | 0.71 | 30.34 | |
| Local GNN | Training | 0.67 | 20.46 | 0.68 | 33.38 |
| Testing | 0.66 | 20.72 | 0.65 | 33.39 | |
| Site-based independent testing | 0.65 | 20.98 | 0.65 | 33.78 | |
| Random forest | Training | 0.94 | 9.31 | 0.94 | 14.95 |
| Testing | 0.79 | 17.34 | 0.78 | 28.87 | |
| Site-based independent testing | 0.77 | 16.35 | 0.76 | 28.56 | |
| XGBoost | Training | 0.68 | 20.89 | 0.65 | 34.78 |
| Testing | 0.67 | 21.56 | 0.65 | 35.78 | |
| Site-based independent testing | 0.66 | 21.69 | 0.62 | 35.45 | |
| Regression kriging | Training | -- | -- | -- | -- |
| Testing | 0.70 | 19.23 | 0.71 | 30.41 | |
| Site-based independent testing | 0.72 | 18.76 | 0.70 | 30.03 | |
| Kriging | Training | -- | -- | -- | |
| Testing | 0.55 | 22.98 | 0.56 | 37.78 | |
| Site-based independent testing | 0.55 | 22.65 | 0.55 | 38.45 | |
| Generalized additive model | Training | 0.54 | 27.41 | 0.42 | 57.92 |
| Testing | 0.54 | 27.34 | 0.45 | 59.67 | |
| Site-based independent testing | 0.53 | 26.89 | 0.46 | 47.13 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L. Geographic Graph Network for Robust Inversion of Particulate Matters. Remote Sens. 2021, 13, 4341. https://doi.org/10.3390/rs13214341
Li L. Geographic Graph Network for Robust Inversion of Particulate Matters. Remote Sensing. 2021; 13(21):4341. https://doi.org/10.3390/rs13214341
Chicago/Turabian StyleLi, Lianfa. 2021. "Geographic Graph Network for Robust Inversion of Particulate Matters" Remote Sensing 13, no. 21: 4341. https://doi.org/10.3390/rs13214341
APA StyleLi, L. (2021). Geographic Graph Network for Robust Inversion of Particulate Matters. Remote Sensing, 13(21), 4341. https://doi.org/10.3390/rs13214341






