Robust GMTI Scheme for Highly Squinted Hypersonic Vehicle-Borne Multichannel SAR in Dive Mode
Abstract
:1. Introduction
- Traditionally, the impacts of high-order phase terms are negligible and may be disregarded in the GMT focusing stage, especially for the case with a side-looking and horizontal orbiting SAR [14,15,20]. However, when dealing with a high-squint, a high-speed, and a dive orbit, the range model of HSV-SAR/GMTI has non-negligible high-order or coupled phase terms and may induce distortion on the GMT envelopes [6,7,8,14,15].
- The HSV-SAR/GMT range model, with a squint angle and a dive orbit, is complex. Some precise models comprise cumbersome expressions, thus limiting their application in subsequent processing of targets. Examples include the fourth-order range model (FORM4) [21] and the fourth-order Doppler range model (DRM4) [22]. While methods such as the advanced hyperbolic range equation (AHRE) [23] model and its modifications [24,25,26] have simplified the expressions, its accuracy is not sufficient to satisfy the high-resolution imaging requirement. In order to reduce the cumbersome range model and form a basis for stationary target processing, the wavenumber-domain imaging algorithm with modified equivalent range model (MERM) has been derived and discussed in [27], but the GMTI processing for HSV-SAR is still not available at present.
- The traditional clutter rejection algorithms are capable of extracting GMT in a region of interest, such algorithms include displaced phase center antenna (DPCA) [28,29,30] and space-time adaptive processing (STAP) [31,32]. However, its Doppler ambiguity (DA) arising from the high-speed and high-resolution wide-swath (HRWS) making it difficult to directly deal with the GMT [6,7,15,20,33,34].
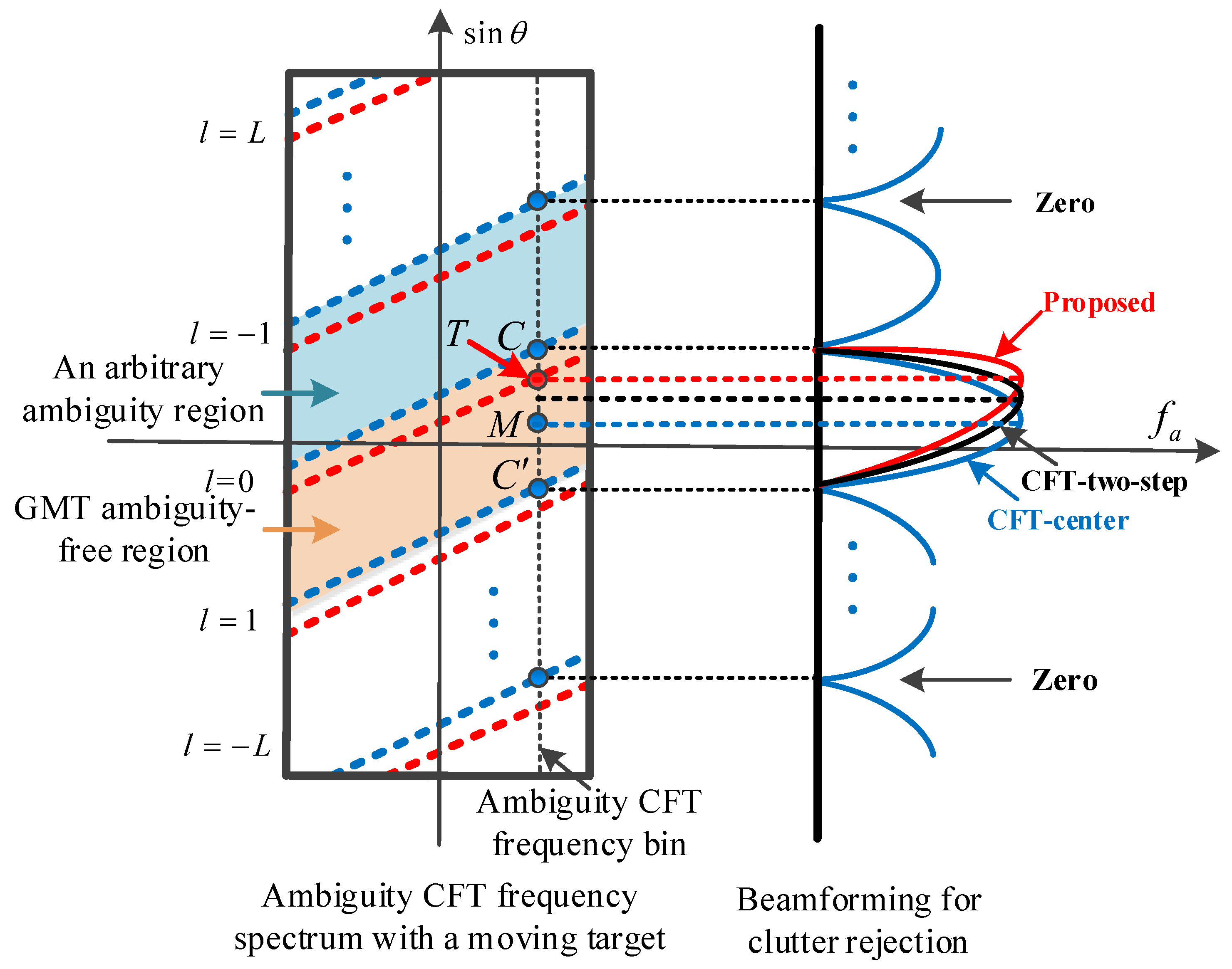
- The improved clutter rejection algorithms can enhance the effective accumulation for GMT and have extensive applications in the detection of faint GMT. These include the extended DPCA (EDPCA) [35,36,37] and the imaging STAP (ISTAP) [38]. Furthermore, the Deramp technique [39] enhances the ability to retrieve the ambiguity-free GMT, as it places the zeros in the DA clutter directions. However, these algorithms would suffer from GMT accumulation degradation when the limited channel number caused by the special aerodynamic characteristics of HSV-SAR are involved [6,7]. The chirp Fourier transform (CFT) and its modified algorithms enjoy a lower demand for the number of channels, because GMT is sparse in the surrounding clutter for coarse-focusing imageries. Examples are the CFT-center [20] and the CFT-two-step [6] algorithms. However, the beamforming mismatch caused by coarse cross-track velocity (CTV) may not be so readily eliminated and GMT energy decline is induced.
- While there are recent researches on highly squinted HSV-MC-SAR/GMTI [14,15], this article, which specifically explores a GMTI scheme in dive mode, is novel. It presents the IERM of a stationary target and GMTs, performs the accurate clutter rejection with matched beamforming, and achieves the GMT imaging and location.
- Derivation of an IERM of stationary target and GMT. Due to its ability to transform the dive orbit into the horizontal orbit, it has a more concise expression compared to [8] and thus mitigating vertical speed impact and simplifying the GMTI processing.
- An improved clutter rejection with a two-step CTV sweep is established. Because of the smaller range of small-interval sweep, it has a shorter calculation time compared to [15]. Moreover, it performs a small-interval sweep of the CTV to form a matched beamforming, thus minimizing the effect of beamforming mismatch in [6,20].
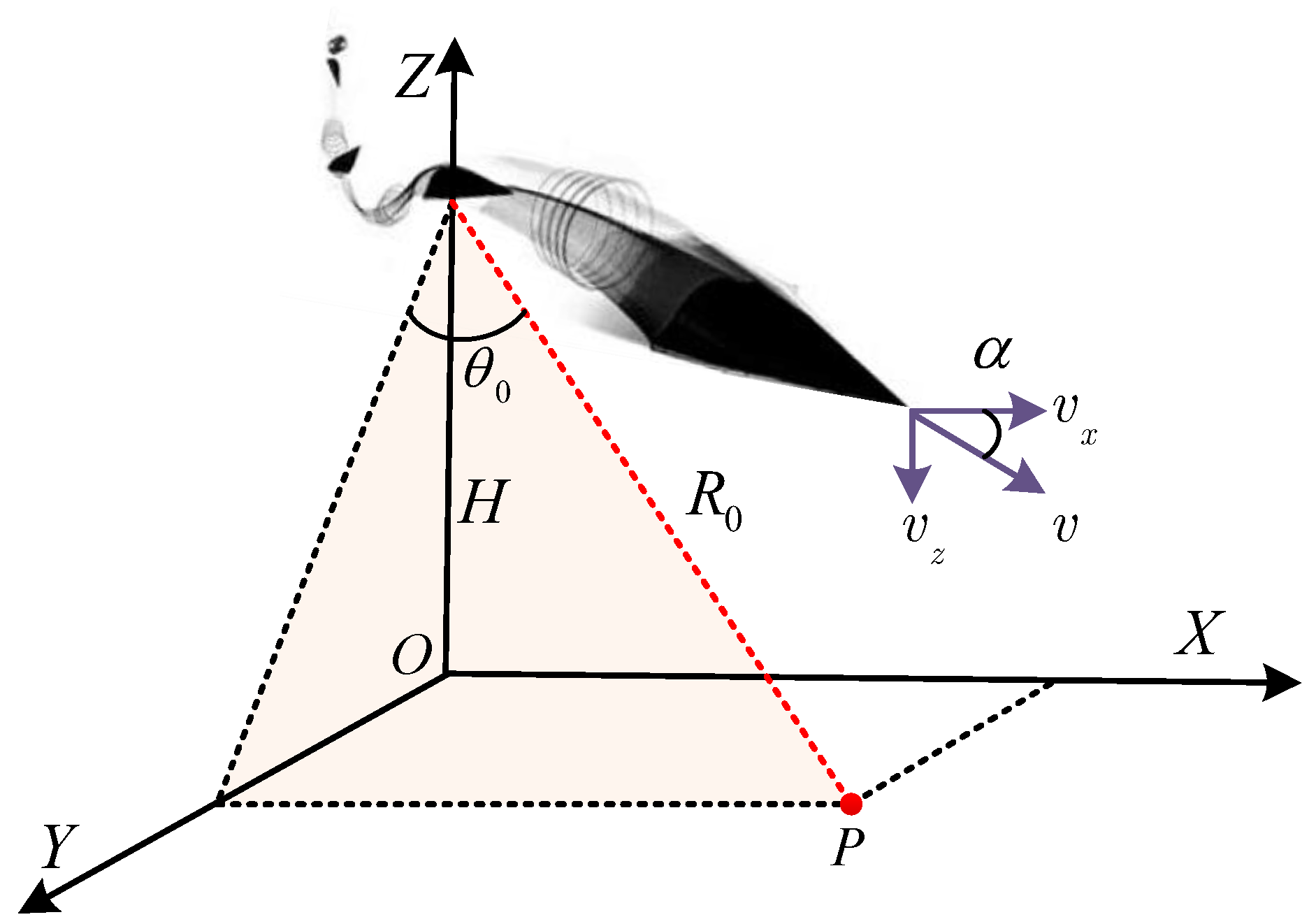
2. Improved Equivalent Range Model
2.1. IERM for Stationary Targets
2.2. IERM for GMT
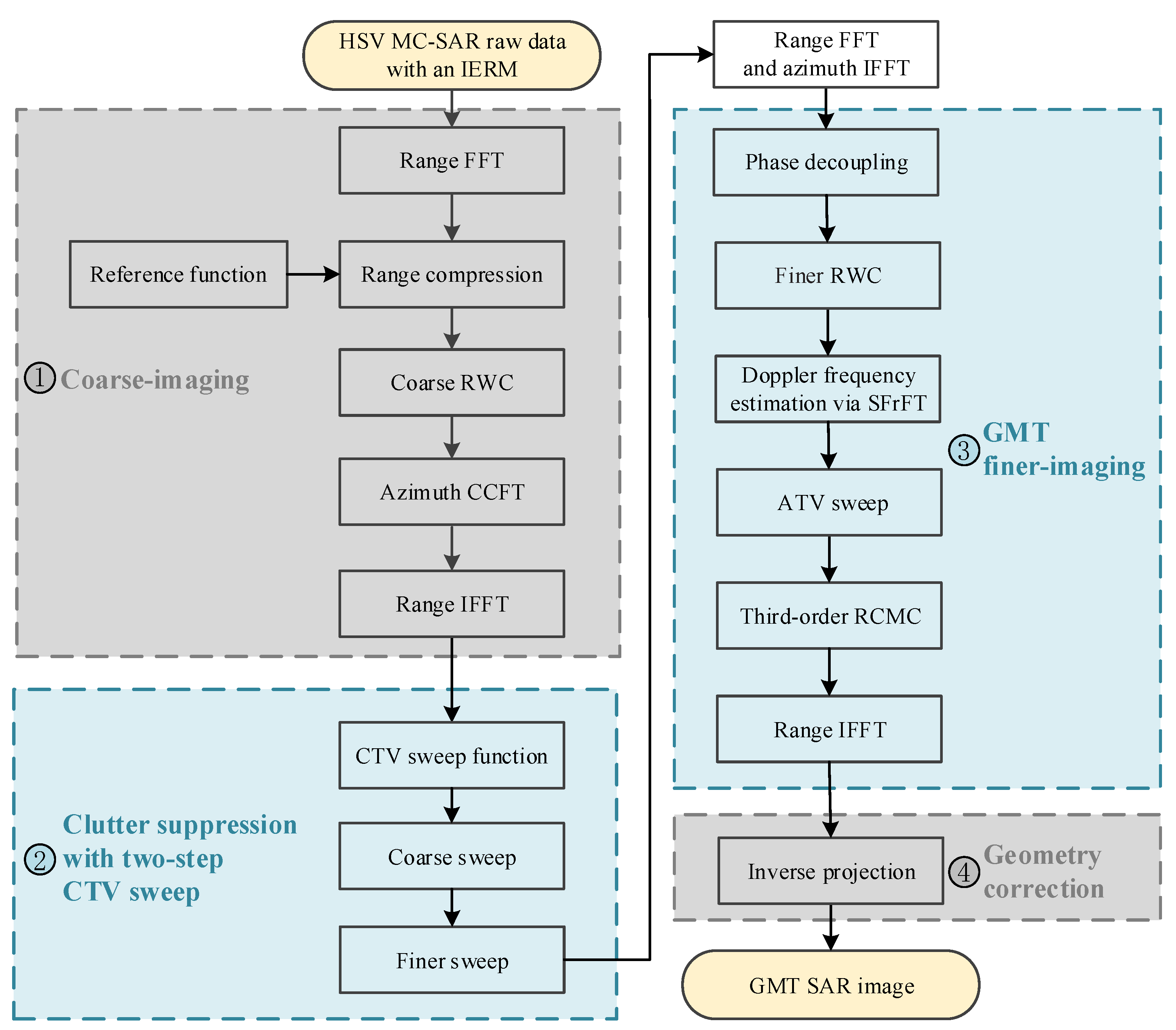
3. Robust GMTI Scheme for Highly Squint-Looking HSV-MC-SAR in Dive Mode
3.1. Coarsely Imaging
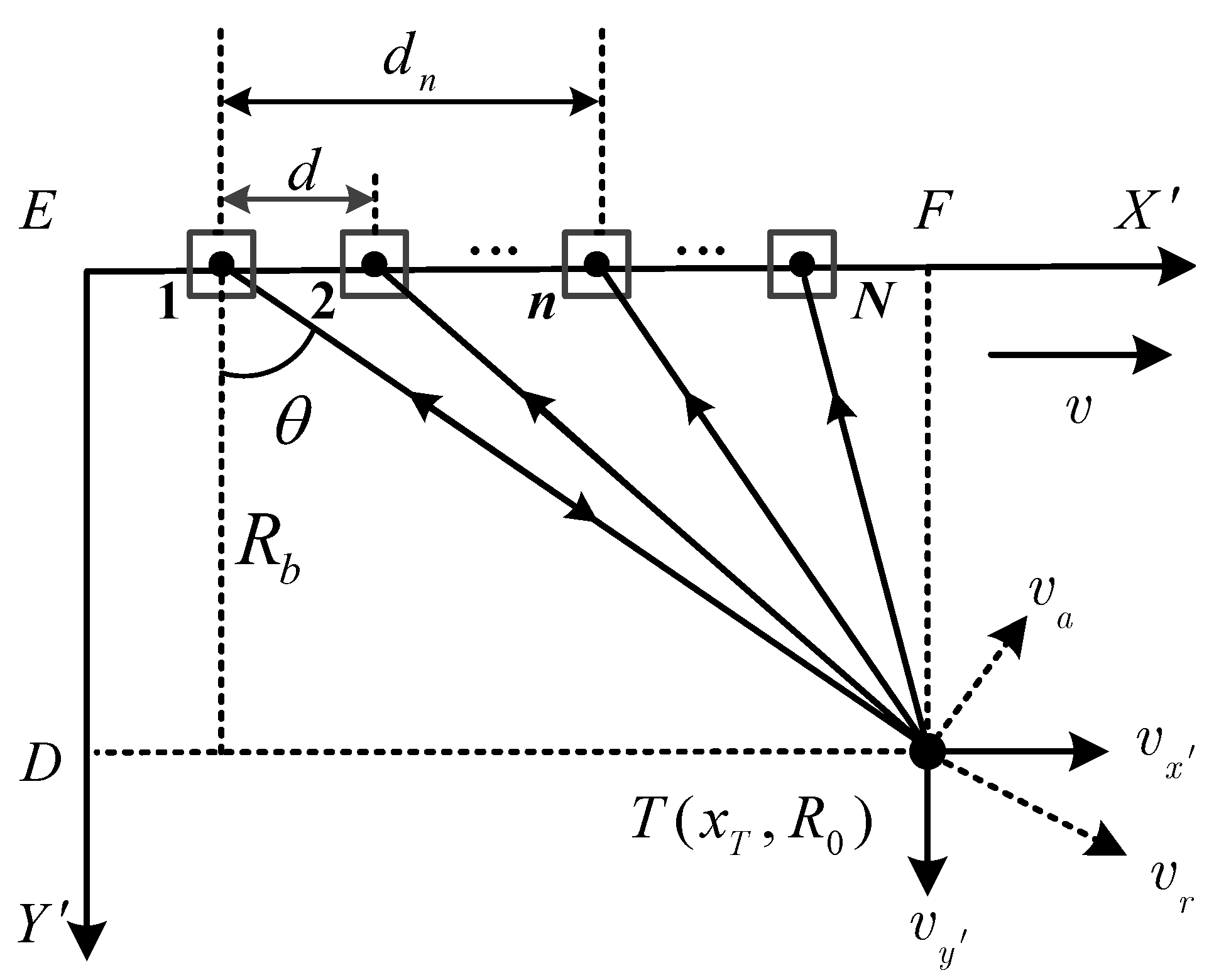
3.2. Improved Clutter Rejection Algorithm with Two-Step CTV Sweep
- CTV estimation with the large-interval sweep. (a) Coarse sweeping in an arbitrary region. Perform the large-interval sweep with the sweep function of (38) in the l-th ambiguity region. (b). Repeat (a) for all ambiguity regions. By sweeping and identifying the maximum output between different ambiguity regions, the GMT true region can be retrieved. (c). Determine the small-interval sweep range. The small-interval sweep range can be determined from the best and second best CTV values generated by large-interval sweep in the GMT ambiguity-free region.
- CTV estimation with the small-interval sweep. Sweeping in the small-interval sweep range, the finer CTV can be estimated from the output that maintains the maximum GMT power.
3.3. GMT Finer-Imaging
3.4. Geometry Correction
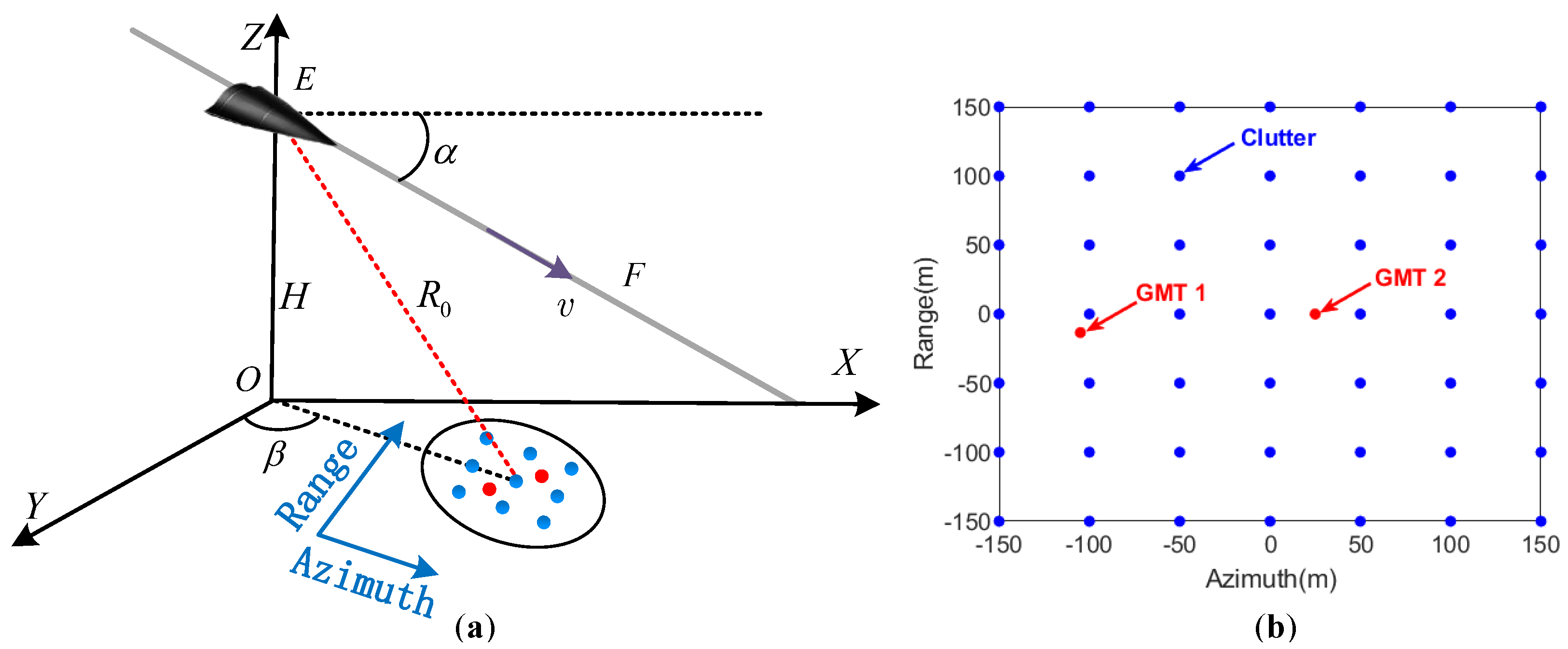
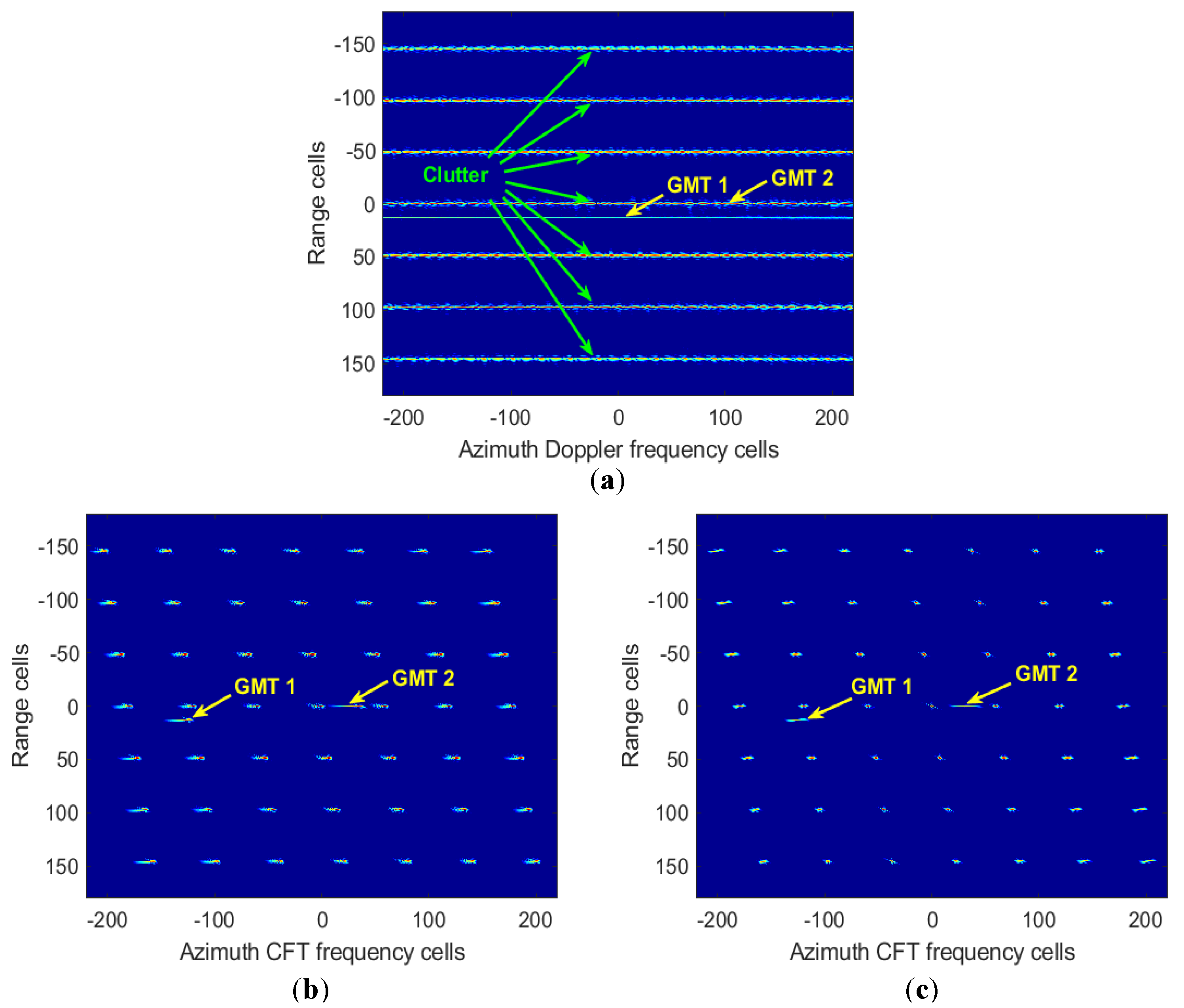
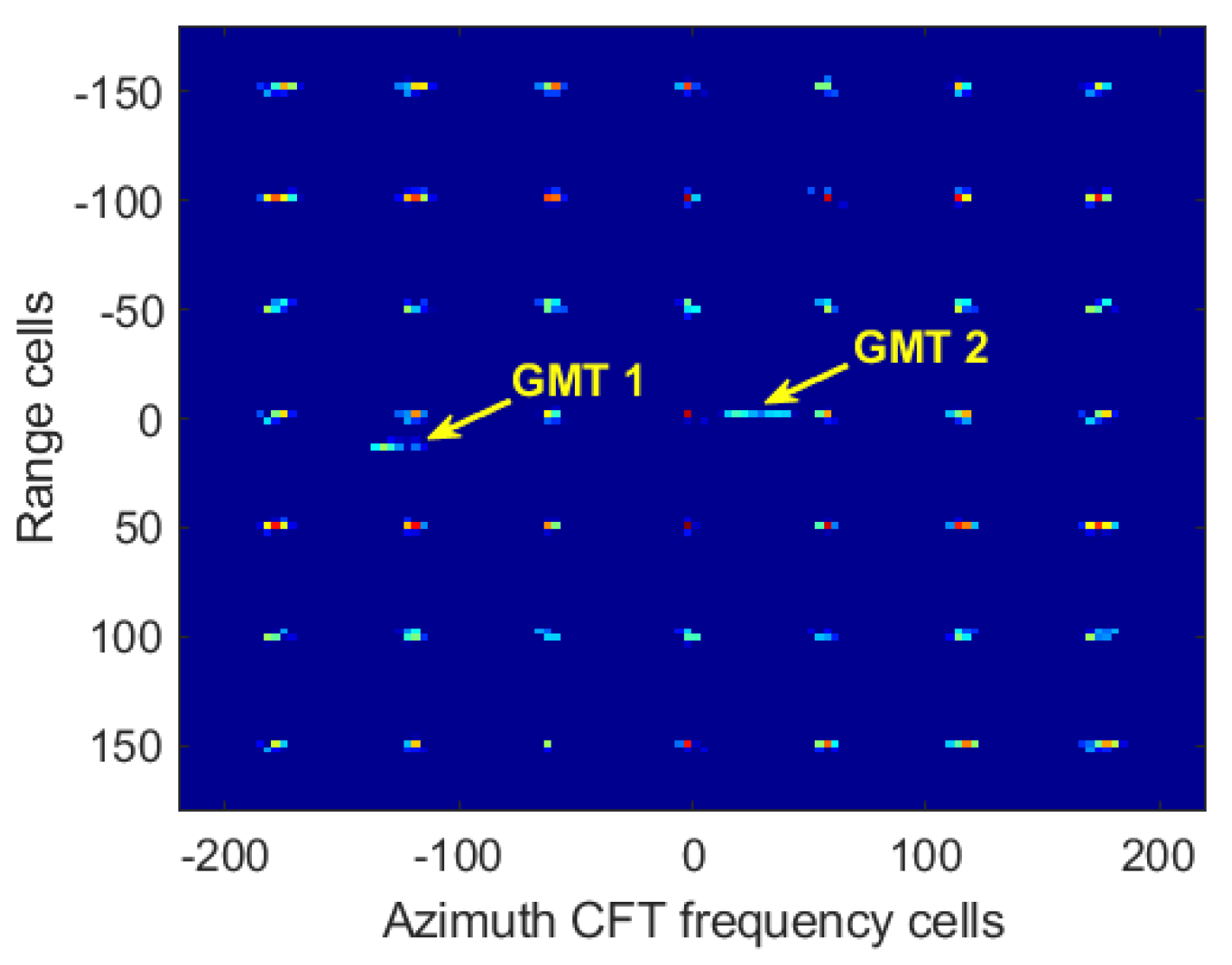
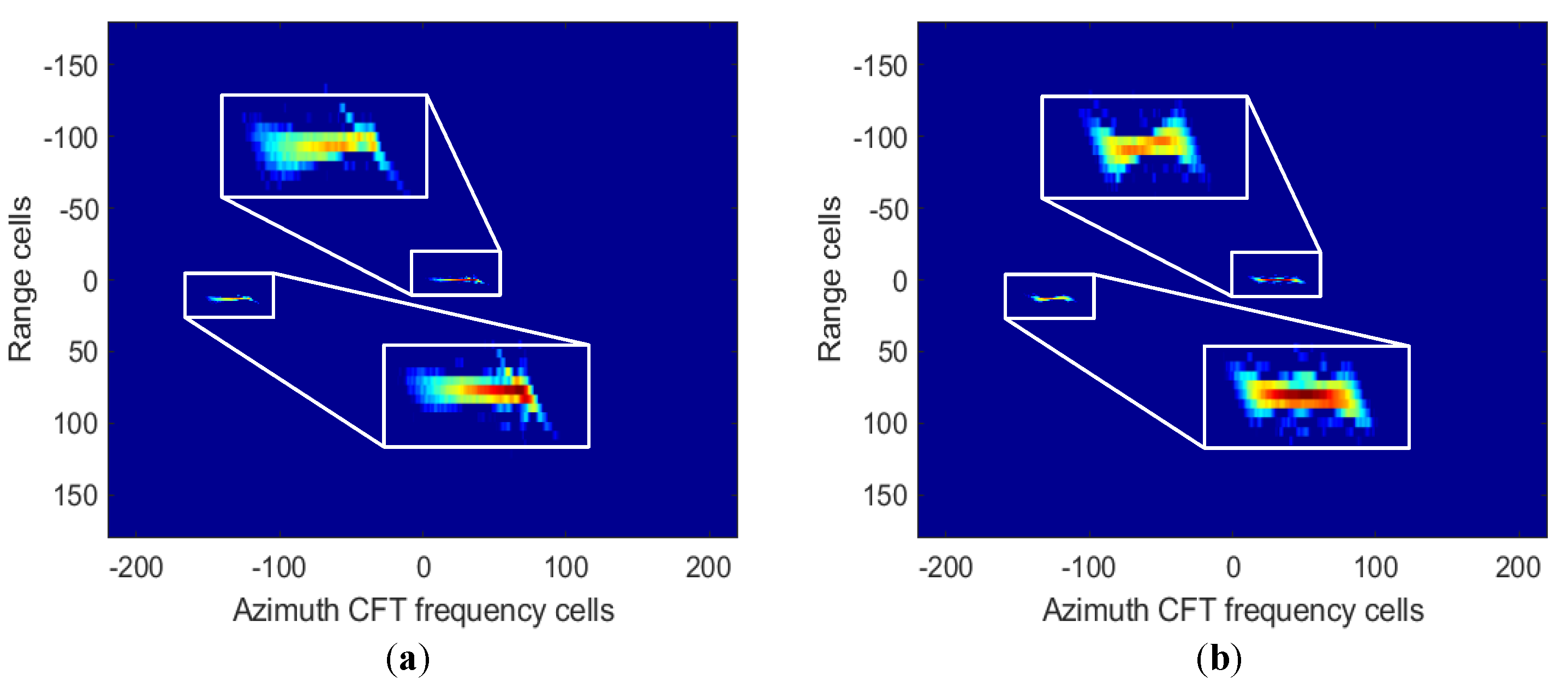
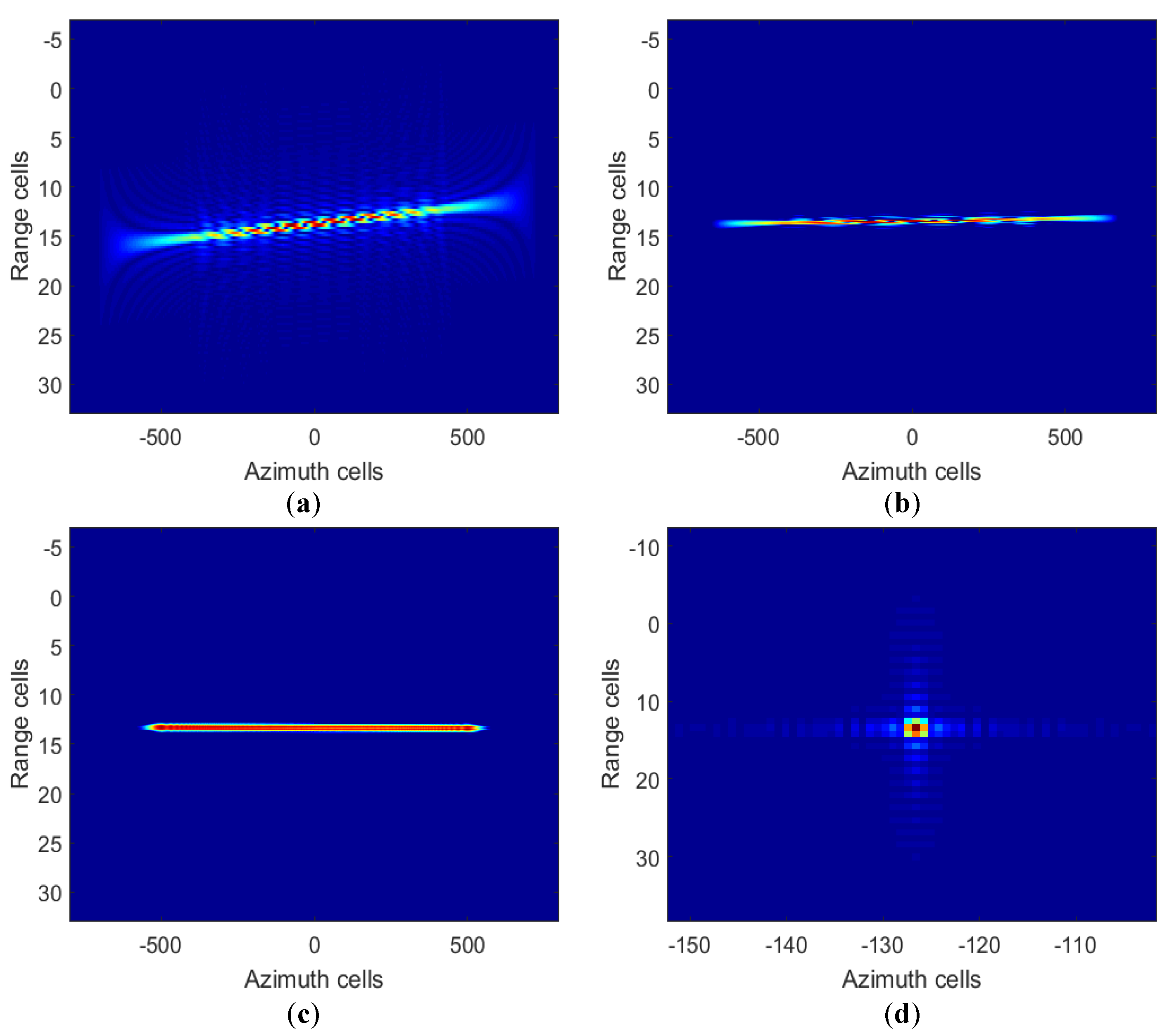
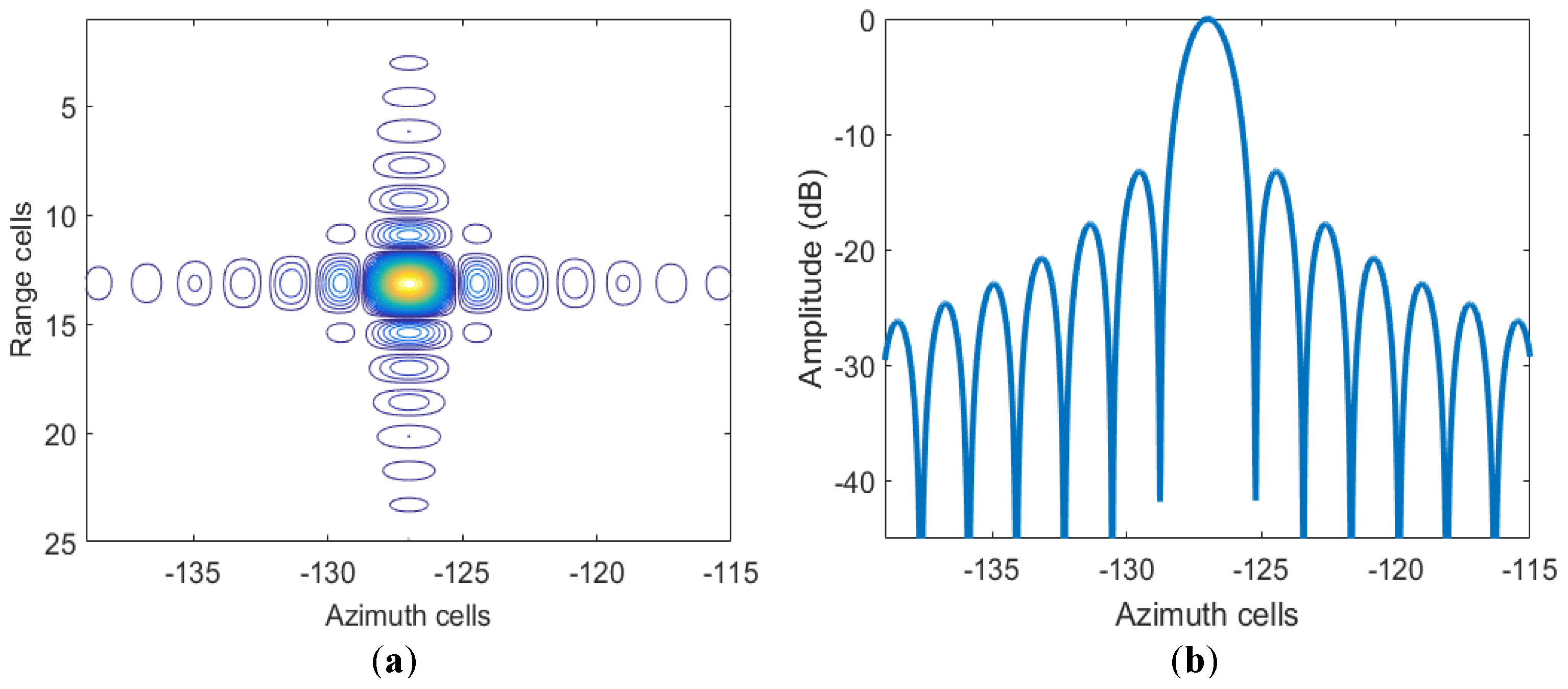
4. Simulations and Examples
4.1. Point Targets
4.2. Surface Targets
4.3. Multiple Targets and Extended Scene
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kang, M.-S.; Kim, K.-T. Ground moving target imaging based on compressive sensing framework with single-channel SAR. IEEE Sens. J. 2020, 20, 1238–1250. [Google Scholar] [CrossRef]
- Wang, W. Near-space vehicle-borne SAR with reflection-antenna for high-resolution and wide-swath remote sensing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 338–348. [Google Scholar] [CrossRef]
- Kang, M.-S.; Won, Y.-J.; Lim, B.-G.; Kim, K.-T. Efficient synthesis of antenna pattern using improved PSO for spaceborne SAR performance and imaging in presence of element failure. IEEE Sens. J. 2018, 18, 6576–6587. [Google Scholar] [CrossRef]
- Khedkar, S.B.; Kasav, S.M.; Khedkar, A.S.; Mahajan, S.M.; Satpute, D.R. A Review on Hypersonic Aircraft. Int. J. Adv. Technol. Eng. Sci. 2015, 3, 1566–1570. [Google Scholar]
- Xu, X.; Liao, G.; Yang, Z.; Wang, C. Moving-in-pulse duration model-based target integration method for HSV-borne high-resolution radar. Digit. Signal Process. 2017, 68, 31–43. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Wang, S.; Su, H. Clutter Suppression and Ground Moving Target Imaging Approach for Hypersonic Vehicle borne multichannel radar based on Two-Step focusing Method. Digit. Signal Process. 2019, 85, 62–76. [Google Scholar] [CrossRef]
- Han, J.; Cao, Y.; Yeo, T.S.; Wang, F.; Liu, S. A novel hypersonic vehicle-borne multichannel SAR-GMTI scheme based on adaptive sum and difference beams within eigenspace. Signal Process. 2021, 187, 108168. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Peng, Z.; Su, H. Clutter suppression and moving target imaging approach for multichannel hypersonic vehicle borne radar. Digit. Signal Process. 2017, 68, 81–92. [Google Scholar] [CrossRef]
- Carter, P.H., II; Pines, D.J.; Rudd, L.V. Approximate Performance of Stageic Hypersonic Trajectories for Global Reach. IBM J. Res. Dev. 2000, 44, 703–714. [Google Scholar] [CrossRef]
- Kang, M.-S.; Bae, J.-H.; Kang, B.-S.; Kim, K.-T. ISAR cross-range scaling using iterative processing via principal component analysis and bisection algorithm. IEEE Trans. Signal Process. 2016, 64, 3909–3918. [Google Scholar] [CrossRef]
- Kang, M.-S.; Bae, J.-H.; Lee, S.-H.; Kim, K.-T. Efficient ISAR autofocus via minimization of Tsallis Entropy. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2950–2960. [Google Scholar] [CrossRef]
- Kang, M.-S.; Kang, B.-S.; Lee, S.-H.; Kim, K.-T. Bistatic-ISAR distortion correction and range and cross-range scaling. IEEE Sens. J. 2017, 17, 5068–5078. [Google Scholar] [CrossRef]
- Tang, S.; Guo, P.; Zhang, L.; So, H.C. Focusing Hypersonic Vehicle-Borne SAR Data Using Radius/Angle Algorithm. IEEE Trans. Geosci. Remote Sens. 2020, 58, 281–293. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Y.; Zhang, L.; Lin, C.; Huang, Y.; Tang, S. Ground Moving Target Imaging and Analysis for Near-Space Hypersonic Vehicle-Borne Synthetic Aperture Radar System with Squint Angle. Remote Sens. 2018, 10, 1966. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Cao, Y.; Yeo, T.S.; Wang, F. Robust Clutter Suppression and Ground Moving Target Imaging Method for a Multichannel SAR with High-Squint Angle Mounted on Hypersonic Vehicle. Remote Sens. 2021, 13, 2051. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, M. A Novel Doppler Chirp Rate and Baseline Estimation Approach in the Time Domain Based on Weighted Local Maximum-Likelihood for an MC-HRWS SAR System. IEEE Trans. Geosci. Remote Sens. Lett. 2017, 14, 299–303. [Google Scholar] [CrossRef]
- Xu, J.; Huang, Z.; Wang, Z.; Xiao, L.; Xia, X.; Long, T. Radial Velocity Retrieval for Multichannel SAR Moving Targets With Time–Space Doppler Deambiguity. IEEE Trans. Geosci. Remote Sens. 2018, 56, 35–48. [Google Scholar] [CrossRef]
- Lv, G.; Li, Y.; Wang, G.; Zhang, Y. Ground Moving Target Indication in SAR Images With Symmetric Doppler Views. IEEE Trans. Geosci. Remote Sens. 2016, 54, 533–543. [Google Scholar] [CrossRef]
- Huang, Y.; Liao, G.; Xu, J.; Yang, D. MIMO SAR OFDM chirp waveform design and GMTI with RPCA based method. Digit. Signal Process. 2016, 51, 184–195. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, M.; Xia, X. Robust clutter suppression and moving target imaging approach for multichannel in azimuth high-resolution and wide-swath synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 687–709. [Google Scholar] [CrossRef]
- Eldhuset, K. A new fourth-order processing algorithm for spaceborne SAR. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 824–835. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Zhao, B.; Han, X.; Wang, R.; Song, H.; Deng, Y. A novel high-order range model and imaging approach for highresolution LEO SAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3473–3485. [Google Scholar] [CrossRef]
- Huang, L.; Qiu, X.; Hu, D.; Ding, C. Focusing of medium-earth-orbit SAR with advanced nonlinear chirp scaling algorithm. IEEE Trans. Geosci. Remote Sens. 2011, 49, 500–508. [Google Scholar] [CrossRef]
- Bao, M.; Xing, M.; Wang, Y.; Li, Y. Two-dimensional spectrum for MEO SAR processing using a modified advanced hyperbolic range equation. Electron. Lett. 2011, 47, 1043–1045. [Google Scholar] [CrossRef]
- Li, Z.; Yi, L.; Xing, M.; Huai, Y.; Gao, Y.; Zeng, L.; Bao, Z. An improved range model and omega-K-based imaging algorithm for high-squint SAR with curved orbit and constant acceleration. IEEE Geosci. Remote Sens. Lett. 2016, 13, 656–660. [Google Scholar] [CrossRef]
- Wang, P.; Liu, W.; Chen, J.; Niu, M.; Yang, W. A high-order imaging algorithm for high-resolution spaceborne SAR based on a modified equivalent squint range model. IEEE Geosci. Remote Sens. 2015, 53, 1225–1235. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Xing, M.; Xing, W.; Liang, Y.; Gao, Y.; Dai, B.; Bao, Z. A Modified Equivalent Range Model and Wavenumber-Domain Imaging Approach for High-Resolution-High-Squint SAR With Curved Trajectory. IEEE Geosci. Remote Sens. 2017, 55, 3721–3734. [Google Scholar] [CrossRef]
- Makhoul, E.; Broquetas, A.; Rodon, J.R.; Zhan, Y.; Ceba, F. A performance evaluation of sar-gmti missions for maritime applications. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2496–2509. [Google Scholar] [CrossRef] [Green Version]
- Faubert, D.; Tam, W. Improvement in the detection performance of a space based radar using a displaced phase centre antenna. In Proceedings of the 1987 Antennas and Propagation Society International Symposium, Blacksburg, VA, USA, 15–19 June 1987; pp. 964–967. [Google Scholar]
- Lightstone, L.; Faubert, D.; Rempel, G. Multiple phase centre DPCA for airborne radar. In Proceedings of the 1991 IEEE National Radar Conference, Los Angeles, CA, USA, 12–13 March 1991; pp. 36–40. [Google Scholar]
- Klemm, R. Introduction to space-time adaptive processing. Electron. Commun. Eng. J. 1999, 11, 5–12. [Google Scholar] [CrossRef]
- Xu, L.; Gianelli, C.; Jian, L. Long-CPI multichannel SAR-based ground moving target indication. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5159–5170. [Google Scholar] [CrossRef]
- Huang, Y.; Liao, G.; Xu, J.; Li, J.; Yang, D. GMTI and Parameter Estimation for MIMO SAR System via Fast Interferometry RPCA Method. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1174–1187. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Peng, Z. Clutter suppression and GMTI for hypersonic vehicle borne SAR system with MIMO antenna. IET Signal Process. 2017, 11, 909–915. [Google Scholar] [CrossRef]
- Maori, D.C.; Sikaneta, I. A generalization of DPCA processing for multichannel SAR/GMTI radars. IEEE Trans. Geosci. Remote Sens. 2013, 51, 560–572. [Google Scholar] [CrossRef]
- Delphine, C.; Ishuwa, S. Optimum GMTI processing for space-based SAR/GMTI systems—Theoretical derivation. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 390–393. [Google Scholar]
- Makhoul, E.; Broquetas, A.; Gonzalez, O. Evaluation of state-ofthe- art GMTI techniques for future space-borne SAR system-simulation validation. In Proceedings of the 9th European Conference on Synthetic Aperture Radar (EUSAR 2012), Nuremberg, Germany, 23–26 April 2012; pp. 376–379. [Google Scholar]
- Cerutti-Maori, D.; Sikaneta, I.C.H. Gierull, Optimum SAR/GMTI Processing and Its Application to the Radar Satellite RADARSAT-2 for Traffic Monitoring. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3868–3881. [Google Scholar] [CrossRef]
- Li, X.; Xing, M.; Xia, X.; Sun, G.; Yi, L.; Zheng, B. Deramp space-time adaptive processing for multichannel SAR systems. IEEE Trans. Geosci. Remote Sens. Lett. 2014, 11, 1448–1452. [Google Scholar]
- Huang, Y.; Liao, G.; Xu, J.; Li, J. GMTI and Parameter Estimation via Time-Doppler Chirp-Varying Approach for Single-Channel Airborne SAR System. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4367–4383. [Google Scholar] [CrossRef]
- Rousseau, L.; Gierull, C.; Chouinard, J. First results from an experimental ScanSAR-GMTI mode on RADARSAT-2. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 5068–5080. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, F.; Sun, G.; Xia, X.; Bao, Z. A new SAR-GMTI high-accuracy focusing and relocation algorithm using instantaneous interferometry. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5564–5577. [Google Scholar] [CrossRef]
- Dragosevic, M.V.; Burwash, W.; Chiu, S. Detection and estimation with RADARSAT-2 moving-object detection experiment modes. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3527–3543. [Google Scholar] [CrossRef]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef] [Green Version]
- Liao, G.; Li, H. Estimation Method for InSAR Interferometric Phase Based on Generalized Correlation Steering Vector. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1389–1403. [Google Scholar] [CrossRef]
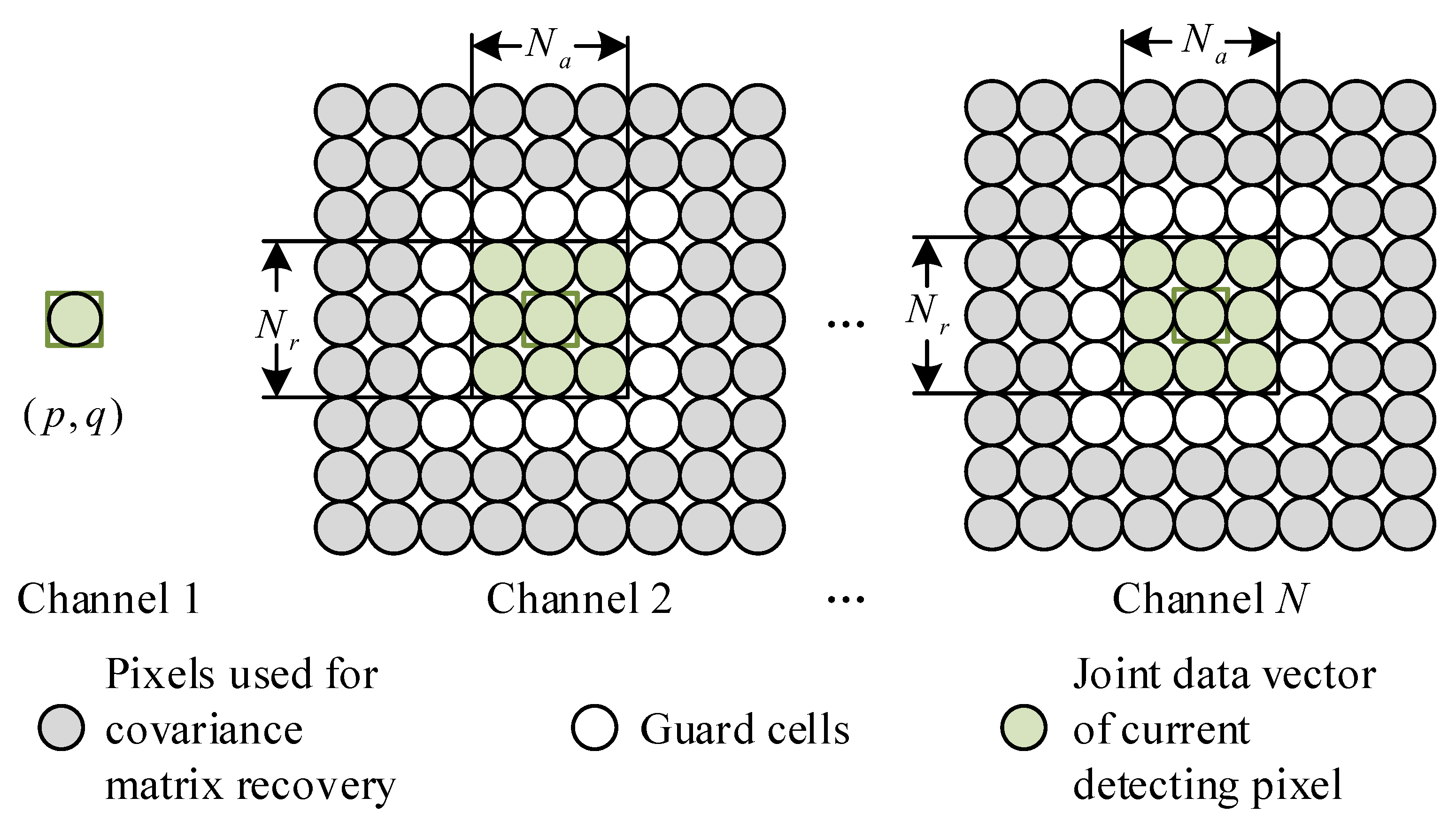
- He, X.; Liao, G.; Xu, J.; Zhu, S. Robust radial velocity estimation based on joint-pixel normalized sample covariance matrix and shift vector for moving targets. IEEE Trans. Geosci. Remote Sens. Lett. 2019, 16, 221–225. [Google Scholar] [CrossRef]
- Yan, H.; Wang, R.; Li, F.; Deng, Y.; Liu, Y. Ground moving target extraction in a multichannel wide-area surveillance sar/gmti system via the relaxed pcp. IEEE Trans. Geosci. Remote Sens. Lett. 2013, 10, 617–621. [Google Scholar] [CrossRef]
- Yu, C.; Wang, Y.; Song, M.; Chang, C. Class Signature-Constrained Background Suppressed Approach to Band Selection for Classification of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 14–31. [Google Scholar] [CrossRef]
- Zuo, S.; Xing, M.; Xia, X.G.; Sun, G. Improved Signal Reconstruction Algorithm for Multichannel SAR Based on the Doppler Spectrum Estimation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 1425–1442. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.G.; Ma, J.; Zheng, J. Ground maneuvering target imaging and high-order motion parameter estimation based on second-order keystone and generalized Hough-HAF transform. IEEE Trans. Geosci. Remote Sens. 2017, 55, 320–335. [Google Scholar] [CrossRef]
- Zeng, C.; Li, D.; Luo, X.; Song, D.; Liu, H.; Su, J. Ground maneuvering targets imaging for synthetic aperture radar based on second-order keystone transform and high-order motion parameter estimation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 12, 4486–4501. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I.; Klare, J.; Gierull, C.H. Mimo sar processing for multichannel high-resolution wide-swath radars. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5034–5055. [Google Scholar] [CrossRef]
- Pei, S.C.; Ding, J.J. Fractional cosine, sine, and Hartley transforms. IEEE Trans. Signal Process. 2002, 50, 1661–1680. [Google Scholar]
- Almeida, L.B. The fractional fourier transform and time-frequencyrepresentations. IEEE Trans. Signal Process. 1994, 42, 3084–3091. [Google Scholar] [CrossRef]
- Wang, W. Approach of multiple moving targets detection for microwave surveillance sensors. Int. J. Inf. Acquisit. 2007, 4, 57–68. [Google Scholar] [CrossRef]
- Li, Z.; Xing, M.; Liang, Y.; Gao, Y.; Chen, J.; Huai, Y.; Zeng, L.; Sun, G.; Bao, Z. A Frequency-Domain Imaging Algorithm for Highly Squinted SAR Mounted on Maneuvering Platforms With Nonlinear Trajectory. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4023–4038. [Google Scholar] [CrossRef]









| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carrier frequency | 10 GHz | Channel number | 5 |
| Doppler bandwidth | 2400 Hz | Squint angle | 63.51° |
| PRF | 800 Hz | Equivalent squint angle | 60° |
| Wave length | 0.03 m | Dive angle | 36.87° |
| Platform altitude | 15 km | Platform horizontal speed | 1920 (m/s) |
| Center slant range | 60 km | Platform vertical speed | 1440 (m/s) |
| Algorithms | SCNR (dB) | CTV Error (m/s) | ATV Error (m/s) |
|---|---|---|---|
| ISTAP | 21.36 | 2.57 | 2.73 |
| CFT-center | 27.19 | 2.02 | / |
| CFT-two-step | 29.74 | 1.21 | 0.23 |
| Proposed | 30.82 | 0.17 | 0.15 |
| Algorithms | Primary Steps | Complexities |
|---|---|---|
| ISTAP | Clutter rejection with 2D velocity sweep | |
| CFT-center | Clutter rejection without velocity sweep | |
| Clutter rejection with coarse CTV sweep | ||
| CFT-two-step | SOKT | |
| SFrFT | ||
| ERTE | ||
| Clutter rejection with finer CTV sweep | ||
| CFT-modified | SOKT | |
| SFrFT | ||
| Clutter rejection with two-step CTV sweep | ||
| Proposed | SOKT | |
| SFrFT |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Cao, Y.; Wu, W.; Wang, Y.; Yeo, T.-S.; Liu, S.; Wang, F. Robust GMTI Scheme for Highly Squinted Hypersonic Vehicle-Borne Multichannel SAR in Dive Mode. Remote Sens. 2021, 13, 4431. https://doi.org/10.3390/rs13214431
Han J, Cao Y, Wu W, Wang Y, Yeo T-S, Liu S, Wang F. Robust GMTI Scheme for Highly Squinted Hypersonic Vehicle-Borne Multichannel SAR in Dive Mode. Remote Sensing. 2021; 13(21):4431. https://doi.org/10.3390/rs13214431
Chicago/Turabian StyleHan, Jiusheng, Yunhe Cao, Wenhua Wu, Yang Wang, Tat-Soon Yeo, Shuai Liu, and Fengfei Wang. 2021. "Robust GMTI Scheme for Highly Squinted Hypersonic Vehicle-Borne Multichannel SAR in Dive Mode" Remote Sensing 13, no. 21: 4431. https://doi.org/10.3390/rs13214431
APA StyleHan, J., Cao, Y., Wu, W., Wang, Y., Yeo, T.-S., Liu, S., & Wang, F. (2021). Robust GMTI Scheme for Highly Squinted Hypersonic Vehicle-Borne Multichannel SAR in Dive Mode. Remote Sensing, 13(21), 4431. https://doi.org/10.3390/rs13214431