Marine Heatwaves in Siberian Arctic Seas and Adjacent Region
Abstract
:1. Introduction
2. Data and Methods
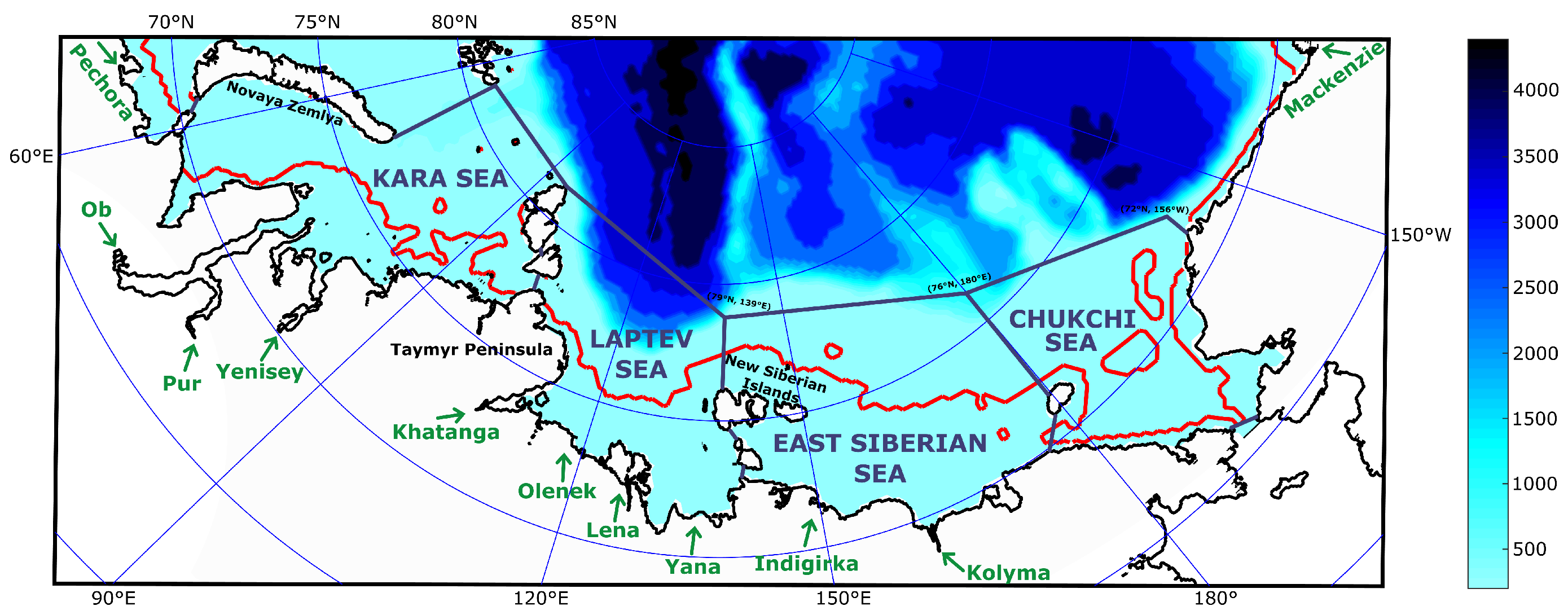
2.1. Data
2.2. Method of MHW Identification
2.3. Method of Numerical Simulation of the Arctic Ocean and Sea Ice State
3. Results
3.1. Marine Heatwaves: Data Analysis
3.2. Marine Heatwaves: Climate Tendency Elimination
3.3. Marine Heatwaves: Model Simulation
3.4. Sensitivity Tests
3.4.1. Analysis of Atmospheric Forcing
3.4.2. Sensitivity to Fast Ice Parameterization
3.4.3. Sensitivity to Riverine Heat Inflow
3.4.4. Sensitivity to Ice Drift
3.4.5. Sensitivity to Initial State of the Ocean and Sea Ice
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hobday, A.J.; Alexander, L.V.; Perkins, S.E.; Smale, D.A.; Straub, S.C.; Oliver, E.C.J.; Benthuysen, J.A.; Burrows, M.T.; Donat, M.G.; Feng, M.; et al. A hierarchical approach to defining marine heatwaves. Prog. Oceanogr. 2016, 141, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Collins, M.; Sutherland, M.; Bouwer, L.; Cheong, S.-M.; Frölicher, T.; Jacot Des Combes, H.; Koll Roxy, M.; Losada, I.; McInnes, K.; Ratter, B.; et al. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., et al., Eds.; Intergovernmental Panel on Climate Change: Genève, Switzerland, 2019; Available online: https://www.ipcc.ch/report/srocc/ (accessed on 3 November 2021).
- Cavole, L.M.; Demko, A.M.; Diner, R.E.; Giddings, A.; Koester, I.; Pagniello, C.M.L.S.; Paulsen, M.-L.; Ramirez-Valdez, A.; Schwenck, S.M.; Yen, N.K.; et al. Biological impacts of the 2013–2015 warm-water anomaly in the Northeast Pacific: Winners, losers, and the future. Oceanography 2016, 29, 273–285. [Google Scholar] [CrossRef] [Green Version]
- Oliver, E.C.J.; Donat, M.G.; Burrows, M.T.; Moore, P.J.; Smale, D.A.; Alexander, L.V.; Benthuysen, J.A.; Feng, M.; Sen Gupta, A.; Hobday, A.J.; et al. Longer and more frequent marine heatwaves over the past century. Nat. Commun. 2018, 9, 1324. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Burrows, M.T.; Donat, M.G.; Sen Gupta, A.; Alexander, L.V.; Perkins-Kirkpatrick, S.E.; Benthuysen, J.A.; Hobday, A.J.; Holbrook, N.J.; Moore, P.J.; et al. Projected Marine Heatwaves in the 21st Century and the Potential for Ecological Impact. Front. Mar. Sci. 2019, 6, 734. [Google Scholar] [CrossRef] [Green Version]
- Holbrook, N.J.; Scannell, H.A.; Sen Gupta, A.; Benthuysen, J.A.; Feng, M.; Oliver, E.C.J.; Alexander, L.V.; Burrows, M.T.; Donat, M.G.; Hobday, A.J.; et al. A global assessment of marine heatwaves and their drivers. Nat. Commun. 2019, 10, 2624. [Google Scholar] [CrossRef] [PubMed]
- Smale, D.A.; Wernberg, T.; Oliver, E.C.J.; Thomsen, M.; Harvey, B.P.; Straub, S.C.; Burrows, M.T.; Alexander, L.V.; Benthuysen, J.A.; Donat, M.G.; et al. Marine heatwaves threaten global biodiversity and the provision of ecosystem services. Nat. Clim. Chang. 2019, 9, 306–312. [Google Scholar] [CrossRef] [Green Version]
- Walsh, J.E. Intensified warming of the Arctic: Causes and impacts on middle latitudes. Glob. Planet. Chang. 2014, 117, 52–63. [Google Scholar] [CrossRef]
- Comiso, J.C.; Parkinson, C.L.; Gersten, R.; Stock, L. Accelerated decline in the Arctic sea ice cover. Geophys. Res. Lett. 2008, 35, L01703. [Google Scholar] [CrossRef] [Green Version]
- Ricker, R.; Girard-Ardhuin, F.; Krumpen, T.; Lique, C. Satellite-derived sea ice export and its impact on Arctic ice mass balance. Cryosphere 2018, 12, 3017–3032. [Google Scholar] [CrossRef] [Green Version]
- Kwok, R. Arctic sea ice thickness, volume, and multiyear ice coverage: Losses and coupled variability (1958–2018). Environ. Res. Lett. 2018, 13, 105005. [Google Scholar] [CrossRef]
- National Snow and Ice Data Center: Sea Ice Index. Available online: https://nsidc.org/data/seaice_index/archives (accessed on 20 June 2021).
- Martin, S.; Munoz, E.A.; Drucker, R. Recent observations of a spring-summer surface warming over the Arctic Ocean. Geophys. Res. Lett. 1997, 24, 1259–1262. [Google Scholar] [CrossRef]
- Comiso, J.C. Warming trends in the Arctic from clear sky satellite observations. J. Clim. 2003, 16, 3498–3510. [Google Scholar] [CrossRef] [Green Version]
- Steele, M.; Ermold, W.; Zhang, J. Arctic Ocean surface warming trends over the past 100 years. Geophys. Res. Lett. 2008, 35, L02614. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.K.; Maheshwari, M.; Oza, S.R.; Kumar, R. Long-term variability in Arctic sea surface temperatures. Polar Sci. 2013, 7, 233–240. [Google Scholar] [CrossRef] [Green Version]
- Timmermans, M.-L.; Labe, Z. Sea Surface Temperature. In Arctic Report Card; update to 2020; National Oceanic and Atmospheric Administration (NOAA): Washington, DC, USA, 2020; pp. 54–58. [Google Scholar] [CrossRef]
- Wassmann, P.; Duarte, C.; Agusti, S.; Sejr, M. Footprints of climate change in the Arctic Marine Ecosystem. Glob. Chang. Biol. 2011, 17, 1235–1249. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Perkins-Kirkpatrick, S.E.; Holbrook, N.J.; Bindoff, N.L. Anthropogenic influences on record 2016 marine heatwaves. Bull. Am. Meteorol. Soc. 2018, 99, S44–S48. [Google Scholar] [CrossRef] [Green Version]
- Walsh, J.E.; Thoman, R.L.; Bhatt, U.S.; Bieniek, P.A.; Brettschneider, B.; Brubaker, M.; Danielson, S.; Lader, R.; Fetterer, F.; Holderied, K.; et al. The high latitude marine heat wave of 2016 and its impacts on Alaska. Bull. Am. Meteorol. Soc. 2018, 99, S39–S43. [Google Scholar] [CrossRef]
- Hu, S.; Zhang, L.; Qian, S. Marine heatwaves in the Arctic region: Variation in different ice covers. Geophys. Res. Lett. 2020, 47, e2020GL089329. [Google Scholar] [CrossRef]
- Carvalho, K.S.; Smith, T.E.; Wang, S. Bering Sea marine heatwaves: Patterns, trends and connections with the Arctic. J. Hydrol. 2021, 600, 126462. [Google Scholar] [CrossRef]
- Review of Hydrometeorological Processes in the Arctic Ocean. 2015–2020. Available online: http://www.aari.ru/main.php?lg=0&id=449 (accessed on 25 October 2021). (In Russian).
- Overland, J.; Hanna, E.; Hanssen-Bauer, I.; Kim, S.-J.; Walsh, J.E.; Wang, M.; Bhatt, U.S.; Thoman, R.L. Surface Air Temperature. In Arctic Report Card; update to 2016; National Oceanic and Atmospheric Administration (NOAA): Washington, DC, USA, 2016; pp. 18–24. Available online: https://arctic.noaa.gov/Portals/7/ArcticReportCard/Documents/ArcticReportCard_full_report2016.pdf (accessed on 23 October 2021).
- Jakobsson, M.; Macnab, R.; Mayer, L.; Anderson, R.; Edwards, M.; Hatzky, J.; Schenke, H.W.; Johnson, P. An improved bathymetric portrayal of the Arctic Ocean: Implications for ocean modeling and geological, geophysical and oceanographic analyses. Geophys. Res. Lett. 2008, 35, L07602. [Google Scholar] [CrossRef] [Green Version]
- Information about Arctic Seas. Available online: http://www.aari.ru/projects/ECIMOt/Docs/reports/21/html/page_2.html (accessed on 20 June 2021). (In Russian).
- Smedsrud, L.H.; Esau, I.; Ingvaldsen, R.B.; Eldevik, T.; Haugan, P.M.; Li, C.; Lien, V.S.; Olsen, A.; Omar, A.M.; Otterå, O.H.; et al. The role of the Barents Sea in the Arctic climate system. Rev. Geophys. 2013, 51, 415–449. [Google Scholar] [CrossRef] [Green Version]
- Onarheim, I.H.; Smedsrud, L.H.; Ingvaldsen, R.B.; Nilsen, F. Loss of sea ice during winter north of Svalbard. Tellus A Dyn. Meteorol. Oceanogr. 2014, 66, 23933. [Google Scholar] [CrossRef] [Green Version]
- Polyakov, I.V.; Pnyushkov, A.V.; Alkire, M.B.; Ashik, I.M.; Baumann, T.M.; Carmack, E.C.; Goszczko, I.; Guthrie, J.; Ivanov, V.V.; Kanzow, T.; et al. Greater role for Atlantic inflows on sea-ice loss in the Eurasian Basin of the Arctic Ocean. Science 2017, 356, 285–291. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Polyakov, I.V.; Alkire, M.B.; Bluhm, B.A.; Brown, K.A.; Carmack, E.C.; Chierici, M.; Danielson, S.L.; Ellingsen, I.; Ershova, E.A.; Gärdfeldt, K.; et al. Borealization of the Arctic Ocean in Response to Anomalous Advection From Sub-Arctic Seas. Front. Mar. Sci. 2020, 7, 491. [Google Scholar] [CrossRef]
- Coachman, L.K.; Barnes, C.A. Surface water in the Eurasian basin of the Arctic Ocean. Arctic 1962, 15, 251–277. [Google Scholar] [CrossRef] [Green Version]
- Polyakov, I.V.; Rippeth, T.P.; Fer, I.; Alkire, M.B.; Baumann, T.M.; Carmack, E.C.; Ingvaldsen, R.; Ivanov, V.V.; Janout, M.; Lind, S.; et al. Weakening of Cold Halocline Layer Exposes Sea Ice to Oceanic Heat in the Eastern Arctic Ocean. J. Clim. 2020, 33, 8107–8123. [Google Scholar] [CrossRef]
- Polyakov, I.V.; Pnyushkov, A.V.; Carmack, E.C. Stability of the Arctic halocline: A new indicator of Arctic climate change. Environ. Res. Lett. 2018, 13, 125008. [Google Scholar] [CrossRef]
- Ivanov, V.V.; Repina, I.A. The Effect of Seasonal Variability of Atlantic Water on the Arctic Sea Ice Cover. Izv. Atmos. Ocean. Phys. 2018, 54, 65–72. [Google Scholar] [CrossRef]
- Whitefield, J.; Winsor, P.; McClelland, J.; Menemenlis, D. A new river discharge and river temperature climatology dataset for the pan-Arctic region. Ocean Model. 2015, 88, 1–15. [Google Scholar] [CrossRef]
- Park, H.; Watanabe, E.; Kim, Y.; Polyakov, I.; Oshima, K.; Zhang, X.; Kimball, J.; Yang, D. Increasing riverine heat influx triggers Arctic sea ice decline and oceanic and atmospheric warming. Sci. Adv. 2020, 6, eabc4699. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, V.F. The role of flaw leads off the edge of fast ice in the hydrological and ice regime of the Laptev Sea. Oceanol. Engl. Transl. 1966, 6, 815–821. [Google Scholar]
- Popov, A.V.; Karelin, I.D.; Rubchenya, A.V. The Role of Winter Flaw Polynyas in the Formation of Ice and Hydrologic Conditions in the Siberian Shelf Seas in the Summer Period. Russ. Meteorol. Hydrol. 2007, 32, 593–599. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily High-Resolution-Blended Analyses for Sea Surface Temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Saha, K.; Zhao, X.; Zhang, H.; Casey, K.S.; Zhang, D.; Baker-Yeboah, S.; Kilpatrick, K.A.; Evans, R.H.; Ryan, T.; Relph, J.M. AVHRR Pathfinder Version 5.3 Level 3 Collated (L3C) Global 4 km Sea Surface Temperature for 1981-Present; 2018 Dataset; NOAA National Centers for Environmental Information: Washington, DC, USA, 2018. [CrossRef]
- WGS 84/NSIDC Sea Ice Polar Stereographic North. Available online: http://epsg.io/3413 (accessed on 20 June 2021).
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Amer. Meteor. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef] [Green Version]
- Shiklomanov, A.I.; Holmes, R.M.; McClelland, J.W.; Tank, S.E.; Spencer, R.G.M. Arctic Great Rivers Observatory. Discharge Dataset, Version 20210527. Available online: https://arcticgreatrivers.org/discharge/ (accessed on 20 June 2021). Discharge Dataset, Version 20210527.
- Golubeva, E.N.; Platov, G.A. On improving the simulation of Atlantic Water circulation in the Arctic Ocean. J. Geophys. Res. 2007, 112, C04S05. [Google Scholar] [CrossRef] [Green Version]
- Golubeva, E.N.; Platov, G.A. Numerical modeling of the Arctic Ocean ice system response to variations in the atmospheric circulation from 1948 to 2007. Izv. Atmos. Ocean. Phys. 2009, 45, 137–151. [Google Scholar] [CrossRef]
- Platov, G.A. Numerical modeling of the Arctic Ocean deepwater formation: Part II. Results of regional and global experiments. Izv. Atmos. Ocean. Phys. 2011, 47, 377–392. [Google Scholar] [CrossRef]
- Hunke, E.C.; Dukowicz, J.K. An elastic-viscous-plastic model for ice dynamics. J. Phys. Oceanography 1997, 27, 1849–1867. [Google Scholar] [CrossRef] [Green Version]
- Bitz, C.M.; Lipscomb, W.H. An energy-conserving thermodynamic model of sea ice. J. Geophys. Res. 1999, 104, 15669–15677. [Google Scholar] [CrossRef]
- Lipscomb, W.H.; Hunke, E.C. Modeling Sea Ice Transport Using Incremental Remapping. Mon. Weather Rev. 2004, 132, 1341–1354. [Google Scholar] [CrossRef]
- Golubeva, E.N.; Platov, G.A.; Iakshina, D.F. Numerical simulations of the current state of waters and sea ice in the Arctic Ocean. Led I sneg 2015, 5, 81–92. (In Russian) [Google Scholar] [CrossRef] [Green Version]
- Platov, G.A.; Golubeva, E.N.; Kraineva, M.V.; Malakhova, V.V. Modeling of climate tendencies in Arctic seas based on atmospheric forcing EOF decomposition. Ocean. Dyn. 2019, 69, 747–767. [Google Scholar] [CrossRef]
- Woodgate, R.A. Increases in the Pacific inflow to the Arctic from 1990 to 2015, and insights into seasonal trends and driving mechanisms from year-round Bering Strait mooring data. Prog. Oceanogr. 2018, 160, 124–154. [Google Scholar] [CrossRef] [Green Version]
- Vorosmarty, C.J.; Fekete, B.M.; Tucker, B.A. Global River Discharge, 1807–1991, V[ersion]. 1.1 (RivDIS); ORNL DAAC: Oak Ridge, TN, USA, 1998. [CrossRef]
- Forum for Arctic Modeling and Observational Synthesis. Available online: https://web.whoi.edu/famos (accessed on 15 September 2021).
- Proshutinsky, A.; Aksenov, Y.; Kinney, C.J.; Gerdes, R.; Golubeva, E.; Holland, D.; Holloway, G.; Jahn, A.; Johnson, M.; Popova, E.; et al. Recent advances in Arctic ocean studies employing models from the Arctic Ocean Model Intercomparison Project. Oceanography 2011, 24, 102–113. [Google Scholar] [CrossRef] [Green Version]
- Proshutinsky, A.; Krishfield, R.; Toole, J.M.; Timmermans, M.-L.; Williams, W.; Zimmermann, S.; Yamamoto-Kawai, M.; Armitage, T.W.K.; Dukhovskoy, D.; Golubeva, E.; et al. Analysis of the Beaufort Gyre freshwater content in 2003–2018. J. Geophys. Res. Oceans 2019, 124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aksenov, Y.; Karcher, M.; Proshutinsky, A.; Gerdes, R.; de Cuevas, B.; Golubeva, E.; Kauker, F.; Nguyen, A.T.; Platov, G.A.; Wadley, M.; et al. Arctic pathways of Pacific Water: Arctic Ocean Model Intercomparison experiments. J. Geophys. Res. Oceans 2016, 121, 27–59. [Google Scholar] [CrossRef] [PubMed]
- Proshutinsky, A.; Timmermans, M.-L.; Ashik, I.; Beszczynska-Moeller, A.; Carmack, E.; Eert, J.; Frolov, I.; Itoh, M.; Kikuchi, T.; Krishfield, R.; et al. Ocean. In Arctic Report Card; update to 2011; National Oceanic and Atmospheric Administration (NOAA): Washington, DC, USA, 2011; pp. 42–54. Available online: https://arctic.noaa.gov/Portals/7/ArcticReportCard/Documents/ArcticReportCard_full_report2011.pdf (accessed on 23 October 2021).
- Timmermans, M.-L.; Proshutinsky, A.; Ashik, I.; Beszczynska-Moeller, A.; Carmack, E.; Frolov, I.; Ingvaldsen, R.; Itoh, M.; Jackson, J.; Kawaguchi, Y.; et al. Ocean. In Arctic Report Card; update to 2012; National Oceanic and Atmospheric Administration (NOAA): Washington, DC, USA, 2012; pp. 43–55. Available online: https://arctic.noaa.gov/Portals/7/ArcticReportCard/Documents/ArcticReportCard_full_report2012.pdf (accessed on 23 October 2021).
- Timmermans, M.-L.; Ashik, I.; Cao, Y.; Frolov, I.; Ha, H.K.; Ingvaldsen, R.; Kikuchi, T.; Kim, T.W.; Krishfield, R.; Loeng, H.; et al. Ocean Temperature and Salinity. In Arctic Report Card; update to 2013; National Oceanic and Atmospheric Administration (NOAA): Washington, DC, USA, 2013; pp. 44–49. Available online: https://arctic.noaa.gov/Portals/7/ArcticReportCard/Documents/ArcticReportCard_full_report2013.pdf (accessed on 23 October 2021).
- Timmermans, M.-L.; Proshutinsky, A. Arctic Ocean Sea Surface Temperature. In Arctic Report Card; update to 2014; National Oceanic and Atmospheric Administration (NOAA): Washington, DC, USA, 2014; pp. 39–43. Available online: https://arctic.noaa.gov/Portals/7/ArcticReportCard/Documents/ArcticReportCard_full_report2014.pdf (accessed on 23 October 2021).
- Timmermans, M.-L.; Proshutinsky, A. Sea Surface Temperature. In Arctic Report Card; update to 2015; National Oceanic and Atmospheric Administration (NOAA): Washington, DC, USA, 2015; pp. 41–43. Available online: https://arctic.noaa.gov/Portals/7/ArcticReportCard/Documents/ArcticReportCard_full_report2015.pdf (accessed on 23 October 2021).
- Fumo, J.T.; Carter, M.L.; Flick, R.E.; Rasmussen, L.L.; Rudnick, D.L.; Iacobellis, S.F. Contextualizing marine heatwaves in the Southern California bight under anthropogenic climate change. J. Geophys. Res. Ocean. 2020, 125, e2019JC015674. [Google Scholar] [CrossRef]
- Overview Maps of the State of the Ice Cover of the Arctic Ocean. Available online: http://www.aari.ru/projects/ECIMO/index.php (accessed on 20 June 2021). (In Russian).
- Platov, G.; Iakshina, D.; Krupchatnikov, V. Characteristics of Atmospheric Circulation Associated with Variability of Sea Ice in the Arctic. Geosciences 2020, 10, 359. [Google Scholar] [CrossRef]
- Golubeva, E.; Platov, G.; Malakhova, V.; Kraineva, M.; Iakshina, D. Modelling the Long-Term and Inter-Annual Variability in the Laptev Sea Hydrography and Subsea Permafrost State. Polarforsch. Bremerhav. Alfred Wegener Inst. Polar Mar. Res. 2017, 87, 195–210. [Google Scholar] [CrossRef]
- Kraineva, M.; Golubeva, E.; Platov, G. Simulation of the near-bottom water warming in the Laptev Sea in 2007–2008. Bull. Nov. Comp. Center Num. Model. in Atmosph. 2019, 17, 21–30. [Google Scholar]
- Golubeva, E.; Kraineva, M.; Platov, G. Simulation of near-bottom water warming in the Laptev Sea. IOP Conf. Ser. Earth Environ. Sci. 2020, 611, 012010. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Lago, V.; Holbrook, N.J.; Ling, S.D.; Mundy, C.N.; Hobday, A.J. Eastern Tasmania Marine Heatwave Atlas; Institute for Marine and Antarctic Studies; University of Tasmania: Hobart, Australia, 2017. [Google Scholar] [CrossRef]
- Martin, S.; Cavalieri, D.J. Contribution of the Siberian Shelf Polynyas to the Arctic Ocean Intermediate and Deep Water. J. Geophys. Res. 1989, 94, 12725–12738. [Google Scholar] [CrossRef]
- Dmitrenko, I.; Kirillov, S.; Tremblay, L.; Kassens, H.; Anisimov, O.; Lavrov, S.; Razumov, S.; Grigoriev, M. Recent changes in shelf hydrography in the Siberian Arctic: Potential for subsea permafrost instability. J. Geophys. Res. 2011, 116, C10027. [Google Scholar] [CrossRef]
- Bauch, D.; Rutgers van der Loeff, M.; Andersen, N.; Torres-Valdes, S.; Bakker, K.; Abrahamsen, P. Origin of freshwater and polynya water in the Arctic Ocean halocline in summer 2007. Prog. Oceanogr. 2011, 91, 482–495. [Google Scholar] [CrossRef] [Green Version]
- Dmitrenko, I.A.; Tyshko, K.N.; Kirillo, S.; Eicken, H.; Hölemann, J.; Kassens, H. Impact of flaw polynyas on the hydrography of the Laptev Sea. Glob. Planet. Chang. 2005, 48, 9–27. [Google Scholar] [CrossRef]
- Willmes, S.; Adams, S.; Schröder, D.; Heinemann, G. Spatio-temporal variability of polynya dynamics and ice production in the Laptev Sea between the winters of 1979/80 and 2007/08. Polar Res. 2011, 30, 5971. [Google Scholar] [CrossRef]
- Wills, R.C.J.; White, R.H.; Levine, X.J. Northern Hemisphere Stationary Waves in a Changing Climate. Curr. Clim. Chang. Rep. 2019, 5, 372–389. [Google Scholar] [CrossRef] [Green Version]
- Platov, G.; Krupchatnikov, V.; Gradov, V.; Borovko, I.; Volodin, E. Analysis of the Northern Hemisphere Atmospheric Circulation Response to Arctic Ice Reduction Based on Simulation Results. Geosciences 2021, 11, 373. [Google Scholar] [CrossRef]


















| 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60–70N | 1.5 | 1.3 | 0.4 | 1.0 | 1.6 | 1.5 | 1.0 | 1.7 | 1.9 | 2.7 | 1.8 | 2.1 | 2.4 | 2.9 |
| 70–85N | 2.4 | 2.1 | 2.6 | 1.9 | 3.1 | 2.9 | 1.9 | 2.6 | 2.5 | 3.9 | 2.7 | 3.0 | 3.4 | 3.6 |
| 60–85N | 1.5 | 1.6 | 2.3 | 2.2 | 1.4 | 2.2 | 2.2 | 3.3 | 2.2 | 2.5 | 2.8 | 3.2 |
| Exps. | Peculiarity of | Period of | Initial Ice State | Initial Ocean |
|---|---|---|---|---|
| Experiment | Simulation | State | ||
| A0 | Control experiment | Jan 2000–Dec 2020 | Jan 2000 | Jan 2000 |
| A1 | No fast ice | Jan 2000–Dec 2020 | Jan 2000 | Jan 2000 |
| A2 | No riverine heat | Jan 2000–Dec 2020 | Jan 2000 | Jan 2000 |
| D1 | No ice drift | Jan 2020–Dec 2020 | Jan 2020 | Jan 2020 |
| Sensitivity to initial ocean and ice state | ||||
| 1 year | ||||
| B1 | Thick ice | Nov 2019–Dec 2020 | Nov 2003 | Nov 2019 |
| B2 | Cold ocean | Nov 2019–Dec 2020 | Nov 2019 | Nov 2003 |
| B3 | Thick ice, cold ocean | Nov 2019–Dec 2020 | Nov 2003 | Nov 2003 |
| 5 years | ||||
| B11 | Thick ice | Jan 2016–Dec 2020 | Jan 2004 | Jan 2016 |
| B33 | Thick ice, cold ocean | Jan 2016–Dec 2020 | Jan 2004 | Jan 2004 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Golubeva, E.; Kraineva, M.; Platov, G.; Iakshina, D.; Tarkhanova, M. Marine Heatwaves in Siberian Arctic Seas and Adjacent Region. Remote Sens. 2021, 13, 4436. https://doi.org/10.3390/rs13214436
Golubeva E, Kraineva M, Platov G, Iakshina D, Tarkhanova M. Marine Heatwaves in Siberian Arctic Seas and Adjacent Region. Remote Sensing. 2021; 13(21):4436. https://doi.org/10.3390/rs13214436
Chicago/Turabian StyleGolubeva, Elena, Marina Kraineva, Gennady Platov, Dina Iakshina, and Marina Tarkhanova. 2021. "Marine Heatwaves in Siberian Arctic Seas and Adjacent Region" Remote Sensing 13, no. 21: 4436. https://doi.org/10.3390/rs13214436
APA StyleGolubeva, E., Kraineva, M., Platov, G., Iakshina, D., & Tarkhanova, M. (2021). Marine Heatwaves in Siberian Arctic Seas and Adjacent Region. Remote Sensing, 13(21), 4436. https://doi.org/10.3390/rs13214436






