Estimation of PM2.5 Concentration Using Deep Bayesian Model Considering Spatial Multiscale
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. MODIS Satellite Data
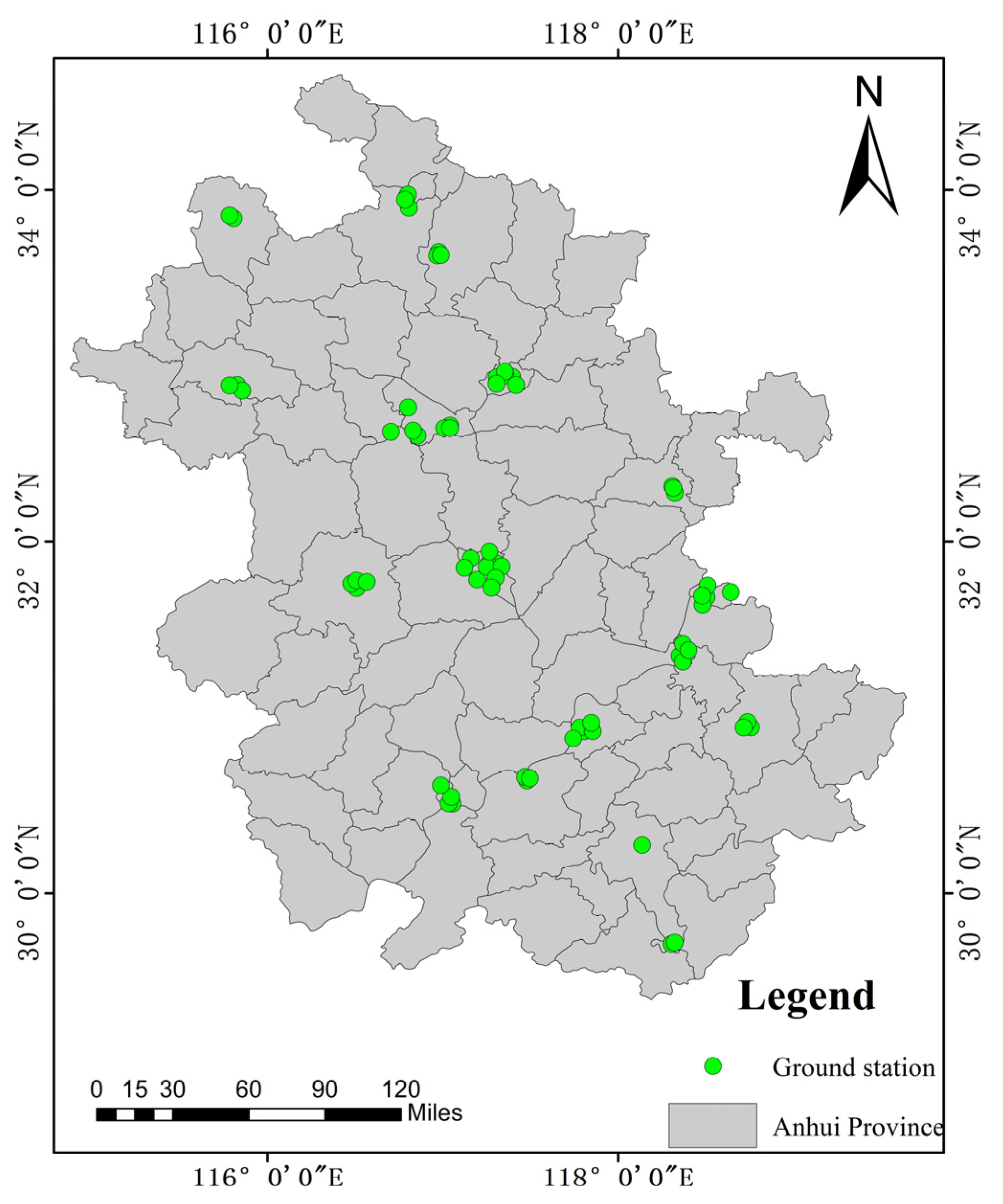
2.3. PM2.5 Measurements from Ground Stations
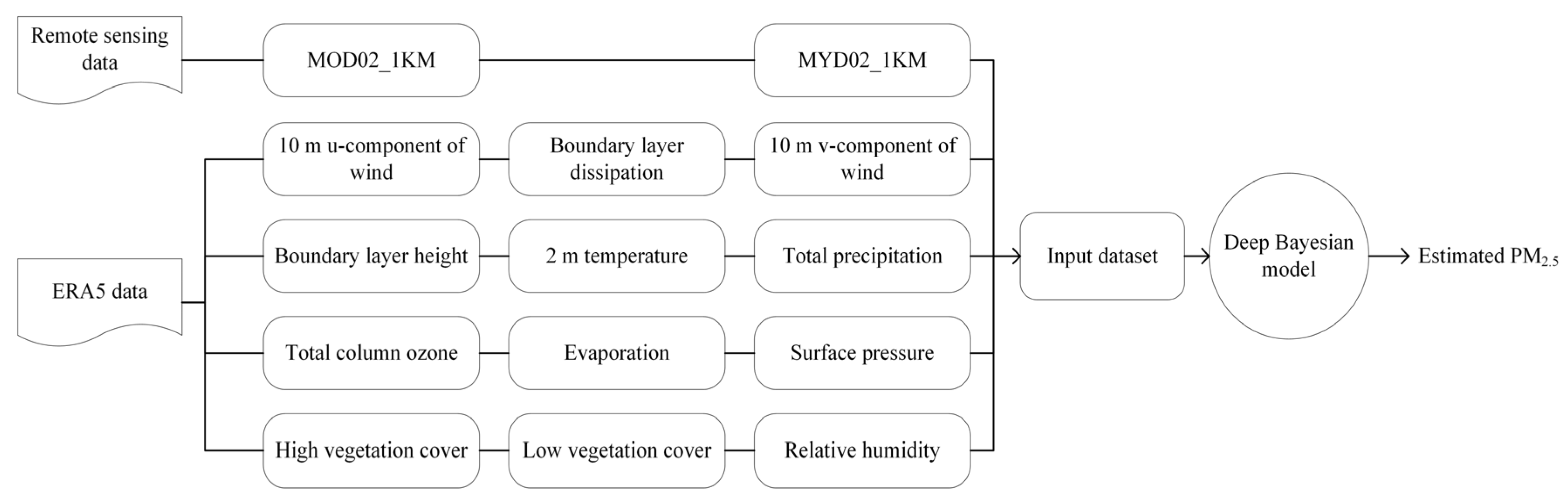
2.4. Weather Reanalysis Data
ERA5 Accuracy Analysis
2.5. Data Preprocessing
3. Methods
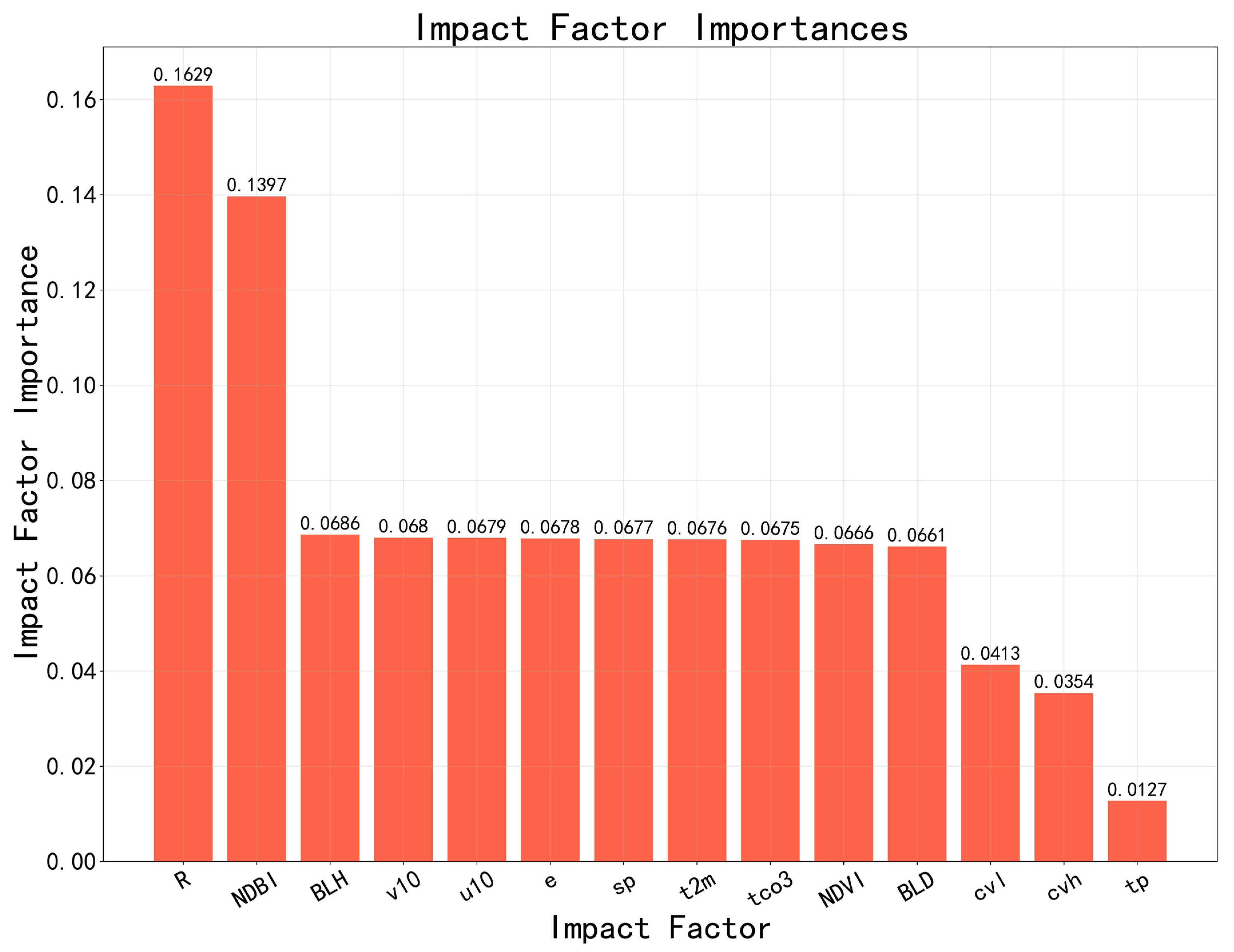
3.1. Impact Factor Screening
3.2. Bayesian Neural Network
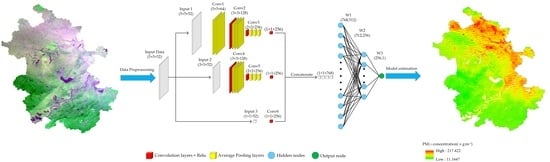
3.3. Deep Bayesian Model
3.4. Model Evaluation
4. Result
4.1. Results of Impact Factor Screening
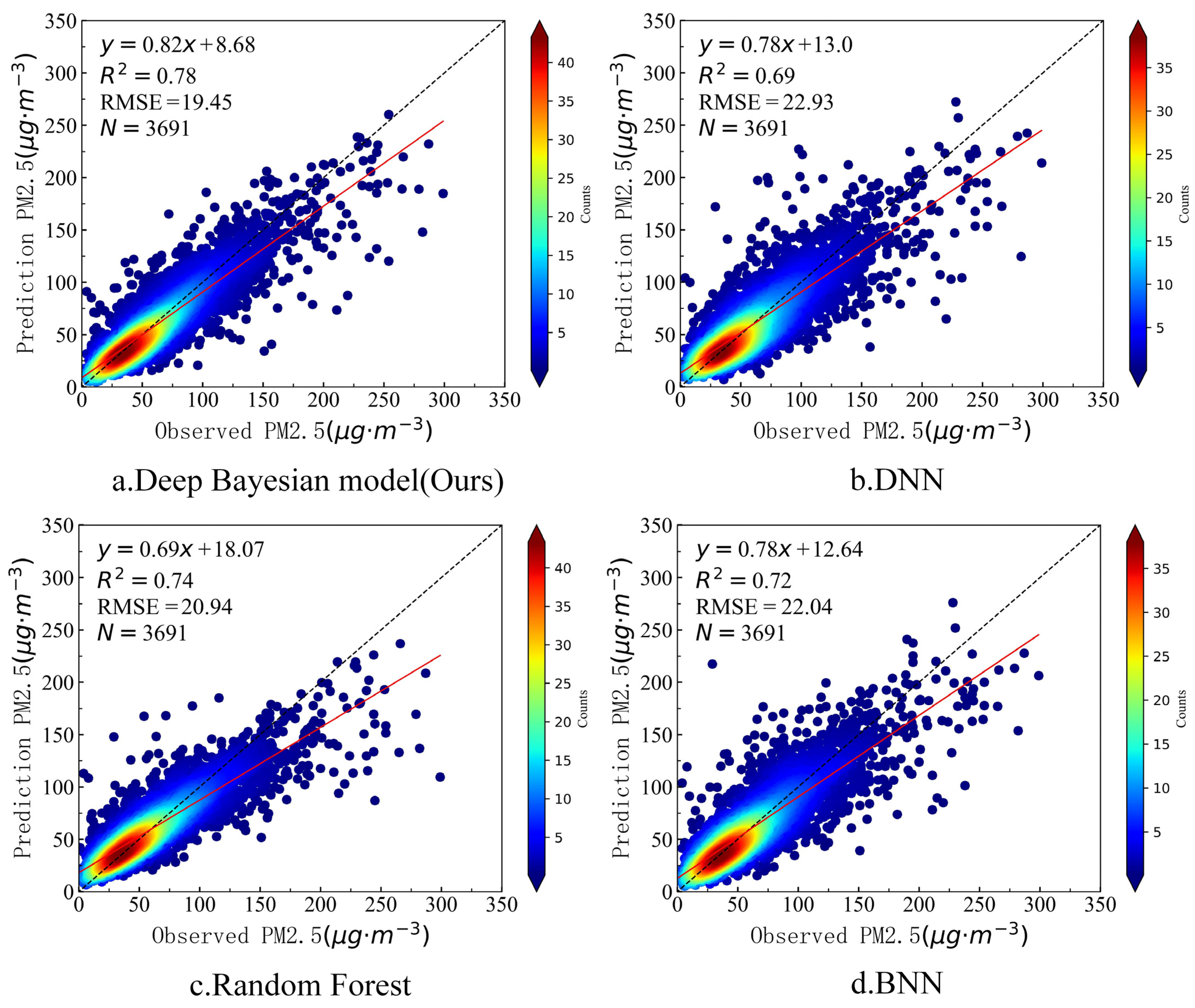
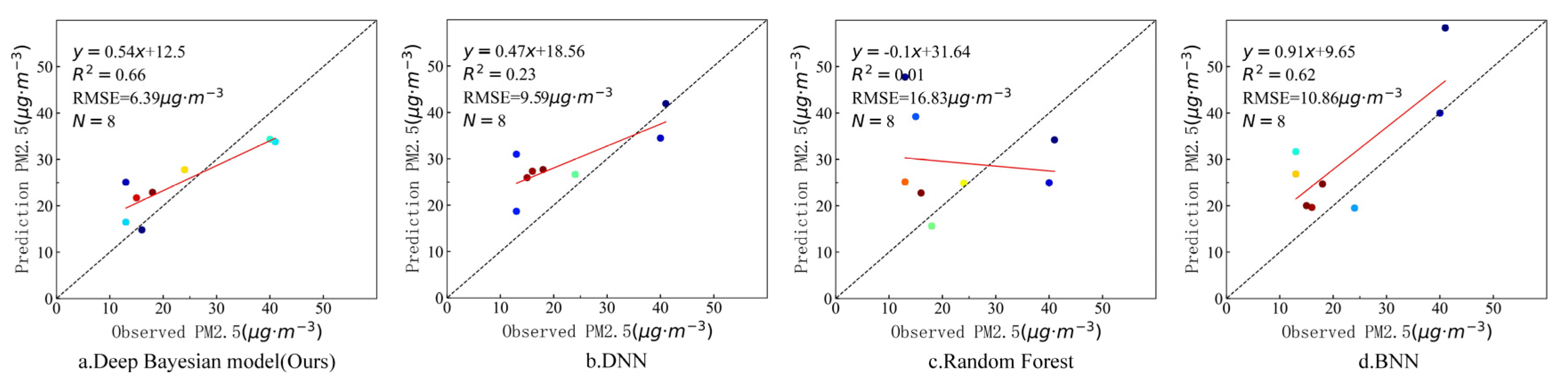
4.2. Comparative Analysis of Model Results
4.2.1. Comparative Analysis of Different Methods
4.2.2. Spatial Scope Impact Analysis
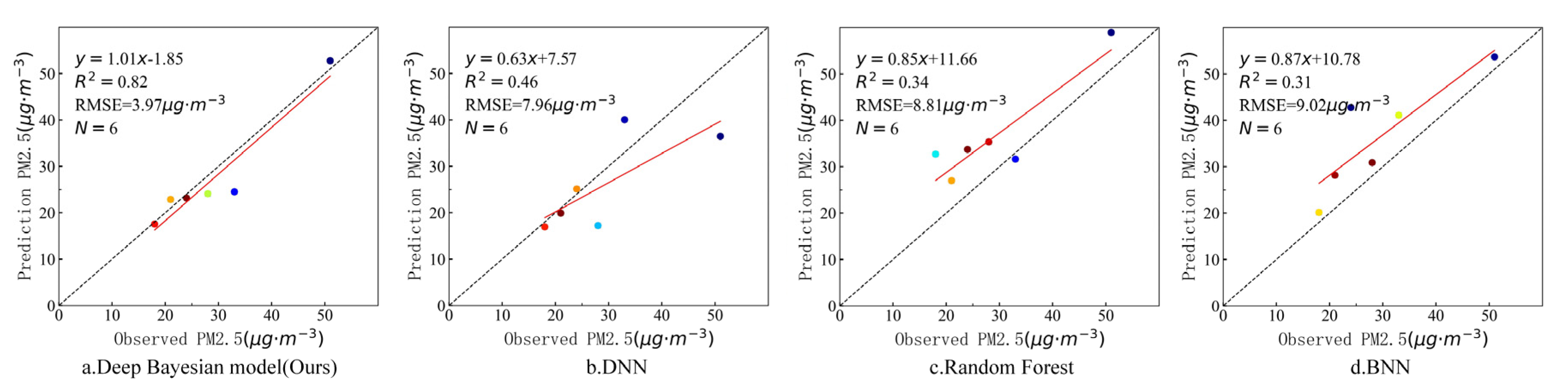
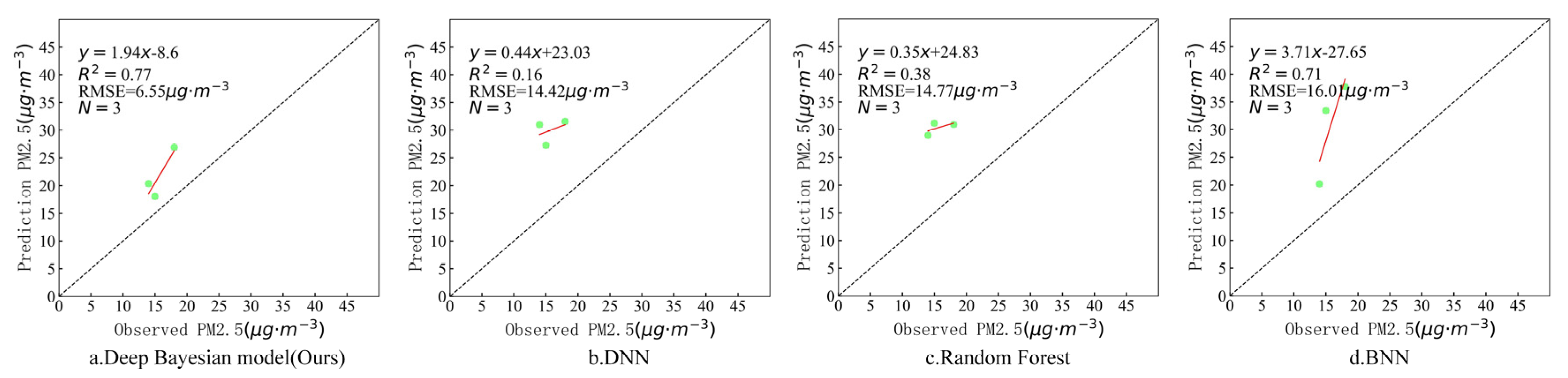
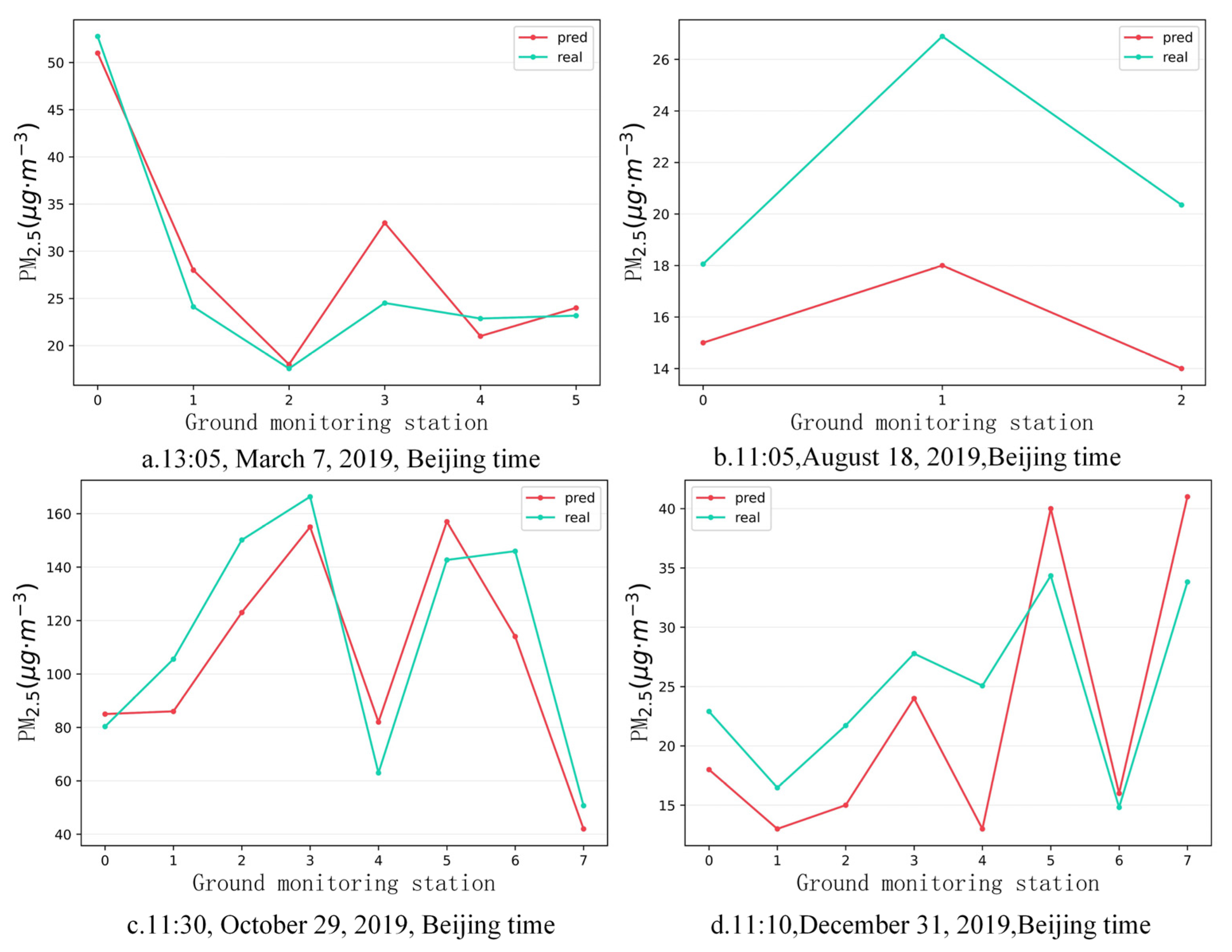
4.3. PM2.5 Concentration Estimation and Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, H.; Guan, Q.; Lin, J.; Wang, Q.; Yang, L.; Tan, Z.; Wang, N. Air pollution characteristics and human health risks in key cities of northwest China. J. Environ. Manag. 2020, 269, 110791. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Wang, Y.; Zeng, Y.; Gao, G.F.; Liang, X.; Zhou, M.; Wan, X.; Yu, S.; Jiang, Y.; Naghavi, M.; et al. Rapid health transition in China, 1990–2010: Findings from the Global Burden of Disease Study 2010. Lancet 2013, 381, 1987–2015. [Google Scholar] [CrossRef]
- Wang, J.; Cristopher, S.A. Intercomparison between satellite-derived aerosol optical thickness and PM2.5 mass: Implications for air quality studies. Geophys. Res. Lett. 2003, 30, 2095. [Google Scholar] [CrossRef]
- Li, R.; Mei, X.; Chen, L.; Wang, Z.; Jing, Y.; Wei, L. Influence of spatial resolution and retrieval frequency on applicability of satellite-predicted PM2.5 in Northern China. Remote Sens. 2020, 12, 736. [Google Scholar] [CrossRef] [Green Version]
- van Donkelaar, A.; Martin, R.V.; Brauer, M.; Hsu, C.; Kahn, R.A.; Levy, R.C.; Lyapustin, A.; Sayer, A.M.; Winker, D.M. Global estimates of fine particulate matter using a combined geophysical-statistical method with information from satellites, models, and monitors. Environ. Sci. Technol. 2016, 50, 3762–3772. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Huang, B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Koelemeijer, R.B.A.; Homan, C.D.; Matthijsen, J. Comparison of spatial and temporal variations of aerosol optical thickness and particulate matter over Europe. Atmos. Environ. 2006, 40, 5304–5315. [Google Scholar] [CrossRef]
- Lin, C.; Li, Y.; Lau, A.; Deng, X.; Tse, T.K.; Fung, J.; Li, C.; Li, Z.; Lu, X.; Zhang, X.; et al. Estimation of long-term population exposure to PM2.5 for dense urban areas using 1-km MODIS data. Remote Sens. Environ. 2016, 179, 13–22. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, Z. Remote sensing of atmospheric fine particulate matter (PM2.5) mass concentration near the ground from satellite observation. Remote Sens. Environ. 2015, 160, 252–262. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Seven year particulate matter air quality assessment from surface and satellite measurements. Atmos. Chem. Phys. 2008, 8, 3311–3324. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Fu, Q.; Ma, Z.; Chen, L.; Zou, B.; Zhang, Y.; Xue, W.; Wang, J.; Wang, D.; Kan, H.; et al. Estimating ground-level PM (10) in a Chinese city by combining satellite data, meteorological information and a land use regression model. Environ. Pollut. 2016, 208, 177–184. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.J.; Liu, Y.; Coull, B.A.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS AOD data to predict PM 2.5 concentrations. Atmos. Chem. Phys. 2011, 11, 7991–8002. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Sarnat, J.A.; Kilaru, V.; Jacob, D.J.; Koutrakis, P. Estimating ground-level PM2.5 in the Eastern United States using satellite remote sensing. Environ. Sci. Technol. 2005, 39, 3269–3278. [Google Scholar] [CrossRef] [Green Version]
- van Donkelaar, A.; Martin, R.V.; Spurr, R.J.D.; Burnett, R.T. High-resolution satellite-derived PM2.5 from optimal estimation and geographically weighted regression over North America. Environ. Sci. Technol. 2015, 49, 10482–10491. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Yuan, Q.; Yue, L.; Li, T.; Shen, H.; Zhang, L. The relationships between PM2.5 and aerosol optical depth (AOD) in mainland China: About and behind the spatio-temporal variations. Environ. Pollut. 2019, 248, 526–535. [Google Scholar] [CrossRef] [PubMed]
- You, W.; Zang, Z.; Zhang, L.; Zhang, M.; Pan, X.; Li, Y. A nonlinear model for estimating ground-level PM10 concentration in Xi’an using MODIS aerosol optical depth retrieval. Atmos. Res. 2016, 168, 169–179. [Google Scholar] [CrossRef]
- He, J.; Christakos, G. Space-time PM2.5 mapping in the severe haze region of Jing-Jin-Ji (China) using a synthetic approach. Environ. Pollut. 2018, 240, 319–329. [Google Scholar] [CrossRef] [PubMed]
- Brokamp, C.; Jandarov, R.; Hossain, M.; Ryan, P. Predicting daily urban fine particulate matter concentrations using a random forest model. Environ. Sci. Technol. 2018, 52, 4173–4179. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Ho, H.C.; Wong, M.S.; Deng, C.; Shi, Y.; Chan, T.-C.; Knudby, A. Evaluation of machine learning techniques with multiple remote sensing datasets in estimating monthly concentrations of ground-level PM2.5. Environ. Pollut. 2018, 242, 1417–1426. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, L. Geographically and temporally weighted neural networks for satellite-based mapping of ground-level PM2.5. ISPRS J. Photogramm. Remote Sens. 2020, 167, 178–188. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Zeng, C.; Yuan, Q.; Zhang, L. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China: Methods and assessment. Atmos. Environ. 2017, 152, 477–489. [Google Scholar] [CrossRef] [Green Version]
- Murillo-Escobar, J.; Sepulveda-Suescun, J.P.; Correa, M.A.; Orrego-Metaute, D. Forecasting concentrations of air pollutants using support vector regression improved with particle swarm optimization: Case study in Aburrá Valley, Colombia. Urban Clim. 2019, 29, 100473. [Google Scholar] [CrossRef]
- Qiao, J.; He, Z.; Du, S. Prediction of PM2.5 concentration based on weighted bagging and image contrast-sensitive features. Stoch. Environ. Res. Risk Assess. 2020, 34, 561–573. [Google Scholar] [CrossRef]
- Tao, M.; Wang, Z.; Tao, J.; Chen, L.; Wang, J.; Hou, C.; Wang, L.; Xu, X.; Zhu, H. How do aerosol properties affect the temporal variation of MODIS AOD bias in Eastern China? Remote Sens. 2017, 9, 800. [Google Scholar] [CrossRef] [Green Version]
- Song, Z.; Fu, D.; Zhang, X.; Han, X.; Song, J.; Zhang, J.; Wang, J.; Xia, X. MODIS AOD sampling rate and its effect on PM2.5 estimation in North China. Atmos. Environ. 2019, 209, 14–22. [Google Scholar] [CrossRef]
- Tao, M.; Wang, J.; Li, R.; Wang, L.; Wang, L.; Tao, J.; Che, H.; Chen, L. Performance of MODIS high-resolution MAIAC aerosol algorithm in China: Characterization and limitation. Atmos. Environ. 2019, 213, 159–169. [Google Scholar] [CrossRef]
- Mao, F.; Hong, J.; Min, Q.; Gong, W.; Zang, L.; Yin, J. Estimating hourly full-coverage PM2.5 over China based on TOA reflectance data from the Fengyun-4 A satellite. Environ. Pollut. 2021, 270, 116119. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Weng, F.; Li, Z. Satellite-based PM2.5 estimation directly from reflectance at the top of the atmosphere using a machine learning algorithm. Atmos. Environ. 2019, 208, 113–122. [Google Scholar] [CrossRef]
- Shen, H.; Li, T.; Yuan, Q.; Zhang, L. Estimating regional ground-level PM2.5 Directly from satellite top-of-atmosphere reflectance using deep belief networks. J. Geophys. Res. Atmos. 2018, 123, 13–875. [Google Scholar] [CrossRef] [Green Version]
- Bai, H.; Zheng, Z.; Zhang, Y.; Huang, H.; Wang, L. Comparison of satellite-based PM2.5 Estimation from aerosol optical depth and top-of-atmosphere reflectance. Aerosol Air Qual. Res. 2020, 21, 200257. [Google Scholar] [CrossRef]
- Imani, M. Particulate matter (PM2.5 and PM10) generation map using MODIS Level-1 satellite images and deep neural network. J. Environ. Manag. 2021, 281, 111888. [Google Scholar] [CrossRef] [PubMed]
- Hong, K.Y.; Pinheiro, P.O.; Weichenthal, S. Predicting global variations in outdoor PM2.5 concentrations using satellite images and deep convolutional neural networks. arXiv 2019, arXiv:1906.03975. [Google Scholar]
- Zheng, T.; Bergin, M.H.; Hu, S.; Miller, J.; Carlson, D.E. Estimating ground-level PM 2.5 using micro-satellite images by a convolutional neural network and random forest approach. Atmos. Environ. 2020, 230, 117451. [Google Scholar] [CrossRef]
- Li, G.; Wu, H.; Zhong, Q.; He, J.; Yang, W.; Zhu, J.; Zhao, H.; Zhang, H.; Zhu, Z.; Huang, F. Six air pollutants and cause-specific mortality: A multi-area study in nine counties or districts of Anhui Province, China. Environ. Sci. Pollut. Res. 2021, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Sun, J.; Chang, X.; Zhang, W.; Arcucci, R.; Guo, Y.; Pain, C.C. Data-driven reduced order model with temporal convolutional neural network. Comput. Methods Appl. Mech. Eng. 2020, 360, 112766. [Google Scholar] [CrossRef]
- Liu, B.; Guo, J.; Gong, W.; Zhang, Y.; Shi, L.; Ma, Y.; Li, J.; Guo, X.; Stoffelen, A.; de Leeuw, G.; et al. Intercomparison of wind observations from ESA’s satellite mission Aeolus, ERA5 reanalysis and radiosonde over China. Atmos. Chem. Phys. 2021, 1–35. [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y.; Bolbasova, L.A.; Kovadlo, P.G.; Kiselev, A.V. Atmospheric parameters at the 6-m Big Telescope Alt-azimuthal site. Mon. Not. R. Astron. Soc. 2020, 493, 723–729. [Google Scholar] [CrossRef]
- Demchev, D.M.; Kulakov, M.Y.; Makshtas, A.P.; Makhotina, I.A.; Fil’chuk, K.V.; Frolov, I.E. Verification of ERA-Interim and ERA5 Reanalyses Data on Surface Air Temperature in the Arctic. Russ. Meteorol. Hydrol. 2020, 45, 771–777. [Google Scholar] [CrossRef]
- Oses, N.; Azpiroz, I.; Marchi, S.; Guidotti, D.; Quartulli, M.; Olaizola, I.G. Analysis of Copernicus’ ERA5 Climate Reanalysis Data as a Replacement for Weather Station Temperature Measurements in Machine Learning Models for Olive Phenology Phase Prediction. Sensors 2020, 20, 6381. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Cai, C.; Chen, B.; Dai, W. Consistency Evaluation of Precipitable Water Vapor Derived From ERA5, ERA-Interim, GNSS, and Radiosondes Over China. Radio Sci. 2019, 54, 561–571. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. VSURF: Variable Selection Using Random Forests. Pattern Recognit. Lett. 2016, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shao, M.; Wang, W.; Yuan, B.; Parrish, D.D.; Li, X.; Lu, K.; Wu, L.; Wang, X.; Mo, Z.; Yang, S. Quantifying the role of PM2.5 dropping in variations of ground-level ozone: Inter-comparison between Beijing and Los Angeles. Sci. Total Environ. 2021, 788, 147712. [Google Scholar] [CrossRef] [PubMed]




| Name | Unit | Definition Description |
|---|---|---|
| 10 m u-component of wind | m/s | This parameter is the eastward component of the 10 m wind |
| Boundary layer height | m | This parameter calculation is based on the bulk Richardson number |
| Total column ozone | kg/m2 | This parameter is the total amount of ozone in a column of air extending from the surface of the Earth to the top of the atmosphere |
| Boundary layer dissipation | J/m2 | This parameter is the accumulated conversion of kinetic energy in the mean flow into heat, over the whole atmospheric column, per unit area |
| 2 m temperature | K | This parameter is the temperature of air at 2 m above the surface of land, sea or inland waters |
| Evaporation | m of water equivalent | This parameter is the accumulated amount of water that has evaporated from the Earth’s surface |
| 10 m v-component of wind | m/s | This parameter is the northward component of the “neutral wind”, at a height of 10 m above the surface of the Earth |
| Total precipitation | m | This parameter is the accumulated liquid and frozen water, comprising rain and snow, that falls to the Earth’s surface |
| Surface pressure | Pa | This parameter is the pressure (force per unit area) of the atmosphere at the surface of land, sea and inland water |
| High vegetation cover | Dimensionless | This parameter is the fraction of the grid box that is covered with vegetation that is classified as “high” |
| Low vegetation cover | Dimensionless | This parameter is the fraction of the grid box that is covered with vegetation that is classified as “low” |
| Relative humidity | % | This parameter is the water vapour pressure as a percentage of the value at which the air becomes saturated (the point at which water vapour begins to condense into liquid water or deposition into ice) |
| Model | Model Training | Model Testing | ||
|---|---|---|---|---|
| R2 Value | RMSE (μg·m−3) | R2 Value | RMSE (μg·m−3) | |
| Deep Bayesian (this study) | 0.97 | 6.84 | 0.78 | 19.45 |
| DNN | 0.92 | 10.93 | 0.69 | 22.93 |
| Random Forest | 0.93 | 10.14 | 0.74 | 20.94 |
| BNN | 0.94 | 9.33 | 0.72 | 22.04 |
| Spatial Range | Model Test Accuracy (R2) |
|---|---|
| 1 km × 1 km | 0.69 |
| 3 km × 3 km | 0.74 |
| 5 km × 5 km | 0.76 |
| 1 km × 1 km, 3 km × 3 km | 0.75 |
| 1 km × 1 km, 3 km × 3 km, 5 km × 5 km | 0.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Kong, P.; Jiang, P.; Wu, Y. Estimation of PM2.5 Concentration Using Deep Bayesian Model Considering Spatial Multiscale. Remote Sens. 2021, 13, 4545. https://doi.org/10.3390/rs13224545
Chen X, Kong P, Jiang P, Wu Y. Estimation of PM2.5 Concentration Using Deep Bayesian Model Considering Spatial Multiscale. Remote Sensing. 2021; 13(22):4545. https://doi.org/10.3390/rs13224545
Chicago/Turabian StyleChen, Xingdi, Peng Kong, Peng Jiang, and Yanlan Wu. 2021. "Estimation of PM2.5 Concentration Using Deep Bayesian Model Considering Spatial Multiscale" Remote Sensing 13, no. 22: 4545. https://doi.org/10.3390/rs13224545
APA StyleChen, X., Kong, P., Jiang, P., & Wu, Y. (2021). Estimation of PM2.5 Concentration Using Deep Bayesian Model Considering Spatial Multiscale. Remote Sensing, 13(22), 4545. https://doi.org/10.3390/rs13224545