Wind Speed Retrieval Algorithm Using Ku-Band Radar Onboard GPM Satellite
Abstract
:1. Introduction
2. Data Source
2.1. DPR Data
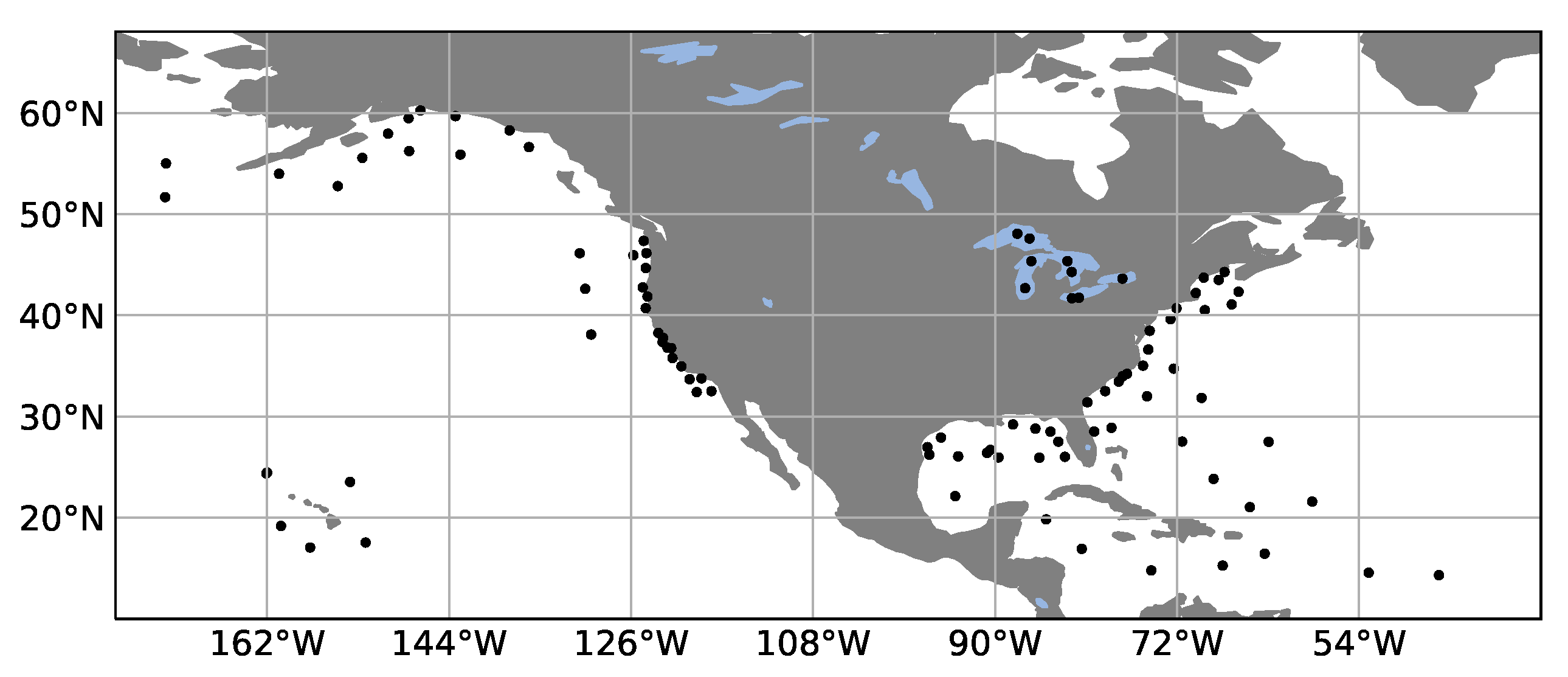
2.2. Buoy Wind Speed Data
3. Wind Speed Retrieval Algorithm
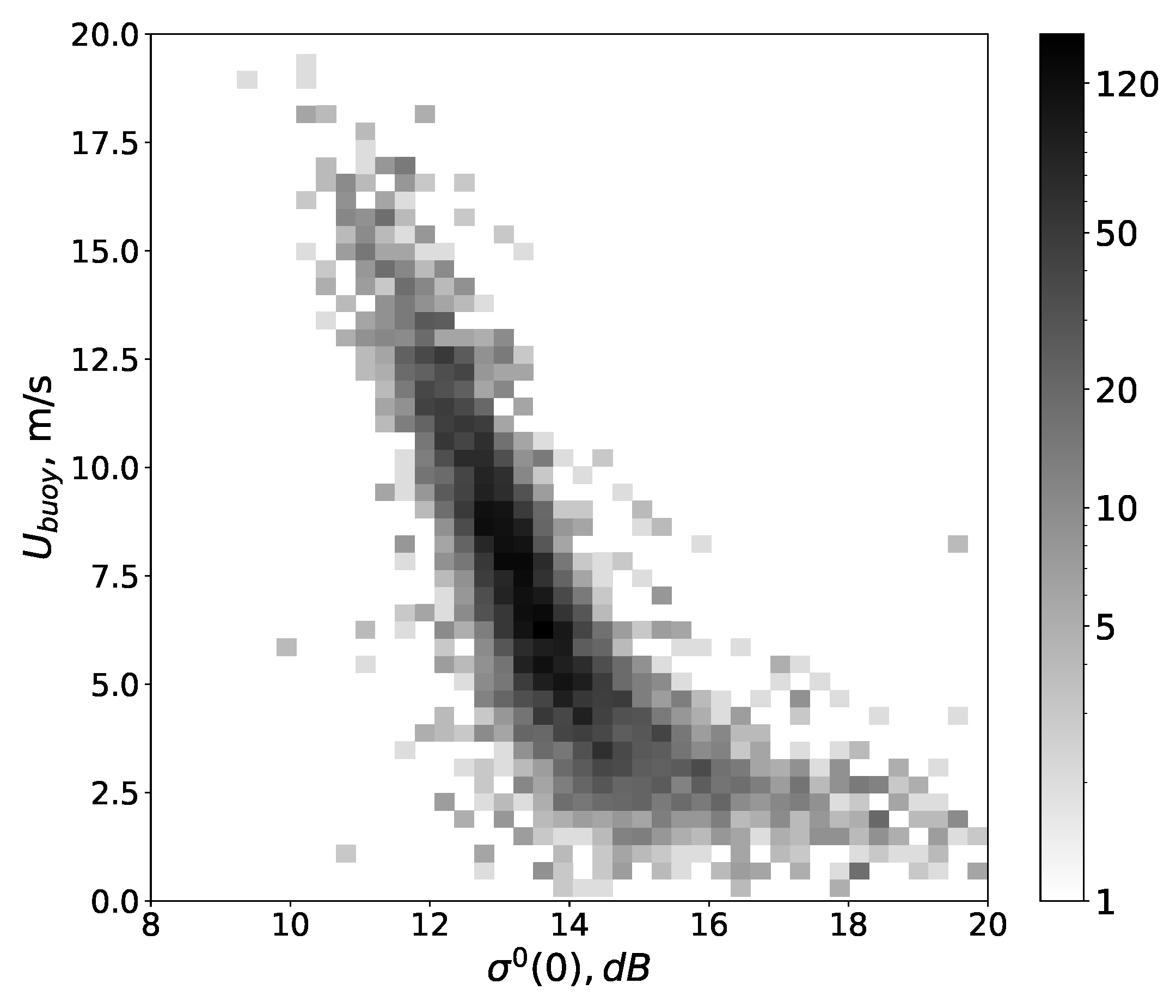
3.1. Data around Buoys
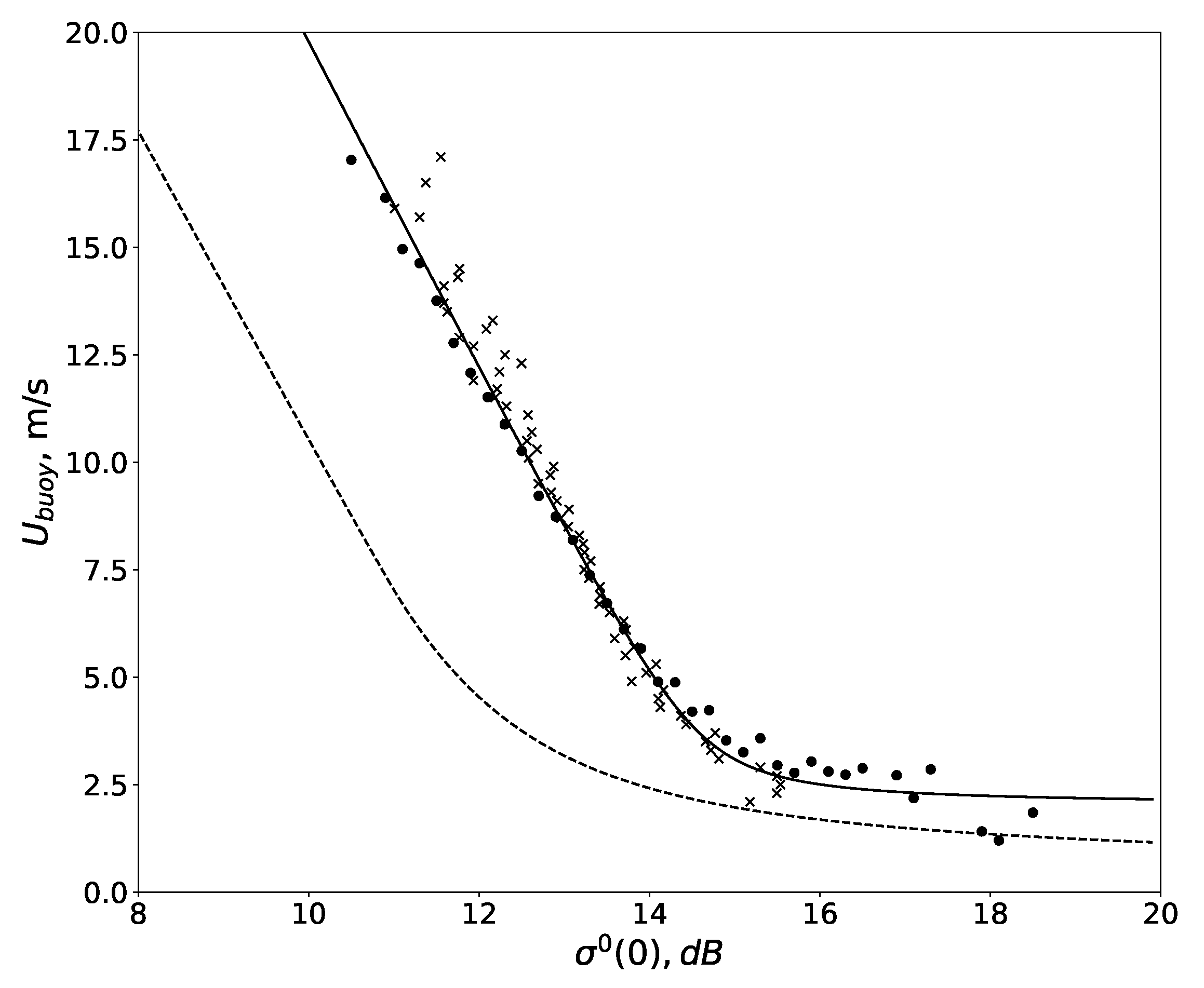
3.2. Regression Model for Wind Speed of NRCS at Nadir
4. Discussion: Wind Speed Retrieval Accuracy
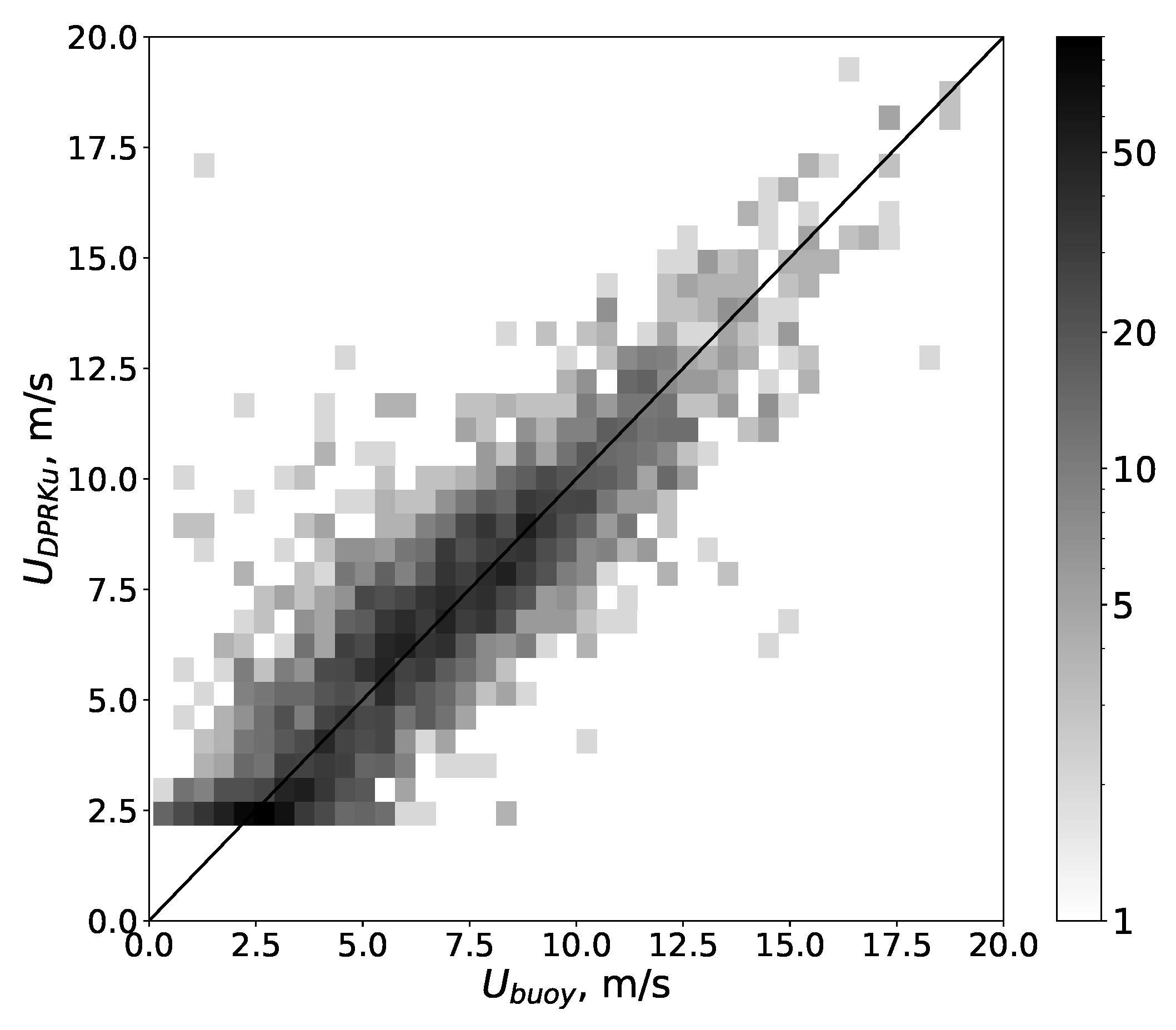
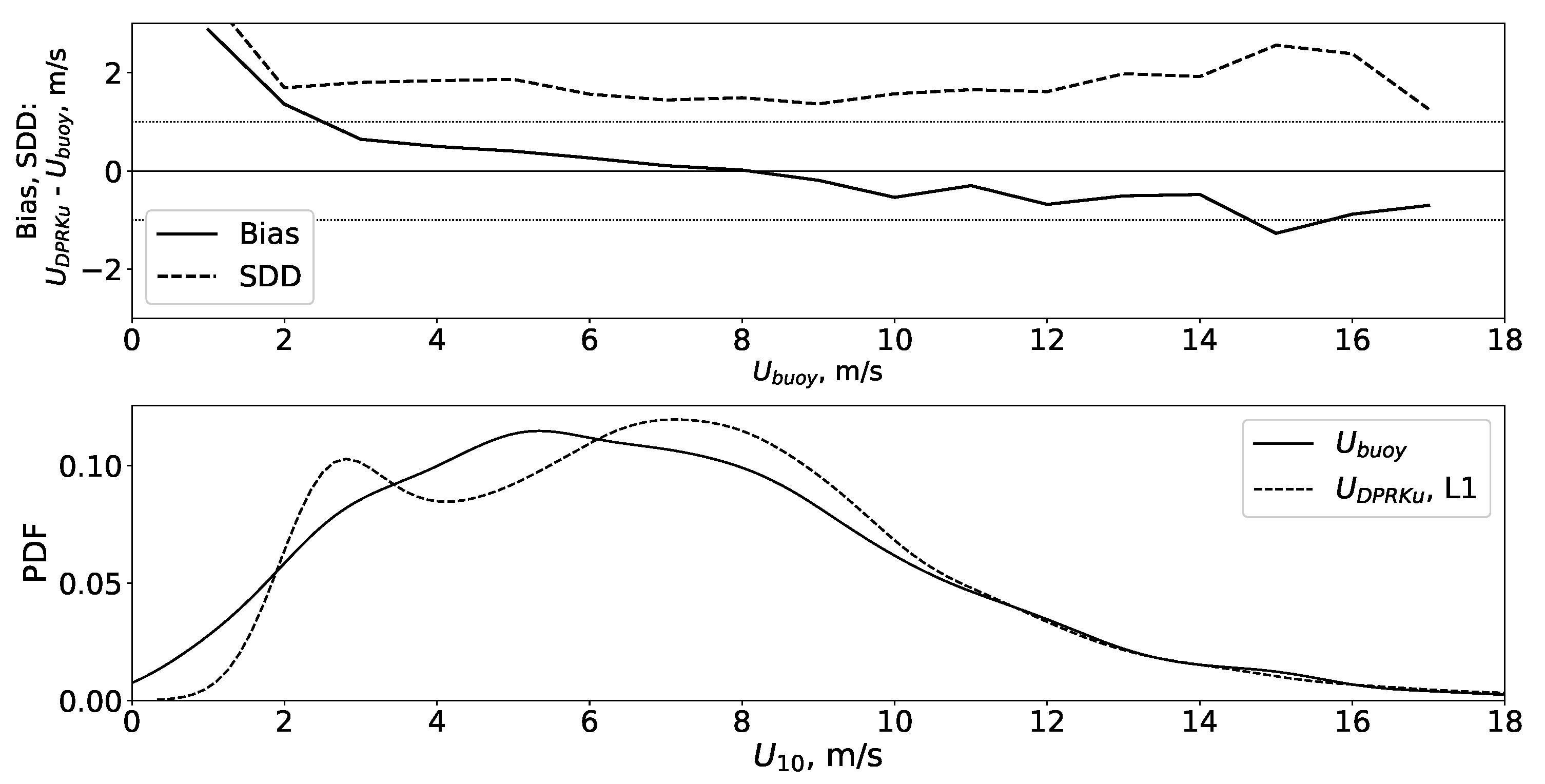
4.1. Comparison with Buoy
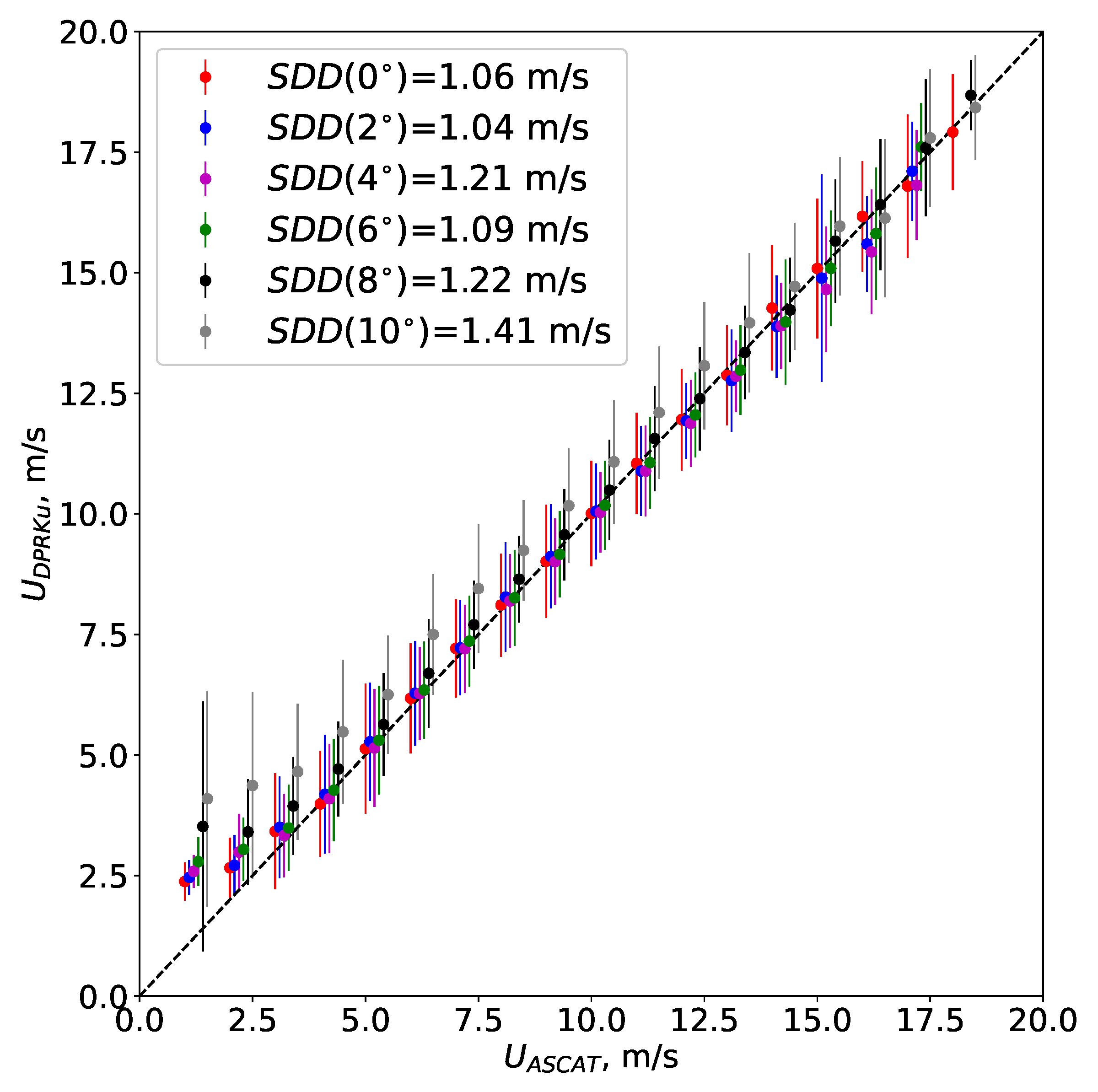
4.2. Comparison with ASCAT
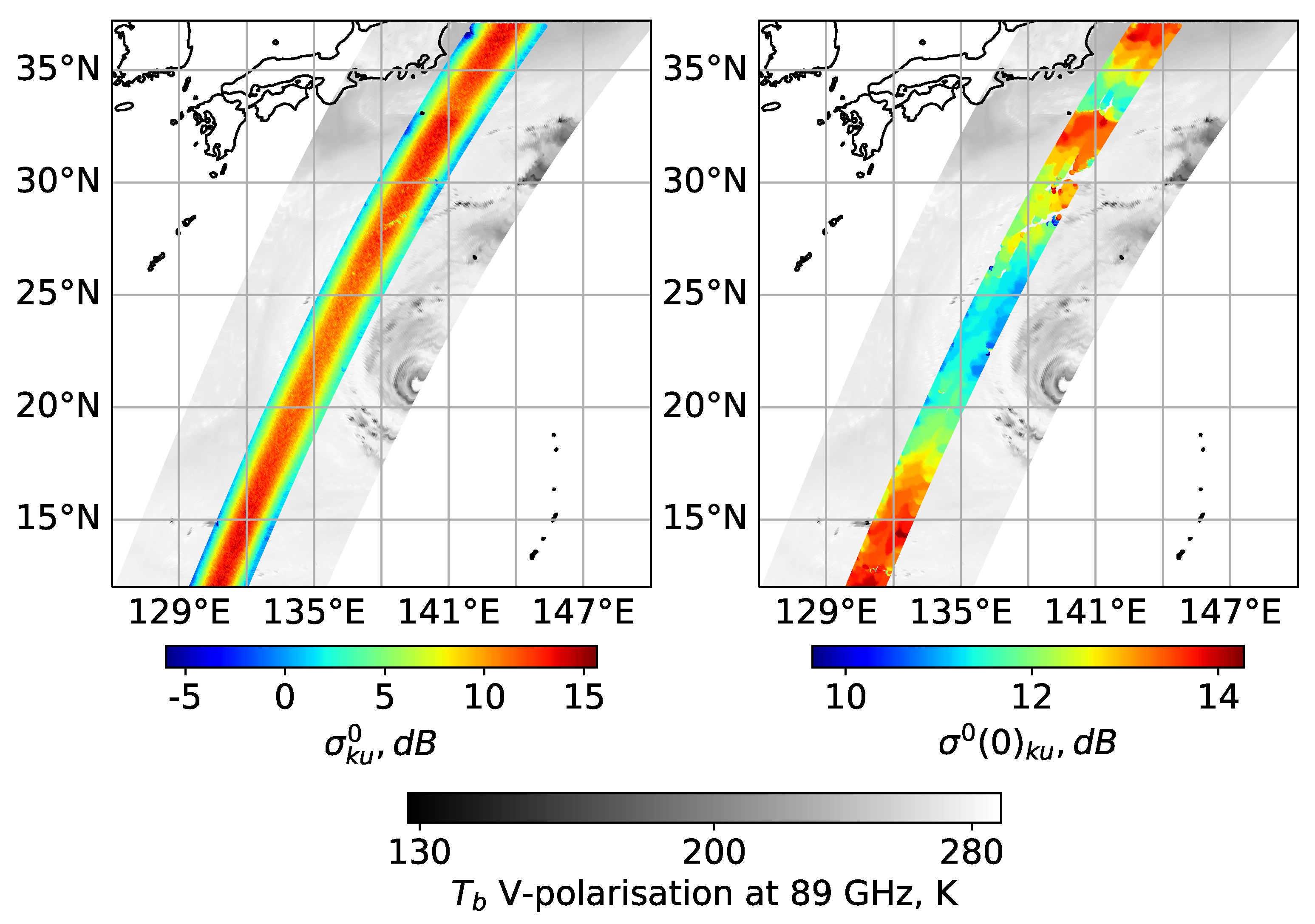
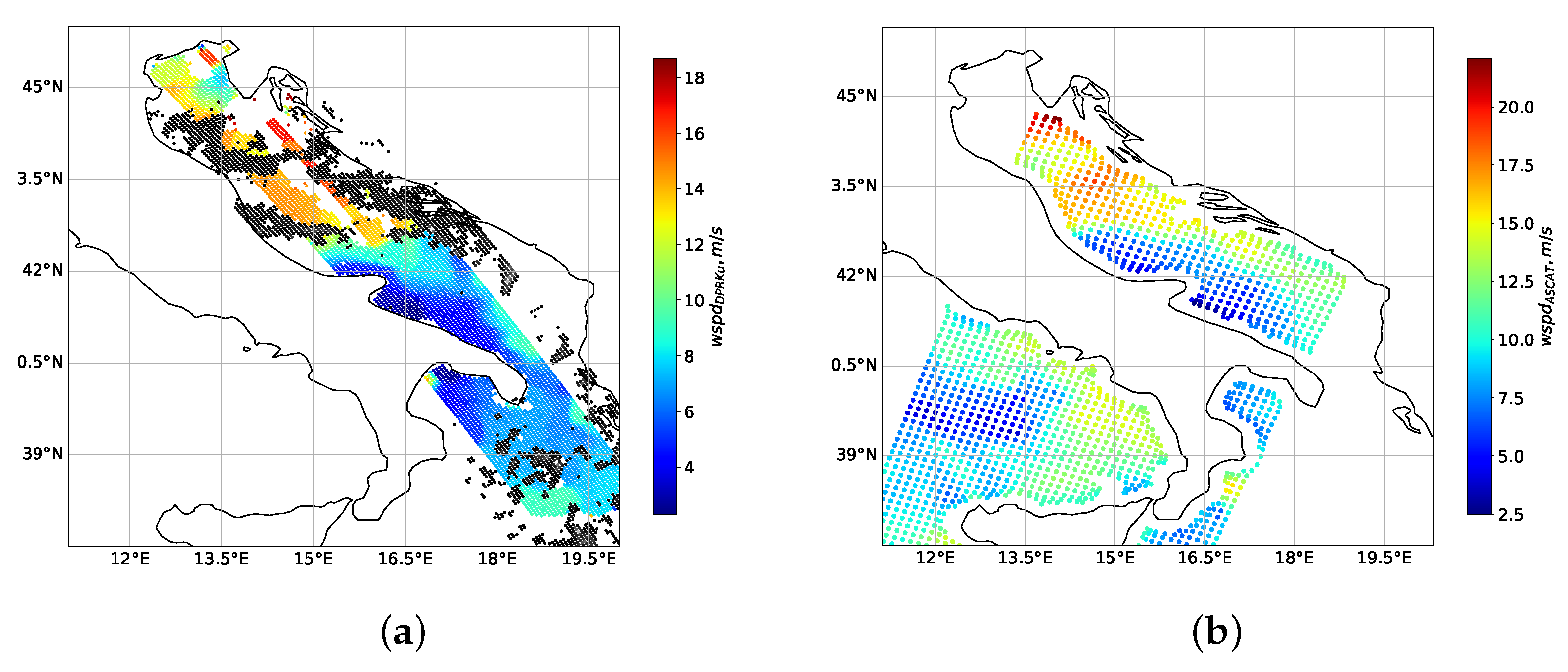
4.3. Local Case of Wind Speed Retrieval from DPR Ku-Band Radar
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASCAT | Advanced Scatterometer |
| DPR | Dual Frequency Precipitation Radar |
| ENVISAT | Environmental Satellite |
| GMI | GPM Microwave Imager |
| GPM | Global Precipitation Measurement |
| mss | Mean square slope |
| NDBC | National Data Buoy Center |
| NRCS | Normalized Radar Cross-section |
| Probability Density Function | |
| TRMM | Tropical Raifall Measurement Mission |
| UTC | Coordinated Universal Time |
Appendix A
References
- Ye, H.; Li, J.; Li, B.; Liu, J.; Tang, D.; Chen, W.; Yang, H.; Zhou, F.; Zhang, R.; Wang, S.; et al. Evaluation of CFOSAT Scatterometer Wind Data in Global Oceans. Remote Sens. 2021, 13, 1926. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Meissner, T.; Cerovecki, I.; Chang, P.S.; Dong, X.; De Chiara, G.; Donlon, C.; Dukhovskoy, D.S.; Elya, J.; Fore, A.; et al. Remotely Sensed Winds and Wind Stresses for Marine Forecasting and Ocean Modeling. Front. Mar. Sci. 2019, 6, 443. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Stoffelen, A.; Haan, S. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. Ocean. 2007, 112, C03006. [Google Scholar] [CrossRef]
- Witter, D.L.; Chelton, D. A geosat altimeter wind speed algorithm and a method for altimeter wind speed algorithm development. J. Geophys. Res. 1991, 96, 8853–8860. [Google Scholar] [CrossRef]
- Gourrion, J.; Vandemark, D.; Bailey, S.; Chapron, B.; Gommenginger, C.P.; Challenor, P.G.; Srokosz, M.A. A Two-Parameter Wind Speed Algorithm for Ku-Band Altimeters. J. Atmos. Ocean. Technol. 2002, 19, 2030–2048. [Google Scholar] [CrossRef]
- Karaev, V.Y.; Kanevsky, M.B.; Balandina, G.N.; Cotton, P.D.; Challenor, P.G.; Gommenginger, C.P.; Srokosz, M.A. On the problem of the near ocean surface wind speed retrieval by radar altimeter: A two-parameter algorithm. Int. J. Remote Sens. 2002, 23, 3263–3283. [Google Scholar] [CrossRef]
- Abdalla, S. Ku-Band Radar Altimeter Surface Wind Speed Algorithm. Mar. Geod. 2012, 35, 276–298. [Google Scholar] [CrossRef] [Green Version]
- Hauser, D.; Tourain, C.; Hermozo, L.; Alraddawi, D.; Aouf, L.; Chapron, B.; Dalphinet, A.; Delaye, L.; Dalila, M.; Dormy, E.; et al. New Observations From the SWIM Radar On-Board CFOSAT: Instrument Validation and Ocean Wave Measurement Assessment. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5–26. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F. The Emissivity of the Ocean Surface Between 6 and 90 GHz Over a Large Range of Wind Speeds and Earth Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3004–3026. [Google Scholar] [CrossRef]
- Gao, J.; Tang, G.; Hong, Y. Similarities and Improvements of GPM Dual-Frequency Precipitation Radar (DPR) upon TRMM Precipitation Radar (PR) in Global Precipitation Rate Estimation, Type Classification and Vertical Profiling. Remote Sens. 2017, 9, 1142. [Google Scholar] [CrossRef] [Green Version]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) Sensor Package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Freilich, M.H.; Vanhoff, B.A. The Relationship between Winds, Surface Roughness, and Radar Backscatter at Low Incidence Angles from TRMM Precipitation Radar Measurements. J. Atmos. Ocean. Technol. 2003, 20, 549–562. [Google Scholar] [CrossRef]
- Chu, X.; He, Y.; Karaev, V.Y. Relationships Between Ku-Band Radar Backscatter and Integrated Wind and Wave Parameters at Low Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4599–4609. [Google Scholar] [CrossRef]
- Chu, X.; He, Y.; Chen, G. Asymmetry and Anisotropy of Microwave Backscatter at Low Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4014–4024. [Google Scholar] [CrossRef]
- Chen, P.; Zheng, G.; Hauser, D.; Xu, F. Quasi-Gaussian probability density function of sea wave slopes from near nadir Ku-band radar observations. Remote Sens. Environ. 2018, 217, 86–100. [Google Scholar] [CrossRef]
- Hossan, A.; Jones, W.L. Ku- and Ka-Band Ocean Surface Radar Backscatter Model Functions at Low-Incidence Angles Using Full-Swath GPM DPR Data. Remote Sens. 2021, 13, 1569. [Google Scholar] [CrossRef]
- Panfilova, M.A.; Karaev, V.Y.; Guo, J. Oil Slick Observation at Low Incidence Angles in Ku-Band. J. Geophys. Res. Ocean. 2018, 123, 1924–1936. [Google Scholar] [CrossRef]
- Li, L.; Im, E.; Connor, L.; Chang, P. Retrieving ocean surface wind speed from the TRMM Precipitation Radar measurements. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1271–1282. [Google Scholar] [CrossRef]
- Ren, L.; Yang, J.; Zheng, G.; Wang, J. Wind speed retrieval from Ku-band Tropical Rainfall Mapping Mission precipitation radar data at low incidence angles. J. Appl. Remote Sens. 2016, 10, 1–14. [Google Scholar] [CrossRef]
- Bao, Q.; Zhang, Y.; Lang, S.; Lin, M.; Gong, P. Sea Surface Wind Speed Inversion Using the Low Incident NRCS Measured by TRMM Precipitation Radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5262–5271. [Google Scholar] [CrossRef]
- Ren, L.; Yang, J.; Xu, Y.; Zhang, Y.; Zheng, G.; Wang, J.; Dai, J.; Jiang, C. Ocean Surface Wind Speed Dependence and Retrieval From Off-Nadir CFOSAT SWIM Data. Earth Space Sci. 2021, 8, e2020EA001505. [Google Scholar] [CrossRef]
- Barrick, D. Rough Surface Scattering Based on the Specular Point Theory. IEEE Trans. Antennas Propag. 1968, 16, 449–454. [Google Scholar] [CrossRef]
- Bass, F.; Fuks, I. (Eds.) Chapter 7—Scattering from Large-Scale Roughness. In Wave Scattering from Statistically Rough Surfaces: International Series in Natural Philosophy; Pergamon Press: Oxford, UK, 1979; Volume 93, pp. 220–315. [Google Scholar]
- Ribal, A.; Young, I.R. 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 2019, 6, 1–15. [Google Scholar]
- Cox, C.; Munk, W. Measurement of the Roughness of the Sea Surface from Photographs of the Sun’s Glitter. J. Opt. Soc. Am. 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Huber, P.; Ronchetti, E. Robust Statistics; J. Wiley, Cop.(Wiley Series in Probability and Statistics); Wiley: Hoboken, NJ, USA, 2009; p. 384. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panfilova, M.; Karaev, V. Wind Speed Retrieval Algorithm Using Ku-Band Radar Onboard GPM Satellite. Remote Sens. 2021, 13, 4565. https://doi.org/10.3390/rs13224565
Panfilova M, Karaev V. Wind Speed Retrieval Algorithm Using Ku-Band Radar Onboard GPM Satellite. Remote Sensing. 2021; 13(22):4565. https://doi.org/10.3390/rs13224565
Chicago/Turabian StylePanfilova, Maria, and Vladimir Karaev. 2021. "Wind Speed Retrieval Algorithm Using Ku-Band Radar Onboard GPM Satellite" Remote Sensing 13, no. 22: 4565. https://doi.org/10.3390/rs13224565
APA StylePanfilova, M., & Karaev, V. (2021). Wind Speed Retrieval Algorithm Using Ku-Band Radar Onboard GPM Satellite. Remote Sensing, 13(22), 4565. https://doi.org/10.3390/rs13224565







