In Situ Determination of Dry and Wet Snow Permittivity: Improving Equations for Low Frequency Radar Applications
Abstract
1. Introduction
Theoretical Background
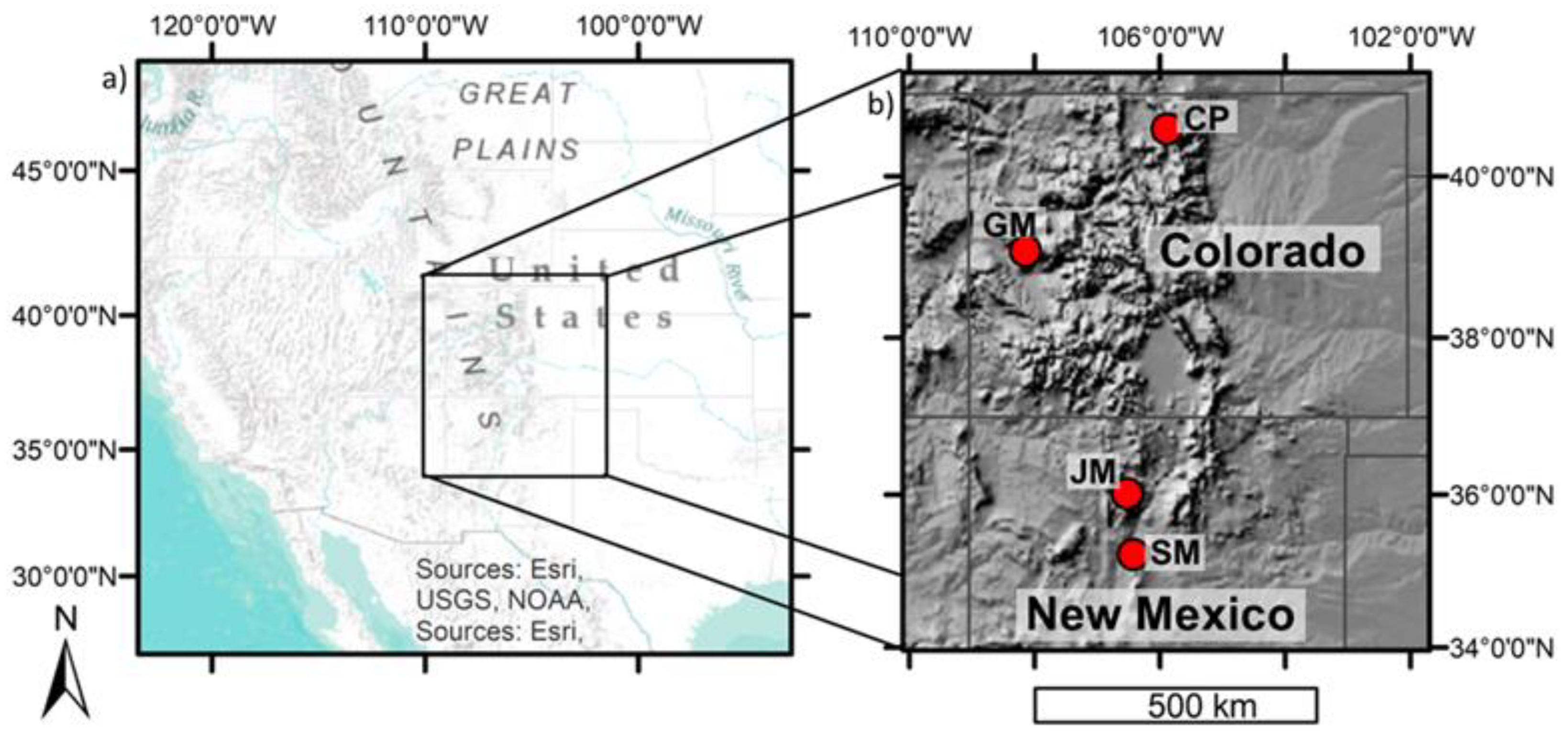
2. Materials and Methods
3. Results
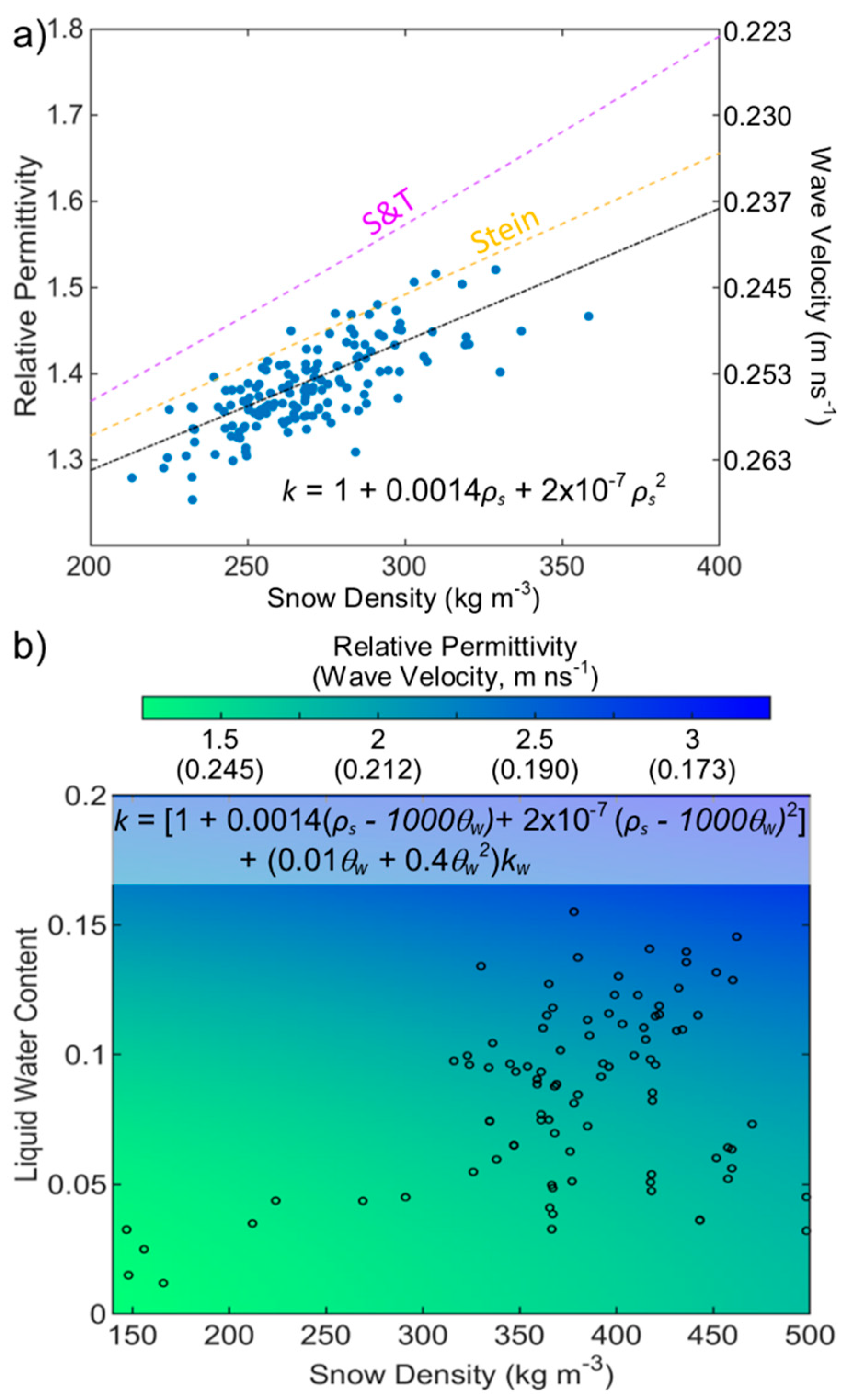
3.1. Dry Snow Observations
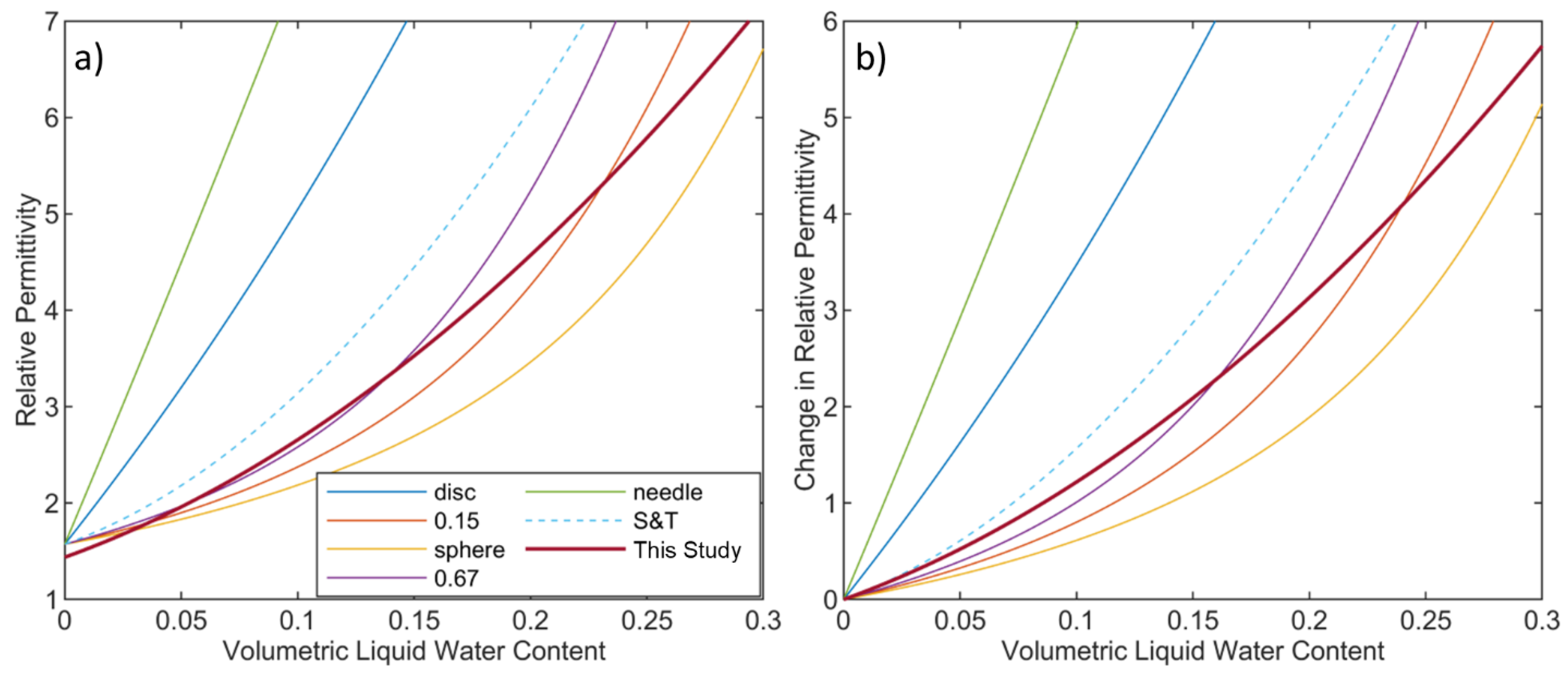
3.2. Wet Snow Observations
4. Discussion
Uncertainty and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
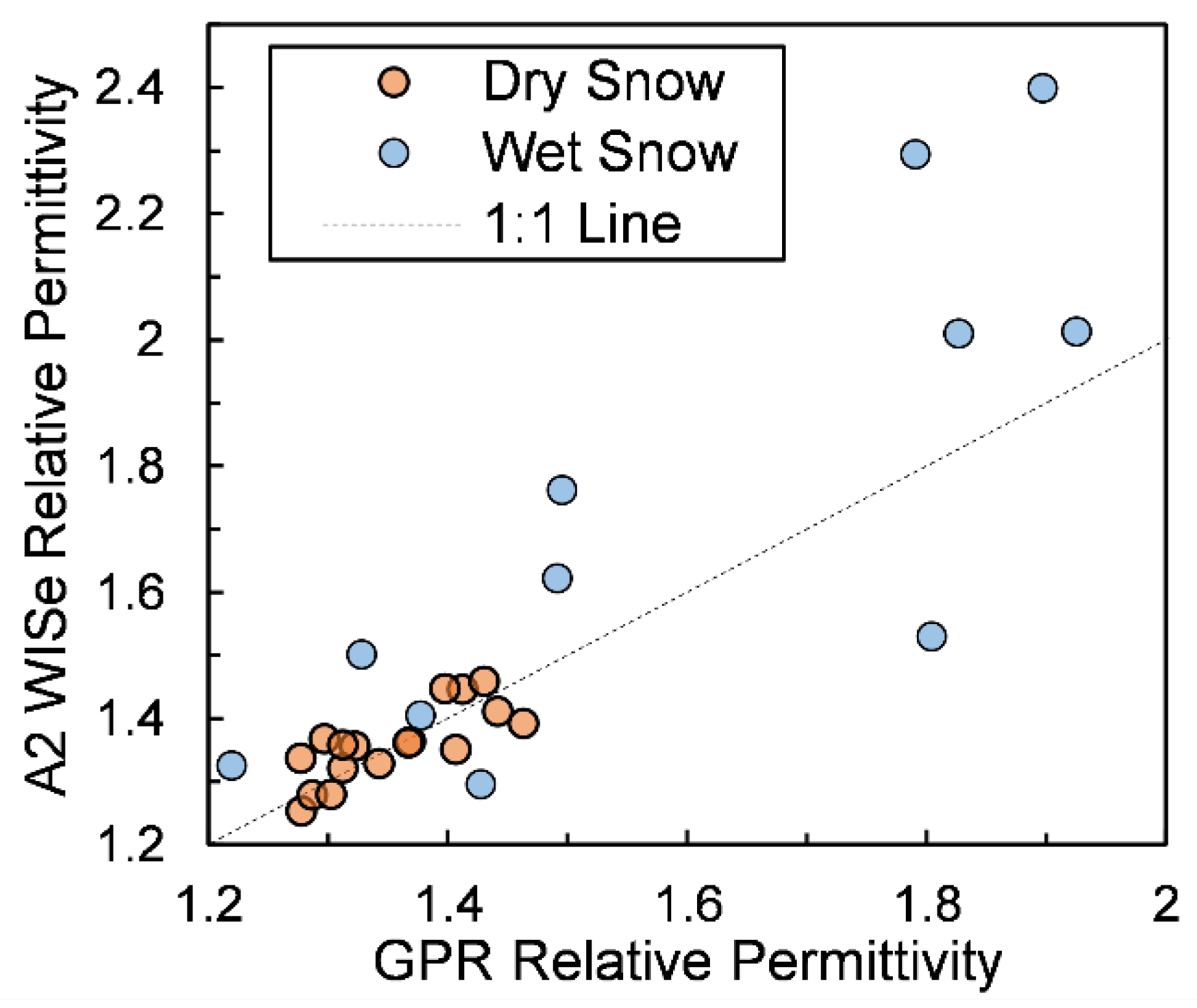
Appendix A. Validation of the A2 Photonics WISe Sensor
References
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Mankin, J.; Viviroli, D.; Singh, D.; Hoekstra, A.; Diffenbaugh, N. The potential for snow to supply human water demand in the present and future. Environ. Res. Lett. 2015, 10, 114016. [Google Scholar] [CrossRef]
- Sturm, M.; Goldstein, M.; Parr, C. Water and life from snow: A trillion dollar science question. Water Resour. Res. 2017, 53, 3534–3544. [Google Scholar] [CrossRef]
- Berghuijs, W.; Woods, R.; Hrachowitz, M. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat. Clim. Chang. 2014, 4, 583–586. [Google Scholar] [CrossRef]
- Barnhart, T.; Molotch, N.; Livneh, B.; Harpold, A.; Knowles, J.; Schneider, D. Snowmelt rate dictates streamflow. Geophys. Res. Lett. 2016, 43, 8006–8016. [Google Scholar] [CrossRef]
- Musselman, K.; Clark, M.; Liu, C.; Ikeda, K.; Rasmussen, R. Slower snowmelt in a warmer world. Nat. Clim. Chang. 2017, 7, 214–219. [Google Scholar] [CrossRef]
- Painter, T.; Berisford, D.; Boardman, J.; Bormann, K.; Deems, J.; Gehrke, F.; Hedrick, A.; Joyce, M.; Laidlaw, R.; Marks, D.; et al. The Airborne Snow Observatory: Fusion of scanning lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo. Remote Sens. Environ. 2016, 184, 139–152. [Google Scholar] [CrossRef]
- Foster, J.; Hall, D.; Kelly, R.; Chiu, L. Seasonal snow extent and snow mass in South America using SMMR and SSM/I passive microwave data (1979–2006). Remote Sens. Environ. 2009, 113, 291–305. [Google Scholar] [CrossRef]
- Li, D.; Durand, M.; Margulis, S. Estimating snow water equivalent in a Sierra Nevada watershed via spaceborne radiance data assimilation. Water Resour. Res. 2017, 53, 647–671. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Karna, J.; Koskinen, J.; Bojkov, B. Estimating northern hemisphere snow water equivalent for climate research through assimilation of space-borne radiometer data and ground-based measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Kelly, R.; Chang, A.; Tsang, L.; Foster, J. A prototype AMSR-E global snow area and snow depth algorithm. IEEE Trans. Geosci. Remote Sens. 2003, 41, 230–242. [Google Scholar] [CrossRef]
- Bair, E.; Rittger, K.; Davis, R.; Painter, T.; Dozier, J. Validating reconstruction of snow water equivalent in California’s Sierra Nevada using measurements from the NASA Airborne Snow Observatory. Water Resour. Res. 2016, 52, 8437–8460. [Google Scholar] [CrossRef]
- McGrath, D.; Webb, R.; Shean, D.; Bonnell, R.; Marshall, H.; Painter, T.; Molotch, N.; Elder, K.; Hiemstra, C.; Brucker, L. Spatially extensive ground-penetrating radar snow depth observations during NASA’s 2017 SnowEx Campaign: Comparison with in situ, airborne, and satellite observations. Water Resour. Res. 2019, 55, 10026–10036. [Google Scholar] [CrossRef]
- Bhushan, S.; Shean, D.; Alexandrov, O.; Henderson, S. Automated digital elevation model (DEM) generation from very-high-resolution Planet SkySat triplet stereo and video imagery. ISPRS J. Photogramm. Remote Sens. 2021, 173, 151–165. [Google Scholar] [CrossRef]
- Guneriussen, T.; Hogda, K.A.; Johnsen, H.; Lauknes, I. InSAR for estimation of changes in snow water equivalent of dry snow. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2101–2108. [Google Scholar] [CrossRef]
- Deeb, E.; Forster, R.; Kane, D. Monitoring snowpack evolution using interferometric synthetic aperture radar on the North Slope of Alaska, USA. Int. J. Remote Sens. 2011, 32, 3985–4003. [Google Scholar] [CrossRef]
- Oveisgharan, S.; Zebker, H. Estimating snow accumulation from InSAR correlation observations. IEEE Trans. Geosci. Remote Sens. 2007, 45, 10–20. [Google Scholar] [CrossRef]
- Bradford, J.; Harper, J.; Brown, J. Complex dielectric permittivity measurements from ground-penetrating radar data to estimate snow liquid water content in the pendular regime. Water Resour. Res. 2009, 45, W08403. [Google Scholar] [CrossRef]
- Clair, J.; Holbrook, W. Measuring snow water equivalent from common-offset GPR records through migration velocity analysis. Cryosphere 2017, 11, 2997–3009. [Google Scholar] [CrossRef]
- Granlund, N.; Lundberg, A.; Feiccabrino, J.; Gustafsson, D. Laboratory test of snow wetness influence on electrical conductivity measured with ground penetrating radar. Hydrol. Res. 2009, 40, 33–44. [Google Scholar] [CrossRef]
- Colombero, C.; Comina, C.; De Toma, E.; Franco, D.; Godio, A. Ice Thickness Estimation from Geophysical Investigations on the Terminal Lobes of Belvedere Glacier (NW Italian Alps). Remote Sens. 2019, 11, 805. [Google Scholar] [CrossRef]
- Marshall, H.; Koh, G.; Forster, R.; MacAyeal, D. Estimating alpine snowpack properties using FMCW radar. Ann. Glaciol. 2005, 40, 157–162. [Google Scholar] [CrossRef]
- Meehan, T.G.; Marshall, H.P.; Bradford, J.H.; Hawley, R.L.; Overly, T.B.; Lewis, G.; Graeter, K.; Osterberg, E.; McCarthy, F. Reconstruction of historical surface mass balance, 1984–2017 from GreenTrACS multi-offset ground-penetrating radar. J. Glaciol. 2021, 67, 219–228. [Google Scholar] [CrossRef]
- Webb, R.W.; Jennings, K.; Fend, M.; Molotch, N. Combining Ground Penetrating Radar with Terrestrial LiDAR Scanning to Estimate the Spatial Distribution of Liquid Water Content in Seasonal Snowpacks. Water Resour. Res. 2018, 54, 10339–10349. [Google Scholar] [CrossRef]
- Kovacs, A.; Gow, A.J.; Morey, R.M. The in-situ dielectric constant of polar firn revisited. Cold Reg. Sci. Technol. 1995, 23, 245–256. [Google Scholar] [CrossRef]
- Denoth, A.; Foglar, A.; Weiland, P.; Mätzler, C.; Aebischer, H.; Tiuri, M.; Sihvola, A. A comparative study of instruments for measuring the liquid water content of snow. J. Appl. Phys. 1984, 56, 2154–2160. [Google Scholar] [CrossRef]
- Kawashima, K.; Endo, T.; Takeuchi, Y. A portable calorimeter for measuring liquid-water content of wet snow. Ann. Glaciol. 1998, 26, 103–106. [Google Scholar] [CrossRef]
- Tiuri, M.; Sihvola, A.; Nyfors, E.; Hallikainen, M. The complex dielectric constant of snow at microwave frequencies. IEEE J. Ocean. Eng. 1984, 9, 377–382. [Google Scholar] [CrossRef]
- Polder, D.; van Santeen, J.H. The effective permeability of mixtures of solids. Physica 1946, 12, 257–271. [Google Scholar] [CrossRef]
- Denoth, A. The monopole-antenna: A Practical snow and soil wetness sensor. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1371–1375. [Google Scholar] [CrossRef]
- Sihvola, A.; Tiuri, M. Snow fork for field determination of the density and wetness profiles of a snow pack. IEEE Trans. Geosci. Remote Sens. 1986, 24, 717–721. [Google Scholar] [CrossRef]
- Roth, K.; Schulin, R.; Fluhler, H.; Attinger, W. Calibration of time domain reflectometry for water-content measurement using a composite dielectric approach. Water Resour. Res. 1990, 26, 2267–2273. [Google Scholar] [CrossRef]
- Koch, F.; Prasch, M.; Schmid, L.; Schweizer, J.; Mauser, W. Measuring Snow Liquid Water Content with Low-Cost GPS Receivers. Sensors 2014, 14, 20975–20999. [Google Scholar] [CrossRef]
- Heilig, A.; Mitterer, C.; Schmid, L.; Wever, N.; Schweizer, J.; Marshall, H.P.; Eisen, O. Seasonal and diurnal cycles of liquid water in snow-Measurements and modeling. J. Geophys. Res. Earth Surf. 2015, 120, 2139–2154. [Google Scholar] [CrossRef]
- Webb, R.W.; Raleigh, M.S.; McGrath, D.; Molotch, N.P.; Elder, K.; Hiemstra, C.; Brucker, L.; Marshall, H.P. Within-Stand Boundary Effects on Snow Water Equivalent Distribution in Forested Areas. Water Resour. Res. 2020, 56, e2019WR024905. [Google Scholar] [CrossRef]
- A2 Photonics Sensors. Wise Snow Liquid Water Content Sensor User Manual; A2 Photonics Sensors: Grenoble, France, 2019. [Google Scholar]
- FPGA Company. SLF Snow Sensor User Manual; FPGA Company GmbH: Tann, Switzerland, 2018. [Google Scholar]
- Sihvola, A.; Kong, J. Effective Permittivity of Dielectric Mixtures. IEEE Trans. Geosci. Remote Sens. 1988, 26, 420–429. [Google Scholar] [CrossRef]
- Di Paolo, F.; Cosciotti, B.; Lauro, S.E.; Mattei, E.; Pettinelli, E. Dry snow permittivity evaluation from density: A critical review. In Proceedings of the 2018 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018; pp. 1–5. [Google Scholar]
- Kendra, J.; Ulaby, F.; Sarabandi, K. Snow Probe for in-situ Determination of Wetness and Density. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1152–1159. [Google Scholar] [CrossRef]
- Lundberg, A.; Thunehed, H. Snow wetness influence on impulse radar snow surveys theoretical and laboratory study. Nord. Hydrol. 2000, 31, 89–106. [Google Scholar] [CrossRef]
- Vuyovich, C.M.; Marshall, H.P.; Elder, K.; Hiemstra, C.; Brucker, L.; McCormick, M. SnowEx20 Grand Mesa Intensive Obs. Period Snow Pit Meas. Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021. [CrossRef]
- Webb, R.; Marziliano, A.; Bonnell, R.; McGrath, D. Snow Pit Permittivity and Liquid Water Observations—Colorado and New Mexico 2020–2021. HydroShare 2021. [Google Scholar] [CrossRef]
- Marziliano, A.; Webb, R.W. Sandia Mountains 10K Site, Hydroshare. 2020. Available online: http://www.hydroshare.org/resource/f9c65581416b4021a860d648688d5d54 (accessed on 16 August 2021).
- Fierz, C.; Armstrong, R.L.; Durand, Y.; Etchevers, P.; Greene, E.; McClung, D.M.; Nishimura, K.; Satyawali, P.K.; Sokratov, S.A. The International Classification for Seasonal Snow on the Ground; Technical Documents in Hydrology; International Association of Cryospheric Sciences; UNESCO-IHP: Paris, France, 2009; p. 90. [Google Scholar]
- Techel, F.; Pielmeier, C. Point observations of liquid water content in wet snow—Investigating methodical, spatial and temporal aspects. Cryosphere 2011, 5, 405–418. [Google Scholar] [CrossRef]
- Stein, J.; Laberge, G.; Levesque, D. Monitoring the dry density and the liquid water content of snow using time domain reflectometry (TDR). Cold Reg. Sci. Technol. 1997, 25, 123–136. [Google Scholar] [CrossRef]
- Staron, P.J.; Adams, E.E.; Miller, D.A. Nonequilibrium thermodynamics of kinetic metamorphism in snow. Cold Reg. Sci. Technol. 2014, 97, 60–71. [Google Scholar] [CrossRef]
- Williams, M.; Erickson, T.; Petrzelka, J. Visualizing meltwater flow through snow at the centimetre-to-metre scale using a snow guillotine. Hydrol. Process. 2010, 24, 2098–2110. [Google Scholar] [CrossRef]
- Eiriksson, D.; Whitson, M.; Luce, C.H.; Marshall, H.P.; Bradford, J.; Benner, S.G.; Black, T.; Hetrick, H.; McNamara, J.P. An evaluation of the hydrologic relevance of lateral flow in snow at hillslope and catchment scales. Hydrol. Process. 2013, 27, 640–654. [Google Scholar] [CrossRef]
- Webb, R.W.; Wigmore, O.; Jennings, K.; Fend, M.; Molotch, N.P. Hydrologic connectivity at the hillslope scale through intra-snowpack flow paths during snowmelt. Hydrol. Process. 2020, 34, 1616–1629. [Google Scholar] [CrossRef]
- Webb, R.; Jennings, K.; Finsterle, S.; Fassnacht, S. Two-dimensional liquid water flow through snow at the plot scale in continental snowpacks: Simulations and field data comparisons. Cryosphere 2021, 15, 1423–1434. [Google Scholar] [CrossRef]



| Reference | θw Range (cm cm−1) | Equation for Relative Permittivity, k (Unless Otherwise Specified) |
|---|---|---|
| Sihvola and Tiuri [31] | 0.005–0.10 | |
| Denoth [30] | 0.0–0.09 | |
| Roth [32] | - | |
| Kendra et al. [40] | 0.0–0.1 | |
| Lundberg and Thunehed [41] | - | |
| A2 Photonics [36] | 0.0–0.2 | |
| FPGA [37] | 0.0–0.2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Webb, R.W.; Marziliano, A.; McGrath, D.; Bonnell, R.; Meehan, T.G.; Vuyovich, C.; Marshall, H.-P. In Situ Determination of Dry and Wet Snow Permittivity: Improving Equations for Low Frequency Radar Applications. Remote Sens. 2021, 13, 4617. https://doi.org/10.3390/rs13224617
Webb RW, Marziliano A, McGrath D, Bonnell R, Meehan TG, Vuyovich C, Marshall H-P. In Situ Determination of Dry and Wet Snow Permittivity: Improving Equations for Low Frequency Radar Applications. Remote Sensing. 2021; 13(22):4617. https://doi.org/10.3390/rs13224617
Chicago/Turabian StyleWebb, Ryan W., Adrian Marziliano, Daniel McGrath, Randall Bonnell, Tate G. Meehan, Carrie Vuyovich, and Hans-Peter Marshall. 2021. "In Situ Determination of Dry and Wet Snow Permittivity: Improving Equations for Low Frequency Radar Applications" Remote Sensing 13, no. 22: 4617. https://doi.org/10.3390/rs13224617
APA StyleWebb, R. W., Marziliano, A., McGrath, D., Bonnell, R., Meehan, T. G., Vuyovich, C., & Marshall, H.-P. (2021). In Situ Determination of Dry and Wet Snow Permittivity: Improving Equations for Low Frequency Radar Applications. Remote Sensing, 13(22), 4617. https://doi.org/10.3390/rs13224617







