A Full-Polarization Radar Image Reconstruction Method with Orthogonal Coding Apertures
Abstract
:1. Introduction
2. Signal Model
2.1. Radar Imaging Model
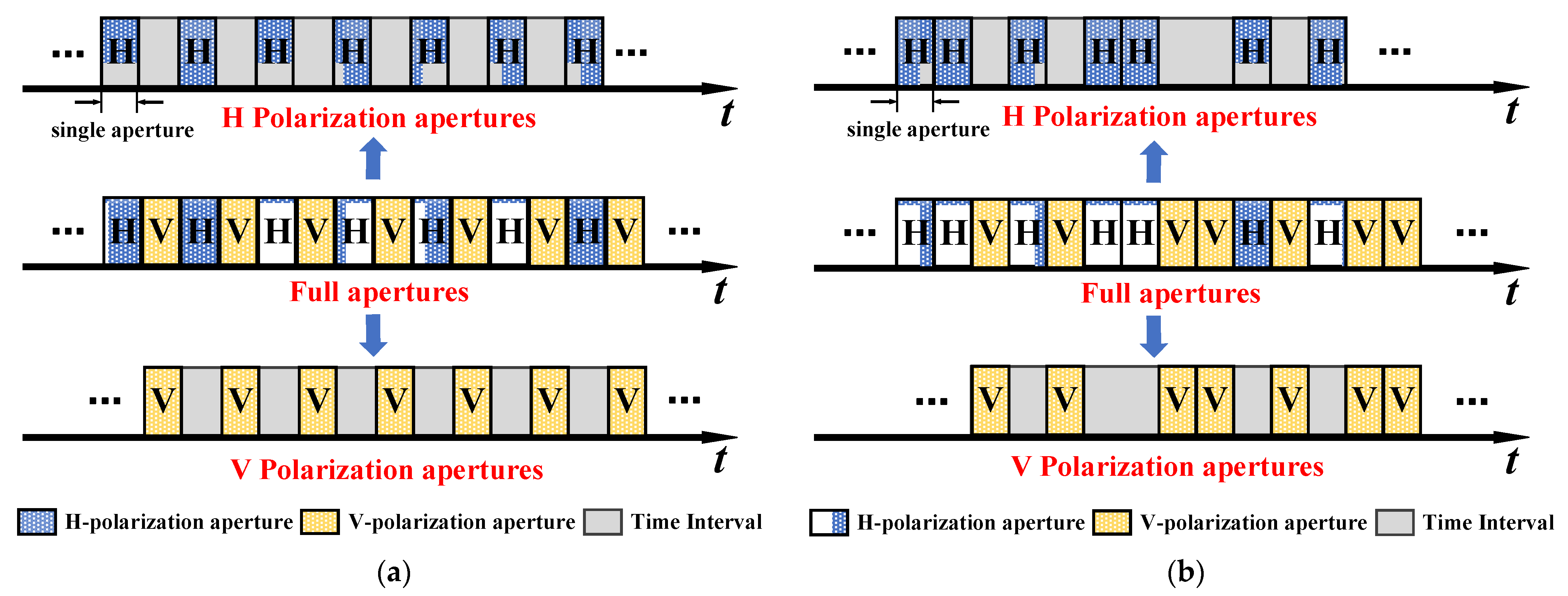
2.2. Orthogonal Coding Apertures for Polarization Radar Imaging
2.3. The Shortcoming of FFT-Based Imaging Method
3. Reconstruction Algorithm Based on CS Theory
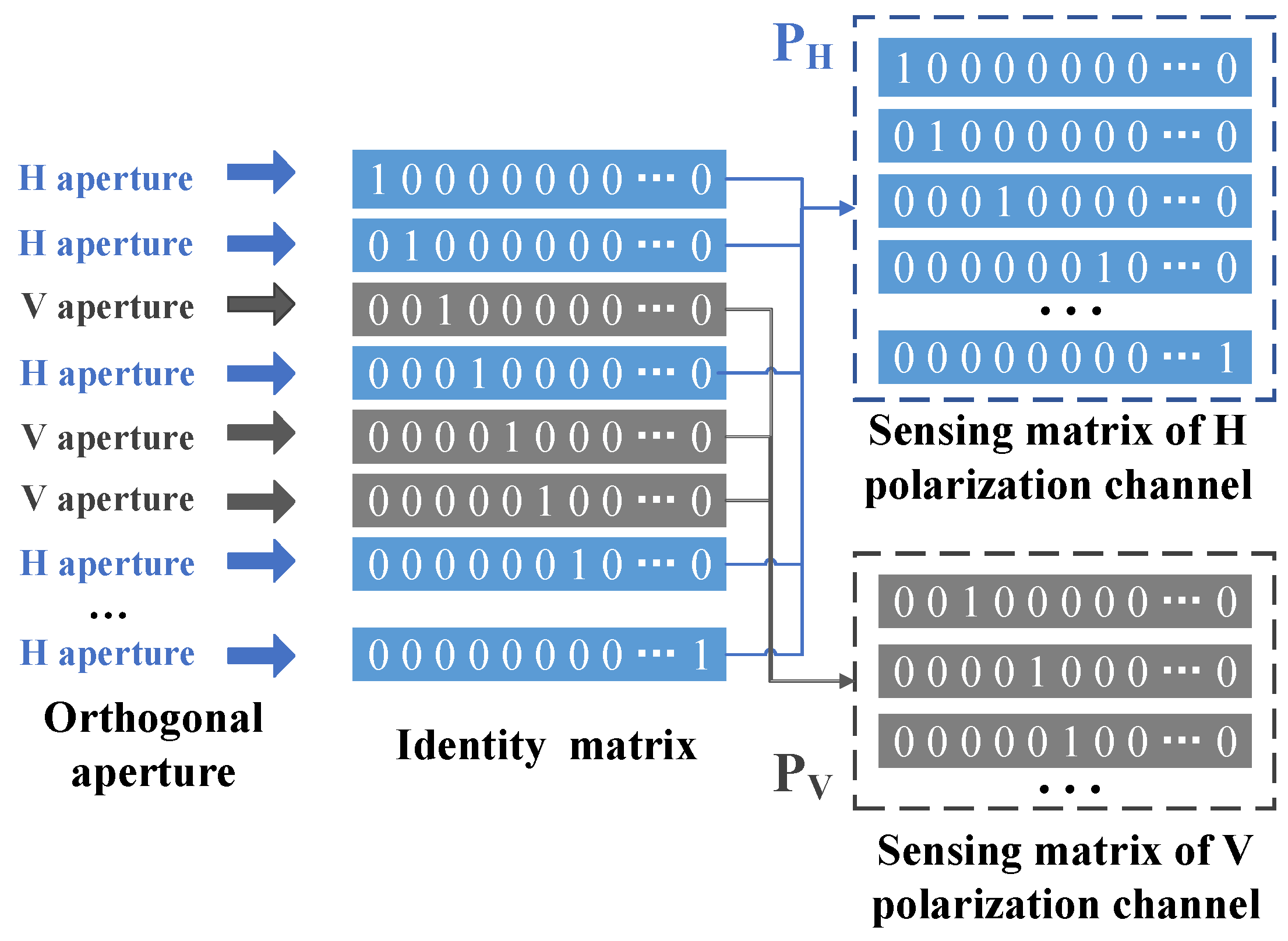
3.1. Sparse Representation of Orthogonal Coding Aperture
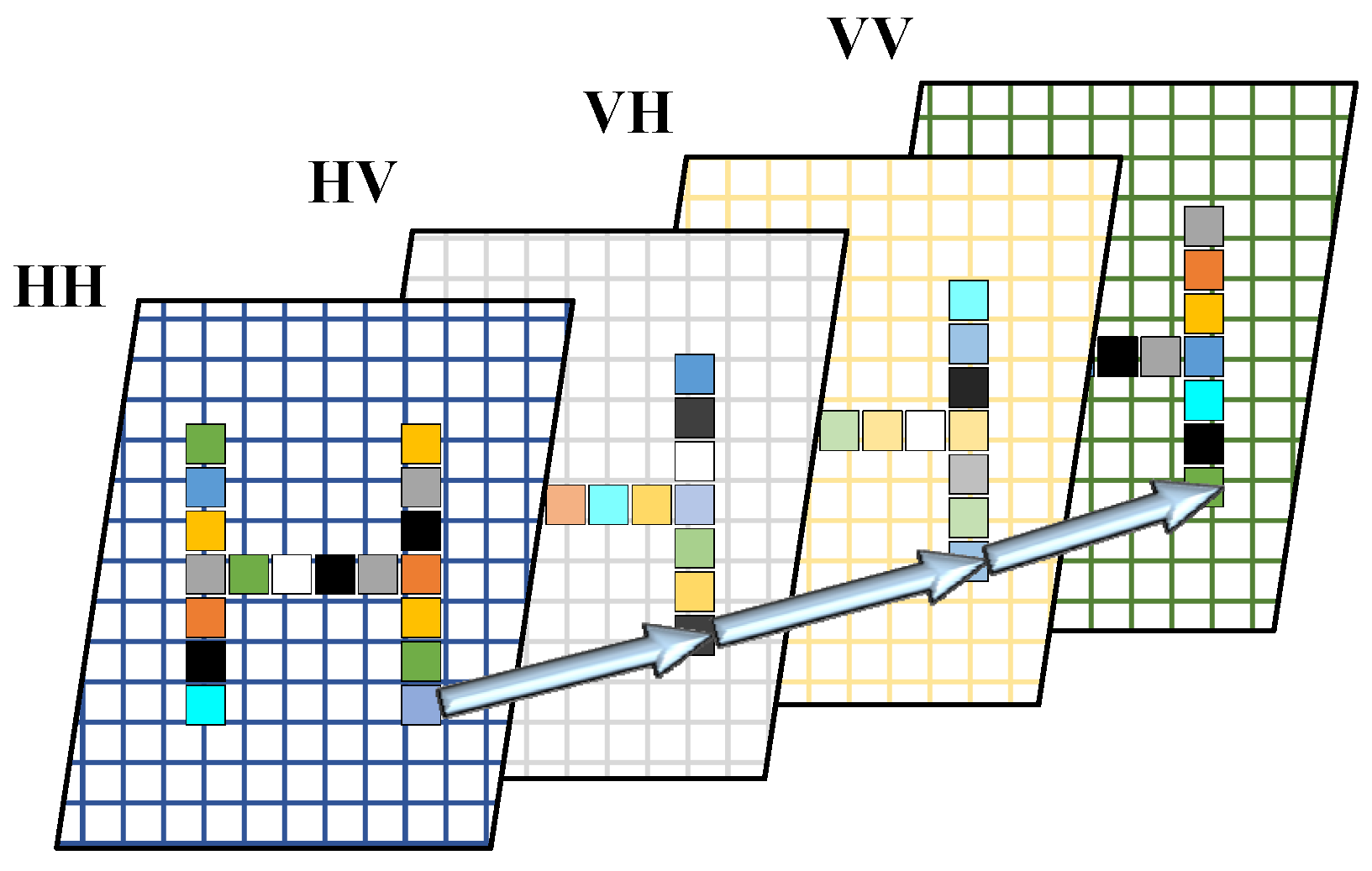
3.2. Multichannel Joint Reconstruction Algorithm Based on CS Theory
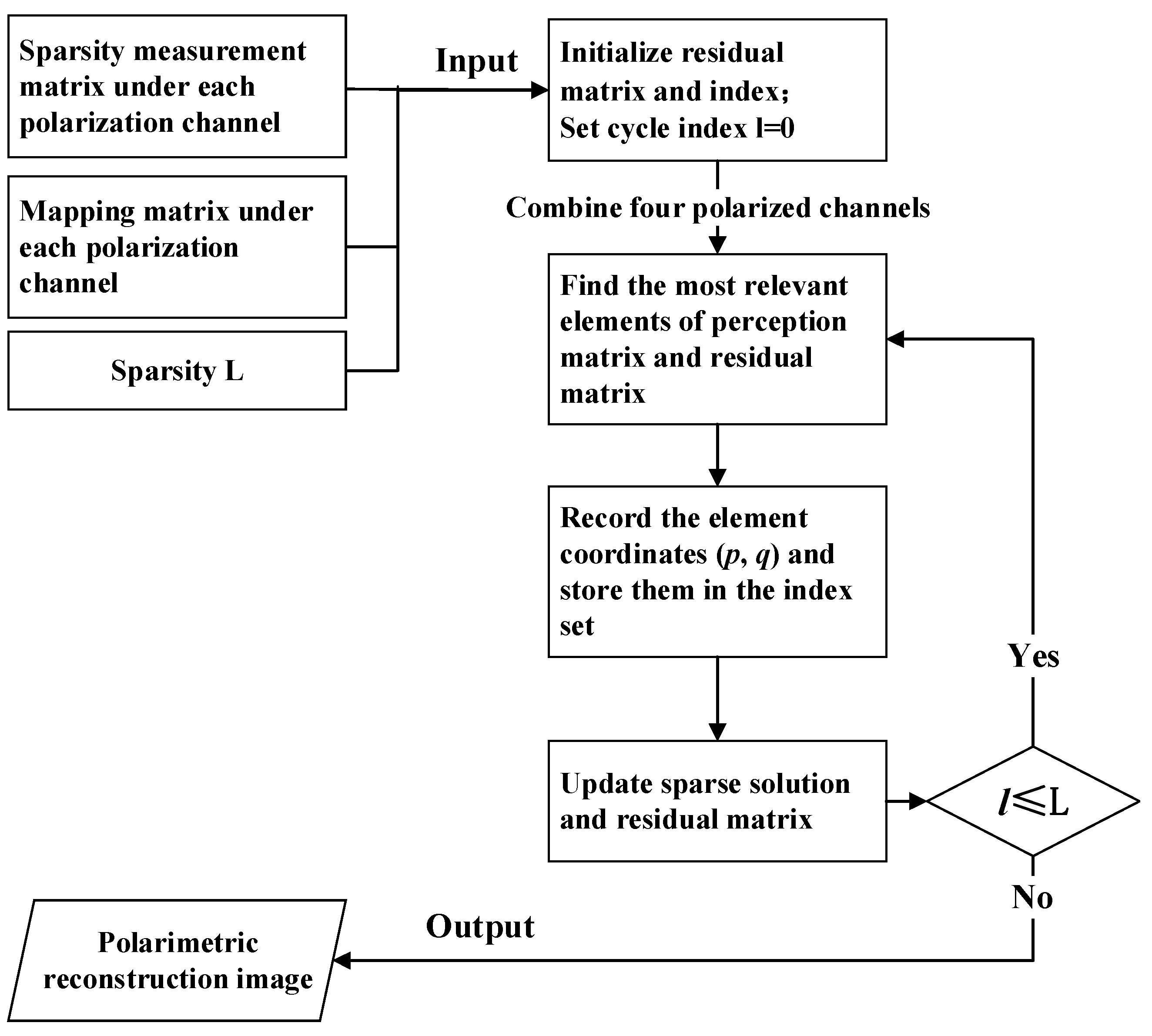
3.3. Procedure of the Proposed Reconstruction Algorithm
4. Simulation and Analysis
4.1. Numerical Simulation
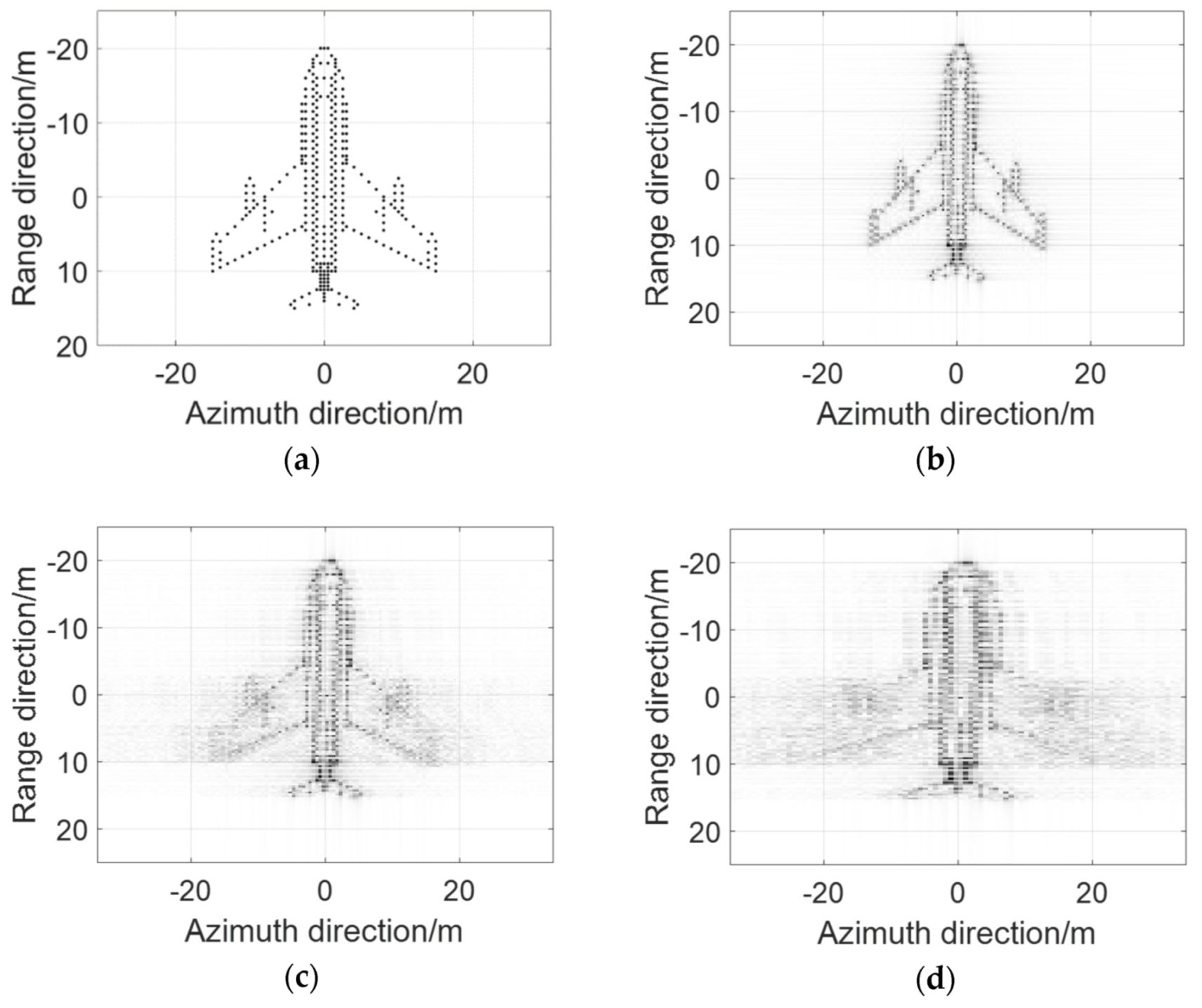
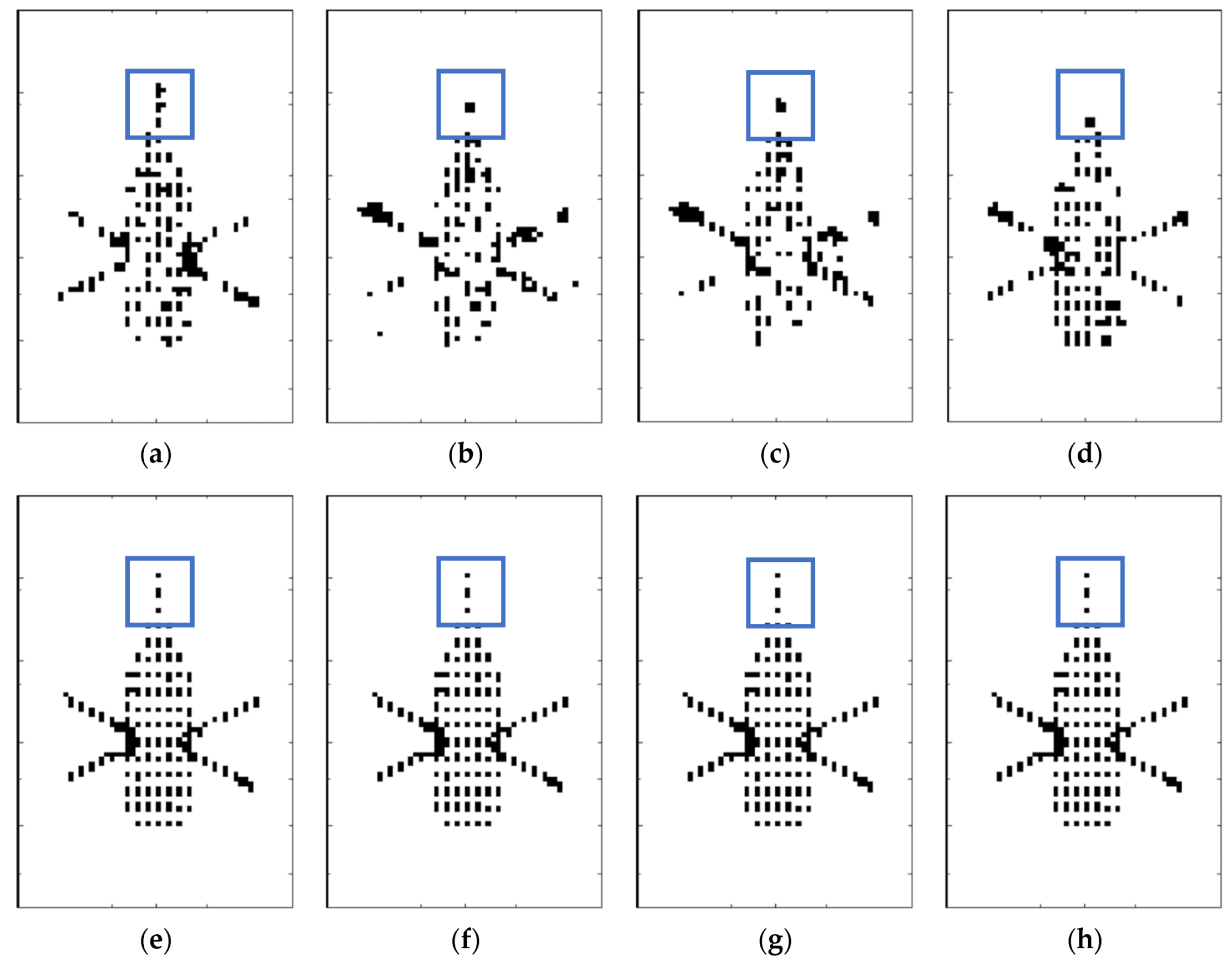
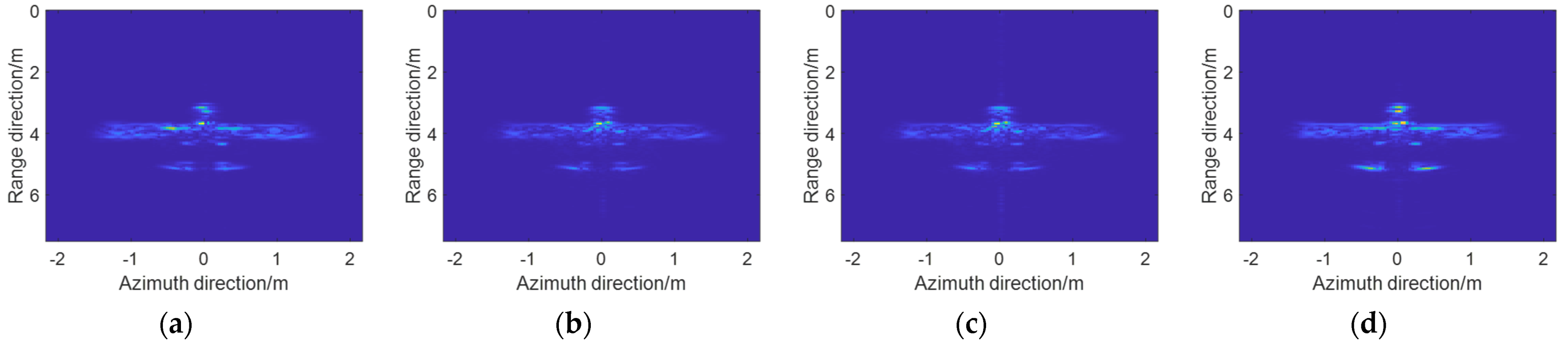
4.1.1. Parameter Setting and Reconstruction Images
4.1.2. Consistency of Reconstruction Images
4.1.3. Reconstructed Image Quality
Image Entropy
Image Contrast
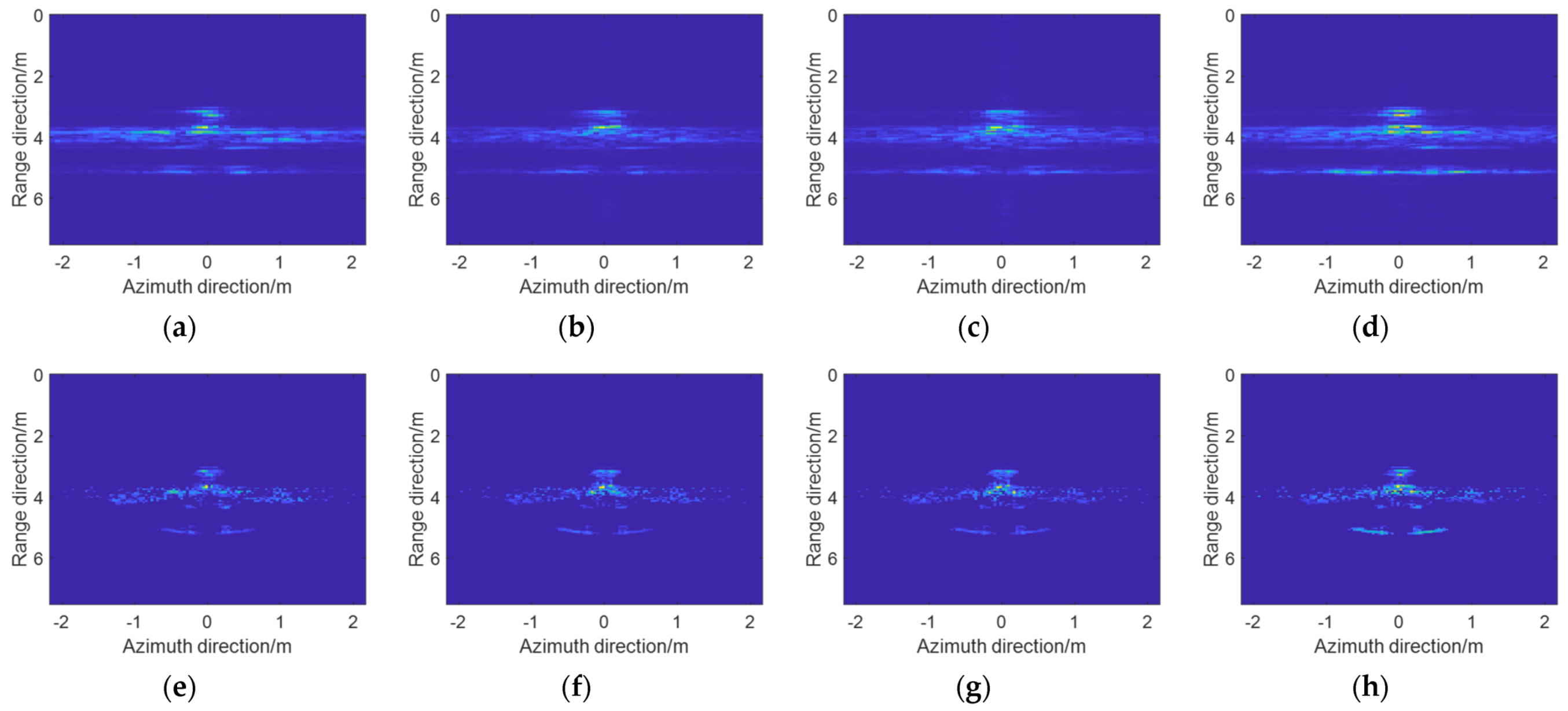
4.2. Measured Data Simulation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ender, J.; Amin, M.; Fornaro, G.; Rosen, P.A. Recent Advances in Radar Imaging [From the Guest Editors]. IEEE Signal Process. Mag. 2014, 31, 15–158. [Google Scholar] [CrossRef]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote Sensing of Mangrove Ecosystems: A Review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef] [Green Version]
- Radecki, K.; Samczynski, P.; Gromek, D. Fast Barycentric-Based Back Projection Algorithm for SAR Imaging. IEEE Sens. J. 2019, 19, 10635–10643. [Google Scholar] [CrossRef]
- Ao, D.; Wang, R.; Hu, C.; Li, Y. A Sparse SAR Imaging Method Based on Multiple Measurement Vectors Model. Remote Sens. 2017, 9, 297. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Narayanan, R.M. Enhanced resolution in SAR/ISAR imaging using iterative sidelobe apodization. IEEE Trans. Image Process. 2005, 14, 537–547. [Google Scholar] [CrossRef]
- Bai, X.R. Study on New Techniques for ISAR Imaging of Aerospace Targets. Ph.D. Dissertation, Xidian University, Xi’an, China, 2014. [Google Scholar]
- Kang, M.-S.; Bae, J.-H.; Lee, S.-H.; Kim, K.-T. Efficient ISAR autofocus via minimization of Tsallis Entropy. IEEE Trans. Aerosp. Electron. Syst. 2017, 52, 2950–2960. [Google Scholar] [CrossRef]
- Tian, B.; Liu, Y.; Hu, P.J. Review of high-resolution imaging techniques of wideband inverse synthetic aperture radar. J. Radars 2020, 9, 765–802. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Jiu, B. PolSAR Coherency Matrix Decomposition Based on Constrained Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5906–5922. [Google Scholar] [CrossRef]
- Guo, H.D. Earth Observation Technology and Sustainable Development; Science Press: Beijing, China, 2001. [Google Scholar]
- Jin, Y.Q.; Xu, F. Theory and Approach for Polarimetric Scattering and Information Retrieval of SAR Remote Sensing; Science Press: Beijing, China, 2008. [Google Scholar]
- Chen, S.W.; Wang, X.S.; Xiao, S.P. Target Scattering Mechanism in Polarimetric Synthetic Aperture Radar: Interpretation and Application; Springer: Singapore, 2018. [Google Scholar]
- Migliaccio, M.; Gambardella, A.; Tranfaglia, M. SAR Polarimetry to Observe Oil Spills. IEEE Trans. Geosci. Remote Sens. 2007, 45, 506–511. [Google Scholar] [CrossRef]
- De Maio, A.; Orlando, D.; Pallotta, L.; Clemente, C. A Multifamily GLRT for Oil Spill Detection. IEEE Trans. Geosci. Remote Sens. 2016, 55, 63–79. [Google Scholar] [CrossRef]
- Dai, H.; Wang, X.; Li, Y.; Liu, Y.; Xiao, S. Main-Lobe Jamming Suppression Method of using Spatial Polarization Characteristics of Antennas. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2167–2179. [Google Scholar] [CrossRef]
- Dai, H.; Chang, Y.; Dai, D.; Li, Y.; Wang, X. Calibration method of phase distortions for cross polarization channel of instantaneous polarization radar system. J. Syst. Eng. Electron. 2010, 21, 211–218. [Google Scholar] [CrossRef]
- Giuli, D.; Facheris, L.; Fossi, M.; Rossettini, A. Simultaneous scattering matrix measurement through signal coding. In Proceedings of the IEEE International Conference on Radar, Arlington, VA, USA, 7–10 May 1990. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Li, C.P. Analysis of synthetic aperture radar ambiguities. J. Electro. Inf. Technol. 2004, 26, 1455–1460. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef] [Green Version]
- Candes, E.J.; Wakin, M. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Hu, C.; Wang, L.; Zhu, D.; Loffeld, O. Inverse Synthetic Aperture Radar Sparse Imaging Exploiting the Group Dictionary Learning. Remote Sens. 2021, 13, 2812. [Google Scholar] [CrossRef]
- Liu, H.C. Study on New Method of High Resolution ISAR Imaging. Ph.D. Dissertation, Xidian University, Xi’an, China, 2014. [Google Scholar]
- Zhang, L.; Wu, S.; Duan, J. Sparse-aperture ISAR imaging of maneuvering targets with sparse representation. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 1623–1626. [Google Scholar] [CrossRef]
- Bi, H.; Zhu, D.; Bi, G.; Zhang, B.; Hong, W.; Wu, Y.-R. FMCW SAR Sparse Imaging Based on Approximated Observation: An Overview on Current Technologies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4825–4835. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, X.; Liu, J.; Zhao, F.; Xiao, S. A Radar Imaging Method Using Nonperiodic Interrupted Sampling Linear Frequency Modulation Signal. IEEE Sensors J. 2018, 18, 1. [Google Scholar] [CrossRef]
- Zhuang, Z.W.; Xiao, S.P.; Wang, X.S. Radar Polarization Information Processing and Application; National Defense Industry Press: Beijing, China, 1999. [Google Scholar]
- Chen, J.; Huo, X. Sparse Representations for Multiple Measurement Vectors (MMV) in an Over-Complete Dictionary. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 23 March 2005. [Google Scholar]
- Chen, J.; Huo, X. Theoretical Results on Sparse Representations of Multiple-Measurement Vectors. IEEE Trans. Signal Process. 2006, 54, 4634–4643. [Google Scholar] [CrossRef] [Green Version]
- Tropp, J.; Gilbert, A.C.; Strauss, M.J. Algorithms for simultaneous sparse approximation. Part I: Greedy pursuit. Signal Process. 2006, 86, 572–588. [Google Scholar] [CrossRef]
- Wipf, D.P.; Rao, B.D. An Empirical Bayesian Strategy for Solving the Simultaneous Sparse Approximation Problem. IEEE Trans. Signal Process. 2007, 55, 3704–3716. [Google Scholar] [CrossRef]
- Chen, W.; Wipf, D.; Wang, Y.; Liu, Y.; Wassell, I.J. Simultaneous Bayesian Sparse Approximation with Structured Sparse Models. IEEE Trans. Signal Process. 2016, 64, 6145–6159. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, P.; Xing, M.; Sun, G.; Li, Y.; Bao, Z. Minimum Entropy via Subspace for ISAR Autofocus. IEEE Geosci. Remote Sens. Lett. 2009, 7, 205–209. [Google Scholar] [CrossRef]




| Parameter Setting | Value |
|---|---|
| carrier frequency f0 | 10 GHz |
| pulse width Tp | 100 |
| bandwidth B | 500 MHz |
| azimuth pulse number | 256 |
| distance sampling number | 1024 |
| pulse repetition interval | 1 ms |
| polarization mode | HH\HV\VH\VV |
| Reconstruction Algorithm | Polarization Channel | Experiment Serial Number | Average Image Entropy | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| RD algorithm | HH channel | 5.955 | 5.785 | 5.710 | 5.809 | 5.803 | 5.813 |
| HV channel | 4.498 | 4.782 | 4.565 | 4.471 | 3.982 | 4.460 | |
| VH channel | 4.518 | 4.739 | 4.636 | 4.476 | 4.024 | 4.479 | |
| VV channel | 5.850 | 5.983 | 5.876 | 5.866 | 5.758 | 5.867 | |
| Full-polarization joint reconstruction algorithm | HH channel | 0.706 | 0.696 | 0.707 | 0.700 | 0.701 | 0.702 |
| HV channel | 0.663 | 0.683 | 0.670 | 0.660 | 0.644 | 0.664 | |
| VH channel | 0.674 | 0.673 | 0.674 | 0.657 | 0.639 | 0.663 | |
| VV channel | 0.696 | 0.697 | 0.704 | 0.704 | 0.705 | 0.701 | |
| Reconstruction Algorithm | Polarization Channel | Experiment Serial Number | Average Image Contrast | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| RD algorithm | HH channel | 347.839 | 307.060 | 273.733 | 295.230 | 303.917 | 305.556 |
| HV channel | 153.530 | 168.654 | 164.888 | 151.233 | 136.719 | 155.005 | |
| VH channel | 156.150 | 166.363 | 163.592 | 149.898 | 136.994 | 154.600 | |
| VV channel | 301.904 | 335.617 | 304.306 | 312.230 | 287.988 | 308.409 | |
| Full-polarization joint reconstruction algorithm | HH channel | 499.981 | 435.572 | 411.414 | 444.382 | 423.317 | 442.933 |
| HV channel | 188.784 | 201.384 | 180.080 | 162.159 | 148.806 | 176.242 | |
| VH channel | 190.817 | 196.223 | 181.416 | 166.137 | 146.995 | 176.317 | |
| VV channel | 452.815 | 510.040 | 510.289 | 467.005 | 493.793 | 486.788 | |
| Parameter Setting | Value |
|---|---|
| initial frequency | 8 GHz |
| terminal frequency | 12 GHz |
| bandwidth B | 4 GHz |
| frequency interval | 20 MHz |
| number of sub pulses | 200 |
| pitch angle | 0° |
| azimuth angle | −180°~180° |
| azimuth interval | 0.2° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Wu, Q.; Zhao, F.; Xu, Z.; Xiao, S. A Full-Polarization Radar Image Reconstruction Method with Orthogonal Coding Apertures. Remote Sens. 2021, 13, 4626. https://doi.org/10.3390/rs13224626
Zhao T, Wu Q, Zhao F, Xu Z, Xiao S. A Full-Polarization Radar Image Reconstruction Method with Orthogonal Coding Apertures. Remote Sensing. 2021; 13(22):4626. https://doi.org/10.3390/rs13224626
Chicago/Turabian StyleZhao, Tiehua, Qihua Wu, Feng Zhao, Zhiming Xu, and Shunping Xiao. 2021. "A Full-Polarization Radar Image Reconstruction Method with Orthogonal Coding Apertures" Remote Sensing 13, no. 22: 4626. https://doi.org/10.3390/rs13224626
APA StyleZhao, T., Wu, Q., Zhao, F., Xu, Z., & Xiao, S. (2021). A Full-Polarization Radar Image Reconstruction Method with Orthogonal Coding Apertures. Remote Sensing, 13(22), 4626. https://doi.org/10.3390/rs13224626







