Investigating the Effects of k and Area Size on Variance Estimation of Multiple Pixel Areas Using a k-NN Technique for Forest Parameters
Abstract
:1. Introduction
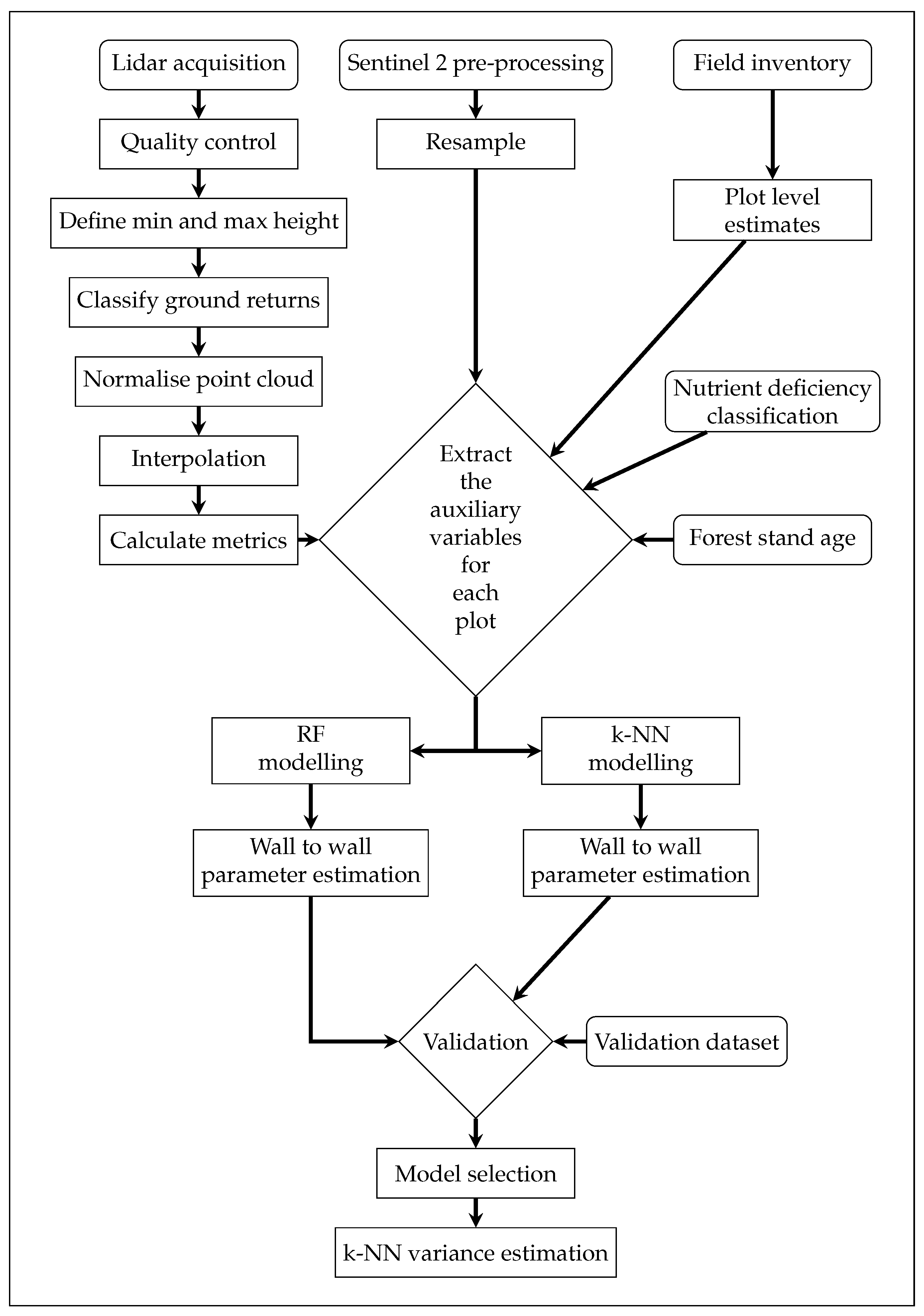
2. Materials and Methods
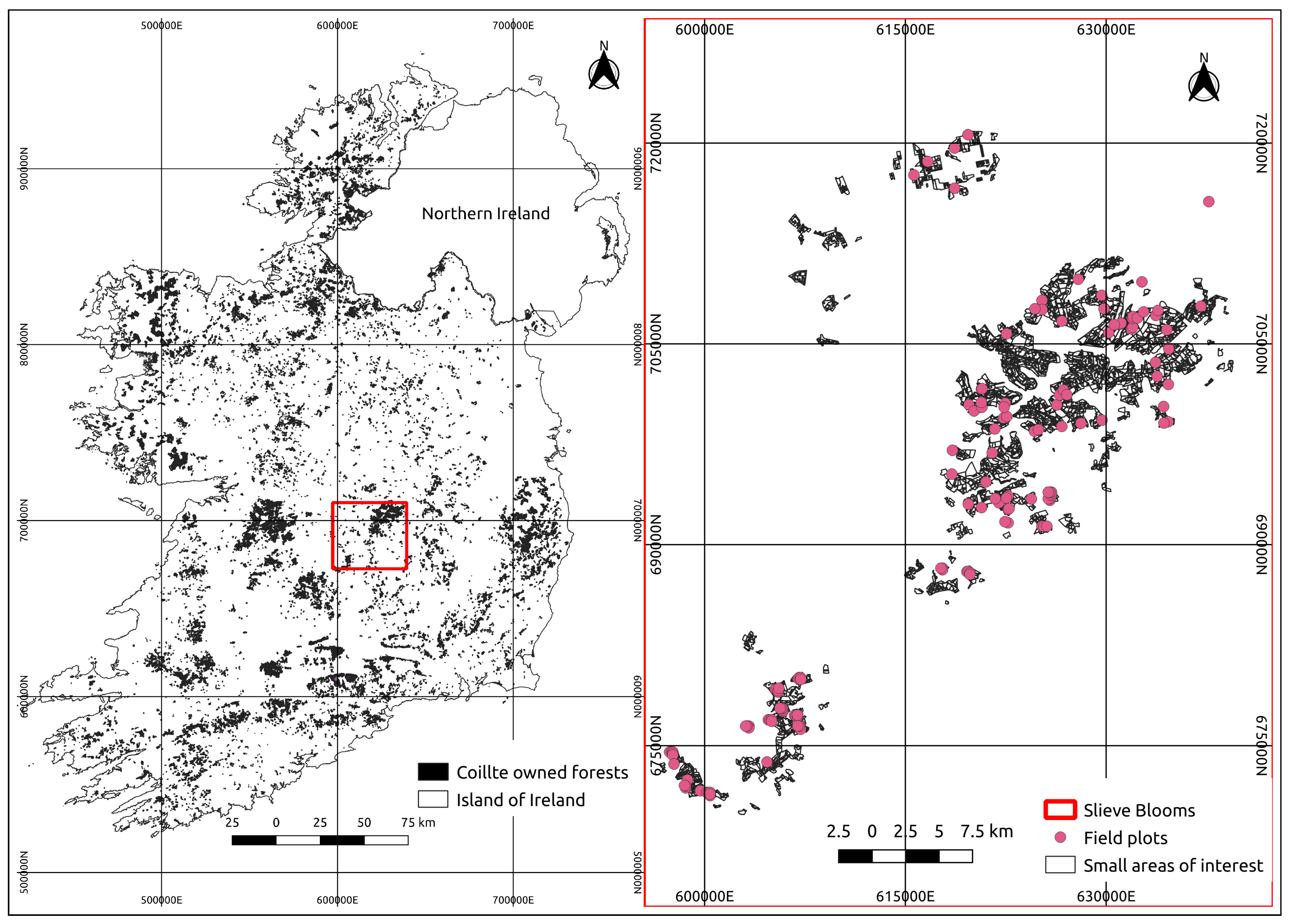
2.1. Study Area
2.2. Field Inventory
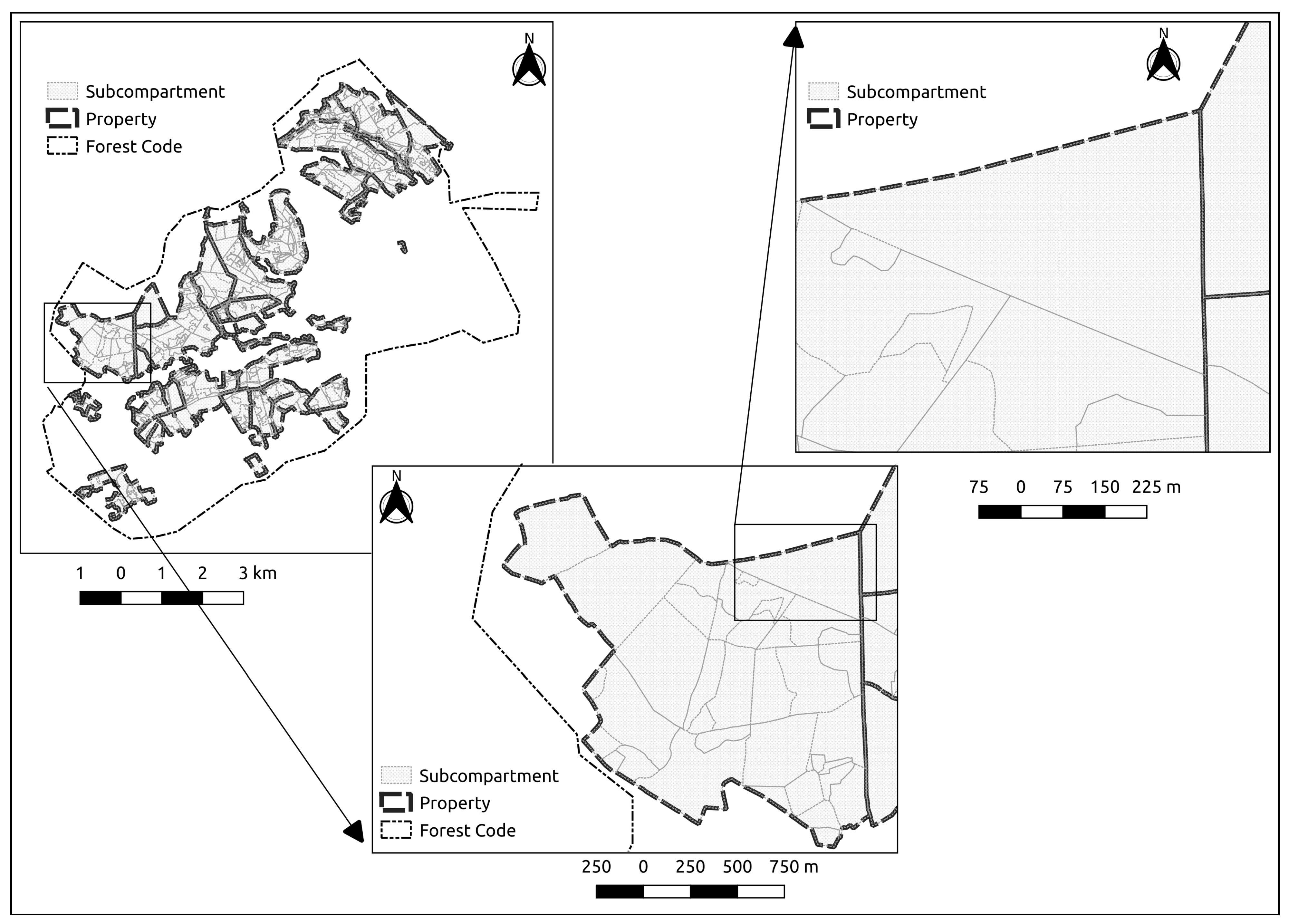
2.3. Spatial Aggregation Layers
2.4. Auxiliary Variables
- a quality control check to ensure the point cloud had no anomalies or issues;
- removing noise by defining a local and global minimum and maximum height threshold;
- point cloud normalisation;
- interpolating surfaces to create a canopy height model (CHM), digital terrain model (DTM), and digital surface model (DSM); and
- calculating metrics.
2.5. Parameter Estimation
2.6. Variance Estimation
3. Results
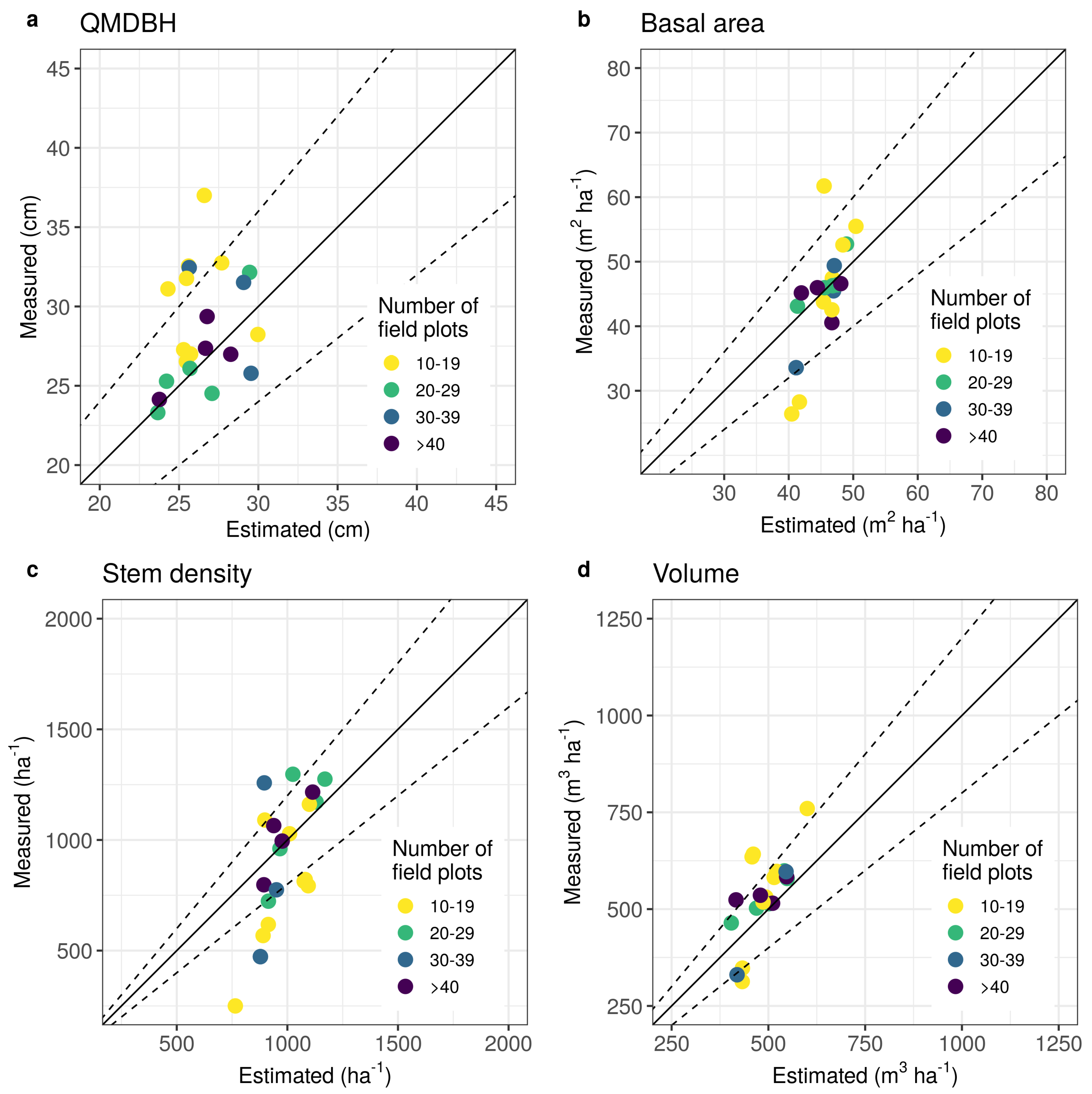
3.1. Parameter Estimation
3.2. Variance Estimation
4. Discussion
4.1. Parameter Estimation
4.2. Variance Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, T.M.F. The Foundations of Survey Sampling: A Review. J. R. Stat. Soc. Ser. A (Gen.) 1976, 139, 183. [Google Scholar] [CrossRef]
- Rao, J.N.K. Small Area Estimation, 1st ed.; Wiley: Hoboken, NJ, USA, 2003; pp. 1–3. [Google Scholar]
- Kangas, A.; Maltamo, M. Forest Inventory: Methodology and Applications; Springer: Dordrecht, The Netherlands, 2006; Volume 10, pp. 39–51. [Google Scholar]
- Gregoire, T.G. Design-based and model-based inference in survey sampling: Appreciating the difference. Can. J. For. Res. 1998, 28, 1429–1447. [Google Scholar] [CrossRef]
- Mandallaz, D. A Unified Approach to Sampling Theory for Forest Inventory Basedon Infinite Population and Superpopulation Models. Ph.D. Thesis, Swiss Federal Institute of Technology (ETH), Zurich, Switzerland, 1991. [Google Scholar]
- Næsset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 49–56. [Google Scholar] [CrossRef]
- Maltamo, M.; Næsset, E.; Vauhkonen, J. Forestry Applications of Airborne Laser Scanning. In Managing Forest Ecosystems, 1st ed.; Springer: Dordrecht, The Netherlands, 2014; Volume 27, Chapter 11; p. 462. [Google Scholar] [CrossRef]
- Tomppo, E. Satellite image-based national forest inventory of Finland. In Proceedings of the Symposium on Global and Environmental Monitoring, Techniques and Impacts, Victoria, BC, Canada, 17–21 September 1990; pp. 419–424. [Google Scholar]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Næsset, E.; Bjerknes, K.O. Estimating tree heights and number of stems in young forest stands using airborne laser scanner data. Remote Sens. Environ. 2001, 78, 328–340. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Breidenbach, J.; Astrup, R. Small area estimation of forest attributes in the Norwegian National Forest Inventory. Eur. J. For. Res. 2012, 131, 1255–1267. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Tomppo, E.O.; Finley, A.O.; Heikkinen, J. Estimating areal means and variances of forest attributes using the k-Nearest Neighbors technique and satellite imagery. Remote Sens. Environ. 2007, 111, 466–480. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Inference for lidar-assisted estimation of forest growing stock volume. Remote Sens. Environ. 2013, 128, 268–275. [Google Scholar] [CrossRef]
- Breidenbach, J.; Nothdurft, A.; Kändler, G. Comparison of nearest neighbour approaches for small area estimation of tree species-specific forest inventory attributes in central Europe using airborne laser scanner data. Eur. J. For. Res. 2010, 129, 833–846. [Google Scholar] [CrossRef]
- Chirici, G.; McRoberts, R.E.; Fattorini, L.; Mura, M.; Marchetti, M. Comparing echo-based and canopy height model-based metrics for enhancing estimation of forest aboveground biomass in a model-assisted framework. Remote Sens. Environ. 2016, 174, 1–9. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Walters, B.F. Multivariate inference for forest inventories using auxiliary airborne laser scanning data. For. Ecol. Manag. 2017, 401, 295–303. [Google Scholar] [CrossRef]
- McInerney, D.; Barrett, F.; McRoberts, R.E.; Tomppo, E. Enhancing the Irish NFI using k-Nearest Neighbors and a genetic algorithim. Can. J. For. Res. 2018, 99, 1482–1494. [Google Scholar] [CrossRef] [Green Version]
- Kangas, A. Small-area estimates using model-based methods. Can. J. For. Res. 1996, 26, 758–766. [Google Scholar] [CrossRef]
- McRoberts, R.E. A model-based approach to estimating forest area. Remote Sens. Environ. 2006, 103, 56–66. [Google Scholar] [CrossRef]
- McInerney, D.; Nieuwenhuis, M. A comparative analysis of kNN and decision tree methods for the Irish National Forest Inventory. Int. J. Remote Sens. 2009, 30, 4937–4955. [Google Scholar] [CrossRef]
- Roberts, O.; Bunting, P.; Hardy, A.; McInerney, D. Sensitivity analysis of the DART model for forest mensuration with airborne laser scanning. Remote Sens. 2020, 12, 247. [Google Scholar] [CrossRef] [Green Version]
- McRoberts, R.E. Estimating forest attribute parameters for small areas using nearest neighbors techniques. For. Ecol. Manag. 2012, 272, 3–12. [Google Scholar] [CrossRef]
- EU-DEM. Copernicus Land Monitoring Service; European Environment Agency: Copenhagen, Denmark, 2017. [Google Scholar]
- Teagasc. Nutrient Deficiencies in Forest Crops; Technical Report 14; Teagasc: Wexford, Ireland, 2007. [Google Scholar]
- Forest Research. How Forest Yield Works; Forest Research: London, UK, 2020. [Google Scholar]
- Matthews, R.; Mackie, E. Forest Mensuration: A Handbook for Practitioners; Forestry Comission: Bristol, UK, 2006. [Google Scholar]
- Bunting, P.; Armston, J.; Lucas, R.M.; Clewley, D. Sorted pulse data (SPD) library. Part I: A generic file format for LiDAR data from pulsed laser systems in terrestrial environments. Comput. Geosci. 2013, 56, 197–206. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, S.C.; Whitman, D.; Shyu, M.L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef] [Green Version]
- Evans, J.S.; Hudak, A.T. A multiscale curvature algorithm for classifying discrete return LiDAR in forested environments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1029–1038. [Google Scholar] [CrossRef]
- Bunting, P.; Clewley, D.; Lucas, R.M.; Gillingham, S. The Remote Sensing and GIS Software Library (RSGISLib). Comput. Geosci. 2014, 62, 216–226. [Google Scholar] [CrossRef]
- Walshe, D.; McInerney, D.; Kerchove, R.V.D.; Goyens, C.; Balaji, P.; Byrne, K.A.; Forest, C. Detecting nutrient deficiency in spruce forests using multispectral satellite imagery. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 101975. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2020. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Schliep, K.; Hechenbichler, K. kknn: Weighted k-Nearest Neighbors; Ludwig-Maximilians University Munich: Munich, Germany, 2016. [Google Scholar]
- Chirici, G.; Mura, M.; McInerney, D.; Py, N.; Tomppo, E.O.; Waser, L.T.; Travaglini, D.; McRoberts, R.E. A meta-analysis and review of the literature on the k-Nearest Neighbors technique for forestry applications that use remotely sensed data. Remote Sens. Environ. 2016, 176, 282–294. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; Wiley: New York, NY, USA, 1998; pp. 28–29. [Google Scholar]
- Woods, M.; Lim, K.; Treitz, P. Predicting forest stand variables from LiDAR data in the Great Lakes - St. Lawrence forest of Ontario. For. Chron. 2008, 84, 827–839. [Google Scholar] [CrossRef] [Green Version]
- Rooker Jensen, J.L.; Humes, K.S.; Conner, T.; Williams, C.J.; DeGroot, J. Estimation of biophysical characteristics for highly variable mixed-conifer stands using small-footprint lidar. Can. J. For. Res. 2006, 36, 1129–1138. [Google Scholar] [CrossRef]
- Holmgren, J.; Jonsson, T. Large scale airborne laser scanning of forest resources in Sweden. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, 157–160. [Google Scholar]
- Bolton, D.K.; White, J.C.; Wulder, M.A.; Coops, N.C.; Hermosilla, T.; Yuan, X. Updating stand-level forest inventories using airborne laser scanning and Landsat time series data. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 174–183. [Google Scholar] [CrossRef]
- Dash, J.P.; Marshall, H.M.; Rawley, B. Methods for estimating multivariate stand yields and errors using k-NN and aerial laser scanning. Forestry 2015, 88, 237–247. [Google Scholar] [CrossRef]
- Holmgren, J. Prediction of tree height, basal area and stem volume in forest stands using airborne laser scanning Prediction of Tree Height, Basal Area and Stem Volume in Forest. Scand. J. For. Res. 2006, 19, 543–553. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikäinen, K.; Pitkänen, J.; Hyyppä, J.; Vehmas, M. Estimation of timber volume and stem density based on scanning laser altimetry and expected tree size distribution functions. Remote Sens. Environ. 2004, 90, 319–330. [Google Scholar] [CrossRef]
- Chirici, G.; Giannetti, F.; McRoberts, R.E.; Travaglini, D.; Pecchi, M.; Maselli, F.; Chiesi, M.; Corona, P. Wall-to-wall spatial prediction of growing stock volume based on Italian National Forest Inventory plots and remotely sensed data. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101959. [Google Scholar] [CrossRef]
- Puliti, S.; Ørka, H.O.; Gobakken, T.; Næsset, E. Inventory of small forest areas using an unmanned aerial system. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef] [Green Version]
- Frank, B.; Mauro, F.; Temesgen, H. Model-based estimation of forest inventory attributes using lidar: A comparison of the area-based and semi-individual tree crown approaches. Remote Sens. 2020, 12, 2525. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Jutras-Perreault, M.C.; Ramtvedt, E.N. Comparing 3D point cloud data from laser scanning and digital aerial photogrammetry for height estimation of small trees and other vegetation in a boreal–alpine ecotone. Remote Sens. 2021, 13, 2469. [Google Scholar] [CrossRef]
- Knapp, N.; Huth, A.; Fischer, R. Tree crowns cause border effects in area-based biomass estimations from remote sensing. Remote Sens. 2021, 13, 1592. [Google Scholar] [CrossRef]
- Katila, M.; Tomppo, E. Stratification by ancillary data in multisource forest inventories employing k-nearest-neighbour estimation. Can. J. For. Res. 2002, 32, 1548–1561. [Google Scholar] [CrossRef]
- Magnussen, S.; McRoberts, R.E.; Tomppo, E.O. Model-based mean square error estimators for k-nearest neighbour predictions and applications using remotely sensed data for forest inventories. Remote Sens. Environ. 2009, 113, 476–488. [Google Scholar] [CrossRef]
- Magnussen, S.; McRoberts, R.E.; Tomppo, E.O. A resampling variance estimator for the k nearest neighbours technique. Can. J. For. Res. 2010, 40, 648–658. [Google Scholar] [CrossRef] [Green Version]
- Breidenbach, J.; McRoberts, R.E.; Astrup, R. Empirical coverage of model-based variance estimators for remote sensing assisted estimation of stand-level timber volume. Remote Sens. Environ. 2016, 173, 274–281. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| Age | Yield Class ≥ 14 m ha year | Yield Class < 14 m ha year |
|---|---|---|
| ≥25 years old | 25% | 15% |
| <25 years old | 52% | 8% |
| Training | Validation | |||||
|---|---|---|---|---|---|---|
| Parameter | Minimum | Maximum | Mean | Minimum | Maximum | Mean |
| QMDBH (cm) | 9 | 43 | 20 | 20 | 44 | 28 |
| Basal area (m2 ha−1) | 2 | 108 | 45 | 26 | 74 | 47 |
| Stems (ha−1) | 275 | 3,250 | 1498 | 279 | 2200 | 953 |
| Volume (m3 ha−1) | 12 | 1308 | 412 | 296 | 872 | 535 |
| Age (Years) | 10 | 50 | 29 | 27 | 55 | 37 |
| Scale | Minimum Area (ha) | Mean Area (ha) | Median Area (ha) | Maximum Area (ha) |
|---|---|---|---|---|
| Subcompartment | 0.5 | 4.3 | 2.5 | 55 |
| Property | 2.4 | 92 | 47 | 660 |
| Forest code | 42 | 797 | 640 | 2216 |
| Parameter | 2018 |
|---|---|
| Sensor | Optech Galaxy T1000 |
| Maximum altitude flown (m) | 1200 |
| Speed of plane (knots) | 110 |
| Scan angle (degrees off nadir) | 14 |
| Flight lines overlap (%) | 20 |
| Pulses (per m—all returns) | 4 |
| Lidar Metric | Return | Details |
|---|---|---|
| Height | All returns that were not ground | Minimum, maximum, mean, median, mode, dominant, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 percentile heights, standard deviation for all height percentiles, kurtosis, variance, skewness, sum. |
| Height | All | Minimum, maximum, mean, median, mode, dominant, standard deviation, kurtosis, variance, skewness, sum. |
| Height | First | Minimum, maximum, mean, median, mode, dominant, standard deviation, kurtosis, variance, skewness, sum. |
| Height | Last | Minimum, maximum, mean, median, mode, dominant, standard deviation, kurtosis, variance, skewness, sum. |
| Density | All returns that were not ground | Between 2 m–40 m, 2.5 m–5 m, 5 m–10 m, 10 m–15 m, 15 m–20 m, 20 m–25 m, 25 m–30 m, 30 m–40 m. |
| Canopy cover percent | All returns that were not ground | Between 2.5 m–5 m, 5 m–7.5 m, 7.5 m–10 m, 10 m–12.5 m, 12.5 m–15 m, 15 m–17.5 m, 17.5 m–20 m, 20 m–22.5 m, 22.5 m–25 m, 25 m–27.5 m, 27.5 m–30 m, 30 m–40 m. |
| Amplitude | All returns that were not ground | Sum, mean, median, max, standard deviation, variance, percentile 10–100 |
| Height density [10] | All | 95th Percentile between 2 m and 40 m height. |
| Sentinel 2 | Bands 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 | |
| Sentinel 2 | Nutrient deficiency classification | |
| Internal database | Age of forest |
| Parameter | AF | Spruce | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | RMSE (%) | R | Bias | RMSE | RMSE (%) | R | Bias | |
| QMDBH (cm) | 3.95 | 19 | 0.70 | 0.0303 | 4.21 | 19 | 0.69 | 0.1179 |
| Basal area (m ha−1) | 9.95 | 22 | 0.67 | 0.0778 | 10.49 | 21 | 0.61 | 0.0775 |
| Stems (ha−1) | 420 | 28 | 0.62 | 1 | 409 | 27 | 0.69 | 8 |
| Volume (m ha−1) | 110 | 26 | 0.77 | 2 | 111 | 23 | 0.75 | 4 |
| Parameter | AF | Spruce | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | RMSE (%) | R | Bias | RMSE | RMSE (%) | R | Bias | |
| QMDBH (cm) | 4.83 | 24 | 0.58 | 0.1141 | 5.40 | 26 | 0.54 | 0.1111 |
| Basal area (m ha−1) | 10.52 | 23 | 0.64 | 0.1380 | 11.23 | 23 | 0.57 | 0.4066 |
| Stems (ha−1) | 461 | 31 | 0.56 | 5 | 465 | 30 | 0.62 | 45 |
| Volume (m ha−1) | 121 | 29 | 0.72 | 3 | 132 | 28 | 0.65 | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walshe, D.; McInerney, D.; Paulo Pereira, J.; Byrne, K.A. Investigating the Effects of k and Area Size on Variance Estimation of Multiple Pixel Areas Using a k-NN Technique for Forest Parameters. Remote Sens. 2021, 13, 4688. https://doi.org/10.3390/rs13224688
Walshe D, McInerney D, Paulo Pereira J, Byrne KA. Investigating the Effects of k and Area Size on Variance Estimation of Multiple Pixel Areas Using a k-NN Technique for Forest Parameters. Remote Sensing. 2021; 13(22):4688. https://doi.org/10.3390/rs13224688
Chicago/Turabian StyleWalshe, Dylan, Daniel McInerney, João Paulo Pereira, and Kenneth A. Byrne. 2021. "Investigating the Effects of k and Area Size on Variance Estimation of Multiple Pixel Areas Using a k-NN Technique for Forest Parameters" Remote Sensing 13, no. 22: 4688. https://doi.org/10.3390/rs13224688






