Shared Blocks-Based Ensemble Deep Learning for Shallow Landslide Susceptibility Mapping
Abstract
:1. Introduction
2. Study Area and Dataset
2.1. Description of the Study Area
2.2. Landslide Inventory Map
2.3. Landslide Predisposing Factors
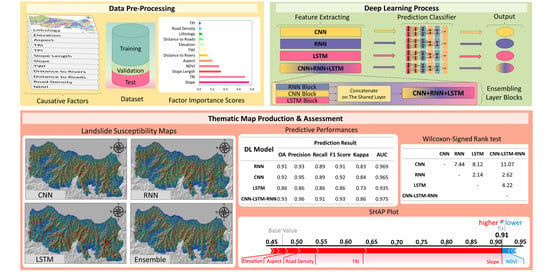
3. Methodology
3.1. Correlation-Based Feature Selection
3.2. Deep Learning Methods
3.2.1. Convolutional Neural Network (CNN)
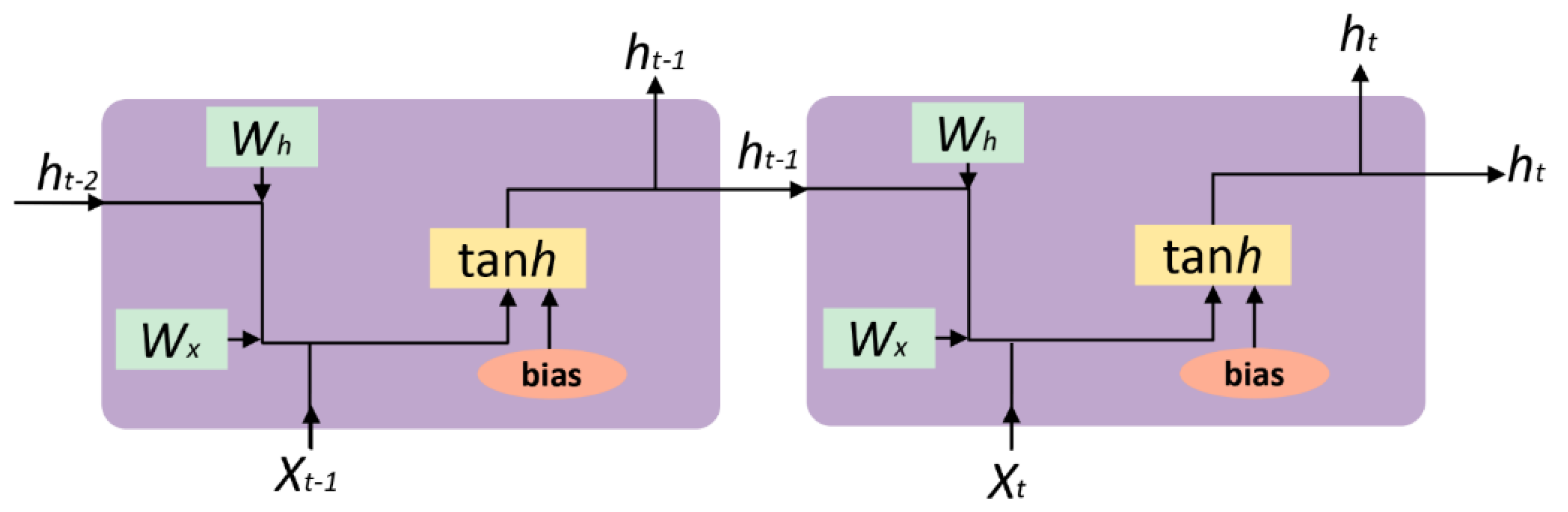
3.2.2. Recurrent Neural Network (RNN)
3.2.3. Long Short-Term Memory (LSTM)
3.2.4. Ensemble DL with Shared Layers Approach
3.2.5. Description of Network Architectures
3.2.6. Interpretation of DL Model Output
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tihon, A. Impact of Natural Disasters, Psychological and Physical Effects on the Population. In Abstracts of The Second Eurasian RISK-2020 Conference and Symposium; Aliyev, V., Ed.; AIJR Publisher: Tbilisi, Georgia, 2020; pp. 133–134. [Google Scholar]
- Lacasse, S.; Nadim, F. Landslide Risk Assessment and Mitigation Strategy. In Bridge Engineering Handbook, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 315–359. [Google Scholar] [CrossRef]
- Highland, L.M.; Bobrowsky, P. The Landslide Handbook-A Guide to Understanding Landslides; Kidd, M., Ed.; U.S. Geological Survey Circular 1325: Reston, VA, USA, 2008; p. 129. ISBN 978-141-132-226-4.
- Pradhan, S.P.; Siddique, T. Mass Wasting: An Overview. Adv. Nat. Technol. Hazards Res. 2019, 50, 3–20. [Google Scholar] [CrossRef]
- Haque, U.; da Silva, P.F.; Devoli, G.; Pilz, J.; Zhao, B.; Khaloua, A.; Wilopo, W.; Andersen, P.; Lu, P.; Lee, J.; et al. The Human Cost of Global Warming: Deadly Landslides and Their Triggers (1995–2014). Sci. Total Environ. 2019, 682, 673–684. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global Fatal Landslide Occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef] [Green Version]
- Guha-Sapir, D.; Below, R.; Hoyois, P. EM-DAT: International Disaster Database. Available online: http://www.emdat.be (accessed on 4 October 2021).
- Dai, F.C.; Lee, C.F.; Ngai, Y.Y. Landslide Risk Assessment and Management: An Overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide Hazard Evaluation: A Review of Current Techniques and Their Application in a Multi-Scale Study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Gómez, H.; Kavzoglu, T. Assessment of Shallow Landslide Susceptibility Using Artificial Neural Networks in Jabonosa River Basin, Venezuela. Eng. Geol. 2005, 78, 11–27. [Google Scholar] [CrossRef]
- Bijukchhen, S.M.; Kayastha, P.; Dhital, M.R. A Comparative Evaluation of Heuristic and Bivariate Statistical Modelling for Landslide Susceptibility Mappings in Ghurmi-Dhad Khola, East Nepal. Arab. J. Geosci. 2013, 6, 2727–2743. [Google Scholar] [CrossRef]
- Soeters, R.; Van Westen, C.J. Slope Instability Recognition, Analysis and Zonation. In Landslides: Investigation and Mitigation. Transportation Research Board National Research Council; Special Report No. 247; Turner, K.T., Schuster, R.L., Eds.; National Academy Press: Washington, DC, USA, 1996; pp. 129–177. [Google Scholar]
- Thiebes, B. Landslide Analysis and Early Warning—Local and Regional Case Study in the Swabian Alb, Germany; Springer: Berlin, Germany, 2012. [Google Scholar]
- Pradhan, B. A Comparative Study on the Predictive Ability of the Decision Tree, Support Vector Machine and Neuro-Fuzzy Models in Landslide Susceptibility Mapping Using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, H.; Mei, H.; Xiao, D.; Li, Y.; Li, M. Landslide Susceptibility Mapping Using the Stacking Ensemble Machine Learning Method in Lushui, Southwest China. Appl. Sci. 2020, 10, 4016. [Google Scholar] [CrossRef]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide Susceptibility Assessment Using SVM Machine Learning Algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Kutlug Sahin, E.; Colkesen, I. An Assessment of Multivariate and Bivariate Approaches in Landslide Susceptibility Mapping: A Case Study of Duzkoy District. Nat. Hazards 2015, 76, 471–496. [Google Scholar] [CrossRef]
- Taalab, K.; Cheng, T.; Zhang, Y. Mapping Landslide Susceptibility and Types Using Random Forest. Big Earth Data 2018, 2, 159–178. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Jirandeh, A.G.; Pradhan, B.; Xu, C.; Gokceoglu, C. Landslide Susceptibility Mapping Using Support Vector Machine and GIS at the Golestan Province, Iran. J. Earth Syst. Sci. 2013, 122, 349–369. [Google Scholar] [CrossRef] [Green Version]
- Merghadi, A.; Abderrahmane, B.; Tien Bui, D. Landslide Susceptibility Assessment at Mila Basin (Algeria): A Comparative Assessment of Prediction Capability of Advanced Machine Learning Methods. ISPRS Int. J. Geo-Inf. 2018, 7, 268. [Google Scholar] [CrossRef] [Green Version]
- Sahin, E.K. Comparative Analysis of Gradient Boosting Algorithms for Landslide Susceptibility Mapping. Geocarto Int. 2020, 1–25. [Google Scholar] [CrossRef]
- Can, R.; Kocaman, S.; Gokceoglu, C. A Comprehensive Assessment of XGBoost Algorithm for Landslide Susceptibility Mapping in the Upper Basin of Ataturk Dam, Turkey. Appl. Sci. 2021, 11, 4993. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H.; Peng, L. Flood Susceptibility Mapping Using Convolutional Neural Network Frameworks. J. Hydrol. 2020, 582, 124482. [Google Scholar] [CrossRef]
- Bjånes, A.; De La Fuente, R.; Mena, P. A Deep Learning Ensemble Model for Wildfire Susceptibility Mapping. Ecol. Inform. 2021, 65, 101397. [Google Scholar] [CrossRef]
- Sublime, J.; Kalinicheva, E. Automatic Post-Disaster Damage Mapping Using Deep-Learning Techniques for Change Detection: Case Study of the Tohoku Tsunami. Remote Sens. 2019, 11, 1123. [Google Scholar] [CrossRef] [Green Version]
- Cui, W.; He, X.; Yao, M.; Wang, Z.; Li, J.; Hao, Y.; Wu, W.; Zhao, H.; Chen, X.; Cui, W. Landslide Image Captioning Method Based on Semantic Gate and Bi-Temporal LSTM. ISPRS Int. J. Geo-Inf. 2020, 9, 194. [Google Scholar] [CrossRef] [Green Version]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Li, W.; Fang, Z.; Wang, Y. Stacking Ensemble of Deep Learning Methods for Landslide Susceptibility Mapping in the Three Gorges Reservoir Area, China. Stoch. Environ. Res. Risk Assess. 2021, 1–22. [Google Scholar] [CrossRef]
- Xiao, L.; Zhang, Y.; Peng, G. Landslide Susceptibility Assessment Using Integrated Deep Learning Algorithm along the China-Nepal Highway. Sensors 2018, 18, 4436. [Google Scholar] [CrossRef] [Green Version]
- Zhong, C.; Liu, Y.; Gao, P.; Chen, W.; Li, H.; Hou, Y.; Nuremanguli, T.; Ma, H. Landslide Mapping with Remote Sensing: Challenges and Opportunities. Int. J. Remote Sens. 2020, 41, 1555–1581. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of Convolutional Neural Networks Featuring Bayesian Optimization for Landslide Susceptibility Assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Chen, H.; Zeng, Z.; Tang, H. Landslide Deformation Prediction Based on Recurrent Neural Network. Neural Process. Lett. 2015, 41, 169–178. [Google Scholar] [CrossRef]
- Mutlu, B.; Nefeslioglu, H.A.; Sezer, E.A.; Ali Akcayol, M.; Gokceoglu, C. An Experimental Research on the Use of Recurrent Neural Networks in Landslide Susceptibility Mapping. ISPRS Int. J. Geo-Inf. 2019, 8, 578. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative Study of Landslide Susceptibility Mapping with Different Recurrent Neural Networks. Comput. Geosci. 2020, 138, 104445. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Fang, Z.; Peng, L.; Hong, H. Potential of Ensemble Learning to Improve Tree-Based Classifiers for Landslide Susceptibility Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4642–4662. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, L.; Li, S.; Ren, F.; Du, Q. A Hybrid Model Considering Spatial Heterogeneity for Landslide Susceptibility Mapping in Zhejiang Province, China. Catena 2020, 188, 104425. [Google Scholar] [CrossRef]
- Ji, J.; Chen, X.; Luo, C.; Li, P. A Deep Multi-Task Learning Approach for ECG Data Analysis. In Proceedings of the 2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; pp. 124–127. [Google Scholar] [CrossRef]
- Yalcin, A. A Geotechnical Study on the Landslides in the Trabzon Province, NE, Turkey. Appl. Clay Sci. 2011, 52, 11–19. [Google Scholar] [CrossRef]
- Ozturk, K. Landslips and the Effects of These on Turkey. Gazi Univ. J. Gazi Educ. Fac. 2002, 22, 35–50. [Google Scholar]
- Bayrak, T.; Ulukavak, M. Trabzon Landslides. Electron. J. Map Technol. 2009, 1, 20–30. [Google Scholar]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide Susceptibility Mapping Using GIS-Based Multi-Criteria Decision Analysis, Support Vector Machines, and Logistic Regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Hussin, H.Y.; Zumpano, V.; Reichenbach, P.; Sterlacchini, S.; Micu, M.; van Westen, C.; Bălteanu, D. Different Landslide Sampling Strategies in a Grid-Based Bi-Variate Statistical Susceptibility Model. Geomorphology 2016, 253, 508–523. [Google Scholar] [CrossRef]
- Yilmaz, I. The Effect of the Sampling Strategies on the Landslide Susceptibility Mapping by Conditional Probability and Artificial Neural Networks. Environ. Earth Sci. 2010, 60, 505–519. [Google Scholar] [CrossRef]
- Xu, C.; Dai, F.; Xu, X.; Lee, Y.H. GIS-Based Support Vector Machine Modeling of Earthquake-Triggered Landslide Susceptibility in the Jianjiang River Watershed, China. Geomorphology 2012, 145–146, 70–80. [Google Scholar] [CrossRef]
- Süzen, M.L.; Doyuran, V. A Comparison of the GIS Based Landslide Susceptibility Assessment Methods: Multivariate versus Bivariate. Environ. Geol. 2004, 45, 665–679. [Google Scholar] [CrossRef]
- Dou, J.; Paudel, U.; Oguch, T.; Uchiyama, S.; Hayakavva, Y.S. Shallow and Deep-Seated Landslide Differentiation Using Support Vector Machines: A Case Study of the Chuetsu Area, Japan. Terr. Atmos. Ocean. Sci. 2015, 26, 227–239. [Google Scholar] [CrossRef] [Green Version]
- Yalcin, A.; Reis, S.; Aydinoglu, A.C.; Yomralioglu, T. A GIS-Based Comparative Study of Frequency Ratio, Analytical Hierarchy Process, Bivariate Statistics and Logistics Regression Methods for Landslide Susceptibility Mapping in Trabzon, NE Turkey. Catena 2011, 85, 274–287. [Google Scholar] [CrossRef]
- Colkesen, I.; Sahin, E.K.; Kavzoglu, T. Susceptibility Mapping of Shallow Landslides Using Kernel-Based Gaussian Process, Support Vector Machines and Logistic Regression. J. Afr. Earth Sci. 2016, 118, 53–64. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Kutlug Sahin, E.; Colkesen, I. Selecting Optimal Conditioning Factors in Shallow Translational Landslide Susceptibility Mapping Using Genetic Algorithm. Eng. Geol. 2015, 192, 101–112. [Google Scholar] [CrossRef]
- Teke, A.; Kavzoglu, T. Determination of Effective Predisposing Factors Using Random Forest-Based Gini Index in Landslide Susceptibility Mapping. In Proceedings of the 2nd International Geoinformation Days (IGD), Mersin, Turkey, 6 May 2021. [Google Scholar]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance Evaluation of the GIS-Based Data Mining Techniques of Best-First Decision Tree, Random Forest, and Naïve Bayes Tree for Landslide Susceptibility Modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef] [PubMed]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference Machine Learning, Lille, France, 6–11 July 2015; Volume 1, pp. 448–456. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; ISBN 978-0-262-03561-3. [Google Scholar]
- Huang, F.; Zhang, J.; Zhou, C.; Wang, Y.; Huang, J.; Zhu, L. A Deep Learning Algorithm Using a Fully Connected Sparse Autoencoder Neural Network for Landslide Susceptibility Prediction. Landslides 2020, 17, 217–229. [Google Scholar] [CrossRef]
- Szandała, T. Review and Comparison of Commonly Used Activation Functions for Deep Neural Networks. In Bio-Inspired Neurocomputing; Springer: Singapore, 2021; pp. 203–224. ISBN 9789811554957. [Google Scholar]
- Zhang, X.; Pun, M.O.; Liu, M. Semi-supervised Multi-temporal Deep Representation Fusion Network for Landslide Mapping from Aerial Orthophotos. Remote Sens. 2021, 13, 548. [Google Scholar] [CrossRef]
- Tan, F.; Yu, J.; Jiao, Y.Y.; Lin, D.; Lv, J.; Cheng, Y. Rapid Assessment of Landslide Risk Level Based on Deep Learning. Arab. J. Geosci. 2021, 14, 1–10. [Google Scholar] [CrossRef]
- Ragab, M.G.; Abdulkadir, S.J.; Aziz, N.; Al-Tashi, Q.; Alyousifi, Y.; Alhussian, H.; Alqushaibi, A. A Novel One-Dimensional Cnn with Exponential Adaptive Gradients for Air Pollution Index Prediction. Sustainability 2020, 12, 10090. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Jian, J. Remote Sensing Landslide Recognition Based on Convolutional Neural Network. Math. Probl. Eng. 2019, 2019, 8389368. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2323. [Google Scholar] [CrossRef] [Green Version]
- Yi, Y.; Zhang, Z.; Zhang, W.; Jia, H.; Zhang, J. Landslide Susceptibility Mapping Using Multiscale Sampling Strategy and Convolutional Neural Network: A Case Study in Jiuzhaigou Region. Catena 2020, 195, 104851. [Google Scholar] [CrossRef]
- Mezaal, M.R.; Pradhan, B.; Sameen, M.I. Optimized Neural Architecture for Automatic Landslide Detection from High-Resolution Airborne Laser Scanning Data. Appl. Sci. 2017, 7, 730. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.; Ma, J.; Wang, Y.; Zhang, J.; Chen, H.; Tang, H. A Novel Decomposition-Ensemble Learning Model Based on Ensemble Empirical Mode Decomposition and Recurrent Neural Network for Landslide Displacement Prediction. Appl. Sci. 2021, 11, 4684. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zhang, L.; Luo, H.; He, J.; Cheung, R.W.M. AI-Powered Landslide Susceptibility Assessment in Hong Kong. Eng. Geol. 2021, 288, 106103. [Google Scholar] [CrossRef]
- Pradhan, B. Landslide Susceptibility Mapping of a Catchment Area Using Frequency Ratio, Fuzzy Logic and Multivariate Logistic Regression Approaches. J. Indian Soc. Remote Sens. 2010, 38, 301–320. [Google Scholar] [CrossRef]
- Lee, S.; Choi, J. Landslide Susceptibility Mapping Using GIS and the Weight-of-Evidence Model. Int. J. Geogr. Inf. Sci. 2004, 18, 789–814. [Google Scholar] [CrossRef]
- Nhu, V.H.; Hoang, N.D.; Nguyen, H.; Ngo, P.T.T.; Thanh Bui, T.; Hoa, P.V.; Samui, P.; Tien Bui, D. Effectiveness Assessment of Keras Based Deep Learning with Different Robust Optimization Algorithms for Shallow Landslide Susceptibility Mapping at Tropical Area. Catena 2020, 188, 104458. [Google Scholar] [CrossRef]
- Mandal, K.; Saha, S.; Mandal, S. Applying Deep Learning and Benchmark Machine Learning Algorithms for Landslide Susceptibility Modelling in Rorachu River Basin of Sikkim Himalaya, India. Geosci. Front. 2021, 12, 101203. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, L.; Ren, Y.; Suganthan, P.; Amaratunga, G. Ensemble Deep Learning for Regression and Time Series Forecasting. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence in Ensemble Learning, Orlando, FL, USA, 9–12 December 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Fan, C.; Matkovic, K.; Hauser, H. Sketch-Based Fast and Accurate Querying of Time Series Using Parameter-Sharing LSTM Networks. IEEE Trans. Vis. Comput. Graph. 2020, 27, 4495–4506. [Google Scholar] [CrossRef]
- Takahashi, R.; Matsubara, T.; Uehara, K. A Novel Weight-Shared Multi-Stage CNN for Scale Robustness. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 1090–1101. [Google Scholar] [CrossRef]
- Yap, M.; Johnston, R.L.; Foley, H.; MacDonald, S.; Kondrashova, O.; Tran, K.A.; Nones, K.; Koufariotis, L.T.; Bean, C.; Pearson, J.V.; et al. Verifying Explainability of a Deep Learning Tissue Classifier Trained on RNA-Seq Data. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4766–4775. [Google Scholar]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A Novel Hybrid Intelligent Model of Support Vector Machines and the MultiBoost Ensemble for Landslide Susceptibility Modeling. Bull. Eng. Geol. Environ. 2019, 78, 2865–2886. [Google Scholar] [CrossRef]
- Sahin, E.K.; Colkesen, I.; Kavzoglu, T. A Comparative Assessment of Canonical Correlation Forest, Random Forest, Rotation Forest and Logistic Regression Methods for Landslide Susceptibility Mapping. Geocarto Int. 2020, 35, 341–363. [Google Scholar] [CrossRef]
- Thai Pham, B.; Tien Bui, D.; Prakash, I. Landslide Susceptibility Modelling Using Different Advanced Decision Trees Methods. Civ. Eng. Environ. Syst. 2018, 35, 139–157. [Google Scholar] [CrossRef]
- Cantor, S.B.; Kattan, M.W. Determining the area under the ROC curve for a binary diagnostic test. Med. Decis. Mak. 2000, 20, 468–470. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Gokceoglu, C.; Sonmez, H. An Assessment on the Use of Logistic Regression and Artificial Neural Networks with Different Sampling Strategies for the Preparation of Landslide Susceptibility Maps. Eng. Geol. 2008, 97, 171–191. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Merghadi, A.; Shirzadi, A.; Nguyen, H.; Hussain, Y.; Avtar, R.; Chen, Y.; Pham, B.T.; Yamagishi, H. Different Sampling Strategies for Predicting Landslide Susceptibilities Are Deemed Less Consequential with Deep Learning. Sci. Total Environ. 2020, 720, 137320. [Google Scholar] [CrossRef]
- Dagdelenler, G.; Nefeslioglu, H.A.; Gokceoglu, C. Modification of Seed Cell Sampling Strategy for Landslide Susceptibility Mapping: An Application from the Eastern Part of the Gallipoli Peninsula (Canakkale, Turkey). Bull. Eng. Geol. Environ. 2016, 75, 575–590. [Google Scholar] [CrossRef]
- Yalcin, A. GIS-Based Landslide Susceptibility Mapping Using Analytical Hierarchy Process and Bivariate Statistics in Ardesen (Turkey): Comparisons of Results and Confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Van Westen, C.J.; Rengers, N.; Soeters, R. Use of Geomorphological Expert Knowledge in Indirect Landslide Hazard Assessment. Nat. Hazards 2003, 30, 399–419. [Google Scholar] [CrossRef]
- Pham, B.T.; Vu, V.D.; Costache, R.; Van Phong, T.; Ngo, T.Q.; Tran, T.H.; Nguyen, H.D.; Amiri, M.; Tan, M.T.; Trinh, P.T.; et al. Landslide Susceptibility Mapping Using State-of-the-Art Machine Learning Ensembles. Geocarto. Int. 2021, 1–25. [Google Scholar] [CrossRef]
- Tanyu, B.F.; Abbaspour, A.; Alimohammadlou, Y.; Tecuci, G. Landslide Susceptibility Analyses Using Random Forest, C4.5, and C5.0 with Balanced and Unbalanced Datasets. Catena 2021, 203, 105355. [Google Scholar] [CrossRef]
- Abedini, M.; Ghasemian, B.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Pham, B.T.; Bin Ahmad, B.; Tien Bui, D. A Novel Hybrid Approach of Bayesian Logistic Regression and Its Ensembles for Landslide Susceptibility Assessment. Geocarto Int. 2019, 34, 1427–1457. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A Review of Statistically-Based Landslide Susceptibility Models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.W.; Han, Z.; Pham, B.T. Improved Landslide Assessment Using Support Vector Machine with Bagging, Boosting, and Stacking Ensemble Machine Learning Framework in a Mountainous Watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
- Van Dao, D.; Jaafari, A.; Bayat, M.; Mafi-Gholami, D.; Qi, C.; Moayedi, H.; Van Phong, T.; Ly, H.B.; Le, T.T.; Trinh, P.T.; et al. A Spatially Explicit Deep Learning Neural Network Model for the Prediction of Landslide Susceptibility. Catena 2020, 188, 104451. [Google Scholar] [CrossRef]












| Major Factors | Sub-Factors | Source | Scale/Resolution |
|---|---|---|---|
| Geology | Lithology | General Directorate of Mineral Research and Exploration of Turkey (http://www.mta.gov.tr (accessed on 4 October 2021)) | 1:100,000 |
| Topographical | Elevation (m)—DEM | Shuttle Radar Topography Mission (SRTM- https://earthexplorer.usgs.gov/ (accessed on 4 October 2021)) | 30 m |
| Aspect | DEM | ||
| TRI | |||
| TPI | |||
| Slope Length | |||
| Slope (°) | |||
| Hydrological | TWI | DEM | 30 m |
| Distance to Rivers | Digitized existing river networks | ||
| Environmental | Distance to Roads | Digitized existing road and river networks | 30 m |
| Road Density | |||
| NDVI | Landsat-8 Operational Land Imager (OLI) multispectral image (2016), (https://earthexplorer.usgs.gov/(accessed on 4 October 2021)) |
| Model Parameters | CNN | RNN | LSTM |
|---|---|---|---|
| Input dimension | 12 × 1 | 12 × 1 | 12 × 1 |
| The number of units | 16 | 16 | 16 |
| Kernel size | 2 | - | - |
| Activation function | ReLu, sigmoid, tanh | sigmoid, tanh | sigmoid, tanh |
| Dense unit | 20, 10 and 1 | 20, 10 and 1 | 20, 10 and 1 |
| Dropout ratio | 0.2 | 0.2 | 0.2 |
| Optimizer | Adagrad | Adagrad | Adagrad |
| Loss function | MSE | MSE | MSE |
| Maximum epoch | 20 | 20 | 140 |
| Batch size | 32 | 32 | 32 |
| Total parameters | 3873 | 913 | 1777 |
| DL Model | Prediction Result | ||||||
|---|---|---|---|---|---|---|---|
| OA | Precision | Recall | F1 Score | Kappa | AUC | Time (sec.) | |
| RNN | 0.91 | 0.93 | 0.89 | 0.91 | 0.83 | 0.969 | 21.04 |
| CNN | 0.92 | 0.95 | 0.89 | 0.92 | 0.84 | 0.965 | 25.06 |
| LSTM | 0.86 | 0.86 | 0.86 | 0.86 | 0.73 | 0.935 | 402.00 |
| CNN–LSTM–RNN | 0.93 | 0.96 | 0.91 | 0.93 | 0.86 | 0.975 | 61.17 |
| CNN | RNN | LSTM | CNN–LSTM–RNN | |
|---|---|---|---|---|
| CNN | - | 7.44 | 8.12 | 11.07 |
| RNN | - | 2.14 | 2.62 | |
| LSTM | - | 4.22 | ||
| CNN–LSTM–RNN | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kavzoglu, T.; Teke, A.; Yilmaz, E.O. Shared Blocks-Based Ensemble Deep Learning for Shallow Landslide Susceptibility Mapping. Remote Sens. 2021, 13, 4776. https://doi.org/10.3390/rs13234776
Kavzoglu T, Teke A, Yilmaz EO. Shared Blocks-Based Ensemble Deep Learning for Shallow Landslide Susceptibility Mapping. Remote Sensing. 2021; 13(23):4776. https://doi.org/10.3390/rs13234776
Chicago/Turabian StyleKavzoglu, Taskin, Alihan Teke, and Elif Ozlem Yilmaz. 2021. "Shared Blocks-Based Ensemble Deep Learning for Shallow Landslide Susceptibility Mapping" Remote Sensing 13, no. 23: 4776. https://doi.org/10.3390/rs13234776
APA StyleKavzoglu, T., Teke, A., & Yilmaz, E. O. (2021). Shared Blocks-Based Ensemble Deep Learning for Shallow Landslide Susceptibility Mapping. Remote Sensing, 13(23), 4776. https://doi.org/10.3390/rs13234776