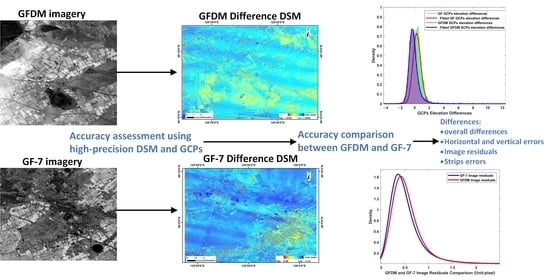
Accuracy Comparison and Assessment of DSM Derived from GFDM Satellite and GF-7 Satellite Imagery
Abstract
:1. Introduction
2. Data
3. Method
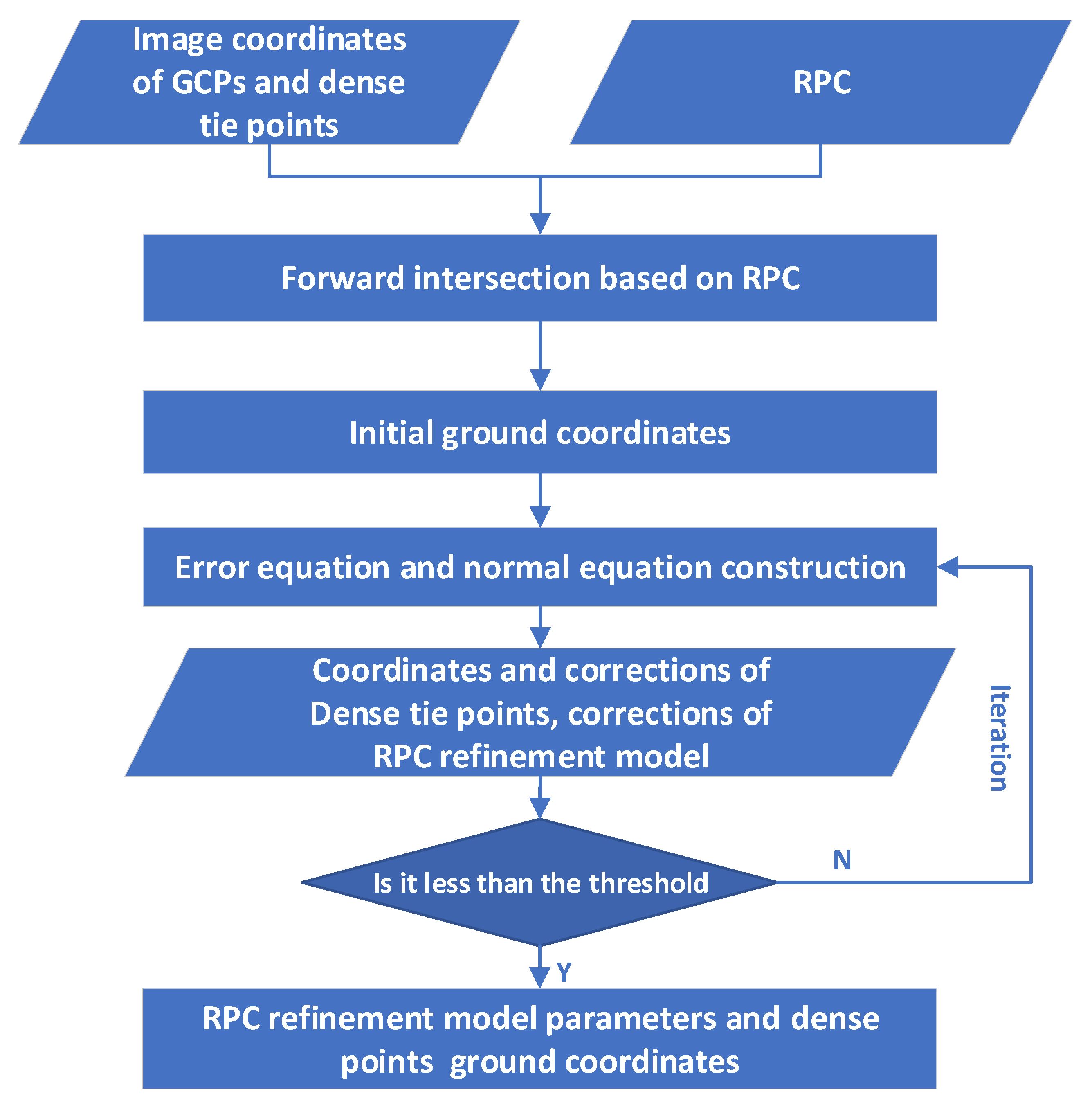
3.1. DSMs Generation and Co-Registration with the Reference DSM
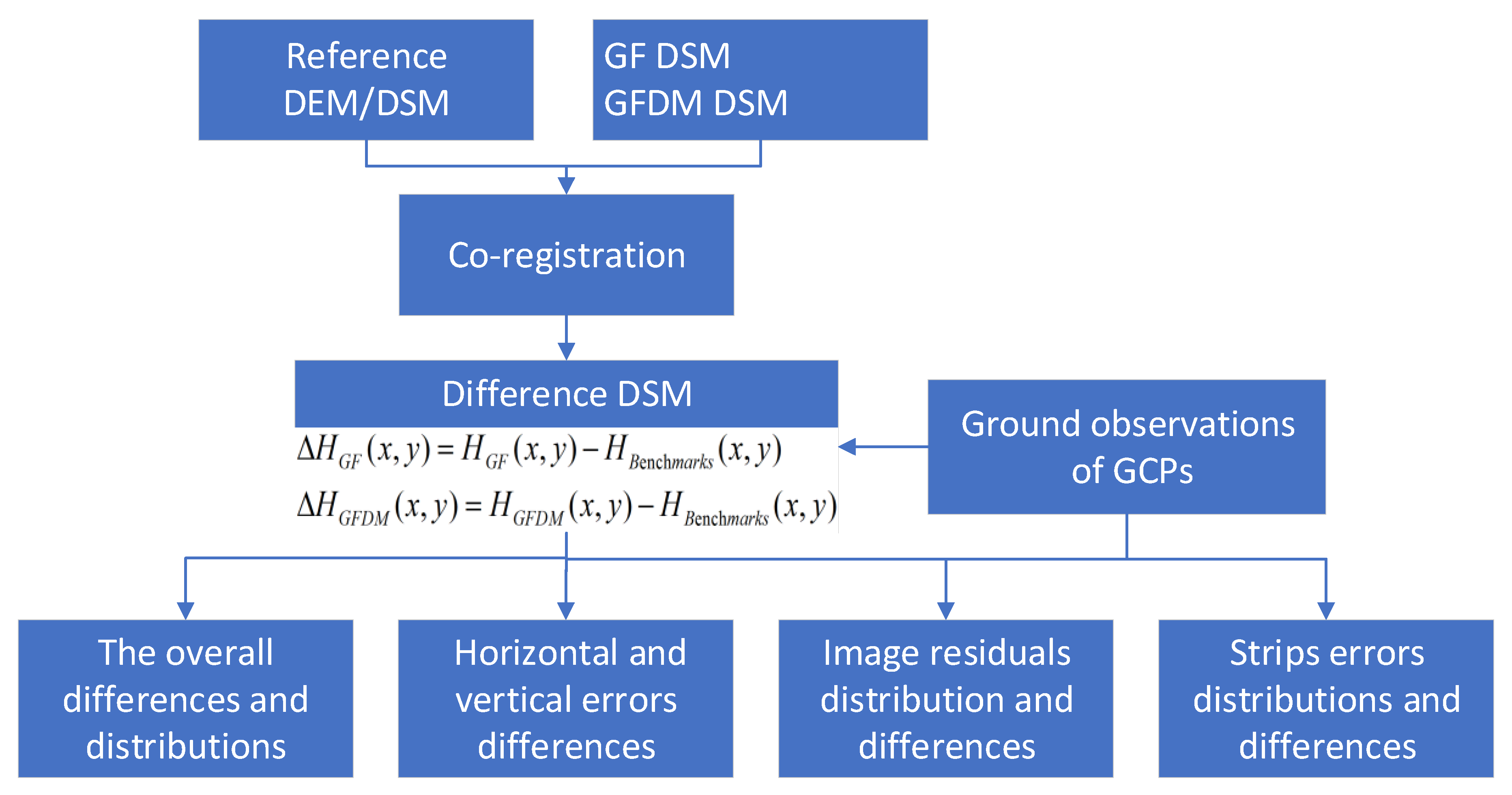
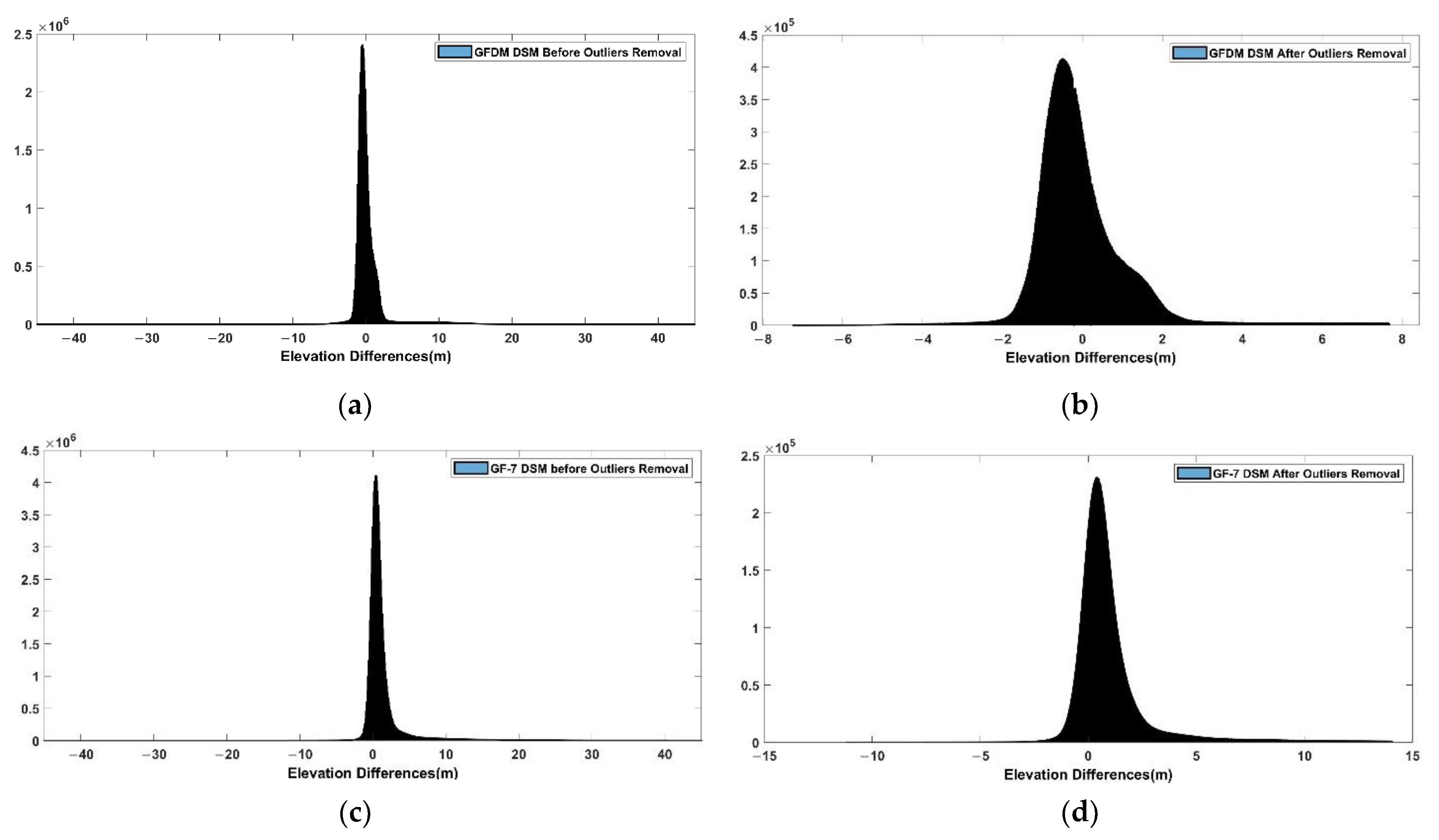
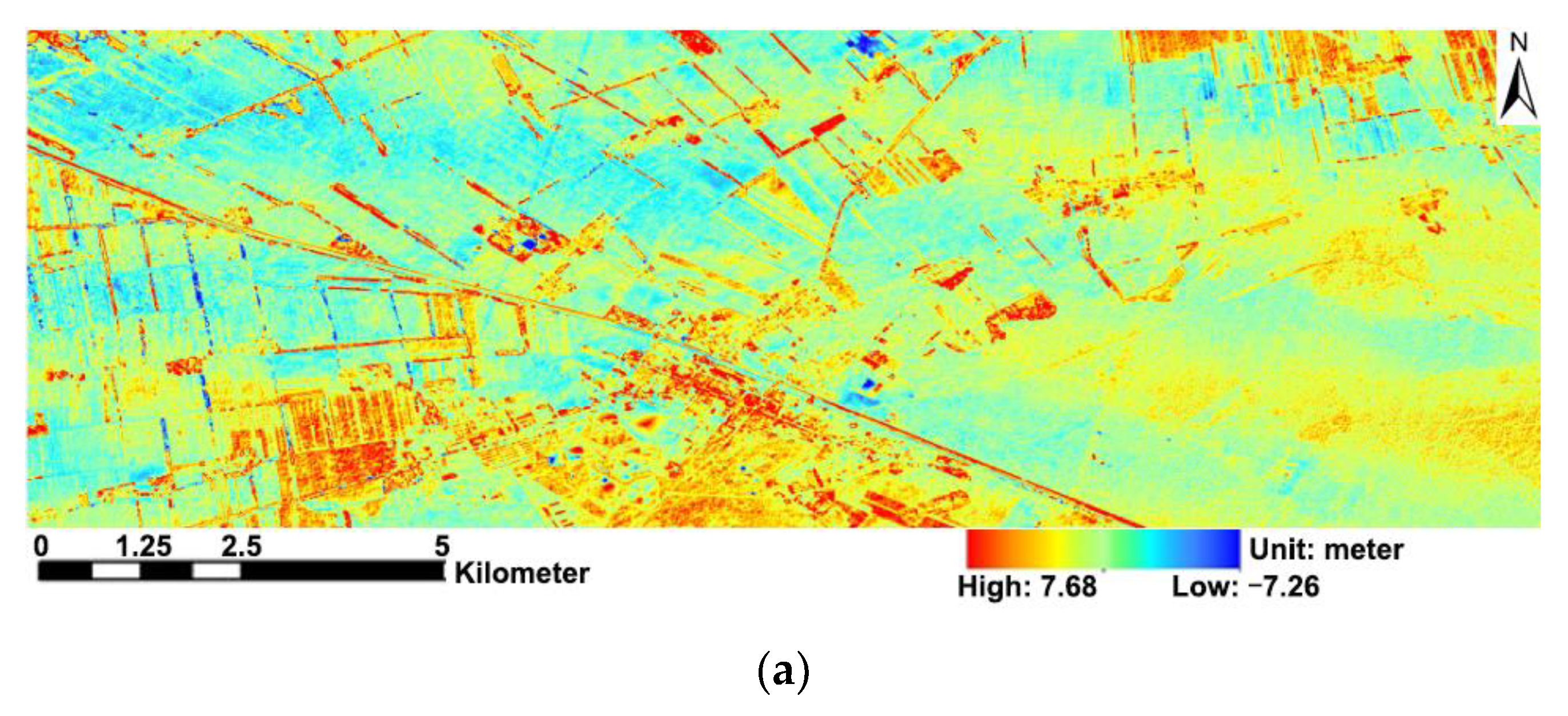
3.2. Calculation of Differences between the Derived DSMs and the Benchmark
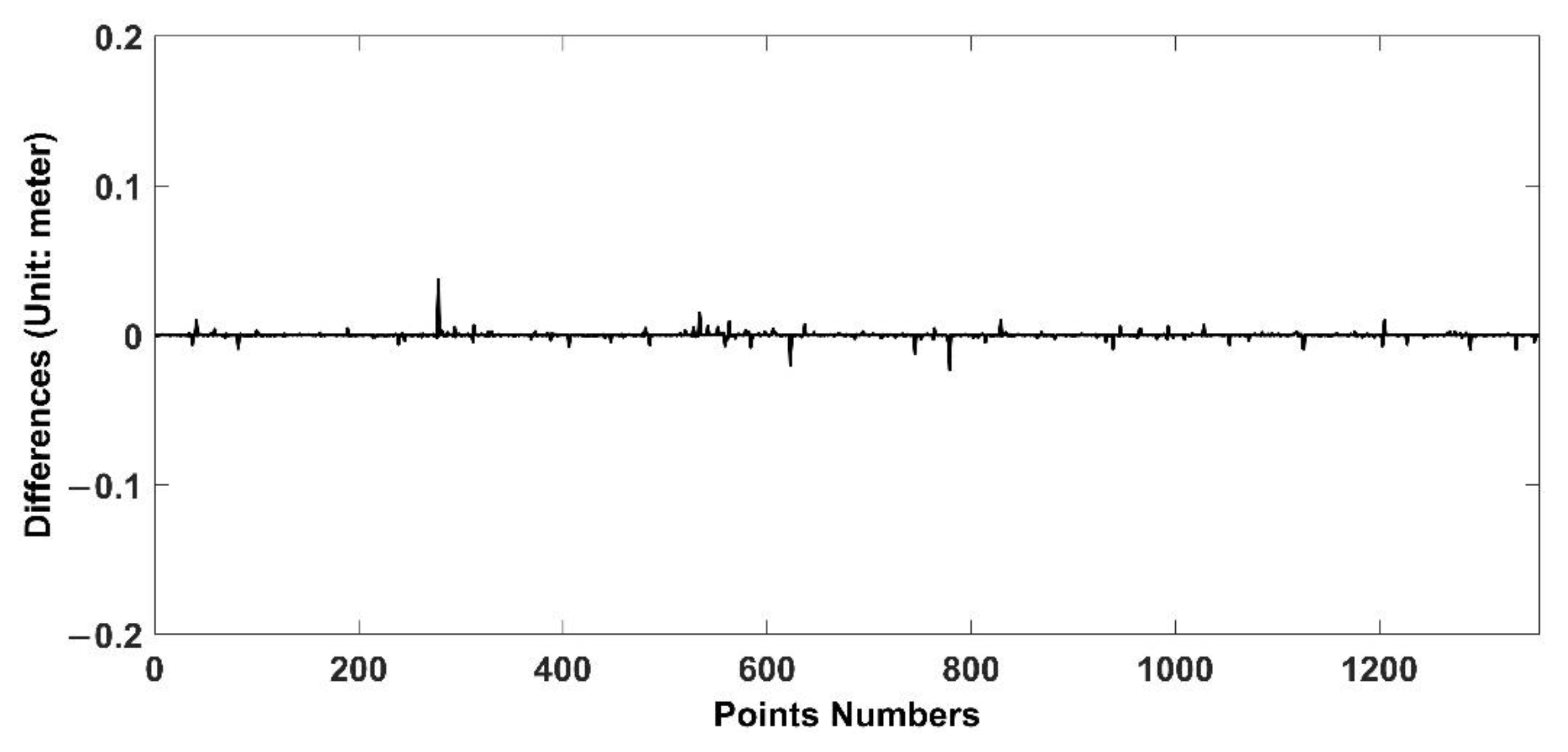
3.3. Accuracy Check in Object and Image Space Using DSM Differences and GCPs
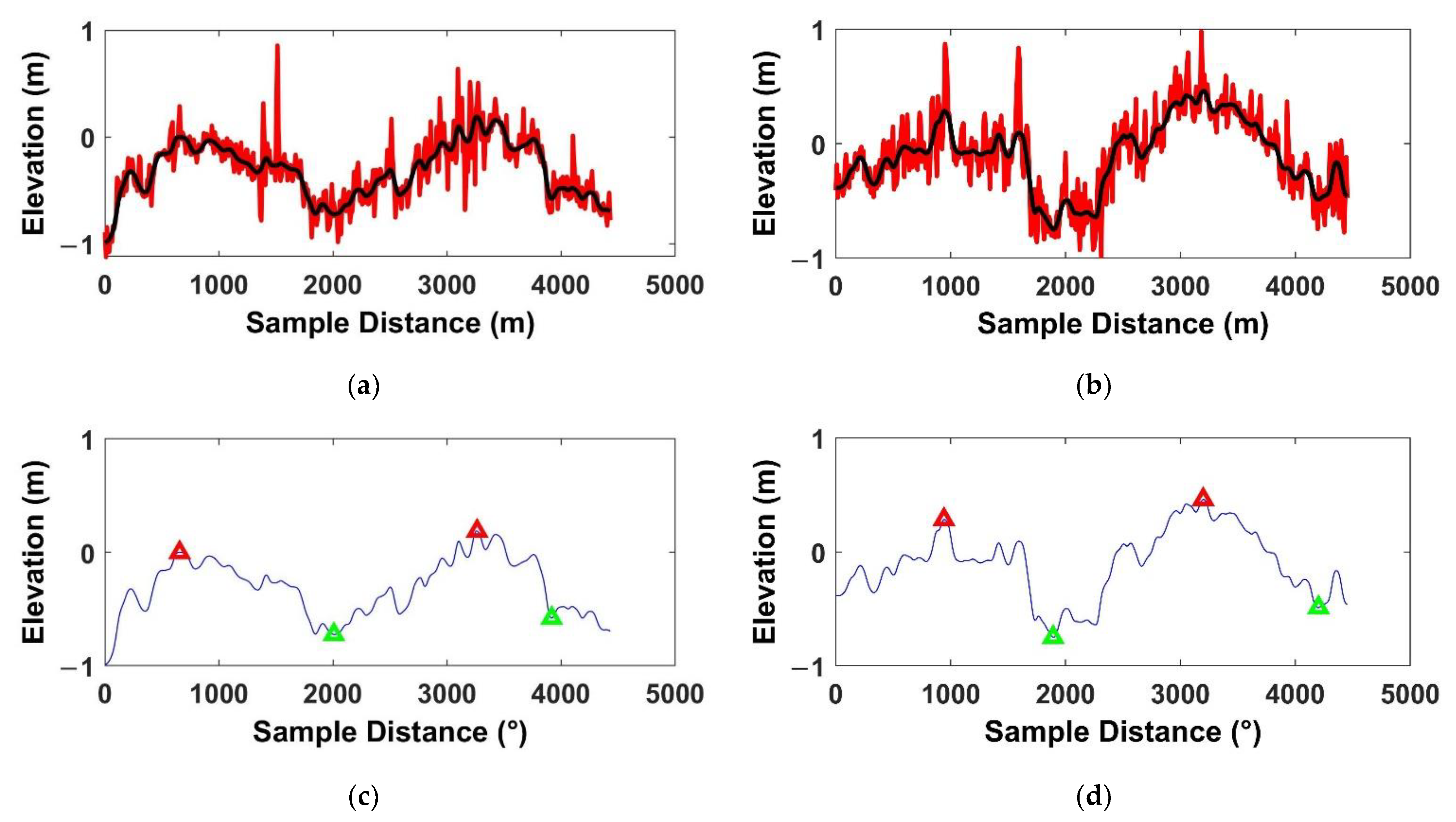
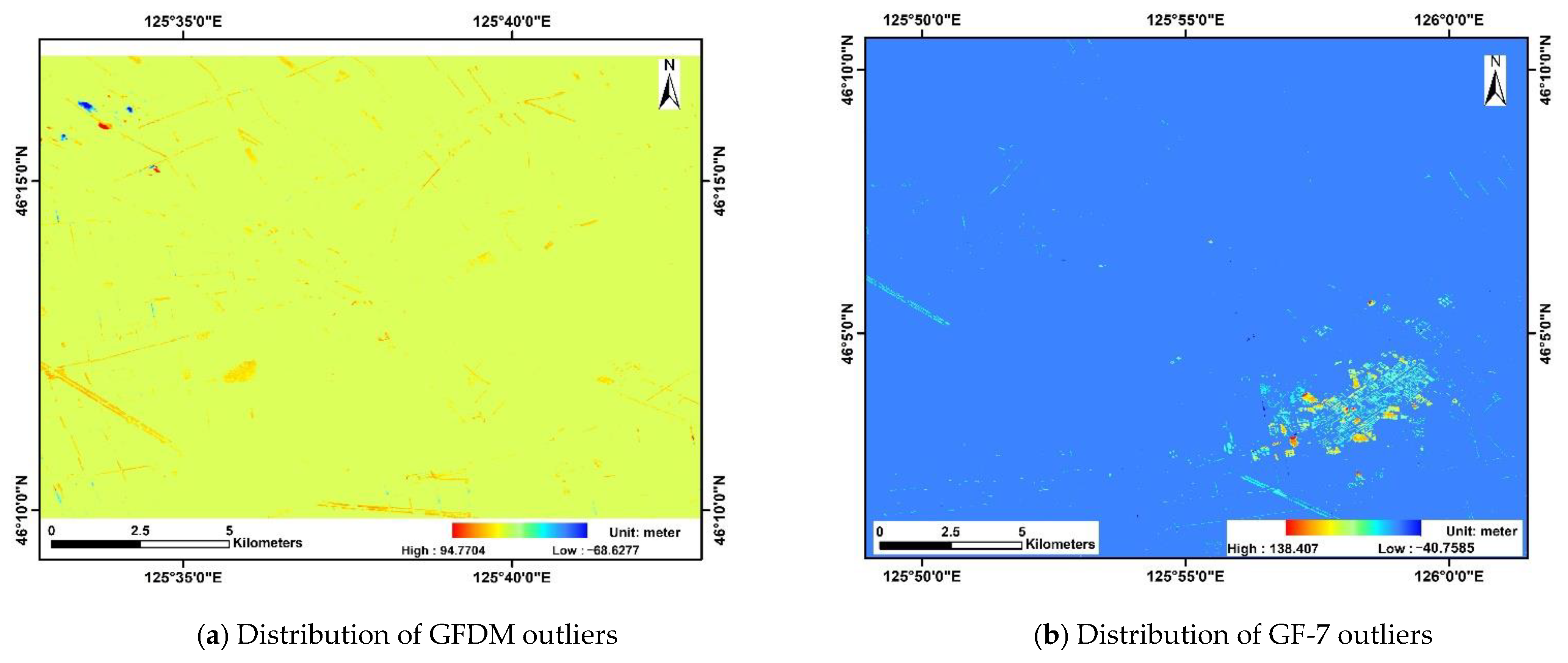
3.4. DSM Differences and Strip Errors
4. Results
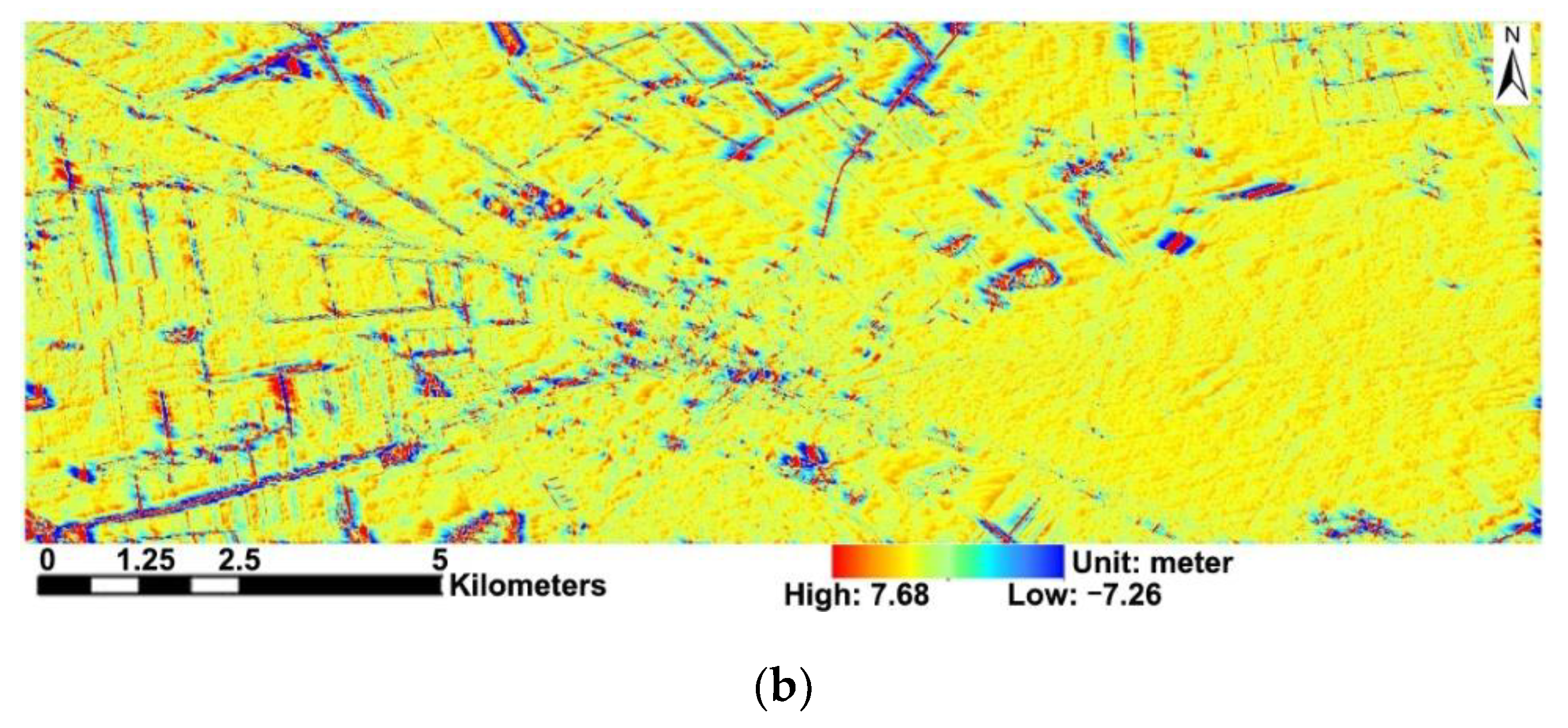
4.1. The Overall Differences between GF-7 DSM and GFDM DSM with High-Precision Reference
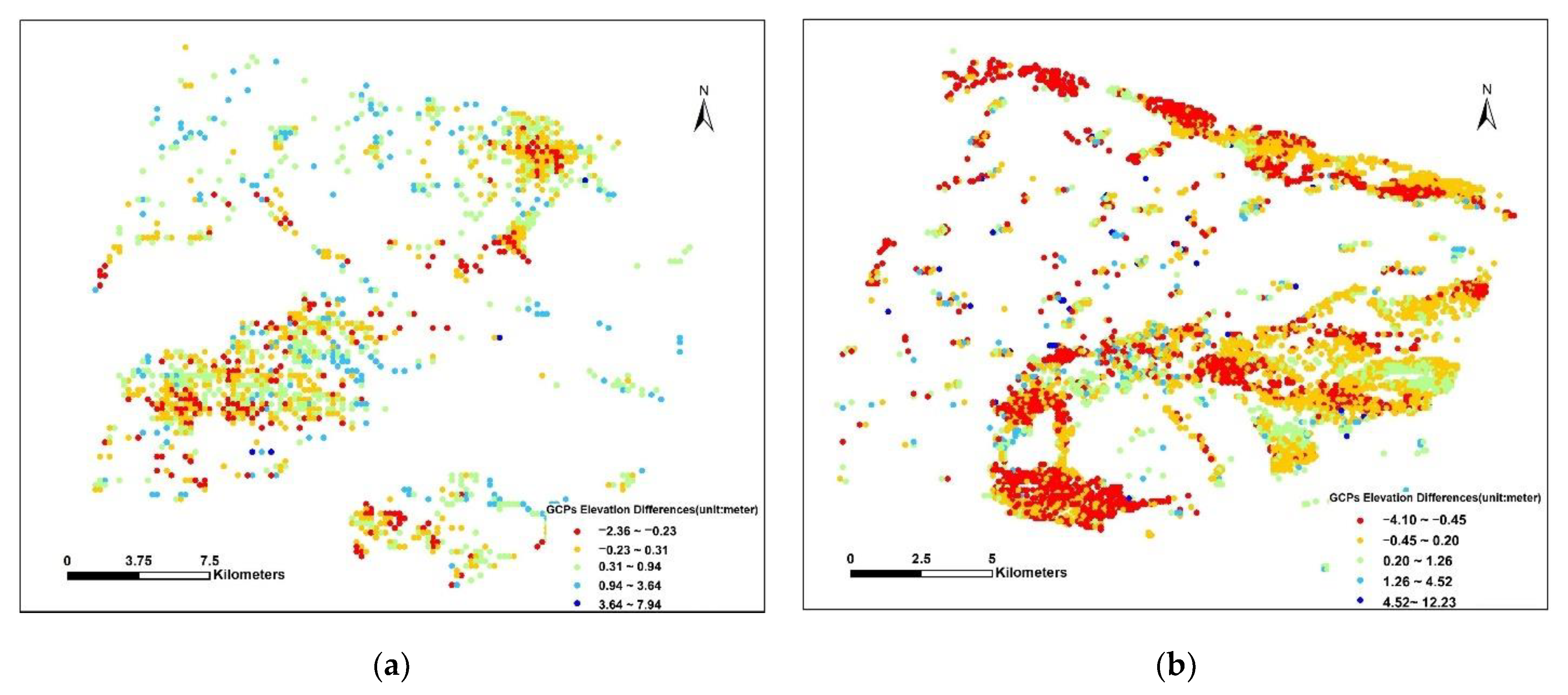
4.2. Differences of Horizontal Displacement Deviations and Vertical Errors
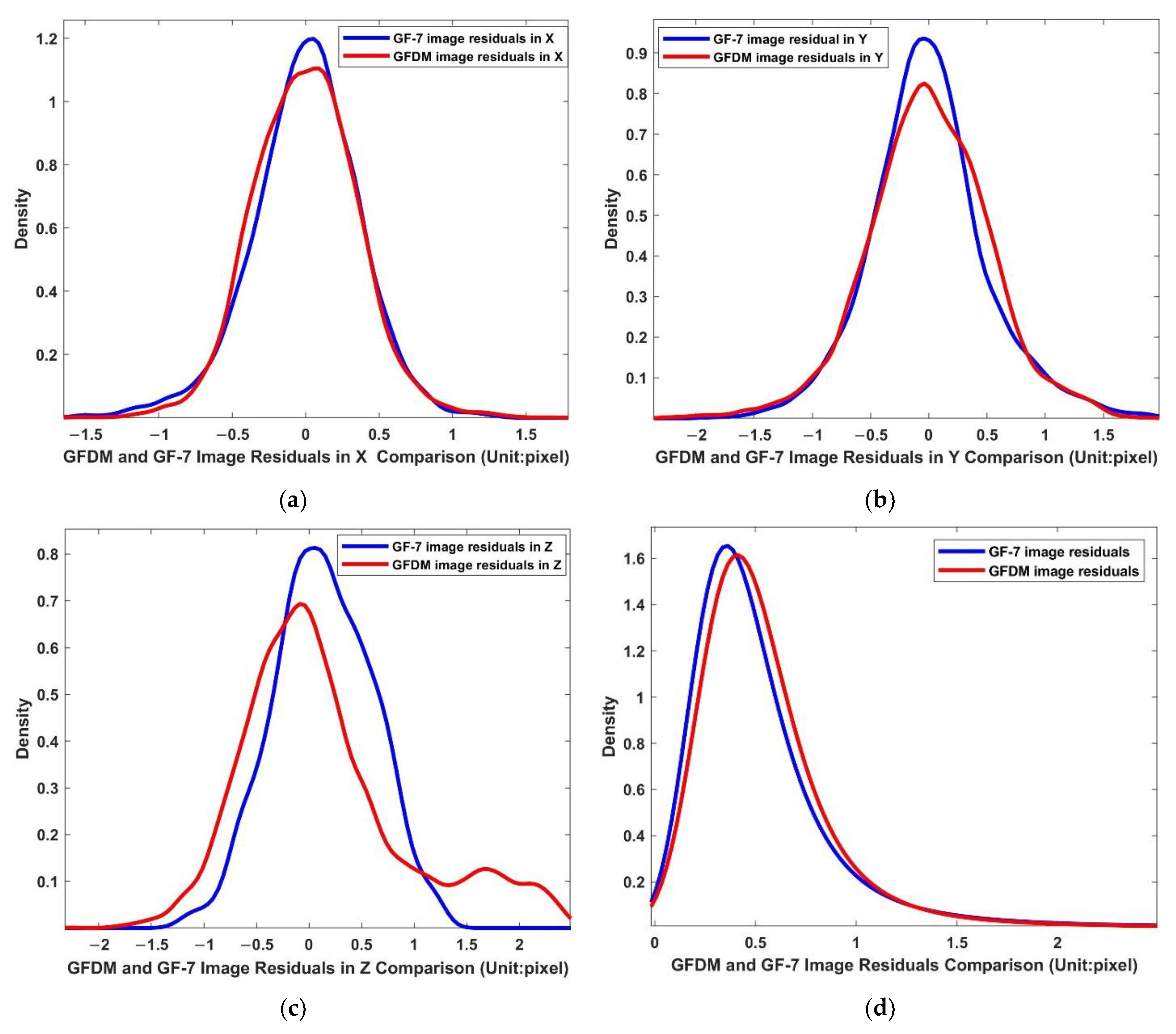
4.3. Residuals Differences in Image Space
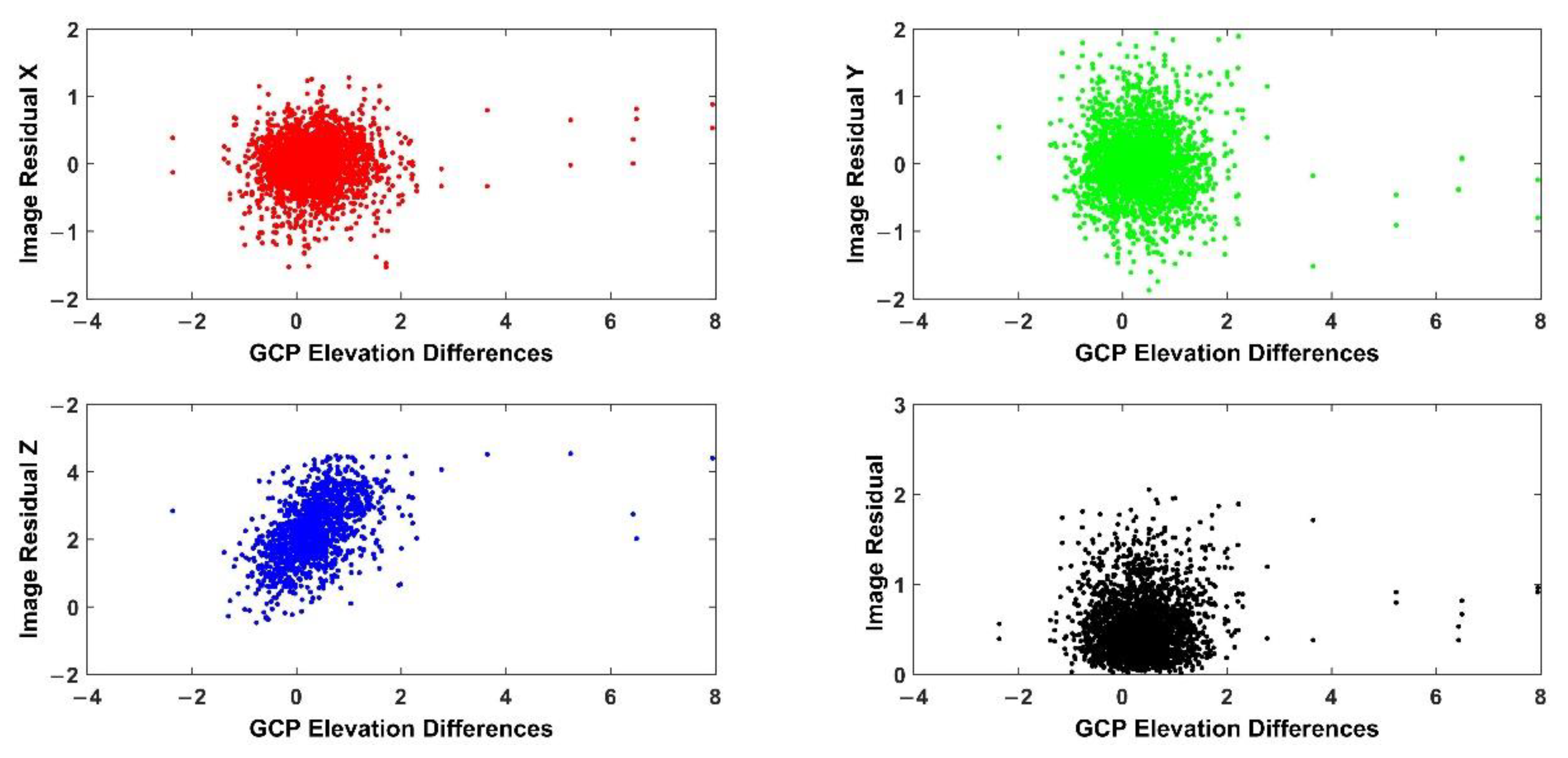
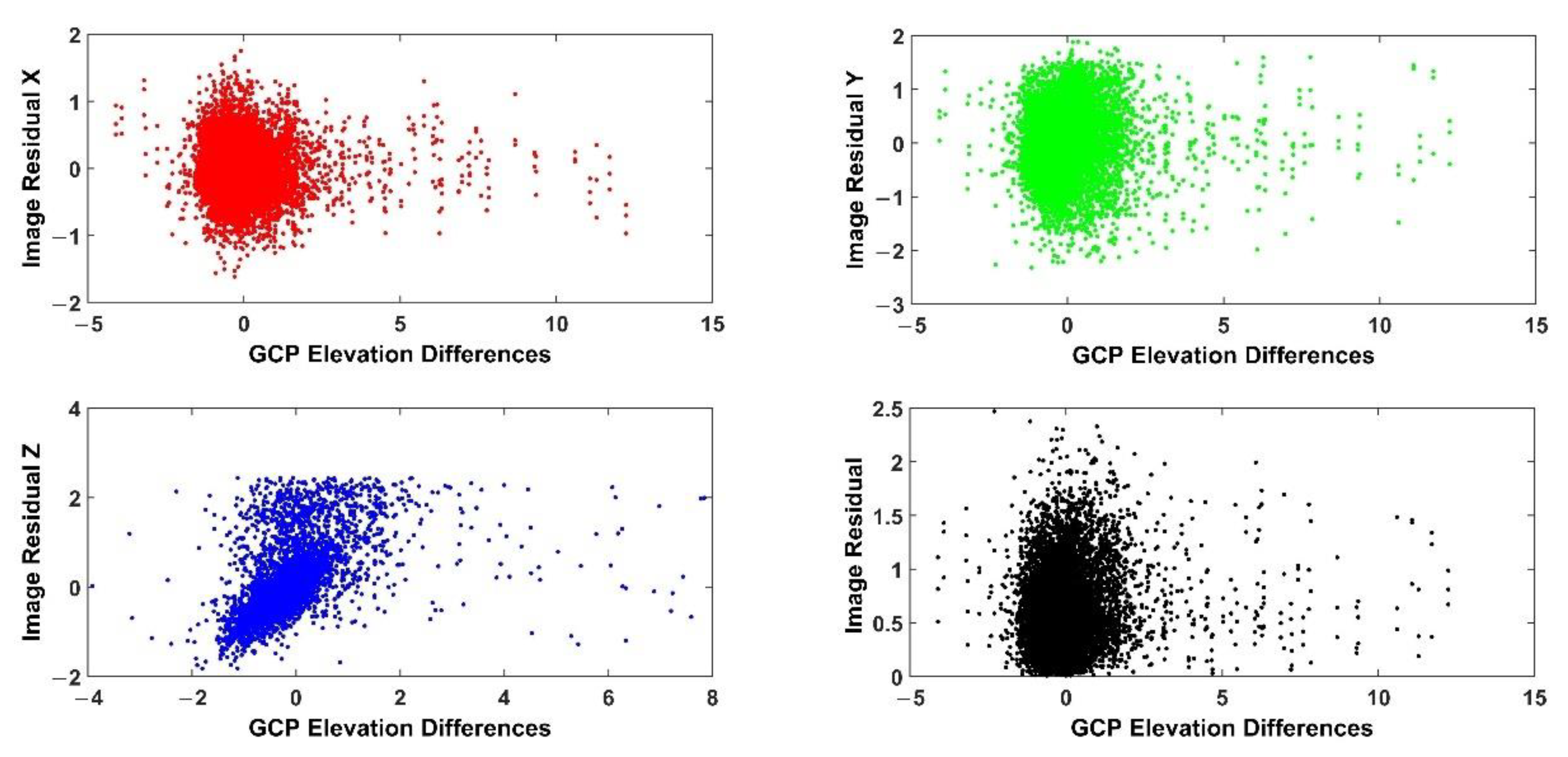
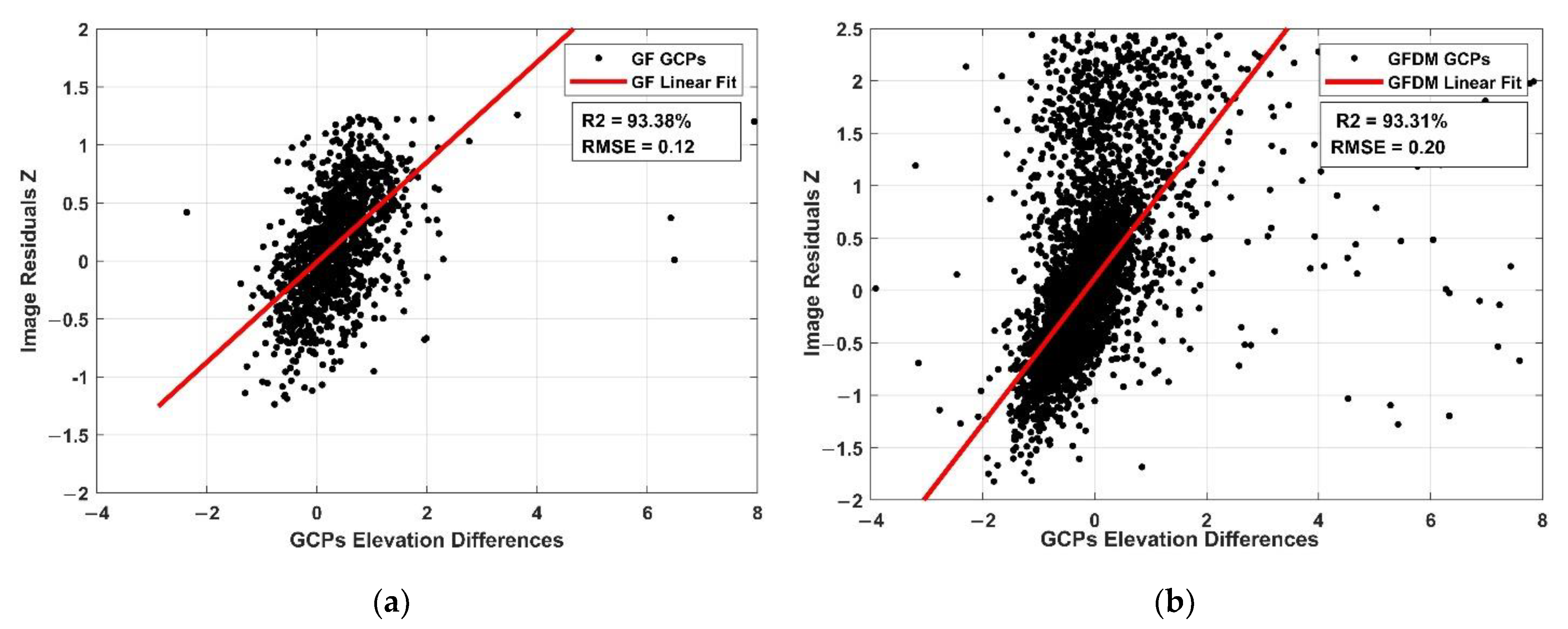
4.4. Coupling Differences between Image Residuals and Vertical Errors
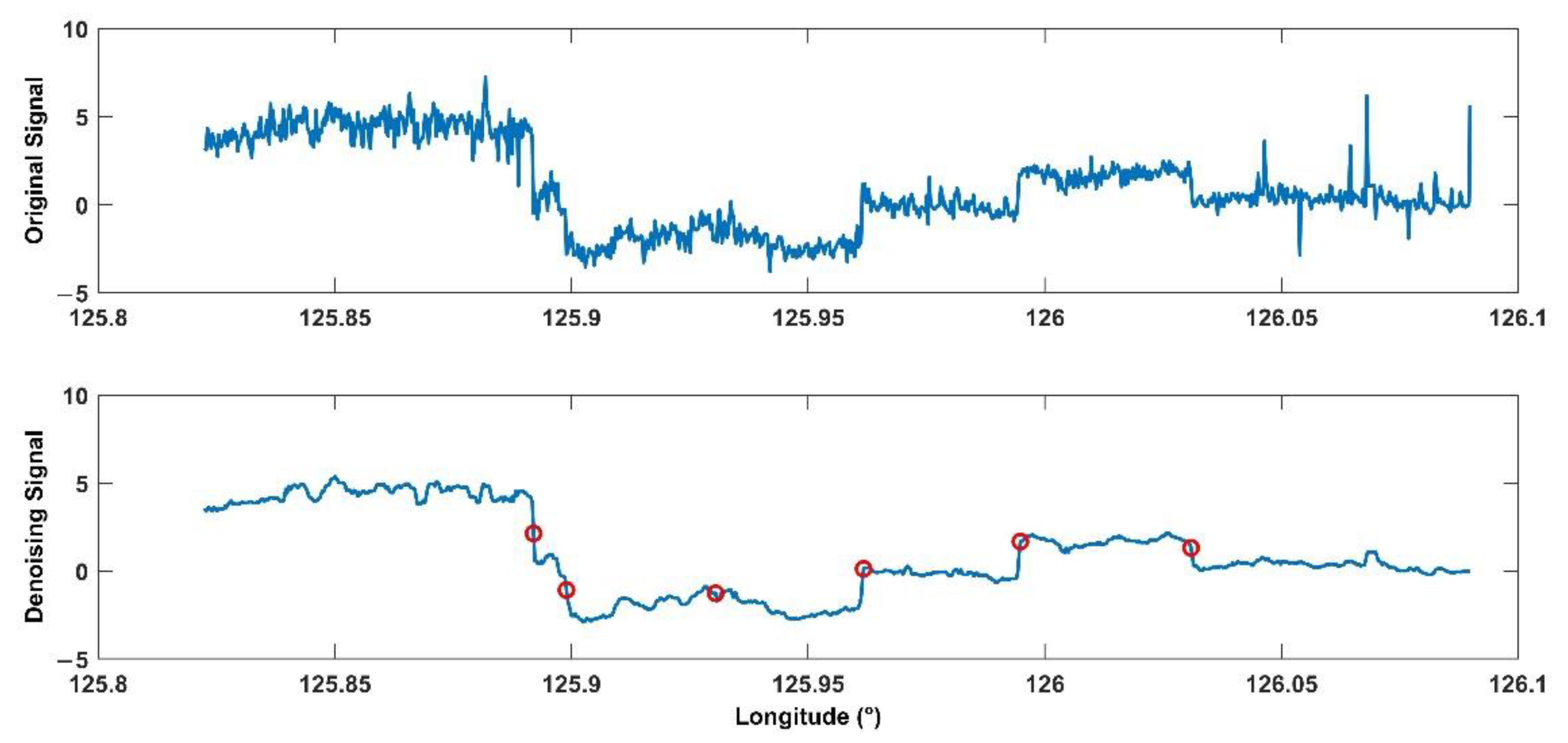
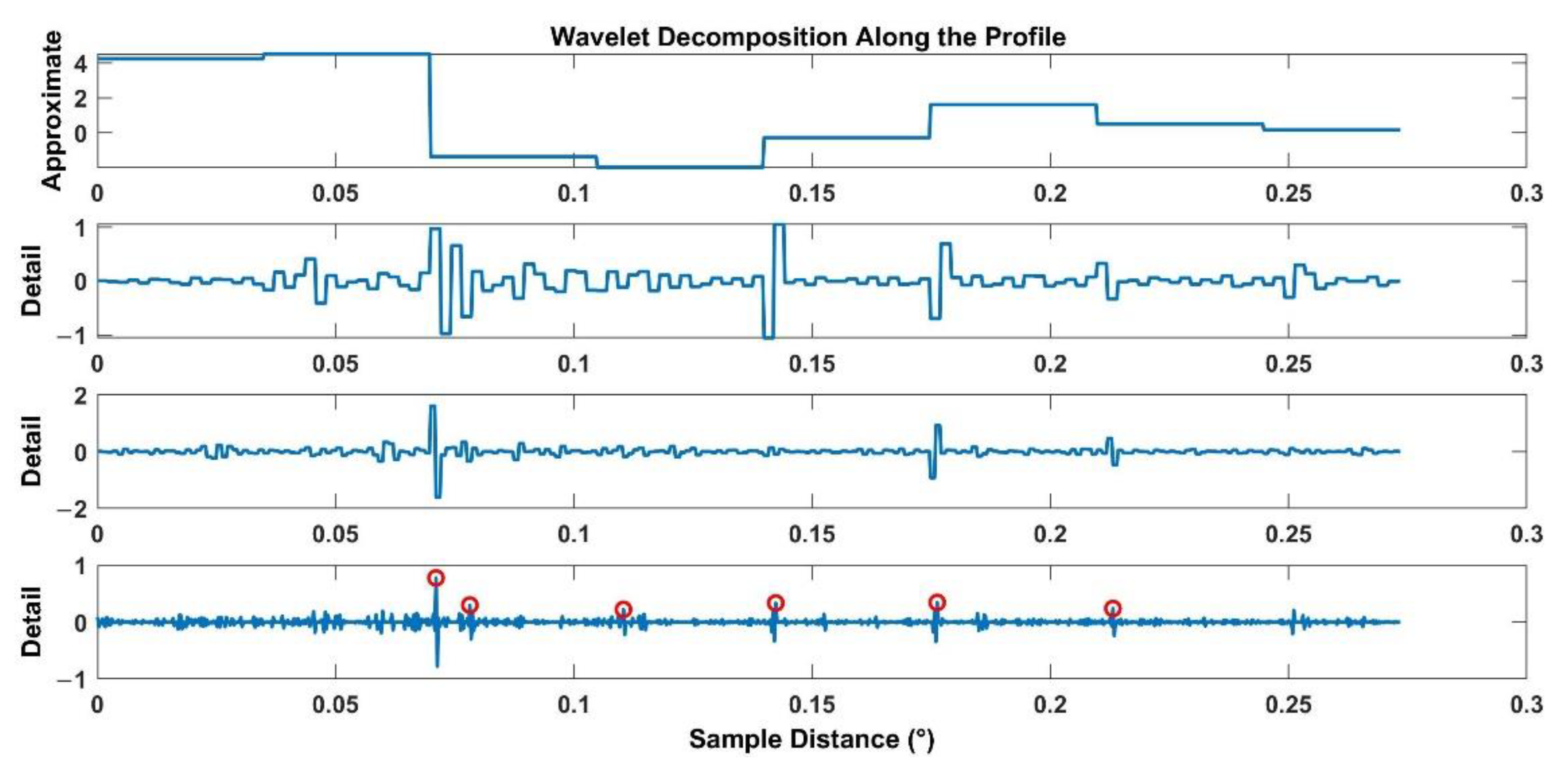
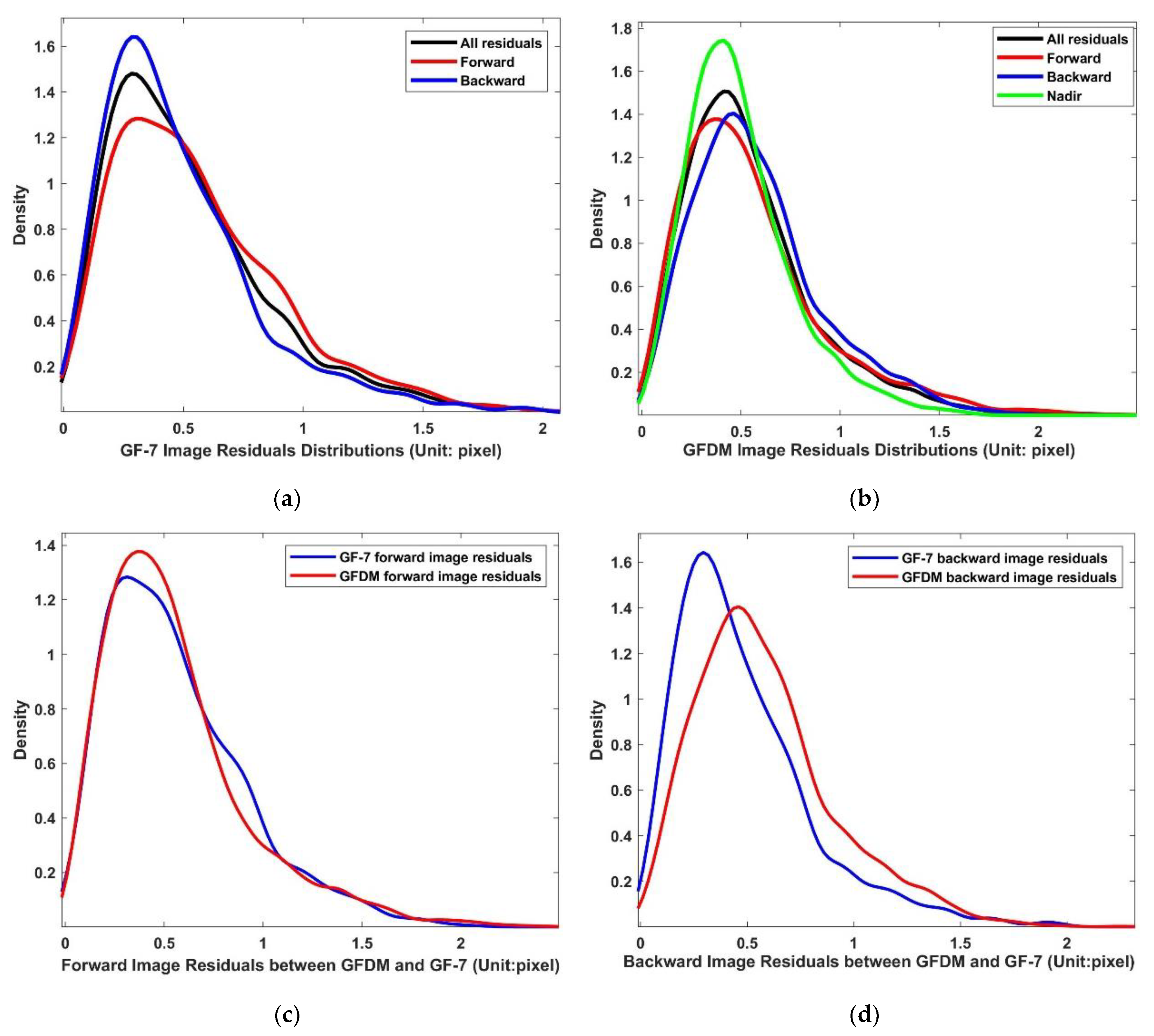
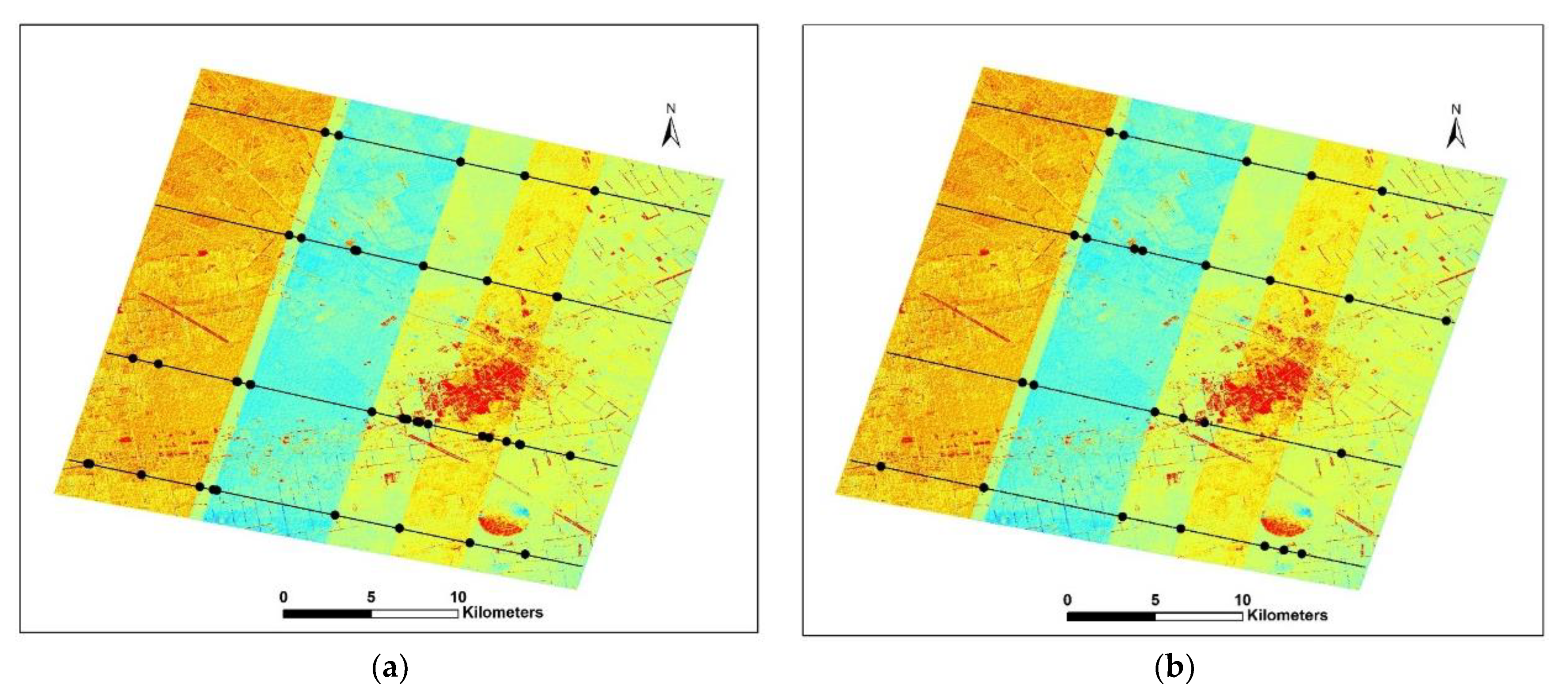
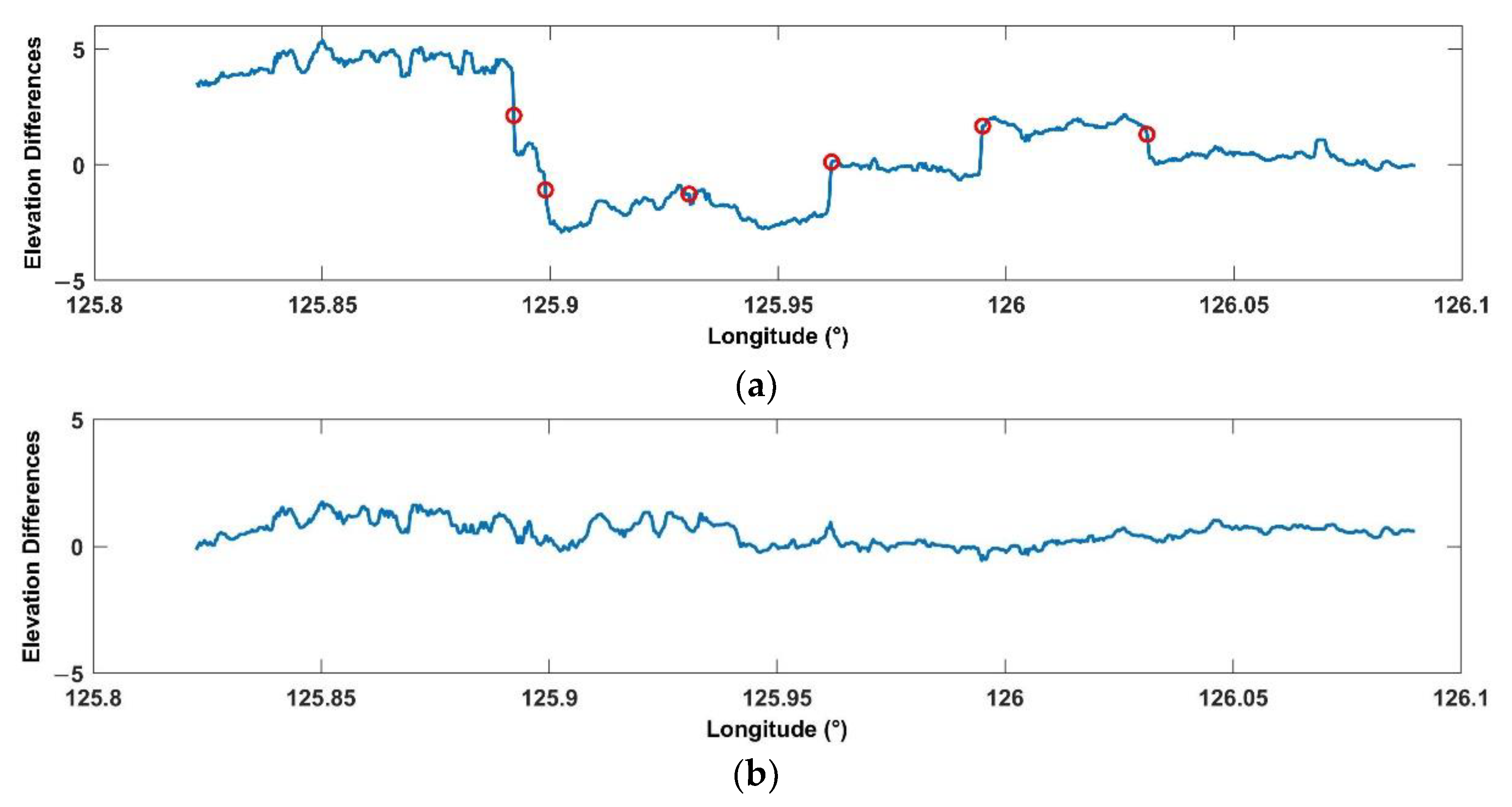
4.5. The Strips Distributions and Differences between GF-7 DSM and GFDM DSM
5. Discussion
5.1. The Factors of Accuracy Differences between the Two DSMs
5.2. The Influence of GCPs on the Accuracy Differences
5.3. The Influence of Data Processing on the Accuracy Differences
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mudd, S.M. Topographic Data from Satellites; Developments in Earth Surface Processes; Elsevier: Amsterdam, The Netherlands, 2020; Volume 23, pp. 91–128. [Google Scholar] [CrossRef]
- Li, D. China’s first civilian three-line-array stereo mapping satellite: ZY-3. Acta Geodaet. Cartograph. Sinica 2012, 41, 317–322. [Google Scholar]
- Gao, X.; Liu, Y.; Li, T.; Wu, D. High Precision DEM Generation Algorithm Based on InSAR Multi-Look Iteration. Remote Sens. 2017, 9, 741. [Google Scholar] [CrossRef] [Green Version]
- Vassilaki, D.I.; Stamos, A.A. TanDEM-X DEM: Comparative performance review employing LIDAR data and DSMs. ISPRS J. Photogramm. Remote Sens. 2020, 160, 33–50. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, Q. Digital Elevation Model; Wuhan University Press: Wuhan, China, 2003. [Google Scholar]
- Tang, G. Digital Terrain Analysis on Loess Plateau of China; Science Press: Beijing, China, 2015. [Google Scholar]
- Rizzoli, P.; Bräutigam, B.; Kraus, T.; Martone, M.; Krieger, G. Relative height error analysis of TanDEM-X elevation data. ISPRS J. Photogramm. Remote Sens. 2012, 73, 30–38. [Google Scholar] [CrossRef] [Green Version]
- Boulton, S.J.; Martin, S. Which DEM Is Best for Analyzing Fluvial Landscape Development in Mountainous Terrains? Geomorphology 2018, 310, 168–187. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, S.; Pu, L.; Yang, J.; Yang, C.; Chen, J.; Guan, C.; Wang, Q.; Chen, D.; Fu, B.; et al. Gully Erosion Mapping and Monitoring at Multiple Scales Based on Multi-Source Remote Sensing Data of the Sancha River Catchment, Northeast China. Int. J. Geo Inf. 2016, 5, 200. [Google Scholar] [CrossRef] [Green Version]
- Frey, H.; Paul, F. International Journal of Applied Earth Observation and Geoinformation On the suitability of the SRTM DEM and ASTER GDEM for the compilation of topographic parameters in glacier inventories. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 480–490. [Google Scholar] [CrossRef]
- Feng, Z.; Shi, D.; Chen, W.; Luo, A. The progress of French remote sensing satellite—From SPOT toward Pleiades. Remote Inf. 2007, 4, 87–92. [Google Scholar]
- Li, D.; Wang, M. A review of high resolution optical satellite surveying and mapping technology. Spacecr. Recov. Remote Sens. 2020, 41, 1–11. [Google Scholar]
- Gong, J. Progress in Data Processing and Analysis of Earth Observation; Wuhan University Press: Wuhan, China, 2007. [Google Scholar]
- Cao, H.; Liu, F.; Zhao, C.; Dai, J. The study of high resolution stereo mapping satellite. Nat. Remote Sens. Bull. 2021, 25, 1400–1410. [Google Scholar]
- Tang, X.; Xie, J.; Zhang, G. Development and status of mapping satellite technology. Spacecr. Recov. Remote Sens. 2012, 33, 17–24. [Google Scholar]
- Tang, X.; Zhang, G.; Zhu, X.; Pan, H.; Jiang, Y.; Zhou, P.; Wang, X.; Guo, L. Triple linear-array imaging geometry model of Ziyuan-3 surveying satellite and its validation. Acta Geod. Cartograph. Sin. 2012, 41, 191–198. [Google Scholar]
- Liu, B.; Sun, X.; Di, K.; Liu, Z. Accuracy analysis and validation of ZY-3′S sensor corrected products. Remote Sens. Land Res. 2012, 24, 36–40. [Google Scholar]
- Zhang, G.; Wang, T.; Li, D.; Tang, X.; Jiang, Y.; Pan, H.; Zhu, X. Block adjustment for ZY-3 satellite standard imagery based on strip constraint. Acta Geod. Cartograph. Sin. 2014, 43, 1158–1164. [Google Scholar]
- Li, G.; Tang, X.; Chen, J.; Yao, J.; Liu, Z.; Gao, X.; Zuo, Z.; Zhou, X. Processing and preliminary accuracy validation of GF-7 satellite laser altimetry data. Acta Geod. Cartograph. Sin. 2021, 50, 1–11. [Google Scholar] [CrossRef]
- Fan, L.; Wang, Y.; Yang, W.; Yu, L.; Zhang, G. GFDM-1 satellite system design and technical characteristics. Spacecr. Eng. 2021, 30, 10–19. [Google Scholar]
- Zhou, Q.; Liu, X. Digital Terrain Analysis; Science Press: Beijing, China, 2006. [Google Scholar]
- Yermolaev, O.; Usmanov, B.; Gafurov, A.; Poesen, J.; Vedeneeva, E.; Lisetskii, F.; Nicu, I.C. Assessment of Shoreline Transformation Rates and Landslide Monitoring on the Bank of Kuibyshev Reservoir (Russia) Using Multi-Source Data. Remote Sens. 2021, 13, 4214. [Google Scholar] [CrossRef]
- Bergstedt, H.; Jones, B.M.; Hinkel, K.; Farquharson, L.; Gaglioti, B.V.; Parsekian, A.D.; Kanevskiy, M.; Ohara, N.; Breen, A.L.; Rangel, R.C.; et al. Remote Sensing-Based Statistical Approach for Defining Drained Lake Basins in a Continuous Permafrost Region, North Slope of Alaska. Remote Sens. 2021, 13, 2539. [Google Scholar] [CrossRef]
- Ali, S.; Liu, D.; Fu, Q.; Cheema, M.J.M.; Pham, Q.B.; Rahaman, M.M.; Dang, T.D.; Anh, D.T. Improving the Resolution of GRACE Data for Spatio-Temporal Groundwater Storage Assessment. Remote Sens. 2021, 13, 3513. [Google Scholar] [CrossRef]
- Panagiotakis, E.; Chrysoulakis, N.; Charalampopoulou, V.; Poursanidis, D. Validation of Pleiades Tri-Stereo DSM in Urban Areas. Int. J. Geo Inf. 2018, 7, 118. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Shi, C.; Li, Z.; Muller, J.P.; Drummond, J.; Li, X.; Li, T.; Li, Y.; Liu, J. Evaluation of ASTER GDEM using GPS benchmarks and SRTM in China. Int. J. Remote Sens. 2013, 34, 1744–1771. [Google Scholar] [CrossRef]
- Courty, L.G.; Soriano-Monzalvo, J.C.; Pedrozo-Acua, A. Evaluation of open-access global digital elevation models (AW3D30, SRTM and ASTER) for flood modelling purposes. J. Flood Risk Manage. 2019, 12, e12550. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhu, J.; Fu, H.; Zhou, C.; Zuo, T. Evaluation of the Vertical Accuracy of Open Global DEMs over Steep Terrain Regions Using ICESat Data: A Case Study over Hunan Province, China. Sensors 2020, 20, 4865. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.; Al, A.; Barbara, M.; Pawan, K. An evaluation of available digital elevation models (DEMs) for geomorphological feature analysis. Environ. Earth Sci. 2020, 79, 1–11. [Google Scholar] [CrossRef]
- Grohmann, C.H. Evaluation of TanDEM-X DEMs on selected Brazilian sites: Comparison with SRTM, ASTER GDEM and ALOS AW3D30. Remote Sens Environ. 2018, 212, 121–133. [Google Scholar] [CrossRef] [Green Version]
- Novak, A.; Oštir, K. Towards Better Visualisation of Alpine Quaternary Landform Features on High-Resolution Digital Elevation Models. Remote Sens. 2021, 13, 4211. [Google Scholar] [CrossRef]
- Grodecki, J.; Dial, G. Block adjustment of high-resolution satellite images described by Rational Polynomials. Photogramm Eng Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
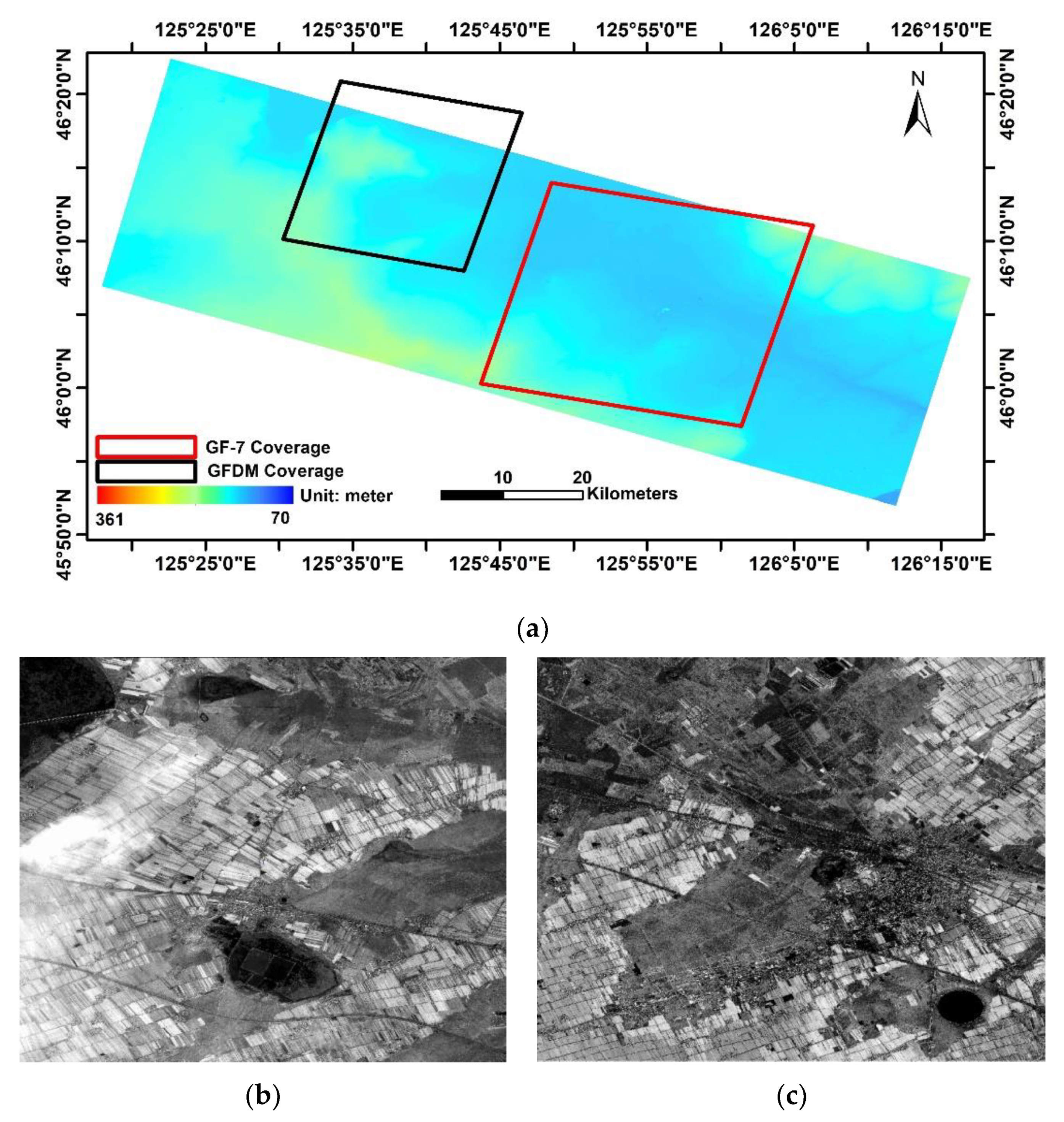



| Satellite Name | Acquired Time | Image Resolution (m) | Central Latitude and Longitude | Observation Angle | Intersection Angle (degree) | Base–Height Ratio |
|---|---|---|---|---|---|---|
| GFDM | 15 November 2020 | 0.42 | E125.6_N46.2 | ~−25° (Forward) ~+25° (backward) | 52.454 | 0.608 |
| GF-7 | 11 November 2020 | 0.8 (Forward) 0.65 (backward) | E125.9_N46.1 | −26° (Forward) +5° (backward) | 33.8 | 0.985 |
| DSM (Unit: m) | Minimum | Maximum | Average | RMS | |
|---|---|---|---|---|---|
| Before outliers | GF-7 DSM | −326.67 | 140.36 | 1.23 | 3.51 |
| GFDM DSM | −340.54 | 96.28 | 0.21 | 2.49 | |
| After outliers | GF-7 DSM | −11.22 | 14.06 | 1.00 | 1.90 |
| GFDM DSM | −7.26 | 7.68 | −0.03 | 1.21 | |
| GCPs | DSM (Unit: m) | Minimum | Maximum | Average | RMS |
|---|---|---|---|---|---|
| Horizontal-X | GF-7 DSM | −1.78 | 2.23 | −0.0017 | 0.53 |
| GFDM DSM | −2.56 | 2.34 | −0.0007 | 0.52 | |
| Horizontal-Y | GF-7 DSM | −2.00 | 1.89 | −0.0012 | 0.51 |
| GFDM DSM | −1.89 | 2.34 | −0.0006 | 0.53 | |
| Vertical errors | GF-7 DSM | −2.36 | 7.94 | 0.35 | 0.67 |
| GFDM DSM | −4.10 | 12.23 | −0.10 | 0.94 |
| GCPs Image Coordinates | DSM (Unit: m) | Minimum | Maximum | Average | RMS |
|---|---|---|---|---|---|
| Image residuals in X | GF-7 DSM | −1.53 | 1.28 | 0.0002 | 0.37 |
| GFDM DSM | −1.61 | 1.75 | 0 | 0.36 | |
| Image residuals in Y | GF-7 DSM | −1.87 | 1.94 | −0.0002 | 0.50 |
| GFDM DSM | −2.32 | 1.89 | 0 | 0.53 | |
| Image residuals in Z | GF-7 DSM | −1.24 | 1.27 | 0.13 | 0.47 |
| GFDM DSM | −2.28 | 2.44 | 0.14 | 0.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Tang, X.; Zhang, G.; Liu, B.; Hu, W. Accuracy Comparison and Assessment of DSM Derived from GFDM Satellite and GF-7 Satellite Imagery. Remote Sens. 2021, 13, 4791. https://doi.org/10.3390/rs13234791
Zhu X, Tang X, Zhang G, Liu B, Hu W. Accuracy Comparison and Assessment of DSM Derived from GFDM Satellite and GF-7 Satellite Imagery. Remote Sensing. 2021; 13(23):4791. https://doi.org/10.3390/rs13234791
Chicago/Turabian StyleZhu, Xiaoyong, Xinming Tang, Guo Zhang, Bin Liu, and Wenmin Hu. 2021. "Accuracy Comparison and Assessment of DSM Derived from GFDM Satellite and GF-7 Satellite Imagery" Remote Sensing 13, no. 23: 4791. https://doi.org/10.3390/rs13234791