Application of Seismic Interferometry by Multidimensional Deconvolution to Earthquake Data Recorded in Malargüe, Argentina
Abstract
1. Introduction
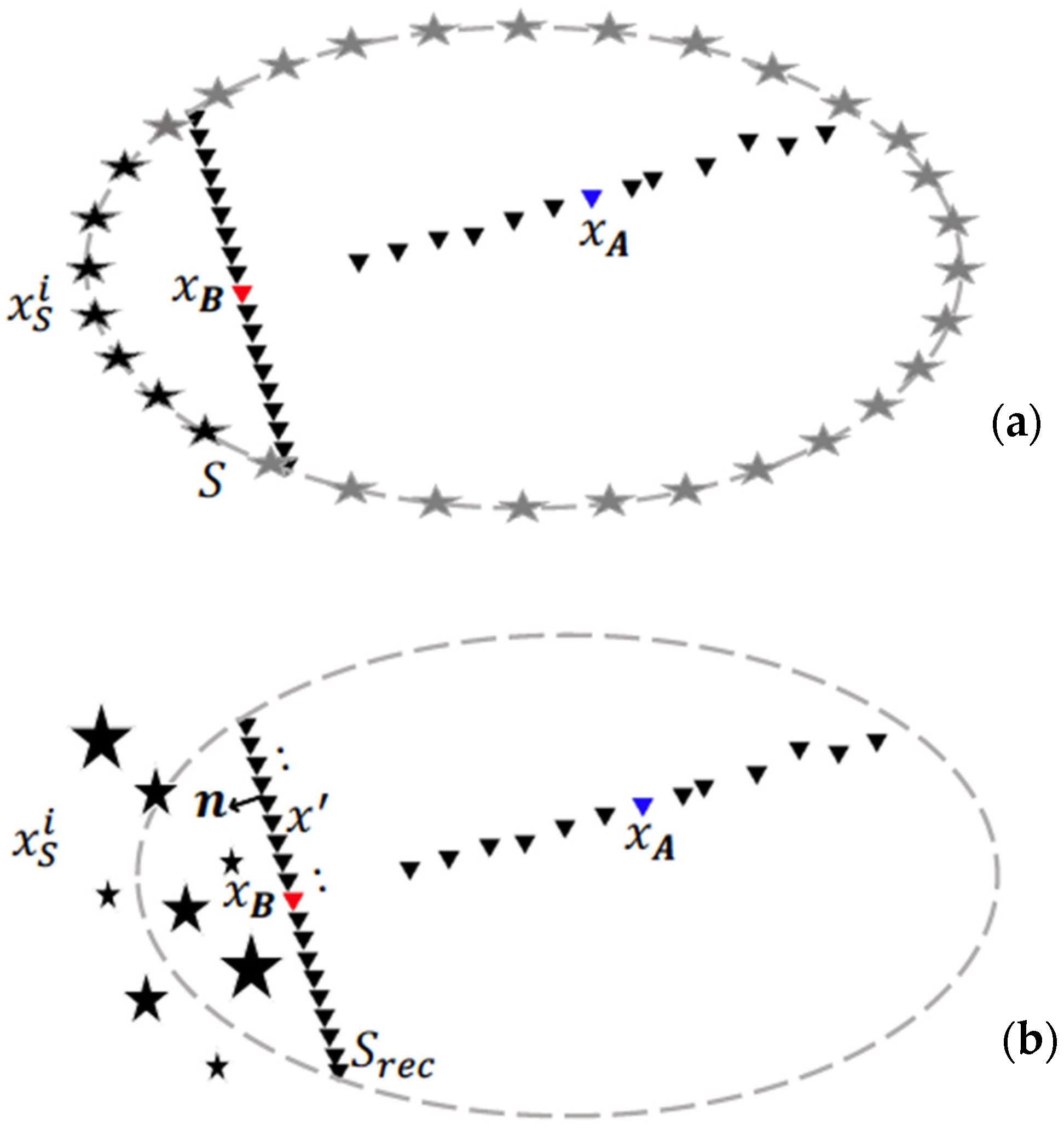
2. Method
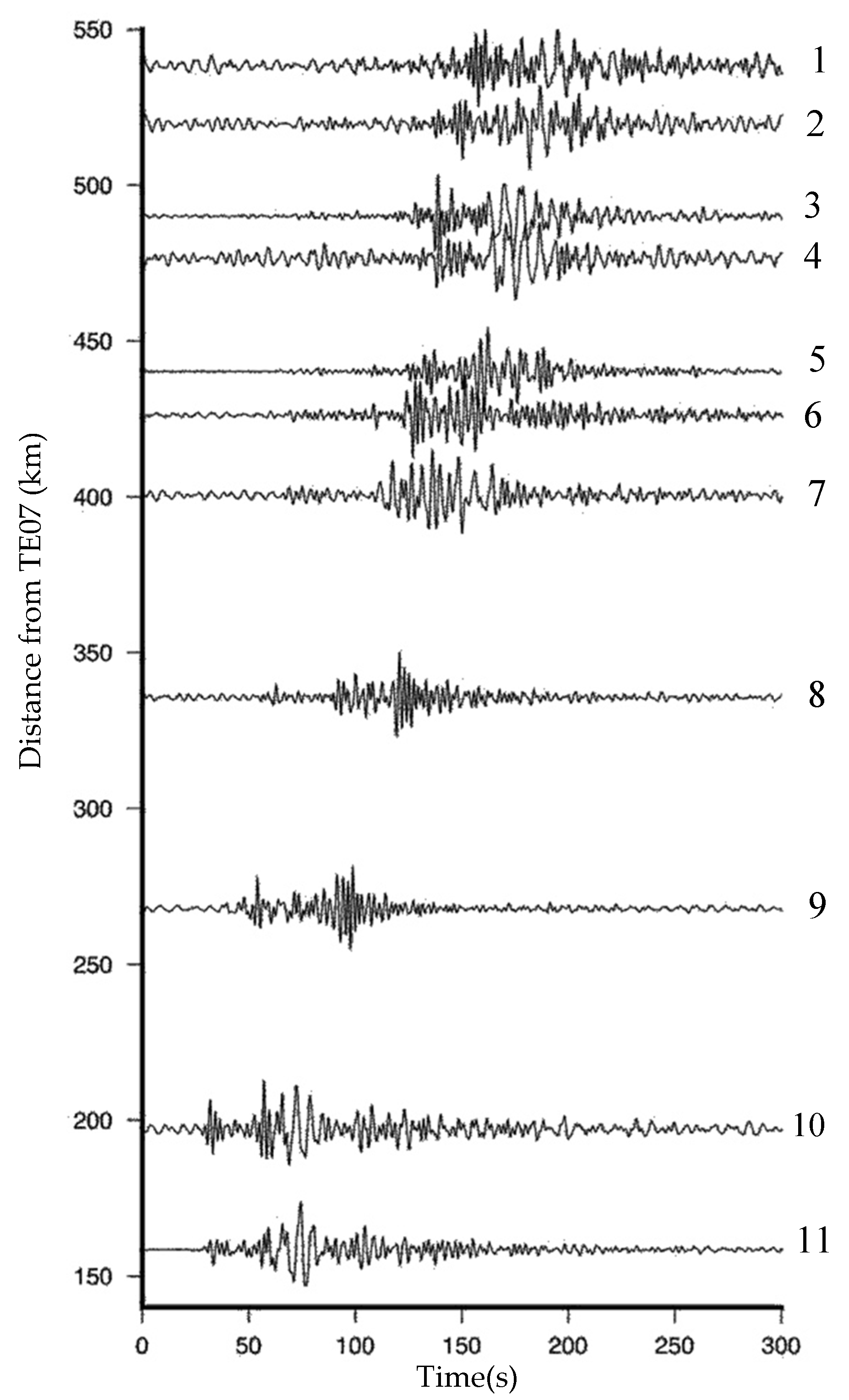
3. MalARRgüe
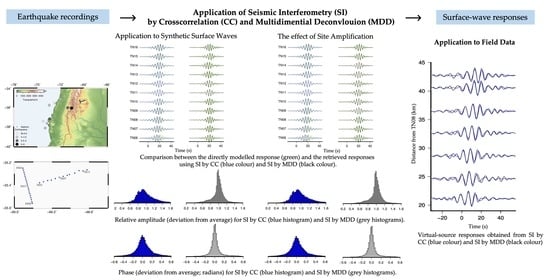
4. Application to Data and Results
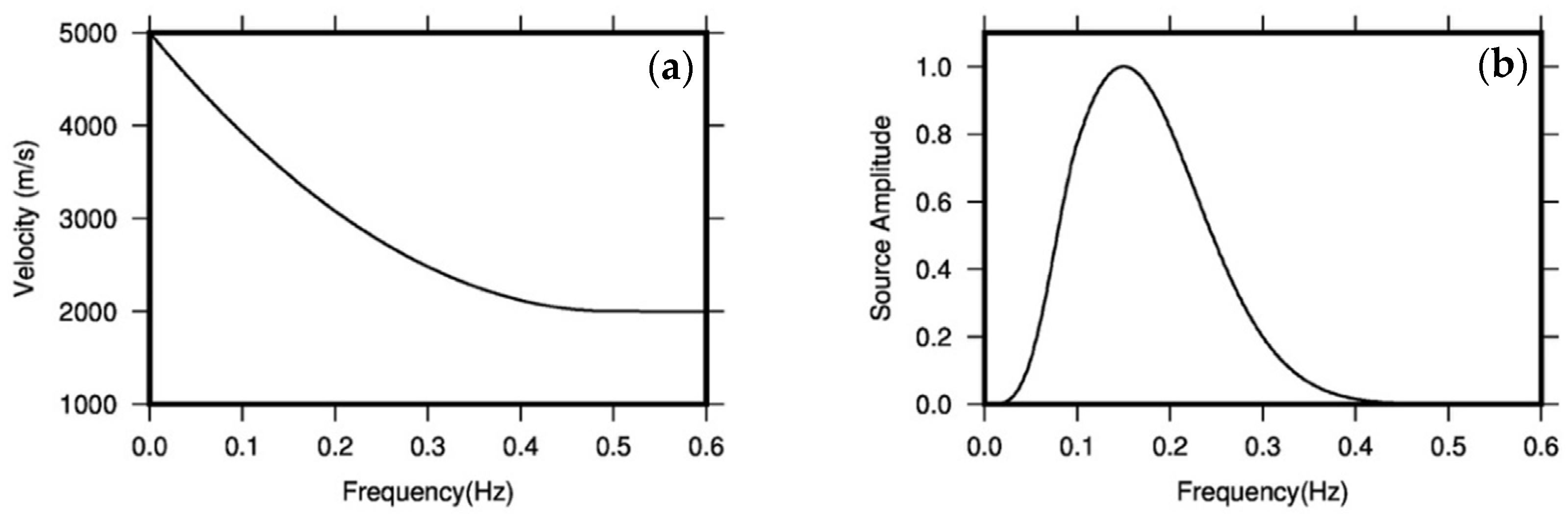
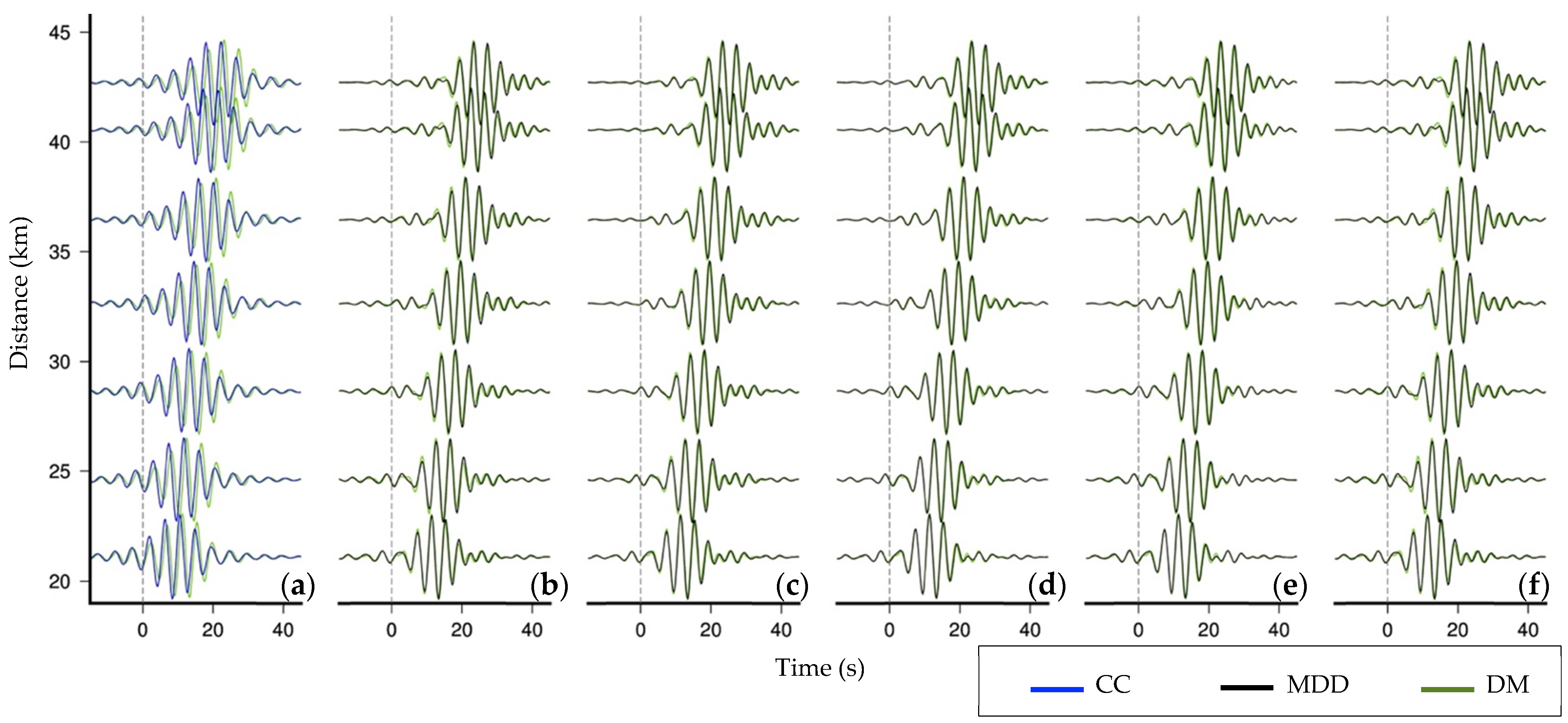
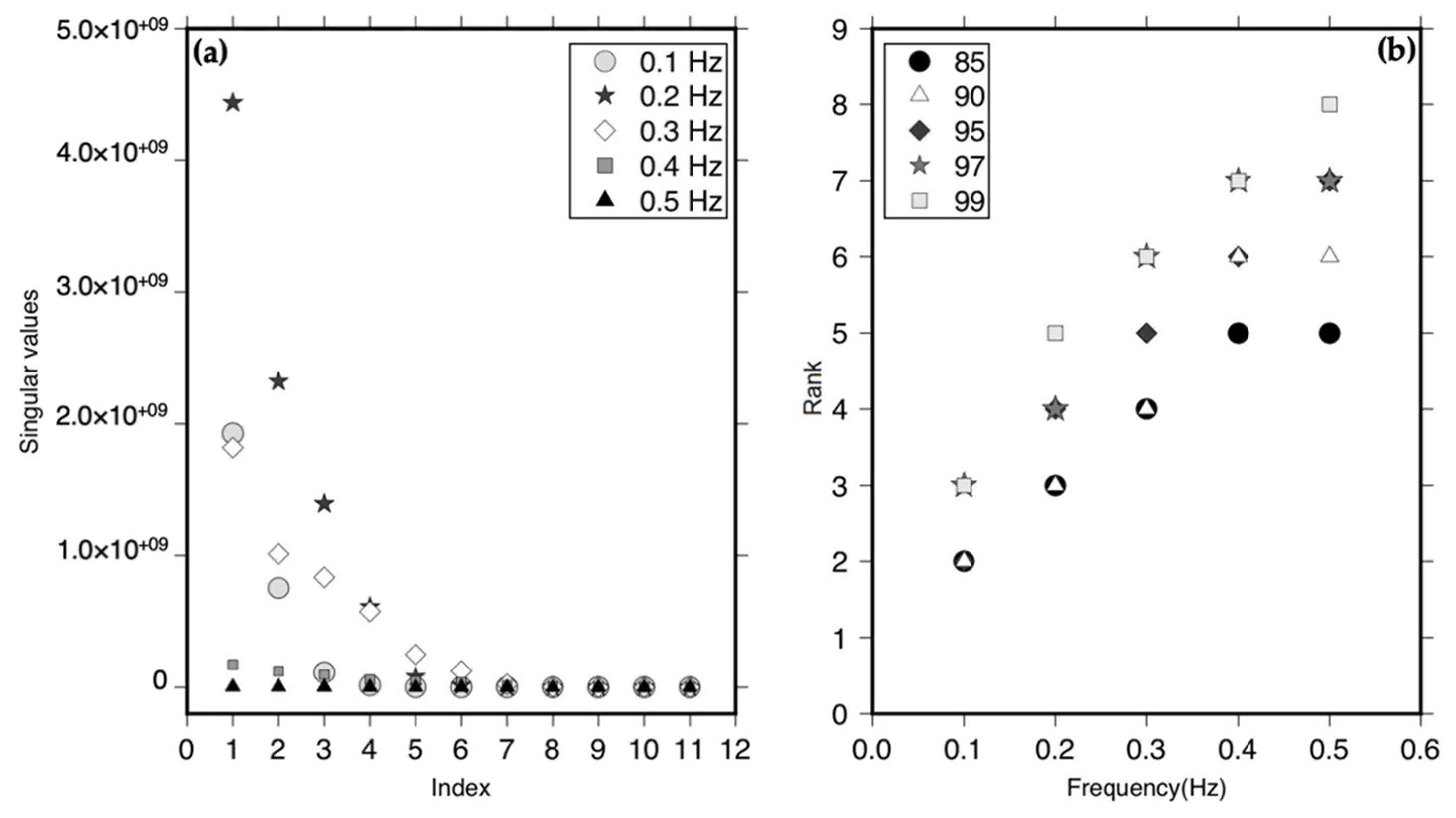
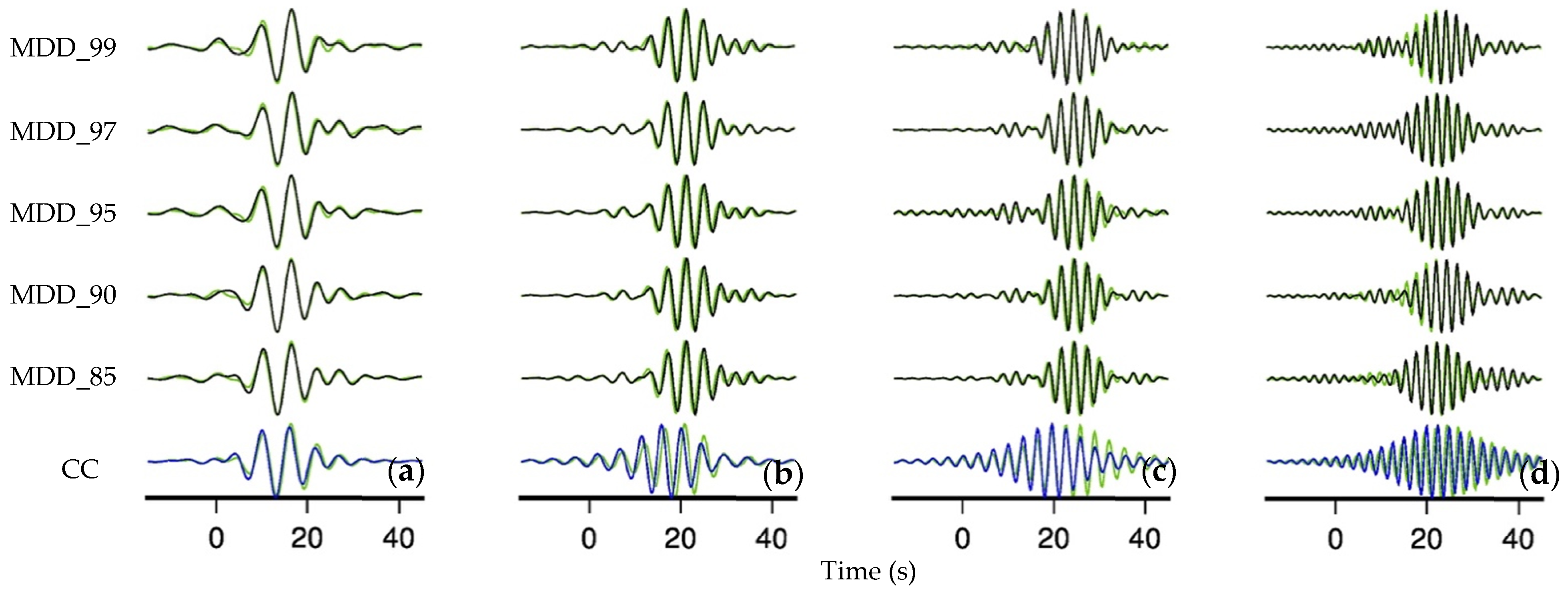
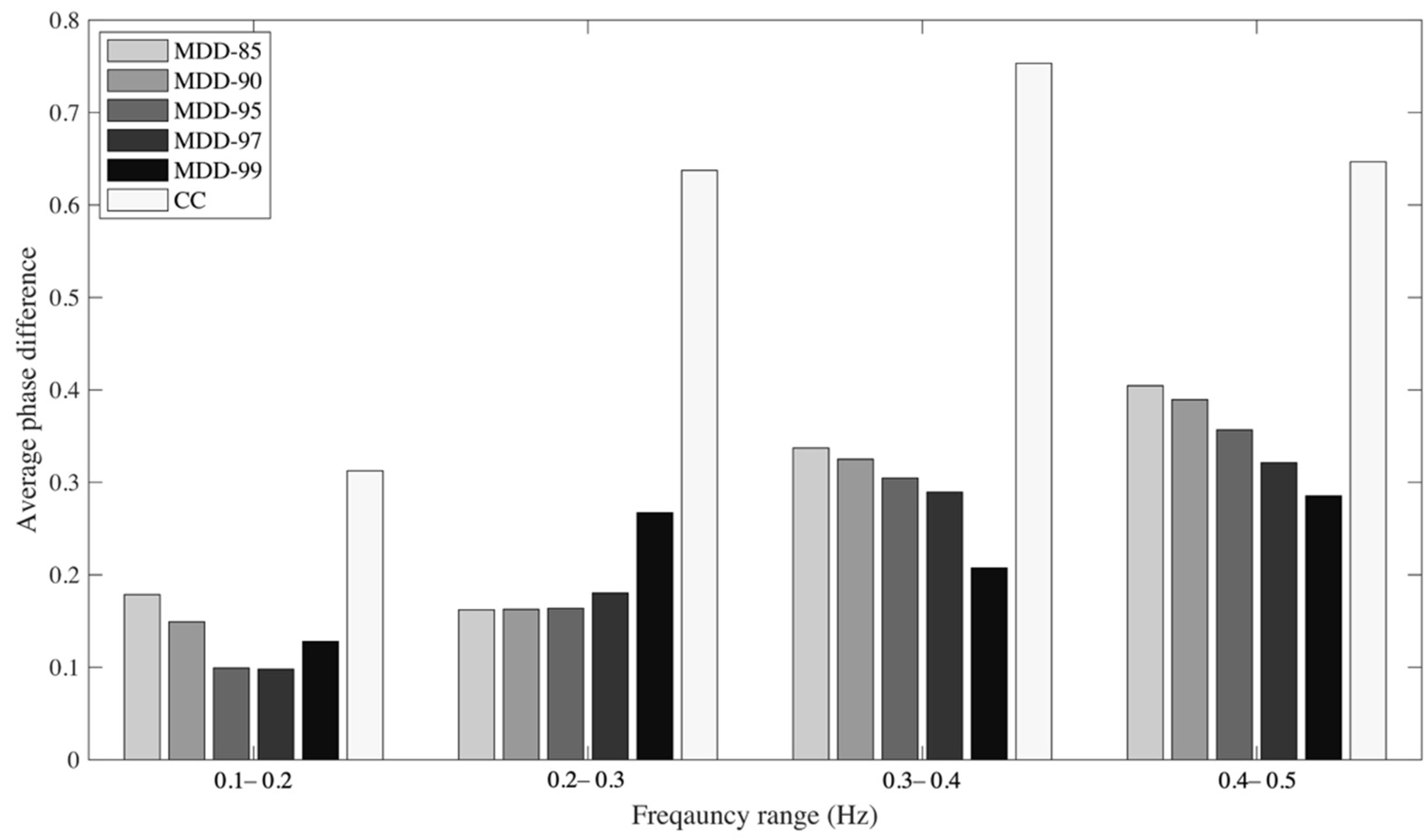
4.1. Application to Synthetic Surface Waves
4.2. The Effect of Site Amplification
4.3. Application to Field Data from Earthquake-Generated Surface Waves
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shapiro, N.M.; Campillo, M. Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Wapenaar, K.; Fokkema, J. Green’s function representations for seismic interferometry. Geophysics 2006, 71, SI33–SI46. [Google Scholar] [CrossRef]
- Campillo, M.; Paul, A. Long-Range Correlations in the Diffuse Seismic Coda. Science 2003, 299, 547–549. [Google Scholar] [CrossRef] [PubMed]
- Roux, P.; Sabra, K.G.; Gerstoft, P.; Kuperman, W.A.; Fehler, M.C. P-waves from cross-correlation of seismic noise. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Draganov, D.; Campman, X.; Thorbecke, J.; Verdel, A.; Wapenaar, K. Reflection images from ambient seismic noise. Geophysics 2009, 74, A63–A67. [Google Scholar] [CrossRef]
- Weemstra, C.; Draganov, D.; Ruigrok, E.; Hunziker, J.; Gomez, M.; Wapenaar, K. Application of seismic interferometry by multidimensional deconvolution to ambient seismic noise recorded in Malargüe, Argentina. Geophys. J. Int. 2016, 208, 693–714. [Google Scholar] [CrossRef][Green Version]
- Ruigrok, E.; Campman, X.; Draganov, D.; Wapenaar, K. High-resolution lithospheric imaging with seismic interferometry. Geophys. J. Int. 2010, 183, 339–357. [Google Scholar] [CrossRef]
- Bakulin, A.; Calvert, R. The virtual source method: Theory and case study. Geophysics 2006, 71, SI139–SI150. [Google Scholar] [CrossRef]
- Draganov, D.; Wapenaar, K.; Thorbecke, J.; Nishizawa, O. Retrieving reflection responses by crosscorrelating transmission responses from deterministic transient sources: Application to ultrasonic data. J. Acoust. Soc. Am. 2007, 122, EL172–EL178. [Google Scholar] [CrossRef]
- Lindner, F.; Weemstra, C.; Walter, F.; Hadziioannou, C. Towards monitoring the englacial fracture state using virtual-reflector seismology. Geophys. J. Int. 2018, 214, 825–844. [Google Scholar] [CrossRef]
- Louie, J. Faster, Better: Shear-Wave Velocity to 100 Meters Depth from Refraction Microtremor Arrays. Bull. Seism. Soc. Am. 2001, 91, 347–364. [Google Scholar] [CrossRef]
- Chávez-García, F.J.; Luzón, F. On the correlation of seismic microtremors. J. Geophys. Res. Space Phys. 2005, 110, 11. [Google Scholar] [CrossRef]
- Zhang, X.; Hansteen, F.; Curtis, A.; De Ridder, S. 1-D, 2-D, and 3-D Monte Carlo Ambient Noise Tomography Using a Dense Passive Seismic Array Installed on the North Sea Seabed. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018552. [Google Scholar] [CrossRef]
- Bommer, J.J.; Dost, B.; Edwards, B.; Kruiver, P.P.; Ntinalexis, M.; Rodriguez-Marek, A.; Stafford, P.J.; van Elk, J. Developing a model for the prediction of ground motions due to earthquakes in the Groningen gas field. Neth. J. Geosci. 2017, 96, s203–s213. [Google Scholar] [CrossRef]
- Olsen, K.B.; Akinci, A.; Rovelli, A.; Marra, F.; Malagnini, L. 3D Ground-Motion Estimation in Rome, Italy. Bull. Seism. Soc. Am. 2006, 96, 133–146. [Google Scholar] [CrossRef]
- Wapenaar, K.; van der Neut, J.; Ruigrok, E.; Draganov, D.; Hunziker, J.; Slob, E.; Thorbecke, J.; Snieder, R. Seismic interfer-ometry by crosscorrelation and by multidimensional deconvolution: A systematic comparison. Geophys. J. Int. 2011, 185, 1335–1364. [Google Scholar] [CrossRef]
- Slob, E.; Wapenaar, K. Electromagnetic Green’s functions retrieval by cross-correlation and cross-convolution in media with losses. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Slob, E.; Draganov, D.; Wapenaar, K. Interferometric electromagnetic Green’s functions representations using propagation invariants. Geophys. J. Int. 2007, 169, 60–80. [Google Scholar] [CrossRef]
- Vasconcelos, I.; Snieder, R. Interferometry by deconvolution: Part 2—Theory for elastic waves and application to drill-bit seismic imaging. Geophysics 2008, 73, S129–S141. [Google Scholar] [CrossRef]
- Wapenaar, K.; Van Der Neut, J.; Ruigrok, E. Passive seismic interferometry by multidimensional deconvolution. Geophysics 2008, 73, A51–A56. [Google Scholar] [CrossRef][Green Version]
- Wapenaar, K.; van der Neut, J. A representation for Green’s function retrieval by multidimensional deconvolution. J. Acoust. Soc. Am. 2010, 128, EL366–EL371. [Google Scholar] [CrossRef] [PubMed]
- Minato, S.; Matsuoka, T.; Tsuji, T.; Draganov, D.; Hunziker, J.; Wapenaar, K. Seismic interferometry using multidimensional deconvolution and crosscorrelation for crosswell seismic reflection data without borehole sources. Geophysics 2011, 76, SA19–SA34. [Google Scholar] [CrossRef]
- van Dalen, K.N.; Wapenaar, K.; Halliday, D.F. Surface wave retrieval in layered media using seismic interferometry by mul-tidimensional deconvolution. Geophys. J. Int. 2013, 196, 230–242. [Google Scholar] [CrossRef][Green Version]
- Hartstra, I.E.; Almagro Vidal, C.; Wapenaar, K. Full-field multidimensional deconvolution to retrieve body-wave reflections from sparse passive sources. Geoph. J. Int. 2017, 210, 609–620. [Google Scholar] [CrossRef]
- Draganov, D.; Hunziker, J.; Heller, K.; Gutkowski, K.; Marte, F. High-Resolution Ultrasonic Imaging of Artworks with Seismic Interferometry for Their Conservation and Restoration. Stud. Conserv. 2018, 63, 277–291. [Google Scholar] [CrossRef]
- Minato, S.; Matsuoka, T.; Tsuji, T. Singular-value decomposition analysis of source illumination in seismic interferometry by multidimensional deconvolution. Geophysics 2013, 78, Q25–Q34. [Google Scholar] [CrossRef][Green Version]
- Ruigrok, E.; Draganov, D.; Gómez, M.; E Ruzzante, J.; Torres, D.F.; Pumarega, I.L.; Barbero, N.; Ramires, A.; Gañan, A.R.C.; van Wijk, K.; et al. Malargüe seismic array: Design and deployment of the temporary array. Eur. Phys. J. Plus 2012, 127, 126. [Google Scholar] [CrossRef]
- Nishitsuji, Y.; Ruigrok, E.; Gòmez, M.; Draganov, D. Global-phase H/V spectral ratio for imaging the basin in the Malargüe region, Argentina. Seism. Res. Lett. 2014, 8, 1004–1011. [Google Scholar] [CrossRef]
- Nishitsuji, Y.; Marin, L.E.F.; Gomez, M.; Rowe, C.; Draganov, D. Tectonic tremor characterized by principal-component analysis in the vicinity of central Chile and Argentina. J. South Am. Earth Sci. 2019, 94, 102178. [Google Scholar] [CrossRef]
- Nishitsuji, Y.; Ruigrok, E.; Gomez, M.; Wapenaar, K.; Draganov, D. Reflection imaging of aseismic zones of the Nazca slab by global-phase seismic interferometry. Interpretation 2016, 4, SJ1–SJ16. [Google Scholar] [CrossRef]
- Nishitsuji, Y.; Minato, S.; Boullenger, B.; Gòmez, M.; Wapenaar, K.; Draganov, D. Crustal-scale reflection imaging and inter-pretation by passive seismic interferometry using local earthquakes. Interpretation 2016, 4, SJ29–SJ53. [Google Scholar] [CrossRef]
- Casas, J.A.; Draganov, D.; Badi, G.A.; Manassero, M.C.; Olivera Craig, V.H.; Franco Marín, L.; Gómez, M.; Ruigrok, E. Seismic interferometry applied to fracture seismicity recorded at Planchón-Peteroa Volcanic Complex, Argentina-Chile. J. South Am. Earth Sci. 2019, 92, 134–144. [Google Scholar] [CrossRef]
- Casas, J.A.; Badi, G.A.; Franco, L.; Draganov, D. Seismic interferometry applied to regional and teleseismic events recorded at Planchón-Peteroa Volcanic Complex, Argentina-Chile. J. Volcanol. Geotherm. Res. 2020, 393, 106805. [Google Scholar] [CrossRef]
- Casas, J.A.; Mikesell, T.D.; Draganov, D.; Lepore, S.; Badi, G.A.; Franco, L.; Gomez, M. Shallow S-Wave Velocity Structure from Ambient Seismic Noise at Planchón-Peteroa Volcanic Complex, Argentina-Chile. Bull. Seism. Soc. Am. 2018, 108, 2183–2198. [Google Scholar]
- Aki, K.; Richards, P.G. Quantitative Seismology, 2nd ed.; University Science Books: Sausalito, CA, USA, 2002; p. 700. [Google Scholar]
- Weemstra, C.; Boschi, L.; Goertz, A.; Artman, B. Seismic attenuation from recordings of ambient noise. Geophysics 2013, 78, Q1–Q14. [Google Scholar] [CrossRef]
- Weemstra, C.; Wapenaar, K.; Dalen, K.N.V. Reflecting boundary conditions for interferometry by multidimensional decon-volution. J. Acoust. Soc. Am. 2017, 142, 2242–2257. [Google Scholar] [CrossRef] [PubMed]
- Wapenaar, K.; Ruigrok, E.; Van Der Neut, J.; Draganov, D. Improved surface-wave retrieval from ambient seismic noise by multi-dimensional deconvolution. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef][Green Version]
- Tsai, V.C. Understanding the amplitudes of noise correlation measurements. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Paolucci, R.; Mazzieri, I.; Piunno, G.; Smerzini, C.; Vanini, M.; Özcebe, A. Earthquake ground motion modeling of induced seismicity in the Groningen gas field. Earthq. Eng. Struct. Dyn. 2021, 50, 135–154. [Google Scholar] [CrossRef]
- Efron, B. The Jackknife, the Bootstrap, and other Resampling Plans; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1982. [Google Scholar]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap Method; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools Version 6. Geochem. Geophys. Geosystems 2019, 20, 5556–5564. [Google Scholar] [CrossRef]


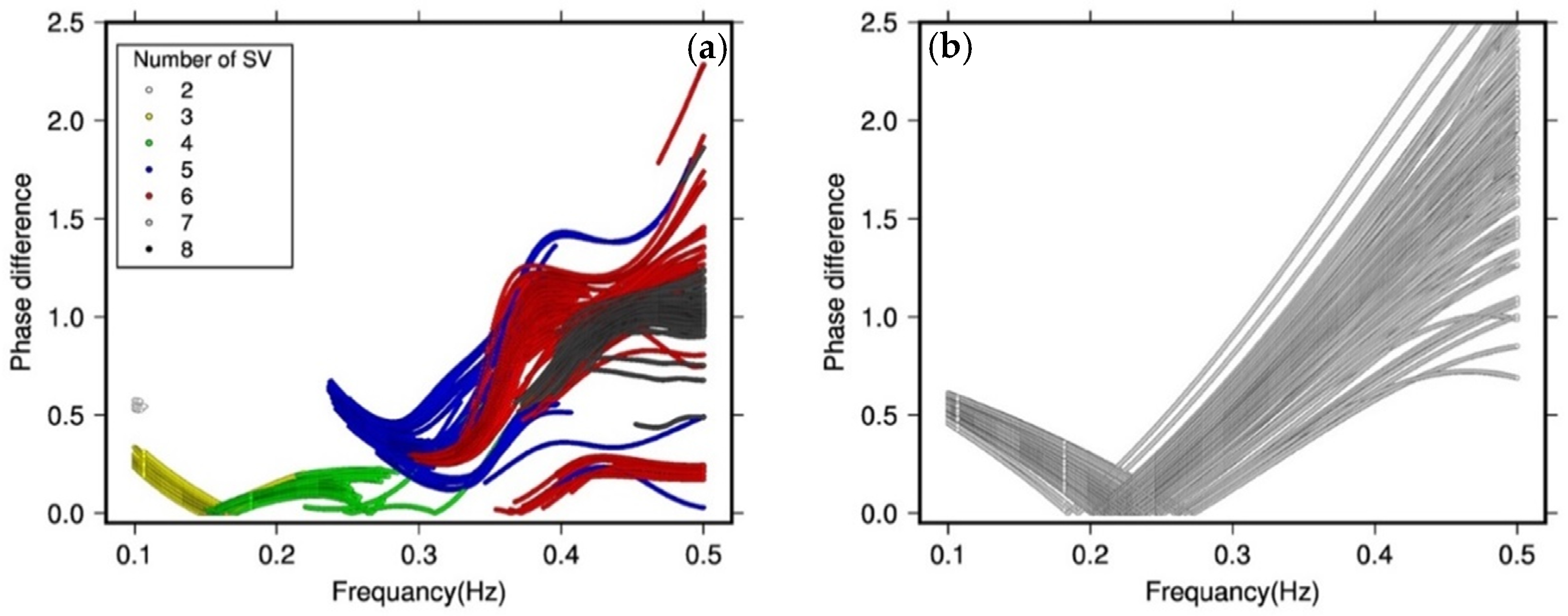
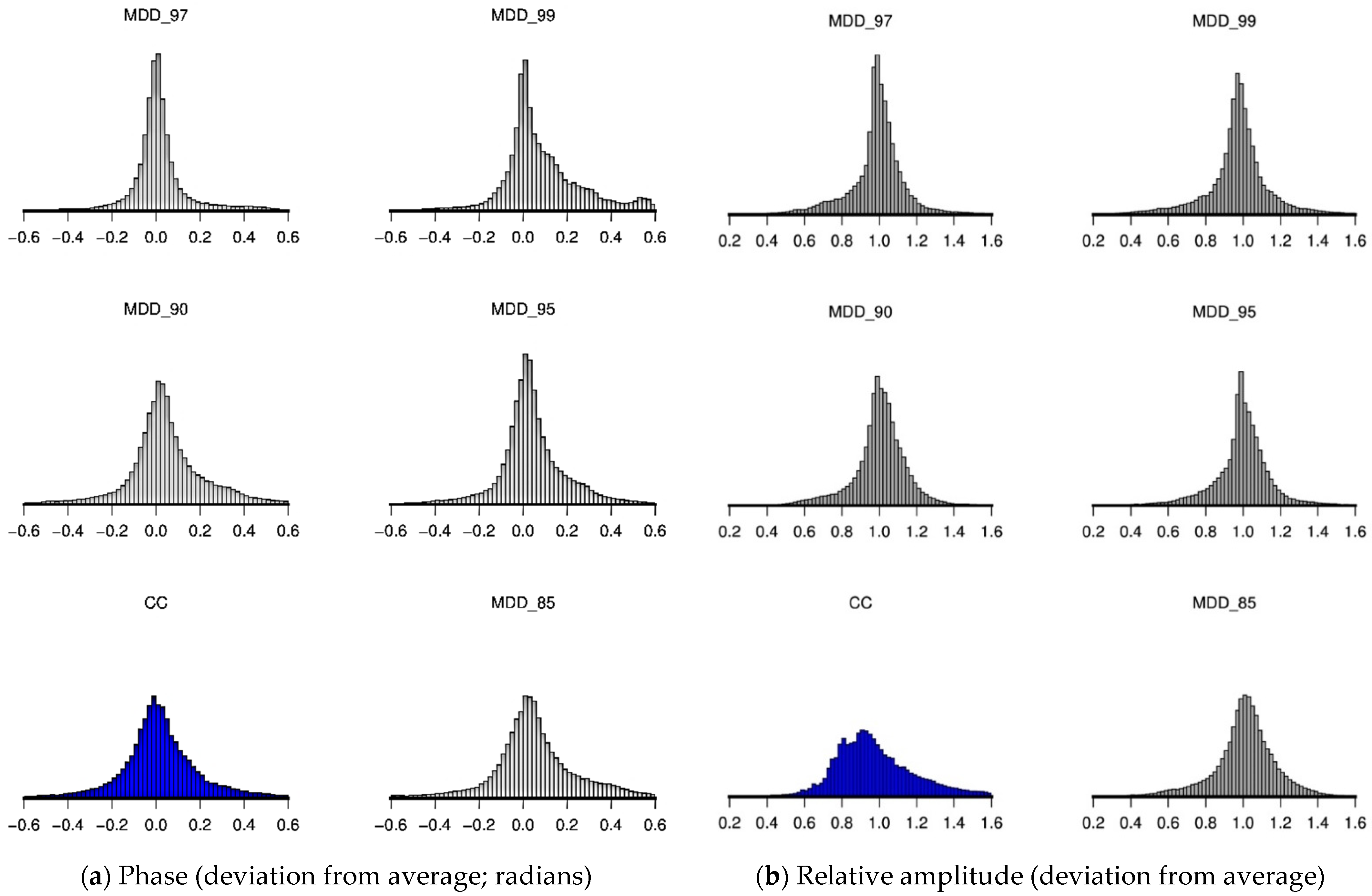


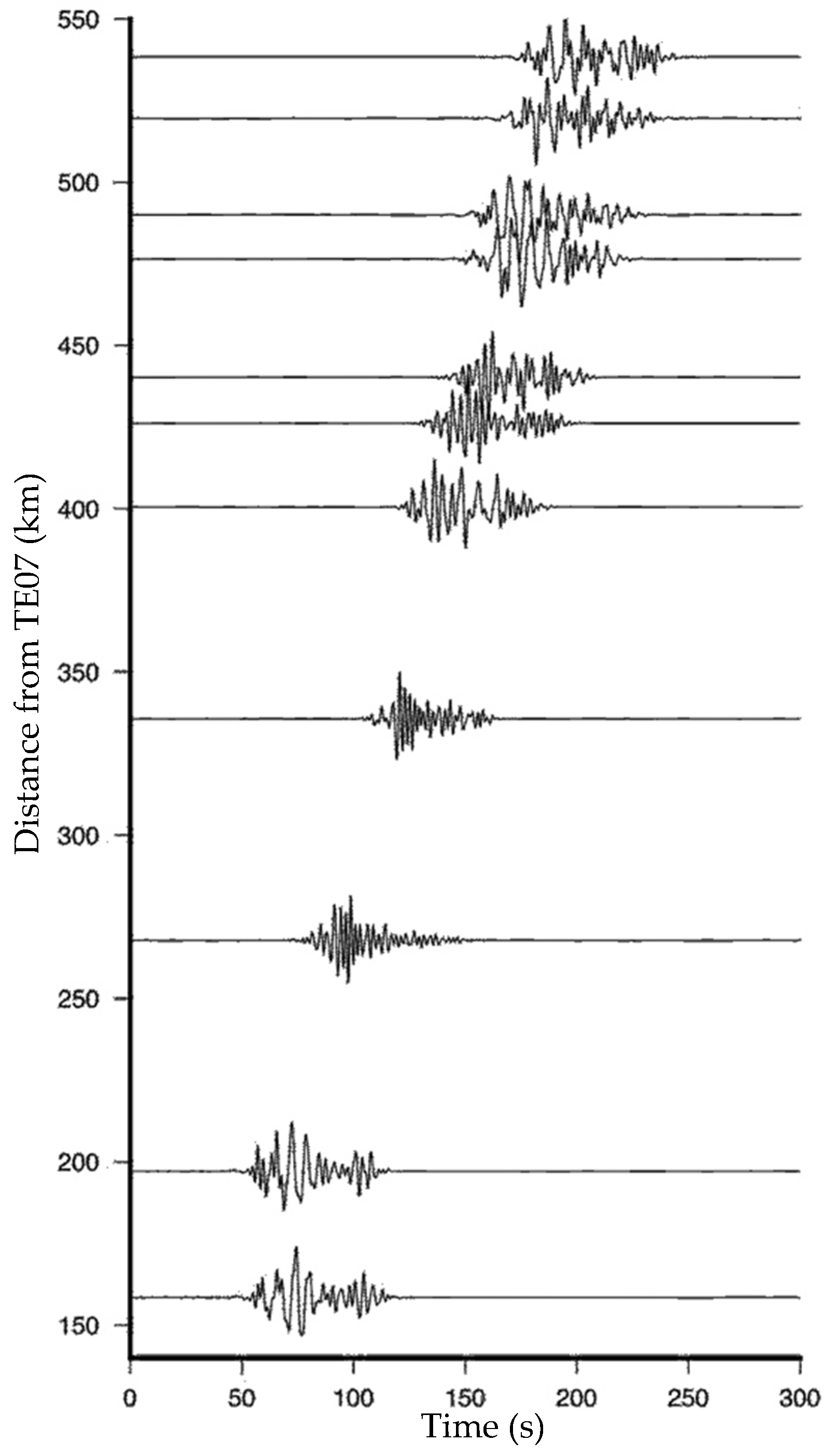
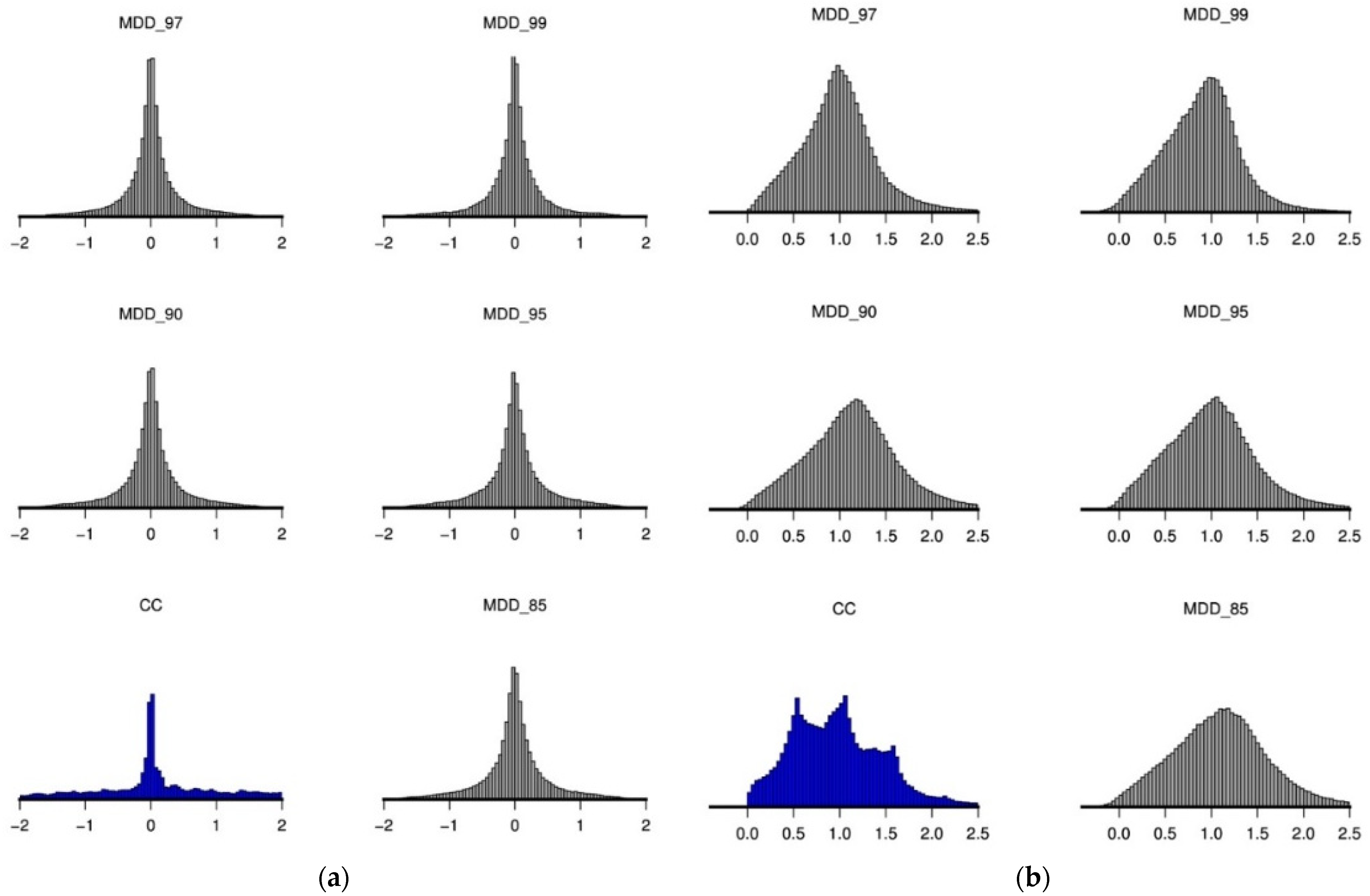

| Num. | Longitude (DD) | Latitude (DD) | Magnitude Scale | Magnitude |
|---|---|---|---|---|
| 1 | −73.981 | −38.148 | MW | 4.5 |
| 2 | −74.237 | −37.455 | ML | 4.1 |
| 3 | −73.723 | −37.658 | MB | 4.5 |
| 4 | −73.547 | −37.654 | ML | 4.2 |
| 5 | −73.397 | −37.199 | MB | 5.0 |
| 6 | −72.985 | −37.512 | MB | 4.8 |
| 7 | −73.462 | −35.776 | MB | 4.8 |
| 8 | −72.766 | −35.541 | MB | 4.3 |
| 9 | −72.012 | −35.127 | MB | 4.7 |
| 10 | −71.075 | −36.036 | MB | 5.0 |
| 11 | −70.570 | −36.074 | MW | 6.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shirmohammadi, F.; Draganov, D.; Hatami, M.R.; Weemstra, C. Application of Seismic Interferometry by Multidimensional Deconvolution to Earthquake Data Recorded in Malargüe, Argentina. Remote Sens. 2021, 13, 4818. https://doi.org/10.3390/rs13234818
Shirmohammadi F, Draganov D, Hatami MR, Weemstra C. Application of Seismic Interferometry by Multidimensional Deconvolution to Earthquake Data Recorded in Malargüe, Argentina. Remote Sensing. 2021; 13(23):4818. https://doi.org/10.3390/rs13234818
Chicago/Turabian StyleShirmohammadi, Faezeh, Deyan Draganov, Mohammad Reza Hatami, and Cornelis Weemstra. 2021. "Application of Seismic Interferometry by Multidimensional Deconvolution to Earthquake Data Recorded in Malargüe, Argentina" Remote Sensing 13, no. 23: 4818. https://doi.org/10.3390/rs13234818
APA StyleShirmohammadi, F., Draganov, D., Hatami, M. R., & Weemstra, C. (2021). Application of Seismic Interferometry by Multidimensional Deconvolution to Earthquake Data Recorded in Malargüe, Argentina. Remote Sensing, 13(23), 4818. https://doi.org/10.3390/rs13234818