Trajectory Tracking and Load Monitoring for Moving Vehicles on Bridge Based on Axle Position and Dual Camera Vision
Abstract
:1. Introduction
2. Methodology
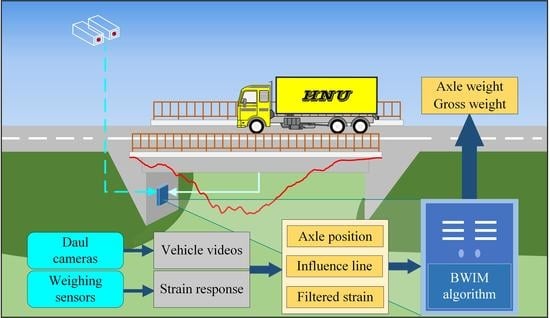
2.1. Framework of the Proposed BWIM
2.2. Automatic Recognizing and Positioning Vehicles and Wheels
2.2.1. Moving Object Detection
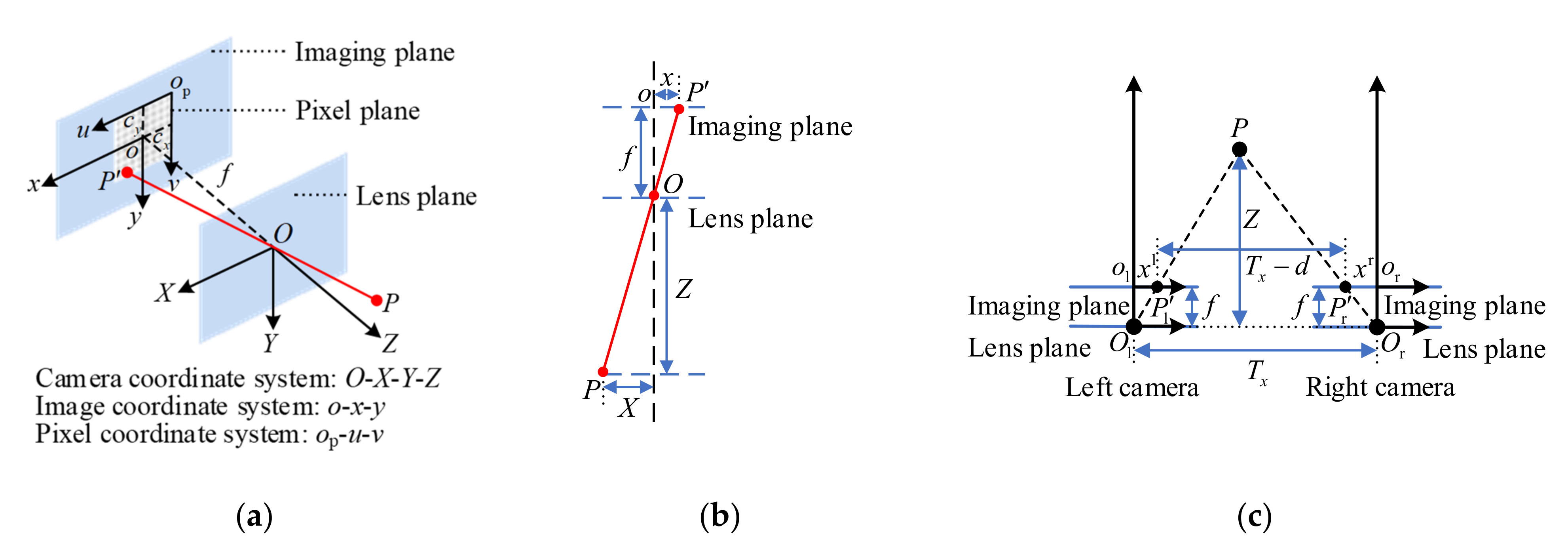
2.2.2. Binocular Ranging and Coordinate Transformation
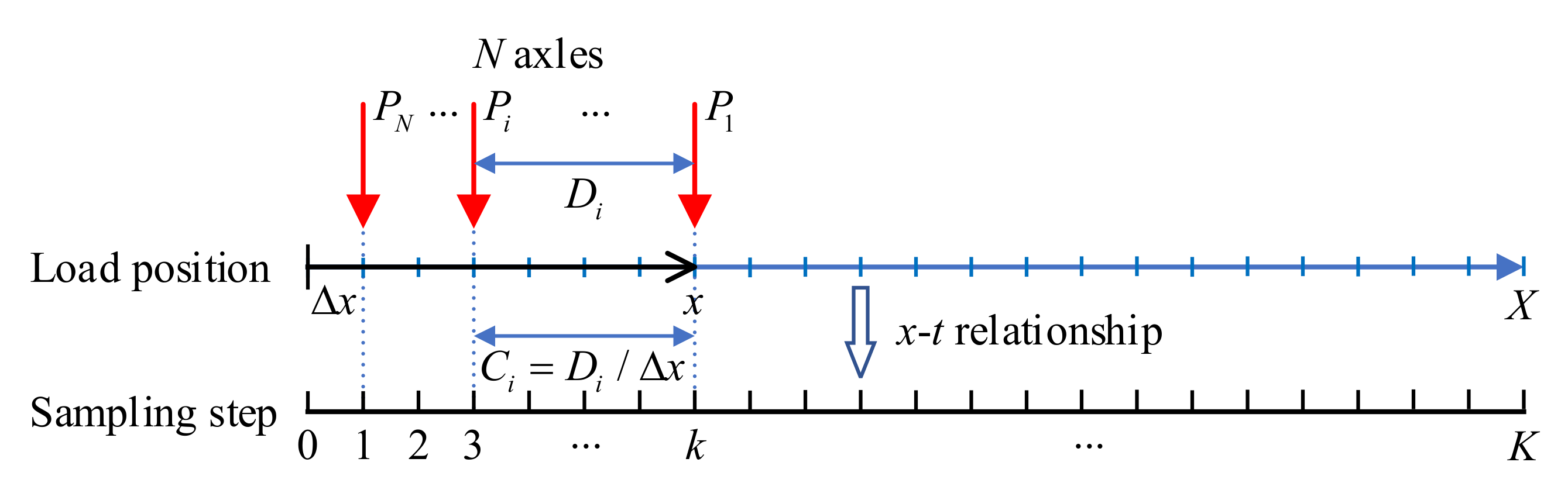
2.3. Influence Line Calibration
2.4. Vehicle Weight Identification
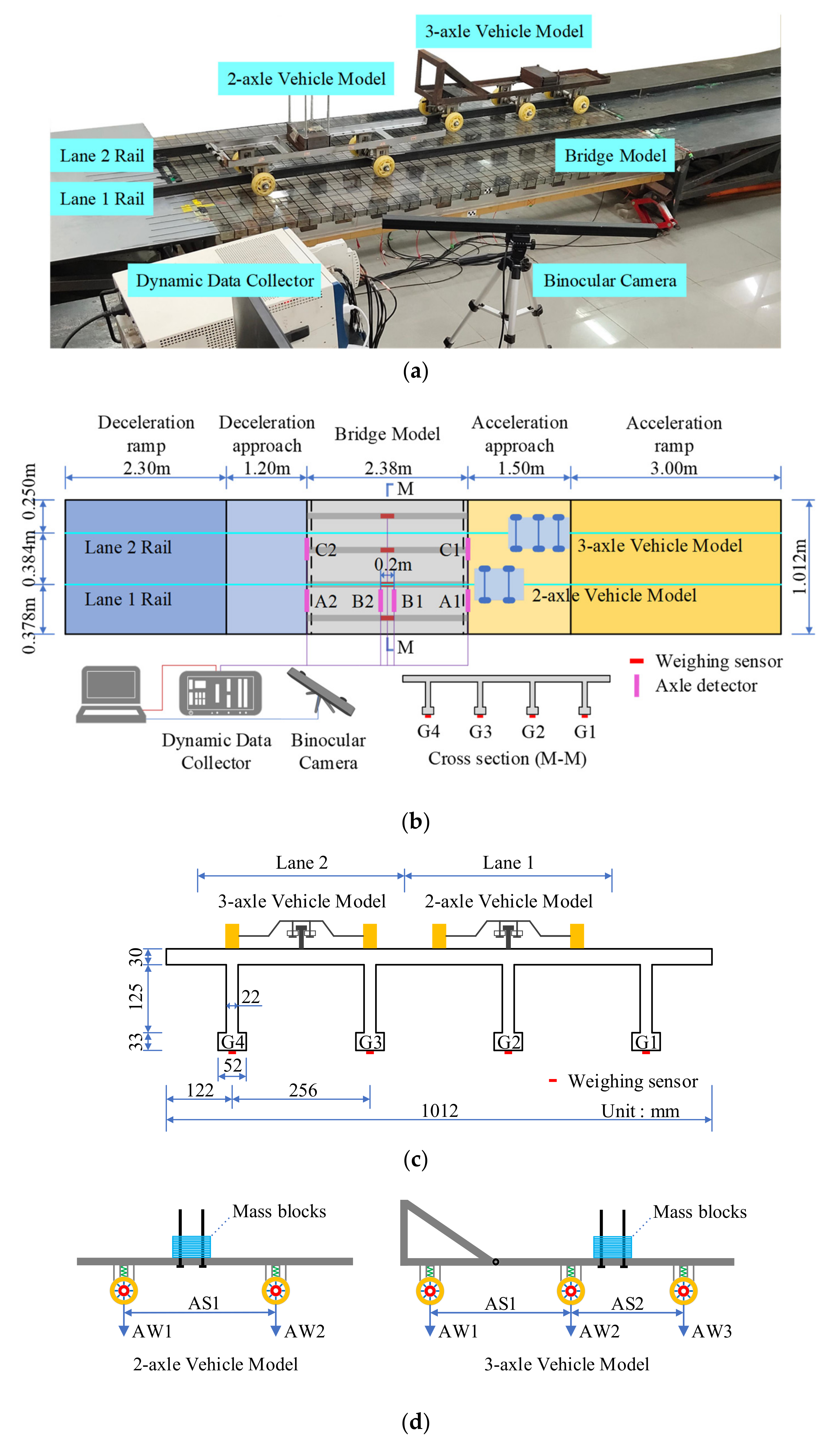
3. Experimental Setup
4. Results and Discussion
4.1. Comparison of the Moving Object Detection Algorithms
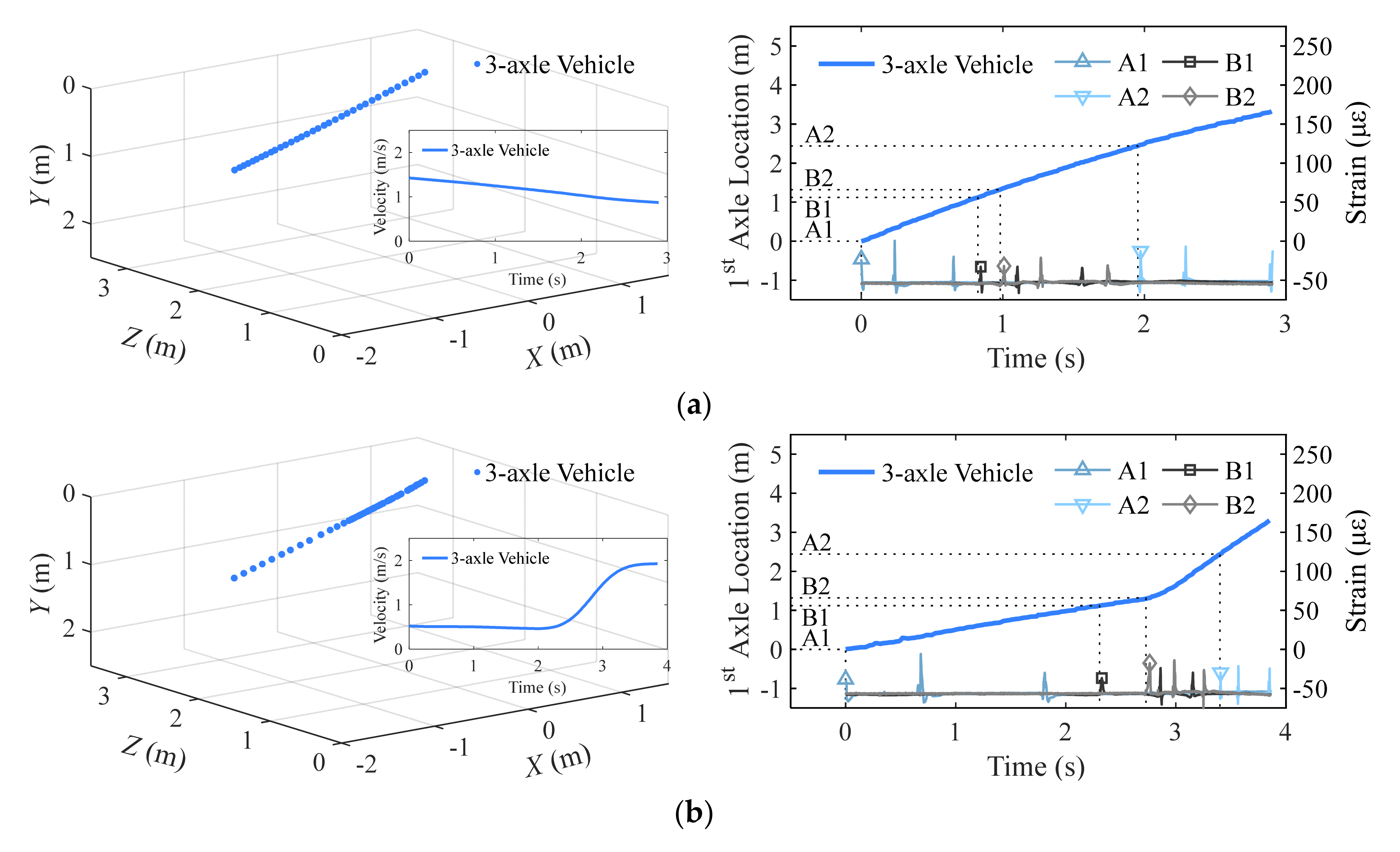
4.2. Vehicle Position Tracking
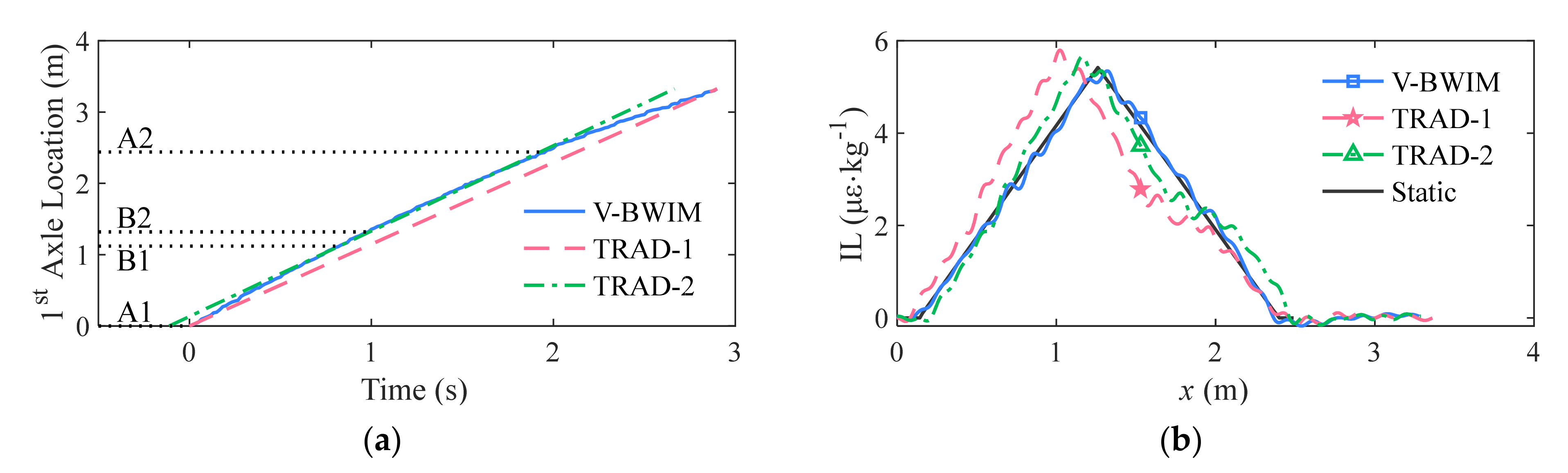
4.3. Influence Line Calibration under Non-Constant Velocity
4.4. Vehicle Weight Identification under Non-Constant Velocity
4.5. Vehicle Weight Identification for Multiple Vehicle Presence
5. Conclusions
- (1)
- For moving vehicle tracking, the deep learning (DL) method based on mask R-CNN had a better accuracy, but the conventional CV method was more efficient. Regarding axle spacing identification, there was no significant difference between the two methods. Generally, both methods could fulfill the requirements of a BWIM system based on the need of vehicle load position identification. In future practical applications, it would be worth combining the two methods to obtain a faster and more accurate vehicle-tracking method.
- (2)
- A slight change of vehicle speed can induce remarkable errors in the influence line calibration results for conventional BWIM methods that are based on constant speed assumption. Test results showed that a larger change of speed caused larger errors, while the mean-square errors of the influence line extracted by the proposed V-BWIM method for all the considered varying speeds were similar, and were 10 times smaller than those of the conventional method. Namely, the proposed method could accurately estimate the bridge influence line despite speed changes during the calibration process.
- (3)
- The largest relative errors of identified axle weight and gross vehicle weight by using the V-BWIM method were 6.18% and 2.23%, respectively, for all single-vehicle-presence tests in which the vehicle ran at a non-constant speed. In contrast, those errors of the conventional method could exceed tens, and even hundreds of percent. The reason for this was mainly because the V-BWIM method constructed the objective function based on the correct relationship between axle load positions and bridge response, while the axle position information that the conventional method used was calculated from vehicle speed and axle spacing, which was not consistent with the real position under the circumstances in which the vehicle did not run at a constant speed. Thus, obtaining accurate load positions and providing them to a BWIM system is vital for axle weight identification.
- (4)
- For a multi-presence scenario in which two vehicles were passing over the test bridge one by one or side by side, the axle and gross weight of the vehicles was successfully obtained, with axle weight errors less than 6% and gross weight errors less than 3%. It also outperformed the traditional method, which, in the conducted slow-deceleration tests, the gross weight error was still controlled within 7%, but the axle weight error was vast and unacceptable.
Author Contributions
Funding
Conflicts of Interest
References
- Deng, L.; Wang, T.; He, Y.; Kong, X.; Dan, D.; Bi, T. Impact of Vehicle Axle Load Limit on Reliability and Strengthening Cost of Reinforced Concrete Bridges. China J. Highw. Transp. 2020, 33, 92–100. [Google Scholar]
- Richardson, J.; Jones, S.; Brown, A.; O’Brien, E.J.; Hajializadeh, D. On the use of bridge weigh-in-motion for overweight truck enforcement. Int. J. Heavy Veh. Syst. 2014, 21, 83–104. [Google Scholar] [CrossRef]
- Yu, Y.; Cai, C.S.; Deng, L. State-of-the-art review on bridge weigh-in-motion technology. Adv. Struct. Eng. 2016, 19, 1514–1530. [Google Scholar] [CrossRef]
- Algohi, B.; Bakht, B.; Khalid, H.; Mufti, A.; Regehr, J. Some observations on BWIM data collected in Manitoba. Can. J. Civ. Eng. 2020, 47, 88–95. [Google Scholar] [CrossRef]
- Algohi, B.; Mufti, A.; Bakht, B. BWIM with constant and variable velocity: Theoretical derivation. J. Civ. Struct. Health 2020, 10, 153–164. [Google Scholar] [CrossRef]
- Cantero, D. Moving point load approximation from bridge response signals and its application to bridge Weigh-in-Motion. Eng. Struct. 2021, 233, 111931. [Google Scholar] [CrossRef]
- Brouste, A. Testing the accuracy of WIM systems: Application to a B-WIM case. Measurement 2021, 185, 110068. [Google Scholar] [CrossRef]
- Ye, X.; Dong, C. Review of Computer Vision-based Structural Displacement Monitoring. China J. Highw. Transp. 2019, 32, 21–39. [Google Scholar]
- Pieraccini, M.; Miccinesi, L. An Interferometric MIMO Radar for Bridge Monitoring. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1383–1387. [Google Scholar] [CrossRef]
- Miccinesi, L.; Consumi, T.; Beni, A.; Pieraccini, M. W-band MIMO GB-SAR for Bridge Testing/Monitoring. Electronics 2021, 10, 2261. [Google Scholar] [CrossRef]
- Tosti, F.; Gagliardi, V.; D’Amico, F.; Alani, A.M. Transport infrastructure monitoring by data fusion of GPR and SAR imagery information. Transp. Res. Proc. 2020, 45, 771–778. [Google Scholar] [CrossRef]
- Lazecky, M.; Hlavacova, I.; Bakon, M.; Sousa, J.J.; Perissin, D.; Patricio, G. Bridge Displacements Monitoring Using Space-Borne X-Band SAR Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2017, 10, 205–210. [Google Scholar] [CrossRef] [Green Version]
- Moses, F. Weigh-in-motion system using instrumented bridges. Transp. Eng. J. 1979, 105, 233–249. [Google Scholar] [CrossRef]
- O’Brien, E.J.; Quilligan, M.J.; Karoumi, R. Calculating an influence line from direct measurements. Proc. Inst. Civ. Eng.-Br. 2006, 159, 31–34. [Google Scholar] [CrossRef]
- Ieng, S.S. Bridge Influence Line Estimation for Bridge Weigh-in-Motion System. J. Comput. Civ. Eng. 2015, 29, 06014006. [Google Scholar] [CrossRef]
- Jacob, B. Weighing-in-Motion of Axles and Vehicles for Europe (WAVE). Rep. of Work Package 1.2; Laboratoire Central des Ponts et Chaussées: Paris, France, 2001. [Google Scholar]
- Lansdell, A.; Song, W.; Dixon, B. Development and testing of a bridge weigh-in-motion method considering nonconstant vehicle speed. Eng. Struct. 2017, 152, 709–726. [Google Scholar] [CrossRef]
- Zhuo, Y. Application of Non-Constant Speed Algorithm in Bridge Weigh-in-Motion System. Master’s Thesis, Hunan University, Changsha, China, 2015. (In Chinese). [Google Scholar]
- Chen, Z.; Li, H.; Bao, Y.; Li, N.; Jin, Y. Identification of spatio-temporal distribution of vehicle loads on long-span bridges using computer vision technology. Struct. Control Health Monit. 2016, 23, 517–534. [Google Scholar] [CrossRef]
- Khuc, T.; Catbas, F.N. Structural Identification Using Computer Vision–Based Bridge Health Monitoring. J. Struct. Eng. 2018, 144, 04017202. [Google Scholar] [CrossRef]
- Zhu, J.; Li, X.; Zhang, C.; Shi, T. An accurate approach for obtaining spatiotemporal information of vehicle loads on bridges based on 3D bounding box reconstruction with computer vision. Measurement 2021, 181, 109657. [Google Scholar] [CrossRef]
- Ojio, T.; Carey, C.H.; O’Brien, E.J.; Doherty, C.; Taylor, S.E. Contactless Bridge Weigh-in-Motion. J. Bridge Eng. 2016, 21, 04016032. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Zhou, L.; Zhang, J. A methodology for obtaining spatiotemporal information of the vehicles on bridges based on computer vision. Comput.-Aided Civ. Inf. 2019, 34, 471–487. [Google Scholar] [CrossRef]
- Dan, D.; Ge, L.; Yan, X. Identification of moving loads based on the information fusion of weigh-in-motion system and multiple camera machine vision. Measurement 2019, 144, 155–166. [Google Scholar] [CrossRef]
- Ge, L.; Dan, D.; Li, H. An accurate and robust monitoring method of full-bridge traffic load distribution based on YOLO-v3 machine vision. Struct. Control Health Monit. 2020, 27, e2636. [Google Scholar] [CrossRef]
- Xia, Y.; Jian, X.; Yan, B.; Su, D. Infrastructure Safety Oriented Traffic Load Monitoring Using Multi-Sensor and Single Camera for Short and Medium Span Bridges. Remote Sens. 2019, 11, 2651. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Pei, Y.; Li, Z.; Fang, L.; Zhao, Y.; Yi, W. Vehicle weight identification system for spatiotemporal load distribution on bridges based on non-contact machine vision technology and deep learning algorithms. Measurement 2020, 159, 107801. [Google Scholar] [CrossRef]
- Quilligan, M.; Karoumi, R.; O’Brien, E.J. Development and Testing of a 2-Dimensional Multi-Vehicle Bridge-WIM Algorithm. In Proceedings of the 3rd International Conference on Weigh-in-Motion (ICWIM3), Orlando, FL, USA, 13–15 May 2002; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Zhao, H.; Uddin, N.; O’Brien, E.J.; Shao, X.; Zhu, P. Identification of Vehicular Axle Weights with a Bridge Weigh-in-Motion System Considering Transverse Distribution of Wheel Loads. J. Bridge Eng. 2014, 19, 04013008. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.Z.; Wu, G.; Feng, D.C. Development of a bridge weigh-in-motion method considering the presence of multiple vehicles. Eng. Struct. 2019, 191, 724–739. [Google Scholar] [CrossRef]
- Liu, Y. Study on the BWIM Algorithm of A Vehicle or Multi-Vehicles Based on the Moses Algorithm. Master’s Thesis, Jilin University, Changchun, China, 2019. (In Chinese). [Google Scholar]
- Marr, D.; Poggio, T. Cooperative Computation of Stereo Disparity. Science 1976, 194, 283–287. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.J. Displacement Measurement Method of Sphere Joints Based on Machine Vision and Deep Learning. Master’s Thesis, Zhejiang University, Hangzhou, China, 2018. (In Chinese). [Google Scholar]
- Yang, B. The Research on Detection and Tracking Algorithm of Moving Target in Video Image Sequence. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2020. (In Chinese). [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 January 2014; pp. 580–587. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Zhang, W.; Wu, Q.M.J.; Wang, G.; Yin, H. An Adaptive Computational Model for Salient Object Detection. IEEE Trans. Multimedia 2010, 12, 300–316. [Google Scholar] [CrossRef]
- He, W.; Ling, T.; O’Brien, E.J.; Deng, L. Virtual axle method for bridge weigh-in-motion systems requiring no axle detector. J. Bridge Eng. 2019, 24, 04019086. [Google Scholar] [CrossRef]








| Vehicle Name | Vehicle Model | AS1 (m) | AS2 (m) | AW1 (kg) | AW2 (kg) | AW3 (kg) | GVW (kg) |
|---|---|---|---|---|---|---|---|
| Calibration vehicle | 3-axle | 0.455 | 0.370 | 5.80 | 11.65 | 7.80 | 25.25 |
| Test vehicle | 2-axle | 0.545 | - | 11.80 | 9.50 | - | 21.30 |
| 3-axle | 0.320 | 0.545 | 5.71 | 17.33 | 18.83 | 41.87 |
| Camera Deflection Angle | Reflection | Frame Count | Recall Rate (%) | Prediction Time Per Frame (s) | ||||
|---|---|---|---|---|---|---|---|---|
| Vehicle | Wheel | |||||||
| CV | DL | CV | DL | CV | DL | |||
| 0° | No | 139 | 98.56 | 100.00 | 97.84 | 100.00 | 0.172 | 1.820 |
| 15° | No | 160 | 98.13 | 100.00 | 96.88 | 100.00 | 0.172 | 1.819 |
| 30° | No | 172 | 97.67 | 99.42 | 84.88 | 98.84 | 0.174 | 1.814 |
| 30° | Yes | 193 | 90.16 | 99.48 | 81.35 | 98.45 | 0.179 | 1.822 |
| Camera Deflection Angle | Reflection | Statistical Indicator | Relative Error (%) | |||
|---|---|---|---|---|---|---|
| CV | DL | |||||
| AS1 | AS2 | AS1 | AS2 | |||
| 0° | No | Mean | −0.42 | 0.52 | −0.20 | 0.14 |
| SD | 1.86 | 2.63 | 1.72 | 2.71 | ||
| 15° | No | Mean | 0.50 | −0.41 | 0.14 | −0.41 |
| SD | 2.35 | 2.11 | 3.03 | 2.34 | ||
| 30° | No | Mean | 1.24 | −1.31 | 0.75 | −0.80 |
| SD | 3.55 | 3.17 | 2.88 | 3.03 | ||
| 30° | Yes | Mean | 0.67 | −1.75 | 0.73 | −1.40 |
| SD | 3.31 | 3.18 | 3.82 | 3.06 | ||
| No. | v (m·s−1) | Δv (%) | MSE (με·kg−1)2 | |||
|---|---|---|---|---|---|---|
| v0 | vend | V-BWIM | TRAD-1 | TRAD-2 | ||
| 1 | 1.36 | 0.87 | −36.10 | 0.0098 | 0.7586 | 0.1941 |
| 2 | 1.37 | 0.91 | −33.69 | 0.0123 | 0.6507 | 0.1624 |
| 3 | 1.64 | 1.25 | −23.65 | 0.0105 | 0.3672 | 0.1204 |
| 4 | 1.67 | 1.32 | −21.01 | 0.0096 | 0.2919 | 0.1059 |
| 5 | 2.04 | 1.67 | −18.23 | 0.0105 | 0.2393 | 0.0930 |
| 6 | 2.09 | 1.74 | −16.75 | 0.0098 | 0.2161 | 0.0872 |
| 7 | 2.60 | 2.26 | −13.08 | 0.0125 | 0.1525 | 0.0712 |
| 8 | 2.67 | 2.38 | −10.75 | 0.0010 | 0.1368 | 0.0654 |
| Mean | - | - | - | 0.0107 | 0.3516 | 0.1125 |
| SD | - | - | - | 0.0011 | 0.2167 | 0.0421 |
| Scenario | Statistical Indicator | Relative Error (%) | r (%) | |||
|---|---|---|---|---|---|---|
| AW1 | AW2 | AW3 | GVW | |||
| VS-I | Mean | 3.41 | −2.28 | 2.59 | 0.69 | 2.71 |
| SD | 4.32 | 3.06 | 3.78 | 1.23 | 3.15 | |
| VS-II | Mean | 3.06 | 0.80 | 3.30 | 2.23 | 2.57 |
| SD | 5.20 | 2.49 | 2.39 | 0.58 | 2.21 | |
| VS-III | Mean | −0.39 | −3.69 | 2.44 | −0.48 | 3.09 |
| SD | 5.33 | 3.84 | 4.81 | 1.06 | 3.72 | |
| VS-IV | Mean | 6.18 | −4.42 | 5.44 | 1.46 | 3.69 |
| SD | 3.41 | 2.49 | 3.15 | 0.94 | 3.27 | |
| Scenario | Statistical Indicator | Relative Error (%) | |||
|---|---|---|---|---|---|
| AW1 | AW2 | AW3 | GVW | ||
| VS-I | Mean | −76.98 | −100.00 | 63.83 | −23.18 |
| SD | 4.32 | 0.00 | 3.36 | 1.84 | |
| VS-II | Mean | 330.14 | −37.14 | −54.54 | 5.12 |
| SD | 17.97 | 3.93 | 2.92 | 0.93 | |
| VS-III | Mean | −76.26 | −100.00 | 64.64 | −22.72 |
| SD | 5.38 | 0.00 | 2.51 | 1.15 | |
| VS-IV | Mean | 46.82 | −100.00 | 64.17 | −6.15 |
| SD | 45.52 | 0.00 | 4.02 | 6.87 | |
| Scenario | Statistical Indicator | Relative Error (%) | |||
|---|---|---|---|---|---|
| AW1 | AW2 | AW3 | GVW | ||
| VS-I | Mean | 229.17 | −92.82 | 29.17 | 5.95 |
| SD | 13.23 | 7.49 | 7.20 | 2.36 | |
| VS-II | Mean | 8.51 | −9.20 | 17.82 | 5.37 |
| SD | 2.99 | 1.60 | 2.11 | 0.74 | |
| VS-III | Mean | 113.68 | −43.33 | 12.79 | 3.32 |
| SD | 15.28 | 5.54 | 2.64 | 1.56 | |
| VS-IV | Mean | 217.11 | −81.05 | 43.13 | 15.46 |
| SD | 30.17 | 23.74 | 20.04 | 6.03 | |
| Scenario | Statistical Indicator | Relative Error (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Two-Axle Vehicle | Three-Axle Vehicle | |||||||||
| Δv (%) | AW1 | AW2 | GVW | Δv (%) | AW1 | AW2 | AW3 | GVW | ||
| M-I | Mean | −14.11 | −2.52 | −1.74 | −2.17 | −29.19 | −2.52 | 0.06 | 1.40 | −0.12 |
| SD | 0.83 | 2.42 | 3.96 | 1.95 | 7.44 | 5.65 | 3.30 | 3.89 | 0.95 | |
| M-II | Mean | −17.28 | 0.74 | −2.75 | −0.82 | −39.20 | 0.10 | 2.99 | 2.93 | 2.31 |
| SD | 2.18 | 1.44 | 2.81 | 0.91 | 7.63 | 4.82 | 1.95 | 4.39 | 0.85 | |
| Scenario | Statistical Indicator | Relative Error (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Two-Axle Vehicle | Three-Axle Vehicle | |||||||||
| Δv (%) | AW1 | AW2 | GVW | Δv (%) | AW1 | AW2 | AW3 | GVW | ||
| M-I | Mean | −14.11 | 22.47 | −34.47 | −2.92 | −29.19 | 112.56 | −20.64 | −42.10 | 3.33 |
| SD | 0.83 | 5.27 | 7.36 | 1.71 | 7.44 | 30.80 | 10.92 | 17.47 | 1.66 | |
| M-II | Mean | −17.28 | 31.66 | −49.68 | −4.62 | −39.20 | 148.95 | −28.98 | −47.39 | 6.20 |
| SD | 2.18 | 2.29 | 6.84 | 2.37 | 7.63 | 24.77 | 10.26 | 7.01 | 1.37 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; He, W.; Deng, L.; Wu, Y.; Xie, H.; Dai, J. Trajectory Tracking and Load Monitoring for Moving Vehicles on Bridge Based on Axle Position and Dual Camera Vision. Remote Sens. 2021, 13, 4868. https://doi.org/10.3390/rs13234868
Zhao D, He W, Deng L, Wu Y, Xie H, Dai J. Trajectory Tracking and Load Monitoring for Moving Vehicles on Bridge Based on Axle Position and Dual Camera Vision. Remote Sensing. 2021; 13(23):4868. https://doi.org/10.3390/rs13234868
Chicago/Turabian StyleZhao, Dongdong, Wei He, Lu Deng, Yuhan Wu, Hong Xie, and Jianjun Dai. 2021. "Trajectory Tracking and Load Monitoring for Moving Vehicles on Bridge Based on Axle Position and Dual Camera Vision" Remote Sensing 13, no. 23: 4868. https://doi.org/10.3390/rs13234868
APA StyleZhao, D., He, W., Deng, L., Wu, Y., Xie, H., & Dai, J. (2021). Trajectory Tracking and Load Monitoring for Moving Vehicles on Bridge Based on Axle Position and Dual Camera Vision. Remote Sensing, 13(23), 4868. https://doi.org/10.3390/rs13234868