Reducing Scaling Effect on Downscaled Land Surface Temperature Maps in Heterogenous Urban Environments
Abstract
:1. Introduction
2. Study Areas and Data Sets
2.1. Study Areas
2.2. Data Sets
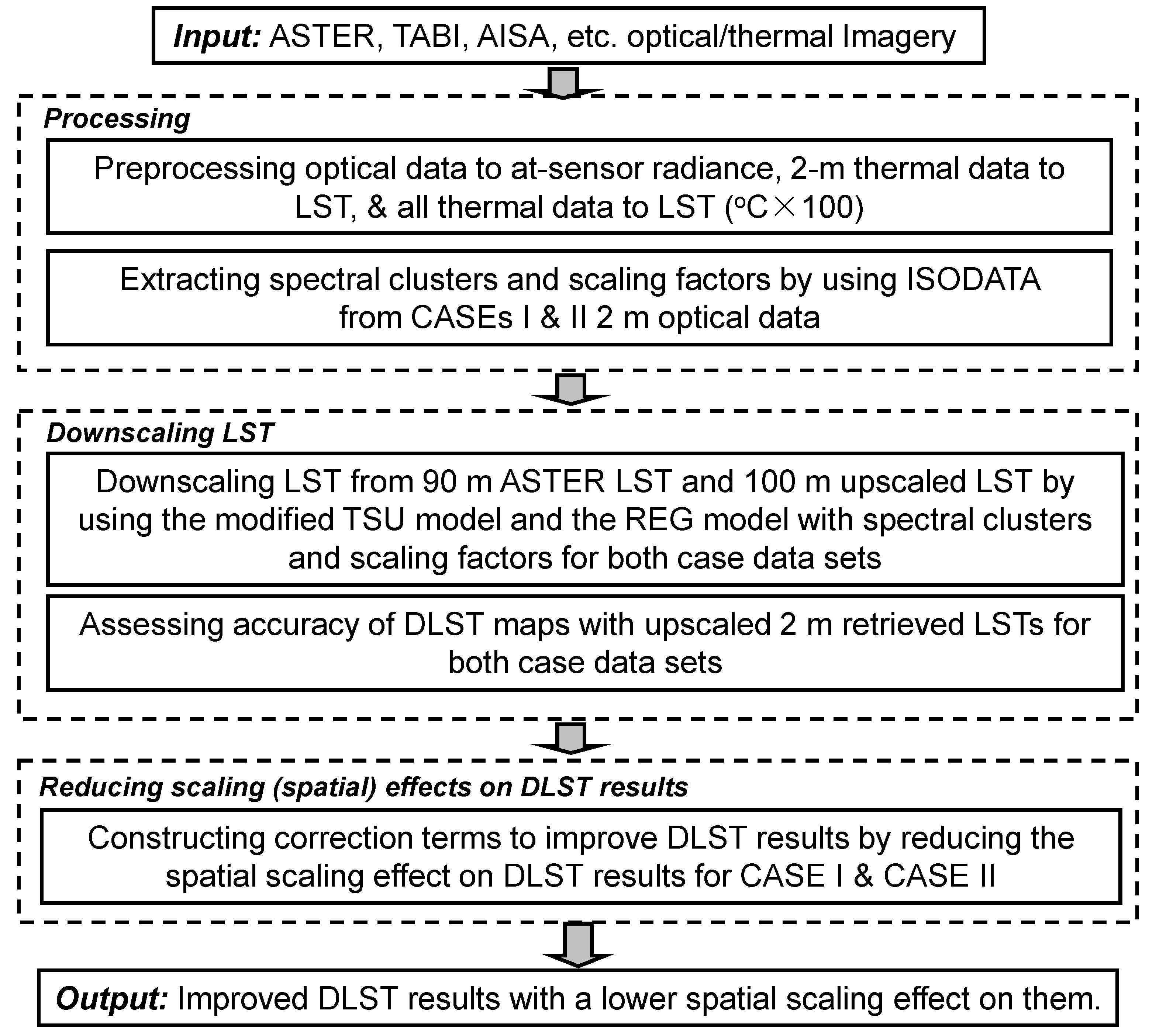
3. Methodology
3.1. Data Preprocessing
3.2. Downscaling Land Surface Temperature (DLST)
3.2.1. A Modified Thermal Spectral Unmixing (TSU) Model
3.2.2. Extraction of Spectral Clusters from High Resolution Optical Data
3.2.3. Thermal Components and Spectral Clusters
3.2.4. Modification of Initial LSTs
3.2.5. Validation of Downscaled LSTs
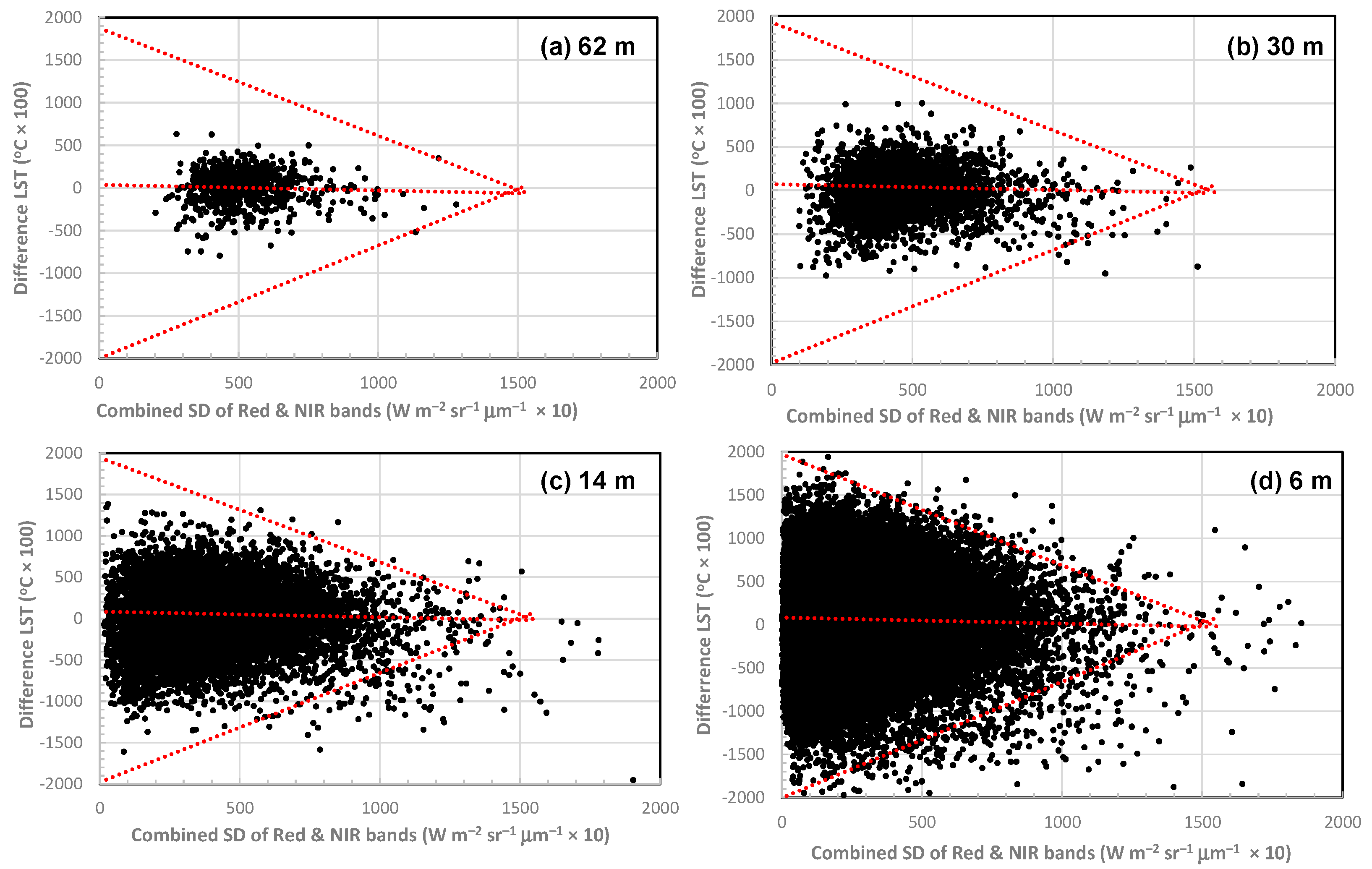
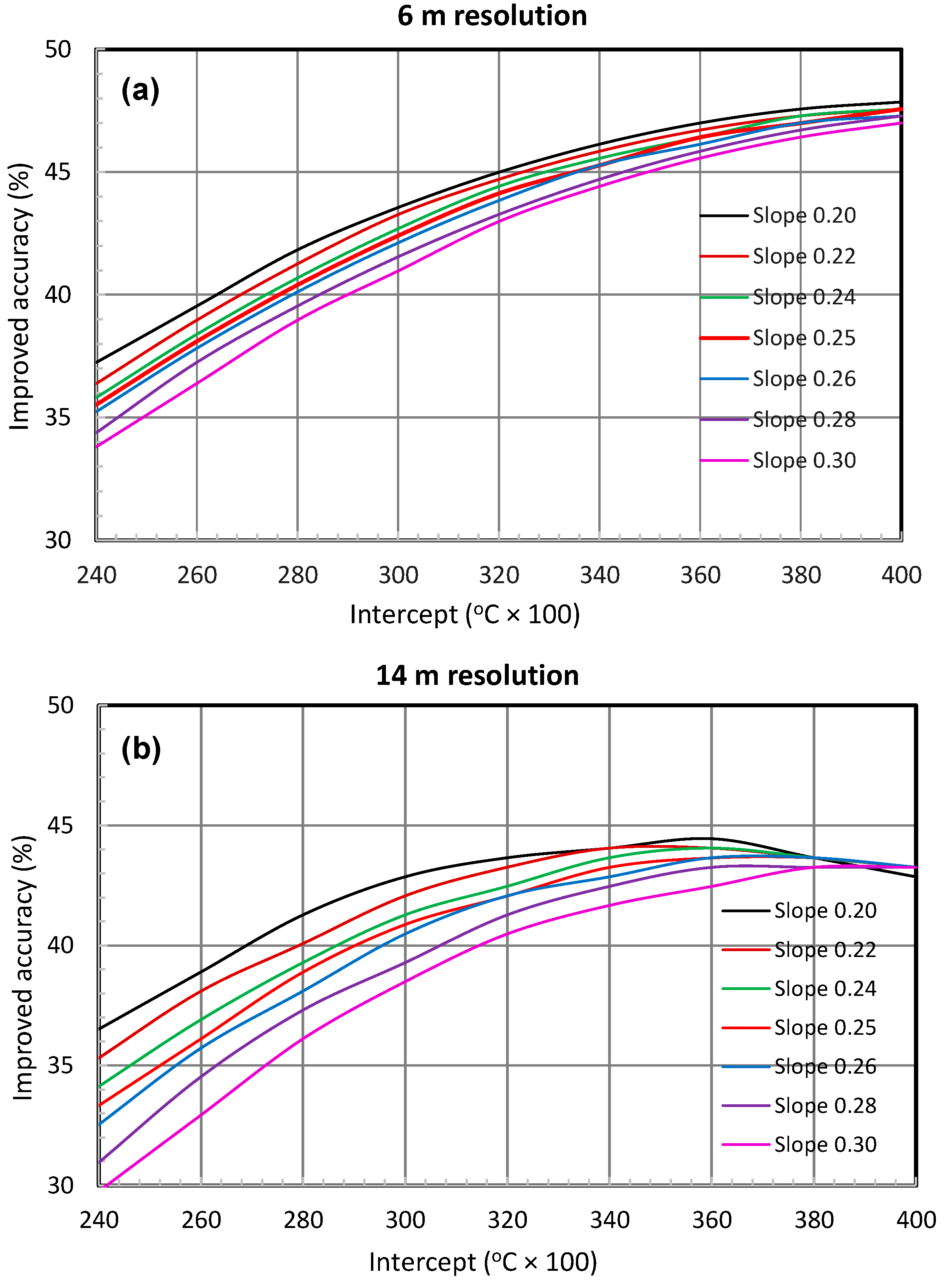
3.3. Correction Term (CT)
3.4. Assessment of DLST Results
4. Results and Analysis
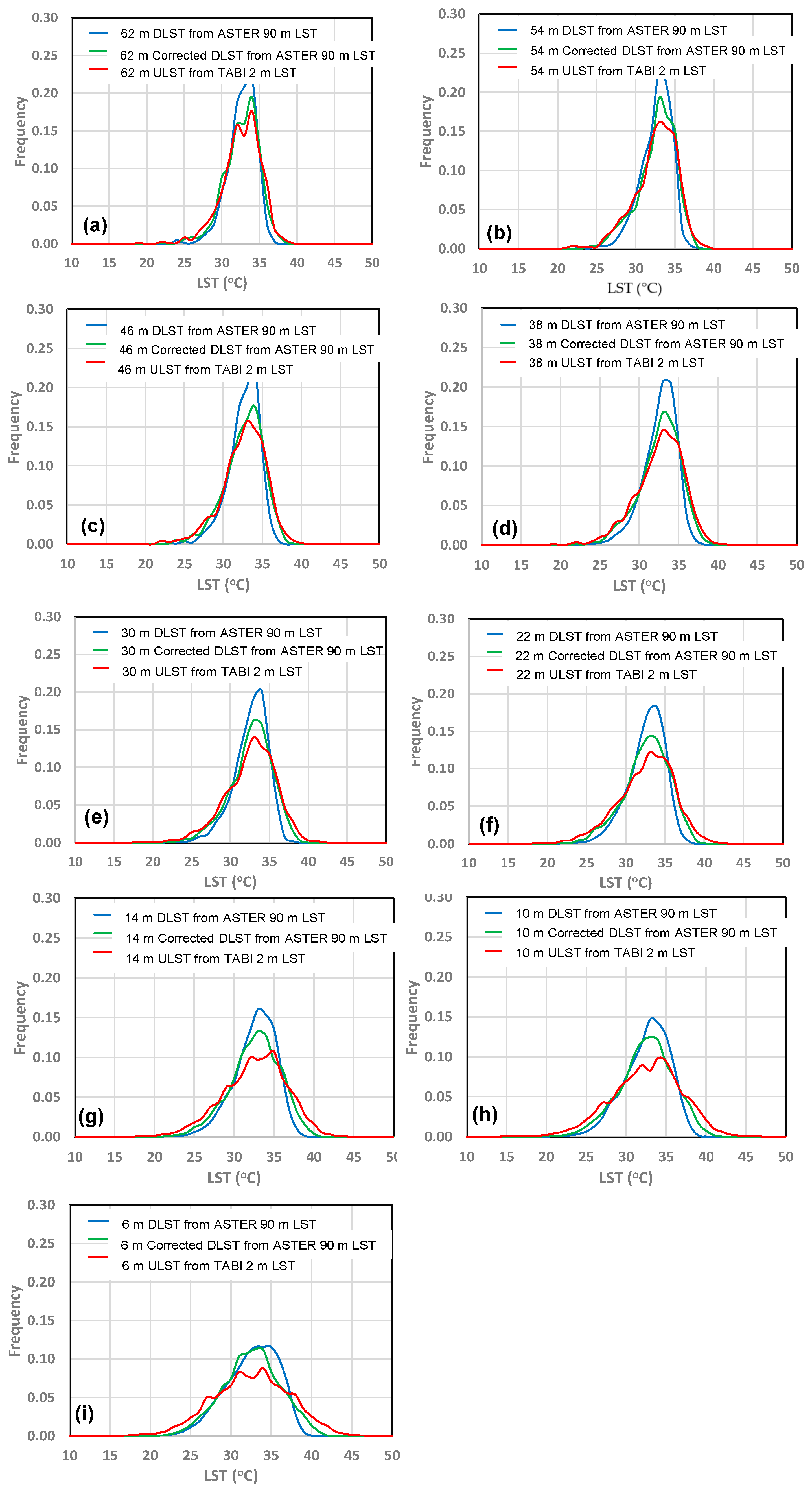
4.1. DLST Maps at Different High Resolutions
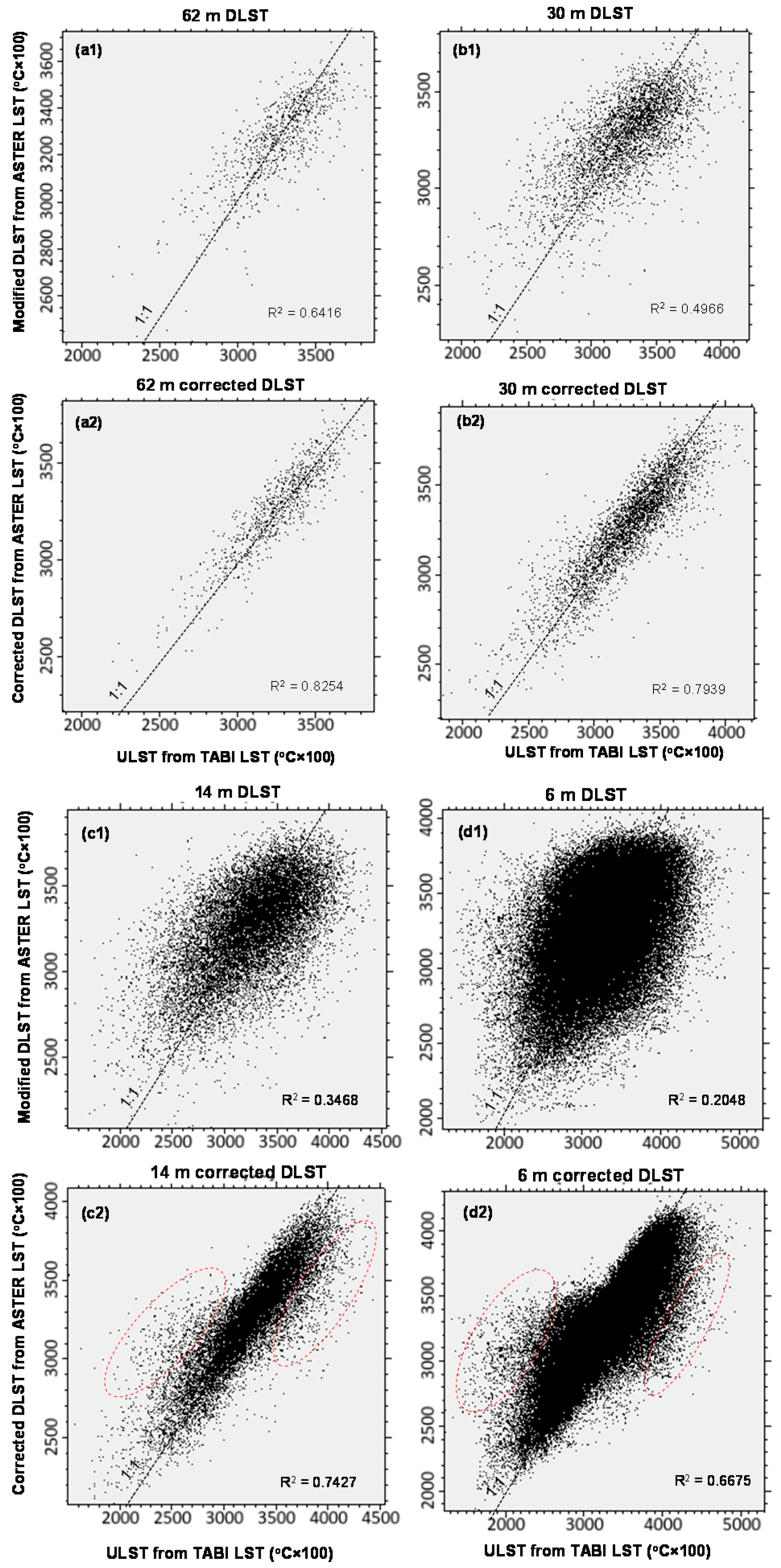
4.2. Accuracy of DLST Maps
5. Discussion
5.1. The Performance of the Modified TSU Model
5.2. Corection Term (CT)
5.3. Limitations and Significance of This Study
6. Conclusions
- The modified TSU model for unmixing thermal component temperatures at the initial high resolution was effective and advanced in downscaling LSTs compared to our previous works and those in existing literature.
- Spectral clusters were intrinsically associated with spectral properties of surface materials/cover types and thermal physical characteristics of corresponding thermal components, and were thus workable and reliable for solving the modified TSU model.
- The proposed method with the CT expression (Equation (6)) was workable and the testing results were reliable and stable for the two data sets; thus, it is effective and novel.
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AISA | Airborne Imaging Spectrometer for different Applications, sensor |
| ASTER | Advanced Spaceborne Thermal Emission and Reflection Radiometer, sensor |
| CT | correction term |
| DisTrad | disaggregation of radiometric temperature |
| DiffLST | difference between ULST image (actual) and DLST image (estimated) |
| TsHARP | temperature sharpening |
| DLST | downscaling land surface temperature or disaggregation of land surface temperature (°C) |
| LST | land surface temperature (°C) |
| MAE | mean absolute error (°C) |
| NIR | near-infrared |
| REG | multiple regression (model) |
| RMSE | root mean squire error (°C) |
| SD | standard deviation |
| TSU | thermal spectral unmixing (model) |
| TIR | thermal infrared (8–14 mm) |
| TABI | Thermal Airborne Broadband Imager, sensor |
| ULST | upscaling land surface temperature (°C) |
| VNIR | visible-near infrared (0.4–1.0 mm) |
| AISA | Airborne Imaging Spectrometer for different Applications, sensor |
References
- Pu, R. Assessing scaling effect in downscaling land surface temperature in a heterogenous urban environment. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102256. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, S.; Li, M.; Zhan, W.; Xu, Z.; Xu, T. Quantification of the scale effect in downscaling remotely sensed land surface temperature. Remote Sens. 2016, 8, 975. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Li, W. Downscaling land surface temperatures using a random forest regression model with multitype predictor variables. IEEE Access 2019, 7, 21904–21916. [Google Scholar] [CrossRef]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Quantifying spatial heterogeneity at the landscape scale using variogram models. Remote Sens. Environ. 2006, 103, 81–96. [Google Scholar] [CrossRef]
- Garrigues, S.; Allard, D.; Baret, F. Influence of the spatial heterogeneity on the nonlinear estimation of Leaf Area Index from moderate resolution remote sensing data. Remote Sens. Environ. 2006, 106, 286–298. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index–radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M.U. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Chen, X.H.; Yamaguchi, Y.; Chen, J.; Shi, Y.S. Scale effect of vegetation-index-based spatial sharpening for thermal imagery: A simulation study by ASTER data. IEEE Geosci. Remote Sens. Lett. 2012, 9, 549–553. [Google Scholar] [CrossRef]
- Ghosh, A.; Joshi, P.K. Hyperspectral imagery for disaggregation of land surface temperature with selected regression algorithms over different land use land cover scenes. ISPRS J. Photogramm. Remote Sens. 2014, 96, 76–93. [Google Scholar] [CrossRef]
- Liu, H.; Weng, Q. Scaling effect of fused ASTER-MODIS land surface temperature in an urban environment. Sensors 2018, 18, 4058. [Google Scholar] [CrossRef]
- Gao, F.; Kustas, W.P.; Anderson, M.C. A data mining approach for sharpening thermal satellite imagery over land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, S.; Joshi, P.; Garg, R. A comparison of different regression models for downscaling Landsat and MODIS land surface temperature images over heterogeneous landscape. Adv. Space Res. 2014, 54, 655–669. [Google Scholar] [CrossRef]
- Bonafoni, S.; Tosi, G. Downscaling of land surface temperature using airborne high-resolution data: A case study on Aprilia, Italy. IEEE Geosci. Remote Sens. Lett. 2017, 14, 107–111. [Google Scholar] [CrossRef]
- Gao, L.; Zhan, W.; Huang, F.; Quan, J.; Lu, X.; Wang, F.; Ju, W.; Zhou, J. Localization or globalization? Determination of the optimal regression window for disaggregation of land surface temperature. IEEE Trans. Geosci. Remote Sens. 2017, 55, 477–490. [Google Scholar] [CrossRef]
- Li, X.; Xin, X.; Jiao, J.; Peng, Z.; Zhang, H.; Shao, S.; Liu, Q. Estimating subpixel surface heat fluxes through applying temperature-sharpening methods to MODIS data. Remote Sens. 2017, 9, 836. [Google Scholar] [CrossRef] [Green Version]
- Zawadzka, J.; Corstanje, R.; Harris, J.; Truckell, I. Downscaling Landsat-8 land surface temperature maps in diverse urban landscapes using multivariate adaptive regression splines and very high resolution auxiliary data. Int. J. Digit. Earth 2020, 13, 899–914. [Google Scholar] [CrossRef] [Green Version]
- Yang, G.; Pu, R.; Zhao, C.; Huang, W.; Wang, J. Estimation of subpixel land surface temperature using an endmember index based technique: A case examination on ASTER and MODIS temperature products over a heterogeneous area. Remote Sens. Environ. 2011, 115, 1202–1219. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Xia, H.; Chen, Y.; Li, Y.; Quan, J. Combining kernel-driven and fusion-based methods to generate daily high spatial resolution land surface temperatures. Remote Sens. Environ. 2019, 224, 259–274. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Q.; Yin, K.; He, G.; Zhang, Z.; Wang, G.; Wen, M.; Zhang, N. Spatial downscaling of land surface temperature based on a multi-factor geographically weighted machine learning model. Remote Sens. 2021, 13, 1186. [Google Scholar] [CrossRef]
- Li, W.; Ni, L.; Li, Z.-L.; Duan, S.-B.; Wu, H. Evaluation of machine learning algorithms in spatial downscaling of MODIS land surface temperature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2299–2307. [Google Scholar] [CrossRef]
- Deng, C.; Wu, C. Examining the impacts of urban biophysical compositions on surface urban heat island: A spectral unmixing and thermal mixing approach. Remote Sens. Environ. 2013, 131, 262–274. [Google Scholar] [CrossRef]
- Deng, C.; Wu, C. Estimating very high resolution urban surface temperature using a spectral unmixing and thermal mixing approach. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 155–164. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, W.; Marinoni, A.; Gao, L.; Zhang, B. An improved spatial and temporal reflectance unmixing model to synthesize time series of Landsat-like images. Remote Sens. 2016, 10, 1388. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Cai, F.; Tian, J.; Williams, T. Spatiotemporal fusion of multisource remote sensing data: Literature survey, taxonomy, principles, applications, and future directions. Remote Sens. 2018, 10, 527. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Schmitz, O.; Lu, M.; Karssenberg, D. Thermal unmixing based downscaling for fine resolution diurnal land surface temperature analysis. ISPRS J. Photogramm. Remote Sens. 2020, 161, 76–89. [Google Scholar] [CrossRef]
- Zhan, W.; Chen, Y.; Zhou, J.; Wang, J.; Liu, W.; Voogt, J.; Zhu, X.; Quan, J.; Li, J. Disaggregation of remotely sensed land surface temperature: Literature survey, taxonomy, issues, and caveats. Remote Sens. Environ. 2013, 131, 119–139. [Google Scholar] [CrossRef]
- Jin, Y.; Yong, G.; Wang, J.; Chen, Y.; Heuvelink, G.B.M.; Peter, M.; Atkinson, P.M. Downscaling AMSR-2 Soil Moisture Data with Geographically Weighted Area-to-Area Regression Kriging. Trans. Geosci. Remote Sens. 2018, 56, 2362–2376. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Wen, F.; Wang, Q.; Sanchez, N.; Piles, M. Seamless downscaling of the ESA CCI soil moisture data at the daily scale with MODIS land products. J. Hydrol. 2021, 603, 126930. [Google Scholar] [CrossRef]
- Garrigues, S.; Allard, D.; Baret, F.; Morisette, J. Multivariate quantification of landscape spatial heterogeneity using variogram models. Remote Sens. Environ. 2008, 112, 216–230. [Google Scholar] [CrossRef]
- Hu, Z.; Islam, S. A framework for analyzing and designing scale invariant remote sensing algorithms. IEEE Trans. Geosci. Remote Sens. 1997, 35, 747–755. [Google Scholar]
- Hu, Z.; Islam, S. Effects of subgrid-scale heterogeneity of soil wetness and temperature on grid-scale evaporation and its parameterization. Int. J. Climatol. 1998, 18, 49–63. [Google Scholar] [CrossRef]
- Liu, H.; Weng, Q. Scaling effect on the relationship between landscape pattern and land surface temperature: A case study of Indianapolis, United States. Photogramm. Eng. Remote Sens. 2009, 75, 291–304. [Google Scholar] [CrossRef] [Green Version]
- Wikipedia, City of Yokohama, Japan. Available online: https://en.wikipedia.org/wiki/Yokohama#Climate (accessed on 23 May 2021).
- World Weather Online, Aprilia Weather, Lazio, IT. Available online: https://www.worldweatheronline.com/aprilia-weather/lazio/it.aspx (accessed on 23 May 2021).
- Yamaguchi, Y.; Kahle, A.B.; Tsu, H.; Kawakami, T.; Pniel, M. Overview of advanced spaceborne thermal emission and reflection radiometer (ASTER). IEEE Trans. Geosci. Remote Sens. 1998, 36, 1062–1071. [Google Scholar] [CrossRef] [Green Version]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jimenez-Munoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT5 TM. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Pu, R.; Gong, P.; Michishita, R.; Sasagawa, T. Assessment of multi-resolution and multi-sensor data for urban surface temperature retrieval. Remote Sens. Environ. 2006, 104, 211–225. [Google Scholar] [CrossRef]
- Pu, R.; Xu, B.; Gong, P. Oakwood crown closure estimation by unmixing of Landsat TM data. Int. J. Remote Sens. 2003, 24, 4433–4445. [Google Scholar] [CrossRef]
- Wilson, J.S.; Clay, M.; Martin, E.; Stuckey, D.; Vedder-Risch, K. Evaluating environmental influences of zoning in urban ecosystems with remote sensing. Remote Sens. Environ. 2003, 86, 303–321. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. Spectral mixture analysis of ASTER images for examining the relationship between urban thermal features and biophysical descriptors in Indianapolis, Indiana, USA. Remote Sens. Environ. 2006, 104, 157–167. [Google Scholar] [CrossRef]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V.; Galve, M.; Valor, E.; Niclòs, R.; Sánchez, J.M.; Rivas, R. Ground measurements for the validation of land surface temperatures derived from AATSR and MODIS data. Remote Sens. Environ. 2005, 97, 288–300. [Google Scholar] [CrossRef]
- White-Newsome, J.L.; Brines, S.J.; Brown, D.G.; Dvonch, J.T.; Gronlund, C.J.; Zhang, K.; Oswald, E.M.; O’Neill, M.S. Validating satellite-derived land surface temperature with in situ measurements: A public health perspective. Environ. Health Perspect. 2013, 12, 925–931. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeganathan, C.; Hamm, N.A.S.; Mukherjee, S.; Atkinson, P.M.; Raju, P.L.N.; Dadhwal, V.K. Evaluating a thermal image sharpening model over a mixed agricultural landscape in India. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 178–191. [Google Scholar] [CrossRef]
- Bisquert, M.; Sánchez, J.M.; Caselles, V. Evaluation of disaggregation methods for downscaling MODIS land surface temperature to Landsat spatial resolution in Barrax test site. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1430–1438. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Oltra-Carrió, R.; Sòria, G.; Bianchi, R.; Paganini, M. Impact of spatial resolution and satellite overpass time on evaluation of the surface urban heat island effects. Remote Sens. Environ. 2012, 117, 50–56. [Google Scholar] [CrossRef]


| LST Products or Optical Data | Acquisition (Date and Time) | DLST or ULST or Optical Data (Bands, Wavelengths) | Spectral Clusters and Scaling Factors |
|---|---|---|---|
| CASE I data set | |||
| ASTER 90 m LST | 04/25/2004, around 10:30 a.m. local time | DLST: 62 m, 54 m, 46 m, 38 m, 30 m, 22 m, 14 m, 10 m, 6 m, 2 m | 6 scaling factors and 10 spectral clusters calculated from the AISA selected 10 VNIR bands |
| TABI 2 m LST | 05/26/2004, 15:00–16:00 p.m. local time | ULST: 62 m, 54 m, 46 m, 38 m, 30 m, 22 m, 14 m, 10 m, 6 m | - |
| AISA 2 m optical data | 01/30/2003, 05/14/2003 | selected 10 VNIR bands | 6 scaling factors and 10 spectral clusters calculated for ASTER LST downscaling |
| CASE II data set | |||
| Thermal retrieved 2 m LST | 03/19/2015, around 12:00 p.m. UTC | ULST: 100 m, 62 m, 54 m, 46 m, 38 m, 30 m, 22 m, 14 m, 10 m, 6 m | - |
| VNIR 0.5 m optical data | 03/19/2015, around 12:00 p.m. UTC | three VNIR bands: green (0.53–0.57 μm), red (0.65–0.69 μm), & NIR (0.76–0.83 μm) | 6 scaling factors and 10 spectral clusters calculated for upscaled 100 m LST downscaling |
| Spectral Cluster | 1 Mean T/SD from 2 m LST (°C) | 2 Thermal Component T (°C) | Surface Cover Materials and Types | 3 Thermal Characteristics |
|---|---|---|---|---|
| SC1 | 32.17/5.07 | 31.38 | shaded areas, very low albedo residential areas, dark soil, water bodies | low—mid thermal radiance, more latent heat exchange |
| SC2 | 32.92/5.09 | 35.99 | low albedo impervious areas (most residential areas and dark road surfaces) | mild—high thermal radiance, more sensible heat exchange |
| SC3 | 34.32/4.93 | 37.23 | light gray road surface and other mild albedo impervious surfaces | high thermal radiance with sensible heat exchange |
| SC4 | 29.92/4.49 | 25.04 | vegetated areas (turf, lawn & shrub) | low thermal radiance with latent heat exchange |
| SC5 | 34.30/4.93 | 35.74 | mild albedo impervious areas (most parking lots, roofs) | mild—high thermal radiance, more sensible heat exchange |
| SC6 | 33.79/5.01 | 28.83 | low albedo impervious areas (most parking lots, roofs) | mild thermal radiance, less sensible heat exchange |
| SC7 | 29.83/4.34 | 30.19 | bright vegetated area (tree canopy) | low thermal radiance with latent heat exchange |
| SC8 | 31.51/4.47 | 25.90 | spare vegetated areas (turf & lawn or wet bare soil) | low thermal radiance, more latent heat exchange |
| SC9 | 32.26/5.67 | 28.71 | playground, gray bare soil. | low—mild thermal radiance, less sensible heat exchange |
| SC10 | 29.81/6.70 | 33.66 | bright roofs | mid thermal radiance with sensible heat exchange |
| DLST (LST) | Min | Max | Mean | SD |
|---|---|---|---|---|
| CASE I with ASTER 90 m LST and AISA optical data (DLST by using the modified TC-based TSU model) | ||||
| ASTER 90 m LST | 23.05 | 36.95 | 32.65 | 2.04 |
| 62 m DLST | 22.16 | 38.19 | 32.69 | 2.31 |
| 54 m DLST | 23.53 | 37.66 | 32.71 | 2.45 |
| 46 m DLST | 22.95 | 38.72 | 32.70 | 2.51 |
| 38 m DLST | 22.22 | 39.24 | 32.68 | 2.65 |
| 30 m DLST | 21.92 | 39.38 | 32.70 | 2.73 |
| 22 m DLST | 21.34 | 40.66 | 32.68 | 2.93 |
| 14 m DLST | 20.76 | 40.87 | 32.67 | 3.15 |
| 10 m DLST | 19.31 | 41.83 | 32.64 | 3.33 |
| 6 m DLST | 18.49 | 43.05 | 32.60 | 3.58 |
| 2 m DLST * | 19.20 | 41.55 | 32.66 | 4.35 |
| TABI 2 m retrieved LST | 11.54 | 52.78 | 32.67 | 5.19 |
| CASE II with high resolution thermal retrieved LST and optical data (DLST by using the REG model) | ||||
| Upscaled 100 m retrieved LST | 9.82 | 30.82 | 20.74 | 2.50 |
| 62 m DLST | 12.89 | 31.27 | 20.77 | 2.62 |
| 54 m DLST | 11.69 | 31.64 | 20.78 | 2.75 |
| 46 m DLST | 12.99 | 31.47 | 20.78 | 2.79 |
| 38 m DLST | 12.91 | 32.09 | 20.80 | 2.86 |
| 30 m DLST | 11.62 | 32.80 | 20.81 | 3.00 |
| 22 m DLST | 11.37 | 32.72 | 20.82 | 3.13 |
| 14 m DLST | 10.42 | 33.65 | 20.82 | 3.36 |
| 10 m DLST | 8.95 | 35.18 | 20.83 | 3.50 |
| 6 m DLST | 5.50 | 35.40 | 20.83 | 3.67 |
| 2 m DLST * | 1.64 | 34.39 | 20.73 | 3.59 |
| 2 m retrieved LST | 0.00 | 50.00 | 20.75 | 4.88 |
| DLST | RMSE (°C) | MAE(°C) | Note | ||||||
|---|---|---|---|---|---|---|---|---|---|
| W/out CT | With CT | Improved with CT (%) | W/out CT | With CT | Improved with CT (%) | ||||
| CASE I with ASTER 90 m LST and AISA optical data (DLST by using the TC-based TSU model) | |||||||||
| 62 m DLST | 1.55 | 1.07 | 30.97 | 1.17 | 0.85 | 27.35 | compared to ULST of TABI 2m LST | ||
| 54 m DLST | 1.67 | 1.14 | 31.74 | 1.28 | 0.89 | 30.47 | compared to ULST of TABI 2m LST | ||
| 46 m DLST | 1.85 | 1.22 | 34.05 | 1.41 | 0.94 | 33.33 | compared to ULST of TABI 2m LST | ||
| 38 m DLST | 2.04 | 1.32 | 35.29 | 1.57 | 1.00 | 36.31 | compared to ULST of TABI 2m LST | ||
| 30 m DLST | 2.30 | 1.48 | 35.65 | 1.77 | 1.11 | 37.29 | compared to ULST of TABI 2m LST | ||
| 22 m DLST | 2.67 | 1.69 | 36.70 | 2.05 | 1.23 | 40.00 | compared to ULST of TABI 2m LST | ||
| 14 m DLST | 3.24 | 2.05 | 36.73 | 2.52 | 1.46 | 42.06 | compared to ULST of TABI 2m LST | ||
| 10 m DLST | 3.69 | 2.33 | 36.86 | 2.90 | 1.64 | 43.45 | compared to ULST of TABI 2m LST | ||
| 6 m DLST | 4.4 | 2.78 | 36.82 | 3.49 | 1.95 | 44.13 | compared to ULST of TABI 2m LST | ||
| Average | 34.98 | 37.15 | |||||||
| CASE II with high resolution thermal retrieved LST and optical data (DLST by using the REG model) | |||||||||
| 62 m DLST | 1.97 | 1.33 | 32.49 | 1.32 | 0.84 | 36.36 | compared to ULST of retrieved 2m LST | ||
| 54 m DLST | 2.02 | 1.33 | 34.16 | 1.34 | 0.81 | 39.55 | compared to ULST of retrieved 2m LST | ||
| 46 m DLST | 2.16 | 1.42 | 34.26 | 1.45 | 0.86 | 40.69 | compared to ULST of retrieved 2m LST | ||
| 38 m DLST | 2.36 | 1.57 | 33.47 | 1.58 | 0.92 | 41.77 | compared to ULST of retrieved 2m LST | ||
| 30 m DLST | 2.50 | 1.61 | 35.60 | 1.67 | 0.95 | 43.11 | compared to ULST of retrieved 2m LST | ||
| 22 m DLST | 2.77 | 1.86 | 32.85 | 1.84 | 1.06 | 42.39 | compared to ULST of retrieved 2m LST | ||
| 14 m DLST | 3.13 | 2.11 | 32.59 | 2.09 | 1.19 | 43.06 | compared to ULST of retrieved 2m LST | ||
| 10 m DLST | 3.39 | 2.29 | 32.45 | 2.28 | 1.30 | 42.98 | compared to ULST of retrieved 2m LST | ||
| 6 m DLST | 3.73 | 2.52 | 32.44 | 2.52 | 1.43 | 43.25 | compared to ULST of retrieved 2m LST | ||
| Average | 33.37 | 41.46 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, R.; Bonafoni, S. Reducing Scaling Effect on Downscaled Land Surface Temperature Maps in Heterogenous Urban Environments. Remote Sens. 2021, 13, 5044. https://doi.org/10.3390/rs13245044
Pu R, Bonafoni S. Reducing Scaling Effect on Downscaled Land Surface Temperature Maps in Heterogenous Urban Environments. Remote Sensing. 2021; 13(24):5044. https://doi.org/10.3390/rs13245044
Chicago/Turabian StylePu, Ruiliang, and Stefania Bonafoni. 2021. "Reducing Scaling Effect on Downscaled Land Surface Temperature Maps in Heterogenous Urban Environments" Remote Sensing 13, no. 24: 5044. https://doi.org/10.3390/rs13245044
APA StylePu, R., & Bonafoni, S. (2021). Reducing Scaling Effect on Downscaled Land Surface Temperature Maps in Heterogenous Urban Environments. Remote Sensing, 13(24), 5044. https://doi.org/10.3390/rs13245044







