Graph SLAM-Based 2.5D LIDAR Mapping Module for Autonomous Vehicles
Abstract
:1. Introduction
2. Key Solution and Proposed Strategy
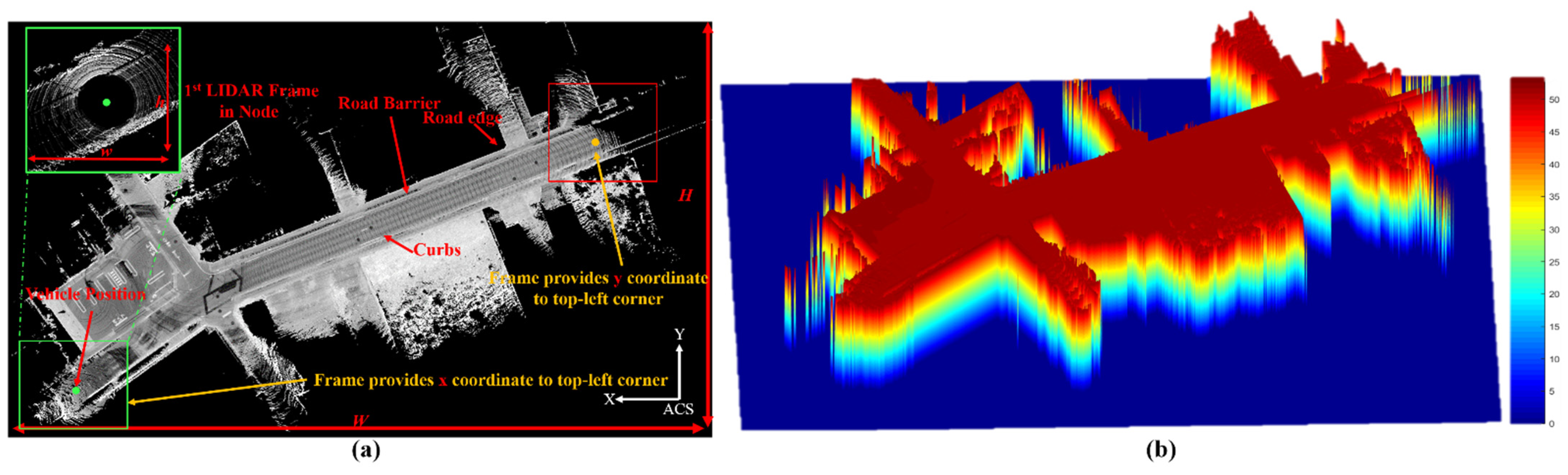
2.1. Node Domain
2.2. GS Optimization Strategy in Node Domain
3. The Proposed Graph SLAM Framework (GS-XYZ)
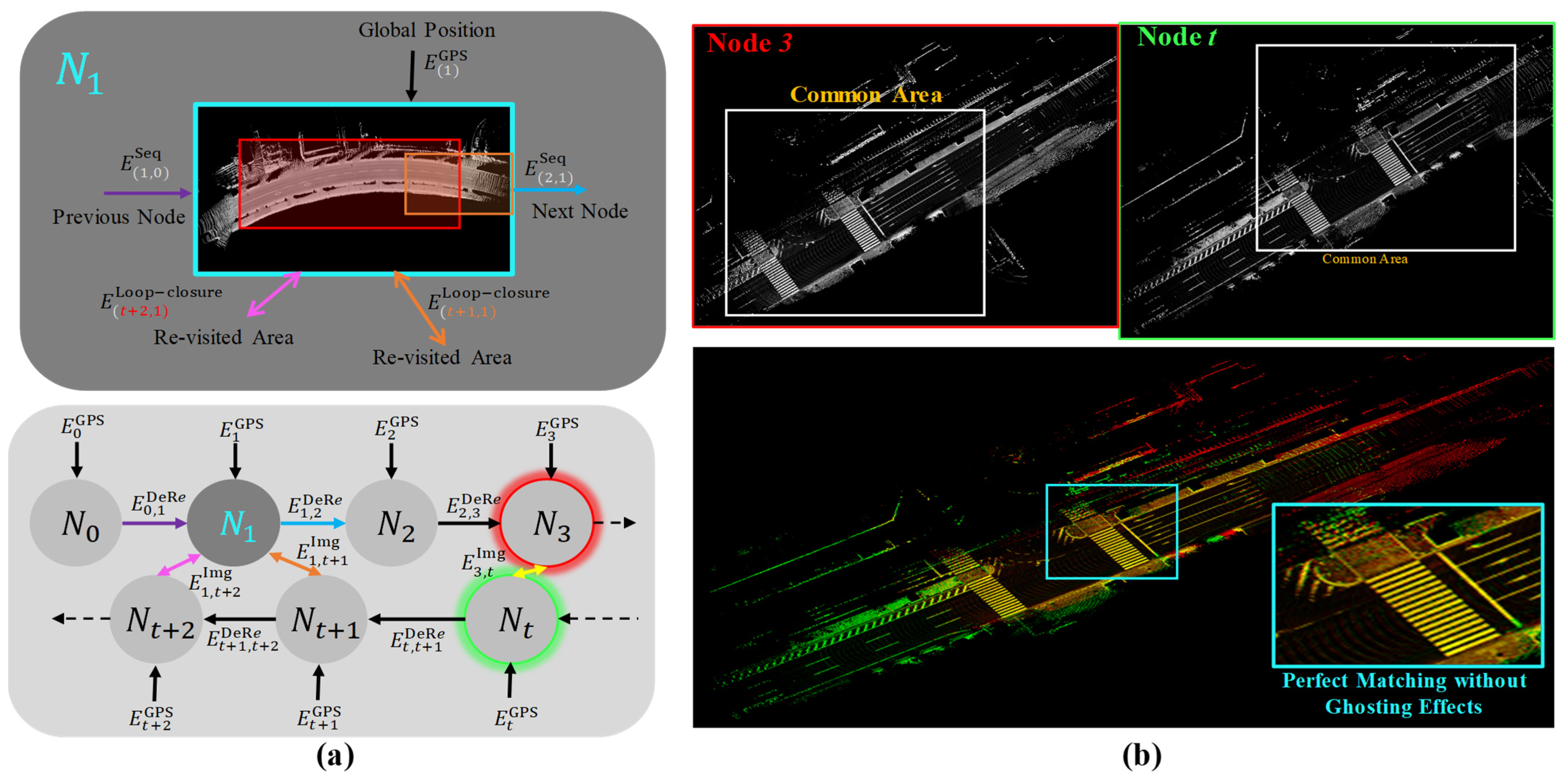
3.1. Edge Selection and Calculation
3.2. Cost Function Concept (Example: GS-XY)
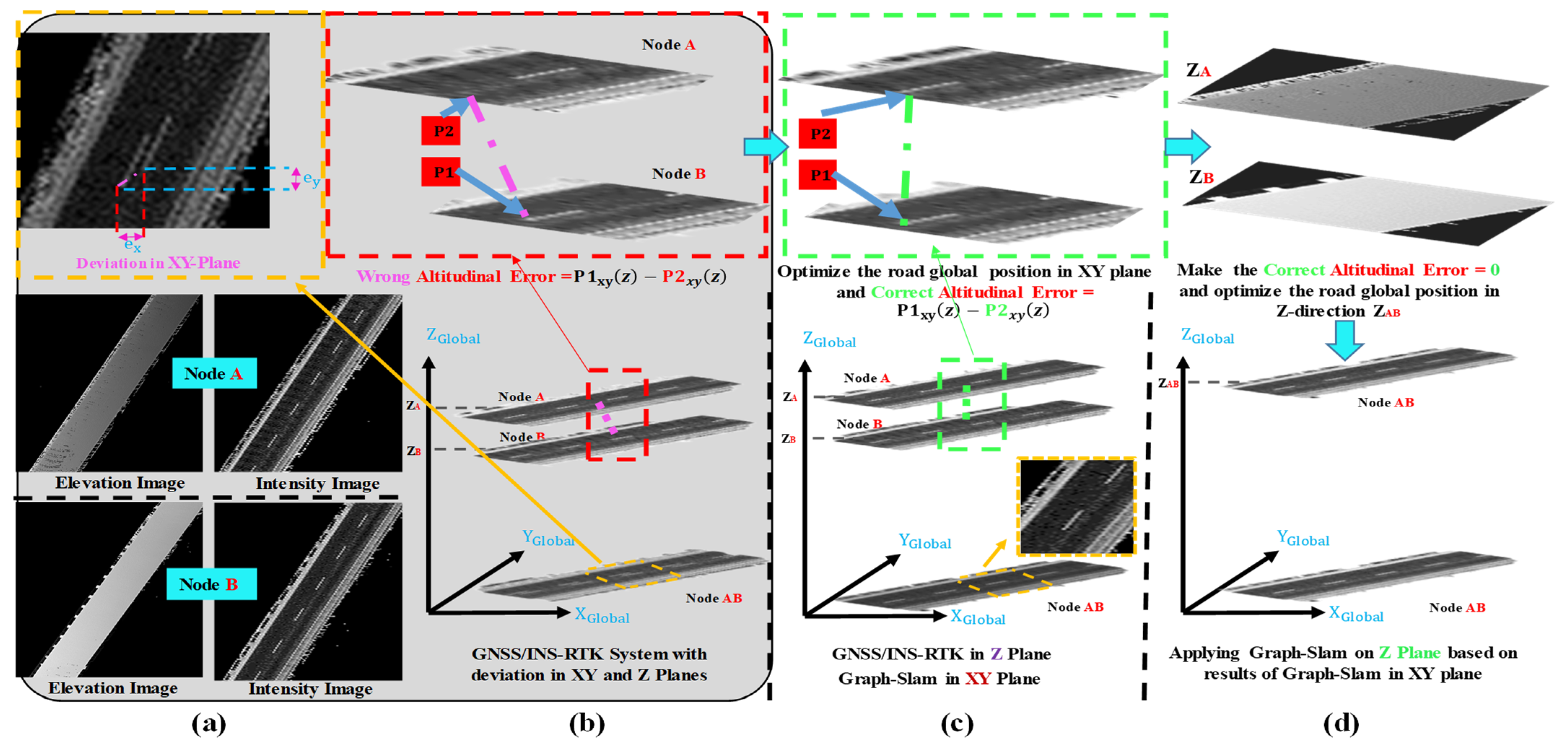
3.3. Transforming GS-XY to GS-Z
4. Experimental Platform and Test Course
4.1. Platform Configuration and Framework Setups
4.2. Test Course
5. Results and Discussion
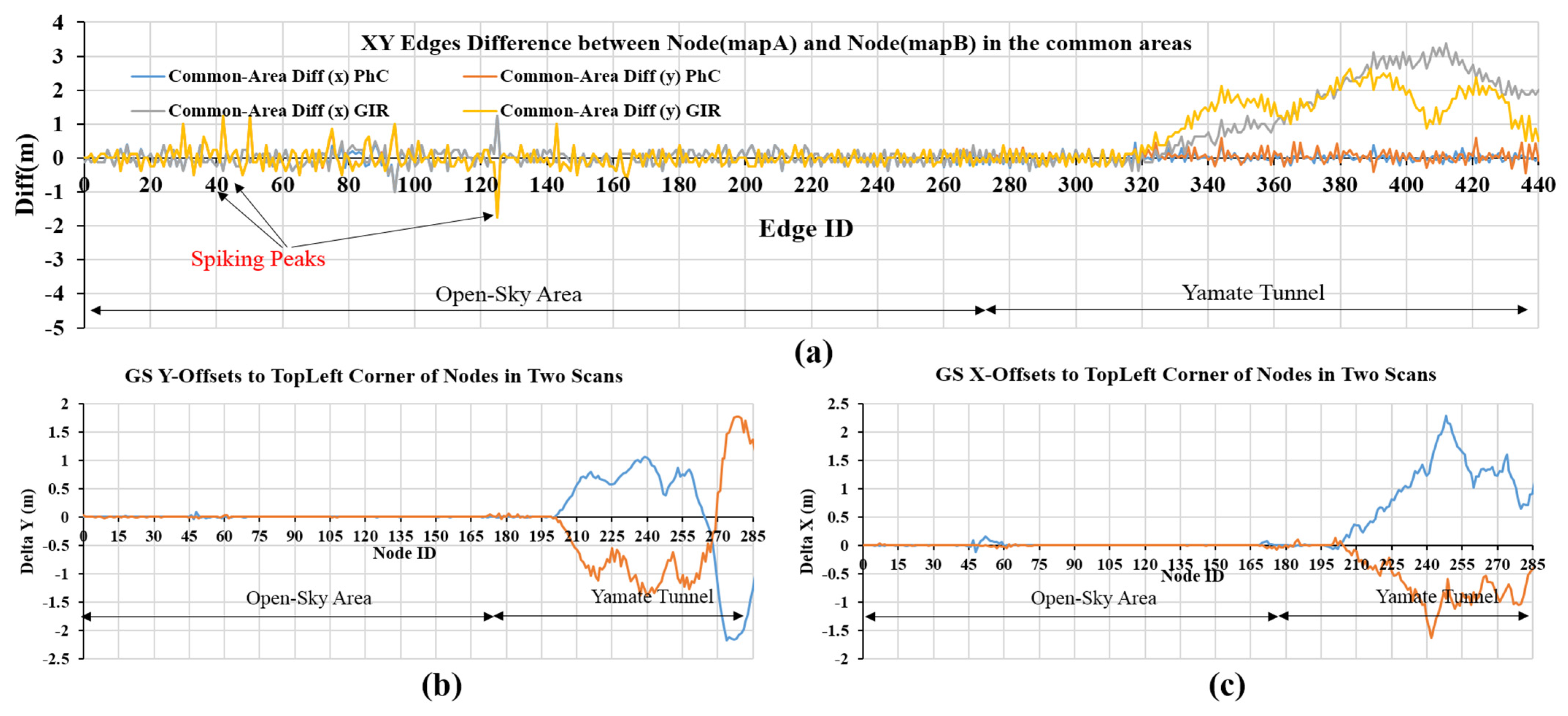
5.1. Graph SLAM in the XY Plane
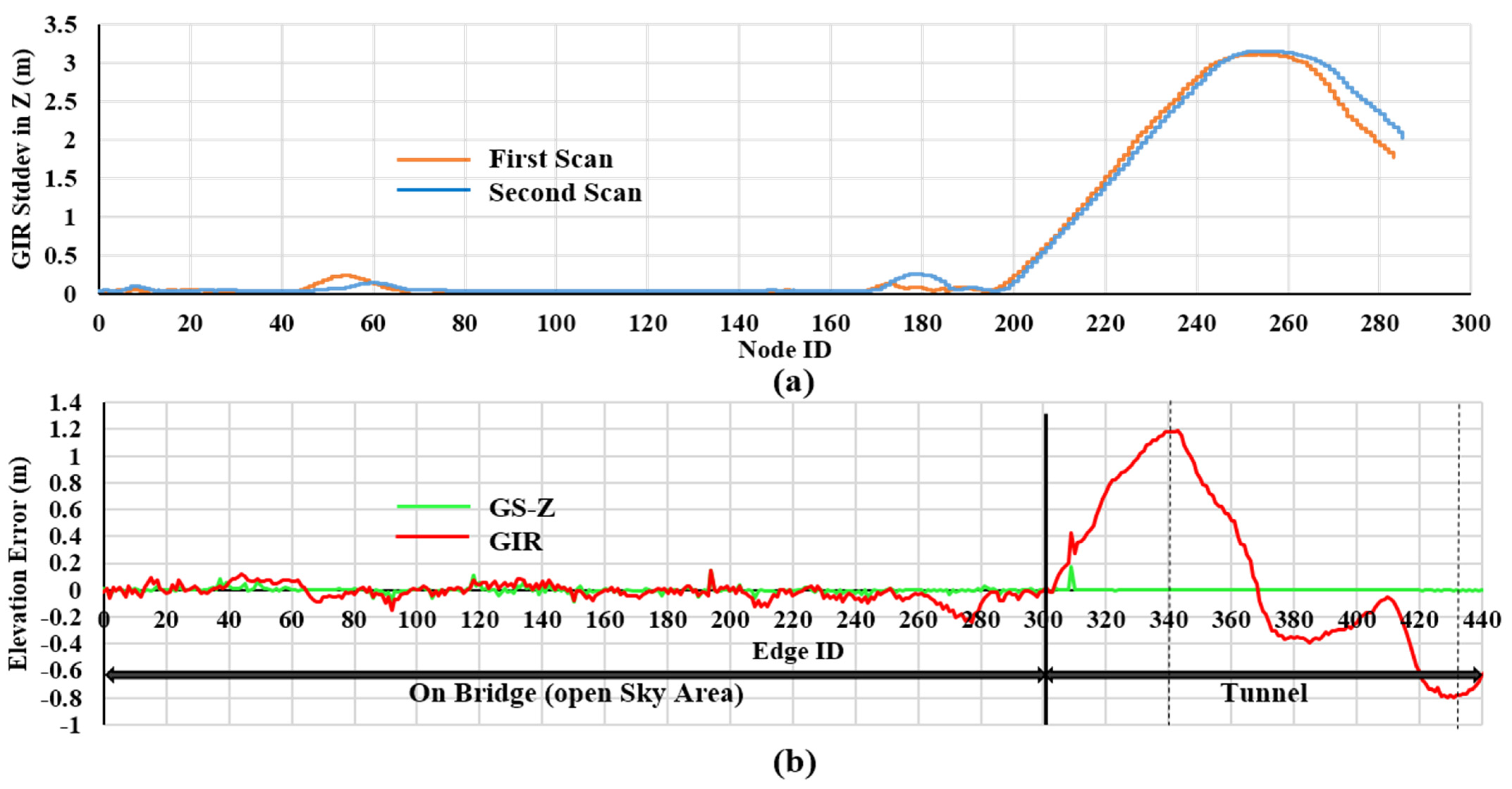
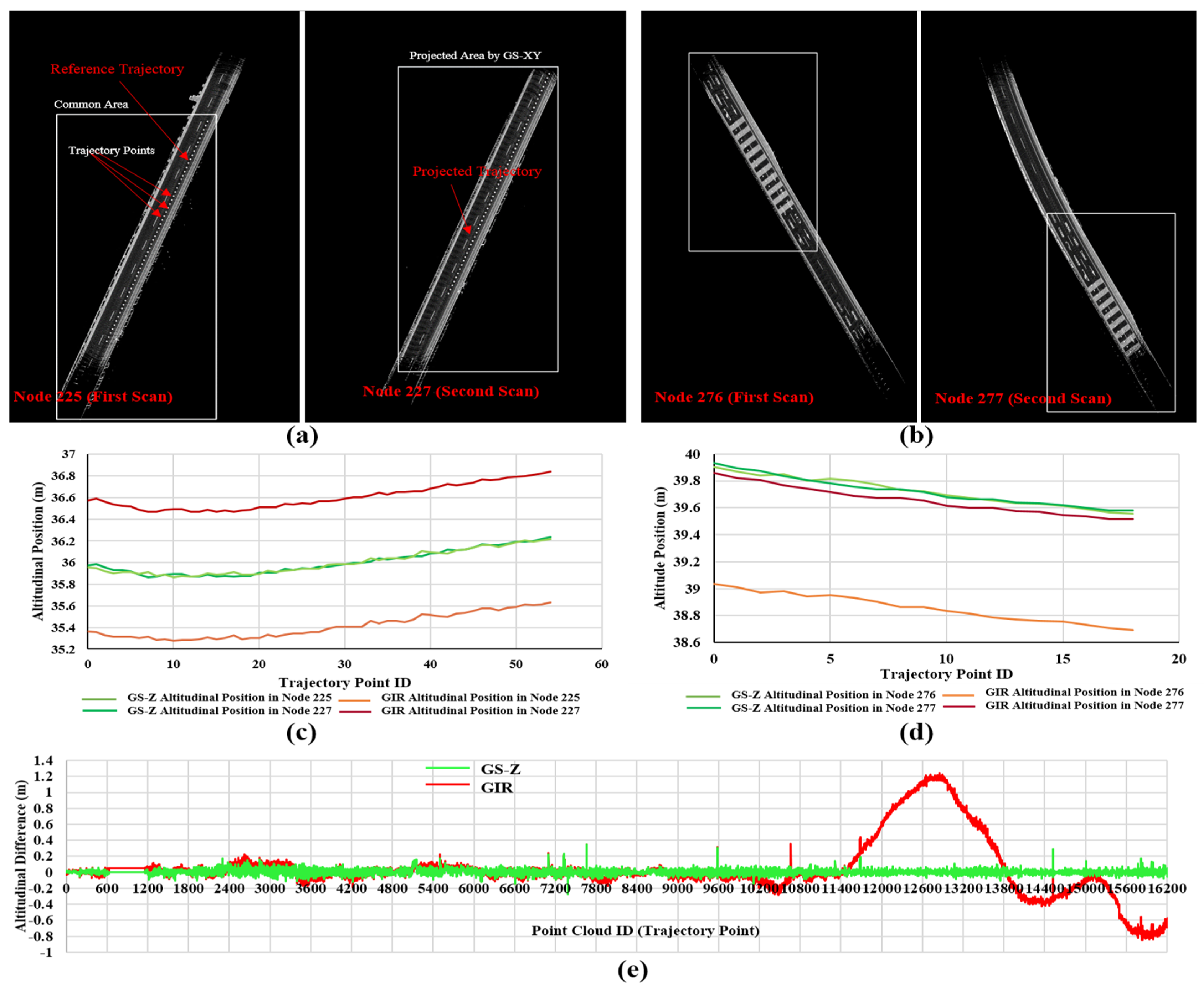
5.2. Graph SLAM in the Z Plane
6. Conclusions
7. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| GS | Graph SLAM |
| DR | Dead Reckoning |
| GIR | GNSS/INS-RTK |
| PhC | Phase Correlation |
| ICP | Iterative Closest Point |
| ACS | Absolute Coordinate System |
| LIDAR | Light Detection and Ranging |
| SLAM | Simultaneous Localization and Mapping |
References
- Aldibaja, M.; Suganuma, N.; Yoneda, K. Robust intensity based localization method for autonomous driving on snow-wet road surface. In Proceedings of the IEEE Transactions on Industrial Informatics; 2017; Volume 13, pp. 2369–2378. Available online: https://ieeexplore.ieee.org/abstract/document/7944675 (accessed on 3 October 2021).
- Pendleton, S.D.; Andersen, H.; Du, X.; Shen, X.; Meghjani, M.; Eng, Y.H.; Rus, D.; Ang, M.H. Perception, planning, control, and coordination for autonomous vehicles. Machines 2017, 5, 6. [Google Scholar] [CrossRef]
- Kuramoto, A.; Aldibaja, M.; Yanase, R.; Kameyama, J.; Yoneda, K.; Suganuma, N. Mono-Camera based 3D object tracking strategy for autonomous vehicles. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 459–464. [Google Scholar]
- Thrun, S.; Montemerlo, M. The graph SLAM algorithm with applications to large-scale mapping of urban structures. Int. J. Robot. Res. 2006, 25, 403. [Google Scholar] [CrossRef]
- Grisetti, G.; Kümmerle, R.; Stachniss, C.; Burgard, W. A Tutorial on Graph-Based SLAM. Proc. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. Available online: https://ieeexplore.ieee.org/document/5681215 (accessed on 3 October 2021). [CrossRef]
- Olson, E.; Agarwal, P. Inference on networks of mixtures for robust robot mapping. Int. J. Robot. Res. 2013, 32, 826–840. [Google Scholar] [CrossRef]
- Roh, H.; Jeong, J.; Cho, Y.; Kim, A. Accurate mobile urban mapping via digital map-based SLAM. Sensors 2016, 16, 1315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Triebel, R.; Pfaff, P.; Burgard, W. Multi-level surface maps for outdoor terrain mapping and loop closing. In Proceedings of the IEEE/RSJ International Conference Intelligent Robots and Systems (IROS), Beijing, China, 9–15 October 2006; pp. 2276–2282. [Google Scholar]
- He, Y.; Liang, B.; Yang, J.; Li, S.; He, J. An iterative closest points algorithm for registration of 3D laser scanner point clouds with Geometric Features. Sensors 2017, 17, 1862. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and ground-optimized Lidar odometry and mapping on variable terrain. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. Lio-sam: Tightly-coupled lidar inertial odometry via smoothing and mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 5135–5142. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.D.; Leonard, J.J. Simultaneous localization and mapping: Present, future, and the robust-perception Age. Proc. IEEE Trans. Robot. 2016, 32, 1309–1332. Available online: https://ieeexplore.ieee.org/document/7747236 (accessed on 3 October 2021). [CrossRef] [Green Version]
- Wolcott, R.; Eustice, R. Fast lidar localization using multiresolution gaussian mixture maps. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2814–2821. [Google Scholar]
- Khot, L.R.; Tang, L.; Steward, B.L.; Han, S. Sensor fusion for roll and pitch estimation improvement of an agricultural sprayer Vehicle. In Proceedings of the American Society of Agricultural and Biological Engineers; 2008; Volume 101, pp. 13–20. Available online: https://dr.lib.iastate.edu/entities/publication/b11aae8f-ccf5-4de8-9a65-d0ec7701be22 (accessed on 3 October 2021).
- Li, X.; Gao, Z.; Chen, X.; Sun, S.; Liu, J. Research on Estimation Method of Geometric Features of Structured Negative Obstacle Based on Single-Frame 3D Laser Point Cloud. Information 2021, 12, 235. [Google Scholar] [CrossRef]
- Lewis, J.P. Fast normalized cross-correlation. Vis. Interface 1993, 10, 120–123. [Google Scholar]
- Besl, P.J.; McKay, H.D. A method for registration of 3-D shapes. Proc. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. Available online: https://ieeexplore.ieee.org/document/121791 (accessed on 3 October 2021). [CrossRef]
- Biber, P.; Straßer, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 27–31 October 2003; pp. 2743–2748. [Google Scholar]
- Sakai, T.; Koide, K.; Miura, J.; Oishi, S. Large-scale 3D outdoor mapping and on-line localization using 3D-2D matching. In Proceedings of the IEEE/SICE International Symposium on System Integration (SII), Taipei, Taiwan, 11–14 December 2017; pp. 829–834. [Google Scholar]
- Nam, T.H.; Shim, J.H.; Cho, Y.I. A 2.5D Map-Based mobile robot localization via cooperation of aerial and ground robots. Sensors 2017, 17, 2730. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aldibaja, M.; Yanase, R.; Kim, T.; Kuramoto, A.; Yoneda, K.; Suganuma, N. Accurate Elevation Maps based Graph-Slam Framework for Autonomous Driving. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 1254–1261. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, J.; He, X.; Ye, C. DLO: Direct LiDAR Odometry for 2.5D Outdoor Environment. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1–5. [Google Scholar]
- Yoon, J.; Kim, B. Vehicle Position Estimation Using Tire Model in Information Science and Applications; Springer: Berlin, Germany, 2015; Volume 339, pp. 761–768. [Google Scholar]
- Ahuja, K.; Tuli, K. Object recognition by template matching using correlations and phase angle method. Int. J. Adv. Res. Comput. Commun. Eng. 2013, 2, 1368–1372. Available online: https://www.ijarcce.com/upload/2013/march/11-kavita%20ahuja%20-%20object%20recognition-c.pdf (accessed on 3 October 2021).
- Sarvaiya, J.; Patnaik, S.; Kothari, K. Image registration using log polar transform and phase correlation to recover higher scale. J. Pattern Recognit. Res. 2012, 7, 90–105. [Google Scholar] [CrossRef]
- Liang, Y. Phase-Correlation Motion Estimation. EE392J Project Report. 2000. Available online: https://web.stanford.edu/class/ee392j/Winter2002/student_projects_final_Winter2000.html (accessed on 3 October 2021).
- Almonacid-Caballer, J.; Pardo-Pascual, J.E.; Ruiz, L.A. Evaluating Fourier cross-correlation sub-pixel registration in landsat images. Remote Sens. 2017, 9, 1051. [Google Scholar] [CrossRef] [Green Version]
- Aldibaja, M.; Suganuma, N.; Yoneda, K. LIDAR-Data accumulation strategy to generate high definition maps for autonomous vehicles. In Proceedings of the IEEE Conference on Multisensor Fusion and Integration for Intelligent Systems, Daegu, Korea, 16–18 November 2017; pp. 422–428. [Google Scholar] [CrossRef]
- Frigo, M.; Johnson, S.G. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. Available online: https://ieeexplore.ieee.org/document/1386650 (accessed on 3 October 2021).





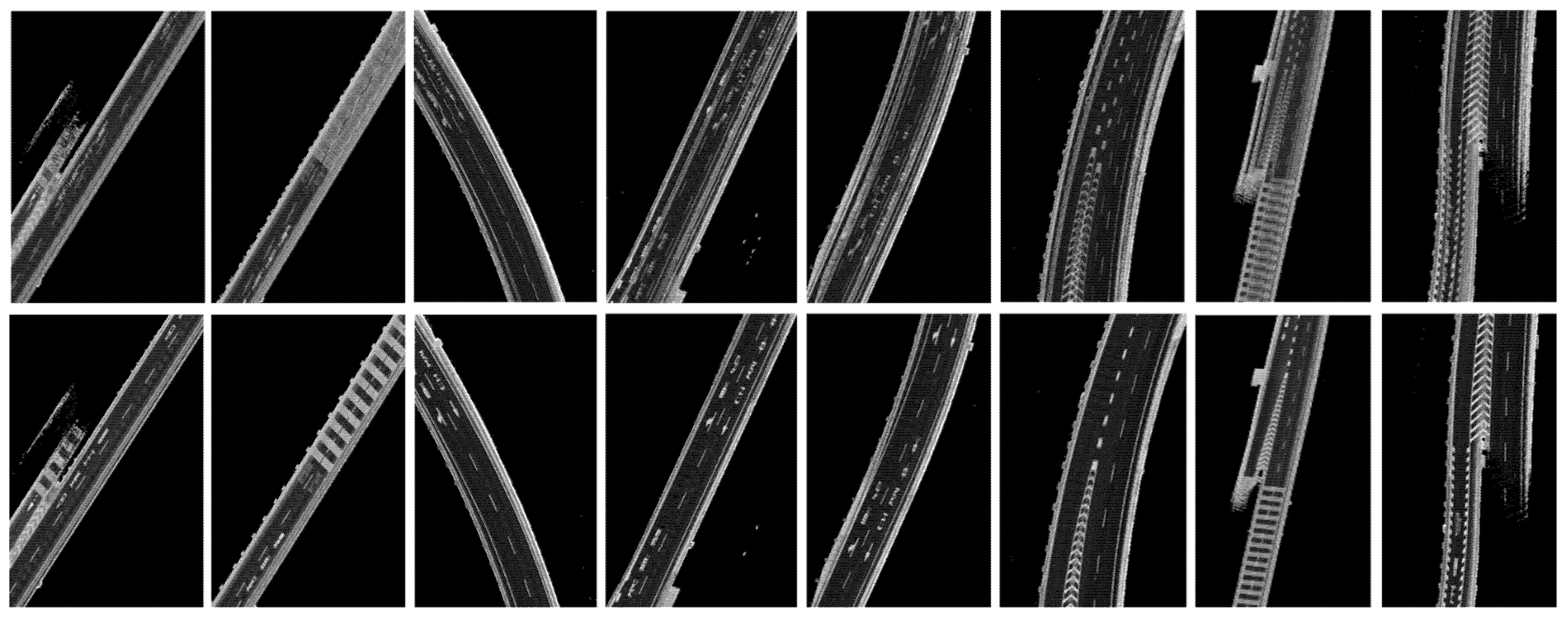

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldibaja, M.; Suganuma, N. Graph SLAM-Based 2.5D LIDAR Mapping Module for Autonomous Vehicles. Remote Sens. 2021, 13, 5066. https://doi.org/10.3390/rs13245066
Aldibaja M, Suganuma N. Graph SLAM-Based 2.5D LIDAR Mapping Module for Autonomous Vehicles. Remote Sensing. 2021; 13(24):5066. https://doi.org/10.3390/rs13245066
Chicago/Turabian StyleAldibaja, Mohammad, and Naoki Suganuma. 2021. "Graph SLAM-Based 2.5D LIDAR Mapping Module for Autonomous Vehicles" Remote Sensing 13, no. 24: 5066. https://doi.org/10.3390/rs13245066
APA StyleAldibaja, M., & Suganuma, N. (2021). Graph SLAM-Based 2.5D LIDAR Mapping Module for Autonomous Vehicles. Remote Sensing, 13(24), 5066. https://doi.org/10.3390/rs13245066






