QDC-2D: A Semi-Automatic Tool for 2D Analysis of Discontinuities for Rock Mass Characterization
Abstract
:1. Introduction
2. Materials and Methods
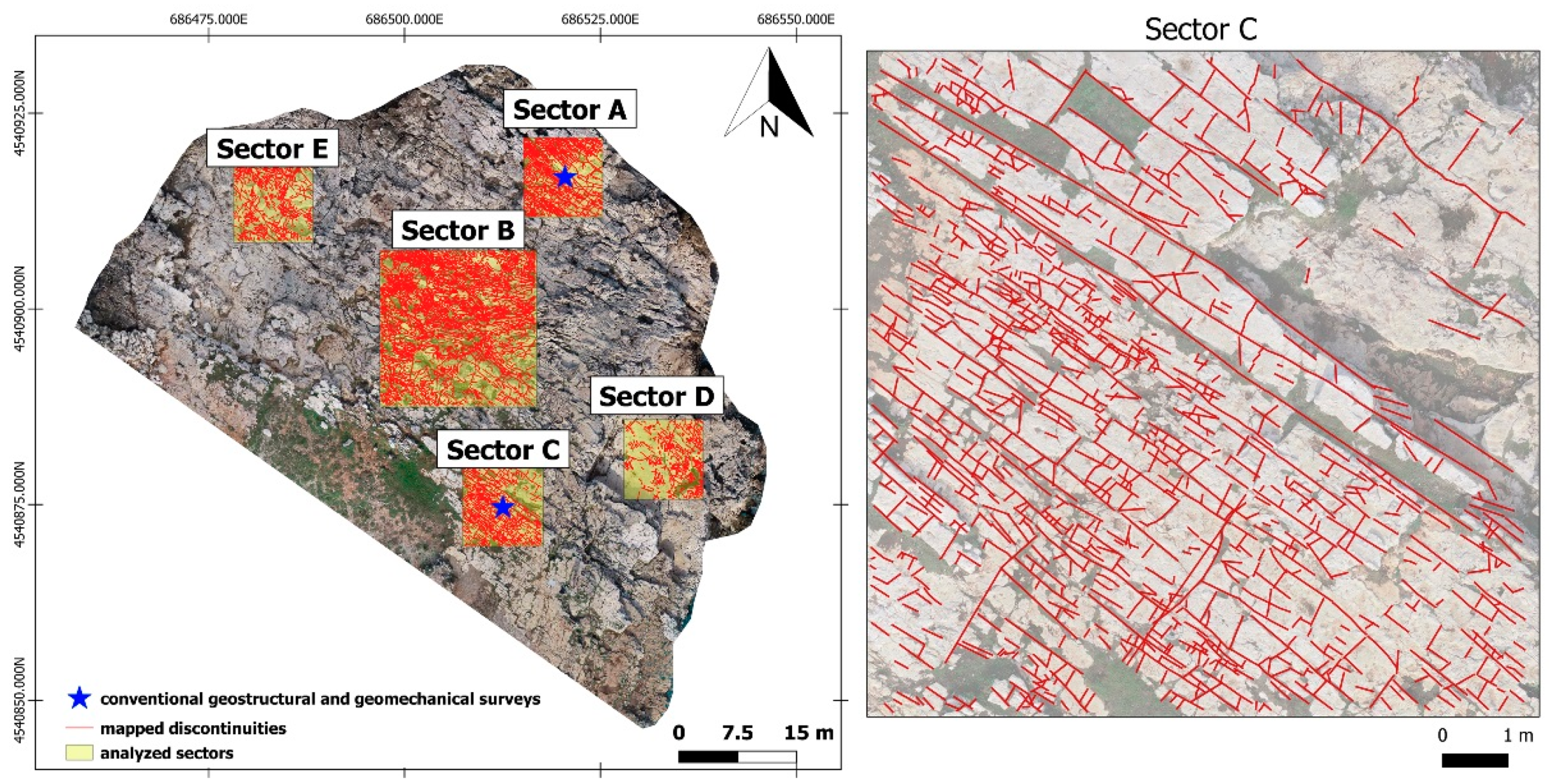
2.1. Study Site
2.2. Generation of the Digital Outcrop Model (DOM)
- (1)
- flight mission planning;
- (2)
- positioning and coordinates’ acquisition of Ground Control Points (GCPs);
- (3)
- flight and image collection;
- (4)
- Structure from Motion (SfM) processing and generation of the dense point cloud; and
- (5)
- building of the orthomosaic.
2.3. Conventional Characterization of Discontinuity Sets
2.4. Manual Mapping of the Fracture Traces
2.5. Methodological Approach for the Digital 2D Quantitative Analysis of Discontinuities
2.6. Workflow of the MATLAB Routine
- graphical representation of the discontinuities;
- semi-automatic classification of the discontinuity sets;
- characterization of one discontinuity set; and
- characterization of the fracture network.
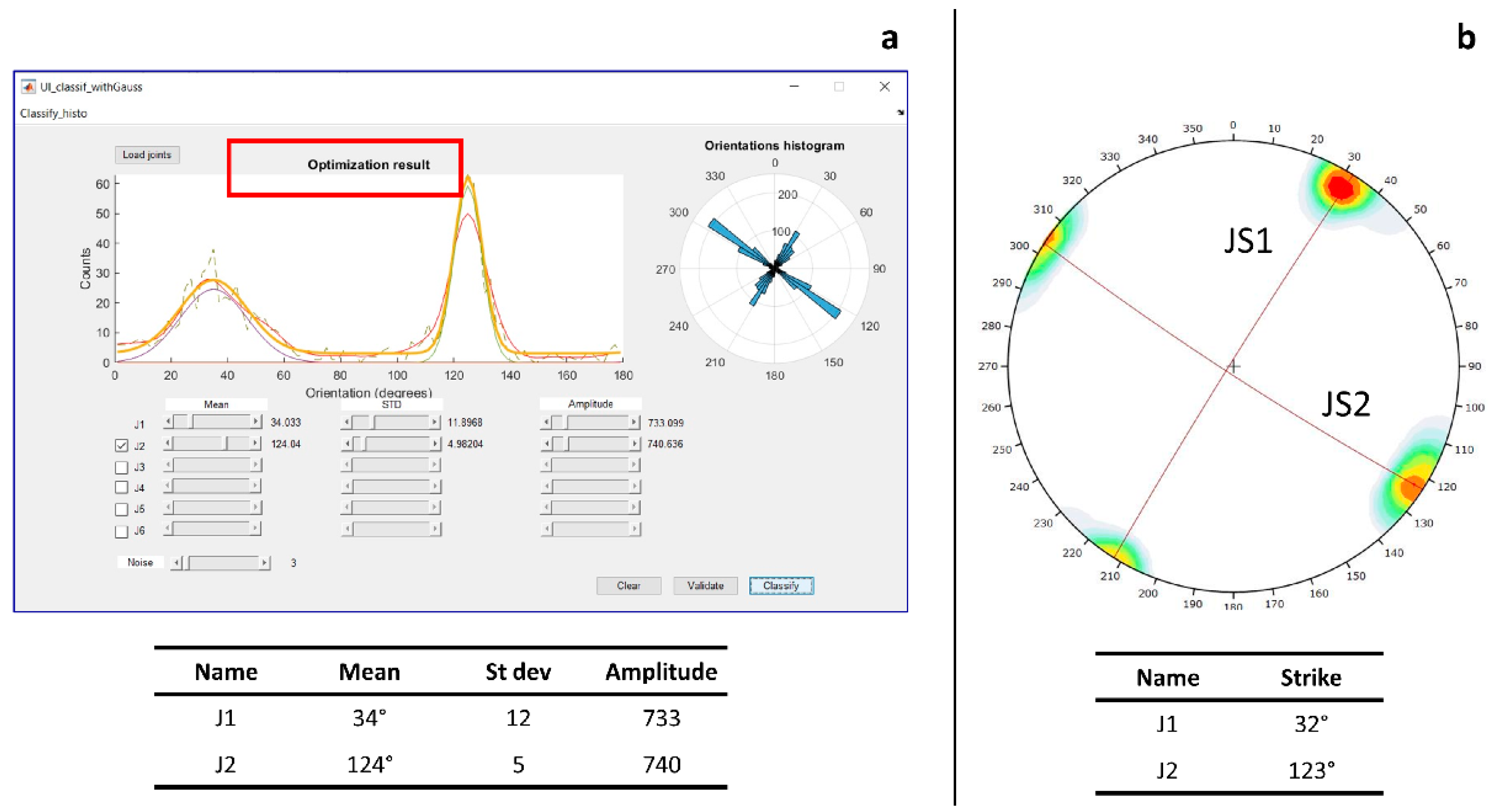
2.6.1. Characterization of the Discontinuity Sets
Orientation
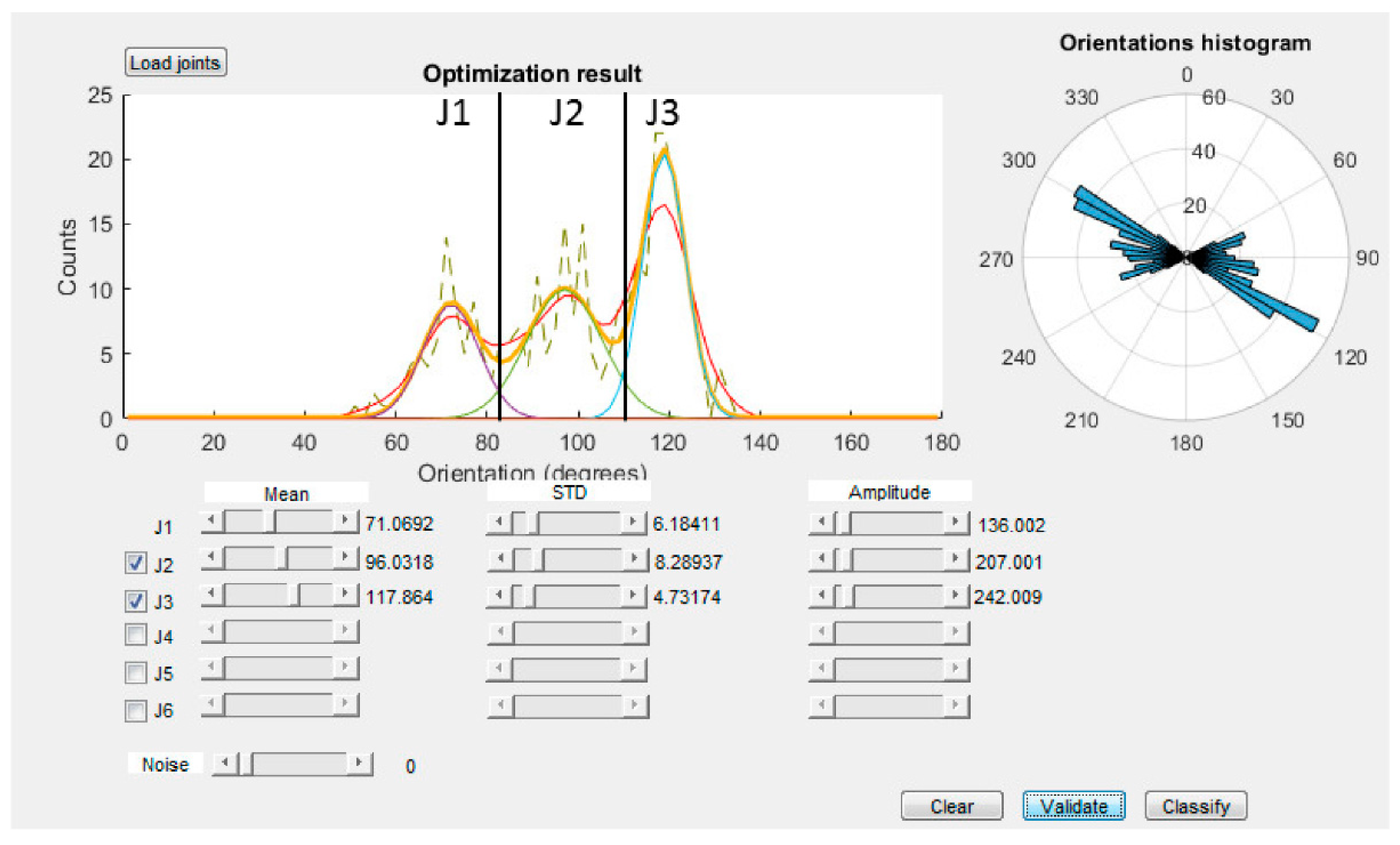
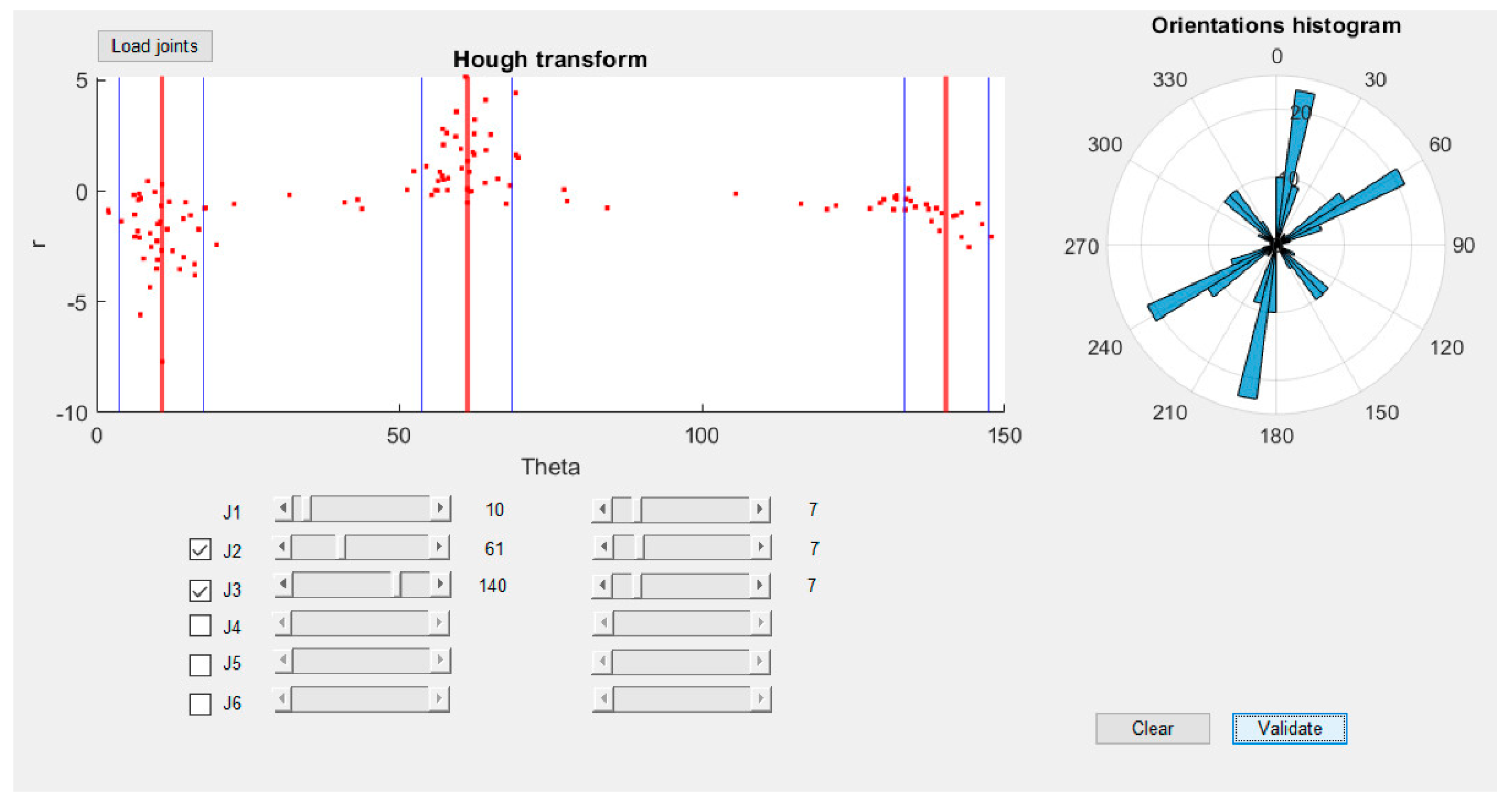
- Method 1: fitting of the composite Gaussian curve
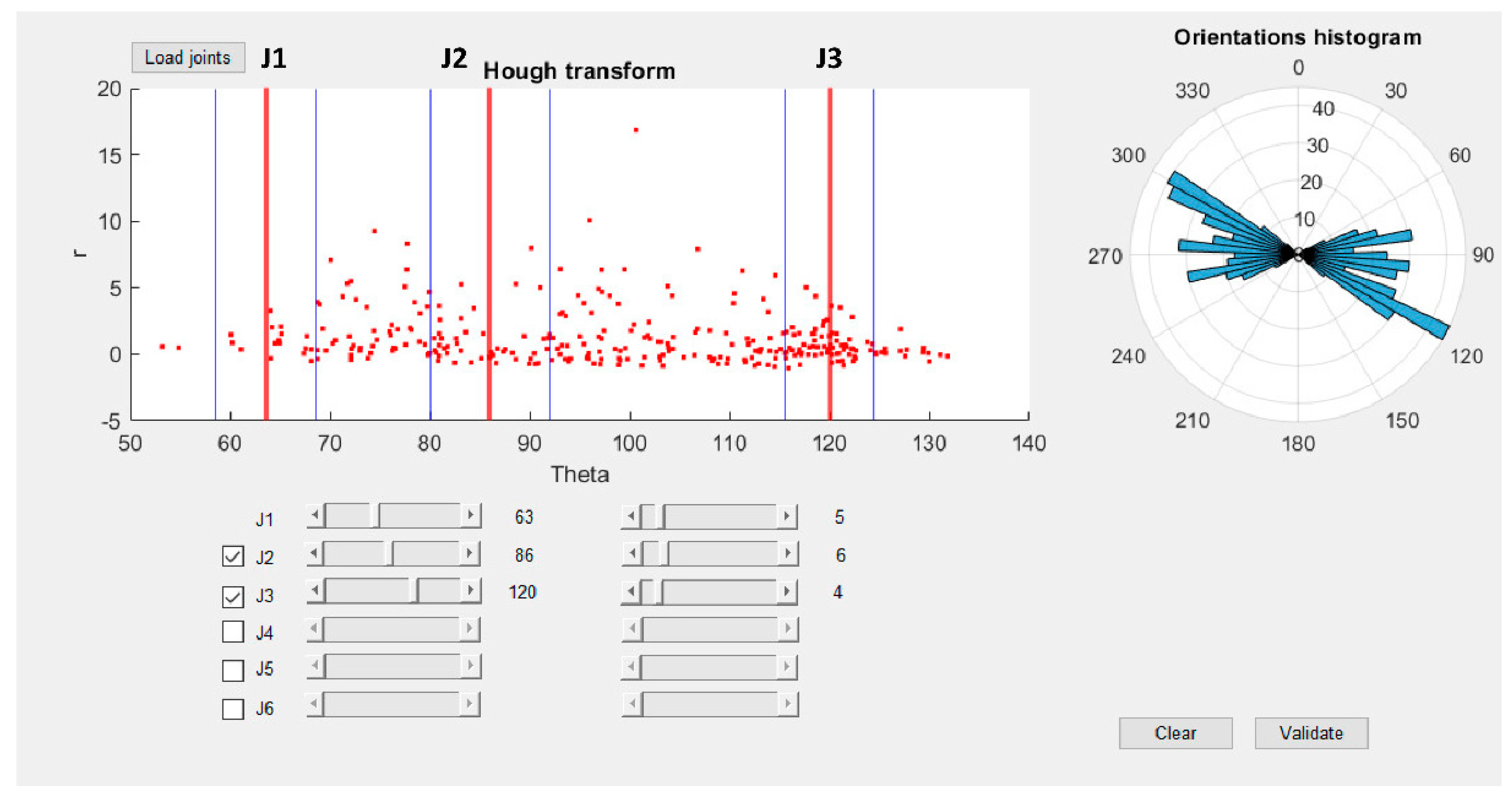
- Method 2: Hough transform
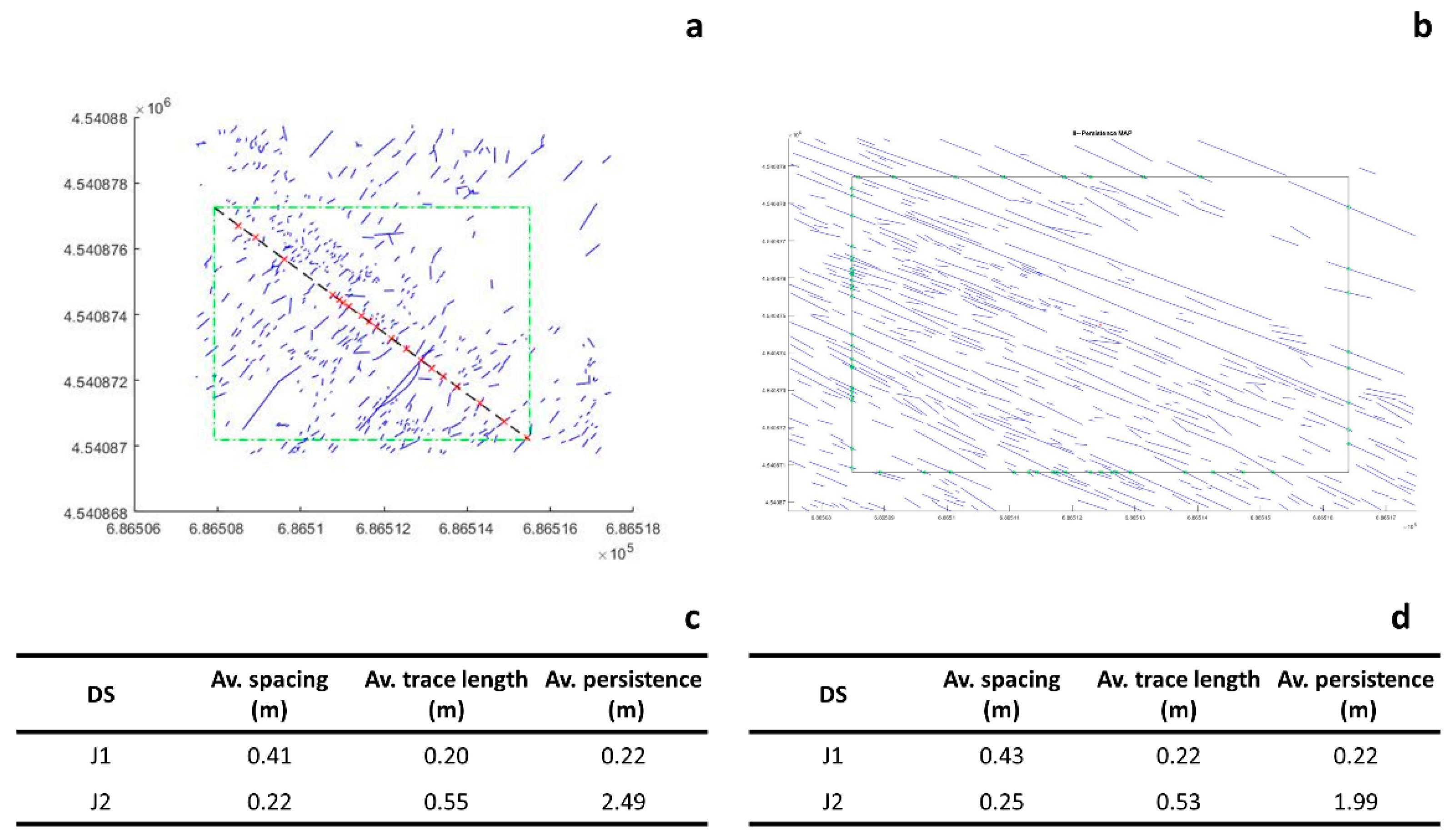
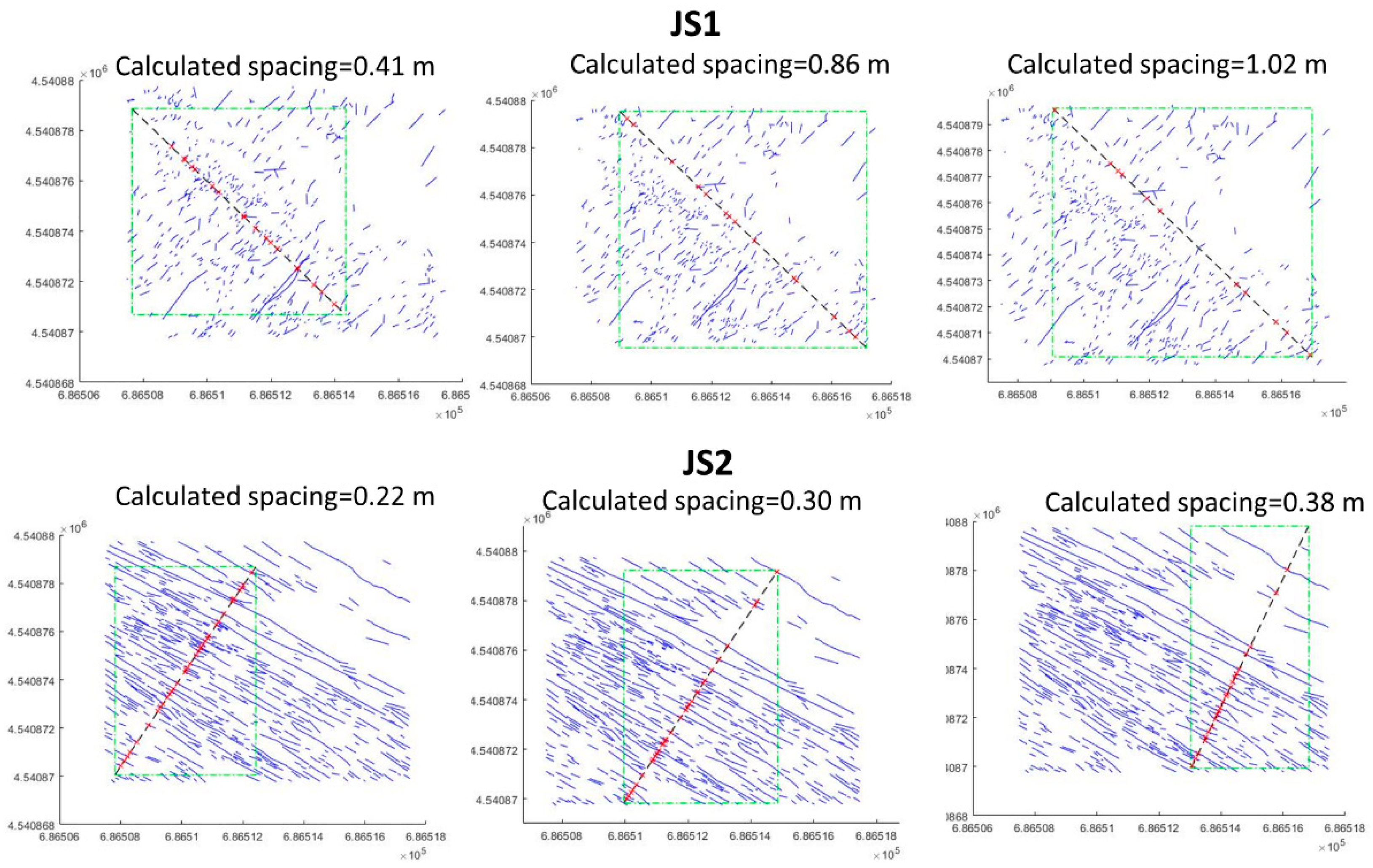
Spacing
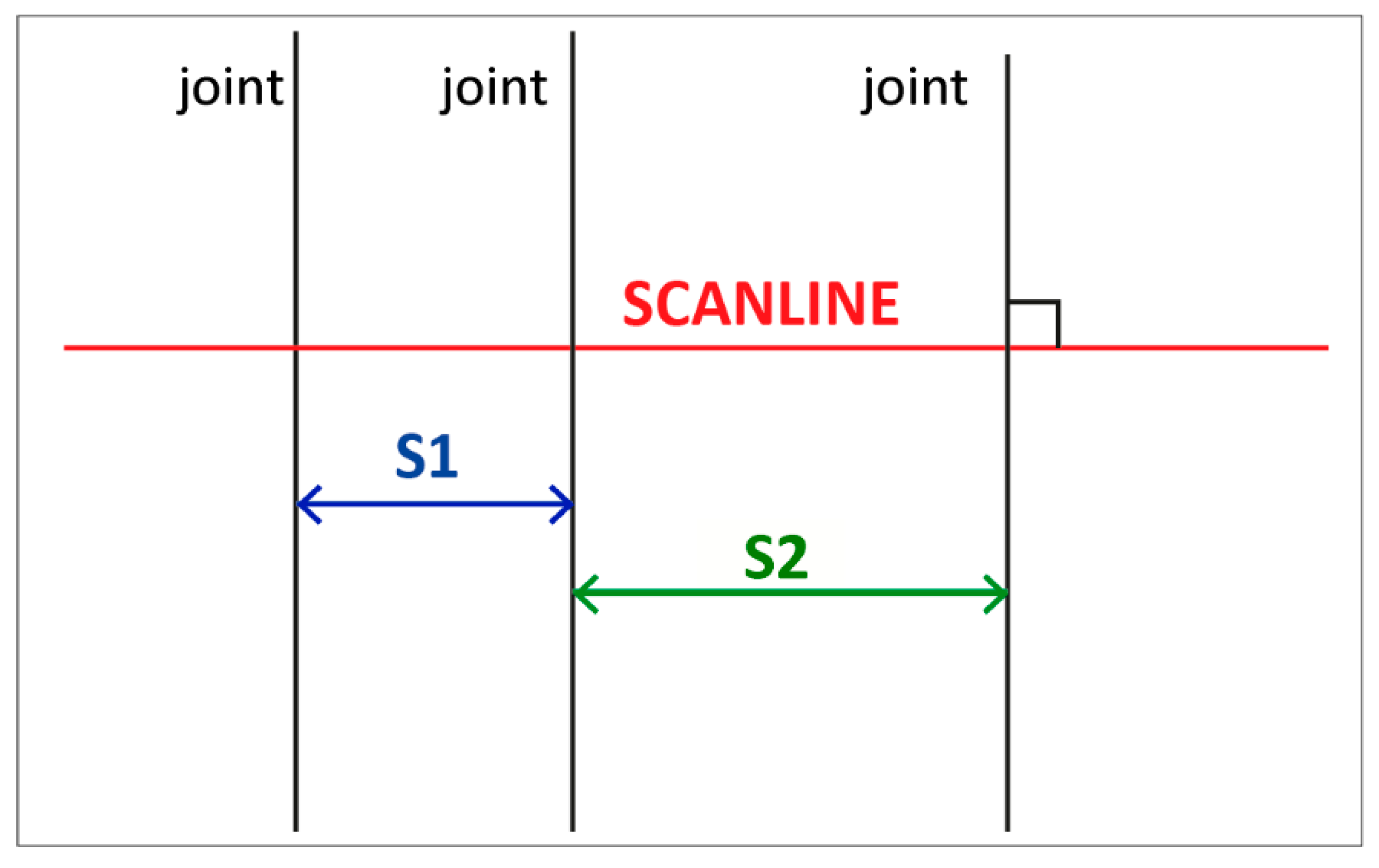
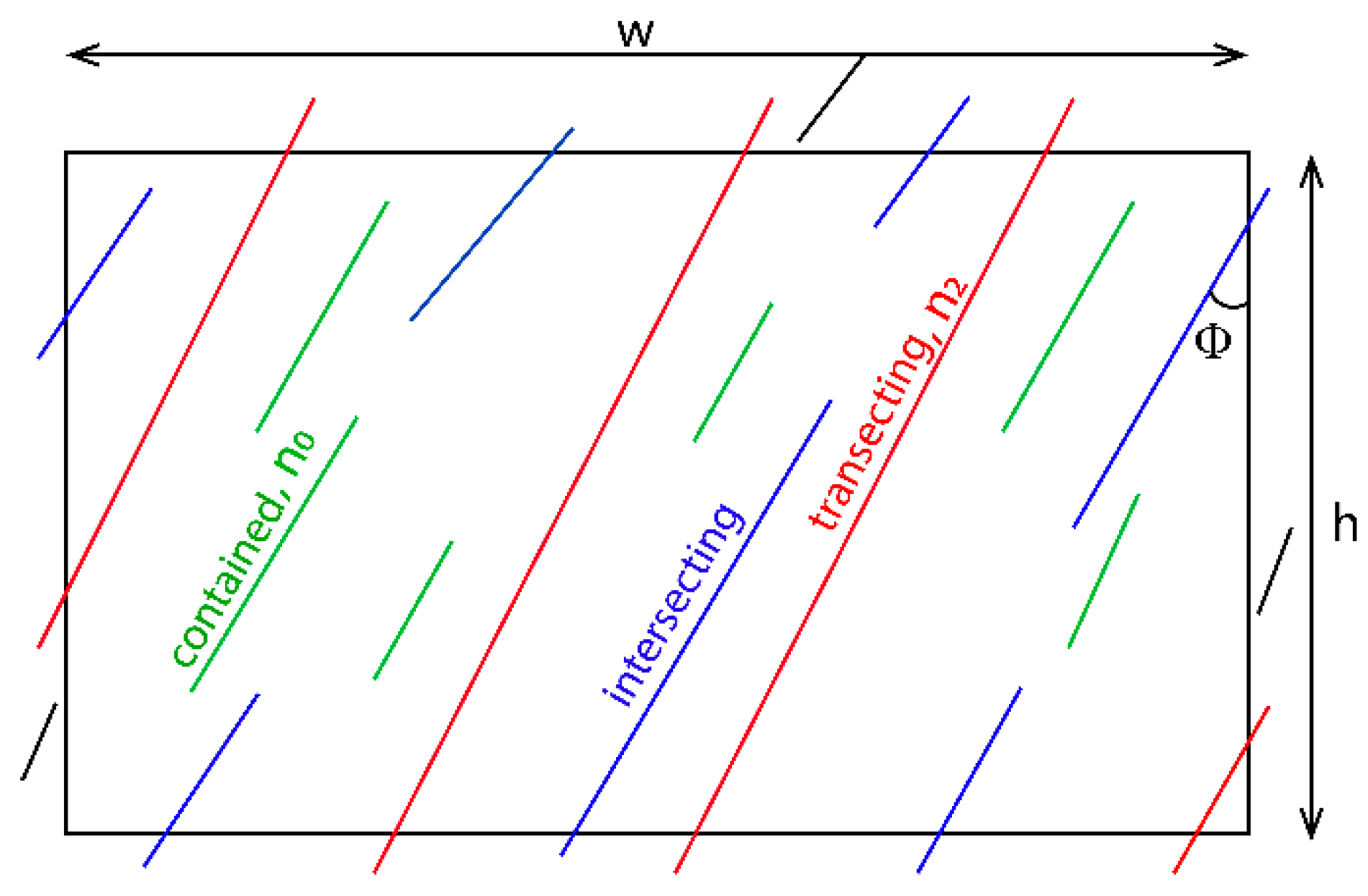
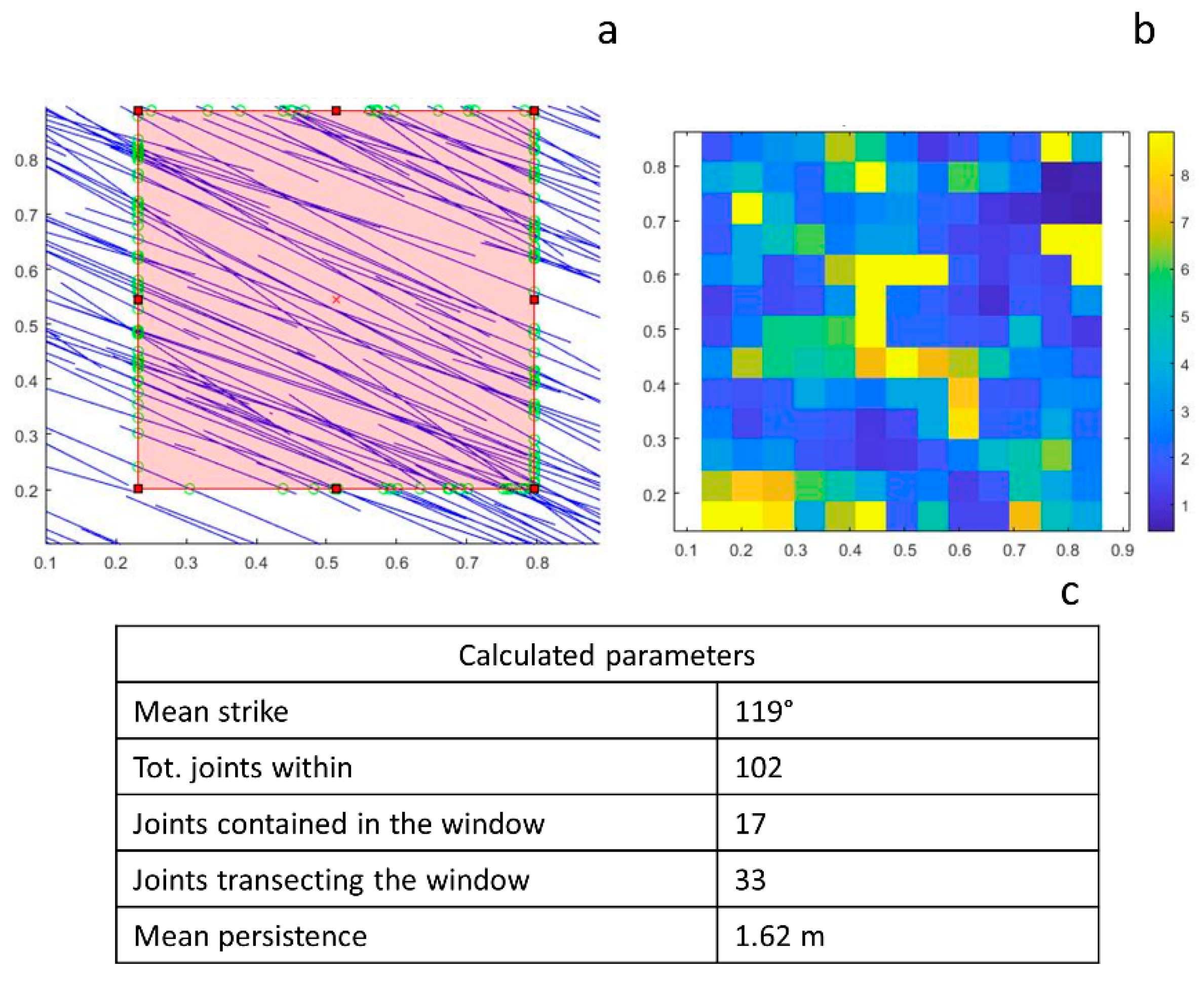
- Spacing for non-persistent joints
- Spacing for persistent joints
Trace Length
Persistence
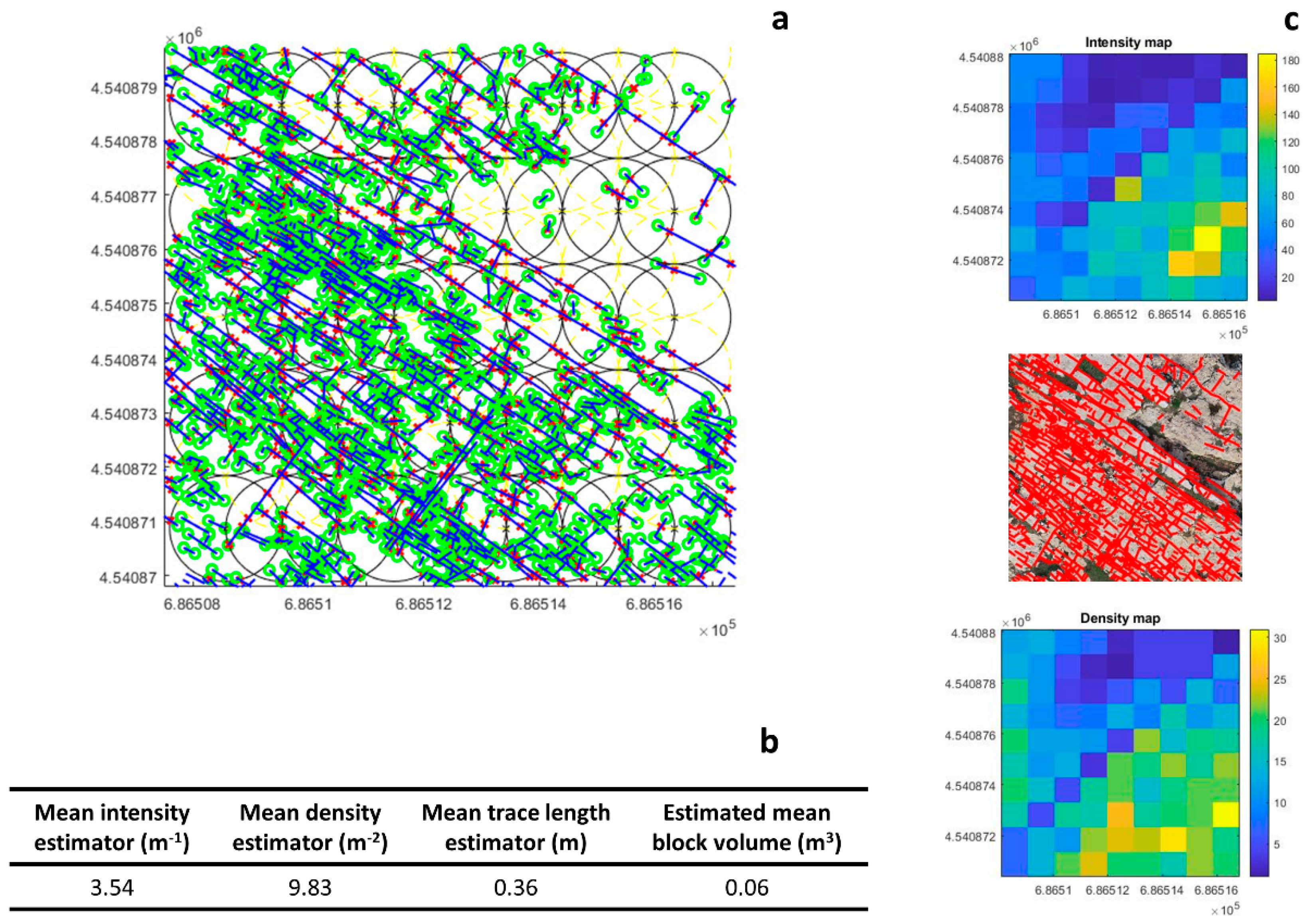
2.6.2. Characterization of the Fracture Network
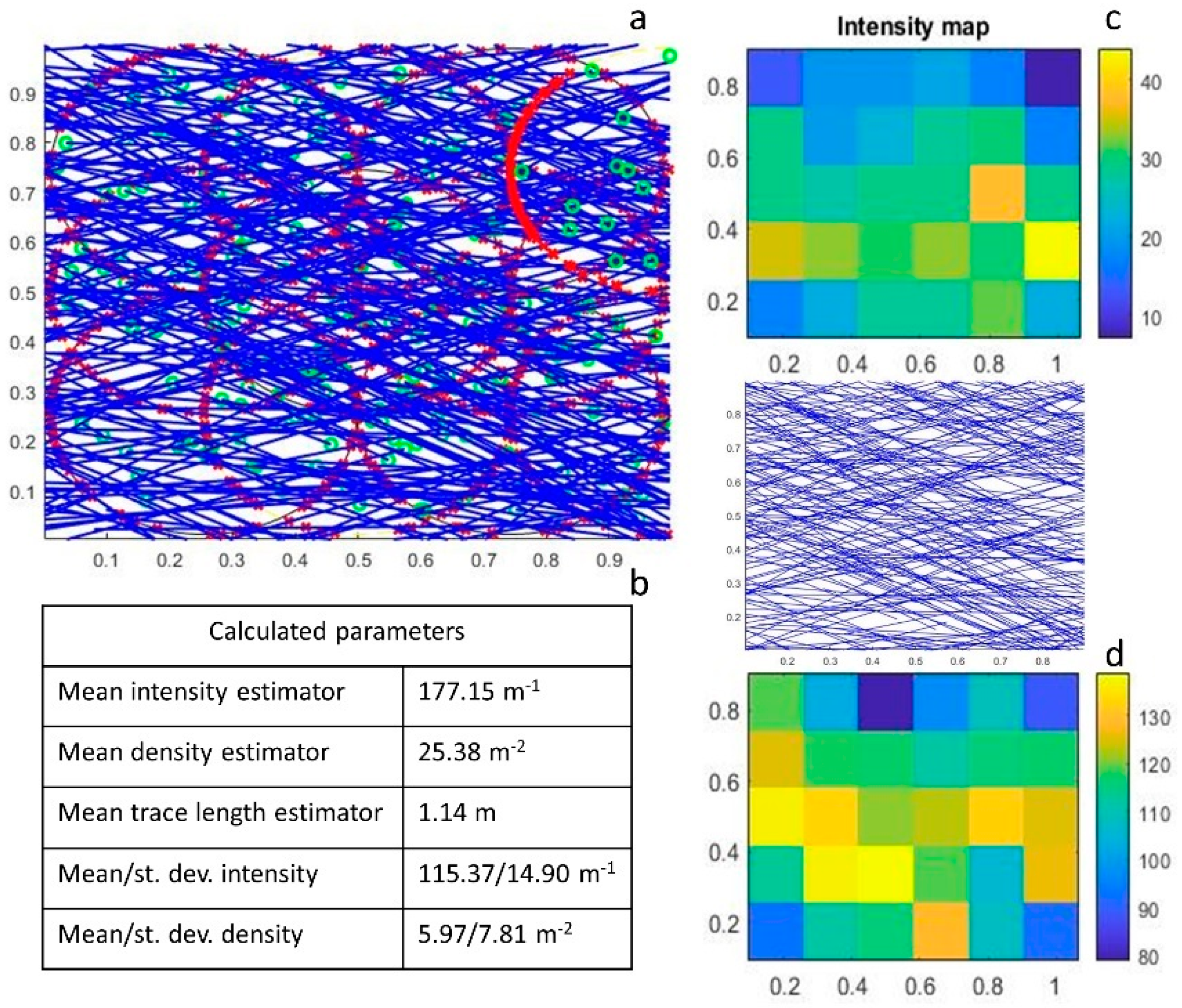
Intensity, Density, and Trace Length Estimators
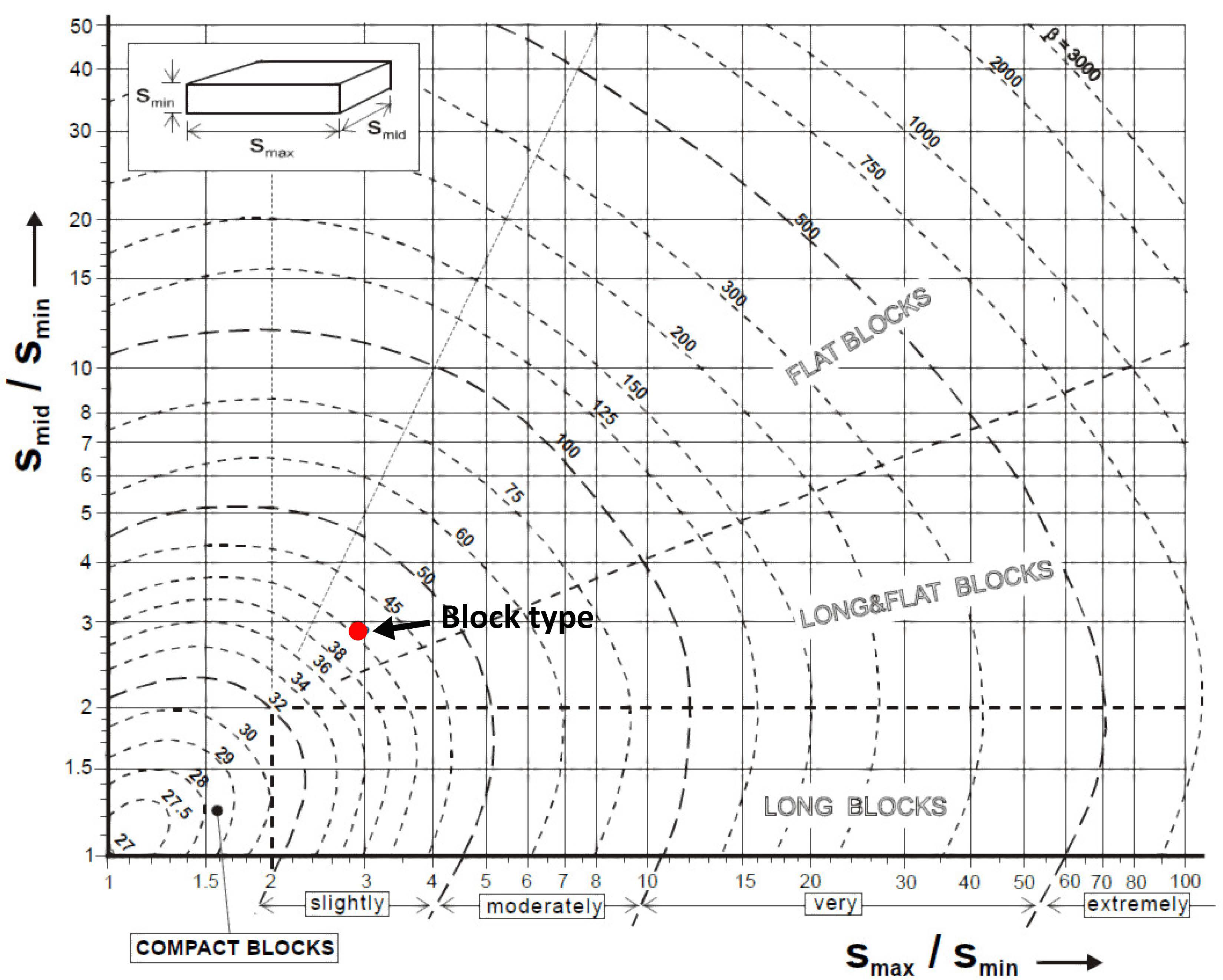
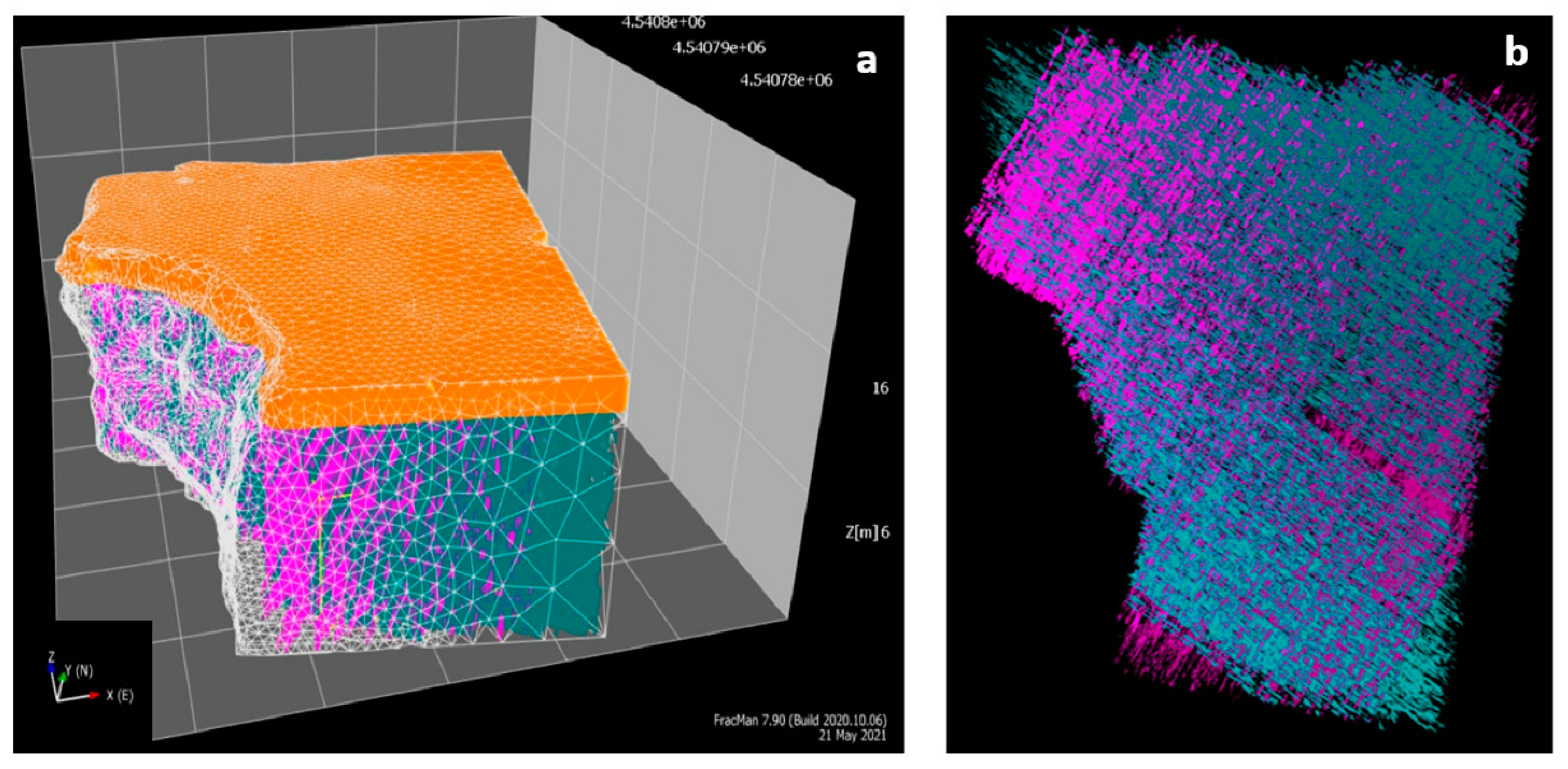
Block Volume and Shape
3. Results
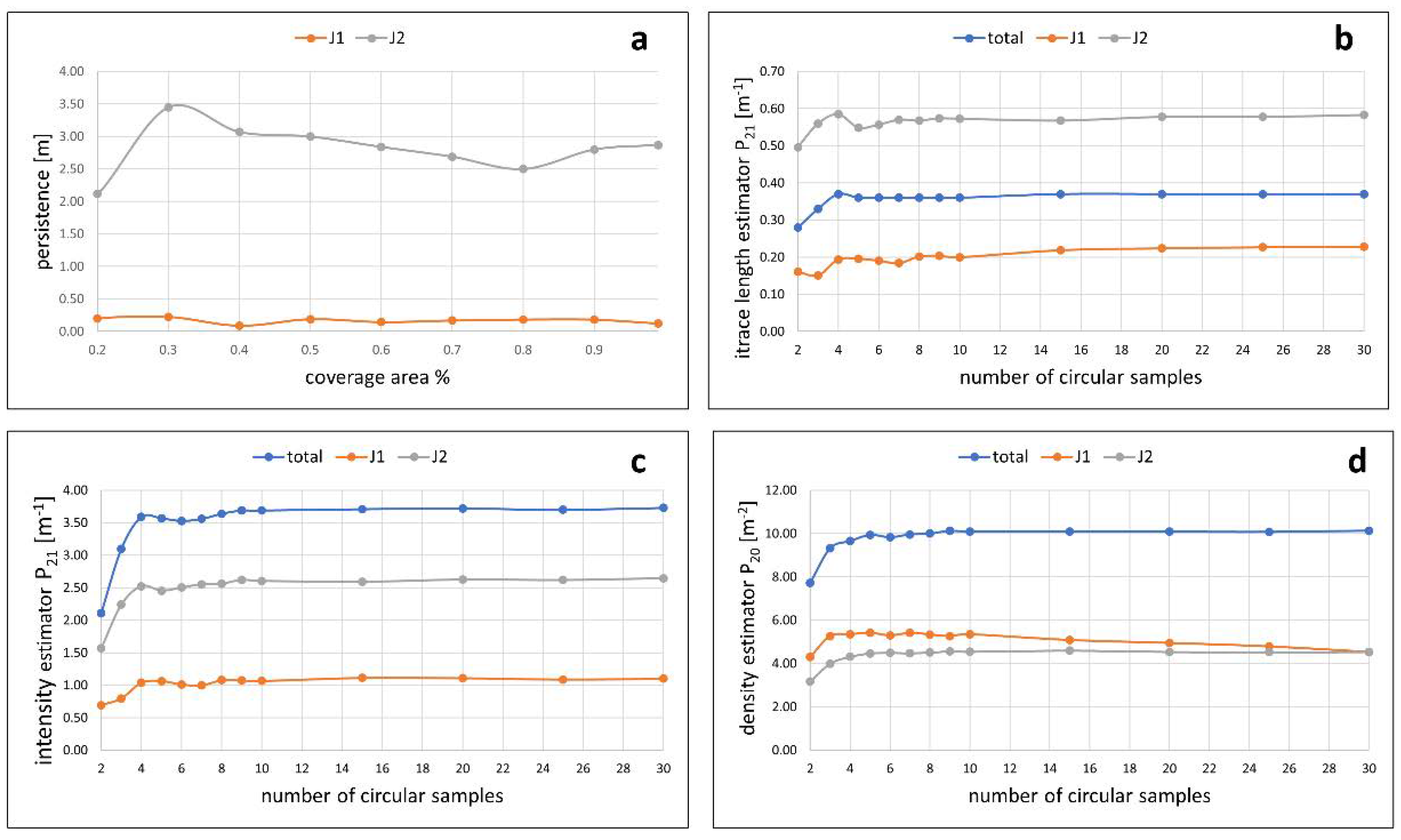
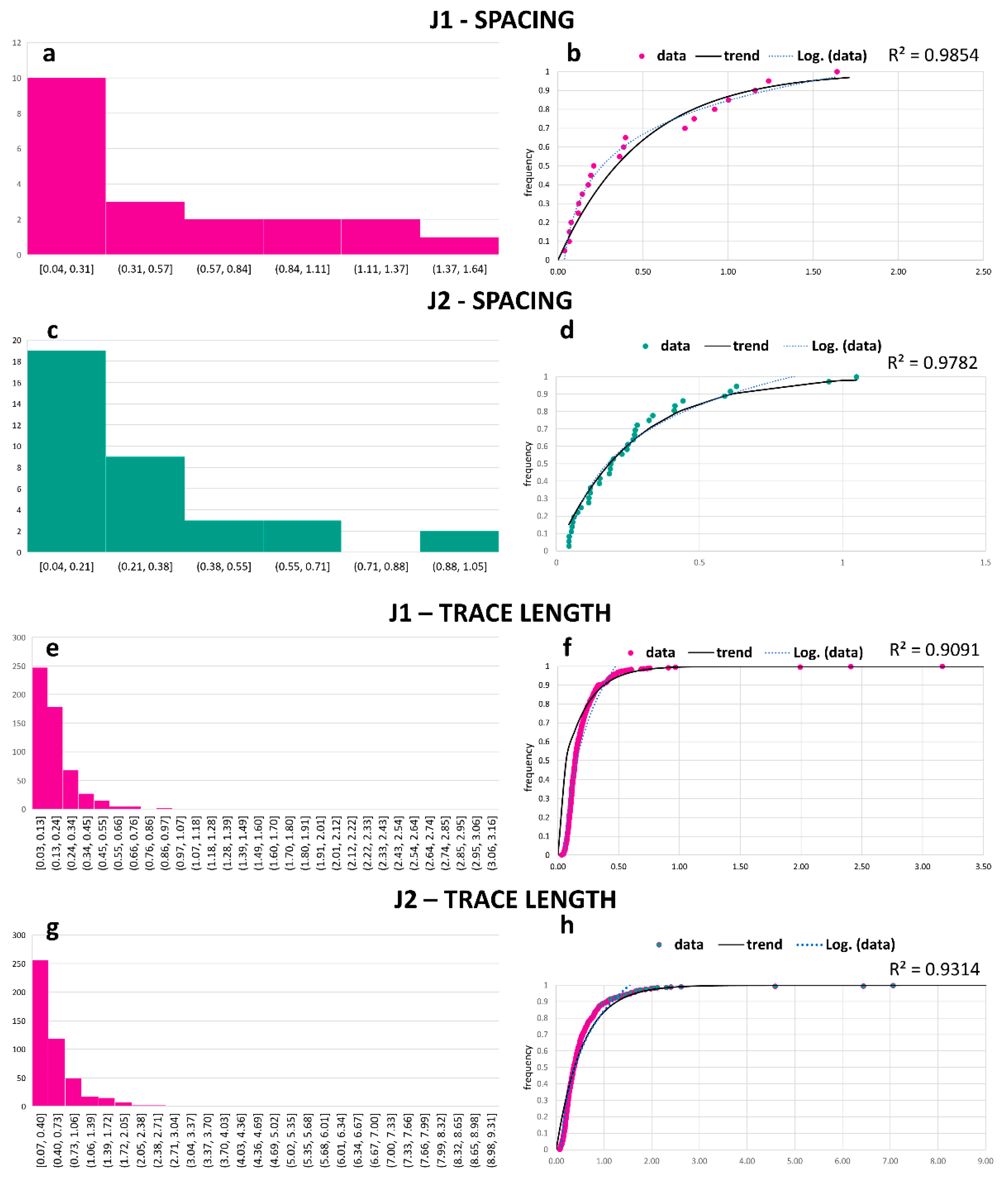
3.1. Results of the Synthetic Dataset
3.2. Application to the Case Study
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barton, N.; Lien, R.; Lunde, J. Engineering Classification of Rock Masses for the Design of Tunnel Support. Rock Mech. Rock Eng. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Franklin, J.A.; Maerz, N.H.; Bennett, C.P. Rock Mass Characterization Using Photoanalysis. Int. J. Min. Geol. Eng. 1988, 6, 97–112. [Google Scholar] [CrossRef]
- Slob, S.; van Knapen, B.; Hack, R.; Turner, K.; Kemeny, J. Method for Automated Discontinuity Analysis of Rock Slopes with Three-Dimensional Laser Scanning. Transp. Res. Rec. J. Transp. Res. Board 2005, 1913, 187–194. [Google Scholar] [CrossRef]
- Slob, S. Method for Automated Discontinuity Analysis of Rock Slopes with Three-Dimensional Laser Scanning. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Tofani, V.; Segoni, S.; Agostini, A.; Catani, F.; Casagli, N. Technical Note: Use of Remote Sensing for Landslide Studies in Europe. Nat. Hazards Earth Syst. Sci. 2013, 13, 299–309. [Google Scholar] [CrossRef]
- Palma, B.; Parise, M.; Ruocco, A. Geo-Mechanical Characterization of Carbonate Rock Masses by Means of Laser Scanner Technique. IOP Conf. Ser. Earth Environ. Sci. 2017, 95, 062007. [Google Scholar] [CrossRef]
- Priest, S.D. Discontinuity Analysis for Rock Engineering; Chapman & Hall: London, UK, 1993. [Google Scholar]
- Hudson, J.; Popescu, M.; Harrison, J. Engineering Rock Mechanics: An Introduction to the Principles. Appl. Mech. Rev. 2002, 55, B30. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Couture, R.; Locat, P. Structural Analysis of Turtle Mountain (Alberta) Using Digital Elevation Model: Toward a Progressive Failure. Geomorphology 2009, 103, 5–16. [Google Scholar] [CrossRef]
- Kainthola, A.; Singh, P.K.; Singh, T.N. Stability Investigation of Road Cut Slope in Basaltic Rockmass, Mahabaleshwar, India. Geosci. Front. 2015, 6, 837–845. [Google Scholar] [CrossRef] [Green Version]
- Goodman, R.E. Methods of Geological Engineering in Discontinuous Rocks; West Pub. Co: St. Paul, MN, USA, 1976; ISBN 0829900667. [Google Scholar]
- Cardia, S.; Palma, B.; Parise, M. The Iterative Pole Density Estimation, a New Approach to Assess the Stability of Rock Masses from 3D Point Clouds. In Proceedings of the 90th Congr. Società Geologica Italiana “Geology without borders”, Trieste, Italy, 14–16 September 2021; p. 239. [Google Scholar]
- Lisjak, A.; Grasselli, G. A Review of Discrete Modeling Techniques for Fracturing Processes in Discontinuous Rock Masses. J. Rock Mech. Geotech. Eng. 2014, 6, 301–314. [Google Scholar] [CrossRef] [Green Version]
- Jing, L. A Review of Techniques, Advances and Outstanding Issues in Numerical Modelling for Rock Mech. Rock Eng. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Jing, L.; Hudson, J.A. Numerical Methods in Rock Mechanics. Int. J. Rock Mech. Min. Sci. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Fardin, N.; Feng, Q.; Stephansson, O. Application of a New in Situ 3D Laser Scanner to Study the Scale Effect on the Rock Joint Surface Roughness. Int. J. Rock Mech. Min. Sci. 2004, 41, 329–335. [Google Scholar] [CrossRef]
- Slob, S.; Hack, R. 3D Terrestrial Laser Scanning as a New Field Measurement and Monitoring Technique; Springer: Berlin/Heidelberg, Germany, 2004; pp. 179–189. [Google Scholar]
- Jaboyedoff, M.; Metzger, R.; Oppikofer, T.; Couture, R.; Derron, M.; Locat, J.; Turmel, D. New Insight Techniques to Analyze Rock-Slope Relief Using DEM and 3D-Imaging Cloud Points. In Rock Mechanics: Meeting Society’s Challenges and Demands; Taylor & Francis: Oxfordshire, UK, 2007; pp. 61–68. [Google Scholar]
- Vöge, M.; Lato, M.J.; Diederichs, M.S. Automated Rockmass Discontinuity Mapping from 3-Dimensional Surface Data. Eng. Geol. 2013, 164, 155–162. [Google Scholar] [CrossRef]
- Mavrouli, O.; Corominas, J.; Jaboyedoff, M. Size Distribution for Potentially Unstable Rock Masses and In Situ Rock Blocks Using LIDAR-Generated Digital Elevation Models. Rock Mech. Rock Eng. 2015, 48, 1589–1604. [Google Scholar] [CrossRef] [Green Version]
- Roncella, R.; Forlani, G.; Remondino, F. Photogrammetry for Geological Applications: Automatic Retrieval of Discontinuity Orientation in Rock Slopes. Videometrics VIII 2005, 5665, 17. [Google Scholar] [CrossRef]
- Voyat, I.; Roncella, R.; Forlani, G.; Ferrero, A.M. Advanced Techniques for Geo Structural Surveys in Modelling Fractured Rock Masses: Application to Two Alpine Sites. In Proceedings of the GoldenRocks 2006: 41st U.S. Rock Mechanics Symposium, Golden, CO, USA, 17–21 June 2006. [Google Scholar]
- Buyer, A.; Schubert, W. Joint Trace Detection in Digital Images. In Proceedings of the ISRM International Symposium—10th Asian Rock Mechanics Symposium, ARMS 2018, OnePetro, Singapore, 29 October 2018. [Google Scholar]
- Buyer, A.; Schubert, W. Calculation the Spacing of Discontinuities from 3D Point Clouds. Procedia Eng. 2017, 191, 270–278. [Google Scholar] [CrossRef]
- Buyer, A.; Schubert, W. Extraction of Discontinuity Orientations in Point Clouds. In Proceedings of the ISRM International Symposium—EUROCK 2016, Ürgüp, Turkey, 29–31 August 2016; pp. 1133–1137. [Google Scholar]
- Lato, M.J.; Vöge, M. Automated Mapping of Rock Discontinuities in 3D Lidar and Photogrammetry Models. Int. J. Rock Mech. Min. Sci. 2012, 54, 150–158. [Google Scholar] [CrossRef]
- Sturzenegger, M.; Stead, D. Close-Range Terrestrial Digital Photogrammetry and Terrestrial Laser Scanning for Discontinuity Characterization on Rock Cuts. Eng. Geol. 2009, 106, 163–182. [Google Scholar] [CrossRef]
- Gigli, G.; Casagli, N. Semi-Automatic Extraction of Rock Mass Structural Data from High Resolution LIDAR Point Clouds. Int. J. Rock Mech. Min. Sci. 2011, 48, 187–198. [Google Scholar] [CrossRef]
- Ferrero, A.M.; Forlani, G.; Roncella, R.; Voyat, H.I. Advanced Geostructural Survey Methods Applied to Rock Mass Characterization. Rock Mech. Rock Eng. 2009, 42, 631–665. [Google Scholar] [CrossRef]
- Slob, S.; Hack, H.R.G.K.; Feng, Q.; Roshoff, K.; Turner, A.K. Fracture Mapping Using 3D Laser Scanning Techniques. In Proceedings of the 11th Congress of the International Society for Rock Mechanics, The Second Half Century of Rock Mechanics, Lisbon, Portugal, 9–13 July 2007; pp. 299–302. [Google Scholar]
- Riquelme, A.J.; Abellán, A.; Tomás, R.; Jaboyedoff, M. A New Approach for Semi-Automatic Rock Mass Joints Recognition from 3D Point Clouds. Comput. Geosci. 2014, 68, 38–52. [Google Scholar] [CrossRef] [Green Version]
- Kong, D.; Saroglou, C.; Wu, F.; Sha, P.; Li, B. Development and Application of UAV-SfM Photogrammetry for Quantitative Characterization of Rock Mass Discontinuities. Int. J. Rock Mech. Min. Sci. 2021, 141, 104729. [Google Scholar] [CrossRef]
- Riquelme, A.; Tomás, R.; Cano, M.; Pastor, J.L.; Abellán, A. Automatic Mapping of Discontinuity Persistence on Rock Masses Using 3D Point Clouds. Rock Mech. Rock Eng. 2018, 51, 3005–3028. [Google Scholar] [CrossRef]
- Oppikofer, T.; Jaboyedoff, M.; Pedrazzini, A.; Derron, M.H.; Blikra, L.H. Detailed DEM Analysis of a Rockslide Scar to Characterize the Basal Sliding Surface of Active Rockslides. J. Geophys. Res. Earth Surf. 2011, 116, 2016. [Google Scholar] [CrossRef]
- Li, X.; Chen, J.; Zhu, H. A New Method for Automated Discontinuity Trace Mapping on Rock Mass 3D Surface Model. Comput. Geosci. 2016, 89, 118–131. [Google Scholar] [CrossRef]
- Battulwar, R.; Zare-Naghadehi, M.; Emami, E.; Sattarvand, J. A State-of-the-Art Review of Automated Extraction of Rock Mass Discontinuity Characteristics Using Three-Dimensional Surface Models. J. Rock Mech. Geotech. Eng. 2021, 13, 920–936. [Google Scholar] [CrossRef]
- 3GSM ShapeMetriX 3D. Available online: www.3GSM.at (accessed on 24 June 2021).
- CREALP Mattercliff Software. Available online: https://www.crealp.ch/fr/accueil/outils-services/logiciels/mattercliff/telechargement-mattercliff.html (accessed on 24 June 2021).
- Healy, D.; Rizzo, R.E.; Cornwell, D.G.; Farrell, N.J.C.; Watkins, H.; Timms, N.E.; Gomez-Rivas, E.; Smith, M. FracPaQ: A MATLABTM Toolbox for the Quantification of Fracture Patterns. J. Struct. Geol. 2017, 95, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Martinelli, M.; Bistacchi, A.; Mittempergher, S.; Bonneau, F.; Balsamo, F.; Caumon, G.; Meda, M. Damage Zone Characterization Combining Scan-Line and Scan-Area Analysis on a Km-Scale Digital Outcrop Model: The Qala Fault (Gozo). J. Struct. Geol. 2020, 140, 104144. [Google Scholar] [CrossRef]
- Cai, M. Rock Mass Characterization and Rock Property Variability Considerations for Tunnel and Cavern Design. Rock Mech. Rock Eng. 2011, 44, 379–399. [Google Scholar] [CrossRef]
- Lyman, G.; Poropat, G.; Elmouttie, M. Uncertainty in Rock Mass Jointing Characterisation. In Proceedings of the First Southern Hemisphere International Rock Mechanics Symposium, Australian Centre for Geomechanics, Perth, Australia, 16 September 2008; pp. 419–432. [Google Scholar]
- Elmo, D.; Stead, D.; Yang, B.; Marcato, G.; Borgatti, L. A New Approach to Characterise the Impact of Rock Bridges in Stability Analysis. Rock Mech. Rock Eng. 2021, 1, 1–19. [Google Scholar] [CrossRef]
- Elmo, D.; Donati, D.; Stead, D. Challenges in the Characterisation of Intact Rock Bridges in Rock Slopes. Eng. Geol. 2018, 245, 81–96. [Google Scholar] [CrossRef]
- Elmo, D.; Stead, D. Disrupting Rock Engineering Concepts: Is There Such a Thing as a Rock Mass Digital Twin and Are Machines Capable of Learning Rock Mechanics? In Proceedings of the 2020 International Symposium on Slope Stability in Open Pit Mining and Civil Engineering, Perth, Australia, 12 May 2020; pp. 565–576. [Google Scholar]
- Tuckey, Z.; Stead, D. Improvements to Field and Remote Sensing Methods for Mapping Discontinuity Persistence and Intact Rock Bridges in Rock Slopes. Eng. Geol. 2016, 208, 136–153. [Google Scholar] [CrossRef]
- Lei, Q.; Latham, J.P.; Tsang, C.F. The Use of Discrete Fracture Networks for Modelling Coupled Geomechanical and Hydrological Behaviour of Fractured Rocks. Comput. Geotech. 2017, 85, 151–176. [Google Scholar] [CrossRef]
- Cacas, M.C.; Ledoux, E.; de Marsily, G.; Tillie, B.; Barbreau, A.; Durand, E.; Feuga, B.; Peaudecerf, P. Modeling Fracture Flow with a Stochastic Discrete Fracture Network: Calibration and Validation: 1. The Flow Model. Water Resour. Res. 1990, 26, 479–489. [Google Scholar] [CrossRef]
- Bruno, G.; del Gaudio, V.; Mascia, U.; Ruina, G. Numerical Analysis of Morphology in Relation to Coastline Variations and Karstic Phenomena in the Southeastern Murge (Apulia, Italy). Geomorphology 1995, 12, 313–322. [Google Scholar] [CrossRef]
- Dini, M.; Mastronuzzi, G.; Sanso, P. The Effects of Relative Sea Level Changes on the Coastal Morphology of Southern Apulia (Italy) during the Holocene. In Geomorphology, Human Activity and Global Environmental Change; Slaymaker, O., Ed.; John Wiley & Sons, LTD: Chichester, UK, 2000; pp. 43–65. [Google Scholar]
- Parise, M. Flood History in the Karst Environment of Castellana-Grotte (Apulia, Southern Italy). Nat. Hazards Earth Syst. Sci. 2003, 3, 593–604. [Google Scholar] [CrossRef]
- Ciaranfi, N.; Pieri, P.; Ricchetti, G. Note Alla Carta Geologica Delle Murge e Del Salento (Puglia Centromeridionale). Mem. Della Soc. Geol. Ital. 1988, 41, 449–460. [Google Scholar]
- Ricchetti, G.; Ciaranfi, N.; Luperto-Sinni, E.; Mongelli, F.; Pieri, P. Geodinamica Ed Evoluzione Sedimentaria e Tettonica Dell’ Avampaese Apulo. Mem. Soc. Geol. It. 1998, 41, 57–82. [Google Scholar]
- Tropeano, M.; Sabato, L. Response of Plio-Pleistocene Mixed Bioclastic-Lithoclastic Temperate-Water Carbonate Systems to Forced Regressions: The Calcarenite Di Gravina Formation, Puglia, SE Italy. Geol. Soc. Spec. Publ. 2000, 172, 217–243. [Google Scholar] [CrossRef]
- Sauro, U. Il Carsismo Marino Della Costa. In Le Grotte di Polignano; Favale, F.F., Ed.; Federazione Speleologica Pugliese, Tiemme Industria Grafica: Manduria, Italy, 1994; pp. 53–72. [Google Scholar]
- Parise, M. Surface and subsurface karst geomorphology in the Murge (Apulia, southern Italy). Acta Carsologica 2011, 4, 79–93. [Google Scholar] [CrossRef]
- Gutiérrez, F. Hazards Associated with Karst. Geomorphol. Hazards Disaster Prev. 2010, 13, 161–176. [Google Scholar] [CrossRef]
- Parise, M. Hazards in karst. Available online: https://www.researchgate.net/publication/233731527_Hazards_in_karst (accessed on 24 June 2021).
- Parise, M. A Procedure for Evaluating the Susceptibility to Natural and Anthropogenic Sinkholes. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2015, 9, 272–285. [Google Scholar] [CrossRef]
- Gutiérrez, F.; Parise, M.; de Waele, J.; Jourde, H. A Review on Natural and Human-Induced Geohazards and Impacts in Karst. Earth-Sci. Rev. 2014, 138, 61–88. [Google Scholar] [CrossRef]
- Agisoft Agisoft Metashape. User Manual: Professional Edition, Version 1.6 2020, 160p. Available online: https://www.agisoft.com/pdf/metashape-pro_1_6_en.pdf (accessed on 24 June 2021).
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef] [Green Version]
- Terzaghi, R.D. Sources of Error in Joint Surveys. Geotechnique 1965, 15, 287–304. [Google Scholar] [CrossRef]
- ISRM Suggested Methods for the Quantitative Description of Discontinuities in Rock Masses. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1988, 20, 189–200. [CrossRef]
- Rocscience Dips—Version 8.015 2021. Available online: www.rocscience.com (accessed on 24 June 2021).
- Pahl, P.J. Estimating the Mean Length of Discontinuity Traces. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1981, 18, 221–228. [Google Scholar] [CrossRef]
- Dershowitz, W.S.; Herda, H.H. Interpretation of Fracture Spacing and Intensity. In Proceedings of the 33rd U.S. Symposium on Rock Mechanics (USRMS), Santa Fe, NM, USA, 3–5 June 1992. [Google Scholar]
- Mauldon, M.; Dershowitz, W.S. A Multi-Dimensional System of Fracture Abundance Measures. Available online: https://docplayer.net/40478836-A-multi-dimensional-system-of-fracture-abundance-measures.html (accessed on 13 July 2021).
- Palmstrøm, A. RMi—A Rock Mass Characterization System for Rock Engineering Purposes. Ph.D. Thesis, Oslo University, Norway, 1995; 400p. Appendix A3-2. Available online: http://rockmass.net/phd/appendix3.pdf (accessed on 5 December 2021).
- Palmstrøm, A. Characterizing Rock Masses by the RMi for Use in Practical Rock Engineering: Part 1: The Development of the Rock Mass Index (RMi). Tunn. Undergr. Space Technol. 1996, 11, 175–188. [Google Scholar] [CrossRef]
- Golder Associates. FracMan7-Interactive Discrete Feature, Data Analysis, Geometric Modeling and Exploration Simulation; Software Manual; Golder Associates: Atlanta, GA, USA, 2018. [Google Scholar]
- Rohrbaugh, M.B.; Dunne, W.M.; Mauldon, M. Estimating Fracture Trace Intensity, Density, and Mean Length Using Circular Scan Lines and Windows. AAPG Bull. 2002, 86, 2089–2104. [Google Scholar] [CrossRef]
- Mauldon, M.; Mauldon, J.G. Fracture Sampling on a Cylinder: From Scanlines to Boreholes and Tunnels. Rock Mech. Rock Eng. 1997, 30, 129–144. [Google Scholar] [CrossRef]
- Baecher, G.; Lanney, N.A. Trace Length Biases in Joint Surveys. In Proceedings of the 19th U.S. Symposium on Rock Mechanics, Reno, NV, USA, 1–3 May 1978; Volume 1, pp. 56–65. [Google Scholar]
- Einstein, H.H.; Baecher, G.B. Probabilistic and Statistical Methods in Engineering Geology. Rock Mech. Rock Eng. 1983, 16, 39–72. [Google Scholar] [CrossRef]
- La Pointe, P.R.; Hudson, J.A.; la Pointe, P.R.; Hudson, J.A. Characterization and Interpretation of Rock Mass Joint Patterns. GSA Spec. Pap. 1985, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Watkins, H.; Bond, C.E.; Healy, D.; Butler, R.W.H. Appraisal of Fracture Sampling Methods and a New Workflow to Characterise Heterogeneous Fracture Networks at Outcrop. J. Struct. Geol. 2015, 72, 67–82. [Google Scholar] [CrossRef]
- Priest, S.D.; Hudson, J.A. Estimation of Discontinuity Spacing and Trace Length Using Scanline Surveys. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1981, 18, 183–197. [Google Scholar] [CrossRef]
- Goldfarb, D. A Family of Variable-Metric Methods Derived by Variational Means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Fletcher, R. A New Approach to Variable Metric Algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef] [Green Version]
- Shanno, D.F. Conditioning of Quasi-Newton Methods for Function Minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Broyden, C.G. The Convergence of a Class of Double-Rank Minimization Algorithms 1. General Considerations. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Hough, P.V.C. Method and Means for Recognizing Complex Patterns. U.S. Patent No. 3,069,654, 18 December 1962. [Google Scholar]
- Duda, R.O.; Hart, P.E. Use of the Hough Transformation to Detect Lines and Curves in Pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Rosenfeld, A. Picture Processing by Computer. ACM Comput. Surv. (CSUR) 1969, 1, 147–176. [Google Scholar] [CrossRef]
- Leavers, V.F. Which Hough Transform? CVGIP Image Underst. 1993, 58, 250–264. [Google Scholar] [CrossRef]
- Mukhopadhyay, P.; Chaudhuri, B.B. A Survey of Hough Transform. Pattern Recognition 2015, 48, 993–1010. [Google Scholar] [CrossRef]
- Einstein, H.H.; Veneziano, D.; Baecher, G.B.; O’reilly, K.J. The Effect of Discontinuity Persistence on Rock Slope Stability. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1983, 20, 227–236. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Philippossian, F.; Mamin, M.; Marro, C.; Rouiller, J.-D. Distribution Spatiale Des Discontinuités Dans Une Falaise. In Approche Statistique et Probabiliste, Rapport de Travail PNR31; Hochschulverlag AG an der ETH Zürich: Zürich, Switzerland, 1996. [Google Scholar]
- Mauldon, M.; Dershowitz, W.S. A Multi-Dimensional System of Fracture Abundance Measures. Geol. Soc. Am. Abstr. Programs 2000, 3, A474. [Google Scholar]
- Priest, S.D.; Hudson, J.A. Discontinuity Spacings in Rock. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1976, 13, 135–148. [Google Scholar] [CrossRef]
- Wallis, R.F.; King, M.S. Discontinuity Spacings in a Crystalline Rock. Int. J. Rock Mech. Min. Sci. Geomeech. Abstr. 1980, 17, 63–66. [Google Scholar] [CrossRef]
- Cruden, D.M. Describing the Size of Discontinuities. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1977, 14, 133–137. [Google Scholar] [CrossRef]
- Tatone, B.S.A.; Grasselli, G. An Investigation of Discontinuity Roughness Scale Dependency Using High-Resolution Surface Measurements. Rock Mech. Rock Eng. 2013, 46, 657–681. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Chen, J.; Zhu, H. Automatic Characterization of Rock Mass Discontinuities Using 3D Point Clouds. Eng. Geol. 2019, 259, 105131. [Google Scholar] [CrossRef]
- Smith, L.; Forster, C.; Evans, J. Interaction Between Fault Zones, Fluid Flow and Heat Transfer at the Basin Scale. Hydrogeol. Low Permeabil. Environ. 1990, 2, 41–67. [Google Scholar]
- Smith, D.A. Sealing and Nonsealing Faults in Louisiana Gulf Coast Salt Basin. AAPG Bull. 1980, 64, 145–172. [Google Scholar]
- Taylor, D.J.; Dietvorst, J.P.A. The Cormorant Field, Blocks 211/21a, 211/26a, UK North Sea. Geol. Soc. London Mem. 1991, 14, 73–82. [Google Scholar] [CrossRef]
- Wiprut, D.; Zoback, M.D. Fault Reactivation, Leakage Potential, and Hydrocarbon Column Heights in the Northern North Sea. AAPG Bull. 2002, 86, 203–219. [Google Scholar]
- Jolley, S.J.; Dijk, H.; Lamens, J.H.; Fisher, Q.J.; Manzocchi, T.; Eikmans, H.; Huang, Y. Faulting and Fault Sealing in Production Simulation Models: Brent Province, Northern North Sea. Pet. Geosci. 2007, 13, 321–340. [Google Scholar] [CrossRef] [Green Version]
- Knai, T.A.; Knipe, R.J. The Impact of Faults on Fluid Flow in the Heidrun Field; Special Publications; Geological Society: London, UK, 1998; Volume 147, pp. 269–282. [Google Scholar] [CrossRef]
- Fisher, Q.J.; Knipe, R.J. The Permeability of Faults within Siliciclastic Petroleum Reservoirs of the North Sea and Norwegian Continental Shelf. Mar. Pet. Geol. 2001, 18, 1063–1081. [Google Scholar] [CrossRef]
- Manzocchi, T. The Connectivity of Two-Dimensional Networks of Spatially Correlated Fractures. Water Resour. Res. 2002, 38, 1–20. [Google Scholar] [CrossRef]
- Saevik, P.N.; Nixon, C.W. Inclusion of Topological Measurements into Analytic Estimates of Effective Permeability in Fractured Media. Water Resour. Res. 2017, 53, 9424–9443. [Google Scholar] [CrossRef]
- Zimmerman, R.; Main, I. Hydromechanical Behavior of Fractured Rocks. Int. Geophys. Ser. 2004, 89, 363–432. [Google Scholar]
- Laubach, S.E.; Lamarche, J.; Gauthier, B.D.M.; Dunne, W.M.; Sanderson, D.J. Spatial Arrangement of Faults and Opening-Mode Fractures. J. Struct. Geol. 2018, 108, 2–15. [Google Scholar] [CrossRef]
- Vera, E.; Lucio, D.; Fernandes, L.A.F.; Velho, L. Hough Transform for Real-Time Plane Detection in Depth Images. Pattern Recognit. Lett. 2018, 103, 8–15. [Google Scholar] [CrossRef]
- Leng, X.; Xiao, J.; Wang, Y. A Multi-Scale Plane-Detection Method Based on the Hough Transform and Region Growing. Photogramm. Rec. 2016, 31, 166–192. [Google Scholar] [CrossRef]
- Wang, Z.; AlRegib, G. Automatic Fault Surface Detection by Using 3D Hough Transform. In Proceedings of the 2014 SEG Annual Meeting, Denver, CO, USA, 26–31 October 2014. [Google Scholar]






| UAV System | |
|---|---|
| UAV device | DJI Inspire 2 |
| Maximum takeoff weight (g) | 4250 g |
| Maximum flight time (min) | 27 |
| Gimbal stabilization | 3-axis (pitch, roll, yaw) |
| On-board camera parameters and setting | |
| Camera model | Zenmuse X5S |
| Supported lens | DJI MFT 15mm 1.7 ASPH |
| Sensor | CMOS, 4/3” |
| FOV | Effective Pixels: 20.8 MPx |
| Photo resolution (mm) | 72° |
| Survey details | |
| Flight mode | automatic |
| Ground Sampling distance (cm/pix) | 0.41 |
| Coverage area (km2) | 0.836 |
| Flight altitude (m) | 18 |
| Number of photos | 248 |
| Front overlap (%) | 75 |
| Side overlap (%) | 75 |
| Frame shooting interval (s) | 1.5 |
| Ground resolution (mm/pix) | 4.71 |
| Number of tie-points | 311,321 |
| Number of projections | 2,290,325 |
| Reprojection error (pix) | 0.541 |
| GCPs XY error (m) | 0.010 |
| GCPs Z error (m) | 0.001 |
| Total GCPs error (m) | 0.010 |
| Orthomosaic pixel size (mm/px) | 4.71 |
| GCP ID | Number of Images | Horizontal Errors (cm) | Vertical Errors (cm) | Total Error | ||
|---|---|---|---|---|---|---|
| X | Y | Z | cm | pix | ||
| GCP1 | 32 | –0.78 | –0.03 | 0.02 | 0.78 | 3.065 |
| GCP2 | 22 | 1.19 | 0.74 | 0.21 | 1.42 | 0.744 |
| GCP3 | 18 | –0.40 | –0.71 | 0.14 | 0.83 | 3.374 |
| Sector | Area (m2) | Number of Traces |
|---|---|---|
| A | 100 | 1472 |
| B | 400 | 5961 |
| C | 100 | 1018 |
| D | 100 | 818 |
| E | 100 | 1044 |
| Property | Orientation | Normal Spacing | Frequency | Persistence | Trace Length Estimator | Intensity Estimator P21 | Density Estimator P20 | Block Volume | Block Shape |
|---|---|---|---|---|---|---|---|---|---|
| Method | Histogram Rose diagram | Scanline | Window mapping | Circular window | From joint sets’ spacing | ||||
| Reference | [8] | [67] | [68,69] | [70,71] | |||||
| Synthetic Dataset | Results of the Classification-Gaussian Fitting | ||||||
|---|---|---|---|---|---|---|---|
| Name | Mean Strike | St. Deviation | N. of Joints | Name | Mean Strike | St. Deviation | Amplitude |
| J1 | 75° | 10° | 100 | J1 | 71° | 6° | 136 |
| J2 | 100° | 7° | 80 | J2 | 96° | 8° | 207 |
| J3 | 120° | 5° | 125 | J3 | 118° | 5° | 242 |
| Results of the Classification-Hough Transform | |||
|---|---|---|---|
| Name | Mean Strike | Minimum Strike | Maximum Strike |
| J1 | 63° | 53° | 73° |
| J2 | 86° | 44° | 98° |
| J3 | 120° | 112° | 128° |
| Characterization of Discontinuity Sets | ||||||
|---|---|---|---|---|---|---|
| Identified DS | Strike | Normal Spacing (m) | Mean Trace Length (m) | Mean Persistence (m) | ||
| Mean Strike (°) | St. Dev. (°) | Amplitude | ||||
| J1 | 34 | 12 | 733 | 0.41 | 0.20 | 0.22 |
| J2 | 124 | 5 | 740 | 0.24 | 0.55 | 2.49 |
| Characterization of the Joint Network | ||||||
| Intensity Estimator P21 (m–1) | Density Estimator P20 (m–2) | Trace Length Estimator (m) | Volumetric Joint Count JV (m–1) | Block Volume VB (m3) | Block Shape Factor β | Block Shape |
| 3 54 | 9.83 | 0.36 | 9.94 | 0.06 | 28.98 | compact |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loiotine, L.; Wolff, C.; Wyser, E.; Andriani, G.F.; Derron, M.-H.; Jaboyedoff, M.; Parise, M. QDC-2D: A Semi-Automatic Tool for 2D Analysis of Discontinuities for Rock Mass Characterization. Remote Sens. 2021, 13, 5086. https://doi.org/10.3390/rs13245086
Loiotine L, Wolff C, Wyser E, Andriani GF, Derron M-H, Jaboyedoff M, Parise M. QDC-2D: A Semi-Automatic Tool for 2D Analysis of Discontinuities for Rock Mass Characterization. Remote Sensing. 2021; 13(24):5086. https://doi.org/10.3390/rs13245086
Chicago/Turabian StyleLoiotine, Lidia, Charlotte Wolff, Emmanuel Wyser, Gioacchino Francesco Andriani, Marc-Henri Derron, Michel Jaboyedoff, and Mario Parise. 2021. "QDC-2D: A Semi-Automatic Tool for 2D Analysis of Discontinuities for Rock Mass Characterization" Remote Sensing 13, no. 24: 5086. https://doi.org/10.3390/rs13245086
APA StyleLoiotine, L., Wolff, C., Wyser, E., Andriani, G. F., Derron, M.-H., Jaboyedoff, M., & Parise, M. (2021). QDC-2D: A Semi-Automatic Tool for 2D Analysis of Discontinuities for Rock Mass Characterization. Remote Sensing, 13(24), 5086. https://doi.org/10.3390/rs13245086









