Assessing Satellite, Land Surface Model and Reanalysis Evapotranspiration Products in the Absence of In-Situ in Central Asia
Abstract
:1. Introduction
2. Materials and Methods
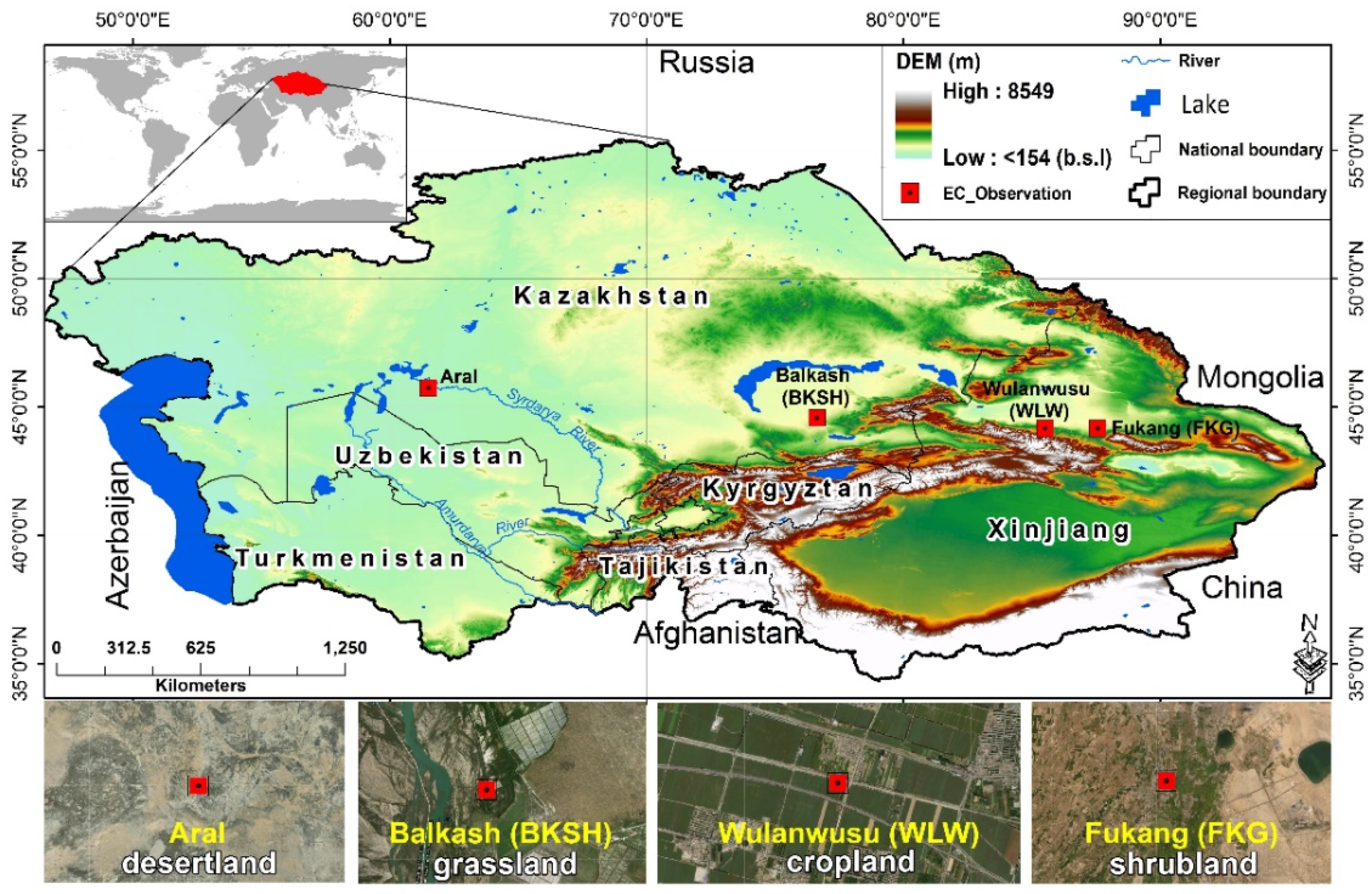
2.1. Study Area
2.2. State-of-the-Art ET Products
2.3. In-Situ Measurements
2.4. Evaluation Approach
2.5. Characterizing Error Variances of the ET Products without In-Situ
2.6. Validation
2.7. Evaluation Metrics
3. Results
3.1. Evaluation of the TC Method in Assessing ET Errors in CA
3.2. Evaluation of the TC Method by Triplet Cross-Validation Performance in CA
3.3. Assessment of the ET Products Using EC Flux Tower Measurements
3.4. Site-Scale TC Analysis of the Triplet Components in CA
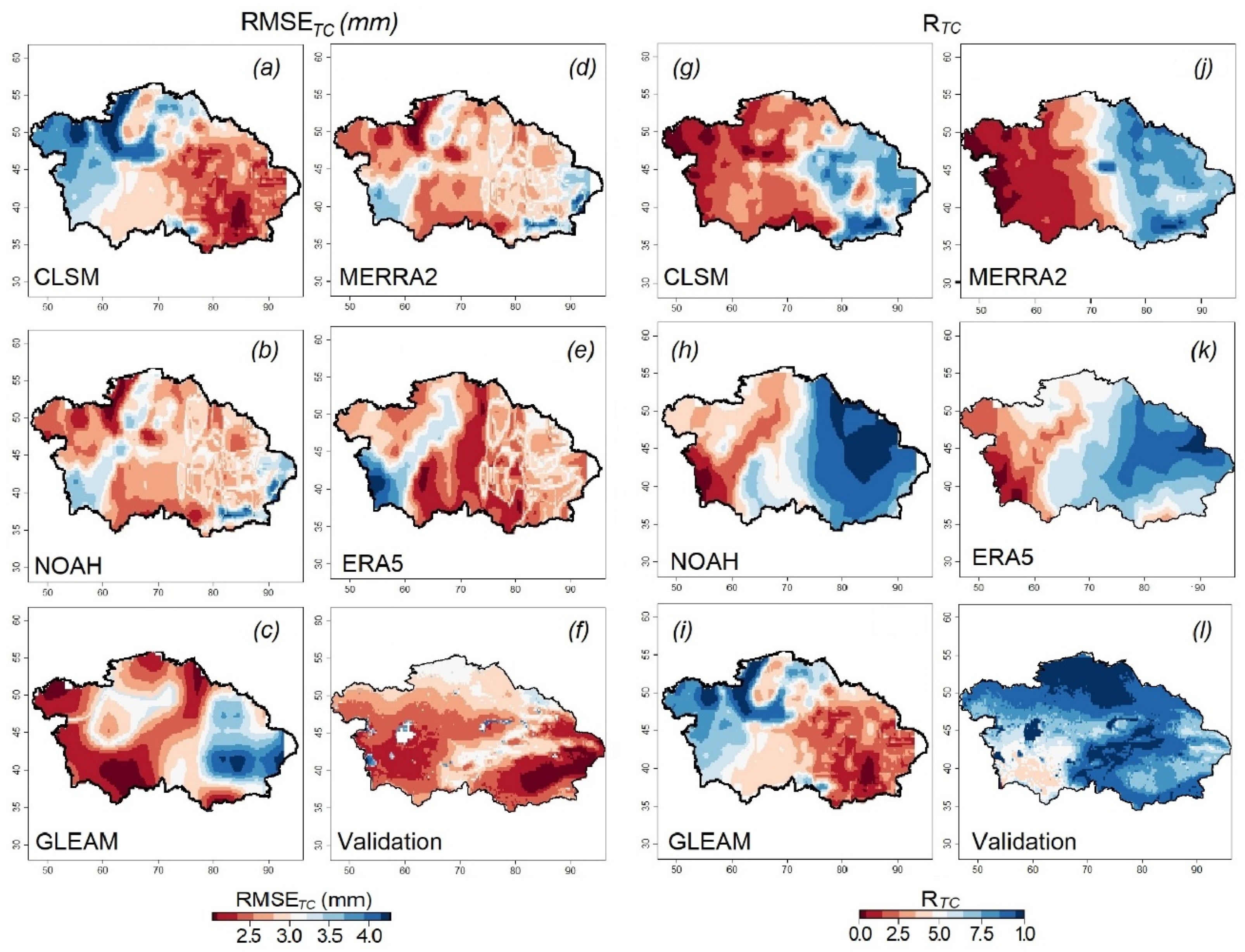
3.5. Spatiotemporal Assessment of the Triplets and Their Individual Components at Continental Scale
3.6. Intercomparison and Evaluation of the TC Analysis against Standard Metric
3.7. Uncertainty Assessment of the ET Products Based on TC Technique
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ET Product | Biome | R | RMSE (mm) | BIAS (mm) | SD | Product Mean (mm/m) | Systematic Errors (∞) |
|---|---|---|---|---|---|---|---|
| CLSM | Crop | 0.90 | 4.18 | −6.18 | 42.37 | 45.50 | 3.13 |
| ERA5 | Crop | 0.88 | 8.51 | −10.16 | 43.72 | 49.48 | 5.76 |
| GLEAM | Crop | 0.46 | 12.42 | 16.14 | 15.51 | 23.18 | 7.67 |
| MERRA2 | Crop | 0.86 | 1.02 | −6.12 | 39.56 | 45.44 | 5.88 |
| NOAH | Crop | 0.90 | 1.14 | −2.83 | 43.16 | 42.14 | −1.02 |
| CLSM | Desert | 0.80 | 4.13 | −15.09 | 23.31 | 60.91 | 37.60 |
| ERA5 | Desert | 0.22 | 6.18 | −13.28 | 9.95 | 12.50 | 2.55 |
| GLEAM | Desert | 0.79 | 2.24 | −21.02 | 9.00 | 35.81 | 26.81 |
| MERRA2 | Desert | 0.93 | 4.87 | −16.98 | 15.13 | 43.84 | 28.71 |
| NOAH | Desert | 0.64 | 5.27 | 4.43 | 27.39 | 36.40 | 9.01 |
| CLSM | Grass | 0.62 | 6.28 | −13.16 | 31.04 | 59.16 | 28.12 |
| ERA5 | Grass | 0.84 | 7.67 | −14.92 | 23.31 | 60.91 | 37.60 |
| GLEAM | Grass | 0.73 | 3.52 | 2.50 | 24.01 | 40.50 | 16.49 |
| MERRA2 | Grass | 0.84 | 7.48 | 4.19 | 9.00 | 35.81 | 26.81 |
| NOAH | Grass | 0.91 | 0.67 | 2.15 | 15.13 | 43.84 | 28.71 |
| CLSM | Shrub | 0.80 | 4.34 | −14.41 | 40.42 | 57.68 | 17.26 |
| ERA5 | Shrub | 0.78 | 5.73 | −14.58 | 40.78 | 64.85 | 24.07 |
| GLEAM | Shrub | 0.70 | 4.24 | 2.27 | 8.67 | 19.00 | 10.33 |
| MERRA2 | Shrub | 0.75 | 5.55 | −15.80 | 34.90 | 54.07 | 19.17 |
| NOAH | Shrub | 0.79 | 1.02 | −17.38 | 46.76 | 60.65 | 13.89 |
References
- Chen, J.M.; Liu, J. Evolution of evapotranspiration models using thermal and shortwave remote sensing data. Remote Sens. Environ. 2020, 237, 111594. [Google Scholar] [CrossRef]
- Ochege, F.U.; Luo, G.; Obeta, M.C.; Owusu, G.; Duulatov, E.; Cao, L.; Nsengiyumva, J.B. Mapping evapotranspiration variability over a complex oasis-desert ecosystem based on automated calibration of Landsat 7 ETM+ data in SEBAL. GISci. Remote Sens. 2019, 56, 1305–1332. [Google Scholar] [CrossRef]
- Martens, B.; Waegeman, W.; Dorigo, W.A.; Verhoest, N.E.C.; Miralles, D.G. Terrestrial evaporation response to modes of climate variability. NPJ Clim. Atmos. Sci. 2018, 1, 43. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Sun, S.; Fiifi Tawia Hagan, D.; Chen, T.; Dolman, H.; Liu, Y. Long-term changes in evapotranspiration over China and attribution to climatic drivers during 1980–2010. J. Hydrol. 2021, 595, 126037. [Google Scholar] [CrossRef]
- Lioubimtseva, E.; Henebry, G.M. Climate and environmental change in arid Central Asia: Impacts, vulnerability, and adaptations. J. Arid Environ. 2009, 73, 963–977. [Google Scholar] [CrossRef]
- Micklin, P.; Aladin, N.V.; Plotnikov, I.S. (Eds.) The Aral Sea. The Devastation and Partial Rehabilitation of a Great Lake; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Crimaldi, M.; Pasquino, V.; Padulano, R.; Chirico, G.B. Bulk Drag Predictions of Riparian Arundo donax Stands through UAV-Acquired Multispectral Images. Water 2021, 13, 1333. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, 54. [Google Scholar] [CrossRef]
- Jung, M.; Koirala, S.; Weber, U.; Ichii, K.; Gans, F.; Camps-Valls, G.; Papale, D.; Schwalm, C.; Tramontana, G.; Reichstein, M. The FLUXCOM ensemble of global land-atmosphere energy fluxes. Sci. Data 2019, 6, 74. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Martens, B.; Gonzalez Miralles, D.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.; Verhoest, N. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46, 21. [Google Scholar] [CrossRef] [Green Version]
- Fisher, J.B.; Lee, B.; Purdy, A.J.; Halverson, G.H.; Dohlen, M.B.; Cawse-Nicholson, K.; Wang, A.; Anderson, R.G.; Aragon, B.; Arain, M.A.; et al. ECOSTRESS: NASA’s Next Generation Mission to Measure Evapotranspiration from the International Space Station. Water Resour. Res. 2020, 56, e2019WR026058. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Jung, H.C.; Getirana, A.; Arsenault, K.R.; Holmes, T.R.; McNally, A. Uncertainties in Evapotranspiration Estimates over West Africa. Remote Sens. 2019, 11, 892. [Google Scholar] [CrossRef] [Green Version]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Yang, X.; Yong, B.; Ren, L.; Zhang, Y.; Long, D. Multi-scale validation of GLEAM evapotranspiration products over China via ChinaFLUX ET measurements. Int. J. Remote Sens. 2017, 38, 5688–5709. [Google Scholar] [CrossRef]
- Baik, J.; Liaqat, U.W.; Choi, M. Assessment of satellite- and reanalysis-based evapotranspiration products with two blending approaches over the complex landscapes and climates of Australia. Agric. For. Meteorol. 2018, 263, 388–398. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Sun, S.; Chen, H.; Bai, P.; Zhou, S.; Huang, Y.; Wang, J.; Deng, P. Assessment of Multi-Source Evapotranspiration Products over China Using Eddy Covariance Observations. Remote Sens. 2018, 10, 1692. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.S.; Liaqat, U.W.; Baik, J.; Choi, M. Stand-alone uncertainty characterization of GLEAM, GLDAS and MOD16 evapotranspiration products using an extended triple collocation approach. Agric. For. Meteorol. 2018, 252, 256–268. [Google Scholar] [CrossRef]
- McColl, K.A.; Vogelzang, J.; Konings, A.G.; Entekhabi, D.; Piles, M.; Stoffelen, A. Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target. Geophys. Res. Lett. 2014, 41, 6229–6236. [Google Scholar] [CrossRef] [Green Version]
- Moshir Panahi, D.; Sadeghi Tabas, S.; Kalantari, Z.; Ferreira, C.S.S.; Zahabiyoun, B. Spatio-Temporal Assessment of Global Gridded Evapotranspiration Datasets across Iran. Remote. Sens. 2021, 13, 1816. [Google Scholar] [CrossRef]
- Dembélé, M.; Ceperley, N.; Zwart, S.J.; Salvadore, E.; Mariethoz, G.; Schaefli, B. Potential of satellite and reanalysis evaporation datasets for hydrological modelling under various model calibration strategies. Adv. Water Resour. 2020, 143, 103667. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef] [Green Version]
- Vinukollu, R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ. 2011, 115, 801–823. [Google Scholar] [CrossRef]
- Chen, J.; Chen, B.; Black, T.A.; Innes, J.L.; Wang, G.; Kiely, G.; Hirano, T.; Wohlfahrt, G. Comparison of terrestrial evapotranspiration estimates using the mass transfer and Penman-Monteith equations in land surface models. J. Geophys. Res. Biogeosci. 2013, 118, 1715–1731. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Xia, Y.; Ferreira, V.G.; Liu, S.; Wang, K.; Yao, Y.; Zhang, X.; Zhao, C. Evaluation of twelve evapotranspiration products from machine learning, remote sensing and land surface models over conterminous United States. J. Hydrol. 2019, 578, 124105. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef] [Green Version]
- Scipal, K.; Dorigo, W.; de Jeu, R. Triple collocation—A new tool to determine the error structure of global soil moisture products. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 4426–4429. [Google Scholar]
- Gruber, A.; Su, C.H.; Zwieback, S.; Crow, W.; Dorigo, W.; Wagner, W. Recent advances in (soil moisture) triple collocation analysis. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 200–211. [Google Scholar] [CrossRef]
- Fang, H.; Wei, S.; Jiang, C.; Scipal, K. Theoretical uncertainty analysis of global MODIS, CYCLOPES, and GLOBCARBON LAI products using a triple collocation method. Remote Sens. Environ. 2012, 124, 610–621. [Google Scholar] [CrossRef]
- Roebeling, R.A.; Wolters, E.L.A.; Meirink, J.F.; Leijnse, H. Triple Collocation of Summer Precipitation Retrievals from SEVIRI over Europe with Gridded Rain Gauge and Weather Radar Data. J. Hydrometeorol. 2012, 13, 1552–1566. [Google Scholar] [CrossRef]
- Miyaoka, K.; Gruber, A.; Ticconi, F.; Hahn, S.; Wagner, W.; Figa-Saldaña, J.; Anderson, C. Triple Collocation Analysis of Soil Moisture from Metop-A ASCAT and SMOS Against JRA-55 and ERA-Interim. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2274–2284. [Google Scholar] [CrossRef]
- Gruber, A.; De Lannoy, G.; Albergel, C.; Al-Yaari, A.; Brocca, L.; Calvet, J.C.; Colliander, A.; Cosh, M.; Crow, W.; Dorigo, W.; et al. Validation practices for satellite soil moisture retrievals: What are (the) errors? Remote Sens. Environ. 2020, 244, 111806. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef] [Green Version]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Falge, E.; Aubinet, M.; Bakwin, P.S.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Black, T.A.; Ceulemans, R.; Davis, K.J.; Dolman, A.J.; et al. FLUXNET Research Network Site Characteristics, Investigators, and Bibliography, 2016; ORNL Distributed Active Archive Center: Oak Ridge, TN, USA, 2017. [CrossRef]
- Li, C.F.; Zhang, C.; Luo, G.P.; Chen, X.; Maisupova, B.; Madaminov, A.A.; Han, Q.F.; Djenbaev, B.M. Carbon stock and its responses to climate change in Central Asia. Glob. Chang. Biol. 2015, 21, 1951–1967. [Google Scholar] [CrossRef]
- Chen, S.; Hamdi, R.; Ochege, F.U.; Du, H.; Chen, X.; Yang, W.; Zhang, C. Added Value of a Dynamical Downscaling Approach for Simulating Precipitation and Temperature over Tianshan Mountains Area, Central Asia. J. Geophys. Res. Atmos. 2019, 124, 11051–11069. [Google Scholar] [CrossRef]
- Li, L.; Luo, G.; Chen, X.; Li, Y.; Xu, G.; Xu, H.; Bai, J. Modelling Evapotranspiration in a Central Asian Desert Ecosystem. Ecol. Model. 2011, 222, 3680–3691. [Google Scholar] [CrossRef]
- Li, B.; Beaudoing, H.; Rodell, M. GLDAS Catchment Land Surface Model L4 daily 0.25 × 0.25 degree GRACE-DA1 V2.2. In GLDAS_CLSM025_DA1_D, V2.2 ed.; NASA, GSFC, Eds.; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2020. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef] [Green Version]
- Albergel, C.; Dutra, E.; Munier, S.; Calvet, J.C.; Munoz-Sabater, J.; de Rosnay, P.; Balsamo, G. ERA-5 and ERA-Interim driven ISBA land surface model simulations: Which one performs better? Hydrol. Earth Syst. Sci. 2018, 22, 3515–3532. [Google Scholar] [CrossRef] [Green Version]
- Koster, R.D.; Suarez, M.J.; Ducharne, A.; Stieglitz, M.; Kumar, P. A catchment-based approach to modeling land surface processes in a general circulation model: 1. Model structure. J. Geophys. Res. Atmos. 2000, 105, 24809–24822. [Google Scholar] [CrossRef]
- Li, L.; Chen, X.; van der Tol, C.; Luo, G.; Su, Z. Growing season net ecosystem CO2 exchange of two desert ecosystems with alkaline soils in Kazakhstan. Ecol. Evol. 2014, 4, 14–26. [Google Scholar] [CrossRef]
- Scipal, K.; Holmes, T.; de Jeu, R.; Naeimi, V.; Wagner, W. A possible solution for the problem of estimating the error structure of global soil moisture data sets. Geophys. Res. Lett. 2008, 35, 4. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, W.A.; Scipal, K.; Parinussa, R.M.; Liu, Y.Y.; Wagner, W.; de Jeu, R.A.M.; Naeimi, V. Error characterisation of global active and passive microwave soil moisture datasets. Hydrol. Earth Syst. Sci. 2010, 14, 2605–2616. [Google Scholar] [CrossRef] [Green Version]
- Pierdicca, N.; Fascetti, F.; Pulvirenti, L.; Crapolicchio, R.; Muñoz-Sabater, J. Analysis of ASCAT, SMOS, in-situ and land model soil moisture as a regionalized variable over Europe and North Africa. Remote Sens. Environ. 2015, 170, 280–289. [Google Scholar] [CrossRef]
- Le, M.-H.; Kim, H.; Moon, H.; Zhang, R.; Lakshmi, V.; Nguyen, L.-B. Assessment of drought conditions over Vietnam using standardized precipitation evapotranspiration index, MERRA-2 re-analysis, and dynamic land cover. J. Hydrol. Reg. Stud. 2020, 32, 100767. [Google Scholar] [CrossRef]
- Abolafia-Rosenzweig, R.; Pan, M.; Zeng, J.L.; Livneh, B. Remotely sensed ensembles of the terrestrial water budget over major global river basins: An assessment of three closure techniques. Remote Sens. Environ. 2021, 252, 112191. [Google Scholar] [CrossRef]
- Lu, J.; Wang, G.; Chen, T.; Li, S.; Hagan, D.F.T.; Kattel, G.; Peng, J.; Jiang, T.; Su, B. A Harmonized Global Land Evaporation Dataset from Reanalysis Products Covering 1980–2017. Earth Syst. Sci. Data Discuss. 2021, 2021, 1–28. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Colliander, A.; Cosh, M.H.; Jackson, T.J.; Bindlish, R.; Reichle, R.H.; Chan, S.K.; Bosch, D.D.; Starks, P.J.; et al. Application of Triple Collocation in Ground-Based Validation of Soil Moisture Active/Passive (SMAP) Level 2 Data Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 489–502. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Bindlish, R.; Colliander, A.; Burgin, M.S.; Asanuma, J.; Aida, K. Global-scale evaluation of SMAP, SMOS and ASCAT soil moisture products using triple collocation. Remote Sens. Environ. 2018, 214, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, M.T.; Crow, W.T. Evaluation of Assumptions in Soil Moisture Triple Collocation Analysis. J. Hydrometeorol. 2014, 15, 1293–1302. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Zhang, C.; Li, C.; Luo, G.; Chen, X. Modeling plant structure and its impacts on carbon and water cycles of the Central Asian arid ecosystem in the context of climate change. Ecol. Model. 2013, 267, 158–179. [Google Scholar] [CrossRef]
- Khan, M.S.; Baik, J.; Choi, M. Inter-comparison of evapotranspiration datasets over heterogeneous landscapes across Australia. Adv. Space Res. 2020, 66, 533–545. [Google Scholar] [CrossRef]
- Badgley, G.; Fisher, J.B.; Jiménez, C.; Tu, K.P.; Vinukollu, R. On Uncertainty in Global Terrestrial Evapotranspiration Estimates from Choice of Input Forcing Datasets. J. Hydrometeorol. 2015, 16, 1449–1455. [Google Scholar] [CrossRef]
- Yang, T.; Li, Q.; Chen, X.; Hamdi, R.; De Maeyer, P.; Kurban, A.; Li, L. Improving snow simulation with more realistic vegetation parameters in a regional climate model in the Tianshan Mountains, Central Asia. J. Hydrol. 2020, 590, 125525. [Google Scholar] [CrossRef]
- Zhang, M.; Luo, G.; Cao, X.; Hamdi, R.; Li, T.; Cai, P.; Ye, H.; He, H. Numerical Simulation of the Irrigation Effects on Surface Fluxes and Local Climate in Typical Mountain-Oasis-Desert Systems in the Central Asia Arid Area. J. Geophys. Res. Atmos. 2019, 124, 12485–12506. [Google Scholar] [CrossRef]











| Product Name | Spatial Resolution | Temporal Resolution | ET Approach/ Reference | Period |
|---|---|---|---|---|
| CLSM L4 V2.2 | 0.25° × 0.25° | Daily | LSM Li, Beaudoing. [42] | February 2003–2020 |
| ERA5 | 0.25° × 0.25° | Monthly | IFS Hersbach, Bell [14] | 2003–2020 |
| NOAH L4 V2.1 | 0.25° × 0.25° | Monthly | LSM Rodell, Houser [10] | 2003–2020 |
| MERRA2 | 0.625° × 0.50° | Monthly | GEOS-5 Gelaro, McCarty [15] | 2003–2020 |
| GLEAM v3.5b | 0.25° × 0.25° | Monthly | Priestly–Taylor algorithm with canopy interception Martens, Gonzalez Miralles [11] | 2003– July 2020 |
| EC Site Name | Biome (Land Cover) | Location | Climatology (Mean/Year) | Period | ||
|---|---|---|---|---|---|---|
| Lat. | Long. | Prec. | Temp. | |||
| Aral Sea | Desert shrubs | 45°58′N | 61°05′E | 140 mm | 6.6 °C | April–Sept. 2012 |
| Balkhash | Grassland | 44°34′N | 76°39′E | 140 mm | 5.7 °C | May–Oct. 2012 |
| Fukang | Shrubland | 44°17′N | 87°56′E | 163 mm | 6.8 °C | 2004–2006, 2009, 2011–2013 |
| Wulanwusu | Cropland | 44°17′N | 85°49′E | 210 mm | 7.0 °C | 2009–2013 |
| Statistics | ET1 | ET2 | ET3 | ET4 | ET5 | ET6 |
|---|---|---|---|---|---|---|
| 75th Percentile | 0.89 | 0.89 | 0.89 | 0.95 | 0.94 | 90 |
| Median | 0.77 | 0.69 | 0.75 | 0.93 | 0.92 | 0.79 |
| 25th Percentile | 0.57 | 0.41 | 0.57 | 0.92 | 0.91 | 0.60 |
| Mean | 35.095 | 32.1975 | 35.47 | 41.66 | 37.38025 | 33.4225 |
| SD | 34.1325 | 31.0725 | 34.2125 | 36.91349 | 33.89 | 32.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ochege, F.U.; Shi, H.; Li, C.; Ma, X.; Igboeli, E.E.; Luo, G. Assessing Satellite, Land Surface Model and Reanalysis Evapotranspiration Products in the Absence of In-Situ in Central Asia. Remote Sens. 2021, 13, 5148. https://doi.org/10.3390/rs13245148
Ochege FU, Shi H, Li C, Ma X, Igboeli EE, Luo G. Assessing Satellite, Land Surface Model and Reanalysis Evapotranspiration Products in the Absence of In-Situ in Central Asia. Remote Sensing. 2021; 13(24):5148. https://doi.org/10.3390/rs13245148
Chicago/Turabian StyleOchege, Friday Uchenna, Haiyang Shi, Chaofan Li, Xiaofei Ma, Emeka Edwin Igboeli, and Geping Luo. 2021. "Assessing Satellite, Land Surface Model and Reanalysis Evapotranspiration Products in the Absence of In-Situ in Central Asia" Remote Sensing 13, no. 24: 5148. https://doi.org/10.3390/rs13245148
APA StyleOchege, F. U., Shi, H., Li, C., Ma, X., Igboeli, E. E., & Luo, G. (2021). Assessing Satellite, Land Surface Model and Reanalysis Evapotranspiration Products in the Absence of In-Situ in Central Asia. Remote Sensing, 13(24), 5148. https://doi.org/10.3390/rs13245148








