The Novel Microwave Temperature Vegetation Drought Index (MTVDI) Captures Canopy Seasonality across Amazonian Tropical Evergreen Forests
Abstract
:1. Introduction
2. Materials and Methods
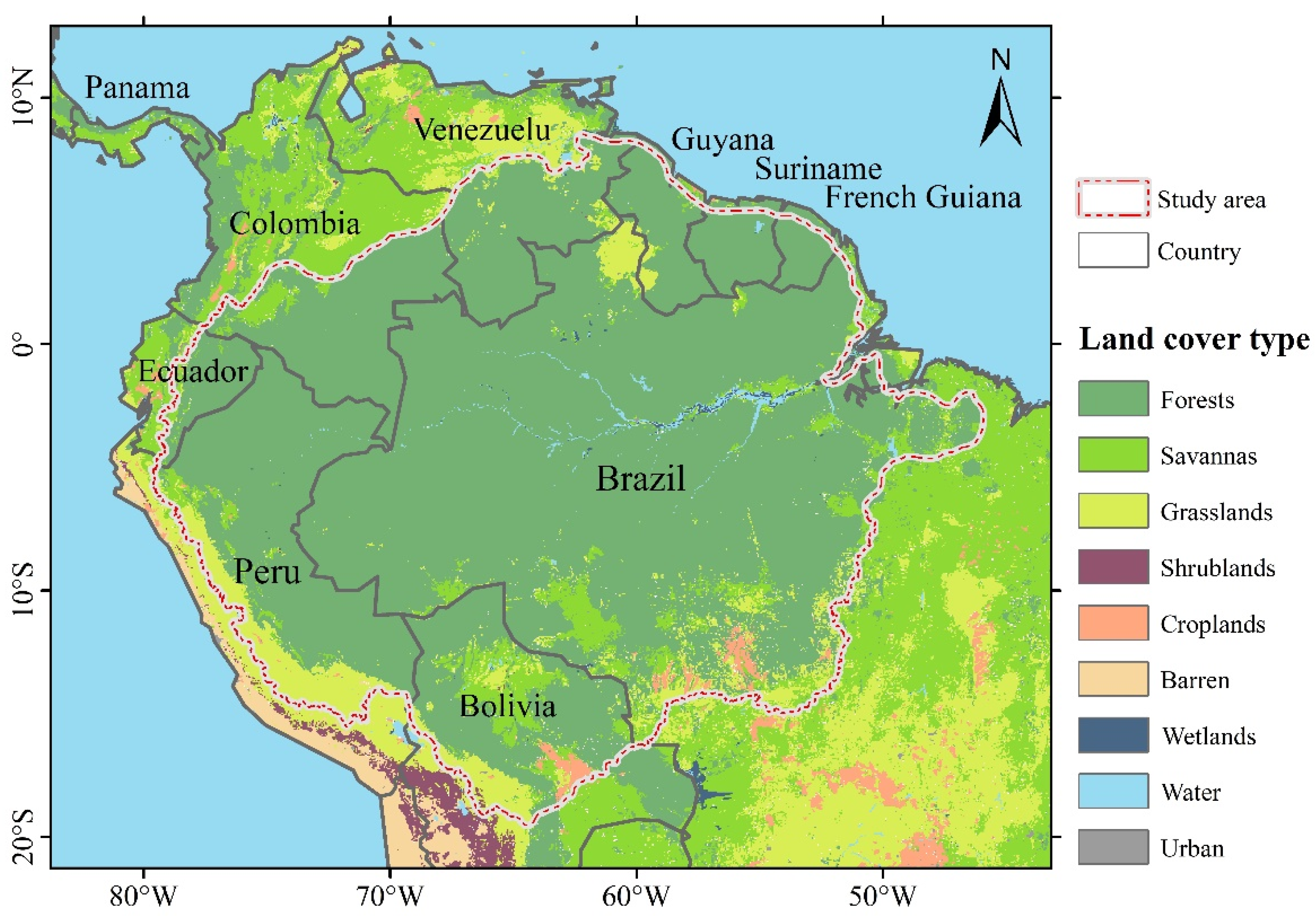
2.1. Study Area
2.2. AMSR-E Data Processing
2.3. Developing MTVDI
2.4. Climatic Dryness Indicators and Canopy Photosynthesis Proxies for Comparing the MTVDI Seasonality
2.4.1. Terrestrial Water Storage
2.4.2. Vapor Pressure Deficit
2.4.3. Palmer Drought Severity Index
2.4.4. Climatological Water Deficit
2.4.5. Enhanced Vegetation Index
2.4.6. Solar-Induced Chlorophyll Fluorescence
2.5. Nash–Sutcliffe Efficiency Coefficient
3. Results
3.1. The MTVDI Triangle Space
3.2. Seasonality of MTVDI
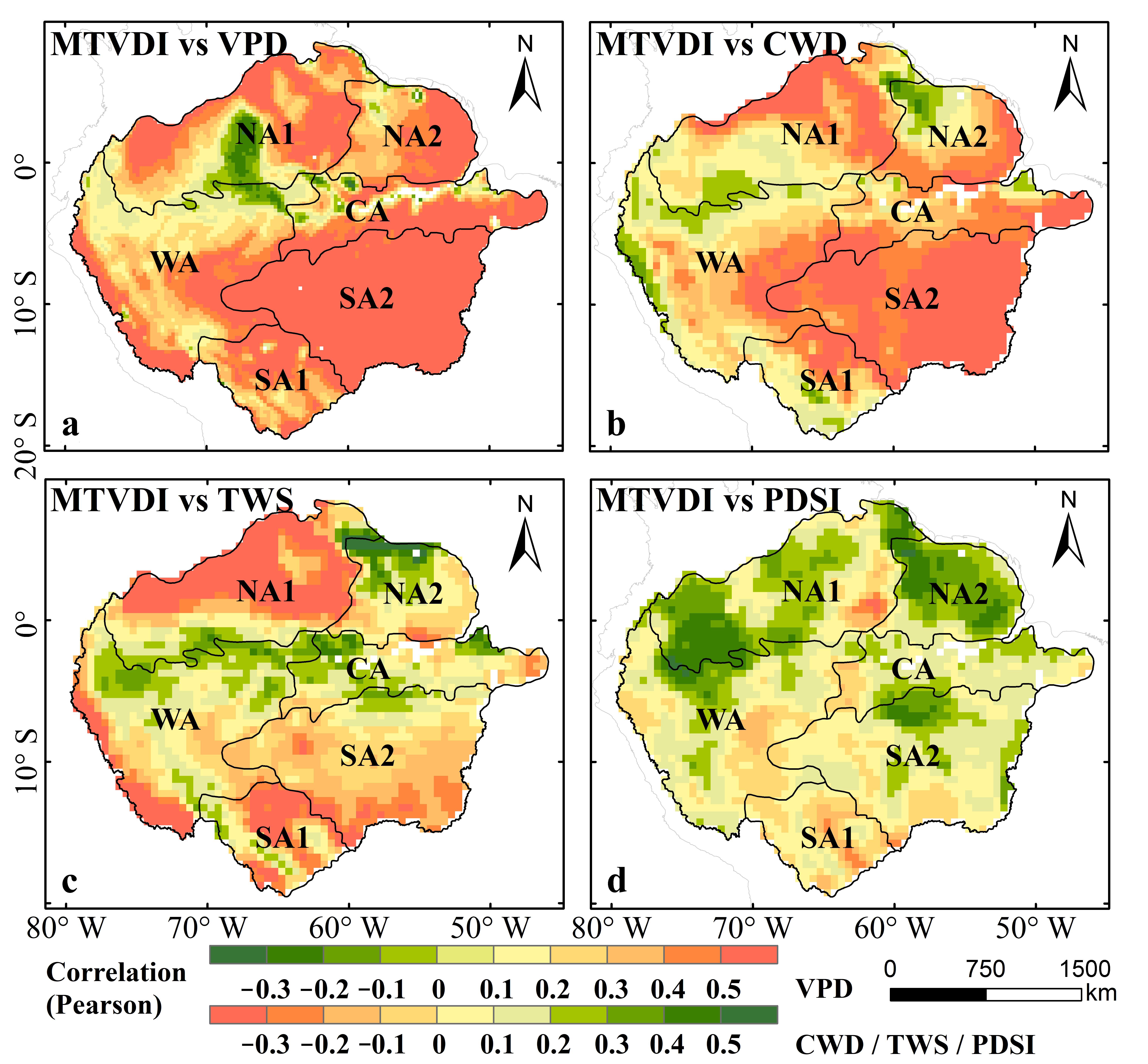
3.3. Compare MTVDI Seasonality against with Climatic Dryness Indicators
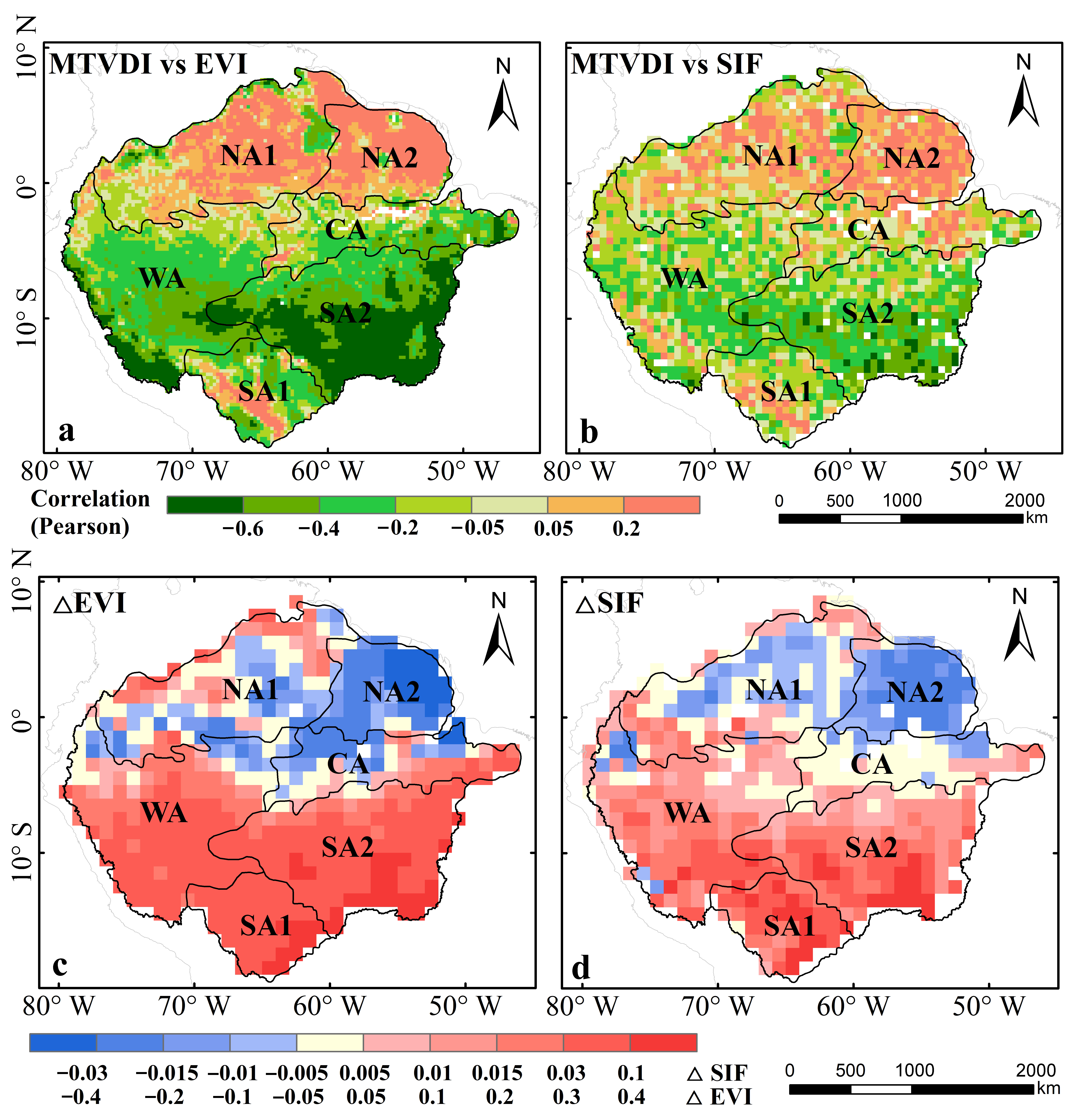
3.4. Capability of MTVDI Seasonality in Representing Canopy Photosynthesis Seasonality
4. Discussions
4.1. MTVDI Captures Amazonian Seasonality
4.2. Light and Water Limitations Identified by MTVDI
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P. Primary Production of the Biosphere: Integrating Terrestrial and Oceanic Components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef] [Green Version]
- Maslin, M.; Malhi, Y.; Phillips, O.; Cowling, S. New Views on an Old Forest: Assessing the Longevity, Resilience and Future of the Amazon Rainforest. Trans. Inst. Br. Geogr. 2005, 30, 477–499. [Google Scholar] [CrossRef]
- Boisier, J.P.; Ciais, P.; Ducharne, A.; Guimberteau, M. Projected Strengthening of Amazonian Dry Season by Constrained Climate Model Simulations. Nat. Clim. Chang. 2015, 5, 656–660. [Google Scholar] [CrossRef]
- Chen, X.; Maignan, F.; Viovy, N.; Bastos, A.; Goll, D.; Wu, J.; Liu, L.; Yue, C.; Peng, S.; Yuan, W.; et al. Novel Representation of Leaf Phenology Improves Simulation of Amazonian Evergreen Forest Photosynthesis in a Land Surface Model. J. Adv. Model. Earth Syst. 2020, 12, e2018MS001565. [Google Scholar] [CrossRef] [Green Version]
- Myneni, R.B.; Yang, W.; Nemani, R.R.; Huete, A.R.; Dickinson, R.E.; Knyazikhin, Y.; Didan, K.; Fu, R.; Juárez, R.I.N.; Saatchi, S.S.; et al. Large Seasonal Swings in Leaf Area of Amazon Rainforests. Proc. Natl. Acad. Sci. USA 2007, 104, 4820–4823. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Argus, D.F.; Freymueller, J.T.; Heflin, M.B. Horizontal Motion in Elastic Response to Seasonal Loading of Rain Water in the Amazon Basin and Monsoon Water in Southeast Asia Observed by GPS and Inferred from GRACE. Geophys. Res. Lett. 2013, 40, 6048–6053. [Google Scholar] [CrossRef]
- Wu, J.; Albert, L.P.; Lopes, A.P.; Restrepo-Coupe, N.; Hayek, M.; Wiedemann, K.T.; Guan, K.; Stark, S.C.; Christoffersen, B.; Prohaska, N.; et al. Leaf Development and Demography Explain Photosynthetic Seasonality in Amazon Evergreen Forests. Science 2016, 351, 972–976. [Google Scholar] [CrossRef] [Green Version]
- Anderson, L.O.; Ribeiro Neto, G.; Cunha, A.P.; Fonseca, M.G.; Mendes de Moura, Y.; Dalagnol, R.; Wagner, F.H.; de Aragão, L.E.O.C. Vulnerability of Amazonian Forests to Repeated Droughts. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373. [Google Scholar] [CrossRef]
- Liu, L.; Liao, J.; Chen, X.; Zhou, G.; Su, Y.; Xiang, Z.; Wang, Z.; Liu, X.; Li, Y.; Wu, J.; et al. The Microwave Temperature Vegetation Drought Index (MTVDI) Based on AMSR-E Brightness Temperatures for Long-Term Drought Assessment across China (2003–2010). Remote Sens. Environ. 2017, 199, 302–320. [Google Scholar] [CrossRef]
- Huete, A.R.; Didan, K.; Shimabukuro, Y.E.; Ratana, P.; Saleska, S.R.; Hutyra, L.R.; Yang, W.; Nemani, R.R.; Myneni, R. Amazon Rainforests Green-up with Sunlight in Dry Season. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Xiao, X.; Zhang, Q.; Saleska, S.; Hutyra, L.; De Camargo, P.; Wofsy, S.; Frolking, S.; Boles, S.; Keller, M.; Moore, B. Satellite-Based Modeling of Gross Primary Production in a Seasonally Moist Tropical Evergreen Forest. Remote Sens. Environ. 2005, 94, 105–122. [Google Scholar] [CrossRef]
- Merrick, T.; Pau, S.; Jorge, M.L.S.P.; Silva, T.S.F.; Bennartz, R. Spatiotemporal Patterns and Phenology of Tropical Vegetation Solar-Induced Chlorophyll Fluorescence across Brazilian Biomes Using Satellite Observations. Remote Sens. 2019, 11, 1746. [Google Scholar] [CrossRef] [Green Version]
- Saleska, S.R.; Wu, J.; Guan, K.; Araujo, A.C.; Huete, A.; Nobre, A.D.; Restrepo-Coupe, N. Dry-Season Greening of Amazon Forests. Nature 2016, 531, E4–E5. [Google Scholar] [CrossRef] [PubMed]
- Morton, D.C.; Nagol, J.; Carabajal, C.C.; Rosette, J.; Palace, M.; Cook, B.D.; Vermote, E.F.; Harding, D.J.; North, P.R.J. Amazon Forests Maintain Consistent Canopy Structure and Greenness during the Dry Season. Nature 2014, 506, 221–224. [Google Scholar] [CrossRef]
- Samanta, A.; Ganguly, S.; Hashimoto, H.; Devadiga, S.; Vermote, E.; Knyazikhin, Y.; Nemani, R.R.; Myneni, R.B. Amazon Forests Did Not Green-up during the 2005 Drought. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Samanta, A.; Ganguly, S.; Myneni, R.B. MODIS Enhanced Vegetation Index Data Do Not Show Greening of Amazon Forests during the 2005 Drought. New Phytol. 2011, 189, 11–15. [Google Scholar] [CrossRef]
- Andela, N.; Liu, Y.Y.; van Dijk, A.I.J.M.; de Jeu, R.A.M.; McVicar, T.R. Global Changes in Dryland Vegetation Dynamics (1988–2008) Assessed by Satellite Remote Sensing: Combining a New Passive Microwave Vegetation Density Record with Reflective Greenness Data. Biogeosci. Discuss. 2013, 10, 8749–8797. [Google Scholar] [CrossRef]
- Liu, Y.Y.; de Jeu, R.A.M.; McCabe, M.F.; Evans, J.P.; van Dijk, A.I.J.M. Global Long-Term Passive Microwave Satellite-Based Retrievals of Vegetation Optical Depth. Geophys. Res. Lett. 2011, 38, L18402. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Samanta, A.; Costa, M.H.; Ganguly, S.; Nemani, R.R.; Myneni, R.B. Widespread Decline in Greenness of Amazonian Vegetation Due to the 2010 Drought. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Jackson, T.; Tao, J.; Du, J.; Bindlish, R.; Lu, L.; Chen, K.S. Microwave Vegetation Indices for Short Vegetation Covers from Satellite Passive Microwave Sensor AMSR-E. Remote Sens. Environ. 2008, 112, 4285–4300. [Google Scholar] [CrossRef]
- Fan, L.; Wigneron, J.-P.; Xiao, Q.; Al-Yaari, A.; Wen, J.; Martin-StPaul, N.; Dupuy, J.-L.; Pimont, F.; Al Bitar, A.; Fernandez-Moran, R.; et al. Evaluation of Microwave Remote Sensing for Monitoring Live Fuel Moisture Content in the Mediterranean Region. Remote Sens. Environ. 2018, 205, 210–223. [Google Scholar] [CrossRef]
- Woodhouse, I.H. Introduction to Microwave Remote Sensing; CRC Press: Boca Raton, FL, USA, 2017; ISBN 1-351-98901-4. [Google Scholar]
- Zhang, A.; Jia, G. Monitoring Meteorological Drought in Semiarid Regions Using Multi-Sensor Microwave Remote Sensing Data. Remote Sens. Environ. 2013, 134, 12–23. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Fan, L.; Ciais, P.; Bastos, A.; Brandt, M.; Chave, J.; Saatchi, S.; Baccini, A.; Fensholt, R. Tropical Forests Did Not Recover from the Strong 2015–2016 El Niño Event. Sci. Adv. 2020, 6, eaay4603. [Google Scholar] [CrossRef] [Green Version]
- Fan, L.; Wigneron, J.-P.; Ciais, P.; Chave, J.; Brandt, M.; Fensholt, R.; Saatchi, S.S.; Bastos, A.; Al-Yaari, A.; Hufkens, K.; et al. Satellite-Observed Pantropical Carbon Dynamics. Nat. Plants 2019, 5, 944–951. [Google Scholar] [CrossRef]
- Saatchi, S.; Asefi-Najafabady, S.; Malhi, Y.; Aragão, L.E.O.C.; Anderson, L.O.; Myneni, R.B.; Nemani, R. Persistent Effects of a Severe Drought on Amazonian Forest Canopy. Proc. Natl. Acad. Sci. USA 2013, 110, 565–570. [Google Scholar] [CrossRef] [Green Version]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A Simple Interpretation of the Surface Temperature/Vegetation Index Space for Assessment of Surface Moisture Status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L. GRACE-REC: A Reconstruction of Climate-Driven Water Storage Changes over the Last Century. Earth Syst. Sci. Data 2019, 11, 1153–1170. [Google Scholar] [CrossRef] [Green Version]
- Yuan, W.; Zheng, Y.; Piao, S.; Ciais, P.; Lombardozzi, D.; Wang, Y.; Ryu, Y.; Chen, G.; Dong, W.; Hu, Z.; et al. Increased Atmospheric Vapor Pressure Deficit Reduces Global Vegetation Growth. Sci. Adv. 2019, 5, eaax1396. [Google Scholar] [CrossRef] [Green Version]
- Palmer, W. Meteorological Drought; Research Paper No. 45; U.S. Department of Commerce Weather Bureau: Washington, DC, USA, 1965.
- Malhi, Y.; Aragão, L.E.O.C.; Galbraith, D.; Huntingford, C.; Fisher, R.; Zelazowski, P.; Sitch, S.; McSweeney, C.; Meir, P. Exploring the Likelihood and Mechanism of a Climate-Change-Induced Dieback of the Amazon Rainforest. Proc. Natl. Acad. Sci. USA 2009, 106, 20610–20615. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Joiner, J.; Guanter, L.; Lindstrot, R.; Voigt, M.; Vasilkov, A.P.; Middleton, E.M.; Huemmrich, K.F.; Yoshida, Y.; Frankenberg, C. Global Monitoring of Terrestrial Chlorophyll Fluorescence from Moderate Spectral Resolution Near-Infrared Satellite Measurements: Methodology, Simulations, and Application to GOME-2. Atmos. Meas. Tech. 2013, 6, 2803–2823. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 Exceptional Amazon Flood and Interannual Terrestrial Water Storage Change Observed by GRACE. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Marengo, J.A. Characteristics and Spatio-Temporal Variability of the Amazon River Basin Water Budget. Clim. Dyn. 2005, 24, 11–22. [Google Scholar] [CrossRef]
- Costa, M.H.; Foley, J.A. A Comparison of Precipitation Datasets for the Amazon Basin. Geophys. Res. Lett. 1998, 25, 155–158. [Google Scholar] [CrossRef]
- Friedl, M.; Sulla-Menashe, D. MCD12C1 MODIS/Terra+ Aqua Land Cover Type Yearly L3 Global 0.05 Deg CMG V006 [Data Set]. NASA EOSDIS Land Process. DAAC 2015. [Google Scholar] [CrossRef]
- McFarland, M.J.; Miller, R.L.; Neale, C.M.U. Land Surface Temperature Derived from the SSM/I Passive Microwave Brightness Temperatures. IEEE Trans. Geosci. Remote Sens. 1990, 28, 839–845. [Google Scholar] [CrossRef]
- Kawanishi, T.; Sezai, T.; Ito, Y.; Imaoka, K.; Takeshima, T.; Ishido, Y.; Shibata, A.; Miura, M.; Inahata, H.; Spencer, R.W. The Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E), NASDA’s Contribution to the EOS for Global Energy and Water Cycle Studies. IEEE Trans. Geosci. Remote Sens. 2003, 41, 184–194. [Google Scholar] [CrossRef]
- Parkinson, C.L. Aqua: An Earth-Observing Satellite Mission to Examine Water and Other Climate Variables. IEEE Trans. Geosci. Remote Sens. 2003, 41, 173–183. [Google Scholar] [CrossRef]
- Imaoka, K.; Kachi, M.; Kasahara, M.; Ito, N.; Nakagawa, K.; Oki, T. Instrument Performance and Calibration of AMSR-E and AMSR2. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2010, 38, 13–16. [Google Scholar]
- Kerr, Y.H.; Njoku, E.G. A Semiempirical Model for Interpreting Microwave Emission from Semiarid Land Surfaces as Seen from Space. IEEE Trans. Geosci. Remote Sens. 1990, 28, 384–393. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor Historical Climatology of Satellite-Derived Global Land Surface Moisture. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Njoku, E.G.; Ashcroft, P.; Chan, T.K.; Li, L. Global Survey and Statistics of Radio-Frequency Interference in AMSR-E Land Observations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 938–947. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of Terrestrial Water Storage Changes from GRACE and GLDAS. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating Groundwater Storage Changes in the Mississippi River Basin (USA) Using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef] [Green Version]
- Reager, J.T.; Famiglietti, J.S. Characteristic Mega-basin Water Storage Behavior Using GRACE. Water Resour. Res. 2013, 49, 3314–3329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crowley, J.W.; Mitrovica, J.X.; Bailey, R.C.; Tamisiea, M.E.; Davis, J.L. Land Water Storage within the Congo Basin Inferred from GRACE Satellite Gravity Data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Ramillien, G.; Famiglietti, J.S.; Wahr, J. Detection of Continental Hydrology and Glaciology Signals from GRACE: A Review. Surv. Geophys. 2008, 29, 361–374. [Google Scholar] [CrossRef]
- Rawson, H.M.; Begg, J.; Woodward, R. The Effect of Atmospheric Humidity on Photosynthesis, Transpiration and Water Use Efficiency of Leaves of Several Plant Species. Planta 1977, 134, 5–10. [Google Scholar] [CrossRef]
- Cunningham, S.C. Stomatal Sensitivity to Vapour Pressure Deficit of Temperate and Tropical Evergreen Rainforest Trees of Australia. Trees 2004, 18, 399–407. [Google Scholar] [CrossRef]
- Tombesi, S.; Nardini, A.; Frioni, T.; Soccolini, M.; Zadra, C.; Farinelli, D.; Poni, S.; Palliotti, A. Stomatal Closure Is Induced by Hydraulic Signals and Maintained by ABA in Drought-Stressed Grapevine. Sci. Rep. 2015, 5, 12449. [Google Scholar] [CrossRef] [PubMed]
- Shirke, P.A.; Pathre, U.V. Influence of Leaf-to-Air Vapour Pressure Deficit (VPD) on the Biochemistry and Physiology of Photosynthesis in Prosopis Juliflora. J. Exp. Bot. 2004, 55, 2111–2120. [Google Scholar] [CrossRef] [PubMed]
- Dee, D.P.; de Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Vitart, F.; et al. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, G.; An, W.; Zou, X.; Li, H.; Hou, M. Timescale Differences between SC-PDSI and SPEI for Drought Monitoring in China. Phys. Chem. Earth Parts ABC 2017, 102, 48–58. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a High-Resolution Global Dataset of Monthly Climate and Climatic Water Balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef] [Green Version]
- Viovy, N. CRUNCEP Version 7–Atmospheric Forcing Data for the Community Land Model. Available online: https://rda.ucar.edu/datasets/ds314.3/ (accessed on 19 May 2020).
- Aragão, L.; Malhi, Y.; Román-Cuesta, R.M.; Saatchi, S.; Anderson, L.; Shimabukuro, Y. Spatial Patterns and Fire Response of Recent Amazonian Droughts. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Rocha, H.; Goulden, M.; Miller, S.; Menton, M.; Pinto, L.; Freitas, H.; Figueira, A. Seasonality of Water and Heat Fluxes over a Tropical Forest in Eastern Amazonia. Ecol. Appl. 2004, 14, 22–32. [Google Scholar] [CrossRef]
- von Randow, C.; Manzi, A.O.; Kruijt, B.; de Oliveira, P.J.; Zanchi, F.B.; Silva, R.L.; Hodnett, M.G.; Gash, J.H.C.; Elbers, J.A.; Waterloo, M.J.; et al. Comparative Measurements and Seasonal Variations in Energy and Carbon Exchange over Forest and Pasture in South West Amazonia. Theor. Appl. Climatol. 2004, 78, 5–26. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Leuning, R.; Black, T.A.; Grace, J.; Jarvis, P.G.; Roberts, J.; Jones, H.G.; Jarvis, P.G.; Monteith, J.L.; Shuttleworth, W.J.; et al. Micrometeorology of Temperate and Tropical Forest. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1989, 324, 299–334. [Google Scholar] [CrossRef]
- Gao, X.; Huete, A.R.; Ni, W.; Miura, T. Optical–Biophysical Relationships of Vegetation Spectra without Background Contamination. Remote Sens. Environ. 2000, 74, 609–620. [Google Scholar] [CrossRef]
- Bertani, G.; Wagner, F.; Aragão, L.; Anderson, L. Remote Sensing of Solar-Induced Chlorophyll Fluorescence for Describing Photosynthesis Seasonality in the Amazon Forest; INPE Press: Santos, SP, Brazil, 2017; ISBN 978-85-17-00088-1. [Google Scholar]
- Guan, K.; Pan, M.; Li, H.; Wolf, A.; Wu, J.; Medvigy, D.; Caylor, K.K.; Sheffield, J.; Wood, E.F.; Malhi, Y.; et al. Photosynthetic Seasonality of Global Tropical Forests Constrained by Hydroclimate. Nat. Geosci. 2015, 8, 284–289. [Google Scholar] [CrossRef]
- Lee, J.-E.; Frankenberg, C.; Tol, C.; Berry, J.; Guanter, L.; Boyce, C.; Fisher, J.; Morrow, E.; Worden, J.; Asefi-Najafabady, S.; et al. Forest Productivity and Water Stress in Amazonia: Observations from GOSAT Chlorophyll Fluorescence. Proc. R. Soc. B Biol. Sci. 2013, 280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frankenberg, C.; O’Dell, C.; Berry, J.; Guanter, L.; Joiner, J.; Köhler, P.; Pollock, R.; Taylor, T.E. Prospects for Chlorophyll Fluorescence Remote Sensing from the Orbiting Carbon Observatory-2. Remote Sens. Environ. 2014, 147, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Joiner, J.; Yoshida, Y.; Guanter, L.; Middleton, E.M. New Methods for the Retrieval of Chlorophyll Red Fluorescence from Hyperspectral Satellite Instruments: Simulations and Application to GOME-2 and SCIAMACHY. Atmos. Meas. Tech. 2016, 9, 3939–3967. [Google Scholar] [CrossRef] [Green Version]
- Campforts, B.; Vanacker, V.; Vanderborght, J.; Baken, S.; Smolders, E.; Govers, G. Simulating the Mobility of Meteoric 10Be in the Landscape through a Coupled Soil-Hillslope Model (Be2D). Earth Planet. Sci. Lett. 2016, 439, 143–157. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007. [Google Scholar] [CrossRef]
- Fernández-Peruchena, C.M.; Blanco, M.; Gastón, M.; Bernardos, A. Increasing the Temporal Resolution of Direct Normal Solar Irradiance Series in Different Climatic Zones. Sol. Energy 2015, 115, 255–263. [Google Scholar] [CrossRef]
- Soltani, S.; Modarres, R.; Eslamian, S.S. The Use of Time Series Modeling for the Determination of Rainfall Climates of Iran. Int. J. Climatol. 2007, 27, 819–829. [Google Scholar] [CrossRef]
- Jim, C.Y.; He, H. Estimating Heat Flux Transmission of Vertical Greenery Ecosystem. Ecol. Eng. 2011, 37, 1112–1122. [Google Scholar] [CrossRef]
- Dass, P.; Rawlins, M.A.; Kimball, J.S.; Kim, Y. Environmental Controls on the Increasing GPP of Terrestrial Vegetation across Northern Eurasia. Biogeosciences 2016, 13, 45–62. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Johnston, C.A. Hydrologic Response to Climatic Variability in a Great Lakes Watershed: A Case Study with the SWAT Model. J. Hydrol. 2007, 337, 187–199. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100, ISBN 0-12-385022-3. [Google Scholar]
- Xu, L.; Saatchi, S.S.; Yang, Y.; Myneni, R.B.; Frankenberg, C.; Chowdhury, D.; Bi, J. Satellite Observation of Tropical Forest Seasonality: Spatial Patterns of Carbon Exchange in Amazonia. Environ. Res. Lett. 2015, 10, 084005. [Google Scholar] [CrossRef]
- Jones, M.O.; Kimball, J.S.; Nemani, R.R. Asynchronous Amazon Forest Canopy Phenology Indicates Adaptation to Both Water and Light Availability. Environ. Res. Lett. 2014, 9, 124021. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Famiglietti, J.S.; Rodell, M. Spatial Sensitivity of the Gravity Recovery and Climate Experiment (GRACE) Time-Variable Gravity Observations. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Phillips, O.L.; Aragão, L.E.O.C.; Lewis, S.L.; Fisher, J.B.; Lloyd, J.; López-González, G.; Malhi, Y.; Monteagudo, A.; Peacock, J.; Quesada, C.A.; et al. Drought Sensitivity of the Amazon Rainforest. Science 2009, 323, 1344–1347. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; de Almeida Castanho, A.D.; Galbraith, D.R.; Moghim, S.; Levine, N.M.; Bras, R.L.; Coe, M.T.; Costa, M.H.; Malhi, Y.; Longo, M.; et al. The Fate of Amazonian Ecosystems over the Coming Century Arising from Changes in Climate, Atmospheric CO2, and Land Use. Glob. Chang. Biol. 2015, 21, 2569–2587. [Google Scholar] [CrossRef]






| Indicator | Evaluation Dataset | Abbr. | Original Spatial Resolution | Original Temporal Resolution | Period | Reference |
|---|---|---|---|---|---|---|
| climatic dryness indicator | GRACE TWS | TWS | 0.50° | Monthly | 2003–2010 | Humphrey and Gudmundsson 2019 [29] |
| ERA-Interim VPD | VPD | 0.125° | Daily | 2003–2010 | Yuan et al., 2019; Dee et al., 2011 [30,56] | |
| Terraclimate PDSI | PDSI | 0.50° | Monthly | 2003–2010 | Abatzoglou et al., 2018 [59] | |
| Climatological Water Deficit | CWD | 0.50° | Monthly | 2003–2010 | Aragão et al., 2007 [61] | |
| canopy photosynthesis proxy | MODIS EVI | EVI | 0.05° | Monthly | 2003–2010 | Huete et al., 2002 [33] |
| GOME-2 SIF v26 | SIF | 0.50° | Monthly | 2007–2010 | Joiner et al., 2013 [34] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Yang, X.; Gong, F.; Su, Y.; Huang, G.; Chen, X. The Novel Microwave Temperature Vegetation Drought Index (MTVDI) Captures Canopy Seasonality across Amazonian Tropical Evergreen Forests. Remote Sens. 2021, 13, 339. https://doi.org/10.3390/rs13030339
Liu L, Yang X, Gong F, Su Y, Huang G, Chen X. The Novel Microwave Temperature Vegetation Drought Index (MTVDI) Captures Canopy Seasonality across Amazonian Tropical Evergreen Forests. Remote Sensing. 2021; 13(3):339. https://doi.org/10.3390/rs13030339
Chicago/Turabian StyleLiu, Liyang, Xueqin Yang, Fanxi Gong, Yongxian Su, Guangqing Huang, and Xiuzhi Chen. 2021. "The Novel Microwave Temperature Vegetation Drought Index (MTVDI) Captures Canopy Seasonality across Amazonian Tropical Evergreen Forests" Remote Sensing 13, no. 3: 339. https://doi.org/10.3390/rs13030339
APA StyleLiu, L., Yang, X., Gong, F., Su, Y., Huang, G., & Chen, X. (2021). The Novel Microwave Temperature Vegetation Drought Index (MTVDI) Captures Canopy Seasonality across Amazonian Tropical Evergreen Forests. Remote Sensing, 13(3), 339. https://doi.org/10.3390/rs13030339






