Multi-Parameter Regularization Method for Synthetic Aperture Imaging Radiometers
Abstract
:1. Introduction
2. Imaging Principle of SAIRs
2.1. Tikhonov Regularization
2.2. Band-Limited Regularization
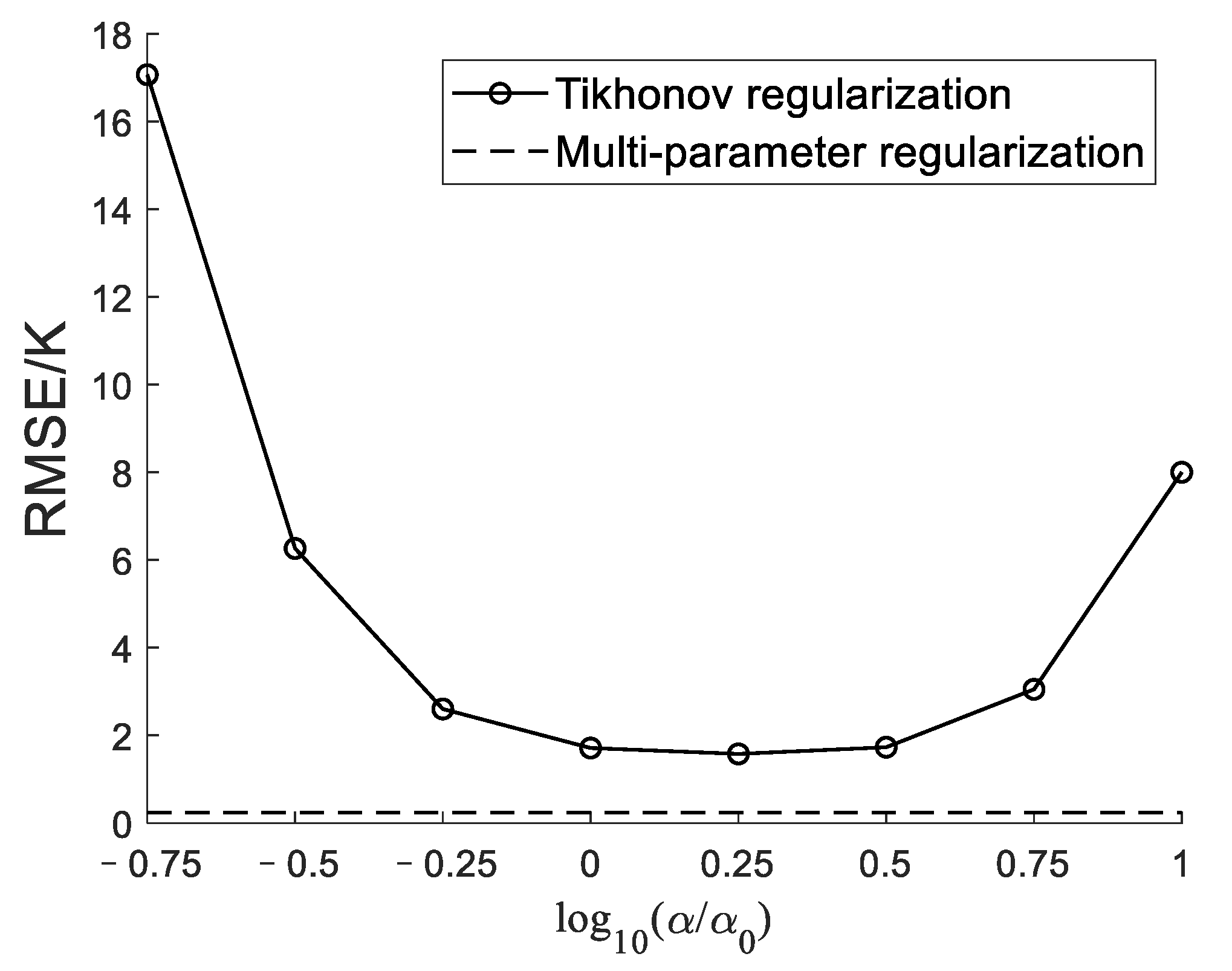
3. Multi-Parameter Regularization
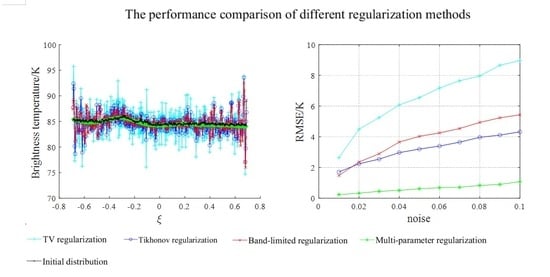
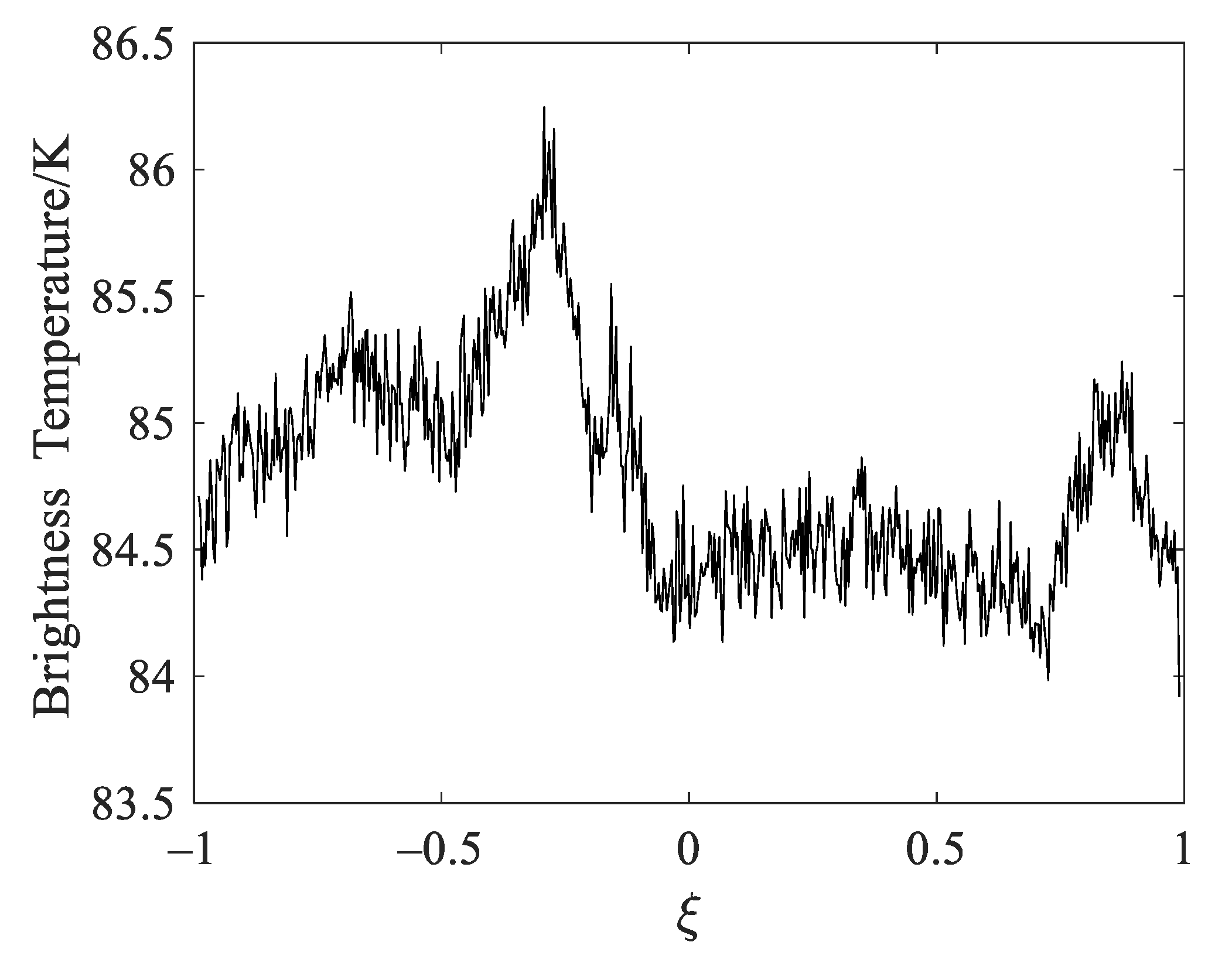
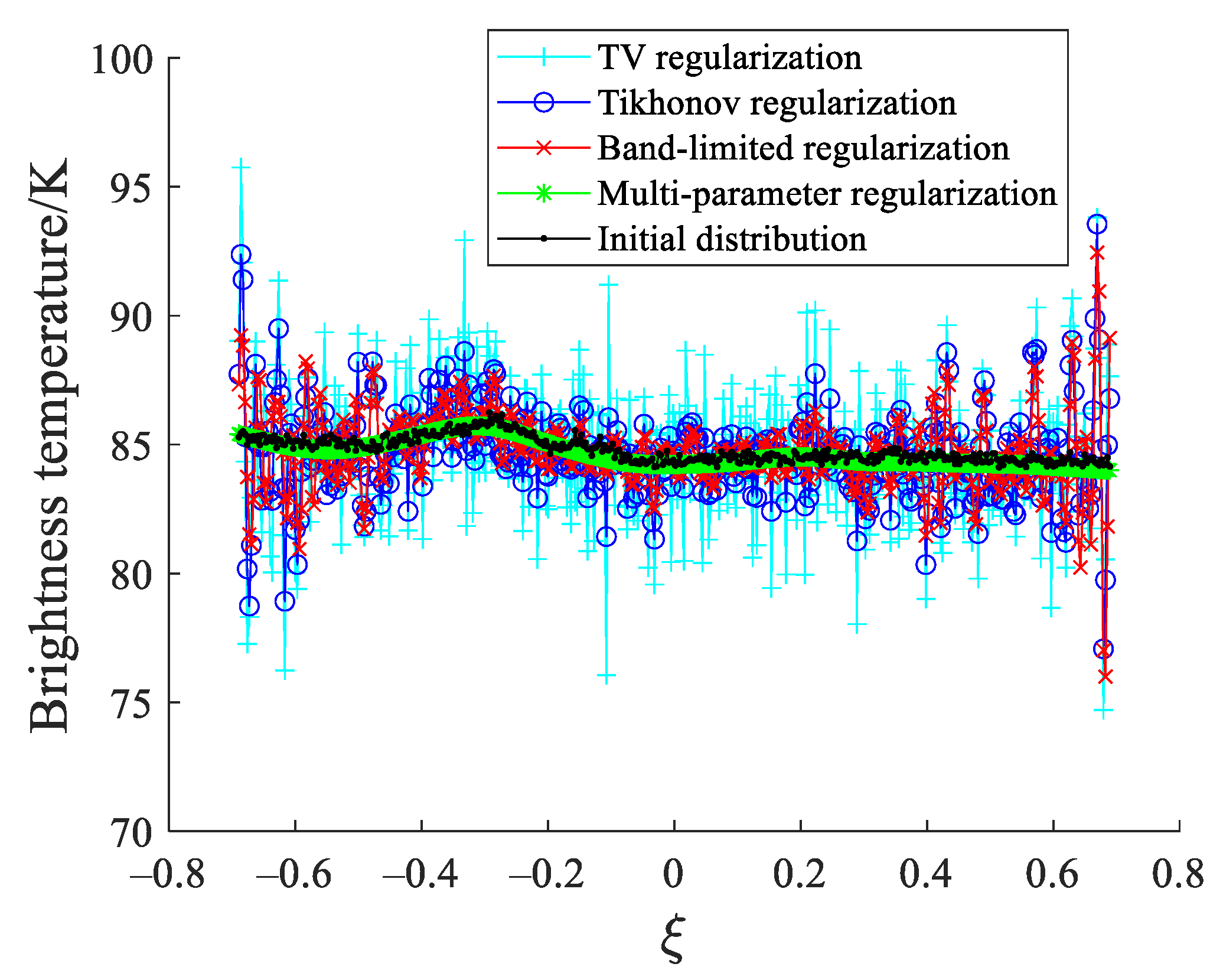
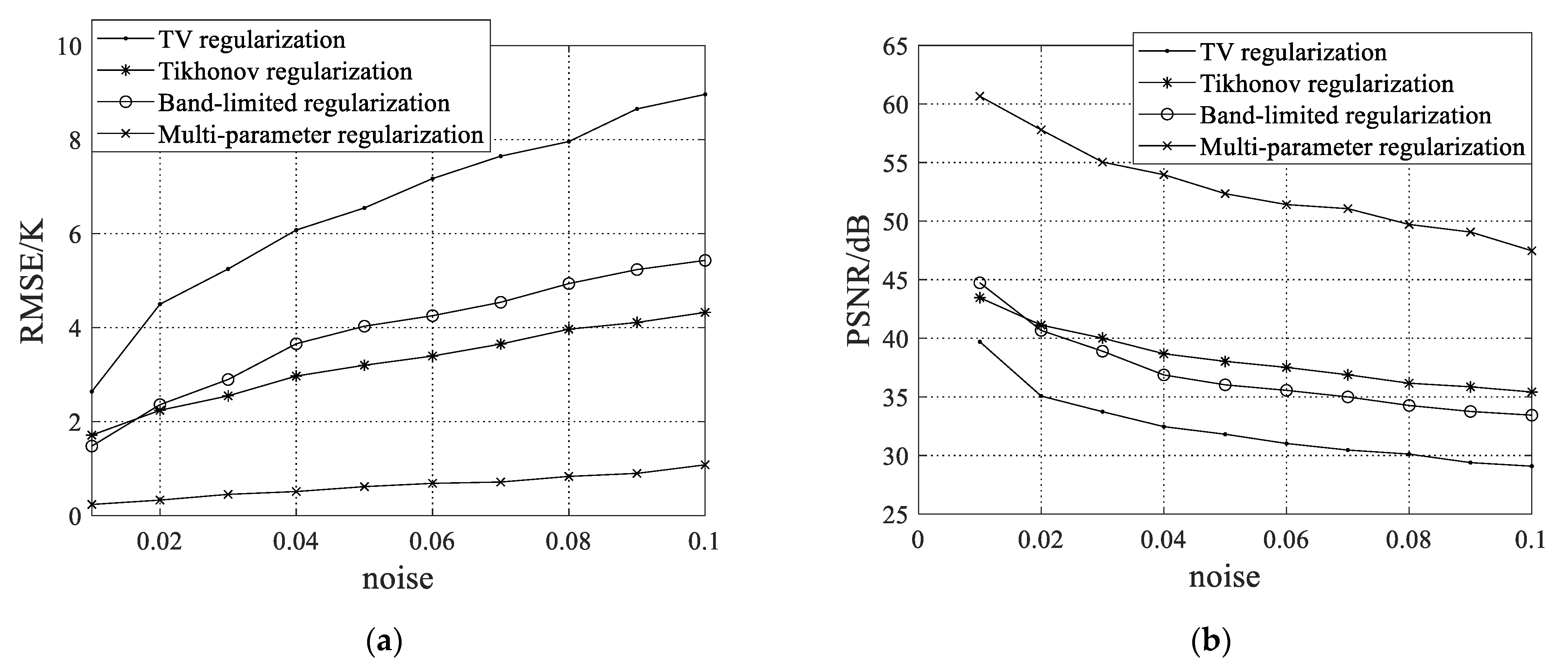
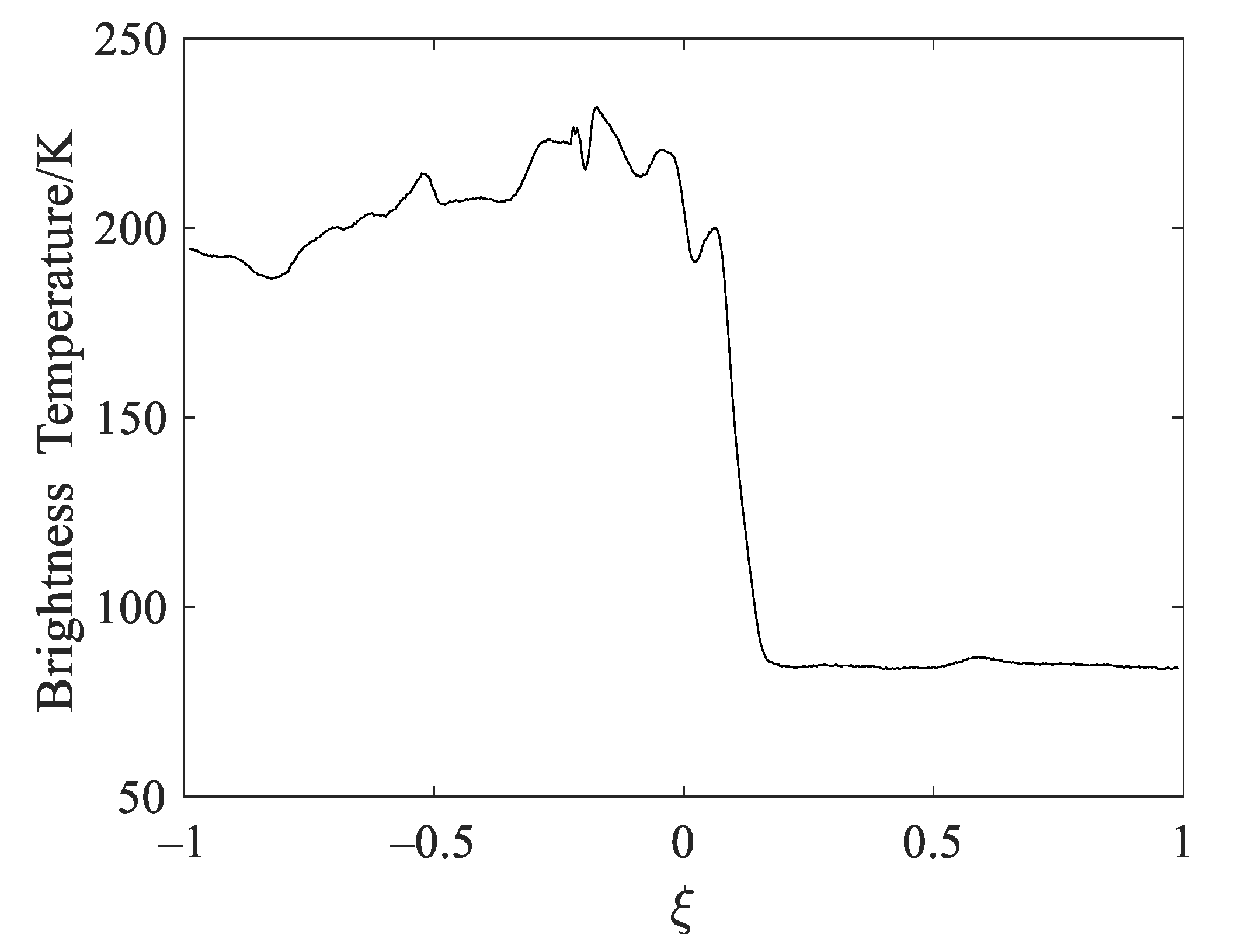
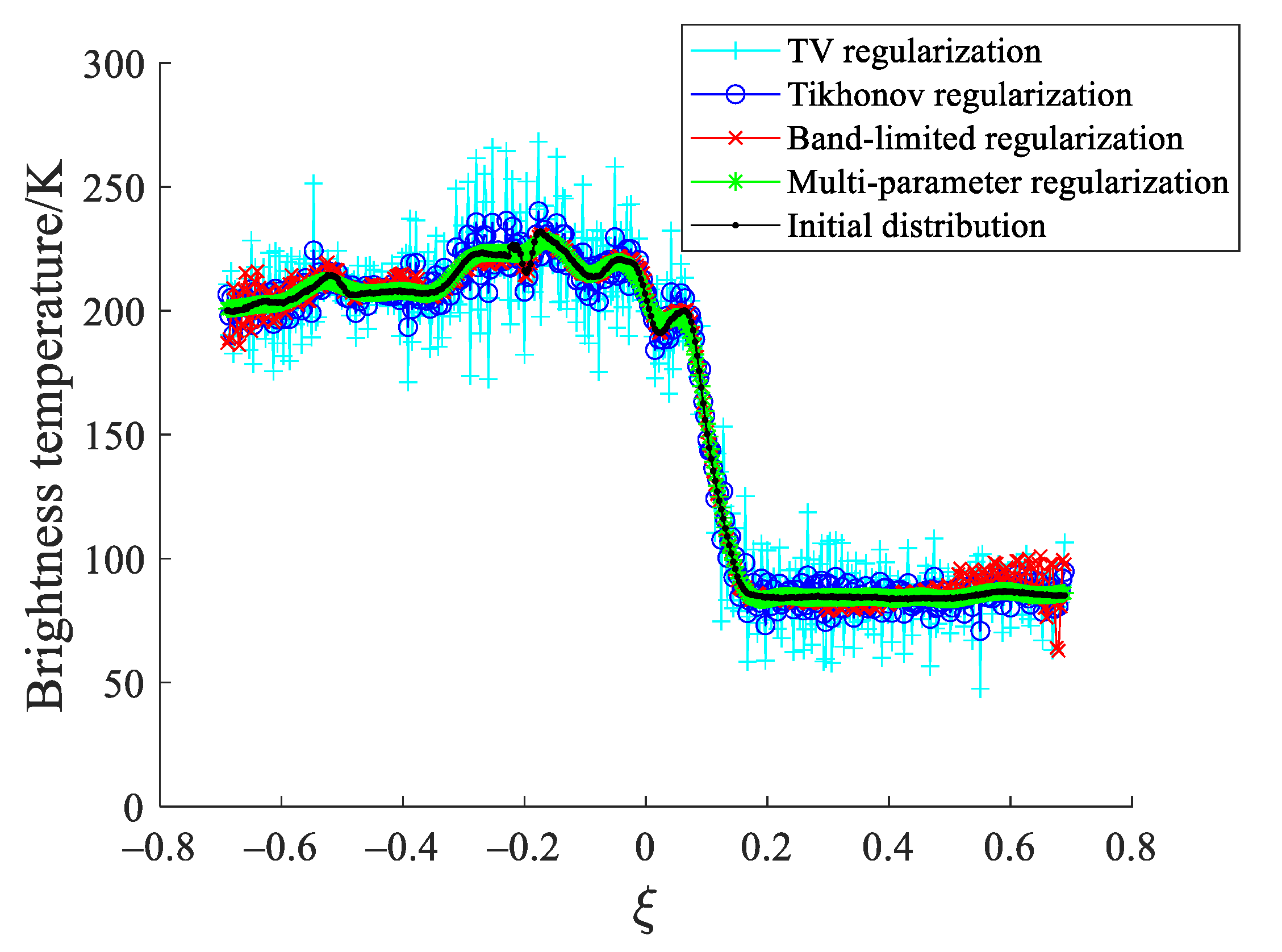
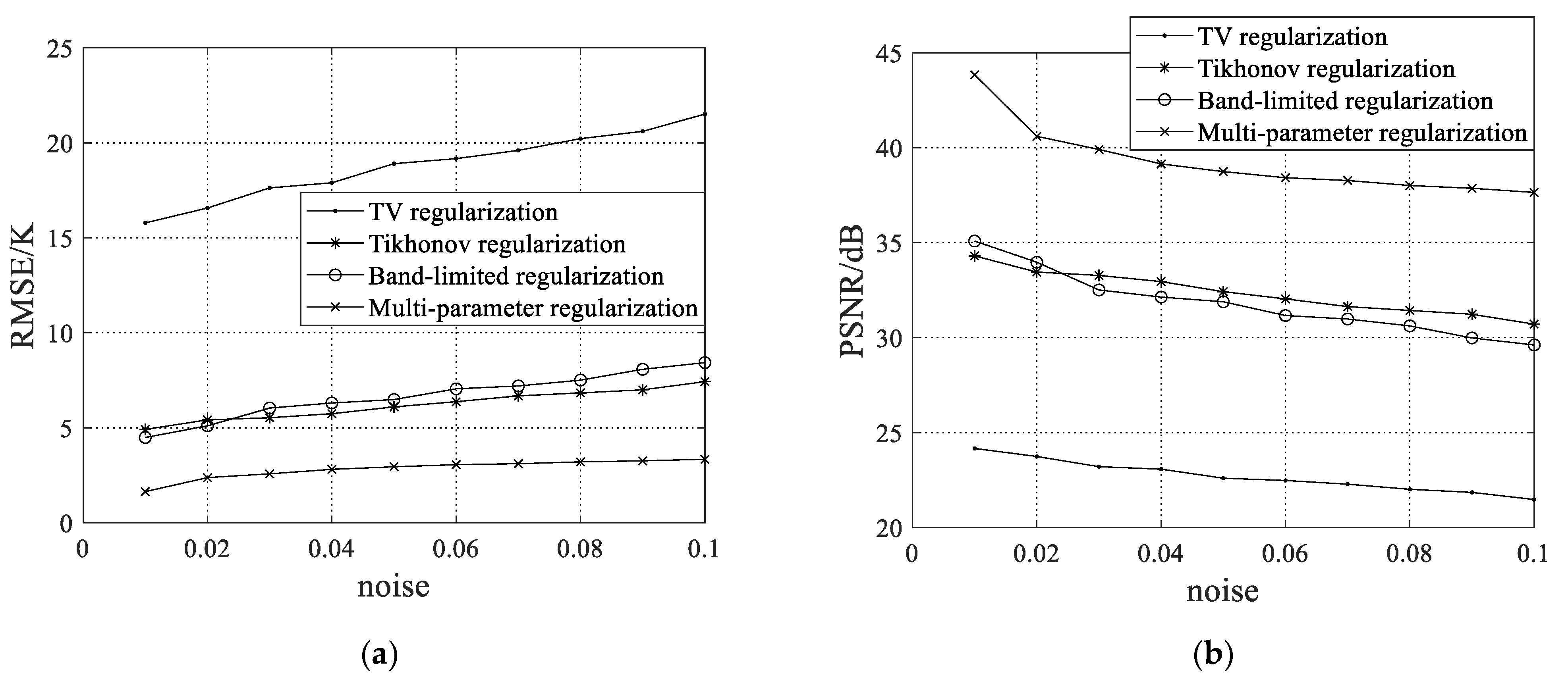
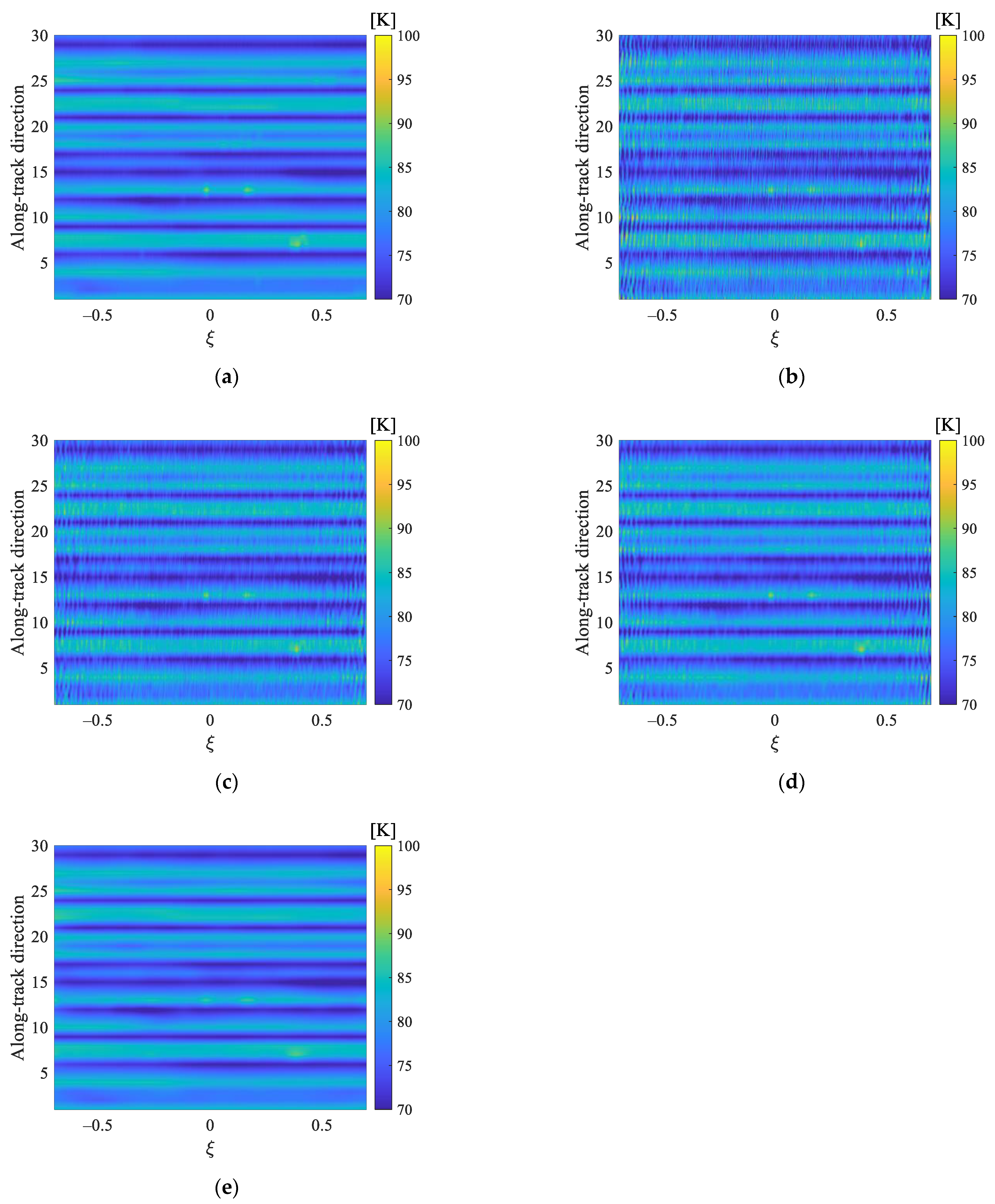
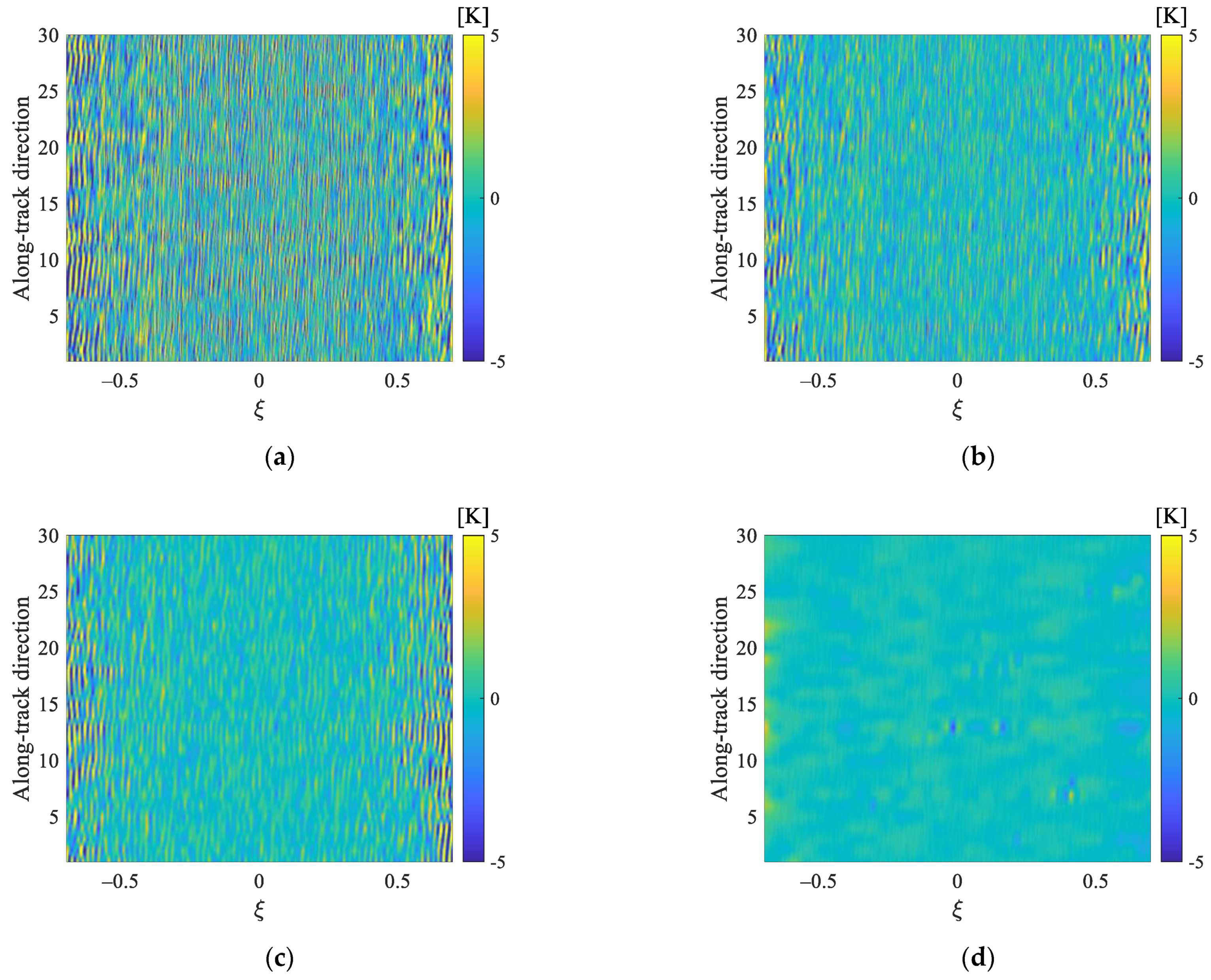
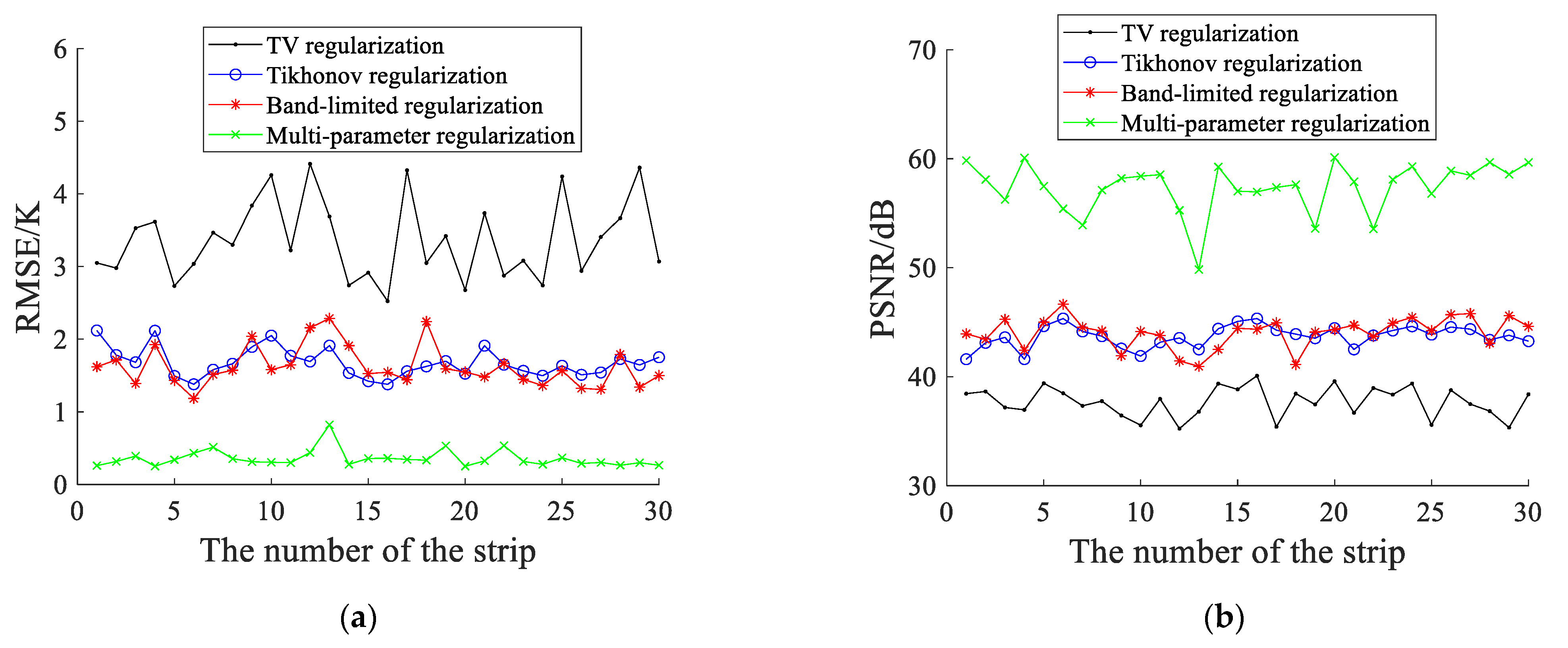
4. Results
4.1. Experiment 1
4.2. Experiment 2
4.3. Experiment 3
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Martin-Neira, M.; LeVine, D.M.; Kerr, Y. Microwave Imaging radiometry in remote sensing: An invited historical review. Radio Sci. 2014, 49, 415–449. [Google Scholar] [CrossRef]
- Reising, S.C.; Gaier, T.C.; Kummerow, C.D.; Padmanabhan, S.; Berg, W. Temporal Experiment for Storms and Tropical Systems Technology Demonstration (TEMPEST-D): Reducing risk for 6U-Class nanosatellite constellations. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Kpré, E.; Vellas, N.; Gaquiére, C.; Decroze, C.; Fromentèze, T.; Mouhamadou, M. A Compressive Millimeter-Wave Imaging Imager for Security Applications. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018. [Google Scholar]
- Levine, D.M.; Griffis, A.J.; Swift, C.T.; Jackson, T.J. ESTAR: A synthetic aperture microwave radiometer for remote sensing spplications. Proc. IEEE 1994, 82, 1787–1801. [Google Scholar] [CrossRef]
- Corbella, I.; Torres, F.; Duffo, N.; Gonzalez-Gambau, V.; Pablos, M.; Duran, I.; Martin-Neira, M. MIRAS calibration and performance: Results from the SMOS in-orbit commissioning phase. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3147–3155. [Google Scholar] [CrossRef]
- Tanner, A.B.; Wilson, W.J.; Lambrigsten, B.H.; Dinardo, S.J.; Brown, S.T.; Kangaslahti, P.P.; Gaier, T.C.; Ruf, C.S.; Gross, S.M.; Lim, L.B.H.; et al. Initial Results of the Geostationary Synthetic Thinned Array Radiometer (GeoSTAR) Demonstrator Instrument. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1947–1957. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, H.; Wu, J.; Zhang, S.; Yan, J.; Niu, L.; Sun, W.; Li, H. Imaging analysis and first results of the geostationary interferometric microwave sounder demonstrator. IEEE Trans. Geosci. Remote Sens. 2015, 53, 207–218. [Google Scholar] [CrossRef]
- Anterrieu, E. A resolving matrix approach for synthetic aperture imaging radiometers. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1649–1656. [Google Scholar] [CrossRef]
- Picard, B.; Anterrieu, E. Comparison of regularized inversion methods in synthetic aperture imaging radiometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 218–224. [Google Scholar] [CrossRef]
- Liang, W.; Fei, H.; Feng, H.; Li, J. Bayesian Inference for Inversion in Synthetic Aperture Imaging Radiometry. IEEE Geosci. Remote Sens. 2016, 13, 1049–1053. [Google Scholar]
- Zhang, Y.; Ren, Y.; Miao, W.; Lin, Z.; Gao, H.; Shi, S. Microwave SAIR Imaging Approach Based on Deep Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10376–10389. [Google Scholar] [CrossRef]
- Yang, X.; Yang, Z.; Yan, J.; Wu, L.; Lyu, W. Reduction of the Reconstruction Error With Lower and Upper Bounds in Synthetic Aperture Imaging Radiometers. IEEE Access 2020, 8, 156964–156971. [Google Scholar] [CrossRef]
- Martin-Neira, M.; Oliva, R.; Corbella, I.; Torres, F.; Duffo, N.; Duran, I.; Kainulainen, J.; Closa, J.; Zurita, A.; Cabot, F.; et al. SMOS instrument performance and calibration after six years in orbit. Remote Sens. Environ. 2016, 180, 19–39. [Google Scholar] [CrossRef]
- Belge, M. Multiscale and Curvature Methods for the Regularization of the Linear Inverse Problems; Northeastern University: Boston, MA, USA, 1999. [Google Scholar]
- Brezinski, C.; Redivo-Zaglia, M.; Rodriguez, G.; Seatzu, S. Multi-parameter regularization techniques for ill-conditioned linear systems. Numer. Math. 2003, 94, 203–228. [Google Scholar] [CrossRef]
- Chen, Z.; Yao, L.; Xu, Y.; Ynag, H. Multi-parameter tikhonov regularization for linear ill-posed operator equations. J. Comput. Math. 2008, 26, 37–55. [Google Scholar]
- Wang, Z. Multi-parameter Tikhonov regularization and model function approach to the damped Morozov principle for choosing regularization parameters. J. Comput. Appl. Math. 2012, 236, 1815–1832. [Google Scholar] [CrossRef] [Green Version]
- Brooks, D.H.; Ahmad, G.F.; MacLeod, R.S.; Maratos, G.M. Inverse electrocardiography by simultaneous imposition of multiple constraints. IEEE Trans. Biomed. Eng. 1999, 46, 3–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, D. A Multi-parameter Regularization Model for Deblurring Images Corrupted by Impulsive Noise. Circ. Syst. Signal Pr. 2017, 36, 3702–3730. [Google Scholar] [CrossRef]
- Zhang, W.; Shen, J.; Thomas, J.C.; Mu, T.; Zhu, X. Particle size distribution recovery in dynamic light scattering by optimized multi-parameter regularization based on the singular value distribution. Powder Technol. 2019, 353, 320–329. [Google Scholar] [CrossRef]
- Aucejo, M.; De Smet, O. Multi-parameter multiplicative regularization: An application to force reconstruction problemse. J. Sound Vib. 2020, 469, 115–135. [Google Scholar] [CrossRef] [Green Version]
- Corbella, I.; Duffo, N.; Vall-llossera, M.; Camps, A.; Torres, F. The visibility function in Imaging aperture synthesis radiometry. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1677–1682. [Google Scholar] [CrossRef]
- Hansen, P.C.; O’Leary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Craven, P.; Wahba, G. Smoothing noisy data with spline functions: Estimating the correct degree of smoothing by the method of Generalized Cross Validation. Numer. Math. 1979, 31, 377–403. [Google Scholar] [CrossRef]
- Wahba, G. Spline Models for Observational Data; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1990; pp. 1–169. [Google Scholar]
- Wu, L.; Yan, J.; Zhao, F.; Lan, A.; Wu, J. FPIR: Demonstrator Integration and Ground-Based Salinity Observation Experiment. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Anterrieu, E.; Waldteufel, P.; Lannes, A. Apodization functions for 2-D hexagonally sampled synthetic aperture imaging radiometers. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2531–2542. [Google Scholar] [CrossRef]

| System Parameters | Values |
|---|---|
| central frequency | f0 = 1.4 GHz |
| antenna number | 16 |
| the shortest baseline | ∆d = 0.589λ |
| the longest baseline | 90∆d |
| bandwidth | B = 20 MHz |
| integration time | τ = 1 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Yang, Z.; Yan, J.; Wu, L.; Jiang, M. Multi-Parameter Regularization Method for Synthetic Aperture Imaging Radiometers. Remote Sens. 2021, 13, 382. https://doi.org/10.3390/rs13030382
Yang X, Yang Z, Yan J, Wu L, Jiang M. Multi-Parameter Regularization Method for Synthetic Aperture Imaging Radiometers. Remote Sensing. 2021; 13(3):382. https://doi.org/10.3390/rs13030382
Chicago/Turabian StyleYang, Xiaocheng, Zhenyi Yang, Jingye Yan, Lin Wu, and Mingfeng Jiang. 2021. "Multi-Parameter Regularization Method for Synthetic Aperture Imaging Radiometers" Remote Sensing 13, no. 3: 382. https://doi.org/10.3390/rs13030382
APA StyleYang, X., Yang, Z., Yan, J., Wu, L., & Jiang, M. (2021). Multi-Parameter Regularization Method for Synthetic Aperture Imaging Radiometers. Remote Sensing, 13(3), 382. https://doi.org/10.3390/rs13030382