Analysis of the Double-Bounce Interaction between a Random Volume and an Underlying Ground, Using a Controlled High-Resolution PolTomoSAR Experiment
Abstract
:1. Introduction
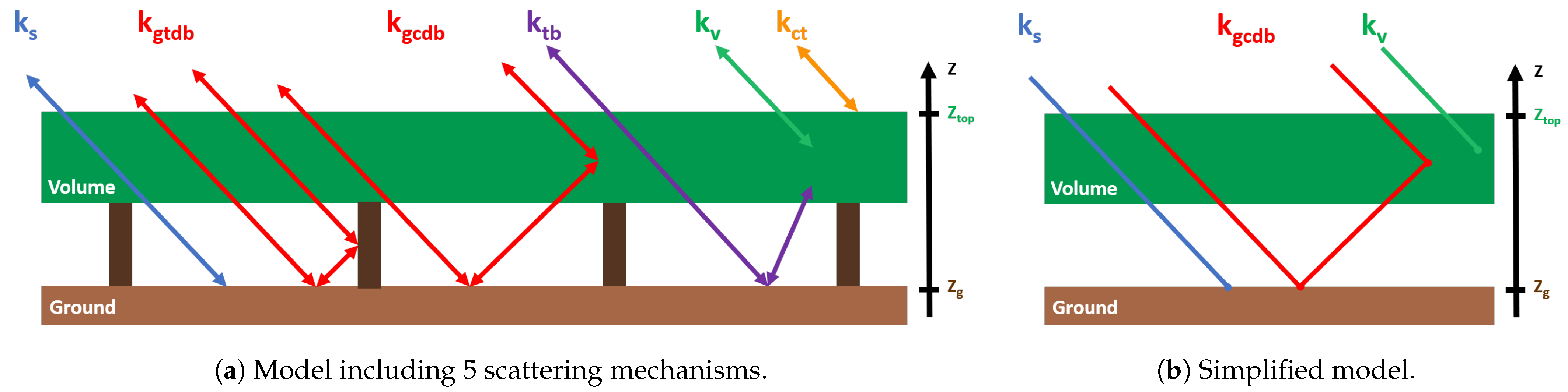
2. Scattering Contributions to the SAR Response of a VoG Scene
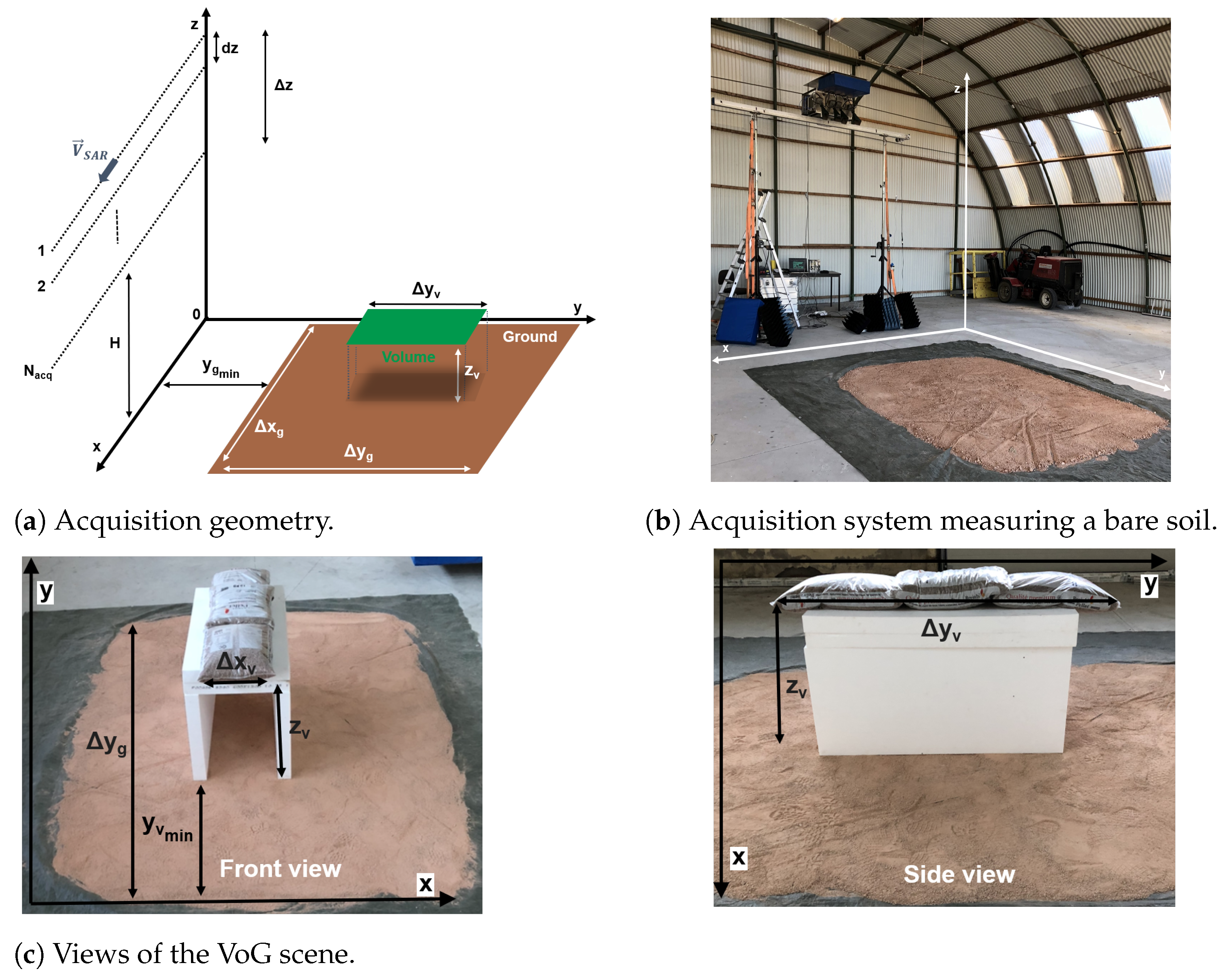
3. Controlled Measurement of a VoG Scene Using a Ground-Based SAR
3.1. Scene and System Configurations
3.2. Imaging Geometry
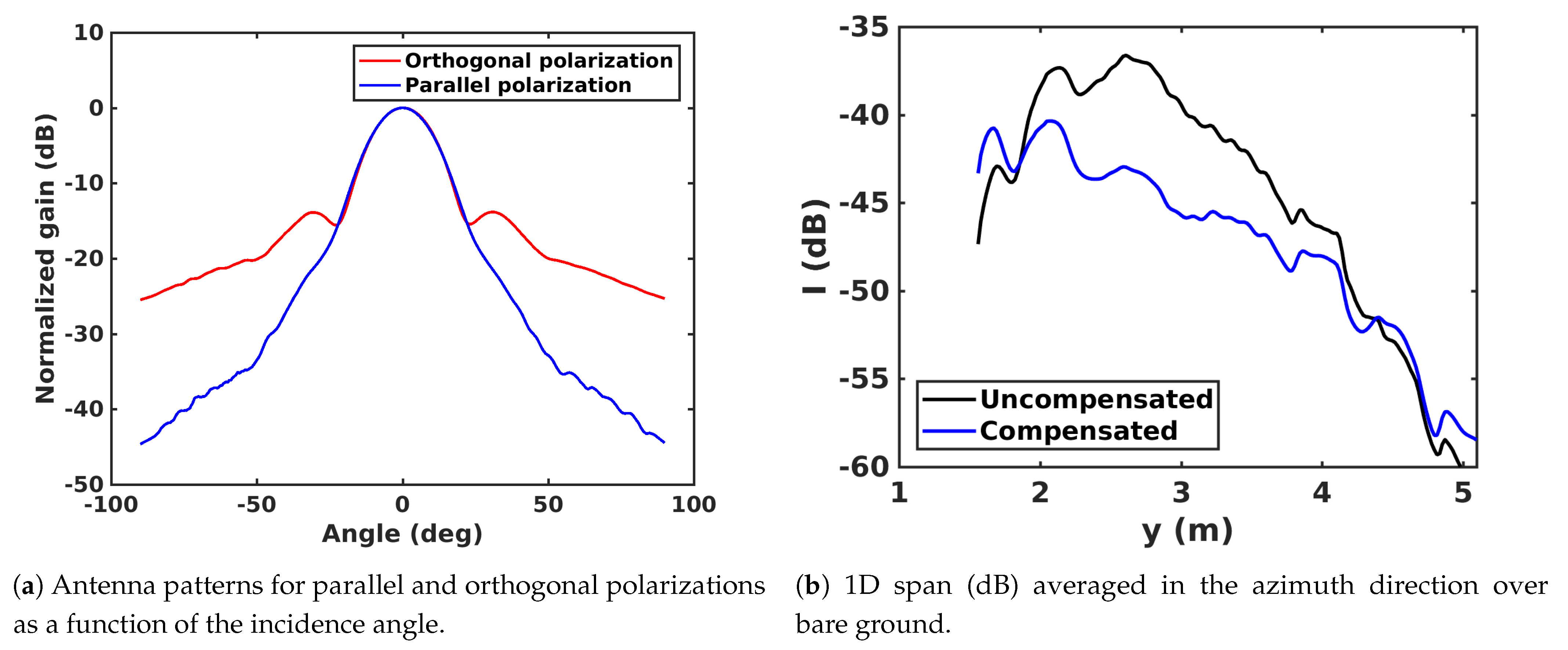
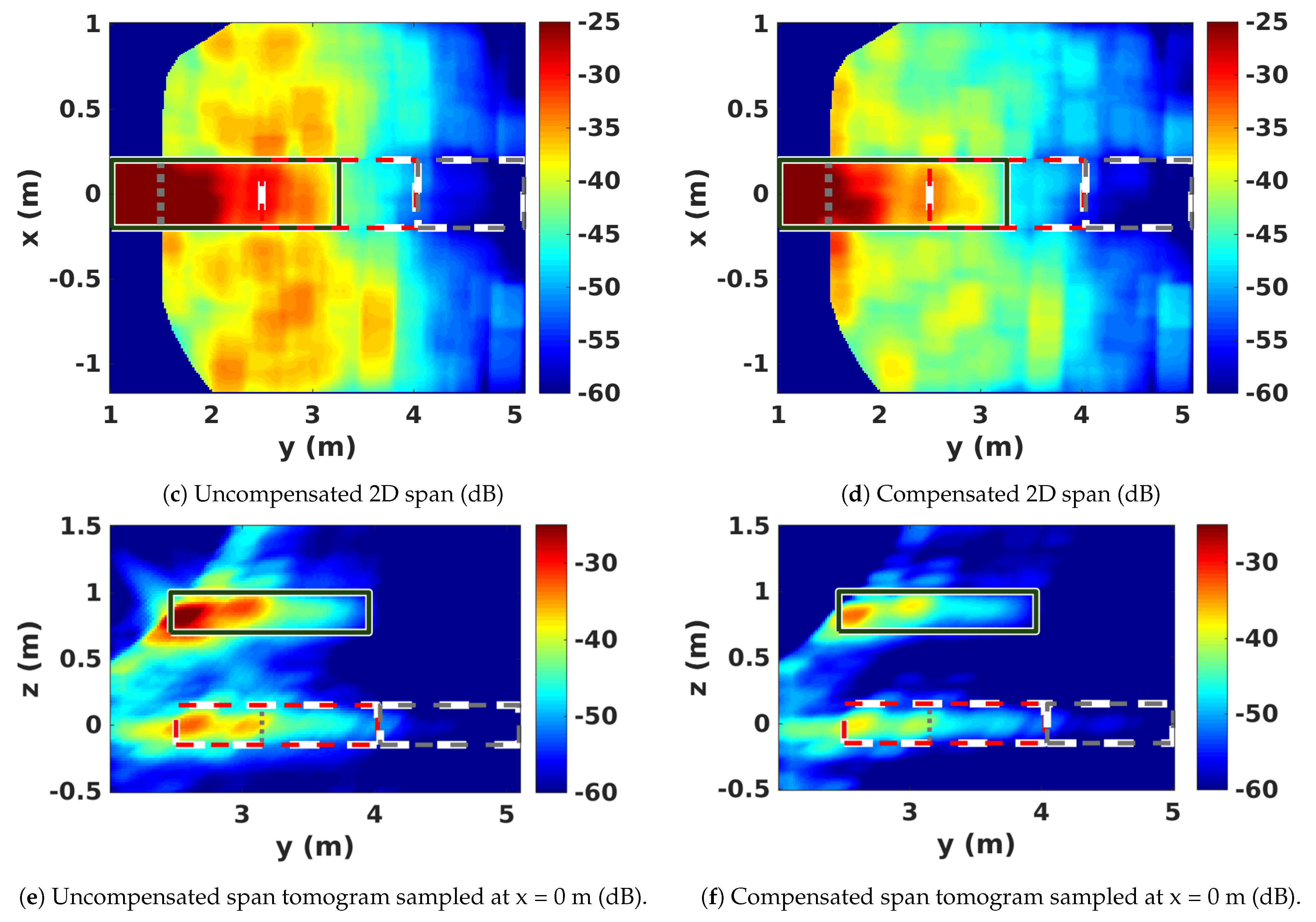
3.3. Radiometric Corrections
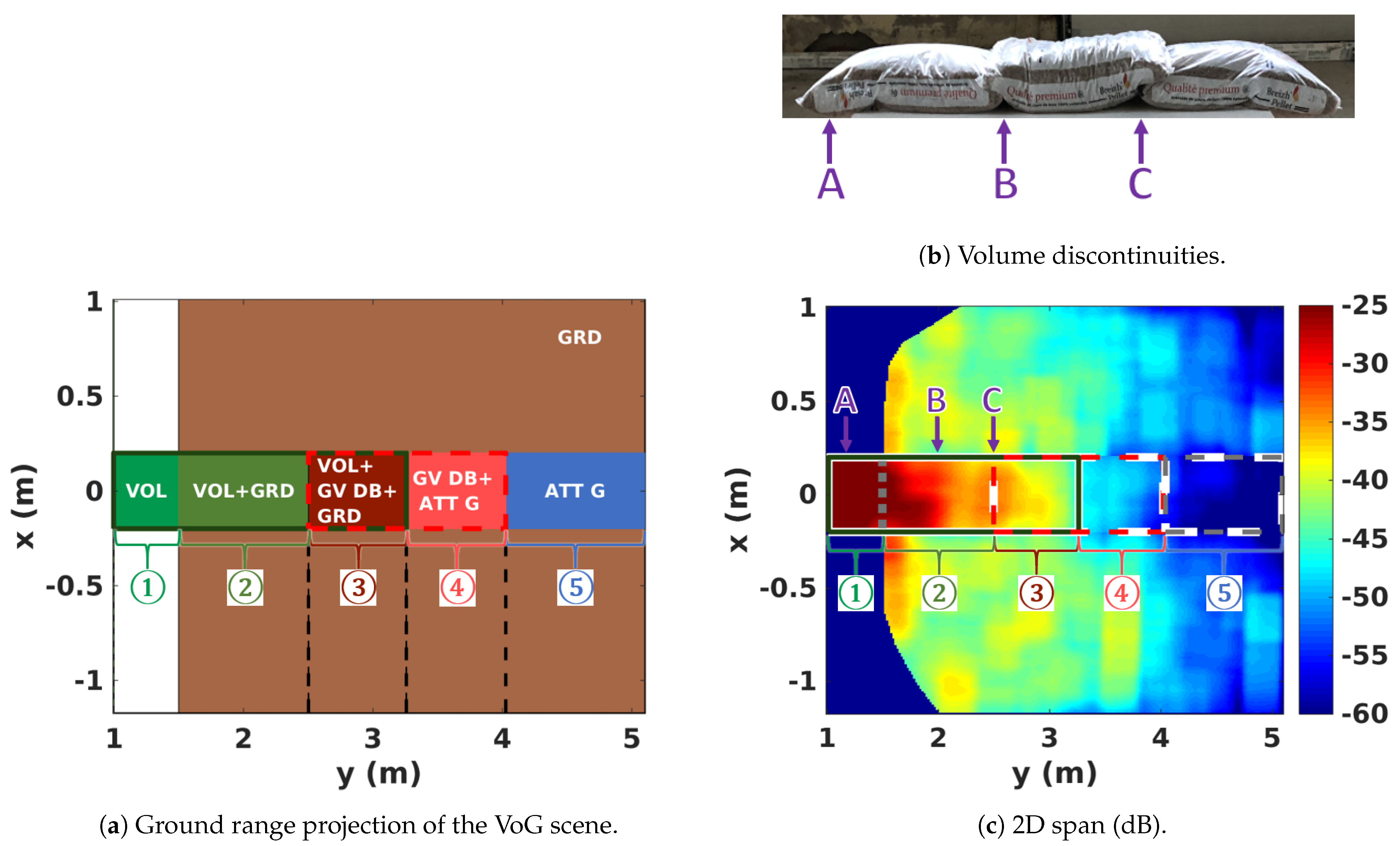
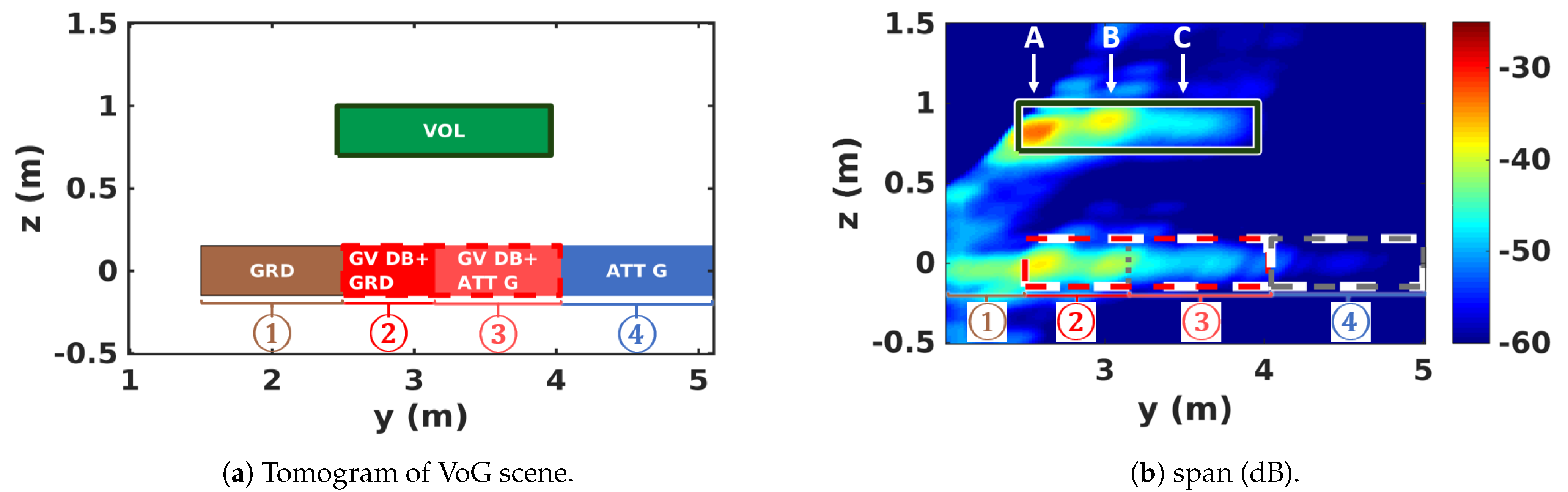
4. 2D SAR Scene Features
4.1. Interpretation of Reflectivity Patterns
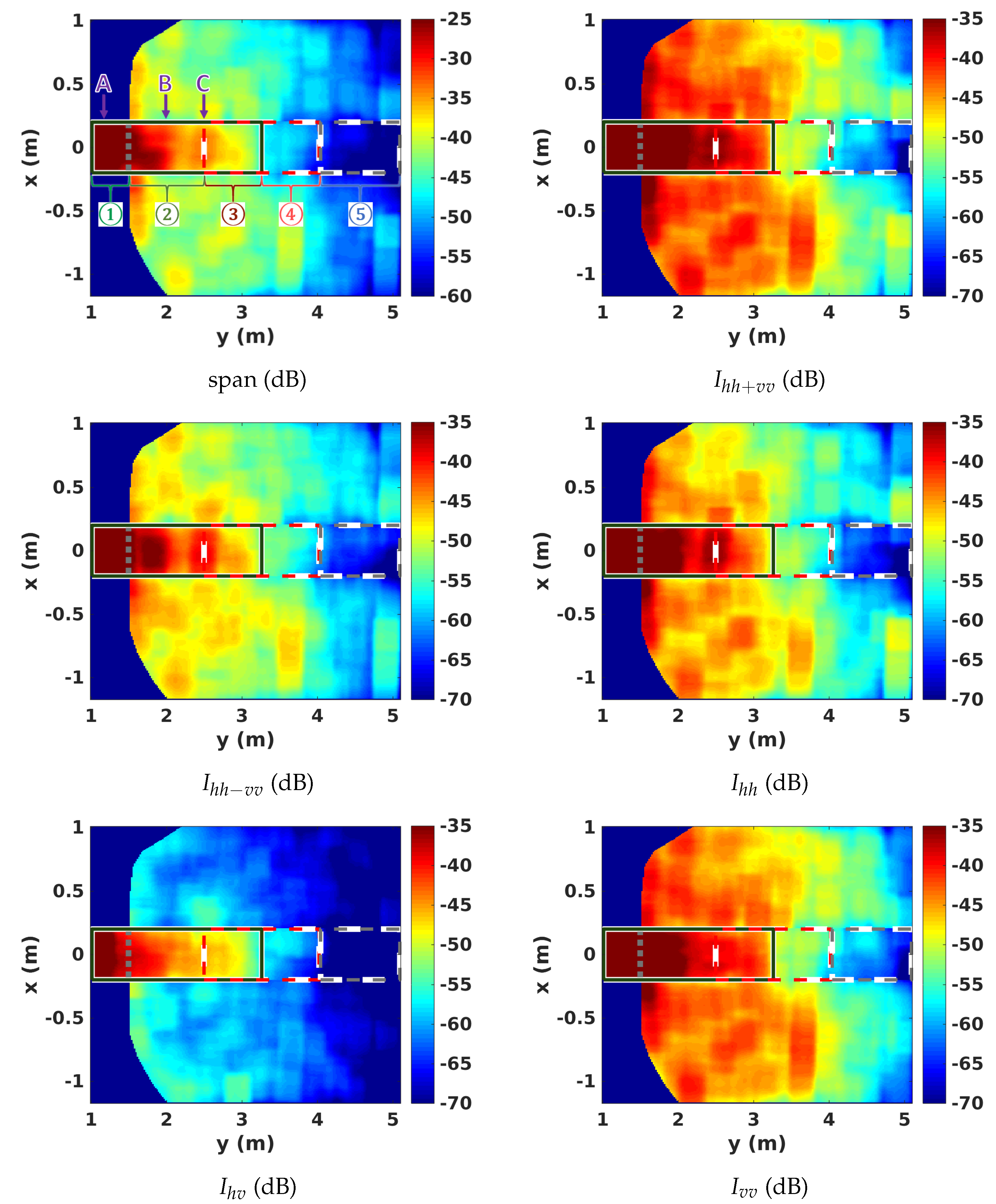
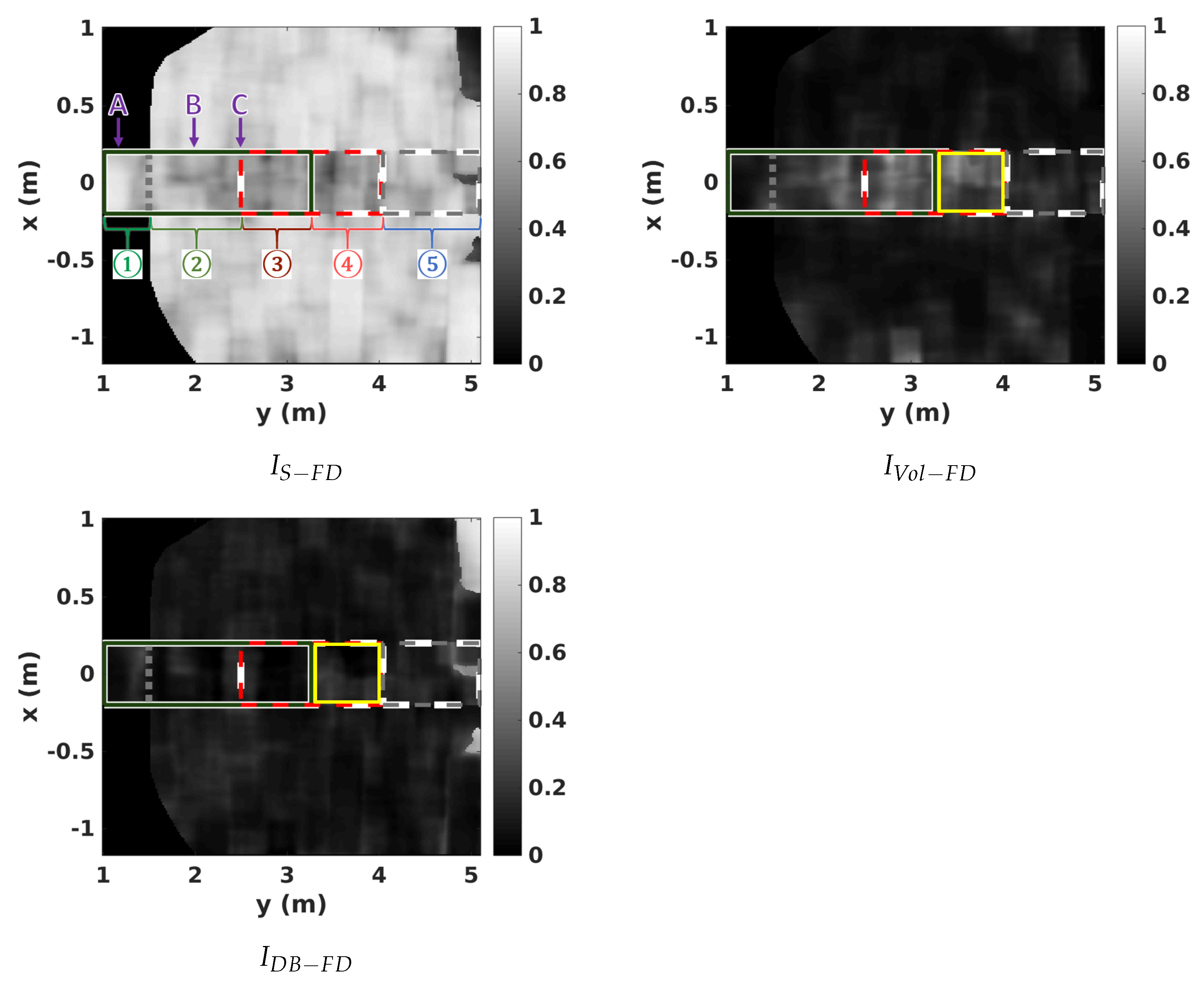
4.2. Polarimetric Analysis
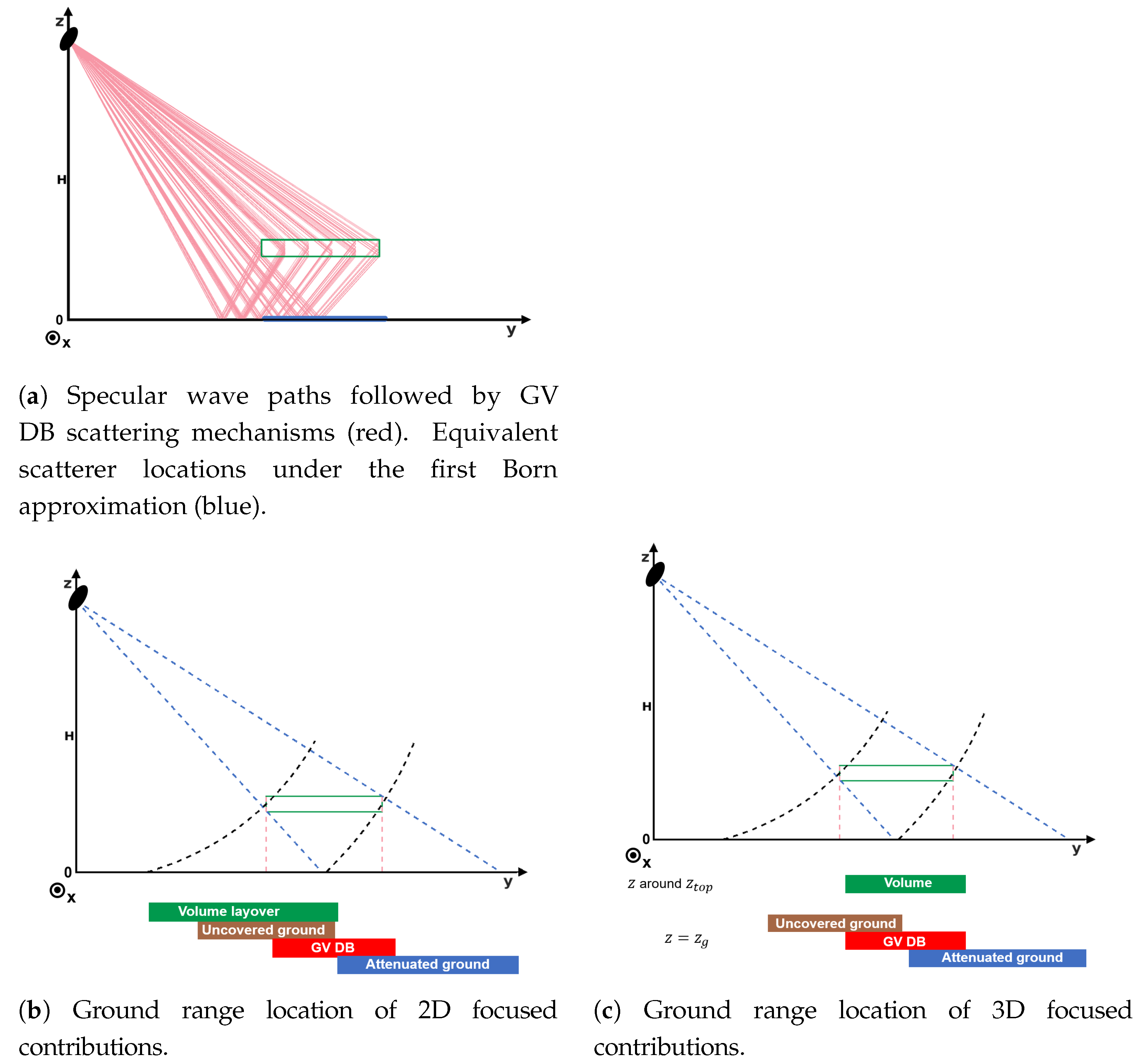
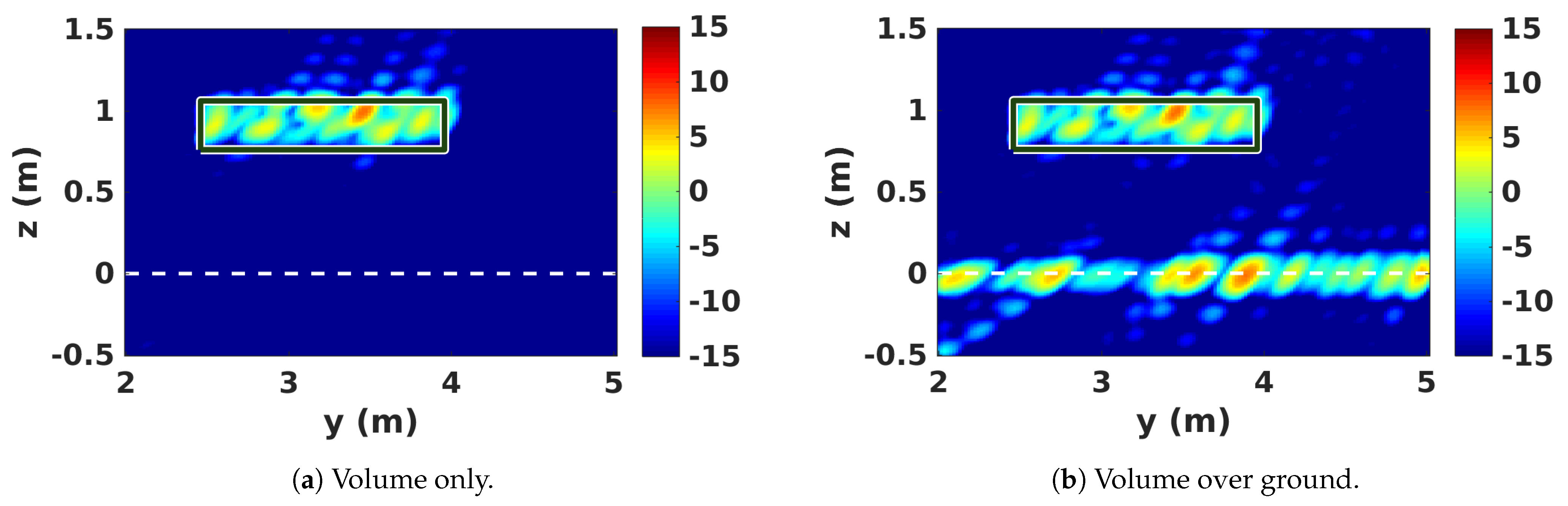
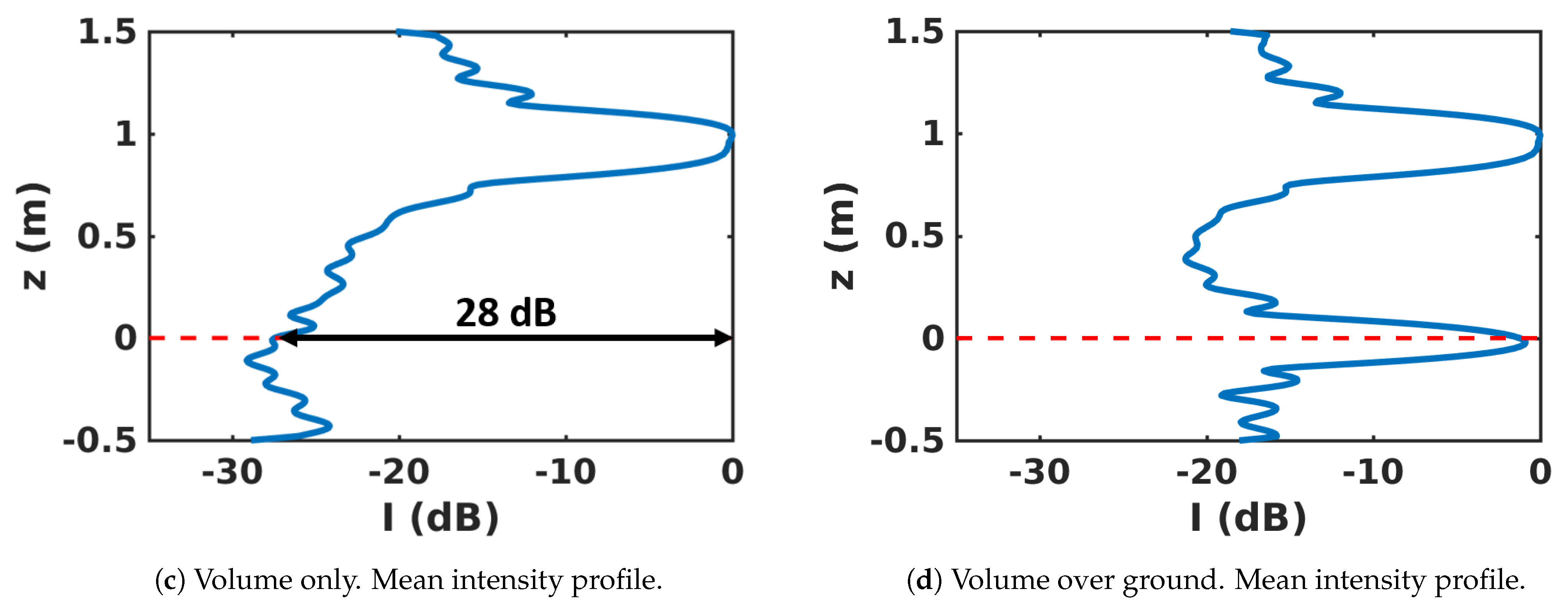
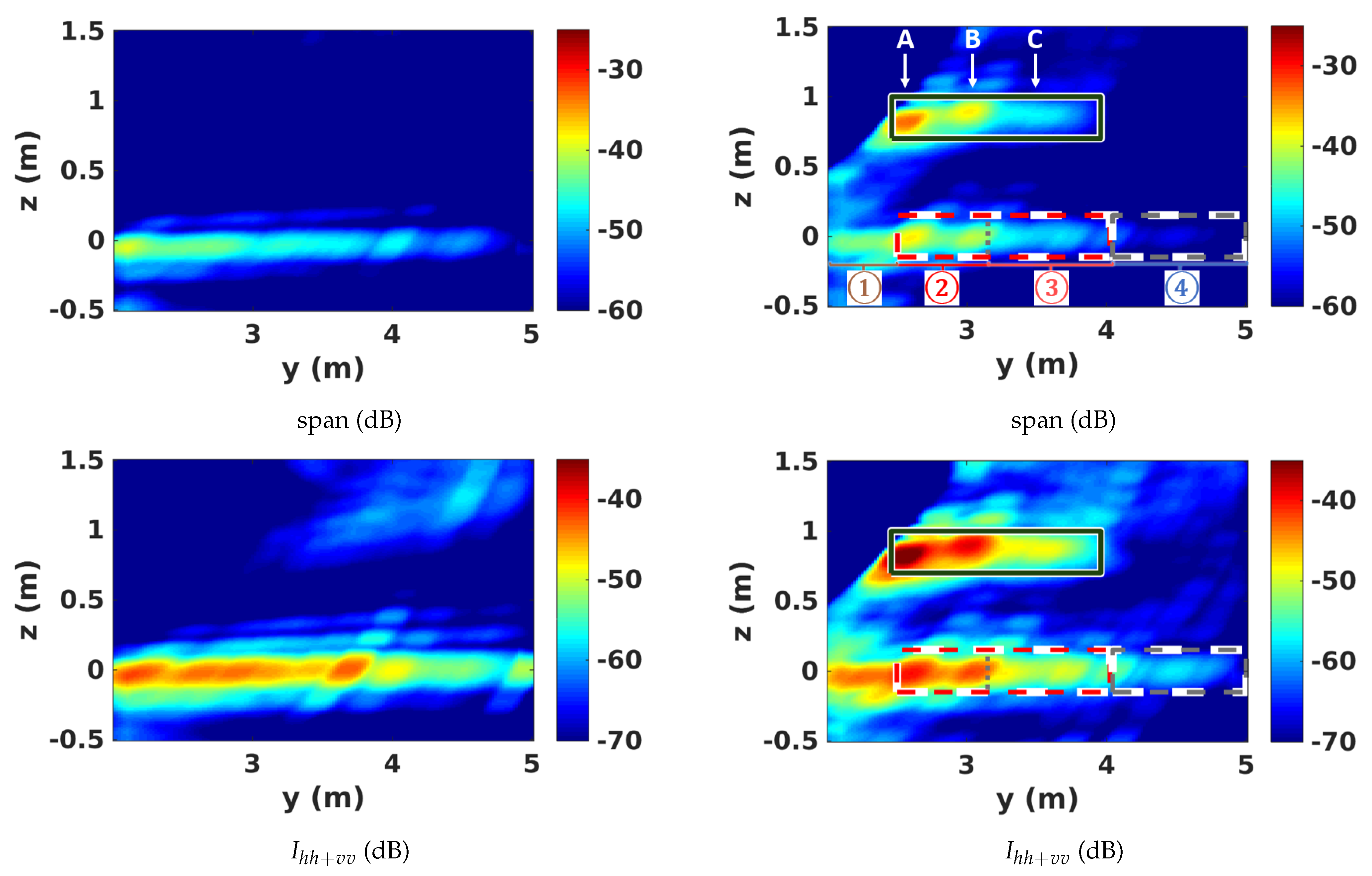
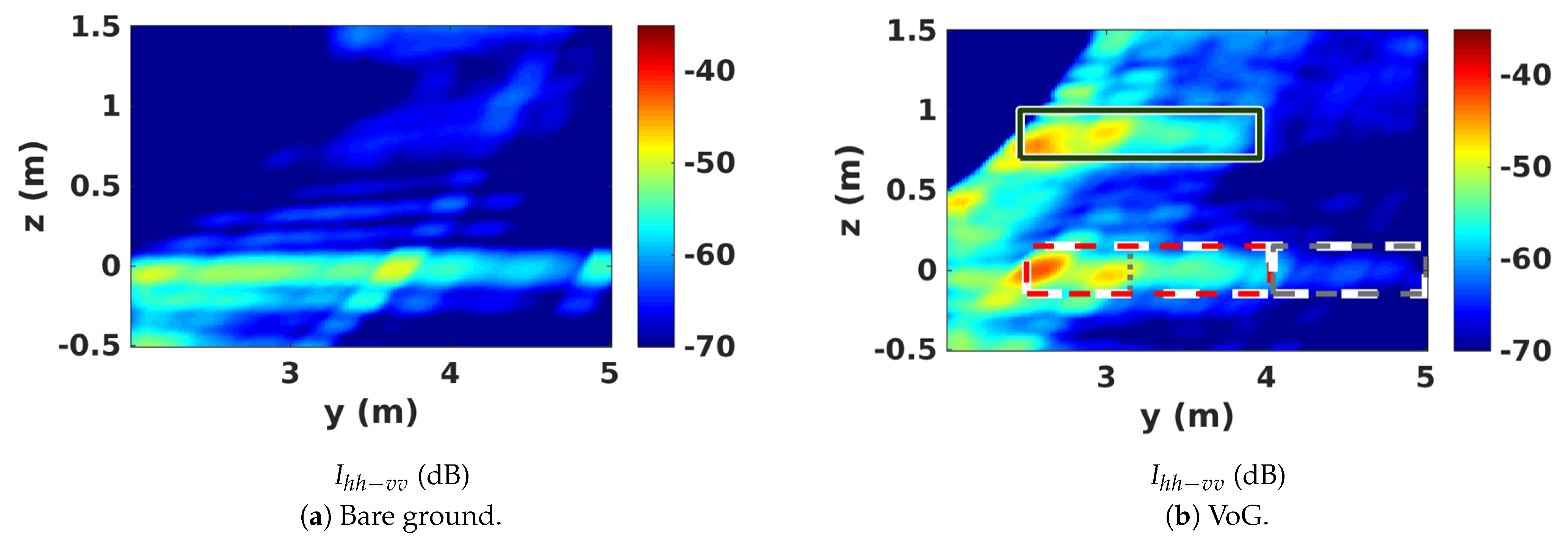
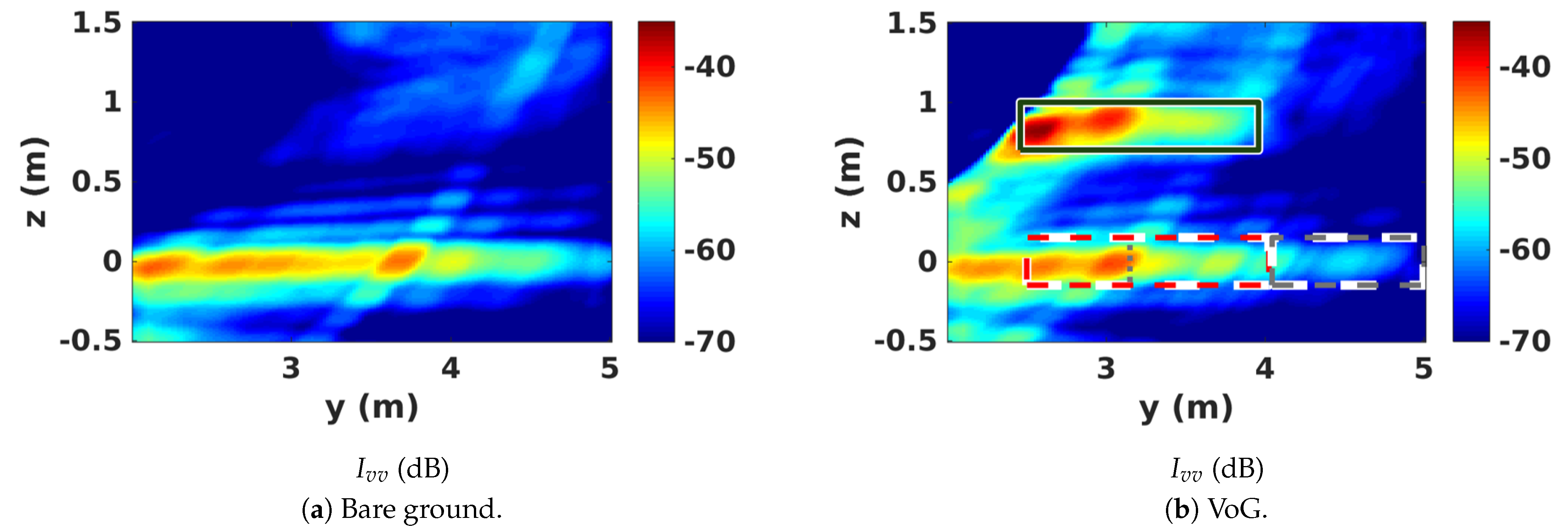
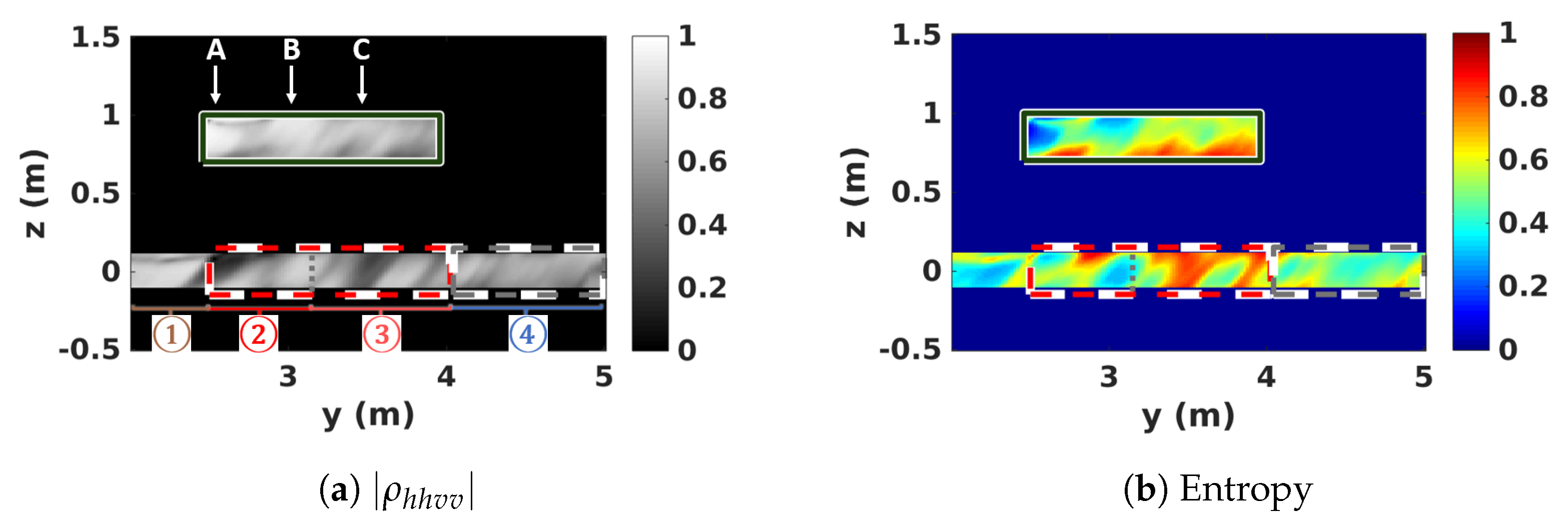
5. 3D SAR Scene Features
5.1. Location of Scattering Contributions in 3D SAR Images
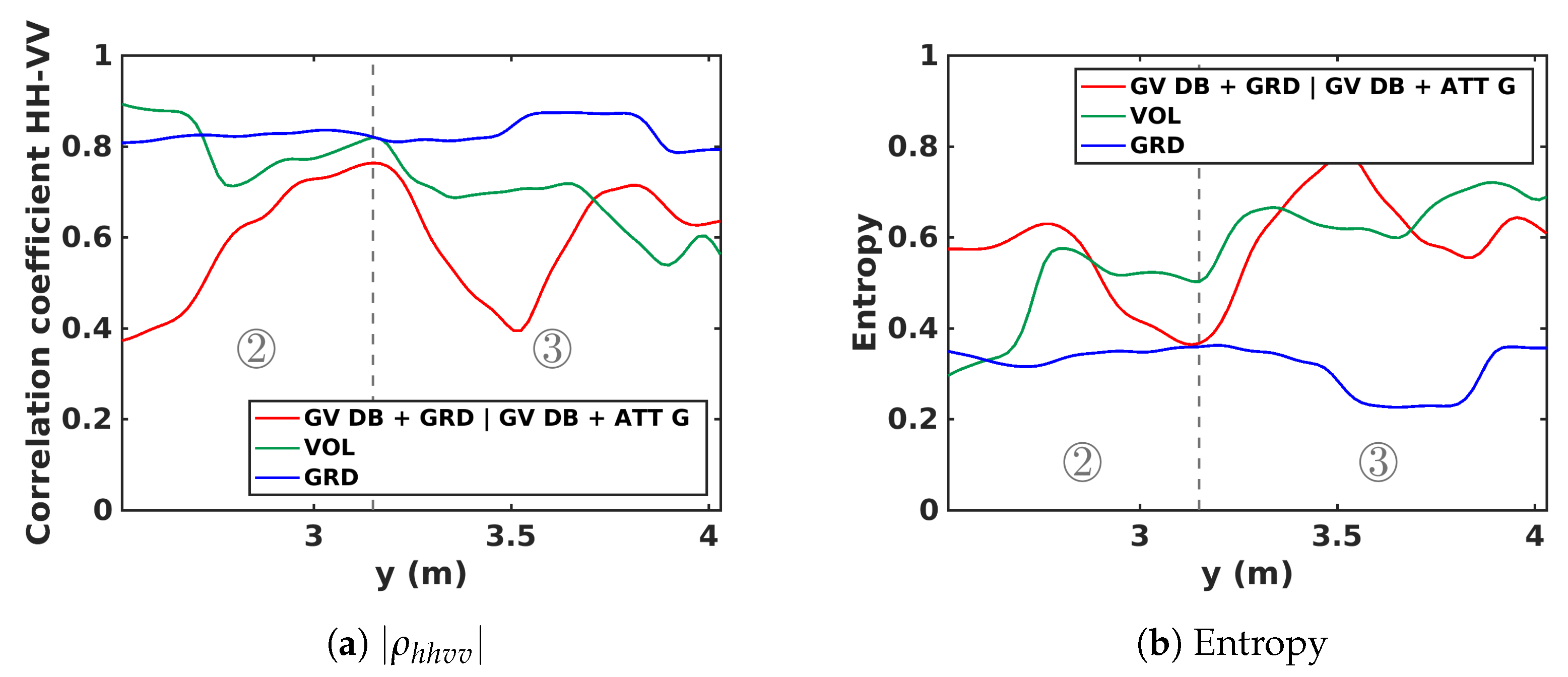
5.2. 3D Polarimetric Analysis
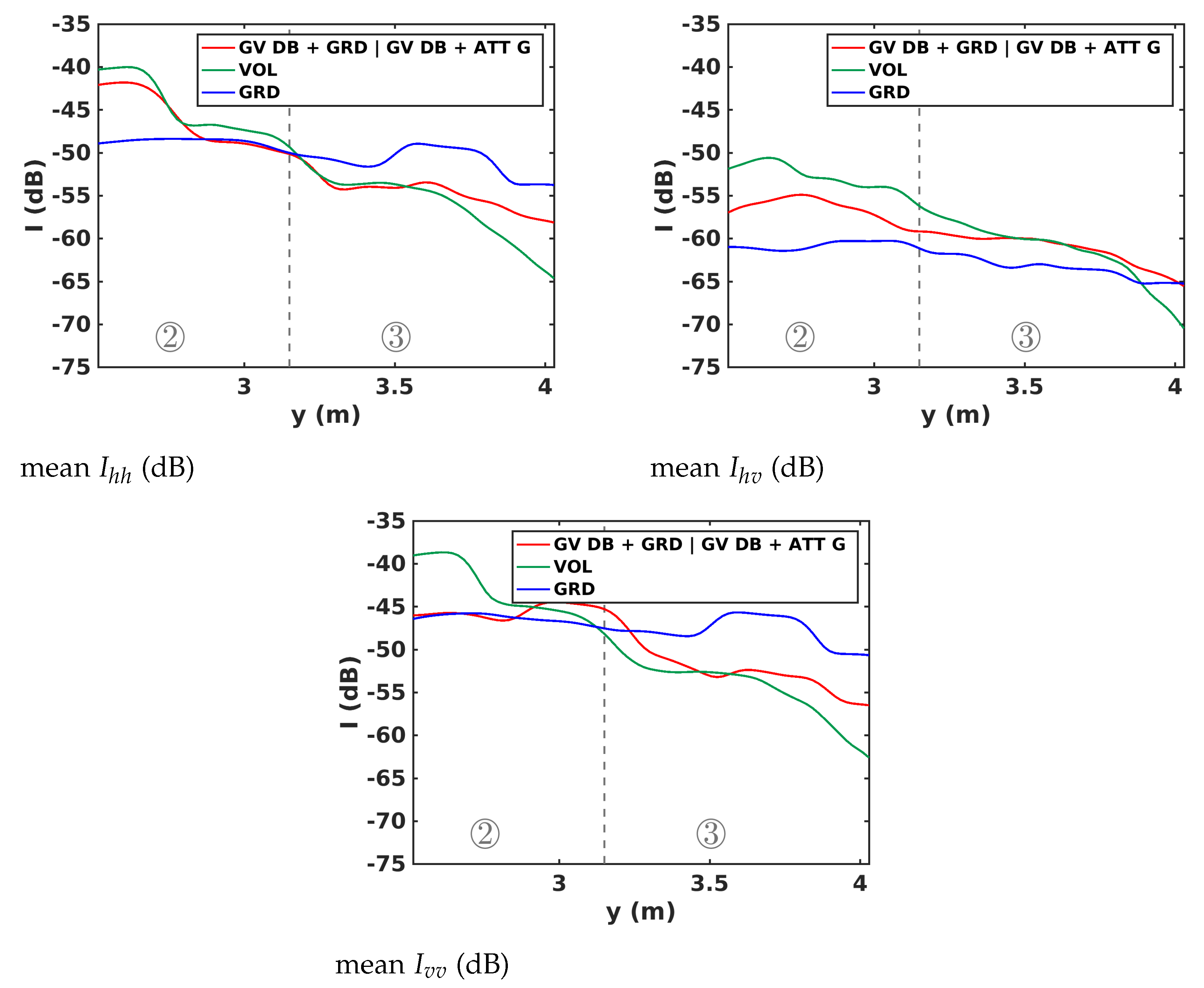
6. Underlying Ground Characterization
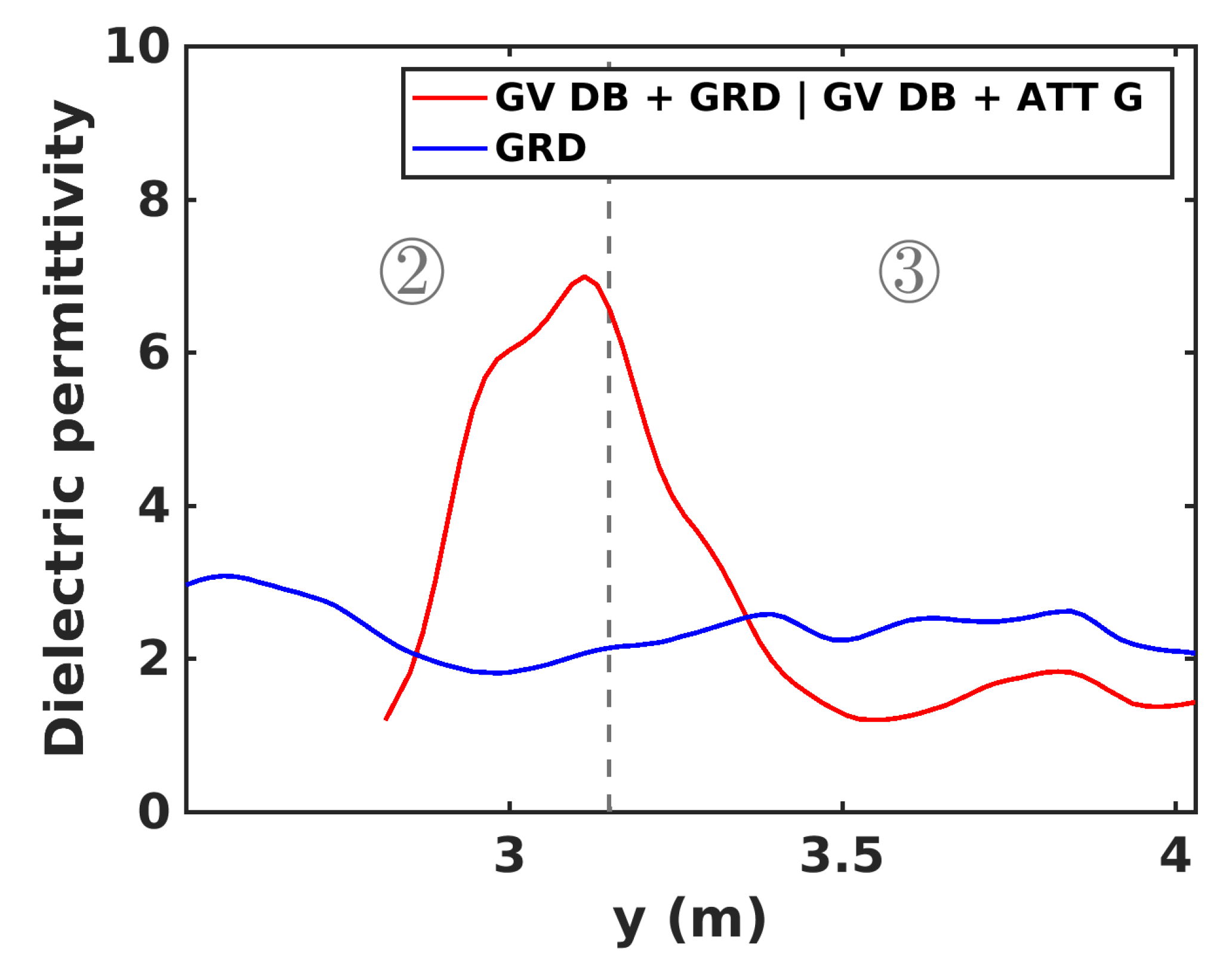
6.1. Dielectric Permittivity Estimation
6.2. Ground Polarimetric Features
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tebaldini, S. Algebraic Synthesis of Forest Scenarios From Multibaseline PolInSAR Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4132–4142. [Google Scholar] [CrossRef]
- Tebaldini, S. Single and Multipolarimetric SAR Tomography of Forested Areas: A Parametric Approach. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2375–2387. [Google Scholar] [CrossRef]
- Tebaldini, S.; Rocca, F. Multibaseline Polarimetric SAR Tomography of a Boreal Forest at P- and L-Bands. IEEE Trans. Geosci. Remote Sens. 2012, 50, 232–246. [Google Scholar] [CrossRef]
- Huang, Y.; Ferro-Famil, L.; Lardeux, C. Polarimetric SAR tomography of tropical forests at P-Band. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1373–1376. [Google Scholar]
- El Hajj Chehade, B.; Ferro-Famil, L. P-band polarimetric SAR tomography for tropical forest structure characterization. In Proceedings of the 2014 11th European Radar Conference, Rome, Italy, 8–10 October 2014; pp. 49–52. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Toan, T.L.; Rocca, F.; Tebaldini, S.; d’Alessandro, M.M.; Villard, L. Relating P-Band Synthetic Aperture Radar Tomography to Tropical Forest Biomass. IEEE Trans. Geosci. Remote Sens. 2014, 52, 967–979. [Google Scholar] [CrossRef]
- Ferro-Famil, L.; Huang, Y.; Pottier, E. Principles and Applications of Polarimetric SAR Tomography for the Characterization of Complex Environments. In International Association of Geodesy Symposia, Proceedings of the VIII Hotine-Marussi Symposium on Mathematical Geodesy, Rome, Italy, 17–21 June 2013; Sneeuw, N., Novàk, P., Crespi, M., Sansò, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 142. [Google Scholar] [CrossRef]
- Kugler, F.; Lee, S.; Hajnsek, I.; Papathanassiou, K.P. Forest Height Estimation by Means of Pol-InSAR Data Inversion: The Role of the Vertical Wavenumber. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5294–5311. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Tebaldini, S.; Rocca, F.; Le Toan, T.; Villard, L.; Dubois-Fernandez, P.C. Capabilities of BIOMASS Tomography for Investigating Tropical Forests. IEEE Trans. Geosci. Remote Sens. 2015, 53, 965–975. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Tebaldini, S.; Rocca, F.; Le Toan, T. The Impact of Temporal Decorrelation on BIOMASS Tomography of Tropical Forests. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1297–1301. [Google Scholar] [CrossRef]
- Pardini, M.; Papathanassiou, K. On the Estimation of Ground and Volume Polarimetric Covariances in Forest Scenarios with SAR Tomography. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1860–1864. [Google Scholar] [CrossRef]
- Joerg, H.; Pardini, M.; Hajnsek, I.; Papathanassiou, K.P. On the Separation of Ground and Volume Scattering Using Multibaseline SAR Data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1570–1574. [Google Scholar] [CrossRef]
- Blomberg, E.; Ferro-Famil, L.; Soja, M.J.; Ulander, L.M.H.; Tebaldini, S. Forest Biomass Retrieval From L-Band SAR Using Tomographic Ground Backscatter Removal. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1030–1034. [Google Scholar] [CrossRef]
- Mariotti D’Alessandro, M.; Tebaldini, S. Digital Terrain Model Retrieval in Tropical Forests Through P-Band SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6774–6781. [Google Scholar] [CrossRef]
- Aghababaei, H.; Ferraioli, G.; Ferro-Famil, L.; Huang, Y.; Mariotti D’Alessandro, M.; Pascazio, V.; Schirinzi, G.; Tebaldini, S. Forest SAR Tomography: Principles and Applications. IEEE Geosci. Remote Sens. Mag. 2020, 8, 30–45. [Google Scholar] [CrossRef]
- Ulaby, F.; Moore, R.; Fung, A. Microwave Remote Sensing: Active and Passive; Number v. 3 in Artech House Microwave Library; Artech House: Norwood, MA, USA, 1981. [Google Scholar]
- Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Madsen, S.N.; Moghaddam, M.; van Zyl, J.J. Vegetation characteristics and underlying topography from interferometric radar. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Dahon, C.; Ferro-Famil, L.; Titin-Schnaider, C.; Pottier, E. Computing the double-bounce reflection coherent effect in an incoherent electromagnetic scattering model. IEEE Geosci. Remote Sens. Lett. 2006, 3, 241–245. [Google Scholar] [CrossRef]
- Thirion, L.; Colin, E.; Dahon, C. Capabilities of a forest coherent scattering model applied to radiometry, interferometry, and polarimetry at P- and L-band. IEEE Trans. Geosci. Remote Sens. 2006, 44, 849–862. [Google Scholar] [CrossRef]
- Lin, Y.C.; Sarabandi, K. A Monte Carlo coherent scattering model for forest canopies using fractal-generated trees. IEEE Trans. Geosci. Remote Sens. 1999, 37, 440–451. [Google Scholar] [CrossRef]
- Yitayew, T.G.; Ferro-Famil, L.; Eltoft, T.; Tebaldini, S. Lake and Fjord Ice Imaging Using a Multifrequency Ground-Based Tomographic SAR System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4457–4468. [Google Scholar] [CrossRef]
- Yitayew, T.G.; Ferro-Famil, L.; Eltoft, T.; Tebaldini, S. Tomographic Imaging of Fjord Ice Using a Very High Resolution Ground-Based SAR System. IEEE Trans. Geosci. Remote Sens. 2017, 55, 698–714. [Google Scholar] [CrossRef]
- Rekioua, B.; Davy, M.; Ferro-Famil, L.; Tebaldini, S. Snowpack permittivity profile retrieval from tomographic SAR data. Comptes Rendus Phys. 2017, 18, 57–65. [Google Scholar] [CrossRef]
- Villard, L.; Borderies, P. On the use of virtual ground scatterers to localize double and triple bounce scattering mechanisms for bistatic SAR. J. Electromagn. Waves Appl. 2015, 29, 626–635. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Kouyate, F.; Fung, A.K.; Sieber, A.J. A backscatter model for a randomly perturbed periodic surface. IEEE Trans. Geosci. Remote Sens. 1982, GE-20, 518–528. [Google Scholar] [CrossRef]
- Tsang, L.; Kong, J.A.; Shin, R.T. Theory of Microwave Remote Sensing; A Wiley-Interscience Publication; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Valenzuela, G. Depolarization of EM waves by slightly rough surfaces. IEEE Trans. Antennas Propag. 1967, 15, 552–557. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. Concept of polarization entropy in optical scattering. Optical Eng. 1995, 34, 1599–1611. [Google Scholar] [CrossRef]





| System Parameters | Image Features | Scene Dimensions | |||
|---|---|---|---|---|---|
| Height | H = 2.99 m | Azimuth resolutions | = 1.75 cm | 1.5 m | |
| Carrier frequency | = 10 GHz | Slant range resolutions | = 3.75 cm | 2.2 m | |
| Bandwidth | B = 4 GHz | Ground range ambiguity | = 6 m | 3.5 m | |
| Incidence angle | = to | Vertical resolution | = 0.13 m to 0.22 m | 0.96 m | |
| Verical baseline between two consecutive acquisitions | dz = 2 cm | Vertical ambiguity | = 2.96 m to 5 m | 0.4 m | |
| Number of acquisitions | = 24 | Polarization | hh, hv, vv | 1.5 m | |
| 0.76 m | |||||
| Zone Index | ① | ② | ③ | ④ | ⑤ |
|---|---|---|---|---|---|
| Ground range domain | 1 m to 1.5 m | 1.5 m to 2.46 m | 2.46 m to 3.15 m | 3.15 m to 3.96 m | 3.96 m to 5.1 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdo, R.; Ferro-Famil, L.; Boutet, F.; Allain-Bailhache, S. Analysis of the Double-Bounce Interaction between a Random Volume and an Underlying Ground, Using a Controlled High-Resolution PolTomoSAR Experiment. Remote Sens. 2021, 13, 636. https://doi.org/10.3390/rs13040636
Abdo R, Ferro-Famil L, Boutet F, Allain-Bailhache S. Analysis of the Double-Bounce Interaction between a Random Volume and an Underlying Ground, Using a Controlled High-Resolution PolTomoSAR Experiment. Remote Sensing. 2021; 13(4):636. https://doi.org/10.3390/rs13040636
Chicago/Turabian StyleAbdo, Ray, Laurent Ferro-Famil, Frederic Boutet, and Sophie Allain-Bailhache. 2021. "Analysis of the Double-Bounce Interaction between a Random Volume and an Underlying Ground, Using a Controlled High-Resolution PolTomoSAR Experiment" Remote Sensing 13, no. 4: 636. https://doi.org/10.3390/rs13040636
APA StyleAbdo, R., Ferro-Famil, L., Boutet, F., & Allain-Bailhache, S. (2021). Analysis of the Double-Bounce Interaction between a Random Volume and an Underlying Ground, Using a Controlled High-Resolution PolTomoSAR Experiment. Remote Sensing, 13(4), 636. https://doi.org/10.3390/rs13040636








