Shoreline Extraction in SAR Image Based on Advanced Geometric Active Contour Model
Abstract
:1. Introduction
2. Background and Related Work
3. Materials and Methods
3.1. Study Area
3.2. Theoretical Background
3.2.1. Traditional Geometric Active Contour Model
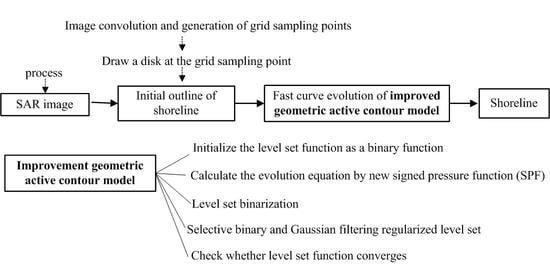
3.2.2. Improvement of Geometric Active Contour model
3.3. Method
3.3.1. Acquisition of Initial Contour
3.3.2. Accurate Extraction of Shoreline
4. Results
5. Validation
6. Discussion
- Although this paper solves the problem of shoreline extraction from SAR images, there is no theoretical basis for the setting of model parameters. As future studies, further research could be conducted to automatically set the parameters.
- In this paper, the GAC model was improved by combining the global region smooth information as the convergence condition of curve evolution. In order to further reduce the iteration times and time, it is necessary to determine the initial contour of shoreline accurately and find a way to eliminate the redundant points in the detected shoreline.
- The energy functional design of the model also needs a set of theories as a guide.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SAR | synthetic aperture radar |
| ACM | active contour model |
| GAC | geometric active contour |
| ESF | edge stopping function |
| SPF | signed pressure function |
| LBF | local binary fitting |
| SBGFRLS | selective binary and Gaussian filtering regularized level set |
References
- Buono, A.; Nunziata, F.; Mascolo, L.; Migliaccio, M. A multipolarization analysis of coastline extraction using X-Band COSMO-SkyMed SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2811–2820. [Google Scholar] [CrossRef]
- Al Fugura, A.; Billa, L.; Pradhan, B. Semi-automated procedures for shoreline extraction using single RADARSAT-1 SAR image. Estuar. Coast. Shelf Sci. 2011, 95, 395–400. [Google Scholar] [CrossRef]
- Nunziata, F.; Buono, A.; Migliaccio, M.; Benassai, G. Dual-Polarimetric C- and X-Band SAR Data for Coastline Extraction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4921–4928. [Google Scholar] [CrossRef]
- Ferrentino, E.; Nunziata, F.; Migliaccio, M. Full-polarimetric SAR measurements for coastline extraction and coastal area classification. Int. J. Remote Sens. 2017, 38, 7405–7421. [Google Scholar] [CrossRef]
- Nunziata, F.; Migliaccio, M.; Li, X.; Ding, X. Coastline extraction using dual-polarimetric COSMO-SkyMed PingPong mode SAR data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 104–108. [Google Scholar] [CrossRef]
- Schmitt, M.; Baier, G.; Zhu, X.X. Potential of nonlocally filtered pursuit monostatic TanDEM-X data for coastline detection. ISPRS J. Photogramm. Remote Sens. 2019, 148, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Shen, Q.; Wang, C.Y.; Zhao, B. Automatic waterline extraction in VHR imagery using geometric active contour model. J. Fudan Univ. (Nat. Sci.) 2012, 51, 77–82. [Google Scholar]
- Michael, K.; Andrew, W.; Demetri, T. Snake: Active Contour Models. In Proceedings of the First International Conference on Computer Vision, London, UK, 8–11 June 1987; pp. 259–269. [Google Scholar]
- Lee, J.-S.; Jurkevich, I. Coastline detection and Tracing in SAr images. IEEE Trans. Geosci. Remote. Sens. 1990, 28, 662–668. [Google Scholar] [CrossRef] [Green Version]
- Baselice, F.; Ferraioli, G. Unsupervised coastal line extraction from SAR images. IEEE Geosci. Remote. Sens. Lett. 2013, 10, 1350–1354. [Google Scholar] [CrossRef]
- Chu, C.; Siao, J.S.; Wang, L.C.; Deng, W.S. Estimation of 2D jump location curve and 3D jump location surface in nonpar-ametric regression. Stat. Comput. 2012, 22, 17–31. [Google Scholar] [CrossRef]
- Wang, D.; Liu, X. Coastline Extraction from SAR Images Using Robust Ridge Tracing. Mar. Geod. 2019, 42, 286–315. [Google Scholar] [CrossRef]
- Descombes, X.; Moctezuma, M.; Maître, H.; Rudant, J.-P. Coastline detection by a Markovian segmentation on SAR images. Signal Process. 1996, 55, 123–132. [Google Scholar] [CrossRef]
- She, X.; Qiu, X.; Lei, B. Accurate sea–land segmentation using ratio of average constrained graph cut for polarimetric synthetic aperture radar data. J. Appl. Remote Sens. 2017, 11, 26023. [Google Scholar] [CrossRef] [Green Version]
- Margarida, S.; Sandra, H. Separation between water and land in SAR Images using Region-Based level sets. IEEE Geosci. Remote Sens. Lett. 2009, 6, 471–475. [Google Scholar]
- Liu, C.; Yang, J.; Yin, J.J.; An, W. Coastline detection in SAR images using a hierarchical level set segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4908–4920. [Google Scholar] [CrossRef]
- Maciel, L.D.S.; Gomide, F.; Ballini, R. A differential evolution algorithm for yield curve estimation. Math. Comput. Simul. 2016, 129, 10–30. [Google Scholar] [CrossRef]
- Modava, M.; Akbarizadeh, G. Coastline extraction from SAR images using spatial fuzzy clustering and the active contour method. Int. J. Remote Sens. 2017, 38, 355–370. [Google Scholar] [CrossRef]
- Niedermeier, A.; Romaneessen, E.; Lehner, S. Detection of coastlines in SAR images using wavelet methods. IEEE Trans. Geosci. Remote. Sens. 2000, 38, 2270–2281. [Google Scholar] [CrossRef]
- Liu, C.; Xiao, Y.; Yang, J. A Coastline Detection Method in Polarimetric SAR Images Mixing the Region-Based and Edge-Based Active Contour Models. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3735–3747. [Google Scholar] [CrossRef]
- Tirandaz, Z.; Akbarizadeh, G. A two-phase algorithm based on kurtosis Curvelet energy and unsupervised spectral regres-sion for segmentation of SAR images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1244–1264. [Google Scholar] [CrossRef]
- Modava, M.; Akbarizadeh, G.; Soroosh, M. Integration of spectral histogram and level set for coastline detection in SAR im-ages. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 810–819. [Google Scholar] [CrossRef]
- Kim, D.-J.; Moon, W.M.; Park, S.-E.; Kim, J.-E.; Lee, H.-S. Dependence of Waterline Mapping on Radar Frequency Used for SAR Images in Intertidal Areas. IEEE Geosci. Remote. Sens. Lett. 2007, 4, 269–273. [Google Scholar] [CrossRef]
- An, M.; Sun, Q.; Hu, J.; Tang, Y.; Zhu, Z. Coastline Detection with Gaofen-3 SAR Images Using an Improved FCM Method. Sensors 2018, 18, 1898. [Google Scholar] [CrossRef] [Green Version]
- Demir, N.; Bayram, B.; Şeker, D.Z.; Oy, S.; Erdem, F. A nonparametric fuzzy shoreline extraction approach from Sentinel-1A by integration of RASAT pan-sharpened imagery. Geo-Mar. Lett. 2019, 39, 401–415. [Google Scholar] [CrossRef]
- Fuse, T.; Ohkura, T. Development of Shoreline Extraction Method Based on Spatial Pattern Analysis of Satellite SAR Images. Remote Sens. 2018, 10, 1361. [Google Scholar] [CrossRef] [Green Version]
- Zollini, S.; Alicandro, M.; Cuevas-Gonzalez, M.; Baiocchi, V.; Dominici, D.; Buscema, M. Shoreline Extraction Based on an Active Connection Matrix (ACM) Image Enhancement Strategy. J. Mar. Sci. Eng. 2019, 8, 9. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Acton, S.T. Automated delineation of coastline from polarimetric SAR imagery. Int. J. Remote Sens. 2004, 25, 3423–3438. [Google Scholar] [CrossRef]
- Di Luccio, D.; Benassai, G.; Di Paola, G.; Mucerino, L.; Buono, A.; Rosskopf, C.M.; Nunziata, F.; Migliaccio, M.; Urciuoli, A.; Montella, R. Shoreline Rotation Analysis of Embayed Beaches by Means of In Situ and Remote Surveys. Sustainability 2019, 11, 725. [Google Scholar] [CrossRef] [Green Version]
- Tajima, Y.; Wu, L.; Fuse, T.; Shimozono, T.; Sato, S. Study on shoreline monitoring system based on satellite SAR imagery. Coast. Eng. J. 2019, 61, 401–421. [Google Scholar] [CrossRef]
- Dellepiane, S.; De Laurentiis, R.; Giordano, F. Coastline extraction from SAR images and a method for the evaluation of the coastline precision. Pattern Recognit. Lett. 2004, 25, 1461–1470. [Google Scholar] [CrossRef]
- Caselles, V.; Kimmel, R.; Sapiro, G. Geodesic active contours. Proc. IEEE Int. Conf. Comput. Vis. 2002, 22, 61–79. [Google Scholar] [CrossRef]
- Malladi, R.; Sethian, J.; Vemuri, B. Shape modeling with front propagation: A level set approach. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 158–175. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Zhang, L.; Song, H.; Zhou, W. Active contours with selective local or global segmentation: A new formulation and level set method. Image Vis. Comput. 2010, 28, 668–676. [Google Scholar] [CrossRef]
- Yang, Y.; Li, C.; Kao, C.-Y.; Osher, S. Split Bregman Method for Minimization of Region-Scalable Fitting Energy for Image Segmentation. Min. Data Financ. Appl. 2010, 2008, 117–128. [Google Scholar] [CrossRef]
- Chan, T.F.; Sandergby, V. Active contours without edges for vector-valued images. J. Vis. Commun. Image Represent. 2000, 11, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Huo, Y.-K.; Wei, G.; Zhang, Y.-D.; Wu, L.-N. An Adaptive Threshold for the Canny Operator of Edge Detection. In Proceedings of the 2010 International Conference on Image Analysis and Signal Processing, Zhejiang, China, 9–11 April 2010; pp. 371–374. [Google Scholar]
















| Improved Canny Operator Method | Boundary Tracking Algorithm | Traditional Geometric Active Contour Modeling Method | Proposed Method | Shoreline Pixels | |
|---|---|---|---|---|---|
| Extraction result | 707 | 789 | 906 | 681 | 663 |
| False extraction pixel | 158 | 184 | 311 | 53 | |
| Missing pixels | 114 | 58 | 68 | 35 | |
| Error rate | 0.410 | 0.365 | 0.572 | 0.133 | |
| Accuracy | 0.828 | 0.913 | 0.897 | 0.947 |
| Improved Canny Operator Method | Boundary Tracking Algorithm | Traditional Geometric Active Contour Modeling Method | Proposed Method | |
|---|---|---|---|---|
| Number of iterations/times | 1693 | 1389 | 1212 | 164 |
| Operation time/second | 363.15 | 289.63 | 267.98 | 25.92 |
| Iteration Number/Times | Operation Time/Second | |
|---|---|---|
| Small initial contour | 6000 | 161.23 |
| Large initial contour | 1593 | 58.48 |
| Global initial contour | 164 | 25.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Zheng, W.; Xi, C.; Shang, S. Shoreline Extraction in SAR Image Based on Advanced Geometric Active Contour Model. Remote Sens. 2021, 13, 642. https://doi.org/10.3390/rs13040642
Wei X, Zheng W, Xi C, Shang S. Shoreline Extraction in SAR Image Based on Advanced Geometric Active Contour Model. Remote Sensing. 2021; 13(4):642. https://doi.org/10.3390/rs13040642
Chicago/Turabian StyleWei, Xueyun, Wei Zheng, Caiping Xi, and Shang Shang. 2021. "Shoreline Extraction in SAR Image Based on Advanced Geometric Active Contour Model" Remote Sensing 13, no. 4: 642. https://doi.org/10.3390/rs13040642
APA StyleWei, X., Zheng, W., Xi, C., & Shang, S. (2021). Shoreline Extraction in SAR Image Based on Advanced Geometric Active Contour Model. Remote Sensing, 13(4), 642. https://doi.org/10.3390/rs13040642