Exploring the Impact of Noise on Hybrid Inversion of PROSAIL RTM on Sentinel-2 Data
Abstract
:1. Introduction
2. Methods
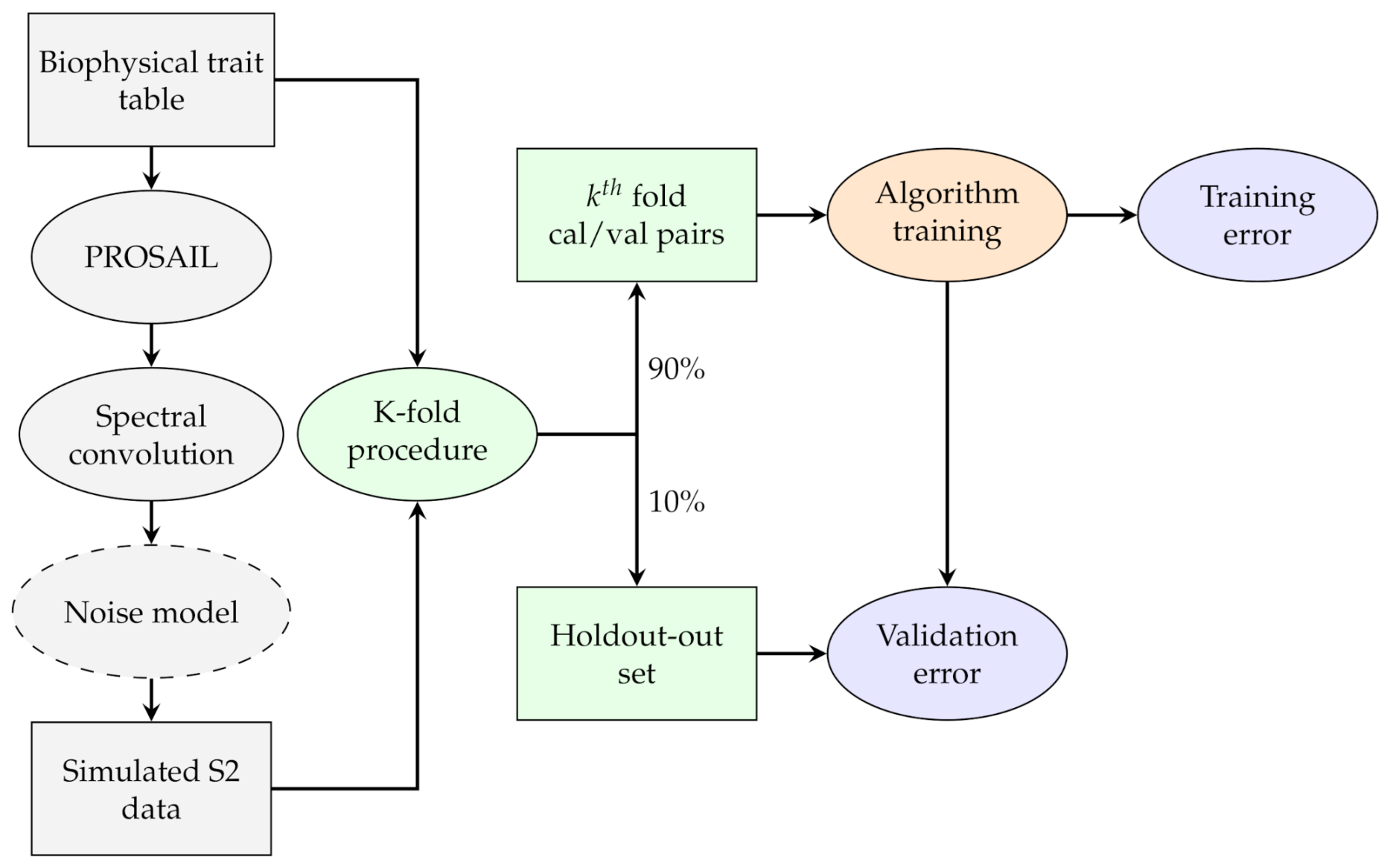
2.1. General Methodology
2.2. PROSAIL
2.3. Machine Learning Algorithms
2.3.1. Random Forest
2.3.2. Artificial Neural Networks
2.3.3. Gaussian Processes
2.4. Step 1: Sensitivity Analysis
2.5. Step 2: Hyperparameter Tuning
2.6. Step 3: RTM Inversion
2.7. Impacts of Noise
3. Results
3.1. Sensitivity Analysis
3.2. Hyperparameter Tuning
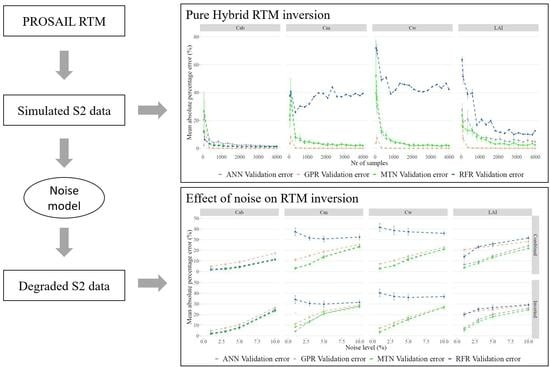
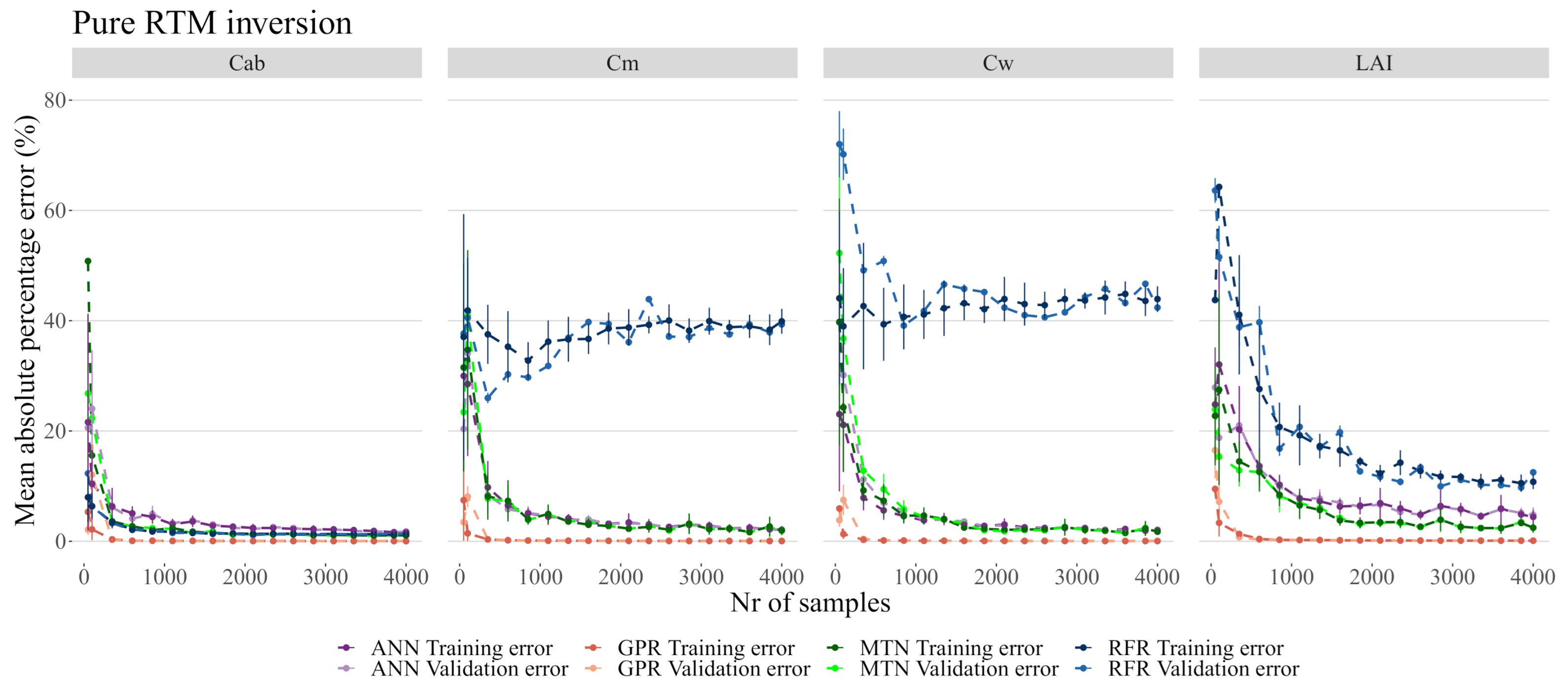
3.3. RTM Inversion
3.4. Impacts of Noise
4. Discussion
5. Conclusions
Author Contributions
Funding
Code Availability
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Spectral Variability in Response to Trait Variability

Appendix A.2. Artificial Neural Networks Mean Absolute Percentage Error in Function of Training Epochs

References
- Pereira, H.M.; Ferrier, S.; Walters, M.; Geller, G.N.; Jongman, R.H.G.; Scholes, R.J.; Bruford, M.W.; Brummitt, N.; Butchart, S.H.M.; Cardoso, A.C.; et al. Essential Biodiversity Variables. Science 2013, 339, 277–278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jetz, W.; McGeoch, M.A.; Guralnick, R.; Ferrier, S.; Beck, J.; Costello, M.J.; Fernandez, M.; Geller, G.N.; Keil, P.; Merow, C.; et al. Essential biodiversity variables for mapping and monitoring species populations. Nat. Ecol. Evol. 2019, 3, 539–551. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vihervaara, P.; Auvinen, A.P.; Mononen, L.; Törmä, M.; Ahlroth, P.; Anttila, S.; Böttcher, K.; Forsius, M.; Heino, J.; Heliölä, J.; et al. How Essential Biodiversity Variables and remote sensing can help national biodiversity monitoring. Glob. Ecol. Conserv. 2017, 10, 43–59. [Google Scholar] [CrossRef]
- Pettorelli, N.; Schulte to Bühne, H.; Tulloch, A.; Dubois, G.; Macinnis-Ng, C.; Queirós, A.M.; Keith, D.A.; Wegmann, M.; Schrodt, F.; Stellmes, M.; et al. Satellite remote sensing of ecosystem functions: Opportunities, challenges and way forward. Remote Sens. Ecol. Conserv. 2017, 4, 71–93. [Google Scholar] [CrossRef]
- Cavender-Bares, J.; Gamon, J.A.; Townsend, P.A. (Eds.) Remote Sensing of Plant Biodiversity; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Ghamisi, P.; Gloaguen, R.; Atkinson, P.M.; Benediktsson, J.A.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; et al. Multisource and Multitemporal Data Fusion in Remote Sensing: A Comprehensive Review of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef] [Green Version]
- Nock, C.A.; Vogt, R.J.; Beisner, B.E. Functional Traits. eLS 2016. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and Biochemical Sources of Variability in Canopy Reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Myneni, R.B.; Pragnère, A.; Knyazikhin, Y. Investigation of a model inversion technique to estimate canopy biophysical variables from spectral and directional reflectance data. Agronomie 2000, 20, 3–22. [Google Scholar] [CrossRef]
- Verrelst, J.; Dethier, S.; Rivera, J.P.; Munoz-Mari, J.; Camps-Valls, G.; Moreno, J. Active Learning Methods for Efficient Hybrid Biophysical Variable Retrieval. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1012–1016. [Google Scholar] [CrossRef]
- Durán, S.M.; Martin, R.E.; Díaz, S.; Maitner, B.S.; Malhi, Y.; Salinas, N.; Shenkin, A.; Silman, M.R.; Wieczynski, D.J.; Asner, G.P.; et al. Informing trait-based ecology by assessing remotely sensed functional diversity across a broad tropical temperature gradient. Sci. Adv. 2019, 5, eaaw8114. [Google Scholar] [CrossRef] [Green Version]
- Schneider, F.D.; Morsdorf, F.; Schmid, B.; Petchey, O.L.; Hueni, A.; Schimel, D.S.; Schaepman, M.E. Mapping functional diversity from remotely sensed morphological and physiological forest traits. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zarco-Tejada, P.; Hornero, A.; Beck, P.; Kattenborn, T.; Kempeneers, P.; Hernández-Clemente, R. Chlorophyll content estimation in an open-canopy conifer forest with Sentinel-2A and hyperspectral imagery in the context of forest decline. Remote Sens. Environ. 2019, 223, 320–335. [Google Scholar] [CrossRef] [PubMed]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Verrelst, J.; Malenovský, Z.; der Tol, C.V.; Camps-Valls, G.; Gastellu-Etchegorry, J.P.; Lewis, P.; North, P.; Moreno, J. Quantifying Vegetation Biophysical Variables from Imaging Spectroscopy Data: A Review on Retrieval Methods. Surv. Geophys. 2018, 40, 589–629. [Google Scholar] [CrossRef] [Green Version]
- Staben, G.; Lucieer, A.; Scarth, P. Modelling LiDAR derived tree canopy height from Landsat TM, ETM+ and OLI satellite imagery—A machine learning approach. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 666–681. [Google Scholar] [CrossRef]
- Moreno-Martínez, Á.; Camps-Valls, G.; Kattge, J.; Robinson, N.; Reichstein, M.; van Bodegom, P.; Kramer, K.; Cornelissen, J.H.C.; Reich, P.; Bahn, M.; et al. A methodology to derive global maps of leaf traits using remote sensing and climate data. Remote Sens. Environ. 2018, 218, 69–88. [Google Scholar] [CrossRef] [Green Version]
- Darvishzadeh, R.; Wang, T.; Skidmore, A.; Vrieling, A.; O’Connor, B.; Gara, T.; Ens, B.; Paganini, M. Analysis of Sentinel-2 and RapidEye for Retrieval of Leaf Area Index in a Saltmarsh Using a Radiative Transfer Model. Remote Sens. 2019, 11, 671. [Google Scholar] [CrossRef] [Green Version]
- Campos-Taberner, M.; Moreno-Martínez, Á.; García-Haro, F.; Camps-Valls, G.; Robinson, N.; Kattge, J.; Running, S. Global Estimation of Biophysical Variables from Google Earth Engine Platform. Remote Sens. 2018, 10, 1167. [Google Scholar] [CrossRef] [Green Version]
- Svendsen, D.H.; Martino, L.; Campos-Taberner, M.; Camps-Valls, G. Joint Gaussian processes for inverse modeling. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 4 December 2017. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Martino, L.; Svendsen, D.H.; Campos-Taberner, M.; Muñoz-Marí, J.; Laparra, V.; Luengo, D.; García-Haro, F.J. Physics-aware Gaussian processes in remote sensing. Appl. Soft Comput. 2018, 68, 69–82. [Google Scholar] [CrossRef]
- Tuia, D.; Verrelst, J.; Alonso, L.; Perez-Cruz, F.; Camps-Valls, G. Multioutput Support Vector Regression for Remote Sensing Biophysical Parameter Estimation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 804–808. [Google Scholar] [CrossRef]
- Annala, L.; Honkavaara, E.; Tuominen, S.; Pölönen, I. Chlorophyll Concentration Retrieval by Training Convolutional Neural Network for Stochastic Model of Leaf Optical Properties (SLOP) Inversion. Remote Sens. 2020, 12, 283. [Google Scholar] [CrossRef] [Green Version]
- Zurita-Milla, R.; Laurent, V.; van Gijsel, J. Visualizing the ill-posedness of the inversion of a canopy radiative transfer model: A case study for Sentinel-2. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 7–18. [Google Scholar] [CrossRef]
- Locherer, M.; Hank, T.; Danner, M.; Mauser, W. Retrieval of Seasonal Leaf Area Index from Simulated EnMAP Data through Optimized LUT-Based Inversion of the PROSAIL Model. Remote Sens. 2015, 7, 10321–10346. [Google Scholar] [CrossRef] [Green Version]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods—A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Brede, B.; Verrelst, J.; Gastellu-Etchegorry, J.P.; Clevers, J.G.P.W.; Goudzwaard, L.; den Ouden, J.; Verbesselt, J.; Herold, M. Assessment of Workflow Feature Selection on Forest LAI Prediction with Sentinel-2A MSI, Landsat 7 ETM+ and Landsat 8 OLI. Remote Sens. 2020, 12, 915. [Google Scholar] [CrossRef] [Green Version]
- Berger, K.; Caicedo, J.P.R.; Martino, L.; Wocher, M.; Hank, T.; Verrelst, J. A Survey of Active Learning for Quantifying Vegetation Traits from Terrestrial Earth Observation Data. Remote Sens. 2021, 13, 287. [Google Scholar] [CrossRef]
- Upreti, D.; Huang, W.; Kong, W.; Pascucci, S.; Pignatti, S.; Zhou, X.; Ye, H.; Casa, R. A Comparison of Hybrid Machine Learning Algorithms for the Retrieval of Wheat Biophysical Variables from Sentinel-2. Remote Sens. 2019, 11, 481. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Dash, J.; Huete, A.; Jiang, A.; Yin, G.; Ding, Y.; Peng, D.; Hall, C.C.; Brown, L.; Shi, Y.; et al. Retrieval of crop biophysical parameters from Sentinel-2 remote sensing imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 187–195. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.P.S. A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D.D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures. In Proceedings of the 30th International Conference, International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. I-115–I-123. [Google Scholar]
- Bergstra, J.; Komer, B.; Eliasmith, C.; Yamins, D.; Cox, D.D. Hyperopt: A Python library for model selection and hyperparameter optimization. Comput. Sci. Discov. 2015, 8, 014008. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Féret, J.B.; Gitelson, A.; Noble, S.; Jacquemoud, S. PROSPECT-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef] [Green Version]
- SUITS, G. The calculation of the directional reflectance of a vegetative canopy. Remote Sens. Environ. 1971, 2, 117–125. [Google Scholar] [CrossRef] [Green Version]
- Berger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the PROSAIL Model Capabilities for Future Hyperspectral Model Environments: A Review Study. Remote Sens. 2018, 10, 85. [Google Scholar] [CrossRef] [Green Version]
- Kattge, J.; Diaz, S.; Lavorel, S.; Prentice, I.C.; Leadley, P.; Bönisch, G.; Garnier, E.; Westoby, M.; Reich, P.B.; Wright, I.J.; et al. TRY—A global database of plant traits. Glob. Chang. Biol. 2011, 17, 2905–2935. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q. An overview of multi-task learning. Natl. Sci. Rev. 2017, 5, 30–43. [Google Scholar] [CrossRef] [Green Version]
- Weiss, M.; Baret, F. S2ToolBox Level 2 Products: LAI, FAPAR, FCOVER; Institut National de la Recherche Agronomique (INRA): Avignon, France, 2016. [Google Scholar]
- Duvenaud, D.; Lloyd, J.R.; Grosse, R.; Tenenbaum, J.B.; Ghahramani, Z. Structure Discovery in Nonparametric Regression through Compositional Kernel Search. In Proceedings of the 30th International Conference, International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. 1166–1174. [Google Scholar]
- Sobol, I. Sensitivity Analysis or Nonlinear Mathematical Models. Math. Model. Comput. Exp. 1993, 4, 407–414. [Google Scholar]
- Gu, C.; Du, H.; Mao, F.; Han, N.; Zhou, G.; Xu, X.; Sun, S.; Gao, G. Global sensitivity analysis of PROSAIL model parameters when simulating Moso bamboo forest canopy reflectance. Int. J. Remote Sens. 2016, 37, 5270–5286. [Google Scholar] [CrossRef]
- Wang, S.; Gao, W.; Ming, J.; Li, L.; Xu, D.; Liu, S.; Lu, J. A TPE based inversion of PROSAIL for estimating canopy biophysical and biochemical variables of oilseed rape. Comput. Electron. Agric. 2018, 152, 350–362. [Google Scholar] [CrossRef]
- The European Space Agency. Sentinel-2 Spectral Response Functions (S2-SRF). Available online: https://earth.esa.int/web/sentinel/user-guides/sentinel-2-msi/document-library (accessed on 1 January 2020).
- Verrelst, J.; Vicent, J.; Rivera-Caicedo, J.P.; Lumbierres, M.; Morcillo-Pallarés, P.; Moreno, J. Global Sensitivity Analysis of Leaf-Canopy-Atmosphere RTMs: Implications for Biophysical Variables Retrieval from Top-of-Atmosphere Radiance Data. Remote Sens. 2019, 11, 1923. [Google Scholar] [CrossRef] [Green Version]
- Pan, H.; Chen, Z.; Ren, J.; Li, H.; Wu, S. Modeling Winter Wheat Leaf Area Index and Canopy Water Content With Three Different Approaches Using Sentinel-2 Multispectral Instrument Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 482–492. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Feurer, M.; Eggensperger, K.; Falkner, S.; Lindauer, M.; Hutter, F. Auto-Sklearn 2.0: The Next Generation. arXiv 2020, arXiv:2007.04074. [Google Scholar]
- Erickson, N.; Mueller, J.; Shirkov, A.; Zhang, H.; Larroy, P.; Li, M.; Smola, A. AutoGluon-Tabular: Robust and Accurate AutoML for Structured Data. arXiv 2020, arXiv:2003.06505. [Google Scholar]
- Lazaro-Gredilla, M.; Titsias, M.K.; Verrelst, J.; Camps-Valls, G. Retrieval of Biophysical Parameters With Heteroscedastic Gaussian Processes. IEEE Geosci. Remote Sens. Lett. 2014, 11, 838–842. [Google Scholar] [CrossRef]
- Svendsen, D.H.; Morales-Álvarez, P.; Ruescas, A.B.; Molina, R.; Camps-Valls, G. Deep Gaussian processes for biogeophysical parameter retrieval and model inversion. ISPRS J. Photogramm. Remote Sens. 2020, 166, 68–81. [Google Scholar] [CrossRef] [PubMed]
- Gewali, U.B.; Monteiro, S.T.; Saber, E. Gaussian Processes for Vegetation Parameter Estimation from Hyperspectral Data with Limited Ground Truth. Remote Sens. 2019, 11, 1614. [Google Scholar] [CrossRef] [Green Version]
- Fröhlich, B.; Rodner, E.; Kemmler, M.; Denzler, J. Efficient Gaussian process classification using random decision forests. Pattern Recognit. Image Anal. 2011, 21, 184–187. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Svendsen, D.H.; Cortés-Andrés, J.; Moreno-Martínez, Á; Pérez-Suay, A.; Adsuara, J.; Martín, I.; Piles, M.; Muñoz-Marí, J.; Martino, L. Living in the Physics and Machine Learning Interplay for Earth Observation. arXiv 2020, arXiv:2010.09031. [Google Scholar]
- Combal, B.; Baret, F.; Weiss, M. Improving canopy variables estimation from remote sensing data by exploiting ancillary information. Case study on sugar beet canopies. Agronomie 2002, 22, 205–215. [Google Scholar] [CrossRef]
- Rivera, J.; Verrelst, J.; Leonenko, G.; Moreno, J. Multiple Cost Functions and Regularization Options for Improved Retrieval of Leaf Chlorophyll Content and LAI through Inversion of the PROSAIL Model. Remote Sens. 2013, 5, 3280–3304. [Google Scholar] [CrossRef] [Green Version]
- Richter, K.; Hank, T.B.; Vuolo, F.; Mauser, W.; D’Urso, G. Optimal Exploitation of the Sentinel-2 Spectral Capabilities for Crop Leaf Area Index Mapping. Remote Sens. 2012, 4, 561–582. [Google Scholar] [CrossRef] [Green Version]
- National Science Foundation. National Ecological Observatory Network. Available online: https://data.neonscience.org/home (accessed on 1 January 2020).







| Model | Domain | Description | Parameter | Units | Range | |
|---|---|---|---|---|---|---|
| PROSPECT | Leaf | Leaf structure index | N | - | 1 | |
| Chlorophyll a + b content | ug/cm | 0 | 120 | |||
| Total carotenoid content | ug/cm | 0 | 60 | |||
| Equivalent water thickness | cm | 0.001 | 0.008 | |||
| Dry matter content | g/cm | 0.001 | 0.008 | |||
| Brown pigments | - | 0 | ||||
| Total anthocyanin content | ug/cm | 0 | ||||
| SAIL | Canopy | Leaf area index | - | 0 | 10 | |
| Average leaf slope | LIDFa | ° | −0.35 | |||
| Leaf distribution bimodality | LIDFb | ° | −0.15 | |||
| Hot spot parameter | hspot | - | 0.01 | |||
| Soil | Soil reflectance | - | 0.5 | |||
| Soil brightness factor | - | 0.1 | ||||
| Positional | Solar zenith angle | tts | ° | 45 | ||
| Sensor zenith angle | tto | ° | 45 | |||
| Relative azimuth angle | phi | ° | 0 | |||
| Model | Parameter | Data Type | Range |
|---|---|---|---|
| Random Forests | Number of trees | Integer | {50, 100, 150, …, 1000} |
| Minimum samples node split | Continuous | [0; 0.5] | |
| Minimum samples leaf node | Continuous | [0; 0.5] | |
| Gaussian Processes | Number of optimizer restarts | Integer | {10, 20, 30, 40, 50, 60, 70, 80, 90, 100} |
| Kernel functions | Categorical | radial basis function, rational quadratic, matérn, dot product | |
| Artificial Neural Network | Number of hidden layers | Integer | 1 to 3 |
| Number of neurons | Integer | {5, 10, 15, 20} | |
| Activation functions | Categorical | Linear, Sigmoid, Tanh, Exponential, Softplus, ReLU, Softsign | |
| Optimizer | Categorical | Adam, RMSprop, Adadelta | |
| Multi-task Neural Network | Number of shared layers | Categorical | {1, 2} |
| Number of single task layers | Integer | {1, 2} | |
| Number of neurons (shared) | Integer | {5, 10, 15, 20} | |
| Number of neurons (single) | Integer | {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} | |
| Activation functions | Categorical | Linear, Sigmoid, Tanh, Exponential, Softplus, ReLU, Softsign | |
| Optimizer | Categorical | Adam, RMSprop, Adadelta |
| Band | |||||
|---|---|---|---|---|---|
| B2 | −0.10 (***) | 0.00 | −0.04 (.) | 0.2 (***) | −0.46 (***) |
| B3 | −0.95 (***) | 0.03 | −0.02 | −0.04 (.) | −0.10 (***) |
| B4 | −0.56 (***) | 0.02 | −0.02 | 0.01 | −0.02 |
| B5 | −0.97 (***) | 0.03 | −0.02 | −0.04 | −0.01 |
| B6 | −0.61 (***) | 0.00 | −0.19 (***) | 0.49 (***) | 0.01 |
| B7 | −0.01 | −0.01 | −0.47 (***) | 0.82 (***) | 0.01 |
| B8A | 0.01 | −0.02 | −0.47 (***) | 0.82 (***) | 0.01 |
| B11 | 0.04 | −0.65 (***) | −0.49 (***) | 0.46 (***) | −0.01 |
| B12 | 0.02 | −0.67 (***) | −0.69 (***) | 0.03 | −0.02 |
| Model | Parameter | Selected |
|---|---|---|
| Random Forests | Number of trees | 850 |
| Minimum samples node split | 0.00053 | |
| Minimum samples leaf node | 0.00286 | |
| Gaussian Processes | Number of optimizer restarts | 80 |
| Kernel functions | Rational Quadratic | |
| Artificial Neural Network | Number of hidden layers | 3 |
| Number of neurons | (20, 20, 15) | |
| Activation functions | Softsign, Softsign, ReLU | |
| Optimizer | Adam | |
| Multi-task Neural network | Number of shared layers | 2 |
| Trait-specific layers | 2 | |
| Number of neurons * | (15, 20) | |
| Activation functions * | Tanh, Exponential | |
| Optimizer | Adam |
| Model | Trait | Parameter | Selected |
|---|---|---|---|
| Multi-task Neural network | Cab | Number of neurons | (3, 6) |
| Activation functions | Softplus, Sigmoid | ||
| Cw | Number of neurons | (3, 4) | |
| Activation functions | Softplus, Tanh | ||
| Cm | Number of neurons | (8, 6) | |
| Activation functions | ReLU, Sigmoid | ||
| LAI | Number of neurons | (6,10) | |
| Activation functions | Softsign, Softsign |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Sá, N.C.; Baratchi, M.; Hauser, L.T.; van Bodegom, P. Exploring the Impact of Noise on Hybrid Inversion of PROSAIL RTM on Sentinel-2 Data. Remote Sens. 2021, 13, 648. https://doi.org/10.3390/rs13040648
de Sá NC, Baratchi M, Hauser LT, van Bodegom P. Exploring the Impact of Noise on Hybrid Inversion of PROSAIL RTM on Sentinel-2 Data. Remote Sensing. 2021; 13(4):648. https://doi.org/10.3390/rs13040648
Chicago/Turabian Stylede Sá, Nuno César, Mitra Baratchi, Leon T. Hauser, and Peter van Bodegom. 2021. "Exploring the Impact of Noise on Hybrid Inversion of PROSAIL RTM on Sentinel-2 Data" Remote Sensing 13, no. 4: 648. https://doi.org/10.3390/rs13040648
APA Stylede Sá, N. C., Baratchi, M., Hauser, L. T., & van Bodegom, P. (2021). Exploring the Impact of Noise on Hybrid Inversion of PROSAIL RTM on Sentinel-2 Data. Remote Sensing, 13(4), 648. https://doi.org/10.3390/rs13040648