Reconstruction of Snow Depth Data at Moderate Spatial Resolution (1 km) from Remotely Sensed Snow Data and Multiple Optimized Environmental Factors: A Case Study over the Qinghai-Tibetan Plateau
Abstract
:1. Introduction
2. Study Area and Data Sources
2.1. Study Area
2.2. Long-Term Passive Microwave Snow Depth Dataset (PMSD)
2.3. Cloud-Free MODIS-SCF
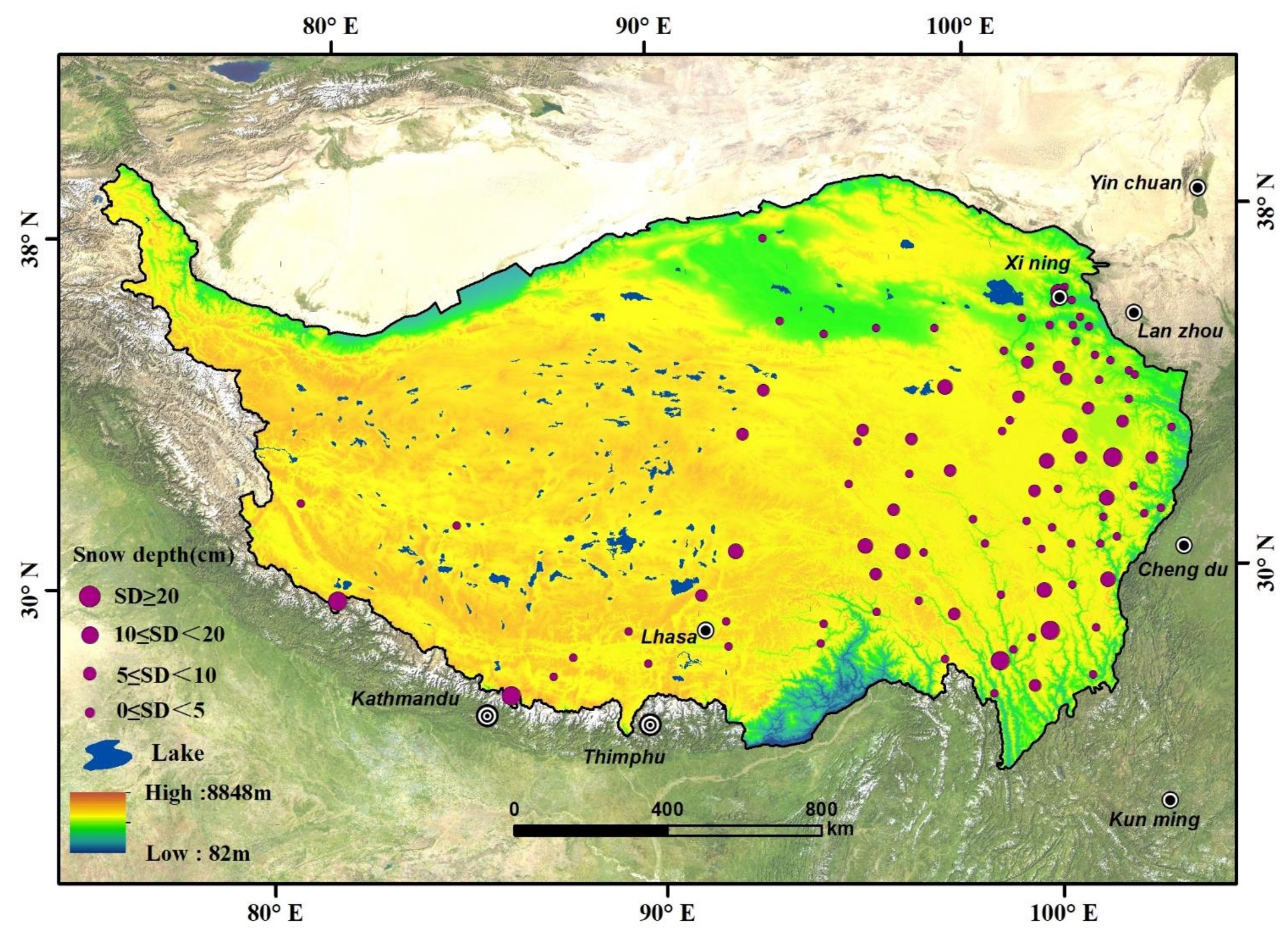
2.4. In-Situ Snow Depth Observations
2.5. Other Data Sources
3. Development of the LMSDR Model
3.1. Multisource Snow Depth Data Fusion
3.2. Snow Depth Reconstruction (SDR) Model Development and Evaluation
4. Results
4.1. Selection of Environmental Factors
4.2. Model Optimization
5. Discussion
5.1. Overall Accuracy Comparison
5.2. Snow Depth Accuracy Comparison of Different Snow Characteristics and Environmental Factors
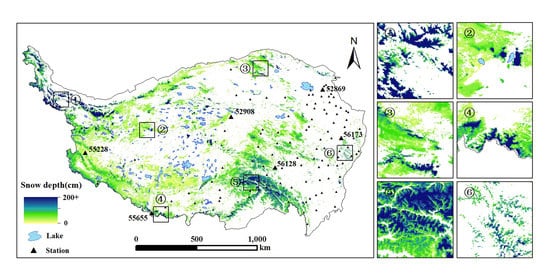
5.3. Spatial Accuracy Comparison of Different Snow Depth Products
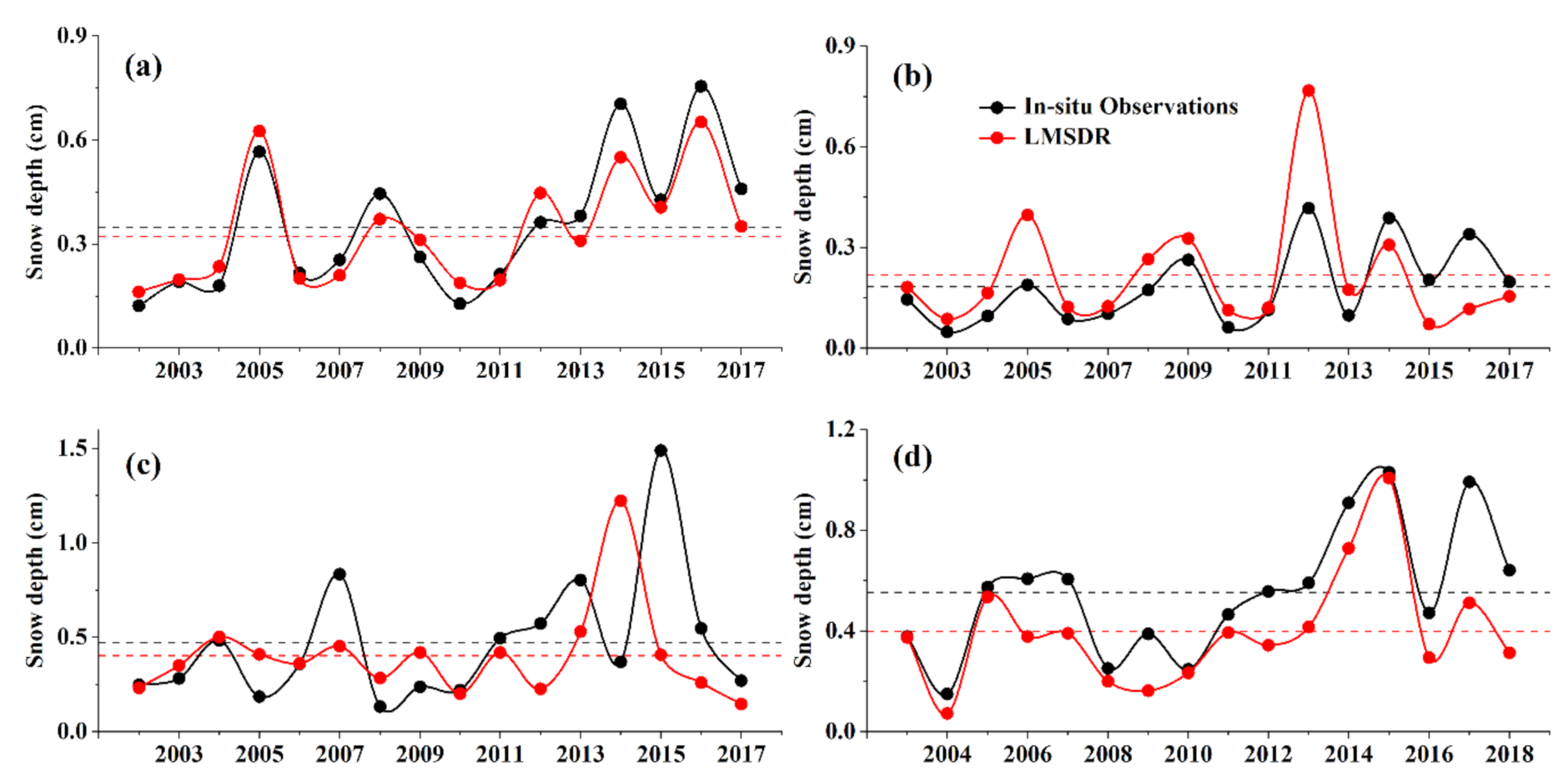
5.4. Interannual Variation of the LMSDR Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| Abbreviated Names | Interpretation |
| AMSR2 | advanced microwave scanning radiometer 2 |
| AVHRR | advanced very high resolution radiometer |
| DEM | digital elevation model |
| EnKF | ensemble Kalman filter method |
| FSD | fused snow depth |
| LMSDR | linear multivariate snow depth reconstruction |
| LOOCV | leave-one-out cross validation |
| LUCC | land-use and land-cover change |
| MAE | mean absolute error |
| MODIS | moderate resolution imaging spectroradiometer |
| NASA | national aeronautics and space administration |
| NDSI | normalized difference snow index |
| NME | negative mean error |
| NSIDC | US national snow and ice data left |
| PME | positive mean error |
| PMSD | passive microwave snow depth dataset |
| QTP | Qinghai-Tibetan Plateau |
| R2 | mean coefficient of determination |
| RMSE | root mean square error |
| SCD | snow cover day |
| SCF | snow cover fraction |
| SDC | snow depletion curve |
| SDR | snow depth reconstruction |
| SMMR | scanning multichannel microwave radiometer |
| SRTM | shuttle radar topography mission |
| SSM/I | special sensor microwave/imager |
| SSMI/S | special sensor microwave imager/sounder |
| TPDC | national Tibetan Plateau data left |
| VNIR | visible and near-infrared |
References
- Andreadis, K.M.; Lettenmaier, D.P. Assimilating remotely sensed snow observations into a macroscale hydrology model. Adv. Water Resour. 2006, 29, 872–886. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Van Beek, L.P.H.; Bierkens, M.F.P. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nat. Cell Biol. 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Tao, C.; Xiaohua, H.; Liyun, D.; Hongyi, L.; Xiaodong, H.; Lin, X. Snow Cover Variation and Its Impacts over the Qinghai-Tibet Plateau. Chin. Acad. Sci. 2019, 34, 1247–1253. [Google Scholar]
- Nosaka, M.; Sasaki, H.; Murata, A.; Kawase, H.; Oh’Izumi, M. Bias Correction of Snow Depth by Using Regional Frequency Analysis in the Non-Hydrostatic Regional Climate Model around Japan. SOLA 2016, 12, 165–169. [Google Scholar] [CrossRef] [Green Version]
- Dressler, K.A.; Leavesley, G.H.; Bales, R.C.; Fassnacht, S.R. Evaluation of gridded snow water equivalent and satellite snow cover products for mountain basins in a hydrologic model. Hydrol. Process. 2006, 20, 673–688. [Google Scholar] [CrossRef]
- Gong, G.; Cohen, J.; Entekhabi, D.; Ge, Y. Hemispheric-scale climate response to Northern Eurasia land surface characteristics and snow anomalies. Glob. Planet. Change 2007, 56, 359–370. [Google Scholar] [CrossRef]
- Cohen, J.; Entekhabi, D. Eurasian snow cover variability and northern hemisphere climate predictability. Geophys. Res. Lett. 1999, 26, 345–348. [Google Scholar] [CrossRef]
- Kuraś, P.K.; Weiler, M.; Alila, Y. The spatiotemporal variability of runoff generation and groundwater dynamics in a snow-dominated catchment. J. Hydrol. 2008, 352, 50–66. [Google Scholar] [CrossRef]
- Damm, A.; Köberl, J.; Prettenthaler, F. Does artificial snow production pay under future climate conditions? A case study for a vulnerable ski area in Austria. Tour. Manag. 2014, 43, 8–21. [Google Scholar] [CrossRef]
- Yao, T.D.; Qin, D.H.; Shen, Y.P.; Zhao, L.; Wang, N.-L.; Lu, A.-X. Cryospheric changes and their impacts on regional water cycle and ecological conditions in the Qinghai-Tibetan Plateau. Chin. J. Nat. 2013, 35, 179–186. [Google Scholar]
- Qian, Y.; Flanner, M.G.; Leung, L.R.; Wang, W. Sensitivity studies on the impacts of Tibetan Plateau snowpack pollution on the Asian hydrological cycle and monsoon climate. Atmos. Chem. Phys. Discuss. 2011, 11, 1929–1948. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Wang, Y.; Wu, R.; Zhu, Z.; Yang, K.; Li, M.; Ma, W.; Zhong, L.; Sun, F.; Chen, X.; et al. Recent advances on the study of atmosphere-land interaction observations on the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2009, 13, 1103–1111. [Google Scholar] [CrossRef] [Green Version]
- Dong, J.; Zhang, G.; Zhang, Y.; Xiao, X. Reply to Wang et al.: Snow cover and air temperature affect the rate of changes in spring phenology in the Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2013, 110, E2856–E2857. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, P. Distribution of Snow Cover Over the High Asia. J. Glaciol. Geocryol. 1995, 17, 291–298. [Google Scholar]
- Stow, D.A.; Hope, A.; McGuire, D.; Verbyla, D.; Gamon, J.; Huemmrich, F.; Houston, S.; Racine, C.; Sturm, M.; Tape, K.; et al. Remote sensing of vegetation and land-cover change in Arctic Tundra Ecosystems. Remote Sens. Environ. 2004, 89, 281–308. [Google Scholar] [CrossRef] [Green Version]
- Pu, Z.; Xu, L. MODIS/Terra observed snow cover over the Tibet Plateau: Distribution, variation and possible connection with the East Asian Summer Monsoon (EASM). Theor. Appl. Clim. 2008, 97, 265–278. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, Z.; Li, J.; Zhong, S.; Wang, L. Possible association of the western Tibetan Plateau snow cover with the decadal to interdecadal variations of northern China heatwave frequency. Clim. Dyn. 2012, 39, 2393–2402. [Google Scholar] [CrossRef]
- Xu, W.; Ma, L.; Ma, M.; Zhang, H.; Yuan, W. Spatial–Temporal Variability of Snow Cover and Depth in the Qinghai–Tibetan Plateau. J. Clim. 2017, 30, 1521–1533. [Google Scholar] [CrossRef]
- Shen, L.H.; Wu, T.; You, Q.L.; Jiang, G.J.; Xie, X.F.; Zhu, L.D.; Yin, J.W. Analysis of the characteristics of spatial and temporal variations of snow depth and their causes over the central and eastern Tibetan Plateau. J. Glaciol. Geocryol. 2019, 41, 1150–1161. [Google Scholar]
- Dai, L.; Che, T.; Xie, H.; Wu, X. Estimation of Snow Depth over the Qinghai-Tibetan Plateau Based on AMSR-E and MODIS Data. Remote Sens. 2018, 10, 1989. [Google Scholar] [CrossRef] [Green Version]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote sensing of snow—A review of available methods. Int. J. Remote Sens. 2011, 33, 4094–4134. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Reichle, R.H.; Arsenault, K.R.; Houser, P.R.; Kumar, S.; Verhoest, N.E.C.; Pauwels, V.R.N. Multiscale assimilation of Advanced Microwave Scanning Radiometer-EOS snow water equivalent and Moderate Resolution Imaging Spectroradiometer snow cover fraction observations in northern Colorado. Water Resour. Res. 2012, 48, 182–205. [Google Scholar] [CrossRef]
- Huang, X.; Deng, J.; Wang, W.; Feng, Q.; Liang, T. Impact of climate and elevation on snow cover using integrated remote sensing snow products in Tibetan Plateau. Remote Sens. Environ. 2017, 190, 274–288. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Gascoin, S.; Grizonnet, M.; Bouchet, M.; Salgues, G.; Hagolle, O. Theia Snow collection: High-resolution operational snow cover maps from Sentinel-2 and Landsat-8 data. Earth Syst. Sci. Data 2019, 11, 493–514. [Google Scholar] [CrossRef] [Green Version]
- Parajka, J.; Bezak, N.; Burkhart, J.; Hauksson, B.; Holko, L.; Hundecha, Y.; Jenicek, M.; Krajčí, P.; Mangini, W.; Molnar, P.; et al. Modis Snowline Elevation Changes During Snowmelt Runoff Events in Europe. J. Hydrol. Hydromech. 2019, 67, 101–109. [Google Scholar] [CrossRef] [Green Version]
- Parajka, J.; Blöschl, G. Validation of MODIS snow cover images over Austria. Hydrol. Earth Syst. Sci. 2006, 10, 679–689. [Google Scholar] [CrossRef] [Green Version]
- Bavera, D.; Bavay, M.; Jonas, T.; Lehning, M.; De Michele, C. A comparison between two statistical and a physically-based model in snow water equivalent mapping. Adv. Water Resour. 2014, 63, 167–178. [Google Scholar] [CrossRef]
- Finger, D. The value of satellite retrieved snow cover images to assess water resources and the theoretical hydropower potential in ungauged mountain catchments. Jokull 2018, 68, 47–66. [Google Scholar]
- Zheng, W.; Du, J.; Zhou, X.; Song, M.; Bian, G.; Xie, S.; Feng, X. Vertical distribution of snow cover and its relation to temperature over the Manasi River Basin of Tianshan Mountains, Northwest China. J. Geogr. Sci. 2017, 27, 403–419. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.; Du, J.; Zhou, X.; Zhang, X.; Feng, X.; Zheng, W.; Li, Z.; Xu, C.-Y. A progressive segmented optimization algorithm for calibrating time-variant parameters of the snowmelt runoff model (SRM). J. Hydrol. 2018, 566, 470–483. [Google Scholar] [CrossRef]
- Zhou, X.; Xie, H.; Hendrickx, J.M. Statistical evaluation of remotely sensed snow-cover products with constraints from streamflow and SNOTEL measurements. Remote Sens. Environ. 2005, 94, 214–231. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; DiGirolamo, N.E.; Bayr, K.J. MODIS snow-cover products. Remote Sens. Environ. 2002, 83, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Foster, J.L.; Hall, D.; Kelly, R.; Chiu, L. Seasonal snow extent and snow mass in South America using SMMR and SSM/I passive microwave data (1979–2006). Remote Sens. Environ. 2009, 113, 291–305. [Google Scholar] [CrossRef] [Green Version]
- Tedesco, M.; Reichle, R.; Low, A.; Markus, T.; Foster, J.L. Dynamic Approaches for Snow Depth Retrieval From Spaceborne Microwave Brightness Temperature. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1955–1967. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Huang, C. Assimilating passive microwave remote sensing data into a land surface model to improve the estimation of snow depth. Remote Sens. Environ. 2014, 143, 54–63. [Google Scholar] [CrossRef]
- Foster, J.L.; Hall, D.; Eylander, J.B.; Riggs, G.A.; Nghiem, S.V.; Tedesco, M.; Kim, E.; Montesano, P.M.; Kelly, R.E.J.; Casey, K.A.; et al. A blended global snow product using visible, passive microwave and scatterometer satellite data. Int. J. Remote Sens. 2011, 32, 1371–1395. [Google Scholar] [CrossRef]
- Liu, Y.; Peters-Lidard, C.D.; Kumar, S.; Foster, J.L.; Shaw, M.; Tian, Y.; Fall, G.M. Assimilating satellite-based snow depth and snow cover products for improving snow predictions in Alaska. Adv. Water Resour. 2013, 54, 208–227. [Google Scholar] [CrossRef]
- Clark, M.P.; Slater, A.G.; Barrett, A.P.; Hay, L.E.; McCabe, G.J.; Rajagopalan, B.; Leavesley, G.H. Assimilation of snow covered area information into hydrologic and land-surface models. Adv. Water Resour. 2006, 29, 1209–1221. [Google Scholar] [CrossRef]
- Toure, A.M.; Reichle, R.H.; Forman, B.A.; Getirana, A.; De Lannoy, G.J.M. Assimilation of MODIS Snow Cover Fraction Observations into the NASA Catchment Land Surface Model. Remote Sens. 2018, 10, 316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. Space Phys. 2003, 108, 1–16. [Google Scholar] [CrossRef]
- Helmert, J.; Şensoy Şorman, A.; Montero, R.A.; De Michele, C.; De Rosnay, P.; Dumont, M.; Finger, D.; Lange, M.; Picard, G.; Potopová, V.; et al. Review of Snow Data Assimilation Methods for Hydrological, Land Surface, Meteorological and Climate Models: Results from a COST HarmoSnow Survey. Geoscience 2018, 8, 489. [Google Scholar] [CrossRef] [Green Version]
- Clark, M.; Hendrikx, J.; Slater, A.G.; Kavetski, D.; Anderson, B.; Cullen, N.J.; Kerr, T.; Hreinsson, E.Ö.; Woods, R.A. Representing spatial variability of snow water equivalent in hydrologic and land-surface models: A review. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Mhawej, M.; Faour, G.; Fayad, A.; Shaban, A. Towards an enhanced method to map snow cover areas and derive snow-water equivalent in Lebanon. J. Hydrol. 2014, 513, 274–282. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, H.; Lu, N.; Yao, T.; Liang, T. Toward advanced daily cloud-free snow cover and snow water equivalent products from Terra–Aqua MODIS and Aqua AMSR-E measurements. J. Hydrol. 2010, 385, 23–35. [Google Scholar] [CrossRef]
- Tang, Z.G.; Li, H.Y.; Wang, J.; Liang, J.; Li, C.; Che, T.; Wang, X. Reconstruction of Snow Depth over the Tibetan Plateau Based on Mutisource Data. J. Geoinf. Sci. 2016, 18, 941–950. [Google Scholar]
- Wang, Y.; Huang, X.; Wang, J.; Zhou, M.; Liang, T. AMSR2 snow depth downscaling algorithm based on a multifactor approach over the Tibetan Plateau, China. Remote Sens. Environ. 2019, 231, 111268. [Google Scholar] [CrossRef]
- Bai, Z.; Dong, J.; Ma, Z. Climatic Characteristics of Qinghai-Xizang Plateau and Its Surrounding. Plateau Meteor. 2004, 6, 890–897. [Google Scholar]
- Yao, T.; Thompson, L.G.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Change 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Che, T.; Li, X. Retrieval of Snow Depth in China by Passive Microwave Remote Sensing Data and Its Accuracy Assessment. Remote Sens. Technol. Appl. 2004, 26, 444–449. [Google Scholar]
- Che, T.; Li, X.; Jin, R.; Armstrong, R.; Zhang, T. Snow depth derived from passive microwave remote-sensing data in China. Ann. Glaciol. 2008, 49, 145–154. [Google Scholar] [CrossRef] [Green Version]
- Che, T. Long-term series of daily snow depth dataset in China (1979–2019). Natl. Tibet. Plateau Data Cent. 2015. [Google Scholar] [CrossRef]
- Gao, J.; Williams, M.W.; Fu, X.; Wang, G.; Gong, T. Spatiotemporal distribution of snow in eastern Tibet and the response to climate change. Remote Sens. Environ. 2012, 121, 1–9. [Google Scholar] [CrossRef]
- Xu, C.; Chen, Y.; Hamid, Y.; Tashpolat, T.; Chen, Y.; Ge, H.; Li, W. Long-term change of seasonal snow cover and its effects on river runoff in the Tarim River basin, northwestern China. Hydrol. Process. 2009, 23, 2045–2055. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, S.; Wang, J.; Sun, P.; Liu, W.; Hartley, D.S. Effects of seasonal snow on the growing season of temperate vegetation in China. Glob. Change Biol. 2013, 19, 2182–2195. [Google Scholar] [CrossRef]
- Liang, T.; Zhang, X.; Xie, H.; Wu, C.; Feng, Q.; Huang, X.; Chen, Q. Toward improved daily snow cover mapping with advanced combination of MODIS and AMSR-E measurements. Remote Sens. Environ. 2008, 112, 3750–3761. [Google Scholar] [CrossRef]
- Qiu, Y.; Wang, X.; Han, L.; Chang, L.; Shi, L. Daily fractional snow cover dataset over High Asia. China Sci. Data 2017. [Google Scholar] [CrossRef]
- Li, C.; Sa, C.; Liu, G.; Wang, M.; Meng, H.; Bao, Y. Spatiotemporal Changes of Snow Cover and its Response to Climate Changes in the Mongolian Plateau from 2000 to 2017. Chin. J. Grassland. 2020, 2, 95–104. [Google Scholar] [CrossRef]
- La, B.Z.; Ci, Z. Snow Cover Variation and Meteorological Factor Research in Yarlung Zangbo Basin of Tibet from 2002 to 2015. Remote Sens. Technol. Appl. 2018, 33, 508–519. [Google Scholar]
- Zhou, M.; Wang, Y.; Liang, H.; Zeng, T.; Huang, W.; Wang, J.; Huang, X. Comparative analysis of the snow coverage products of Soumi-NPP and MODIS in the Qinghai-Tibet Plateau. J. Glaciol. Geocryol. 2019, 41, 36–44. [Google Scholar]
- Tang, Z.; Wang, J.; Wang, X.; Li, C.; Liang, J.; Peng, H. Extraction and Spatiotemporal Analysis of Snow Covered Days over Tibetan Plateau Based on MODIS Data. MT Res. 2017, 35, 412–419. [Google Scholar]
- Jiang, L.; Xu, W.; Zhang, J.; Wang, G.; Liu, X.; Zhao, S. A dataset for automatically measured snow depth on the Tibetan Plateau (2015—2016). China Sci. Data 2017. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. Available online: http://srtm.csi.cgiar.org/ (accessed on 18 December 2019).
- Shangguan, W.; Dai, Y. A China soil characteristics dataset. Natl. Tibet. Plateau Data Cent. 2010. [Google Scholar] [CrossRef]
- Shangguan, W.; Dai, Y.; Liu, B.; Ye, A.; Yuan, H. A soil particle-size distribution dataset for regional land and climate modelling in China. Geoderma 2012, 171, 85–91. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L.C. Fast exact leave-one-out cross-validation of sparse least-squares support vector machines. Neural Netw. 2004, 17, 1467–1475. [Google Scholar] [CrossRef] [PubMed]
- Liang, T.; Yang, S.; Feng, Q.; Liu, B.; Zhang, R.; Huang, X.; Xie, H. Multi-factor modeling of above-ground biomass in alpine grassland: A case study in the Three-River Headwaters Region, China. Remote Sens. Environ. 2016, 186, 164–172. [Google Scholar] [CrossRef]
- Durand, M.; Liu, D. The need for prior information in characterizing snow water equivalent from microwave brightness temperatures. Remote Sens. Environ. 2012, 126, 248–257. [Google Scholar] [CrossRef]
- Dong, J.; Walker, J.P.; Houser, P.R. Factors affecting remotely sensed snow water equivalent uncertainty. Remote Sens. Environ. 2005. [Google Scholar] [CrossRef]
- Li, D.; Durand, M.; Margulis, S.A. Potential for hydrologic characterization of deep mountain snowpack via passive microwave remote sensing in the Kern River basin, Sierra Nevada, USA. Remote Sens. Environ. 2012, 125, 34–48. [Google Scholar] [CrossRef]
- Li, H.; Wang, J. Key Research Topics and Their Advances on Modeling Snow Hydrological Processes. J. Glaciol. Geocryol. 2013, 35, 430–437. [Google Scholar]
- Mätzler, C.; Standley, A. Technical note: Relief effects for passive microwave remote sensing. Int. J. Remote Sens. 2000, 21, 2403–2412. [Google Scholar] [CrossRef]
- Smith, T.; Bookhagen, B. Assessing uncertainty and sensor biases in passive microwave data across High Mountain Asia. Remote Sens. Environ. 2016, 181, 174–185. [Google Scholar] [CrossRef]
- Durand, Y.; Giraud, G.; Laternser, M.; Etchevers, P.; Mérindol, L.; Lesaffre, B. Reanalysis of 47 Years of Climate in the French Alps (1958–2005): Climatology and Trends for Snow Cover. J. Appl. Meteorol. Clim. 2009, 48, 2487–2512. [Google Scholar] [CrossRef]
- Lehning, M.; Grünewald, T.; Schirmer, M. Mountain snow distribution governed by an altitudinal gradient and terrain roughness. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Grünewald, T.; Bühler, Y.; Lehning, M. Elevation dependency of mountain snow depth. Cryosphere 2014, 8, 2381–2394. [Google Scholar] [CrossRef] [Green Version]
- Sevruk, B. Regional Dependency of Precipitation-Altitude Relationship in The Swiss Alps. Clim. Change 1997, 36, 355–369. [Google Scholar] [CrossRef]
- Guo, Y.; Shi, J.; Du, J.; Fu, X. Evaluation of terrain effect on microwave radiometer measurement and its correction. Int. J. Remote Sens. 2011, 32, 8899–8913. [Google Scholar] [CrossRef]
- Tian, L.; Li, W.; Zhang, Y.; Tian, L.J.; Zhu, Q.; Peng, C.H.; Chen, H. The analysis of snow information from 1979 to 2007 in Qinghai-Tibetan Plateau. Acta Ecol. Sin. 2014, 34, 5974–5983. [Google Scholar]
- Xiaoge, X.; Zhou, T.; Yu, R. Increased Tibetan Plateau snow depth: An indicator of the connection between enhanced winter NAO and late-spring tropospheric cooling over East Asia. Adv. Atmos. Sci. 2010, 27, 788–794. [Google Scholar] [CrossRef]
- Ke, C.-Q.; Yu, T.; Yu, K.; Tang, G.-D.; King, L. Snowfall trends and variability in Qinghai, China. Theor. Appl. Clim. 2009, 98, 251–258. [Google Scholar] [CrossRef]
- Bai, S.; Wu, Q.; Shi, J.; Gu, H. Relationship between the spatial and temporal distribution of snow depth and the terrain over the Tibetan Plateau. Remote Sens. Land Resour. 2015, 27, 171–178. [Google Scholar] [CrossRef]
- Dadic, R.; Mott, R.; Lehning, M.; Burlando, P. Wind influence on snow depth distribution and accumulation over glaciers. J. Geophys. Res. Space Phys. 2010, 115, 115. [Google Scholar] [CrossRef] [Green Version]
- Shao, D.; Li, H.; Wang, J.; Pan, X.; Hao, X. Distinguishing the Role of Wind in Snow Distribution by Utilizing Remote Sensing and Modeling Data: Case Study in the Northeastern Tibetan Plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4445–4456. [Google Scholar] [CrossRef]





| Figure | Independent Variable | Model Formula | R |
|---|---|---|---|
| Location | Latitude | y = −0.643 x + 22.515 | 0.31 * |
| Longitude | y = −0.604 x + 61.030 | 0.50 * | |
| Topographical features | Elevation | y = 0.002 x − 4.388 | 0.26 * |
| Slope | y = 0.716 x − 1.232 | 0.42 * | |
| Aspect | y = 0.003 x + 0.275 | 0.07 | |
| Surface roughness | y = 628.822 x − 629.301 | 0.61 * | |
| Surface relief | y = 0.04 x − 0.254 | 0.32 * | |
| Land use and soil types | LUCC | y= −0.871 x + 2636 | 0.11 * |
| Percentage of clay | y = −0.093 x + 2.152 | 0.12 * | |
| Proportion of sand | y = 0.032 x − 0.359 | 0.16 * | |
| Snow | SCD | y = 0.463 x − 1.395 | 0.69 * |
| Form | Model Formula | R2 | RMSE (cm) |
|---|---|---|---|
| Linear | y = 11.61 X1 −12.74 X2 − 5.53 X3 + 0.93 X4 + 185.28 X5 + 5.51 X6 + 89.46 X7 + 3.11 | 0.63 * | 2.28 |
| Logarithmic | y = 0.09 Ln (X1) − 339.49 Ln (X2) − 2.48 Ln (X3) −10.02 Ln (X4) + 169.72 Ln (X5) + 0.61 Ln (X6) + 1.86 ln (X7) + 72.19 | 0.59 * | 6.89 |
| Power | y = 219.77 × X10.02 × X2−20.08 × X3−0.19 × X4−0.93 × X510.05 × X6−9.1×10−3 × X70.19 | 0.63 * | 6.94 |
| Inverse | y = 2.17 × 10−11/X1 − 4.92 × 10−3/X2 + 3/X3 + 3.68/X4 − 4.24 × 10−6/X5 – 3 × 10−3/X6 −0.02/X7 − 4.76 | 0.58 * | 6.84 |
| Sample Capacity | PMSD (cm) | SDC (cm) | FSD (cm) | LMSDR (cm) | ||
|---|---|---|---|---|---|---|
| LUCC | Cultivated land | 18,787 | 4.30 | 1.64 | 2.41 | 1.58 |
| Forest | 25,805 | 4.32 | 1.86 | 5.08 | 2.26 | |
| Grassland | 73,938 | 3.99 | 2.34 | 8.60 | 2.28 | |
| Construction land | 24,725 | 3.07 | 2.25 | 5.97 | 1.86 | |
| Bare land | 5019 | 2.79 | 2.78 | 2.96 | 1.90 | |
| Altitude (m) | 1000–2000 | 7532 | 1.48 | 1.16 | 3.11 | 1.13 |
| 2000–2500 | 14,210 | 2.12 | 0.87 | 2.57 | 1.37 | |
| 2500–3000 | 33,704 | 3.14 | 1.15 | 2.26 | 1.32 | |
| 3000–3500 | 38,263 | 3.43 | 2.35 | 5.78 | 2.07 | |
| 3500–4000 | 24,270 | 4.51 | 2.28 | 9.24 | 2.28 | |
| 4000+ | 30,295 | 3.41 | 3.26 | 5.72 | 3.15 | |
| Slope (°) | 5° | 94,178 | 2.99 | 2.30 | 7.07 | 1.80 |
| 5°–15° | 36,254 | 3.79 | 1.95 | 6.94 | 1.89 | |
| 15° | 17,842 | 5.16 | 4.58 | 4.78 | 4.54 | |
| SCD (days) | 0–30 | 99,709 | 2.86 | 1.48 | 3.50 | 1.18 |
| 30–60 | 38,796 | 3.64 | 1.65 | 4.32 | 1.57 | |
| 60 | 9769 | 3.88 | 2.71 | 8.38 | 2.50 |
| Station ID | Name | Latitude, Longitude (°) | Elevation (m) | Annual Snow Depth (cm) | PMSD (%) | SDC (%) | FSD (%) | LMSDR (%) |
|---|---|---|---|---|---|---|---|---|
| 52,869 | Huang Zhong | 36.50, 101.59 | 2629 | 2.43 | 86 | 88 | 88 | 88 |
| 52,908 | Wu Dao Liang | 35.22, 93.09 | 4615 | 2.29 | 84 | 88 | 87 | 87 |
| 55,228 | Shi Quan He | 32.50, 80.08 | 4311 | 3.49 | 65 | 95 | 95 | 95 |
| 55,655 | Nyalam | 28.18, 85.96 | 4456 | 19.74 | 36 | 70 | 69 | 69 |
| 56,128 | Rioche | 31.22, 96.60 | 3802 | 2.22 | 36 | 93 | 93 | 93 |
| 56,173 | Hong Yuan | 32.80, 102.55 | 3491 | 4.00 | 61 | 80 | 78 | 78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, P.; Zhang, T.; Zhou, X.; Yi, G.; Li, J.; Wang, N.; Wen, B. Reconstruction of Snow Depth Data at Moderate Spatial Resolution (1 km) from Remotely Sensed Snow Data and Multiple Optimized Environmental Factors: A Case Study over the Qinghai-Tibetan Plateau. Remote Sens. 2021, 13, 657. https://doi.org/10.3390/rs13040657
Wei P, Zhang T, Zhou X, Yi G, Li J, Wang N, Wen B. Reconstruction of Snow Depth Data at Moderate Spatial Resolution (1 km) from Remotely Sensed Snow Data and Multiple Optimized Environmental Factors: A Case Study over the Qinghai-Tibetan Plateau. Remote Sensing. 2021; 13(4):657. https://doi.org/10.3390/rs13040657
Chicago/Turabian StyleWei, Pengtao, Tingbin Zhang, Xiaobing Zhou, Guihua Yi, Jingji Li, Na Wang, and Bo Wen. 2021. "Reconstruction of Snow Depth Data at Moderate Spatial Resolution (1 km) from Remotely Sensed Snow Data and Multiple Optimized Environmental Factors: A Case Study over the Qinghai-Tibetan Plateau" Remote Sensing 13, no. 4: 657. https://doi.org/10.3390/rs13040657
APA StyleWei, P., Zhang, T., Zhou, X., Yi, G., Li, J., Wang, N., & Wen, B. (2021). Reconstruction of Snow Depth Data at Moderate Spatial Resolution (1 km) from Remotely Sensed Snow Data and Multiple Optimized Environmental Factors: A Case Study over the Qinghai-Tibetan Plateau. Remote Sensing, 13(4), 657. https://doi.org/10.3390/rs13040657