An Effective Method for Generating Spatiotemporally Continuous 30 m Vegetation Products
Abstract
:1. Introduction
2. Methods
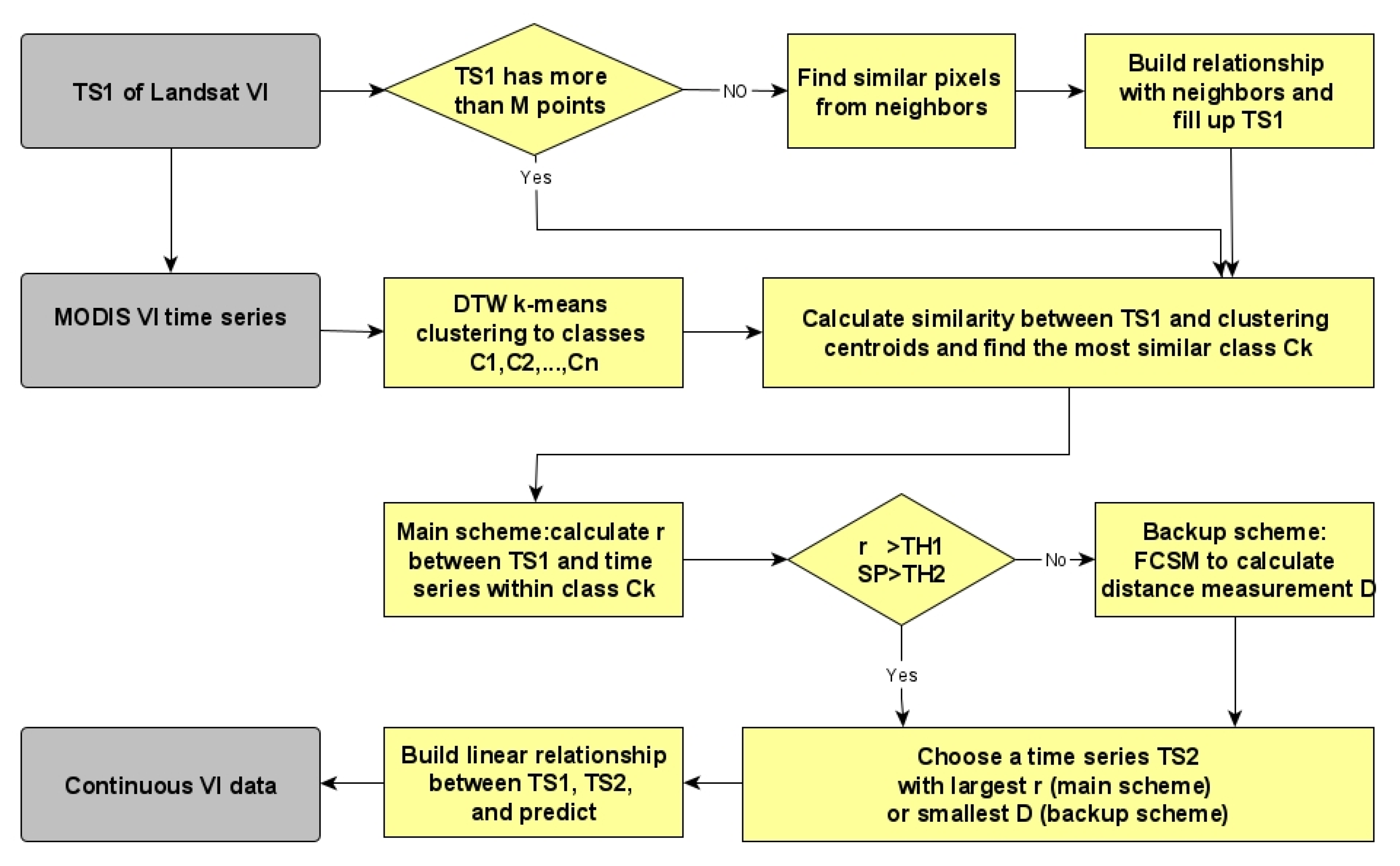
2.1. SIM Method
2.1.1. Selection of Candidate MODIS Pixels
- Randomly select k original clustering centroids.
- For each time series, calculate the DTW distance and cluster to the closest centroid.
- Average all the time series for each clustering class and generate new k centroids based on the averages.
- Repeat steps 2 and 3 until steady centroids are derived.
2.1.2. Correlation Measurement
2.1.3. Fourier Component-Based Shape Similarity Measure
2.2. STF Methods
2.3. Quantitative Evaluation
3. Data and Study Areas
3.1. Study Areas
3.2. Data and Preprocessing
4. Results
4.1. NDVI and LAI Results in the CSD Area
- NDVI results
- LAI results
- Comparison with STF methods
4.2. NDVI Results in the NRM Area
- NDVI Results
- Comparison with STF methods
4.3. LAI Results in the CCN Area
- LAI Results
- Comparison with STF methods
5. Discussions
5.1. Temporal Profile of VI
5.2. Accuracy of Coarse-Resolution Data
5.3. Potentials and Limitations of SIM
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liang, S. Quantitative Remote Sensing of Land Surfaces; John Wiley & Sons, Inc.: New York, NY, USA, 2003; pp. 525–527. [Google Scholar]
- Yang, Y.; Erskine, P.D.; Lechner, A.M.; Mulligan, D.; Zhang, S.; Wang, Z. Detecting the dynamics of vegetation disturbance and recovery in surface mining area via Landsat imagery and LandTrendr algorithm. J. Clean. Prod. 2018, 178, 353–362. [Google Scholar] [CrossRef]
- Zhang, H.K.K.; Huang, B.; Zhang, M.; Cao, K.; Yu, L. A generalization of spatial and temporal fusion methods for remotely sensed surface parameters. Int. J. Remote Sens. 2015, 36, 4411–4445. [Google Scholar] [CrossRef]
- Senf, C.; Leitão, P.J.; Pflugmacher, D.; van der Linden, S.; Hostert, P. Mapping land cover in complex Mediterranean landscapes using Landsat: Improved classification accuracies from integrating multi-seasonal and synthetic imagery. Remote Sens. Environ. 2015, 156, 527–536. [Google Scholar] [CrossRef]
- Johnson, B.A.; Iizuka, K. Integrating OpenStreetMap crowdsourced data and Landsat time-series imagery for rapid land use/land cover (LULC) mapping: Case study of the Laguna de Bay area of the Philippines. Appl. Geogr. 2016, 67, 140–149. [Google Scholar]
- Wulder, M.A.; White, J.C.; Goward, S.N.; Masek, J.G.; Irons, J.R.; Herold, M.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Landsat continuity: Issues and opportunities for land cover monitoring. Remote Sens. Environ. 2008, 112, 955–969. [Google Scholar] [CrossRef]
- Boori, M.S.; Vozenlek, V.; Balzter, H.; Choudhary, K.J.J.o.G.; Sensing, R. Land Surface Temperature with Land Cover Classes in ASTER and Landsat Data. 2015, 04, 1–4. J. Remote Sens. GIS 2015, 4, 1–4. [Google Scholar]
- Xia, H.; Chen, Y.; Li, Y.; Quan, J. Combining kernel-driven and fusion-based methods to generate daily high-spatial-resolution land surface temperatures. Remote Sens. Environ. 2019, 224, 259–274. [Google Scholar] [CrossRef]
- Manjula, R.; Estoque, R.C.; Yuji, M.J.I.I.J.o.G.-I. An Urban Heat Island Study of the Colombo Metropolitan Area, Sri Lanka, Based on Landsat Data (1997–2017). ISPRS Int. J. Geo-Inf. 2017, 6, 17. [Google Scholar]
- Shen, H.; Huang, L.; Zhang, L.; Wu, P.; Zeng, C. Long-term and fine-scale satellite monitoring of the urban heat island effect by the fusion of multi-temporal and multi-sensor remote sensed data: A 26-year case study of the city of Wuhan in China. Remote Sens. Environ. 2016, 172, 109–125. [Google Scholar] [CrossRef]
- Sholihah, R.I.; Trisasongko, B.H.; Shiddiq, D.; Iman, L.O.S.; Kusdaryanto, S.; Manijo;Panuju, D.R. Identification of Agricultural Drought Extent Based on Vegetation Health Indices of Landsat Data: Case of Subang and Karawang, Indonesia. Procedia Environ. Sci. 2016, 33, 14–20. [Google Scholar]
- Reschke, J.; Hüttich, C.; Geoinformation. Continuous field mapping of Mediterranean wetlands using sub-pixel spectral signatures and multi-temporal Landsat data. Int. J. Appl. Earth Obs. 2014, 28, 220–229. [Google Scholar]
- Veettil;Bijeesh, K. Glacier mapping in the Cordillera Blanca, Peru, tropical Andes, using Sentinel-2 and Landsat data. Singapore J. Trop. Geogr. 2018, 39, 351–363. [Google Scholar] [CrossRef]
- Leckie, D.G. Advances in remote sensing technologies for forest surveys and management. Canadian J. For. Res. 1990, 20, 464–483. [Google Scholar] [CrossRef]
- Wu, M.Q.; Zhang, X.Y.; Huang, W.J.; Niu, Z.; Wang, C.Y.; Li, W.; Hao, P.Y. Reconstruction of Daily 30 m Data from HJ CCD, GF-1 WFV, Landsat, and MODIS Data for Crop Monitoring. Remote Sens. 2015, 7, 16293–16314. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Anderson, M.C.; Zhang, X.; Yang, Z.; Alfieri, J.G.; Kustas, W.P.; Mueller, R.; Johnson, D.M.; Prueger, J.H. Toward mapping crop progress at field scales through fusion of Landsat and MODIS imagery. Remote Sens. Environ. 2017, 188, 9–25. [Google Scholar] [CrossRef] [Green Version]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; Mcdermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Gärtner, P.; Förster, M.; Kleinschmit, B. The benefit of synthetically generated RapidEye and Landsat 8 data fusion time series for riparian forest disturbance monitoring. Remote Sens. Environ. 2016, 177, 237–247. [Google Scholar] [CrossRef] [Green Version]
- Lu, M.; Chen, B.; Liao, X.; Yue, T.; Yue, H.; Ren, S.; Li, X.; Zhen, N.; Xu, B. Forest Types Classification Based on Multi-Source Data Fusion. 2017, 9, 1153. Remote Sens. 2017, 9, 1153. [Google Scholar] [CrossRef] [Green Version]
- McCabe, M.F.; Rodell, M.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.; Franz, T.E. The future of Earth observation in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3879. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Huang, B.; Xu, B. Comparison of Spatiotemporal Fusion Models: A Review. Remote Sens. 2015, 7, 1798–1835. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Knight, J.F.; Ediriwickrema, J.; Lyon, J.G.; Worthy, L.D. Land-cover change detection using multi-temporal MODIS NDVI data. Remote Sens. Environ. 2006, 105, 142–154. [Google Scholar] [CrossRef]
- Liang, S.; Wang, J. Advanced Remote Sensing: Terrestrial Information Extraction and Applications; Academic Press/Elsevier: Cambridge, UK, 2019. [Google Scholar]
- Knyazikhin, Y.; Martonchik, J.; Myneni, R.B.; Diner, D.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Z.; Liang, S.; Wang, J.; Xiang, Y.; Zhao, X.; Song, J. Long-time-series global land surface satellite leaf area index product derived from MODIS and AVHRR surface reflectance. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5301–5318. [Google Scholar] [CrossRef]
- Liang, S.; Cheng, J.; Jia, K.; Jiang, B.; Liu, Q.; Xiao, Z.; Yao, Y.; Yuan, W.; Zhang, X.; Zhao, X. The Global LAnd Surface Satellite (GLASS) product suite. Bull. Am. Meteorol. Soc. 2020, 1–37. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION: Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Qu, Y.; Zhang, Y.; Xue, H. Retrieval of 30-m-resolution leaf area index from China HJ-1 CCD data and MODIS products through a dynamic Bayesian network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 222–228. [Google Scholar]
- Ghassemian, H. A review of remote sensing image fusion methods. Inf. Fus. 2016, 32, 75–89. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.; Anders, K.; Gloaguen, R.; et al. Multisource and Multitemporal Data Fusion in Remote Sensing: A Comprehensive Review of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. Geosci. Remote Sens. IEEE Trans. 2006, 44, 2207–2218. [Google Scholar]
- Zhu, X.L.; Jin, C.; Feng, G.; Chen, X.H.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Lhermitte, S.; Verbesselt, J.; Verstraeten, W.W.; Coppin, P. A comparison of time series similarity measures for classification and change detection of ecosystem dynamics. Remote Sens. Environ. 2011, 115, 3129–3152. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, P.; Huo, L.; Zhou, Z.J.I.J.o.W.; Processing, I. MODIS NDVI time series clustering under dynamic time warping. Int. J. Wavel. Multiresolut. Inf. Process. 2014, 12, 1461011. [Google Scholar] [CrossRef]
- Zhang, Y.; Hepner, G.F. The Dynamic-Time-Warping-based k-means++ clustering and its application in phenoregion delineation. Int. J. Remote Sens. 2017, 38, 1720–1736. [Google Scholar] [CrossRef]
- Wang, B.; Chen, Z.; Zhu, A.; Hao, Y.; Xu, C. Multi-level classification based on trajectory features of time series for monitoring impervious surface expansions. Remote Sens. 2019, 11, 640. [Google Scholar] [CrossRef] [Green Version]
- Brown, J.C.; Jepson, W.E.; Kastens, J.H.; Wardlow, B.D.; Lomas, J.M.; Price, K. Multitemporal, moderate-spatial-resolution remote sensing of modern agricultural production and land modification in the Brazilian Amazon. GISci. Remote Sens. 2007, 44, 117–148. [Google Scholar]
- Wang, L.; Chen, J.; Gong, P.; Shimazaki, H.; Tamura, M. Land cover change detection with a cross-correlogram spectral matching algorithm. Int. J. Remote Sens. 2009, 30, 3259–3273. [Google Scholar] [CrossRef]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Evans, J.; Geerken, R. Classifying rangeland vegetation type and coverage using a Fourier component based similarity measure. Remote Sens. Environ. 2006, 105, 1–8. [Google Scholar] [CrossRef]
- Zhu, X.L.; Helmer, E.H.; Gao, F.; Liu, D.S.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, J.; Chen, X.; Zhu, X.; Qiu, Y.; Song, H.; Rao, Y.; Zhang, C.; Cao, X.; Cui, X. Sensitivity of six typical spatiotemporal fusion methods to different influential factors: A comparative study for a normalized difference vegetation index time series reconstruction. Remote Sens. Environ. 2021, 252, 112130. [Google Scholar] [CrossRef]
- Gevaert, C.M.; García-Haro, F.J. A comparison of STARFM and an unmixing-based algorithm for Landsat and MODIS data fusion. Remote Sens. Environ. 2015, 156, 34–44. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar]
- Jin, H.; Li, A.; Xu, W.; Xiao, Z.; Jiang, J.; Xue, H. Evaluation of topographic effects on multiscale leaf area index estimation using remotely sensed observations from multiple sensors. ISPRS J. Photogramm. Remote Sens. 2019, 154, 176–188. [Google Scholar] [CrossRef]
- Jin, H.; Li, A.; Yin, G.; Xiao, Z.; Bian, J.; Nan, X.; Jing, J. A Multiscale Assimilation Approach to Improve Fine-Resolution Leaf Area Index Dynamics. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8153–8168. [Google Scholar] [CrossRef]
- Li, J.; Xiao, Z. Evaluation of the version 5.0 global land surface satellite (GLASS) leaf area index product derived from MODIS data. Int. J. Remote Sens. 2020, 41, 9140–9160. [Google Scholar]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product From Time-Series MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.J.I.J.o.D.E. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int. J. Dig. Earth 2013, 6, 5–33. [Google Scholar]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef] [Green Version]
- Morisette, J.T.; Privette, J.L.; Justice, C.O. A framework for the validation of MODIS land products. Remote Sens. Environ. 2002, 83, 77–96. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]














| DOY | 143 | 175 | 183 | 191 | 199 | 207 | 215 | 223 | 231 | 239 | 255 | 263 | 271 |
| SSIM(%) | 93.4 | 99.0 | 99.2 | 98.1 | 98.5 | 98.7 | 99.5 | 99.0 | 99.4 | 99.4 | 98.4 | 98.7 | 97.1 |
| DOY | 143 | 175 | 183 | 191 | 199 | 207 | 215 | 223 | 231 | 239 | 255 | 263 | 271 |
| MAE | 0.07 | 0.08 | 0.06 | 0.06 | 0.06 | 0.05 | 0.05 | 0.05 | 0.04 | 0.04 | 0.04 | 0.05 | 0.07 |
| RMSE | 0.09 | 0.10 | 0.07 | 0.08 | 0.08 | 0.07 | 0.06 | 0.07 | 0.05 | 0.06 | 0.06 | 0.06 | 0.09 |
| R | 0.54 | 0.90 | 0.97 | 0.91 | 0.95 | 0.97 | 0.98 | 0.97 | 0.98 | 0.98 | 0.95 | 0.97 | 0.90 |
| DOY | 143 | 175 | 191 | 207 | 223 | 239 | 255 | 271 |
| SSIM(%) | 79.5 | 99.2 | 98.8 | 99.5 | 99.7 | 99.6 | 99.2 | 95.9 |
| DOY | 143 | 175 | 191 | 207 | 223 | 239 | 255 | 271 |
| MAE | 0.73 | 0.87 | 0.81 | 1.01 | 0.77 | 0.73 | 0.42 | 0.50 |
| RMSE | 1.02 | 1.15 | 1.06 | 1.44 | 1.06 | 1.02 | 0.67 | 0.69 |
| r | 0.78 | 0.71 | 0.54 | 0.84 | 0.812 | 0.78 | 0.82 | 0.68 |
| NDVI | LAI | |||||
|---|---|---|---|---|---|---|
| Methods | MAE | RMSE | r | MAE | RMSE | r |
| SIM | 0.06 | 0.08 | 0.91 | 0.71 | 1.00 | 0.64 |
| STARFM | 0.11 | 0.145 | 0.67 | 0.80 | 1.00 | 0.64 |
| ESTARFM | 0.12 | 0.17 | 0.60 | 0.88 | 1.17 | 0.56 |
| FSDAF | 0.10 | 0.13 | 0.72 | 0.90 | 1.15 | 0.59 |
| DOY | 43 | 59 | 75 | 83 | 91 | 107 | 115 | 123 | 131 |
| SSIM(%) | 86.0 | nan | 94.01 | 97.2 | 98.9 | 98.8 | 96.9 | 97.5 | 96.2 |
| DOY | 139 | 171 | 179 | 187 | 195 | 203 | 211 | 219 | 227 |
| SSIM(%) | 94.6 | 91.6 | 97.8 | 97.9 | 98.0 | 98.4 | 98.9 | 98.7 | 98.8 |
| DOY | 235 | 243 | 251 | 259 | 275 | 283 | 307 | 315 | 323 |
| SSIM(%) | 97.4 | 98.6 | 97.4 | 93.1 | 94.0 | 94.7 | 98.8 | 84.2 | 97.1 |
| DOY | 83 | 91 | 107 | 123 | 131 | 139 | 171 | 179 |
| MAE | 0.17 | 0.09 | 0.09 | 0.12 | 0.09 | 0.10 | 0.05 | 0.04 |
| RMSE | 0.24 | 0.15 | 0.12 | 0.18 | 0.12 | 0.15 | 0.06 | 0.05 |
| r | 0.68 | 0.73 | 0.83 | 0.74 | 0.78 | 0.62 | 0.93 | 0.98 |
| DOY | 187 | 195 | 203 | 211 | 219 | 227 | 235 | 243 |
| MAE | 0.06 | 0.04 | 0.03 | 0.02 | 0.04 | 0.02 | 0.06 | 0.05 |
| RMSE | 0.05 | 0.05 | 0.04 | 0.03 | 0.06 | 0.03 | 0.07 | 0.06 |
| r | 0.97 | 0.98 | 0.97 | 0.98 | 0.97 | 0.97 | 0.97 | 0.97 |
| DOY | 251 | 259 | 275 | 283 | 307 | 323 | ||
| MAE | 0.04 | 0.04 | 0.05 | 0.05 | 0.15 | 0.07 | ||
| RMSE | 0.04 | 0.05 | 0.06 | 0.056 | 0.21 | 0.09 | ||
| r | 0.96 | 0.97 | 0.96 | 0.95 | 0.62 | 0.789 |
| DOY 171 | DOY 307 | |||||
|---|---|---|---|---|---|---|
| Methods | MAE | RMSE | r | MAE | RMSE | r |
| SIM | 0.09 | 0.12 | 0.83 | 0.21 | 0.27 | 0.62 |
| STARFM | 0.11 | 0.13 | 0.83 | 0.16 | 0.21 | 0.78 |
| ESTARFM | / | / | / | 0.15 | 0.21 | 0.79 |
| FSDAF | 0.11 | 0.14 | 0.82 | 0.17 | 0.22 | 0.79 |
| DOY | 40 | 72 | 104 | 120 | 191 | 200 | 207 | 239 | 248 | 287 | 351 | 360 |
| SSIM(%) | 94.2 | 90.5 | 96.0 | 95.9 | 92.5 | 90.2 | 92.5 | 84.3 | 89.9 | 94.3 | 96.7 | 96.5 |
| DOY | 40 | 72 | 104 | 120 | 191 | 200 | 207 | 239 | 248 | 287 | 351 | 361 |
| MAE | 0.58 | 0.47 | 0.43 | 0.57 | 0.44 | 0.46 | 0.48 | 0.69 | 0.46 | 0.49 | 0.26 | 0.25 |
| RMSE | 0.78 | 0.59 | 0.55 | 0.72 | 0.59 | 0.63 | 0.53 | 1.14 | 0.62 | 0.63 | 0.34 | 0.34 |
| r | 0.59 | 0.77 | 0.79 | 0.81 | 0.76 | 0.70 | 0.67 | 0.63 | 0.73 | 0.70 | 0.90 | 0.89 |
| DOY 104 | DOY 200 | |||||
|---|---|---|---|---|---|---|
| Methods | MAE | RMSE | r | MAE | RMSE | r |
| SIM | 0.43 | 0.55 | 0.79 | 0.46 | 0.63 | 0.70 |
| STARFM | 1.06 | 1.21 | 0.40 | 0.87 | 1.13 | 0.41 |
| ESTARFM | 0.48 | 0.65 | 0.71 | 0.78 | 0.99 | 0.49 |
| FSDAF | 0.80 | 0.96 | 0.81 | 0.74 | 0.97 | 0.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Liang, S.; Jin, H. An Effective Method for Generating Spatiotemporally Continuous 30 m Vegetation Products. Remote Sens. 2021, 13, 719. https://doi.org/10.3390/rs13040719
Li X, Liang S, Jin H. An Effective Method for Generating Spatiotemporally Continuous 30 m Vegetation Products. Remote Sensing. 2021; 13(4):719. https://doi.org/10.3390/rs13040719
Chicago/Turabian StyleLi, Xiuxia, Shunlin Liang, and Huaan Jin. 2021. "An Effective Method for Generating Spatiotemporally Continuous 30 m Vegetation Products" Remote Sensing 13, no. 4: 719. https://doi.org/10.3390/rs13040719
APA StyleLi, X., Liang, S., & Jin, H. (2021). An Effective Method for Generating Spatiotemporally Continuous 30 m Vegetation Products. Remote Sensing, 13(4), 719. https://doi.org/10.3390/rs13040719








