Phase Center Corrections for BDS IGSO and MEO Satellites in IGb14 and IGSR3 Frame
Abstract
:1. Introduction
2. Basic Information
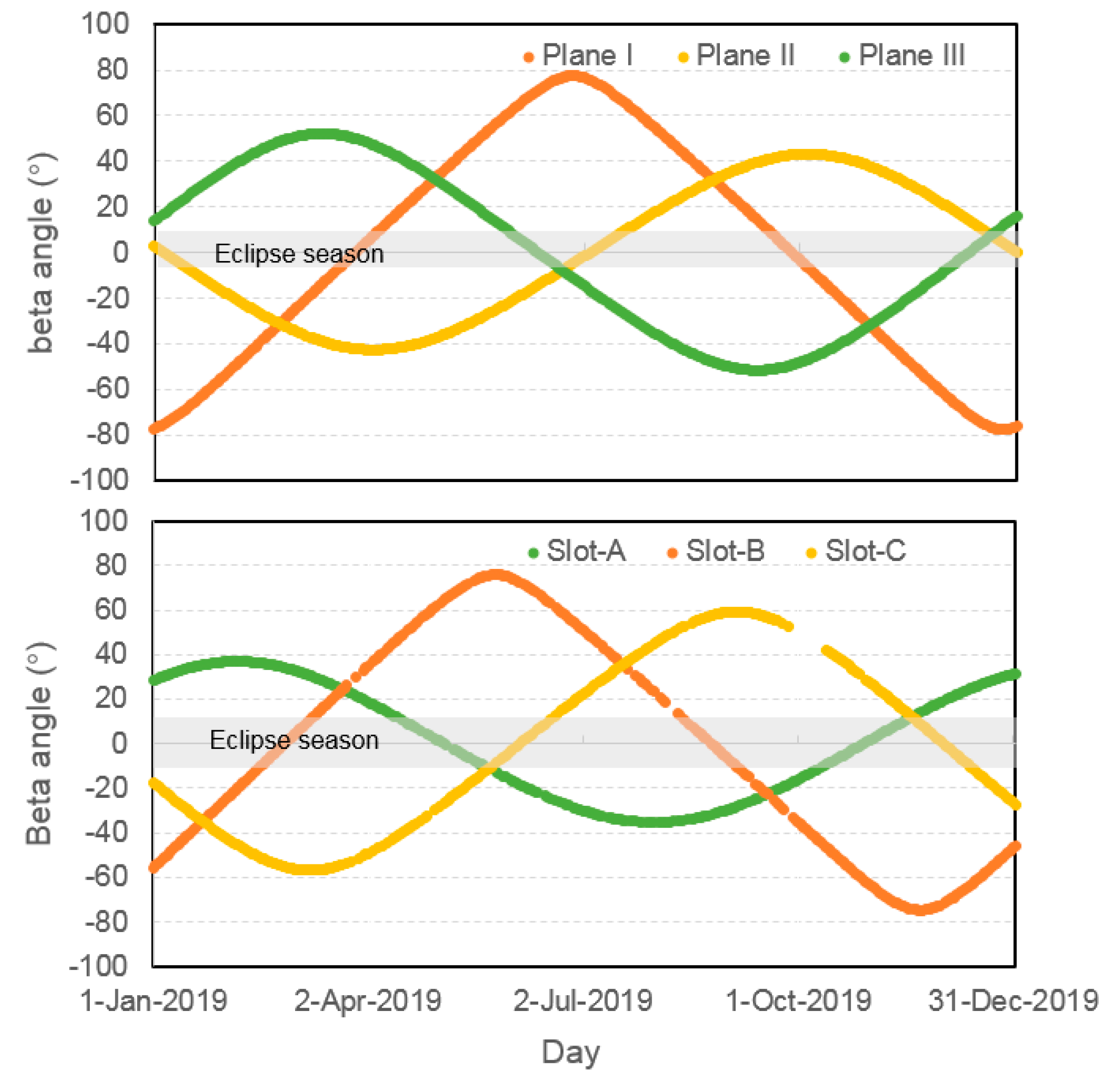
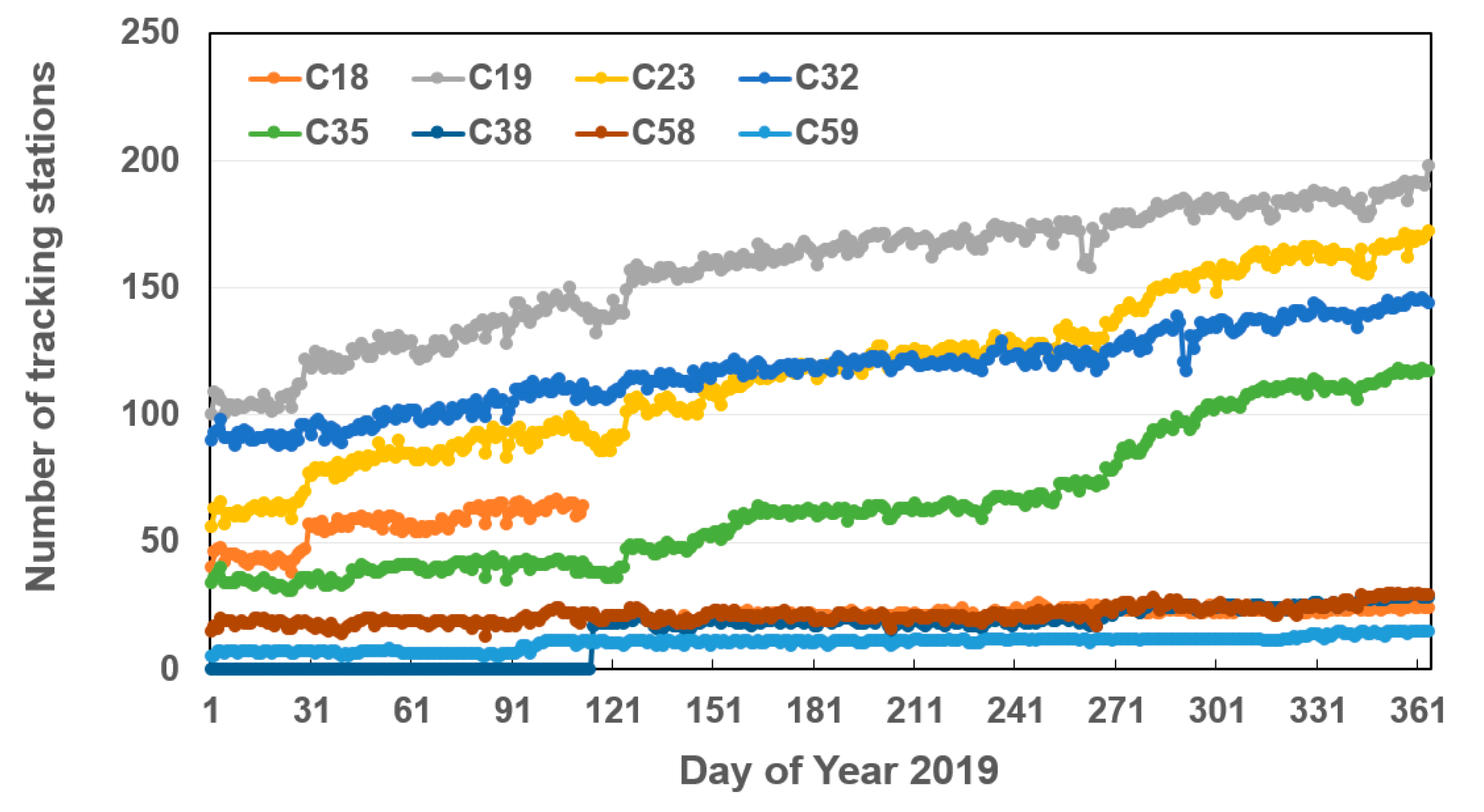
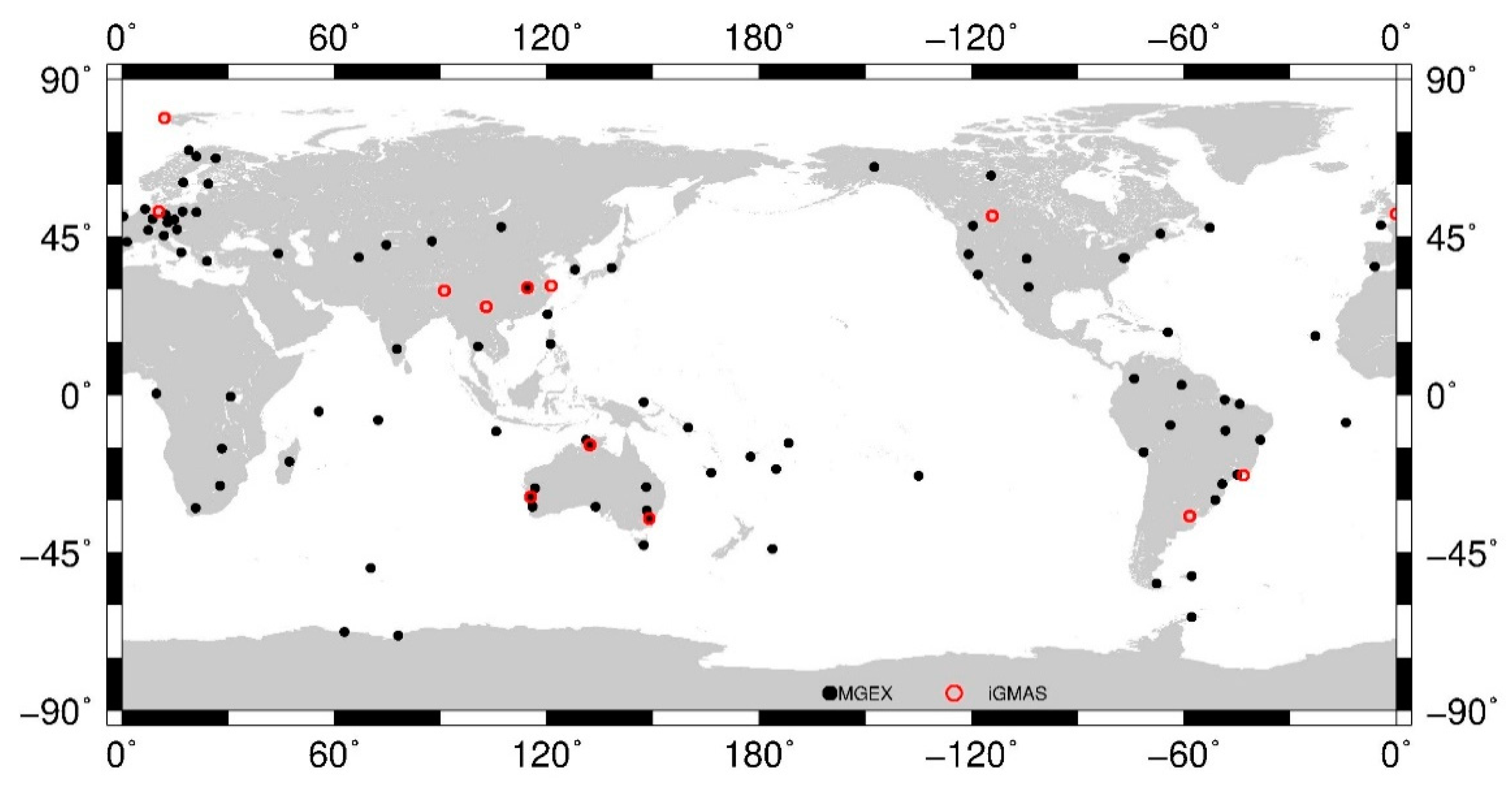
2.1. Status of BDS Satellites and Tracking Network
2.2. Satellite and Receiver Antenna Phase Center Corrections
3. Data Processing
4. Results and Validation
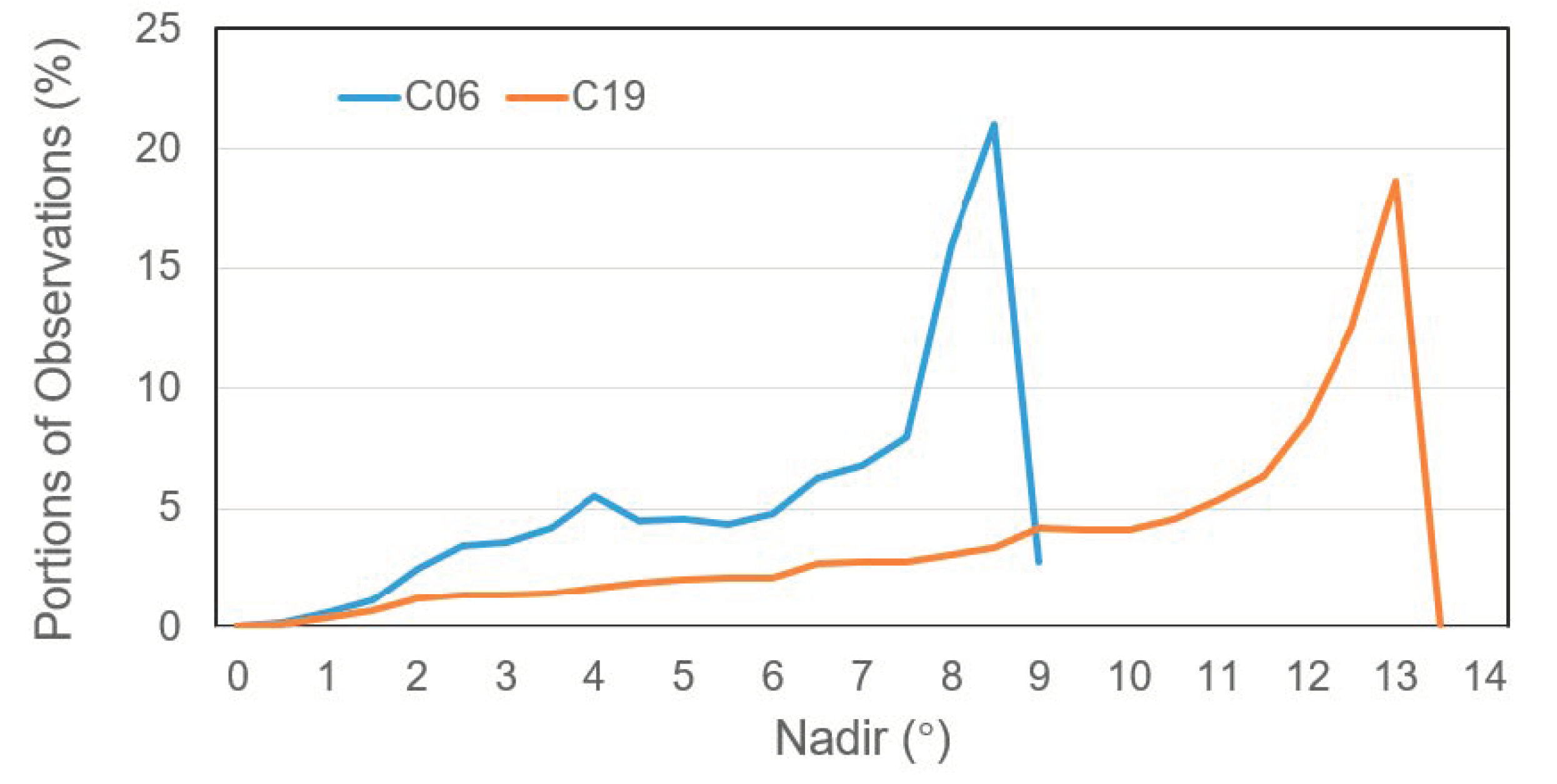
4.1. Distribution of Observations
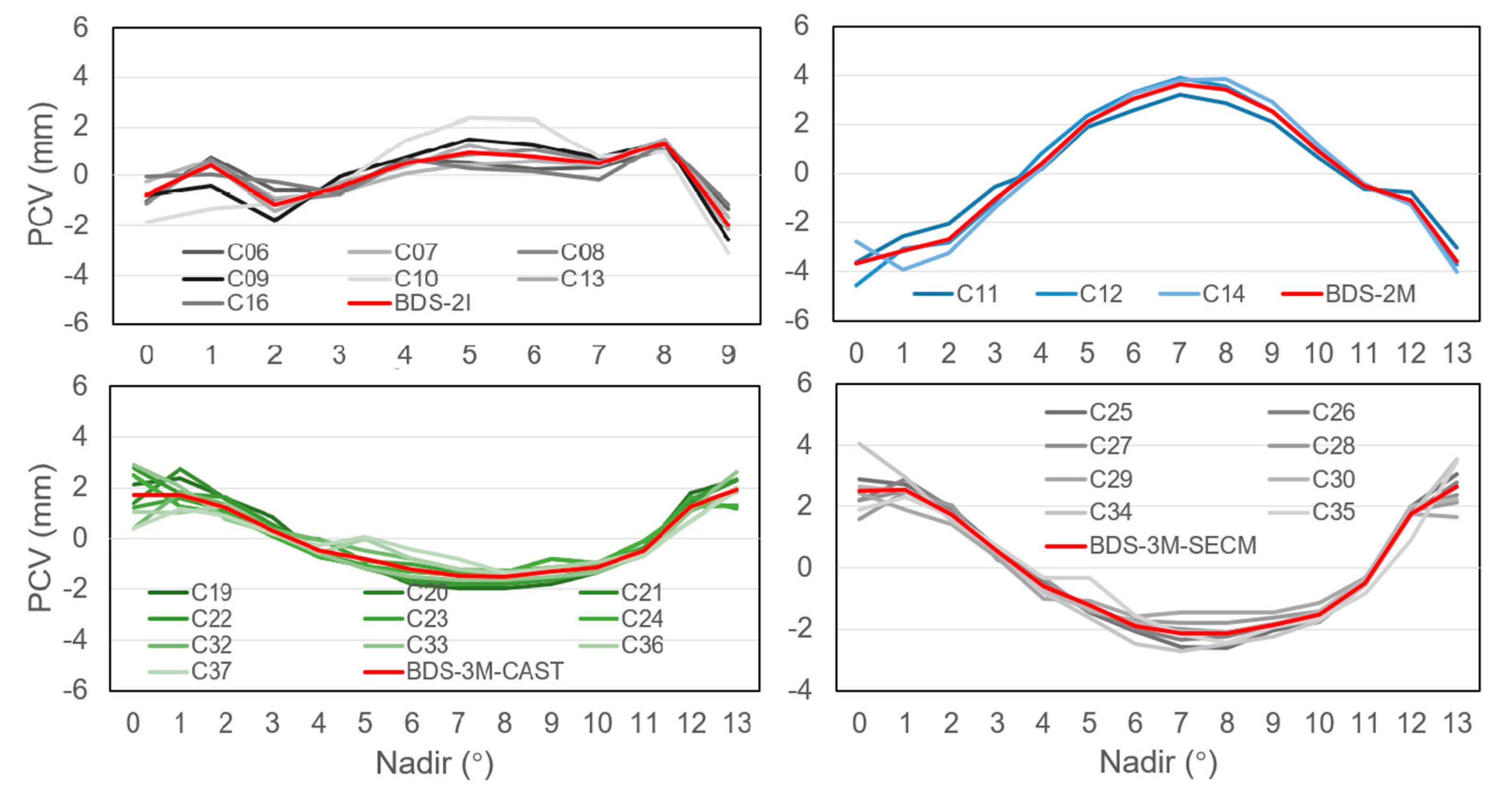
4.2. Phase Center Variations
4.3. Estimated Phase Center Offsets
4.4. Validation
4.4.1. Orbit Consistency
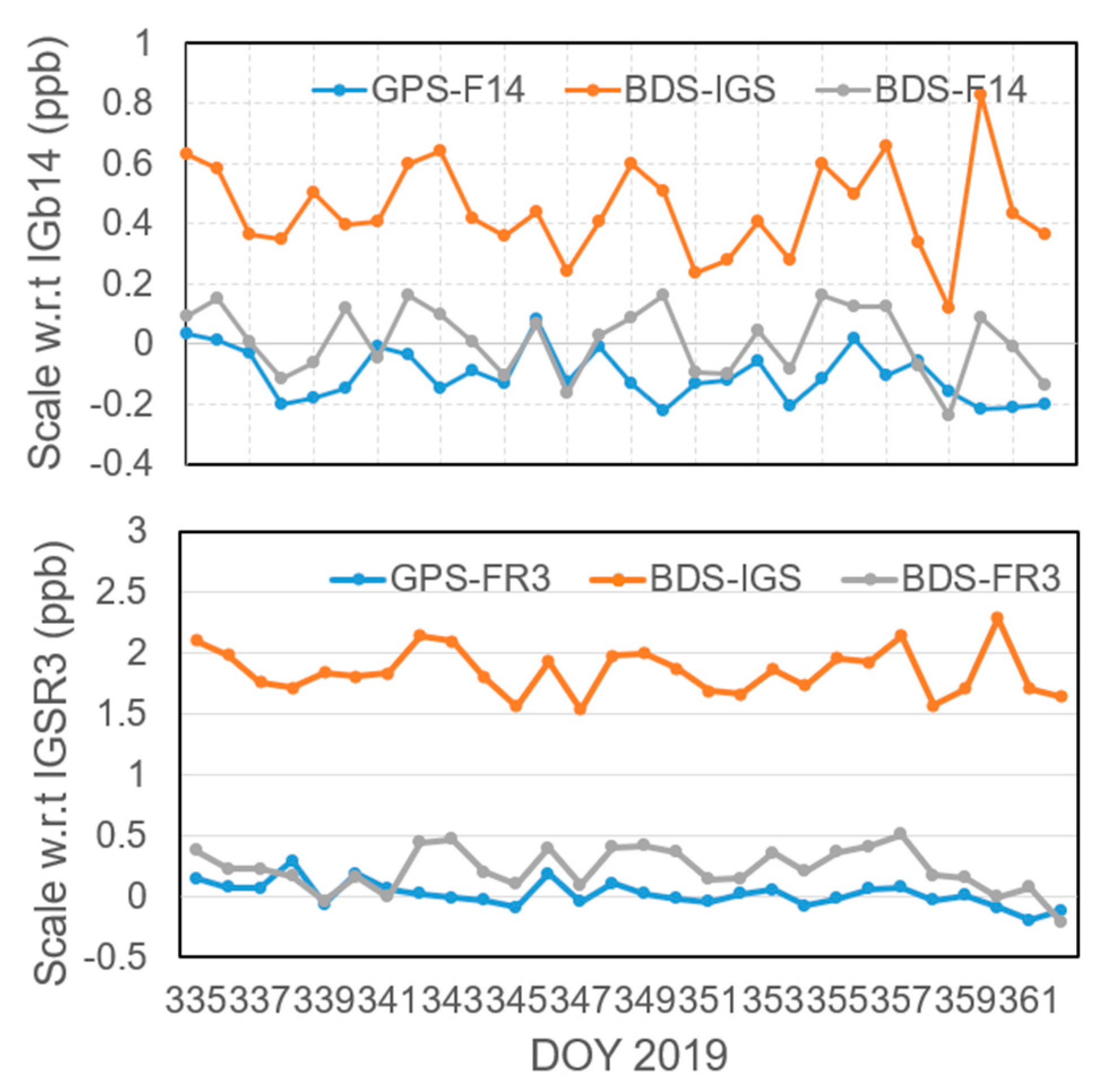
4.4.2. Coordinates
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- CSNO. Development of the BeiDou Navigation Satellite System. China Satellite Navigation Office. Available online: http://www.beidou.gov.cn/xt/gfxz/201912/P020191227430565455478.pdf (accessed on 30 December 2020).
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Sakic, P.; Mansur, G.; Männel, B. A Prototype for a Multi-GNSS Orbit Combination. In Proceedings of the European Navigation Conference, Bonn, Germany, 23–24 November 2020; pp. 1–11. [Google Scholar] [CrossRef]
- Schmid, R.; Steigenberger, P.; Gendt, G.; Ge, M.; Rothacher, M. Generation of a consistent absolute phase-center correction model for GPS receiver and satellite antennas. J. Geod. 2007, 81, 781–798. [Google Scholar] [CrossRef] [Green Version]
- Dilssner, F.; Springer, T.; Flohrer, C.; Dow, J. Estimation of phase center corrections for GLONASS-M satellite antennas. J. Geod. 2010, 84, 467–480. [Google Scholar] [CrossRef]
- Montenbruck, O.; Schmid, R.; Mercier, F.; Steigenberger, P.; Noll, C.; Fatkulin, R.; Kogure, S.; Ganeshan, A. GNSS satellite geometry and attitude models. Adv. Space Res. 2015, 56, 1015–1029. [Google Scholar] [CrossRef] [Green Version]
- Steigenberger, P.; Fritsche, M.; Dach, R.; Schmid, R.; Montenbruck, O.; Uhlemann, M.; Prange, L. Estimation of satellite antenna phase center offsets for Galileo. J. Geod. 2016, 90, 773–785. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.; Reigber, C. Impact of GPS satellite antenna offsets on scale changes in global network solutions. Geophys. Res. Lett. 2005, 32, L06310. [Google Scholar] [CrossRef]
- Zhu, S.Y.; Massmann, F.-H.; Yu, Y.; Reigber, C. Satellite antenna phase center offsets and scale errors in GPS solutions. J. Geod. 2003, 76, 668–672. [Google Scholar] [CrossRef]
- Schmid, R.; Rothacher, M.; Thaller, D.; Steigenberger, P. Absolute phase center corrections of satellite and receiver antennas. GPS Solut. 2005, 9, 283–293. [Google Scholar] [CrossRef]
- Dilssner, F.; Springer, T.; Schönemann, E. Estimation of Satellite Antenna Phase Center Corrections for BeiDou. In Proceedings of the IGS Network, Data and Analysis Center Workshop, Pasadena, CA, USA, 23–27 June 2014. [Google Scholar]
- Guo, J.; Xu, X.; Zhao, Q.; Liu, J. Precise orbit determination for quad-constellation satellites at Wuhan University: Strategy, result validation, and comparison. J. Geod. 2016, 90, 143–159. [Google Scholar] [CrossRef]
- Huang, G.; Yan, X.; Zhang, Q.; Liu, C.; Wang, L.; Qin, Z. Estimation of antenna phase center offset for BDS IGSO and MEO satellites. GPS Solut. 2018, 22, 49. [Google Scholar] [CrossRef]
- Guo, J. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites. Ph.D. Thesis, Wuhan University, Wuhan, China, 2014. [Google Scholar]
- GSC. Galileo Satellite Metadata, European GNSS Service Centre. Available online: https://www.gsc-europa.eu/support-to-developers/galileo-satellite-metadata (accessed on 1 January 2021).
- Villiger, A.; Dach, R.; Schaer, S.; Prange, L.; Zimmermann, F.; Kuhlmann, H.; Wübbena, G.; Schmitz, M.; Beutler, G.; Jäggi, A. GNSS scale determination using calibrated receiver and Galileo satellite antenna patterns. J. Geod. 2020, 94, 93. [Google Scholar] [CrossRef]
- Männel, B.; Brandt, A.; Bradke, M.; Sakic, P.; Brack, A.; Nischan, T. Status of IGS Reprocessing Activities at GFZ. In International Association of Geodesy Symposia; Springer: Berlin, Germany, 2020. [Google Scholar] [CrossRef]
- Huang, W.; Männel, B.; Brack, A.; Schuh, H. Two methods to determine scale-independent GPS PCOs and GNSS-based terrestrial scale: Comparison and cross-check. GPS Solut. 2020, 25, 4. [Google Scholar] [CrossRef]
- CSNO. Satellite Information of BDS. China Satellite Navigation Office. Available online: http://en.beidou.gov.cn/SYSTEMS/Officialdocument/201912/P020200103556125703019.rar (accessed on 30 December 2020).
- Springer, T.; Agrotis, L.; Dilssner, F.; Feltens, J.; Van Kints, M.; Mayer, V.; Romero, I.; Enderle, W.; Schoenemann, E.; Zandbergen, R. The ESA/ESOC IGS Analysis Centre Technical Report. 2019. Available online: ftp://ftp.aiub.unibe.ch/users/villiger/2019_techreport.pdf (accessed on 30 December 2020).
- Xia, F.; Ye, S.; Chen, D.; Wu, J.; Wang, C.; Sun, W. Estimation of antenna phase center offsets for BeiDou IGSO and MEO satellites. GPS Solut. 2020, 24, 90. [Google Scholar] [CrossRef]
- CSNO. BeiDou Navigation Satellite System Signal in Space Interface Control Document. China Satellite Navigation Office. Available online: http://www.beidou.gov.cn/xt/gfxz/201902/P020190227593621142475.pdf (accessed on 30 December 2020).
- Liu, J.; Ge, M. PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géodésique 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.E.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 25. [Google Scholar] [CrossRef] [Green Version]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short Note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Beutler, G.; Brockmann, E.; Gurtner, W.; Hugentobler, U.; Mervart, L.; Rothacher, M.; Verdun, A. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics (IGS): Theory and Initial Results. Manuscr. Geod. 1994, 19, 367–386. [Google Scholar]
- Wang, C. Solar Radiation Pressure Modeling for BeiDou Navigation Satellites. Ph.D. Thesis, Wuhan University, Wuhan, China, 2019. [Google Scholar]
- Yan, X.; Huang, G.; Zhang, Q.; Wang, L.; Qin, Z.; Xie, S. Estimation of the Antenna Phase Center Correction Model for the BeiDou-3 MEO Satellites. Remote Sens. 2019, 11, 2850. [Google Scholar] [CrossRef] [Green Version]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08.atx: Status and potential improvements. J. Geod. 2016, 90, 343–364. [Google Scholar] [CrossRef] [Green Version]

| PRN | SVN | B1 | B3 | IF of B1 and B3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | X | Y | Z | ||
| C06 | C005 | 0.7526 | −0.0027 | 0.8793 | 0.7473 | −0.0051 | 1.1980 | 0.76290 | 0.00197 | 0.25985 |
| C07 | C007 | 0.7455 | 0.001 | 0.9824 | 0.7536 | −0.0051 | 1.1888 | 0.72976 | 0.01286 | 0.58122 |
| C08 | C008 | 0.7494 | −0.0016 | 1.0 | 0.7493 | −0.0028 | 1.1895 | 0.7496 | 0.00073 | 0.63167 |
| C09 | C009 | 0.5940 | −0.0112 | 1.0071 | 0.5960 | −0.00840 | 1.1805 | 0.59011 | −0.01664 | 0.67007 |
| C10 | C010 | 0.59870 | −0.00430 | 0.99540 | 0.60 | −0.0014 | 1.19480 | 0.59617 | −0.00994 | 0.60783 |
| C11 | C012 | 0.5766 | −0.0034 | 1.0742 | 0.57650 | −0.0051 | 1.1863 | 0.57679 | −0.00010 | 0.85631 |
| C12 | C013 | 0.5973 | 0.0134 | 1.0604 | 0.6009 | 0.009 | 1.1717 | 0.59030 | 0.02195 | 0.85507 |
| C13 | C017 | 0.6003 | 0.0008 | 1.3672 | 0.6009 | −0.0009 | 1.2718 | 0.59913 | 0.00410 | 1.55263 |
| C14 | C015 | 0.5834 | −0.001 | 1.0545 | 0.5835 | −0.0084 | 1.141 | 0.58321 | 0.01338 | 0.88637 |
| C16 | C019 | 0.6142 | −0.0011 | 1.3623 | 0.6142 | −0.0019 | 1.2671 | 0.6142 | 0.00046 | 1.54734 |
| C19 | C201 | −0.20810 | −0.00270 | 1.48720 | −0.20940 | 0.00100 | 1.21280 | −0.2056 | −0.0099 | 2.0205 |
| C20 | C202 | −0.21870 | 0.00100 | 1.52430 | −0.21860 | 0.00410 | 1.22630 | −0.2189 | −0.0050 | 2.1035 |
| C21 | C206 | −0.20885 | 0.00083 | 1.50330 | −0.21322 | 0.00469 | 1.21584 | −0.2004 | −0.0067 | 2.0620 |
| C22 | C205 | −0.21084 | −0.00318 | 1.50573 | −0.21469 | 0.00043 | 1.23800 | −0.2034 | −0.0102 | 2.0261 |
| C23 | C209 | −020963 | 0.00336 | 1.49440 | −0.20963 | 0.00637 | 1.22850 | −0.20963 | −0.00249 | 2.01122 |
| C24 | C210 | −0.2090 | 0.00296 | 1.51730 | −0.20913 | 0.00662 | 1.24475 | −0.20875 | −0.00415 | 2.04705 |
| C25 | C212 | 0.07346 | −0.00352 | 1.09270 | 0.07351 | −0.00355 | 1.08500 | 0.07336 | −0.00346 | 1.10767 |
| C26 | C211 | 0.07292 | −0.00508 | 1.09380 | 0.07292 | −0.00518 | 1.08170 | 0.07292 | −0.00489 | 1.11732 |
| C27 | C203 | 0.02741 | −0.00456 | 1.10509 | 0.02761 | −0.00439 | 1.09889 | 0.02702 | −0.00489 | 1.11714 |
| C28 | C204 | 0.02590 | −0.00470 | 1.10311 | 0.02614 | −0.00483 | 1.09761 | 0.02543 | −0.00445 | 1.11380 |
| C29 | C207 | 0.02838 | −0.00700 | 1.10430 | 0.02876 | −0.00581 | 1.09110 | 0.02764 | −0.00931 | 1.12996 |
| C30 | C208 | 0.02877 | −0.00569 | 1.09300 | 0.02895 | −0.00448 | 1.09190 | 0.02842 | −0.00804 | 1.09514 |
| C32 | C213 | −0.18501 | −0.00179 | 1.48822 | −0.18584 | 0.00208 | 1.19864 | −0.18340 | −0.00931 | 2.05107 |
| C33 | C214 | −0.18725 | −0.00375 | 1.46997 | −0.18613 | −0.00030 | 1.17864 | −0.18943 | −0.01046 | 2.03622 |
| C34 | C216 | 0.08972 | −0.00933 | 1.09747 | 0.08972 | −0.00935 | 1.08985 | 0.08972 | −0.00929 | 1.11228 |
| C35 | C215 | 0.08940 | −0.01104 | 1.09074 | 0.08950 | −0.01092 | 1.08515 | 0.08921 | −0.01127 | 1.10160 |
| C36 | C218 | −0.19519 | −0.00966 | 1.33701 | −0.19414 | −0.00672 | 1.05641 | −0.19723 | −0.01537 | 1.88241 |
| C37 | C219 | −0.19944 | −0.0104 | 1.33811 | −0.19914 | −0.00753 | 1.06623 | −0.20002 | −0.01604 | 1.86656 |
| C38 | C220 | −0.06959 | −0.30985 | 1.99959 | −0.06807 | −0.30985 | 1.66409 | −0.07254 | −0.30985 | 2.65170 |
| C39 | C221 | −0.06568 | −0.30570 | 1.97259 | −0.06472 | −0.30769 | 1.58615 | −0.06755 | −0.30183 | 2.72371 |
| C40 | C224 | −0.0671 | −0.3082 | 1.9702 | −0.0672 | −0.3113 | 1.5901 | −0.06691 | −0.30217 | 2.70899 |
| C41 | C227 | −0.19657 | −0.01113 | 1.05419 | −0.19682 | −0.00771 | 0.78121 | −0.19608 | −0.01778 | 1.58478 |
| C42 | C228 | −0.20104 | −0.00917 | 1.06171 | −0.20082 | −0.00682 | 0.78875 | −0.20147 | −0.01374 | 1.59226 |
| C43 | C226 | 0.05095 | −0.00794 | 1.09514 | 0.0508 | −0.00802 | 1.08752 | 0.051242 | −0.00778 | 1.10995 |
| C44 | C225 | 0.05177 | −0.00836 | 1.09280 | 0.05163 | −0.0084 | 1.0862 | 0.05204 | −0.00828 | 1.10563 |
| C45 | C223 | −0.28248 | −0.00739 | 1.39522 | −0.27872 | −0.00686 | 1.10793 | −0.28979 | −0.00842 | 1.95362 |
| C46 | C222 | −0.2831 | −0.00291 | 1.38556 | −0.27902 | −0.00155 | 1.0848 | −0.29103 | −0.00555 | 1.97014 |
| Antenna | Radom | Frequency | Calibration Type |
|---|---|---|---|
| ASH700936D_M | SCIS | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| ASH701945B_M | SCIS | B1I/B2b/B3I/B1c/B2a/B2a+B2b | COPIED |
| ASH701945E_M | SCIS SCIT | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| JAV_GRANT-G3T | NONE | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| JAVRINGANT_DM | NONE SCIS | B1I/B2b/B3I/B1c/B2a B2b: only Radom ‘NONE’ has | ROBOT |
| JAVRINGANT_G5T | JAVC | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| LEIAR20 | NONE LEIM | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| LEIAR25.R3 | NONE LEIT | B1I/B2b/B3I/B1c/B2a B2b: only Radom ‘LEIT’ has | ROBOT |
| LEIAR25.R4 | NONE LEIT | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| LEIAT504GG | NONE | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| RNG80971.00 | NONE | B1I/B2b/B3I/B1c/B2a/B2a+B2b | COPIED |
| SEPCHOKE_B3E6 | SPKE | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| TPSCR.G3 | NONE SCIS | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| TPSCR.G5 | TPSH | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| TRM115000.00 | NONE | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| TRM57971.00 | NONE | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| TRM59800.00 | NONE SCIS | B1I/B2b/B3I/B1c/B2a/B2a+B2b | ROBOT |
| TRM59800.80 | NONE SCIS | B1I/B2b/B3I/B1c/B2a/B2a+B2b | COPIED |
| Items | Description |
|---|---|
| Number of stations | About 130 stations from MGEX and iGMAS |
| Time interval | DOY 1 to 365, 2019 |
| Software | PANDA [23] |
| Observation | Zero-difference ionosphere-free combination of phase and code observations of GPS L1/L2 and BDS B1I/B3I |
| Sampling rate | 300 s |
| Elevation cut-off angle | 7° |
| Weighting | Elevation-dependent |
| Inter-system-bias | A constant value per day for each station |
| Station Coordinates | Align to IGb14 or IGSR3 frame with no-net-scale and no-net-rotation constraint |
| Troposphere | GPT2w used as the empirical meta data; Saastamoinen model with VMF mapping function [24,25,26] Hourly estimation as piece-wise constant |
| Ionosphere | The first-order effect eliminated by the ionosphere-free linear combination; the higher-order effects are ignored |
| Receiver Clock | Epoch estimation as white noise |
| Orbits | 24-h orbital arcs 6 initial position and velocities parameters BDS-3 MEO: 5-parameter Extended CODE Orbit Model (ECOM1) [27] + A prior box-wing model [28] Other: ECOM1+Constant acceleration in along-tracking direction |
| Satellites PCOs | GPS: igsR3_2077.atx used for FR3 solution, and igs14_2101.atx used for F14 solution. BDS: The PCO values in igs14_2101.atx used as the initial and estimated as daily constant with 10, 0.1, 10 m constraint for X-PCO, Y-PCO and Z-PCO. |
| Satellites PCVs | GPS: igsR3_2077.atx used for FR3 solution, and igs14_2101.atx used for F14 solution. BDS: the initial values of nadir-depended set as zero for PCVs estimation, and fixed as the estimated satellite-block-specific values for BDS PCO estimation. |
| Receiver PCOs and PCVs | GPS: igsR3_2077.atx used for FR3 solution, and igs14_2101.atx used for F14 solution. BDS: igsR3_2077.atx; and GPS L1 and L2 used in case of no corrections for BDS signals. |
| Nadir (°) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BDS-2I | −0.79 | 0.41 | −1.14 | −0.46 | 0.47 | 0.92 | 0.77 | 0.49 | 1.34 | −1.97 | ||||
| BDS-2M | −3.65 | −3.18 | −2.70 | −1.05 | 0.40 | 2.09 | 3.03 | 3.62 | 3.43 | 2.50 | 0.91 | −0.53 | −1.10 | −3.58 |
| BDS-3M-CAST | 1.73 | 1.71 | 1.22 | 0.33 | −0.47 | −0.79 | −1.23 | −1.45 | −1.51 | −1.29 | −1.14 | −0.47 | 1.25 | 1.91 |
| BDS-3M-SECM | 2.50 | 2.53 | 1.74 | 0.52 | −0.60 | −1.22 | −1.88 | −2.14 | −2.14 | −1.85 | −1.52 | −0.50 | 1.75 | 2.65 |
| PRN | Days | F14 w.r.t CSNO | FR3 w.r.t F14 | ||
|---|---|---|---|---|---|
| Δx | Δy | Δz | δz | ||
| C06 | 324 | −16.6 ± 0.11 | −1.56 ± 0.06 | +212.70 ± 1.21 | −42.54 ± 1.18 |
| C07 | 336 | −12.02 ± 0.14 | −2.34 ± 0.07 | +222.28 ± 1.07 | −42.17 ± 1.10 |
| C08 | 335 | −16.40 ± 0.10 | −1.81 ± 0.07 | +247.64 ± 1.13 | −41.87 ± 1.12 |
| C09 | 318 | +1.46 ± 0.12 | −0.29 ± 0.07 | +264.44 ± 1.23 | −41.06 ± 1.22 |
| C10 | 336 | +0.26 ± 0.12 | −0.24 ± 0.06 | +272.69 ± 1.05 | −39.68 ± 1.05 |
| C13 | 331 | +1.34 ± 0.15 | −1.50 ± 0.05 | +107.27 ± 1.12 | −40.30 ± 1.11 |
| C16 | 276 | −3.64 ± 0.16 | −1.88 ± 0.05 | +120.83 ± 1.72 | −42.78 ± 1.74 |
| C11 | 355 | +2.31 ± 0.06 | +0.38 ± 0.06 | +105.12 ± 0.47 | −17.37 ± 0.46 |
| C12 | 341 | −2.97 ± 0.00 | −2.19 ± 0.00 | +126.29 ± 0.50 | −17.68 ± 0.47 |
| C14 | 345 | −2.26 ± 0.01 | −1.34 ± 0.00 | +111.15 ± 0.51 | −17.28 ± 0.52 |
| C19 | 313 | −1.45 ± 0.09 | +0.34 ± 0.05 | −1.14 ± 0.50 | −17.42 ± 0.48 |
| C20 | 310 | +0.49 ± 0.07 | −0.59 ± 0.05 | −4.16 ± 0.56 | −17.45 ± 0.52 |
| C21 | 321 | −0.99 ± 0.07 | +0.15 ± 0.05 | −3.64 ± 0.56 | −17.65 ± 0.55 |
| C22 | 323 | −1.42 ± 0.08 | +0.18 ± 0.05 | −0.55 ± 0.53 | −17.36 ± 0.68 |
| C23 | 285 | −0.61 ± 0.08 | +0.12 ± 0.05 | +6.83 ± 0.73 | −17.28 ± 0.73 |
| C24 | 279 | −0.52 ± 0.08 | +0.14 ± 0.05 | +8.52 ± 0.71 | −17.35 ± 0.77 |
| C32 | 272 | +0.02 ± 0.07 | +0.57 ± 0.05 | +16.53 ± 0.80 | −17.63 ± 0.80 |
| C33 | 295 | +0.24 ± 0.06 | +0.49 ± 0.05 | +19.02 ± 0.76 | −17.00 ± 0.74 |
| C36 | 247 | +0.12 ± 0.06 | +1.31 ± 0.03 | +17.27 ± 1.13 | −17.21 ± 1.13 |
| C37 | 212 | +0.08 ± 0.05 | +1.36 ± 0.04 | +17.56 ± 1.10 | −17.23 ± 1.15 |
| C25 | 271 | −0.68 ± 0.19 | −0.67 ± 0.05 | −4.00 ± 0.75 | −17.40 ± 0.79 |
| C26 | 269 | −0.73 ± 0.22 | −0.32 ± 0.05 | +6.98 ± 0.79 | −17.30 ± 0.70 |
| C27 | 287 | +1.30 ± 0.00 | −0.51 ± 0.00 | +16.74 ± 0.70 | −17.32 ± 0.56 |
| C28 | 305 | +1.70 ± 0.086 | −0.18 ± 0.05 | +22.58 ± 0.56 | −17.29 ± 0.58 |
| C29 | 293 | +1.82 ± 0.08 | −0.12 ± 0.05 | +26.72 ± 0.56 | −17.16 ± 0.80 |
| C30 | 294 | +1.96 ± 0.08 | +0.29 ± 0.06 | +16.53 ± 0.68 | −17.36 ± 0.66 |
| C34 | 294 | −3.14 ± 0.07 | +0.29 ± 0.05 | +14.77 ± 0.65 | −17.69 ± 0.66 |
| C35 | 231 | −3.58 ± 0.08 | +0.20 ± 0.05 | +1.29 ± 1.12 | −18.10 ± 1.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Z.; Guo, J.; Zhao, Q. Phase Center Corrections for BDS IGSO and MEO Satellites in IGb14 and IGSR3 Frame. Remote Sens. 2021, 13, 745. https://doi.org/10.3390/rs13040745
Qu Z, Guo J, Zhao Q. Phase Center Corrections for BDS IGSO and MEO Satellites in IGb14 and IGSR3 Frame. Remote Sensing. 2021; 13(4):745. https://doi.org/10.3390/rs13040745
Chicago/Turabian StyleQu, Ziyang, Jing Guo, and Qile Zhao. 2021. "Phase Center Corrections for BDS IGSO and MEO Satellites in IGb14 and IGSR3 Frame" Remote Sensing 13, no. 4: 745. https://doi.org/10.3390/rs13040745
APA StyleQu, Z., Guo, J., & Zhao, Q. (2021). Phase Center Corrections for BDS IGSO and MEO Satellites in IGb14 and IGSR3 Frame. Remote Sensing, 13(4), 745. https://doi.org/10.3390/rs13040745






