Multi-Feature Fusion for Weak Target Detection on Sea-Surface Based on FAR Controllable Deep Forest Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. IPIX Dataset and Processing
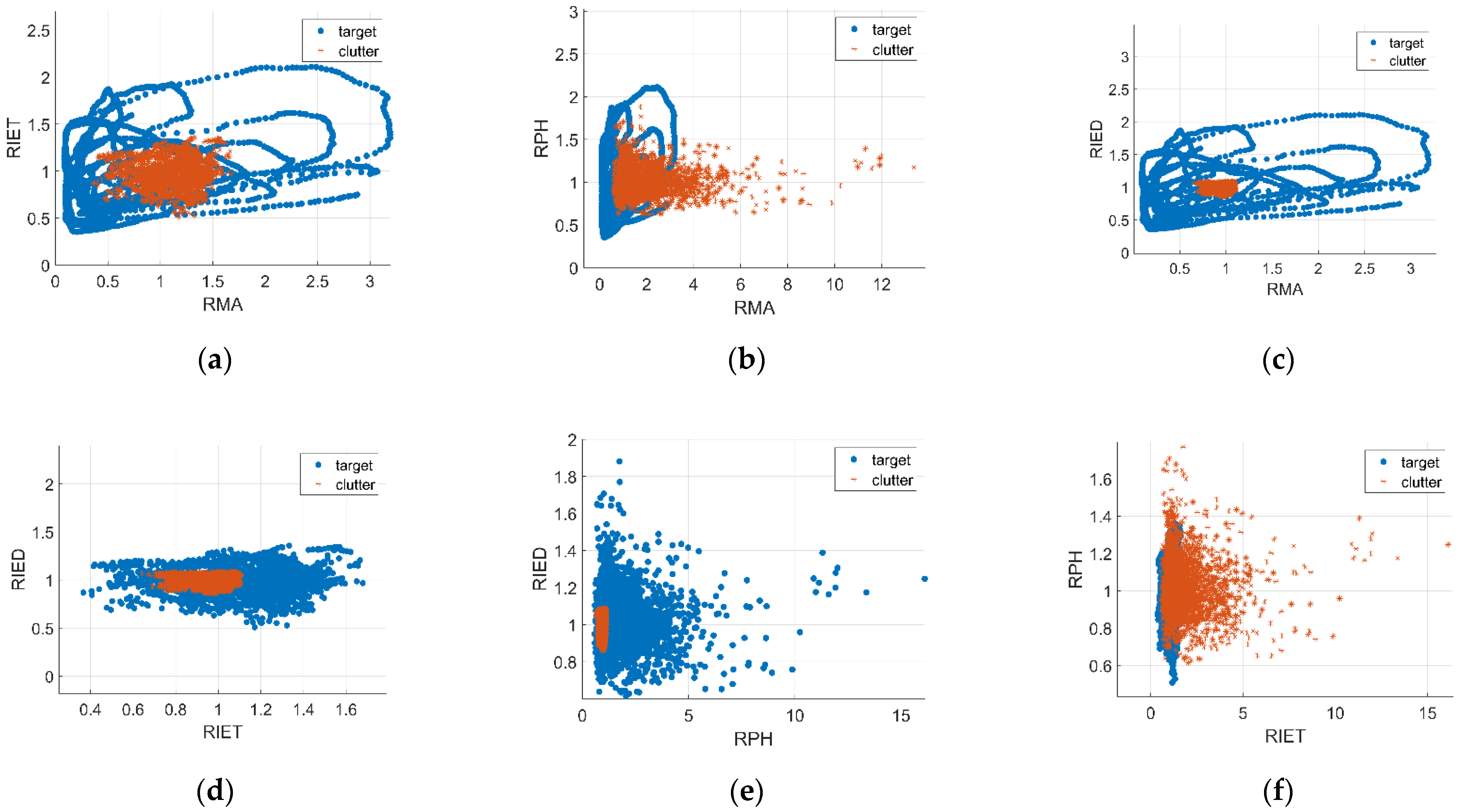
2.2. Features in Experiments
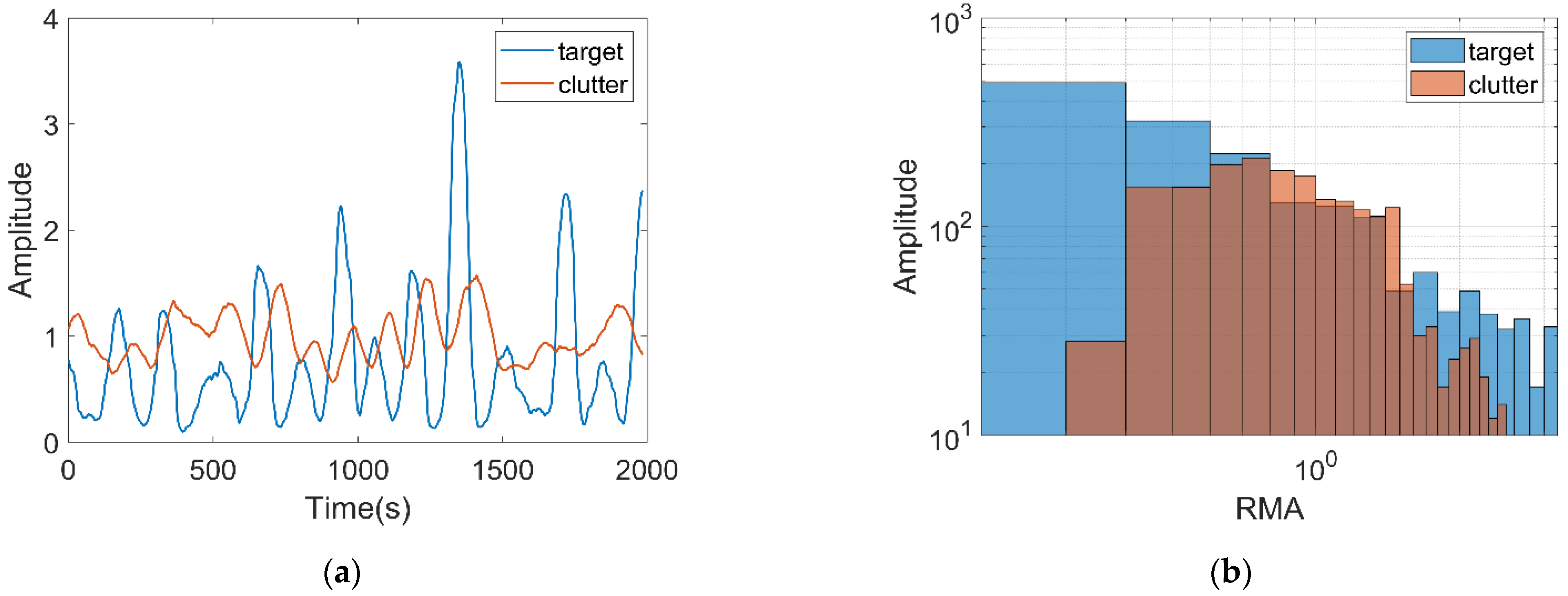
2.2.1. Relative Mean Amplitude
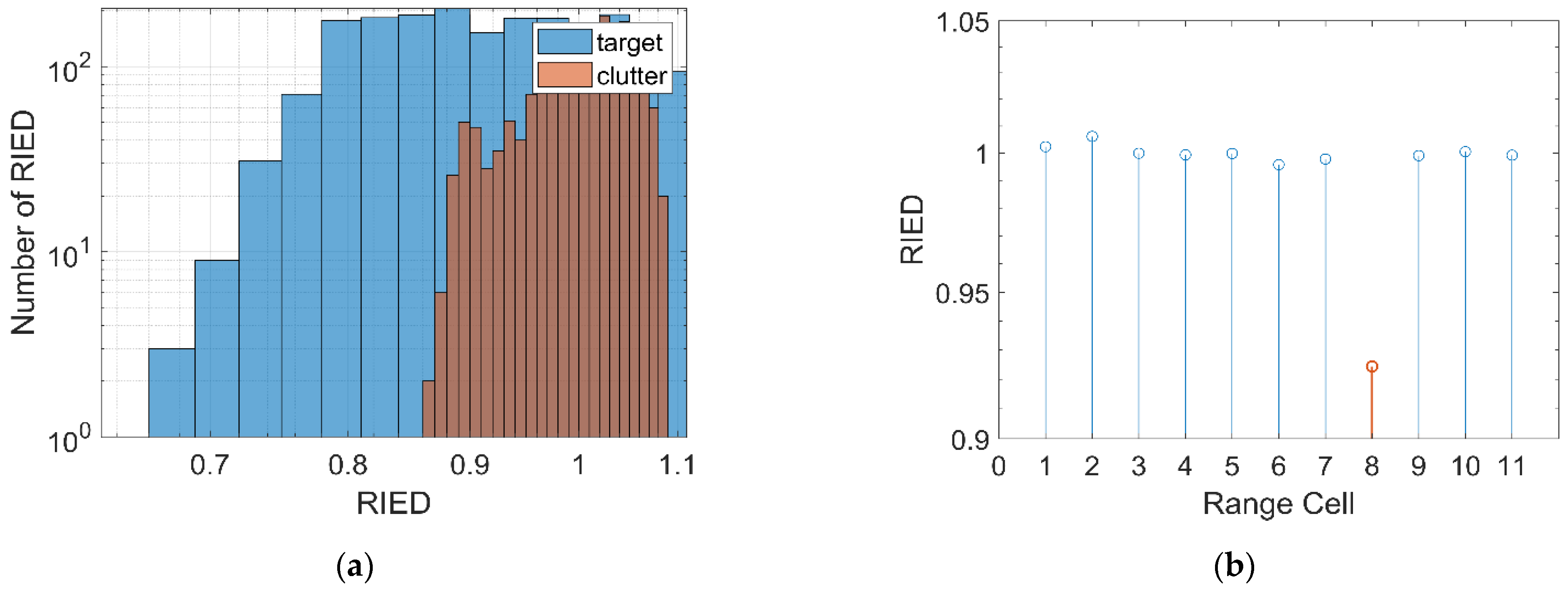
2.2.2. Relative Information Entropy in Time Domain
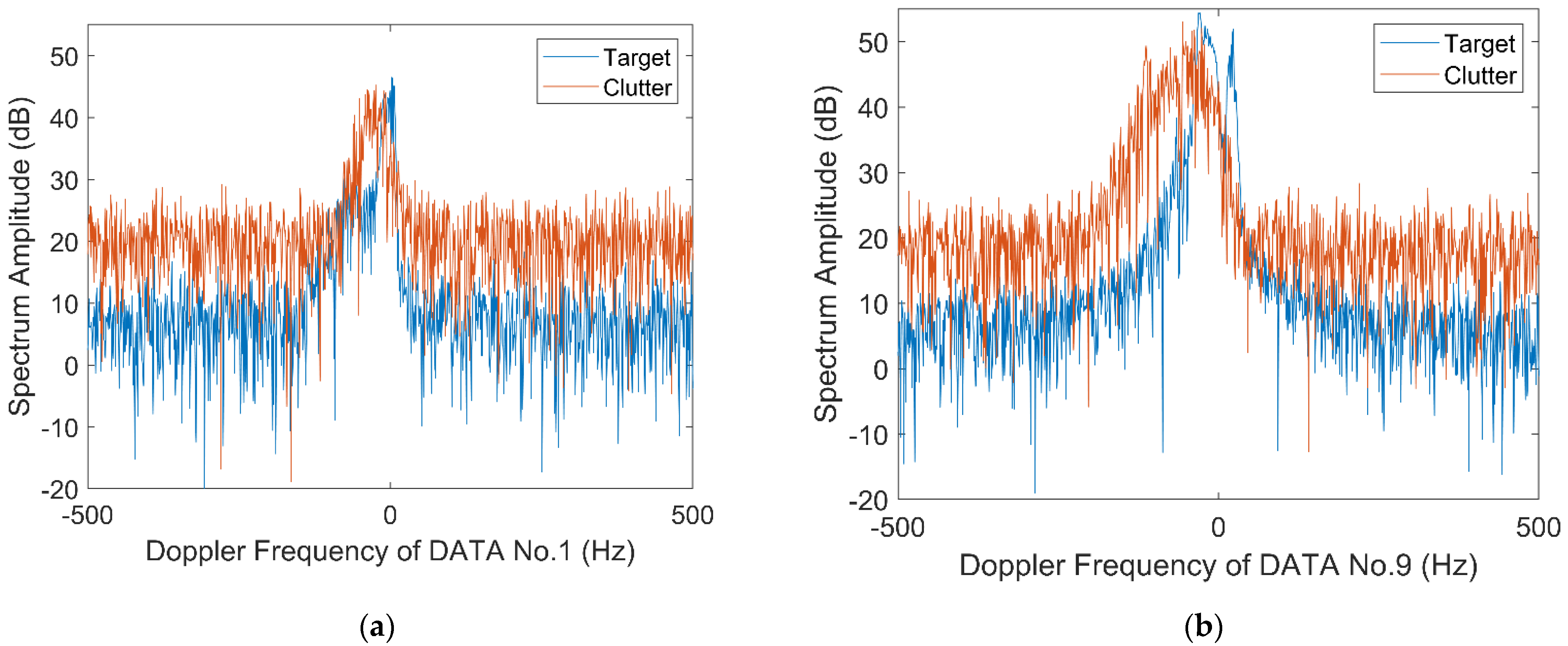
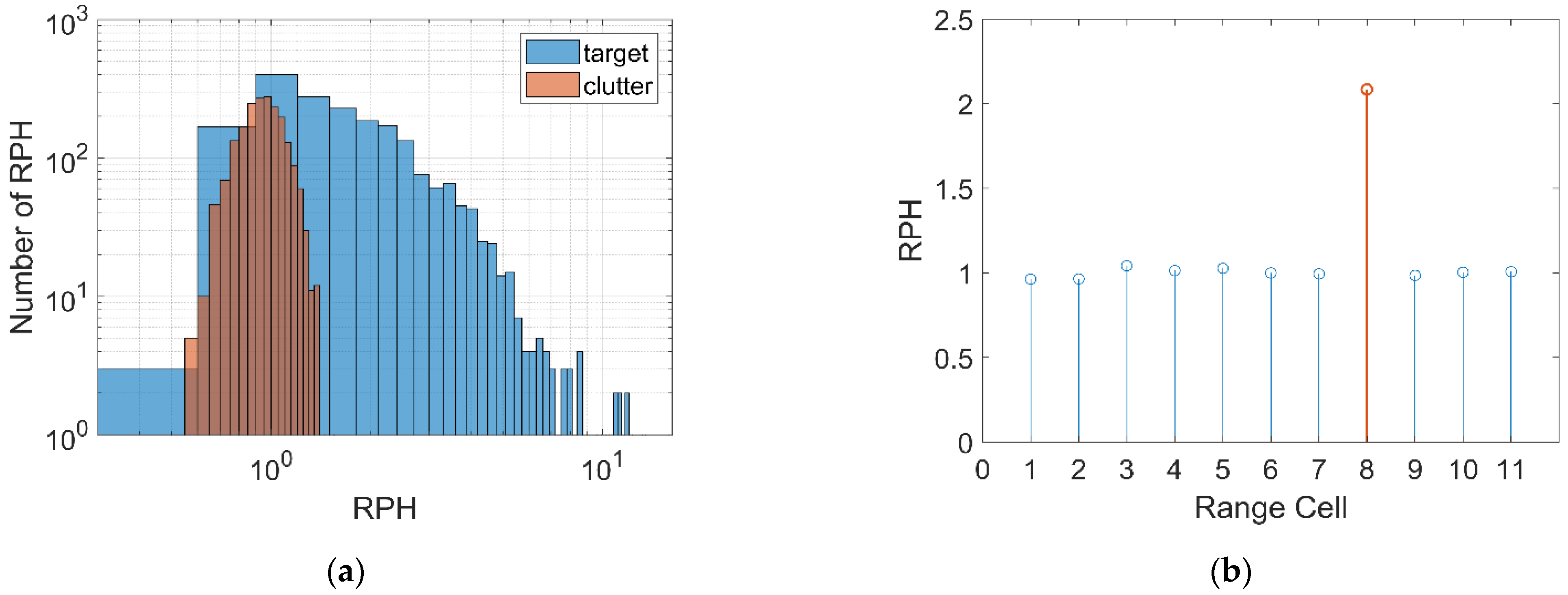
2.2.3. Relative Value of Doppler Peak Height
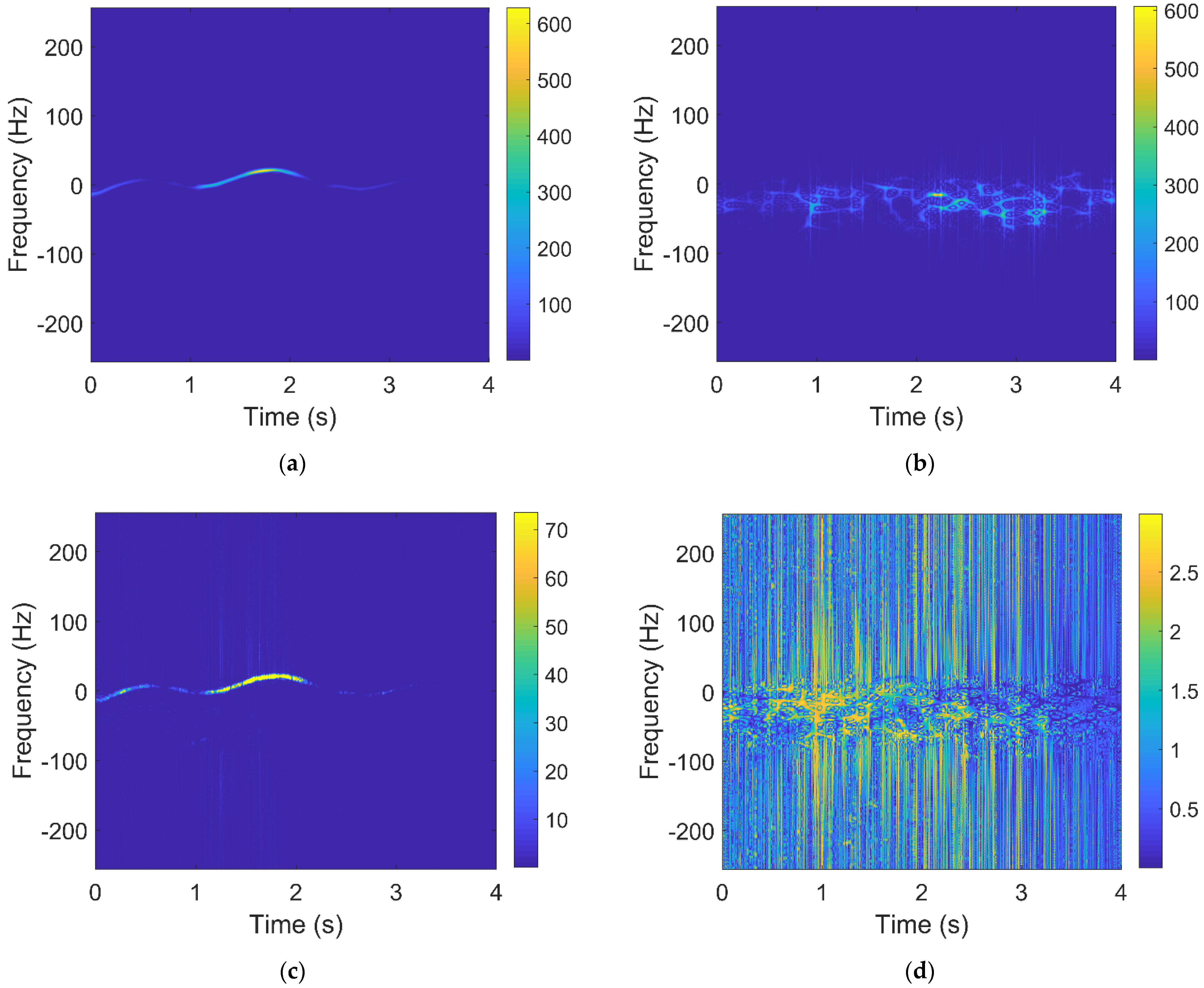
2.2.4. Relative Information Entropy in Doppler Domain
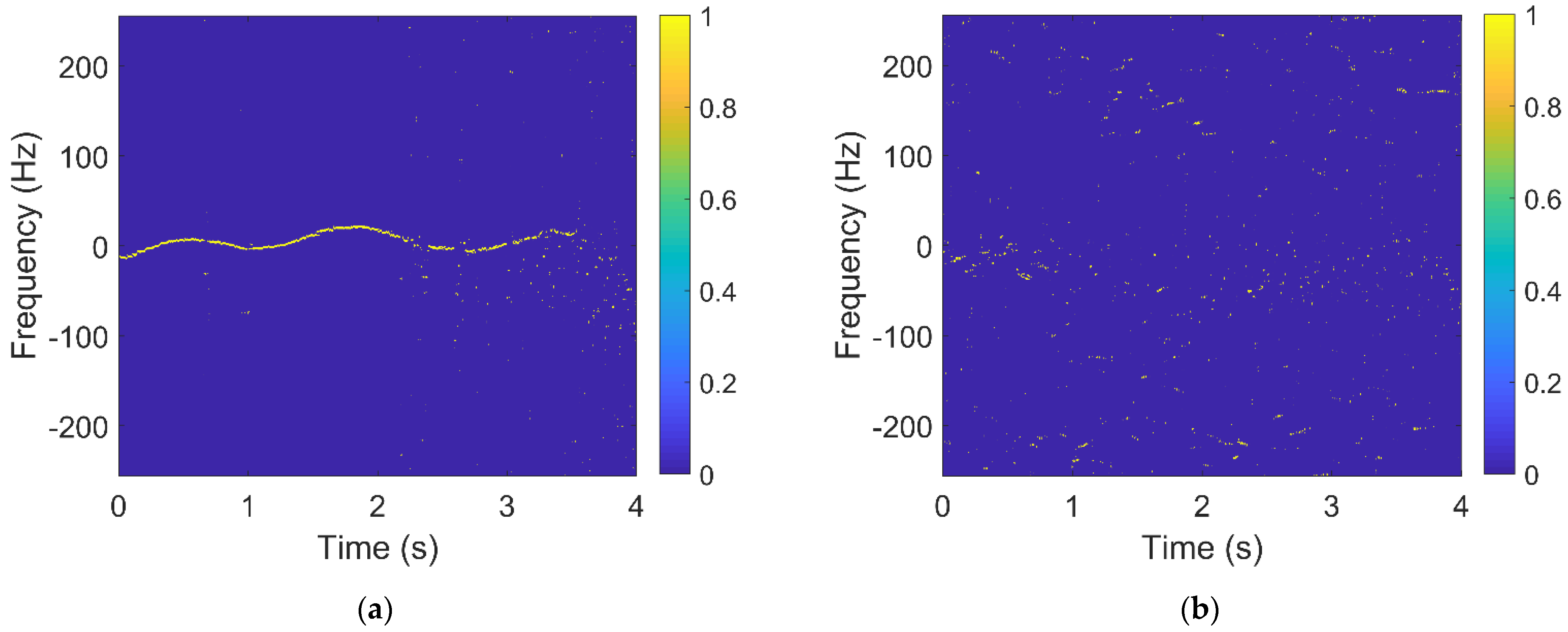
2.2.5. The Number of Connected Regions and Maximum Size of Connected Regions
2.2.6. Summary
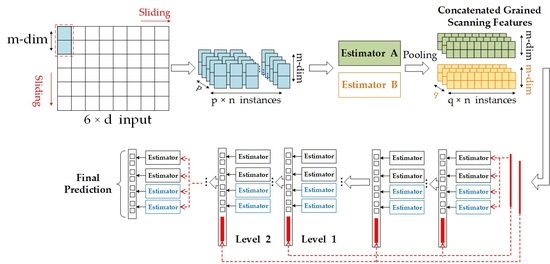
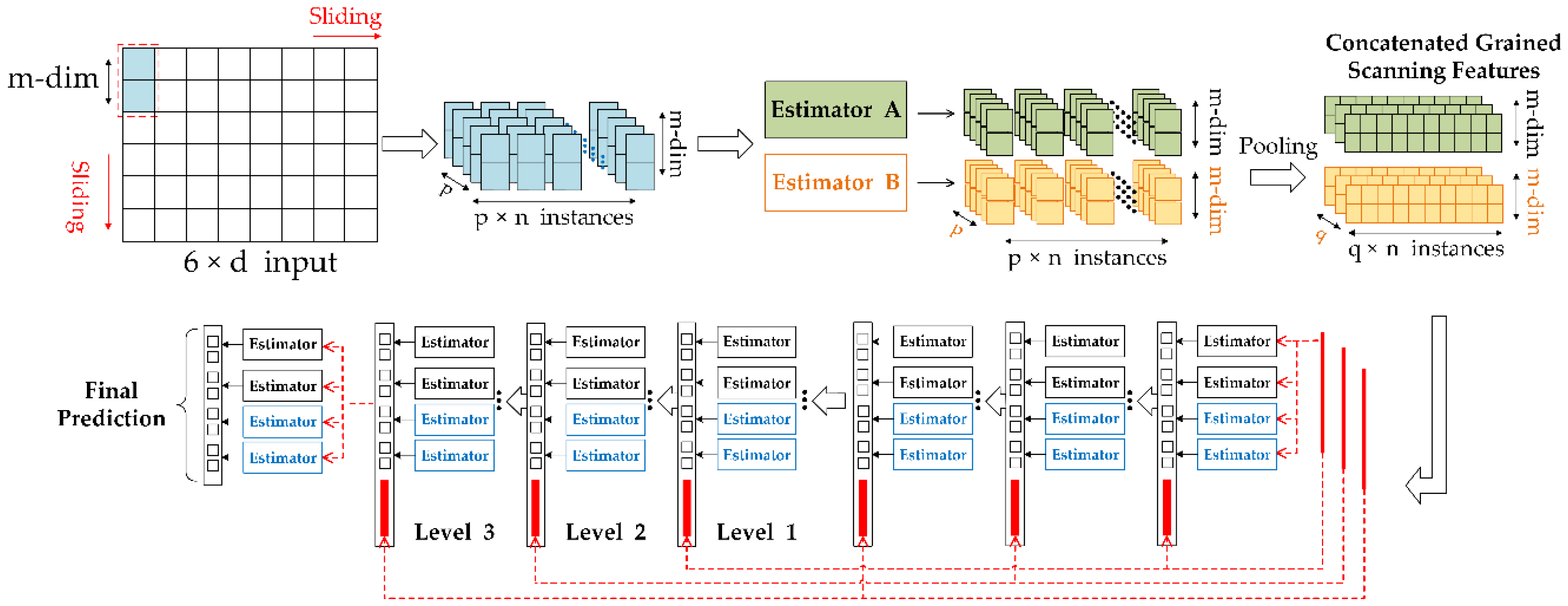
2.3. False-Alarm Rate Controllable Deep Forest Method
3. Results
3.1. Performance Analysis of Detection Framework
3.2. Average Detection Probability of Different Conditions
4. Discussion
4.1. Performance Analysis of Detection Framework
4.1.1. Multi-Grained Scanning Layer
4.1.2. Cascade Layer
4.2. Performance Analysis of Data
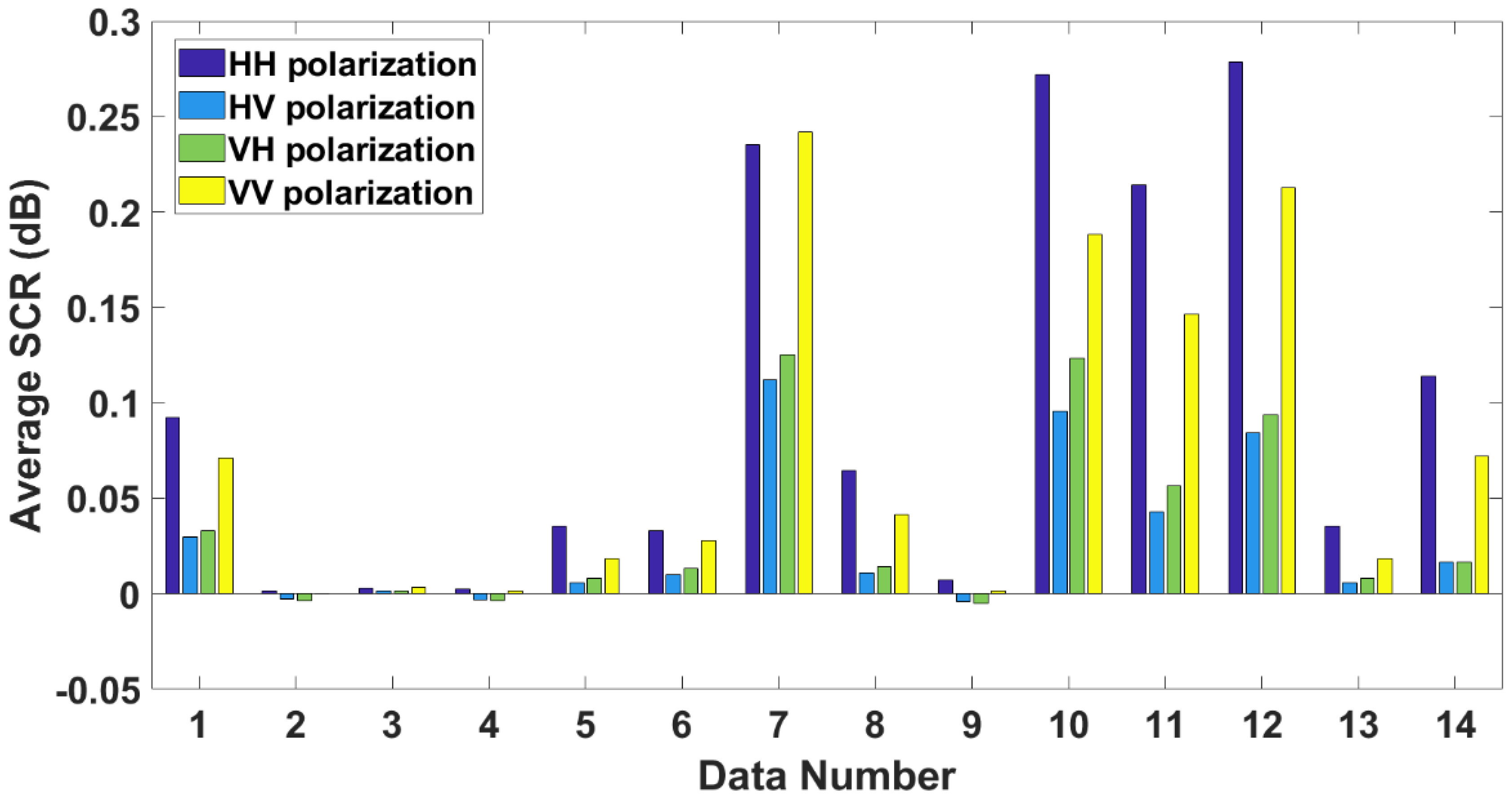
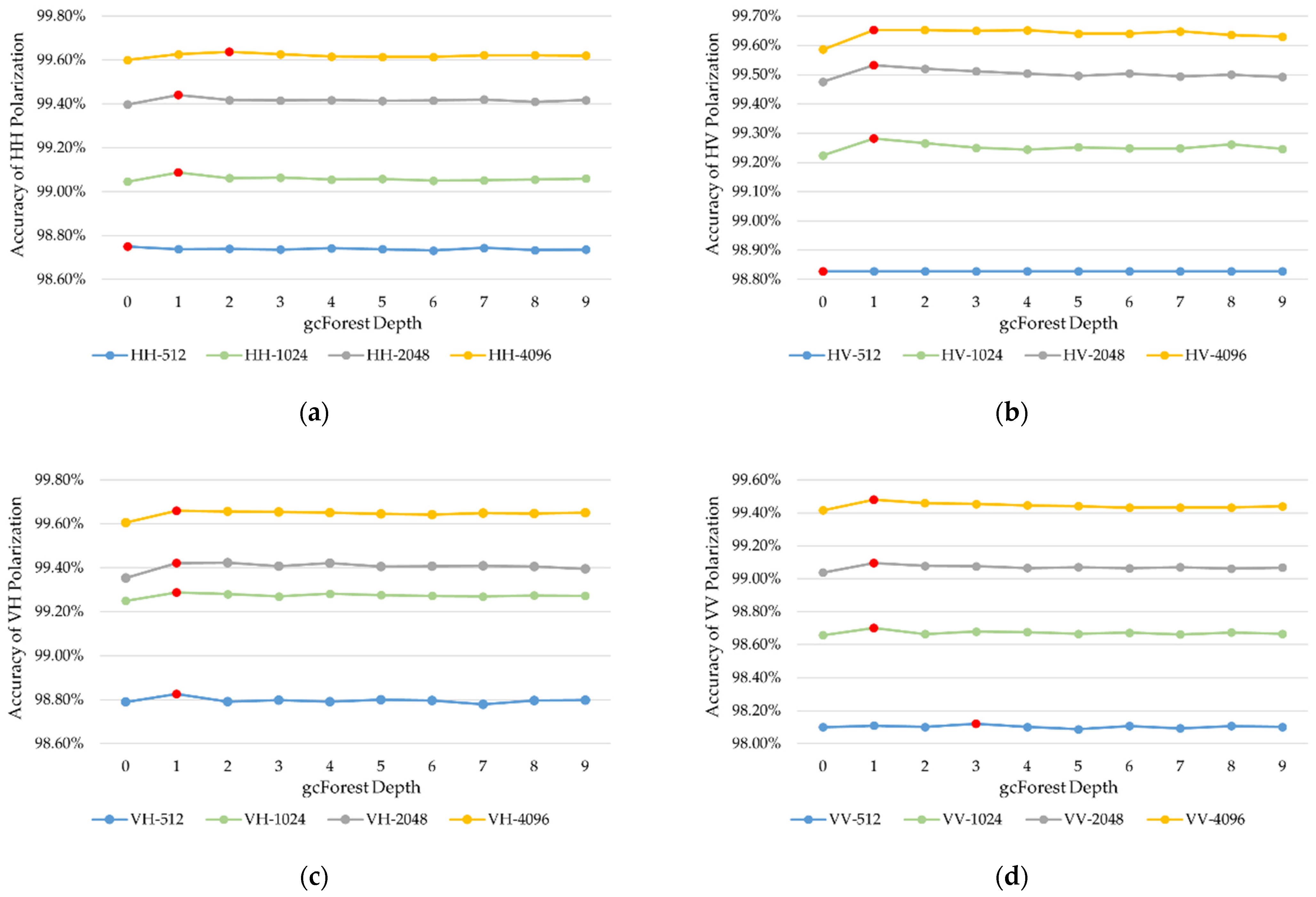
4.2.1. Influence of Polarization and Observation Length
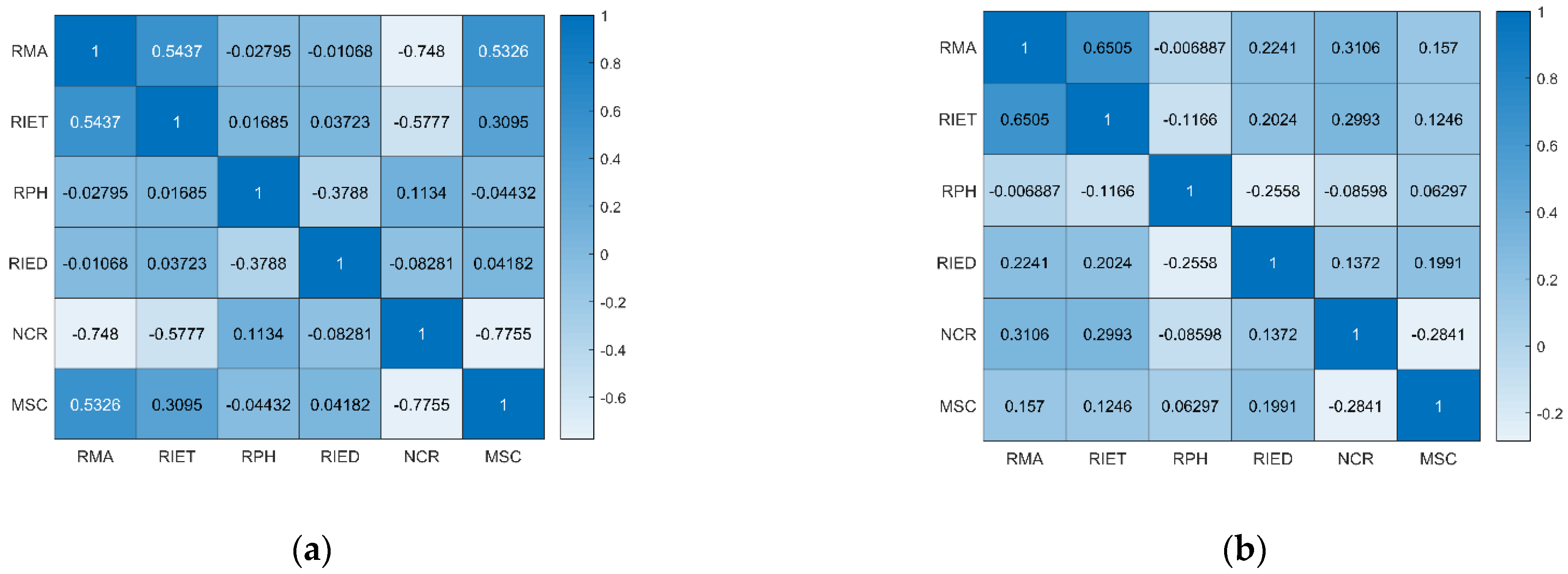
4.2.2. Feature Importance
4.3. The Comparision of Results of Different Methods
4.3.1. Model Validity Check
4.3.2. Comparison of Detection Performance
5. Conclusions
- Six features are selected from three domains to construct feature vectors for detection. Ocean conditions are complex and constantly changing; a single feature cannot effectively detect weak targets on the sea surface. In order to obtain efficient and accurate detection results, this paper extracts six features that can distinguish weak targets and clutter from the time domain, frequency domain, and time–frequency domain, namely RMA, RIET, RPH, RIED, NCR and MSC;
- The deep forest model is used as the weak target detection framework for the first time, and the main algorithm used is gcForest. The model is improved by introducing the expected FAR value into the stop growth judgment condition of the gcForest cascade level to construct a FAR controllable model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng-Lang, S.; Bao, Z.; Su, H. Nonparametric detection of FM signals using time-frequency ridge energy. IEEE Trans. Signal Process. 2008, 56, 1749–1760. [Google Scholar] [CrossRef]
- Xiaolong, C.; Jian, G.; Yong, H.; You, H. Radar low-observable target detection. Sci. Technol. Rev. 2017, 35, 30–38. [Google Scholar]
- You, H.; Yong, H.; Jian, G.; Chen, X. An overview on radar target detection in sea clutter. Mod. Radar. 2014, 36, 1–9. [Google Scholar]
- Yufang, T. Research on Weak Target Detection in Sea Clutter. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2013. [Google Scholar]
- Chen, Y.; Li, Y.; Wang, J.; Chen, W.; Zhang, X. Remote Sensing Image Ship Detection under Complex Sea Conditions Based on Deep Semantic Segmentation. Remote Sens. 2020, 12, 625. [Google Scholar] [CrossRef] [Green Version]
- Dongchen, L. A feature Detection Method for Small Targets in Sea Clutter. Ph.D. Thesis, Xidian University, Xi’an, China, 2013. [Google Scholar]
- Liu, G.; Zhang, X.; Meng, J. A Small Ship Target Detection Method Based on Polarimetric SAR. Remote Sens. 2019, 11, 2938. [Google Scholar] [CrossRef] [Green Version]
- Joshi, S.K.; Baumgartner, S.V.; da Silva, A.B.C.; Krieger, G. Range-Doppler Based CFAR Ship Detection with Automatic Training Data Selection. Remote Sens. 2019, 11, 1270. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Bai, X.; Guo, Z.; Shui, P. Status and prospects of feature-based detection methods for floating targets on the sea surface. J. Radars 2020, 9, 684–714. [Google Scholar] [CrossRef]
- Dugundji, J.; Ackerlind, E. Automatic bias control for a threshold detector. IRE Trans. Inf. Theory 1957, 3, 65–70. [Google Scholar] [CrossRef]
- Endresen, K.; Hedemark, R. Coincidence techniques for radar receivers employing a double-threshold method of detection. Proc. IRE 1961, 49, 1561–1567. [Google Scholar] [CrossRef]
- Watts, S. Cell-averaging CFAR gain in spatially correlated K-distributed clutter. IEE Proc. Radar Sonar Navig. 1996, 143, 321–327. [Google Scholar] [CrossRef]
- Steenson, B.O. Detection performance of a mean-level threshold. IEEE Trans. Aerosp. Electron. Syst. 1968, 4, 529–534. [Google Scholar] [CrossRef]
- Conte, E.; Longo, M.; Lops, M. Performance analysis of CA-CFAR in the presence of compound Gaussian clutter. Electron. Lett. 1988, 24, 782–783. [Google Scholar] [CrossRef]
- Hansen, V.G. Constant false alarm rate processing in search radars. In Proceedings of the IEEE 1973 International Radar Conference, London, UK, 23–25 October 1973; pp. 325–332. [Google Scholar]
- Weiss, M. Analysis of some modified cell-averaging CFAR processors in multiple-target situations. IEEE Trans. Aerosp. Electron. Syst. 1982, 1, 102–114. [Google Scholar] [CrossRef]
- Trunk, G.V. Range resolution of targets using automatic detectors. IEEE Trans. Aerosp. Electron. Syst. 1978, 5, 750–755. [Google Scholar] [CrossRef]
- Rohling, H. Radar CFAR thresholding in clutter and multiple target situations. IEEE Trans. Aerosp. Electron. Syst. 1983, 4, 608–621. [Google Scholar] [CrossRef]
- Rohling, H. New CFAR-processor based on an ordered statistic. In Proceedings of the International Radar Conference, Arlington, VA, USA, 6–9 May 1985; pp. 271–275. [Google Scholar]
- Kelly, E.J. An adaptive detection algorithm. IEEE Trans. Aerosp. Electron. Syst. 1986, 2, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar]
- Conte, E.; Lops, M.; Ricci, G. Asymptotically optimum radar detection in compound-Gaussian clutter. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 617–625. [Google Scholar] [CrossRef] [Green Version]
- Richmond, C.D. Analysis of an adaptive detection algorithm for non-homogeneous environments. In Proceedings of the 1998 23rd IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP 1998, Seattle, WA, USA, 12–15 May 1998. [Google Scholar]
- Lo, T.; Leung, H.; Litva, J.; Haykin, S. Fractal characterisation of sea-scattered signals and detection of sea-surface targets. In IEEE Proceedings F (Radar and Signal Processing); IET Digital Library: New York, NY, USA, 1993; Volume 140. [Google Scholar]
- Hu, J.; Tung, W.W.; Gao, J.B. Detection of low observable targets with sea clutter by structure function based multifractal analysis. IEEE Trans. Antennas Propag. 2006, 54, 136–143. [Google Scholar] [CrossRef]
- Xu, X.-K. Low observable targets detection by joint fractal properties of sea clutter: An experimental study of IPIX OHGR datasets. IEEE Trans. Antennas Propag. 2010, 58, 1425–1429. [Google Scholar]
- Jian, G.; Ning-bo, L.; Jian, Z.; Jie, S. Multifractal Correlation Characteristic of Real Sea Clutter and Low-Observable Targets Detection. J. Electron. Inf. Technol. 2010, 32, 54–61. [Google Scholar] [CrossRef]
- Fan, Y.; Luo, F.; Li, M.; Hu, C.; Chen, S. The Multifractal Properties of AR Spectrum and Weak Target Detection in Sea Clutter Background. J. Electron. Inf. Technol. 2016, 38, 455–463. [Google Scholar] [CrossRef]
- Guan, J.; Liu, N.B.; Huang, Y.; He, Y. Fractal characteristic in frequency domain for target detection within sea clutter. IET Radar Sonar Navig. 2012, 6, 293–306. [Google Scholar] [CrossRef]
- Chen, X.L.; Guan, J.; He, Y.; Zhang, J. Detection of low observable moving target in sea clutter via fractal characteristics in fractional Fourier transform domain. IET Radar Sonar Navig. 2013, 7, 635–651. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Liu, H. Small target detection in sea clutter based on Doppler spectrum features. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar]
- Shui, P.-L.; Li, D.; Xu, S. Tri-feature-based detection of floating small targets in sea clutter. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1416–1430. [Google Scholar] [CrossRef]
- Li, Y.; Xie, P.; Tang, Z.; Jiang, T.; Qi, P. SVM-based sea-surface small target detection: A false-alarm-rate-controllable approach. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1225–1229. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Tao, J. Decision tree based sea-surface weak target detection with false alarm rate controllable. IEEE Signal Process. Lett. 2019, 26, 793–797. [Google Scholar] [CrossRef]
- Guo, Z.; Shui, P.; Bai, X.; Xu, S.; Li, D. Sea-Surface small target detection based on K-NN with controlled false alarm rate in sea clutter. J. Radars 2020, 9, 654–663. [Google Scholar] [CrossRef]
- Shi, S.-N.; Shui, P.-L. Sea-surface floating small target detection by one-class classifier in time-frequency feature space. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6395–6411. [Google Scholar] [CrossRef]
- Zhou, A.-H.; Feng, J. Deep forest: Towards an alternative to deep neural networks. In Proceedings of the 26th International Joint Conference on Artificial Intelligence (IJCAI’17), Melbourne, Australia, 19–25 August 2017; pp. 3553–3559. [Google Scholar]
- Zhang, J.; Song, H.; Zhou, B. SAR Target Classification Based on Deep Forest Model. Remote Sens. 2020, 12, 128. [Google Scholar] [CrossRef] [Green Version]
- Shui, P.; Guo, Z.; Shi, S. Feature-Compression-Based Detection of Sea-Surface Small Targets. IEEE Access 2019, 8, 8371–8385. [Google Scholar] [CrossRef]
- The Dartmouth Database [DB/OL]. Available online: http://soma.ece.mcmaster.ca/ipix/dartmouth/index.html (accessed on 10 November 2020).
- Maps and Pictures of the IPIX Radar at OHGR/Dartmouth [DB/OL]. Available online: http://soma.ece.mcmaster.ca/ipix/dartmouth/ohgrmaps.html (accessed on 10 November 2020).
- Wind, Waves, Weather during Data Collection at OHGR/Dartmouth [DB/OL]. Available online: http://soma.ece.mcmaster.ca/ipix/dartmouth/windwave.html (accessed on 10 November 2020).
- Guo, L.; Cheyoung, K. Light-scattering models for a spherical particle above a slightly dielectric rough surface. Microw. Opt. Technol. Lett. 2002, 33, 142–146. [Google Scholar]
- Guo, L.; Wang, Y.; Wu, Z. Research on Backward Compound Electromagnetic Scattering and Doppler Spectrum of Dynamic Sea Surface and Moving Spherical Target. Sci. China Ser. G 2008, 38, 34–45. [Google Scholar]
- Jia, L.; Guo, L.; Li, J. Research on Compound Electromagnetic Scattering from Sea Surface and Three-dimensional Floating Target Above Based on FDTD Method. Aero Weaponry 2015, 6, 8–13. [Google Scholar]
- Long, M.W. Radar reflectivity of land and sea. DCHC 1975. [Google Scholar] [CrossRef]
- Wang, X.S.; Yang, Y. Overview on cognition of clutter and target polarization characteristics for maritime radar. Chin. J. Radio Sci. 2019, 34, 665–6675. (In Chinese) [Google Scholar] [CrossRef]
- Zuo, L.; Chan, X.; Lu, X.; Li, M. A weak target detection method in sea clutter based on joint space-time-frequency decomposition. J. Radars 2019, 8, 335–343. [Google Scholar] [CrossRef]
- Gini, F.; Farina, A.; Montanari, M. Vector subspace detection in compound-Gaussian clutter, part II: Performance analysis. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 1312–1323. [Google Scholar] [CrossRef]
- Conte, E.; Farina, A.; De Maio, A. Design and analysis of a knowledge-aided radar detector for doppler processing. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1058–1079. [Google Scholar] [CrossRef]
- Jeong, J.; Williams, W.J. Kernel design for reduced interference distributions. IEEE Trans. Signal Process 1992, 40, 402–412. [Google Scholar] [CrossRef]
- Krogh, A.; Vedelsby, J. Neural Network Ensembles, Cross Validation, and Active Learning. In International Conference on Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1995; pp. 231–238. [Google Scholar]
- Liu, N.; Dong, Y.; Wang, G.; Ding, H.; He, Y. Sea-detecting X-band radar and data acquisition program. J. Radars 2019, 8, 656–667. [Google Scholar] [CrossRef]







| Parameter Name | Value |
|---|---|
| Radar carried frequency | 9.39 GHz |
| Pulse length | 200 nanoseconds |
| PRF | 1000 Hz |
| Antenna beamwidth | 0.9 degrees |
| Antenna gain | 45.7 dB |
| Range cell | (2574 2589 … nrange … 2769) meters |
| Azimuth angle | (129.4958 129.4958 … nsweep … 129.5453) degrees |
| Elevation angle | (359.5111 359.5111 … nsweep … 359.5111) degrees |
| Unambiguous velocity | 7.892 m/s |
| Range resolution | 30 m |
| Data format | (nsweep × ntxpol × nrange × nadc) ADC output |
| nsweep | 131,072 |
| ntxpol | 2 |
| nrange | 14 |
| nadc | 4 |
| Working mode | Resident mode |
| Number | Data Name | Target Cell (Primary) | Target Cell (Secondary) | Wave Height (m) 1 | Wind Speed (km/h) |
|---|---|---|---|---|---|
| 1 | 19931107_135603_starea | 9 | 8–11 | 2.01 | 9 |
| 2 | 19931107_141630_starea | 9 | 8–11 | 2.01 | 9 |
| 3 | 19931107_145028_starea | 8 | 7–9 | 2.01 | 13 |
| 4 | 19931108_213827_starea | 7 | 6–8 | 0.98 | 9 |
| 5 | 19931108_220902_starea | 7 | 6–8 | 1.10 | 9 |
| 6 | 19931109_191449_starea | 7 | 6–8 | 0.89 | 19 |
| 7 | 19931109_202217_starea | 7 | 6–9 | 0.89 | 19 |
| 8 | 19931110_001635_starea | 7 | 5–8 | 1.01 | 9 |
| 9 | 19931111_163625_starea | 8 | 7–10 | 0.63 | 20 |
| 10 | 19931118_023604_stareC0000 | 8 | 7–10 | 1.69 | 10 |
| 11 | 19931118_035737_stareC0000 | 10 | 8–12 | 1.69 | 7 |
| 12 | 19931118_162155_stareC0000 | 7 | 6–9 | 0.91 | 33 |
| 13 | 19931118_162658_stareC0000 | 7 | 6–9 | 0.91 | 33 |
| 14 | 19931118_174259_stareC0000 | 7 | 6–9 | 0.91 | 28 |
| Predicted Class | Summary | |||
|---|---|---|---|---|
| Target | Clutter | |||
| Actual Class | Target | True target (TT) | False clutter (FC) | Actual Target (TT + FC) |
| Clutter | False target (FT) | True clutter (TC) | Actual Clutter (FT + TC) | |
| Summary | Predicted target (TT + FT) | Predicted clutter (FC + TC) | TT + FT + FC + TC | |
| Algorithm: FAR-Controllable Deep Forest Model. |
| Input: |
| Dataset: eigenvector matrix , is 6-dim eigenvector ; |
| Label set: ; |
| Expected FAR: ; |
| Error threshold: ; |
| Preset depth of gcForest: ; |
| Step length of depth: ; |
| Maximum depth of gcForest: |
| Parameters of gcForest. |
| Process: |
| 1: Set the parameters and feed the features into the gcForest for training. |
| 2: Calculate the minimum achievable FAR, |
| . |
| 3: if or then |
| 4: save all that satisfies the condition in |
| 5: else |
| 6: while do |
| 7: if then |
| 8: continue training the cascade layer of gcForest |
| 9: calculate the new outputs’ of the cascade layer |
| 10: else |
| 11: set |
| 12: if then |
| 13: break |
| 14: continue training the cascade layer of gcForest |
| 15: calculate the new outputs’ of cascade layer |
| 16: save all the in |
| 17: end if |
| 18: end while |
| 19: end if |
| 20: return FAR = max (). |
| Output: |
| The ideal FAR model and its prediction results of the training set. |
| gcForest Models | Parameter Setting | |
|---|---|---|
| Multi-Grained Scanning | Number of classifiers | 6 |
| Types of classifiers | ExtraTreesClassifier | |
| RandomForestClassifier | ||
| LogisticRegression | ||
| Size of sliding panes | 4, 5, 6 | |
| Cascade | Number of classifiers | 5 |
| Types of classifiers | RandomForestClassifier | |
| ExtraTreesClassifier | ||
| XGBClassifier | ||
| SGDClassifier | ||
| LogisticRegression | ||
| Preset depth of gcForest | 6 | |
| Step length of gcForest | 2 | |
| Maximum depth of gcForest | 14 | |
| Different Polarization Mode | ||||
| Polarization Mode | HH | HV | VH | VV |
| Average | 99.24% | 99.33% | 99.31% | 98.86% |
| Different Observation Time | ||||
| Observation Time (s) | 0.512 | 1.024 | 2.048 | 4.096 |
| Average | 98.65% | 99.10% | 99.38% | 99.62% |
| Layers of gcForest | Parameter |
|---|---|
| Multi-Grained Scanning | Number of classifiers |
| Types of classifiers | |
| Size of sliding panes | |
| Cascade | Number of classifiers |
| Types of classifiers | |
| Preset depth of gcForest | |
| Step length of gcForest | |
| Maximum depth of gcForest |
| Size of Sliding Panes | ExtraTreesClassifier | RandomForestClassifier | LogisticRegression | |||
|---|---|---|---|---|---|---|
| Train Avg. | Test Avg. | Train Avg. | Test Avg. | Train Avg. | Test Avg. | |
| 1 | 91.11% | 91.03% | 91.62% | 91.52% | 91.11% | 91.03% |
| 2 | 91.47% | 91.03% | 98.22% | 98.20% | 91.11% | 91.03% |
| 3 | 91.11% | 91.03% | 99.03% | 99.03% | 91.11% | 91.03% |
| 4 | 98.30% | 98.37% | 99.23% | 99.24% | 93.97% | 93.98% |
| 5 | 99.02% | 99.01% | 99.40% | 99.37% | 94.51% | 94.50% |
| 6 | 99.25% | 99.23% | 99.50% | 99.46% | 97.09% | 97.07% |
| Observation Time (s) | Polarization Mode | Average FAR of Different Observation Time | |||
|---|---|---|---|---|---|
| HH | HV | VH | VV | ||
| 0.512 | 0.0097 | 0.0094 | 0.0093 | 0.0109 | 0.0098 |
| 1.024 | 0.0075 | 0.0059 | 0.0059 | 0.0105 | 0.0075 |
| 2.048 | 0.0045 | 0.0041 | 0.0051 | 0.0082 | 0.0055 |
| 4.096 | 0.0031 | 0.0029 | 0.0027 | 0.0047 | 0.0034 |
| Average FAR of Different Polarization Mode | 0.0062 | 0.0056 | 0.0057 | 0.0086 | |
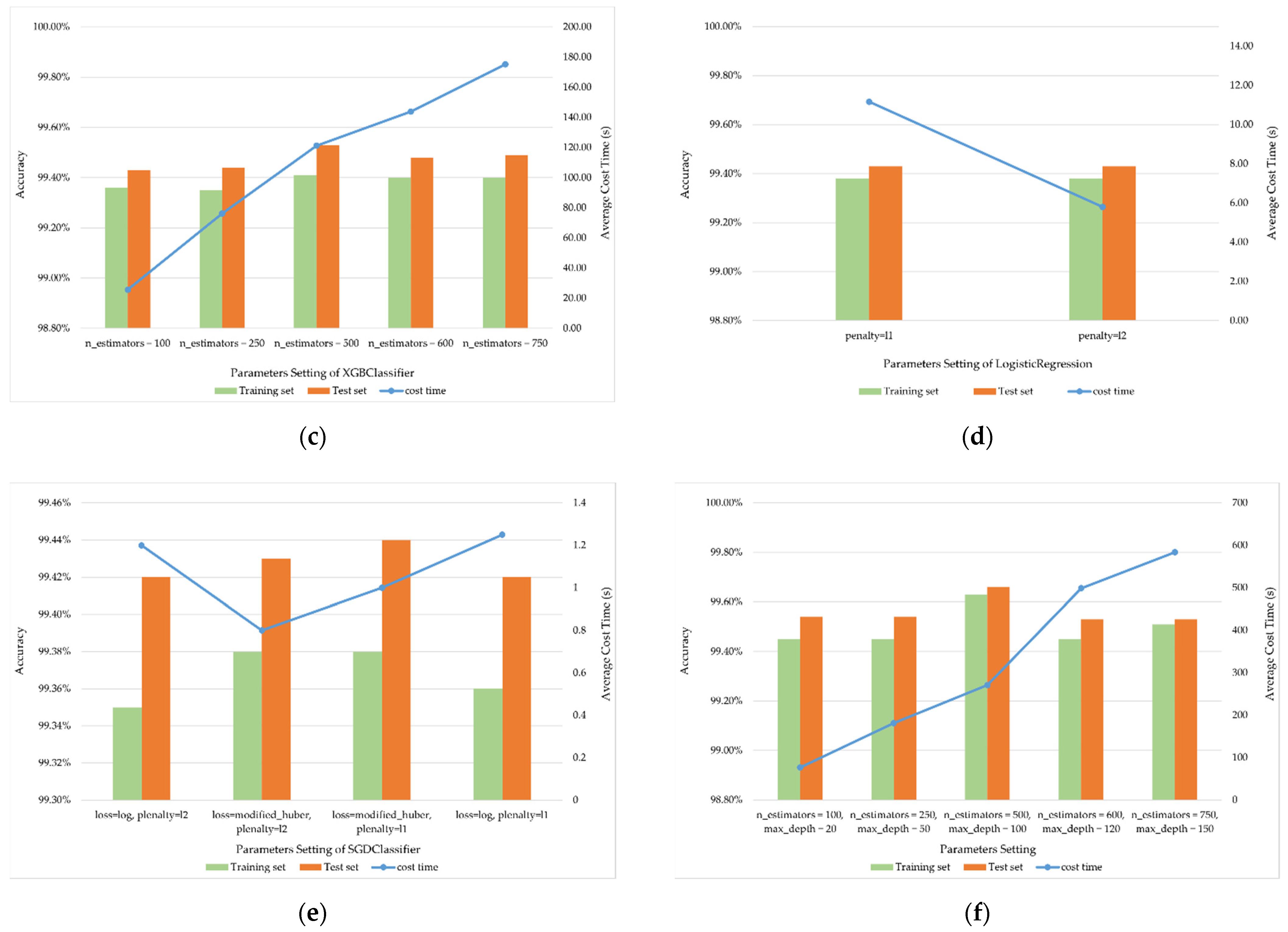
| Estimator | RandomForestClassifier | ExtraTreesClassifier | XGBClassifer | LogisticRegression | SGDClassifier |
|---|---|---|---|---|---|
| Parameters setting | n_estimators = 100, max_depth = 20 | n_estimators = 100 | penalty = l1 | loss = log penalty = l1 | |
| n_estimators = 250, max_depth = 50 | n_estimators = 250 | loss = modified_huber penalty = l1 | |||
| n_estimators = 500, max_depth = 100 | n_estimators = 500 | ||||
| n_estimators = 600, max_depth = 120 | n_estimators = 600 | penalty = l2 | loss = log penalty = l2 | ||
| n_estimators = 750, max_depth = 150 | n_estimators = 750 | loss = modified_huber penalty = l2 | |||
| Observation Time (s) | Polarization Mode | Average of Different Observation Time | |||
|---|---|---|---|---|---|
| HH | HV | VH | VV | ||
| 0.512 | 98.76% | 98.85% | 98.84% | 98.13% | 98.65% |
| 1.024 | 99.09% | 99.29% | 99.30% | 98.72% | 99.10% |
| 2.048 | 99.45% | 99.53% | 99.43% | 99.10% | 99.38% |
| 4.096 | 99.64% | 99.66% | 99.67% | 99.49% | 99.62% |
| Averageof Different Polarization Mode | 99.24% | 99.33% | 99.31% | 98.86% | |
| Removed Feature | RMA | RIET | RPH | RIED | NCR | MSC | |
|---|---|---|---|---|---|---|---|
| Train | HH | 0.15% | 0.12% | 0.40% | 0.32% | 0.14% | 0.45% |
| HV | 2.69% | 0.10% | 0.41% | 0.33% | 0.14% | 0.48% | |
| VH | 0.19% | 0.14% | 0.45% | 0.37% | 0.18% | 0.71% | |
| VV | 0.19% | 0.15% | 0.55% | 0.56% | 0.22% | 0.64% | |
| Average Loss | 0.80% | 0.13% | 0.45% | 0.39% | 0.17% | 0.57% | |
| Test | HH | 0.16% | 0.12% | 0.39% | 0.31% | 0.16% | 0.49% |
| HV | 2.69% | 0.13% | 0.46% | 0.35% | 0.20% | 0.51% | |
| VH | 0.19% | 0.14% | 0.50% | 0.37% | 0.18% | 0.69% | |
| VV | 0.21% | 0.14% | 0.55% | 0.61% | 0.22% | 0.64% | |
| Average Loss | 0.81% | 0.13% | 0.48% | 0.41% | 0.19% | 0.58% | |
| Model | Average Train Accuracy | Average Test Accuracy |
|---|---|---|
| gcForest | 99.63% | 99.66% |
| Multi-layer Perceptron Classifier | 91.11% | 91.02% |
| SVM (Linear Classifier) | 96.91% | 96.96% |
| Logistic Regression | 98.25% | 98.21% |
| K-Nearest Neighbors | 98.50% | 98.24% |
| Gaussian Naive Bayes | 97.52% | 97.44% |
| Xgboost | 99.18% | 99.07% |
| Observation Time (s) | Polarization Mode | ||||
|---|---|---|---|---|---|
| HH | HV | VH | VV | ||
| Proposed detector | 0.512 | 98.76% | 98.85% | 98.84% | 98.13% |
| 1.024 | 99.09% | 99.29% | 99.30% | 98.72% | |
| 2.048 | 99.45% | 99.53% | 99.43% | 99.10% | |
| 4.096 | 99.64% | 99.66% | 99.67% | 99.49% | |
| Fractal-based detector [26] | 0.512 | 58.50% | 68.80% | 69.20% | 58.10% |
| 1.024 | 61.00% | 71.50% | 71.00% | 58.00% | |
| 2.048 | 68.90% | 81.20% | 81.20% | 65.40% | |
| 4.096 | -- | -- | -- | -- | |
| Tri-feature-based detector [32] | 0.512 | 71.40% | 72.60% | 72.70% | 64.50% |
| 1.024 | 75.00% | 76.40% | 76.60% | 72.50% | |
| 2.048 | 82.00% | 82.60% | 82.30% | 72.50% | |
| 4.096 | -- | -- | -- | -- | |
| TF-tri-feature-based detector [36] | 0.512 | 74.70% | 82.60% | 84.20% | 70.60% |
| 1.024 | 82.10% | 88.20% | 87.80% | 78.90% | |
| 2.048 | -- | -- | -- | -- | |
| 4.096 | -- | -- | -- | -- | |
| Feature-compression-based detector [39] | 0.512 | 80.70% | 88.00% | 88.80% | 78.80% |
| 1.024 | 84.10% | 92.00% | 91.40% | 83.90% | |
| 2.048 | -- | -- | -- | -- | |
| 4.096 | -- | -- | -- | -- | |
| Decision tree-based detector [34] | 0.512 | 85.00% | -- | -- | -- |
| 1.024 | 86.00% | -- | -- | -- | |
| 2.048 | 87.00% | -- | -- | -- | |
| 4.096 | 89.00% | -- | -- | -- | |
| K-NN FAR-controlled detector [35] | 0.512 | 82.10% | 88.70% | 89.50% | 80.00% |
| 1.024 | 86.80% | 92.20% | 92.10% | 85.80% | |
| 2.048 | -- | -- | -- | -- | |
| 4.096 | -- | -- | -- | -- | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Song, H. Multi-Feature Fusion for Weak Target Detection on Sea-Surface Based on FAR Controllable Deep Forest Model. Remote Sens. 2021, 13, 812. https://doi.org/10.3390/rs13040812
Zhang J, Song H. Multi-Feature Fusion for Weak Target Detection on Sea-Surface Based on FAR Controllable Deep Forest Model. Remote Sensing. 2021; 13(4):812. https://doi.org/10.3390/rs13040812
Chicago/Turabian StyleZhang, Jiahuan, and Hongjun Song. 2021. "Multi-Feature Fusion for Weak Target Detection on Sea-Surface Based on FAR Controllable Deep Forest Model" Remote Sensing 13, no. 4: 812. https://doi.org/10.3390/rs13040812
APA StyleZhang, J., & Song, H. (2021). Multi-Feature Fusion for Weak Target Detection on Sea-Surface Based on FAR Controllable Deep Forest Model. Remote Sensing, 13(4), 812. https://doi.org/10.3390/rs13040812