Hyperspectral Image Clustering with Spatially-Regularized Ultrametrics

Abstract

We propose a method for the unsupervised clustering of hyperspectral images based on spatially regularized spectral clustering with ultrametric path distances. The proposed method efficiently combines data density and spectral-spatial geometry to distinguish between material classes in the data, without the need for training labels. The proposed method is efficient, with quasilinear scaling in the number of data points, and enjoys robust theoretical performance guarantees. Extensive experiments on synthetic and real HSI data demonstrate its strong performance compared to benchmark and state-of-the-art methods. Indeed, the proposed method not only achieves excellent labeling accuracy, but also efficiently estimates the number of clusters. Thus, unlike almost all existing hyperspectral clustering methods, the proposed algorithm is essentially parameter-free.

1. Introduction

Remote sensing image processing has been revolutionized by machine learning, in particular the labeling of material classes in remotely sensed images. This can take the form of supervised classification, when many labeled pixels are available to help guide the algorithm, or unsupervised clustering, when no labeled pixels are available to the algorithm. When large labeled training sets are available, supervised methods such as kernel methods [1,2,3] and deep neural networks [4,5,6] accurately label pixels in a wide range of imaging modalities. However, it is often impractical to acquire the large training sets necessary for these methods to work well. When human-annotated data is limited, it is necessary to develop unsupervised clustering methods which label the entire data set without the need for training data.

Unsupervised clustering is a classical problem in machine learning, and many methods for unsupervised clustering have been proposed [7]. However, most only enjoy theoretical performance guarantees under very restrictive assumptions on the underlying data. For example, K-means clustering works well for clusters that are roughly spherical and well-separated, but provably fails when the clusters become nonlinear or poorly separated [8]. Clustering methods based on deep learning may perform well in some instances, but are sensitive to metaparameters and lack robust mathematical performance guarantees even in highly idealized settings [9,10,11].

Clustering of remotely sensed hyperspectral images (HSI) is particularly challenging, due to their high-dimensionality, noise, and often poor spatial resolution. Moreover, most existing HSI clustering methods require the number of clusters to be input as a parameter to the algorithm, which is impractical in the unsupervised setting. Despite their challenges, unsupervised HSI clustering methods are increasingly important, because the lack of large training sets prevents supervised learning from being effective on the deluge of HSI data being collected.

Recently, ultrametric path distances (UPD) have been proven to provide state-of-the-art theoretical results for clustering high-dimensional data [12]. In particular, only very weak assumptions on the data are required, namely that the underlying clusters exhibit intrinsically low-dimensional structure and are separated by regions of low density. This suggests UPD are well-suited for HSI [13], which while very high-dimensional, are typically such that each class in the data depends (perhaps nonlinearly) on only a small number of latent variables, and in this sense are intrinsically low-dimensional.

In this paper, we develop an HSI clustering algorithm based on ultrametric spectral clustering. Taking advantage of recent theoretical developments, our approach constructs a weighted graph with nodes corresponding to HSI pixels and edge weights determined by the UPD metric. Crucially, the proposed method spatially regularizes the graph in order to capture important spatial correlations in the HSI. After constructing this spatially regularized UPD graph, the proposed method runs K-means clustering on the lowest frequency eigenfunctions of the graph Laplacian. We call the proposed method spatially regularized ultrametric spectral clustering (SRUSC). SRUSC scales quasilinearly in the number of data points, and has few tunable parameters. Moreover, the proposed method outperforms a range of benchmark and state-of-the-art unsupervised and even supervised classification methods on several synthetic and real HSI in terms of clustering accuracy and efficient estimation of the number of latent clusters. The detection of the number of clusters is particularly significant, because it makes the proposed method essentially parameter-free, unlike nearly all existing methods for clustering HSI.

To summarize, this paper makes three major contributions:

• We propose the SRUSC algorithm for HSI clustering. This method enjoys rich theoretical justification and is intuitively simple, with few sensitive parameters to tune. In particular, SRUSC detects the number of clusters in the HSI.
• We prove performance guarantees on the runtime of SRUSC. This ensures fast performance of SRUSC on high-dimensional data that exhibits intrinsically low-dimensional structure, allowing the proposed method to scale.
• We demonstrate that SRUSC effectively clusters synthetic and real HSI with higher accuracy than a range of benchmark and state-of-the-art methods. Moreover, we show that SRUSC efficiently estimates the number of clusters in these datasets, thereby addressing a major outstanding problem in the HSI clustering literature.

The remainder of this article is organized as follows. In Section 2, we provide background on unsupervised HSI clustering and ultrametric path distances. In Section 3, we motivate and detail the proposed algorithm and discuss its theoretical properties and complexity. In Section 4, we introduce several data sets and perform comparisons between the proposed method and related methods, demonstrating the strong performance of SRUSC not only compared to state-of-the-art unsupervised methods, but compared to supervised methods as well. This section investigates both clustering accuracy and estimation of the number of clusters. We conclude and discuss potential directions for future research in Section 5.

2. Background

We present a problem statement and background on clustering in Section 2.1 before reviewing UPD and spectral clustering in Section 2.2 and Section 2.3, respectively.

2.1. Background on Unsupervised Clustering

The problem of unsupervised clustering consists in providing a data set $X={\left\{x_i\right\}}_{i=1}^n\subset {\mathbb{R}}^D$ with natural group labels corresponding to clusters formed by the data points. Mathematically, there is a set of latent labels ${\left\{y_i\right\}}_{i=1}^n$, where each $y_i\in \{1,2,\dots ,K\}$ and K is the number of latent classes in X. The goal of unsupervised clustering is to learn these labels given X alone; in particular, no training pairs of the form $(x_i,y_i)$ are provided to guide the process. So, labeling decisions must be made entirely based on latent geometrical and statistical properties of the data. The lack of training pairs of the form $(x_i,y_i)$ is the primary challenge of unsupervised clustering, and differentiates it from supervised classification.

A range of methods for clustering data have been developed, including K-means clustering and Gaussian mixture models, which assume the underlying data is a mixture of well-separated, roughly spherical Gaussians [7]; density-driven methods that characterize clusters as high-density regions separated from other high-density regions by regions of low density [14,15]; and spectral graph methods that attempt to find communities in networks generated from the underlying data [8,16].

In the case of HSI, the data may be understood as an $M\times N\times D$ tensor, so that $n=M\times N$ is the number of D-dimensional pixels in the data set and D is the number of spectral bands. For clustering HSI, methods taking advantage of the intrinsically low-dimensional (though potentially nonlinear) structure of the HSI clusters [17,18] are particularly important, because capturing such low-dimensional structures significantly lowers the sampling complexity necessary to defeat the curse of dimensionality [7]. This observation is leveraged by state-of-the-art techniques based on subspace clustering [19,20,21], matrix factorizations [22,23] and nonlinear manifold learning techniques [24,25,26,27]. Recent deep-learning methods can achieve high clustering accuracy [28,29] by computing low-dimensional features using overparametrized neural networks. However, these approaches may perform poorly if the metric used by the deep network to compare pixels cannot discriminate between pixels in the same and different classes, or if the spatial structure of the HSI is not accounted for.

We note that the proposed approach is most comparable with manifold learning methods, though crucially our approach integrates UPD and spatial regularization into the manifold estimation procedure.

2.2. Background on Ultrametric Path Distances

In many clustering algorithms, decisions are based on pairwise distances between data points. The choice of distance metric is thus critical, and a range of non-Euclidean metrics have been developed for high-dimensional HSI, including those based on global covariance matrices [30,31], ${\ell }^1$ geodesic distances [17,32], Laplacian eigenmap distances [33], and diffusion distances [27,34]. Crucially, the selected metric should have the property that points in the same cluster appear close together, while points in different clusters appear far apart. For this reason, we propose to use UPDs, which achieve the desired within-cluster and between-cluster distance properties for a wide class of data.

Let ${\mathcal{G}}_0=(X,W)$ be an undirected Euclidean k-nearest neighbor graph on X, with $k\sim log\left(n\right)$. In the case that ${\mathcal{G}}_0$ is a disconnected graph, edges (weighted by the Euclidean norm) are introduced between the closest points in distinct connected components. For any $x_i,x_j\in X$, let $\mathcal{P}(x_i,x_j)$ be the set of paths connecting $x_i,x_j$ in ${\mathcal{G}}_0$. So, a path ${\left\{{\gamma }_{\ell }\right\}}_{\ell =1}^L\in \mathcal{P}(x_i,x_j)$ is such that ${\gamma }_1=x_i$ and ${\gamma }_L=x_j$. Define the Euclidean ultrametric path distance (UPD) between $x_i,x_j\in X$ as

$$\begin{array}{c}\hfill {\rho }_{\infty }(x_i,x_j)=\underset{{\left\{{\gamma }_{\ell }\right\}}_{\ell =1}^L\in \mathcal{P}(x_i,x_j)}{min}\left(\underset{\ell =1,\dots ,L-1}{max}{\parallel {\gamma }_{\ell +1}-{\gamma }_{\ell }\parallel }_2\right).\end{array}$$

(1)

Intuitively, UPD computes the maximal edge length in each path, then minimizes this quantity over all paths. It may be understood as an ${\ell }^{\infty }$-geodesic, while the classical shortest path is the ${\ell }^1$-geodesic. Two points are far apart in the UPD if every path between them has at least one large edge. Compared to the ${\ell }^1$ geodesic, which is density-agnostic, the UPD prefers paths that avoid low-density regions. Like classical shortest paths, it may be computed efficiently using a Dijkstra-type algorithm [35]. A comparison of Euclidean distances and UPD is in Figure 1.

For clustering data generated from mixtures of manifolds, the UPD is extremely robust to diffuse background noise (e.g., uniformly sampled background points), and enjoys excellent performance guarantees for distinguishing between points in the same and different clusters [12]. Indeed, UPD have the property that for separated clusters with sufficiently many points, ${\rho }_{\infty }(x,y)$ is uniformly small when $x,y$ lie in the same cluster and uniformly large when x and y lie in distinct clusters. This holds even for high-dimensional data, as long as the underlying clusters are low-dimensional (e.g., localize near noisy subspaces or Riemannian manifolds) and background noise does not concentrate in high density regions. These desirable properties are not held by classical metrics such as Euclidean distances, and suggest the utility of UPD for HSI clustering. In particular, we propose to leverage the desirable properties of UPD by incorporating it into the spectral clustering algorithm.

We remark that UPD are not universally appropriate as a metric for clustering, and in particular will fail to distinguish overlapping clusters that are generated by sampling uniformly (i.e., the overlapping clusters with approximately constant density). However, overlapping clusters in which the overlapping regions are low-density are suitable for UPD [36], for example overlapping Gaussian clusters.

2.3. Background on Spectral Clustering

Spectral clustering uses low-frequency eigenfunctions of a graph Laplacian as new coordinates for high-dimensional, nonlinear data, on which a traditional clustering algorithm can be run (e.g., K-means or Gaussian mixture models) [37]. For data $X={\left\{x_i\right\}}_{i=1}^n\subset {\mathbb{R}}^D$ and metric $\rho :{\mathbb{R}}^D\times {\mathbb{R}}^D\to [0,\infty )$, define a weighted, undirected graph $\mathcal{G}$ with nodes X and weighted edges $W_{ij}=exp(-\rho {(x_i,x_j)}^2/{\sigma }^2)$. The scaling parameter $\sigma$ can be tuned manually, or set automatically [38]. Intuitively, there will be a strong edge between $x_i,x_j$ in $\mathcal{G}$ if and only if $\rho (x_i,x_j)$ is small relative to $\sigma$.

A natural approach to clustering is to partition $\mathcal{G}$ into K communities that are internally large and well-connected and externally weakly connected. This may be formulated precisely in terms of the normalized cuts functional, which leads to an NP-hard computational problem [16]. This graph cut problem may be relaxed by considering eigenvectors of the graph Laplacian, which determine natural clusters in $\mathcal{G}$ in polynomial time [8,16]. Indeed, let D be the diagonal degree matrix with $D_{ii}={\sum }_{j=1}^n{W}_{ij}$. Let $L=I-D^{-1/2}W{D}^{-1/2}$ be the (symmetric normalized) graph Laplacian. Note $L\in {\mathbb{R}}^{n\times n}$ is positive semi-definite, with a number of zero eigenvalues equal to the number of connected components in $\mathcal{G}$.

The spectral clustering algorithm (Algorithm 1) computes the lowest frequency eigenvectors ${\left\{{\varphi }_k\right\}}_{k=1}^K$ of L (those with smallest eigenvalues) and uses them as features in K-means clustering [8]. Note that we formulate Algorithm 1 as taking only W and a number of clusters K as an input. In practice, W must be computed using some metric $\rho$. While the Euclidean metric $\rho (x_i,x_j)={\parallel x_i-x_j\parallel }_2$ is common, other metrics may provide superior performance [12,39,40]. Indeed, the metric should be chosen so that points in the same cluster appear well-connected, while points in different clusters are well-separated [41]. Our approach recognizes that spatially-regularized UPD achieves this for high-dimensional, noisy HSI.

Algorithm 1 Spectral Clustering (SC)

Input:W, K; Output:${\left\{y_i\right\}}_{i=1}^n$ 1: Compute the diagonal degree matrix $D\in {\mathbb{R}}^{n\times n}$.   2: Compute $L=I-D^{-\frac{1}{2}}W{D}^{-\frac{1}{2}}$.   3: Compute the K lowest-frequency eigenvector and eigenvalue pairs ${\left\{({\varphi }_k,{\lambda }_k)\right\}}_{k=1}^K$, sorted so that $0={\lambda }_1\le {\lambda }_2\le \dots \le {\lambda }_K$.   4: For $1\le i\le n$, let $$\tilde{\varphi }\left(x_i\right)=\frac{({\varphi }_1\left(x_i\right),{\varphi }_2\left(x_i\right),\dots ,{\varphi }_K\left(x_i\right))}{\left|\right|({\varphi }_1\left(x_i\right),{\varphi }_2\left(x_i\right),\dots ,{\varphi }_K\left(x_i\right)){\left|\right|}_2}.$$ 5: Compute labels ${\left\{y_i\right\}}_{i=1}^n$ by running K-means on the data ${\left\{\tilde{\varphi }\left(x_i\right)\right\}}_{i=1}^n$ using K as the number of clusters.

3. Algorithm

The proposed SRUSC method (Algorithm 2) consists in performing spectral clustering using the UPD ${\rho }_{\infty }$ and a spatially regularized graph Laplacian. The use of ${\rho }_{\infty }$ makes points in the same cluster appear close together, as long as there is a high-density path connecting them, while pushing apart points in distinct clusters separated by a density gap. The spatial regularization accounts for the image structure of the HSI and the latent spatial smoothness of the labels on the HSI.

Mathematically, let

$$\begin{array}{c}\hfill W_{ij}=\left\{\begin{array}{cc}exp(-{\rho }_{\infty }{(x_i,x_j)}^2/{\sigma }^2),\hfill & x_i\in B_r\left(x_j\right),\hfill \\ 0,\hfill & x_i\notin B_r\left(x_j\right),\hfill \end{array}\right.\end{array}$$

(2)

where $B_r$ is the set of all pixels in the full image whose spatial coordinates lie inside the square with side lengths r centered at $x_i$. For points within spatial distance r of an image boundary, no periodic extension of the spatial square is applied; these points are simply connected to fewer points than interior points. The constraint that $W_{ij}=0$ if $x_i\notin B_r\left(x_j\right)$ or $x_j\notin B_r\left(x_i\right)$ enforces spatial regularity in the graph: a pixel can only be connected to spatially proximal pixels. Spatial regularization has been shown to improve clustering performance for HSI, by producing clusters that are smoother with respect to the underlying spatial structure [24,34]. It also has a sparsifying effect, since W has only $\sim r^{2}n$ non-zero entries. This affords a substantial computational advantage in the subsequent eigenvector calculation when $r^2\ll n$. Note also that outlier denoising may be performed as a pre-processing step, by removing any points whose $k^{th}$ nearest neighbor distance in ${\rho }_{\infty }$ exceeds a threshold $T>0$. This accounts for high-dimensional outliers that are known to be problematic for spectral clustering [36]. The labels of these (typically very few) points are computed by a majority vote in a local spatial neighborhood at the final step. In some of our experiments, we found this a helpful pre-processing step. While not strictly necessary, we include this optional pre-processing step as part of Algorithm 2.

Algorithm 2 Spatially Regularized Ultrametric SC (SRUSC), $K,\sigma$ known

Input:${\left\{x_i\right\}}_{i=1}^n,r,\sigma ,K;(\mathrm{Optional}:k,T,r_v$); Output:${\left\{y_i\right\}}_{i=1}^n$ 1: (Optional) Denoise the data by removing all points whose $k^{th}$ nearest neighbor distance in ${\rho }_{\infty }$ exceeds T.   2: Construct W on the remaining points as in (2).   3: Run Algorithm 1 with inputs W, K.   4: (Optional) Assign labels to the points removed by denoising according to a majority vote in a spatial neighborhood of radius $r_v$.

By connecting pixels with strong edges only if they are (i) spectrally close in UPD and (ii) spatially proximal, the resulting graph Laplacian detects communities corresponding to well-connected and spatially coherent clusters. This makes it well-suited to HSI, which often exhibit classes with those properties.

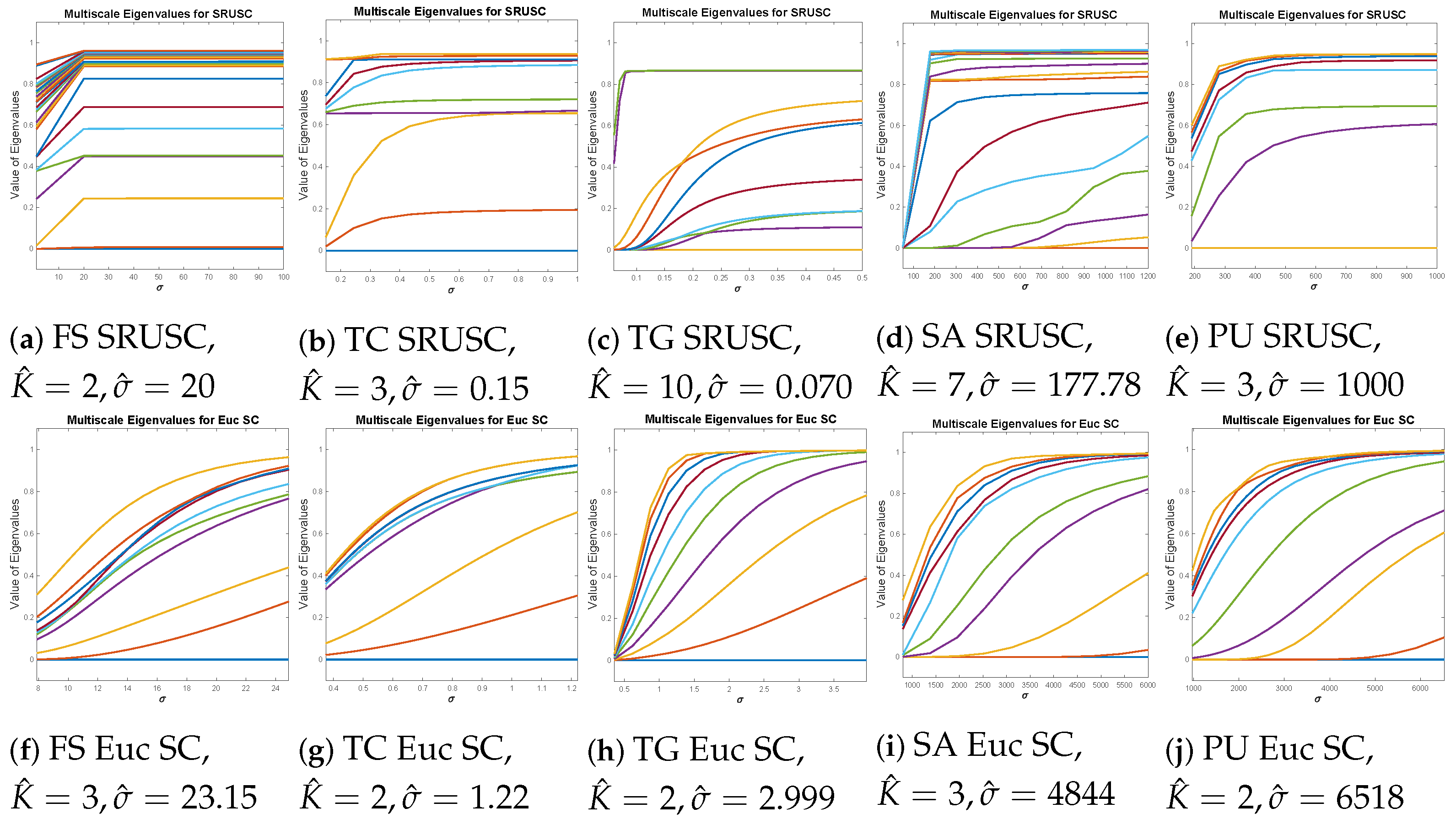
3.1. Discussion of Parameters

The parameters of Algorithm 2 are $r,\sigma$, and K, along with the optional denoising parameters $k,T,r_v$. Spatially regularized spectral graph methods are typically robust to the choice of spatial radius r, and many automated methods exist for determining the scaling parameter $\sigma$ in spectral clustering [38]. Theoretically, the denoising is highly robust to the choice of k and T, because there is a clear gap between inliers and outliers when using ${\rho }_{\infty }$ [12]. In practice on the datasets for which we denoised, we set $k=20$ and the voting radius $r_v$ to be as small as possible while maintaining that at least 10 non-denoised points are in each ball.

Estimation of K

On the other hand, the number of clusters K is notoriously challenging to estimate, particularly for data with nonlinear or elongated shapes. A commonly employed heuristic in spectral clustering is the eigengap heuristic, which estimates $\widehat{K}={arg\; max}_k{\lambda }_{k+1}-{\lambda }_k$. However, this depends strongly on the scaling parameter $\sigma$ used to construct the underlying graph. One can instead consider a multiscale eigengap [12,42], which simultaneously maximizes over the eigenvalue index and over $\sigma$:

$$(\widehat{K},\widehat{\sigma })=\underset{\sigma \in S,k\in \{1,\dots ,K_0\}}{arg\; max}({\lambda }_{k+1}\left(\sigma \right)-{\lambda }_k\left(\sigma \right)),$$

(3)

where $S={\left\{{\sigma }_j\right\}}_{j=1}^J$ is a predetermined range of scaling parameter values, $K_0$ is an upper bound on the number of clusters, and ${\lambda }_k\left(\sigma \right)$ is the $k^{th}$-largest eigenvalue of the graph Laplacian L when it is computed using a weight matrix W with scaling parameter $\sigma$. The estimated optimal parameters $(\widehat{K},\widehat{\sigma })$ are chosen to maximize this multiscale eigengap by varying over k and $\sigma$ simultaneously. This yields a nearly totally unsupervised algorithm, in which the user need only specify the spatial radius r, a range S of candidate $\sigma$ values, and an upper bound on the number of clusters $K_0$. Making the choices suggested above, this nearly parameter-free algorithm is summarized in Algorithm 3.

Algorithm 3 Spatially Regularized Ultrametric SC (SRUSC), $K,\sigma$ unknown

Input:${\left\{x_i\right\}}_{i=1}^n,r,S,K_0$; Output:${\left\{y_i\right\}}_{i=1}^n$ 1: For $\sigma \in S$, construct $W_{\sigma }$ as in (2).   2: For $\sigma \in S$, compute the eigenvalues ${\left\{{\lambda }_k\left(\sigma \right)\right\}}_{k=1}^{K_0}$ of the Laplacian constructed from $W_{\sigma }$.   3: Compute (${\displaystyle \widehat{K},\widehat{\sigma })=\underset{\sigma \in S,k\in \{1,\dots ,K_0\}}{arg\; max}({\lambda }_{k+1}\left(\sigma \right)-{\lambda }_k\left(\sigma \right))}$.   4: Run Algorithm 1 with inputs $W_{\widehat{\sigma }}$, $\widehat{K}$.

Computationally, Algorithm 3 loops over the elements of S, and is therefore slower than Algorithm 2. However, under the very reasonable assumptions that $\left|S\right|=O\left(1\right)$ with respect to n (i.e., the number of candidate scaling parameters does not increase with n) and that $K_0=O\left(1\right)$ with respect to n (i.e., the number of clusters is constant with respect to n) the computational complexity of Algorithm 3 is still quasilinear in n. In practice, we set $K_0=20$ for all experiments and S to be 20 equally spaced points covering the range of ${\rho }_{\infty }$-distances in the data.

3.2. Computational Complexity

A benefit of the proposed method is that when r is small and the number of clusters K does not grow with n, Algorithm 2 (and similarly Algorithm 3) is fast, as quantified in the following theorem.

Theorem 1.

The computational complexity of Algorithm 2 is $O(r^{2}nlog\left(n\right))$.

Proof. 

Note that the graph Laplacian L constructed in the proposed method is $r^2$-sparse. Since the cost of computing ${\rho }_{\infty }(x_i,x_j)$ is proportional to the number of edges in the underlying graph ${\mathcal{G}}_0$, the complexity of computing L is $O\left(r^{2}nk\right)$, where k is the number of nearest neighbors in ${\mathcal{G}}_0$. It is known that $k\sim log\left(n\right)$ is sufficient to ensure that with high probability the UPD on a k-nearest neighbors graph and UPD on the fully connected graph are the same [12,43]. For such a k, the computation of L is $O(r^{2}nlog\left(n\right))$. Once L is computed, getting the $K=O\left(1\right)$ lowest frequency eigenvectors is $O\left(r^{2}n\right)$ using iterative methods [44]. Finally, running K-means via Lloyd’s algorithm on these eigenvectors is $O\left(n\right)$ when the number of iterations is constant with respect to n. This gives an overall complexity of

$$O(r^{2}nlog\left(n\right)+r^{2}n+n)=O(r^{2}nlog\left(n\right)).$$

 □

This scaling is essentially optimal with respect to n, since loading the underlying data into memory already has complexity $O\left(n\right)$. Note, however, that sparsity of the underlying matrix L is necessary to achieve quasilinear scaling. In particular, if r is too large, then SRUSC may not scale to large data sets. We remark that the quasilinear scaling of SRUSC matches the quasilinear scaling achieved by traditional spectral clustering on sparse graphs.

4. Experimental Analysis

To validate the proposed method, we perform clustering experiments on five data sets: three synthetic HSI and two real HSI.

The first synthetic data set is denoted “Four Spheres" (FS), and is generated as follows. Consider four centers in ${\mathbb{R}}^2$, $(1,3),(1,5),(1,7)$, and $(5,5)$, and a fixed radius 1.7. To generate a synthetic pixel associated to one of these centers, 99 samples are generated from the corresponding sphere with the given center and radius $1.7+ϵ$, $ϵ$ generated uniformly at random from $[0,1]$. These 99 samples are concatenated to form a vector in ${\mathbb{R}}^{198}$, with uniform samples from ${[0,1]}^2$ used to pad and create a vector in ${\mathbb{R}}^{200}$. We generate 4900 points associated to each center in this way. There are 2 clusters: the union of points associated to the centers $(1,3),(1,5)$ and $(1,7)$; and the points associated to the center $(5,5)$. The idea is that each of the four centers generate samples that are separable by a nonlinear boundary, but the fourth center is substantially further from the first three. Thus, the most natural number of clusters is 2. It is expected that this data set will be challenging due to the nonlinear cluster boundaries, lack of separability in the last two coordinates, and large within-cluster variances. Each of the 4 groups of 4900 points are spatially arrayed to be $140\times 35$, then are concatenated spatially into a $140\times 140\times 200$ synthetic HSI; see Figure 2.

The second synthetic data set is denoted “Three Cubes” (TC) and consists of three clusters, generated as follows. Vectors are sampled uniformly from ${[0,1]}^3$, then padded with zeros to make vectors in ${\mathbb{R}}^{199}$. These points are then concatenated and rotated by an orthogonal matrix sampled uniformly at random by performing a QR-decomposition on a random Gaussian matrix. The data is then embedded in ${\mathbb{R}}^{200}$ by padding all the data with 0 in the 200^th coordinate. Finally, the second cluster is translated by $(0,0,\dots ,0,.1)$ and the third cluster by $(0,0,\dots ,0,.2)$. In this sense, the clusters are intrinsically 3-dimensional cubes, embedded and separated in a high-dimensional ambient space [45]. Each cube contains 13824 points, spatially arrayed to be $144\times 96$. These clusters are concatenated spatially into a $144\times 288\times 200$ synthetic HSI; see Figure 3. To demonstrate the necessity of spatial regularization, we randomly select 30 points from the middles of cluster 1 and cluster 3 and swap them. This can be understood as adversarial noise, to which we expect spatially regularized methods to be robust. This presupposes a kind of spatial regularity in this synthetic image that is often, but not always, reasonable for real data (e.g., it may be reasonable for HSI of natural scenes, but not urban ones).

The third synthetic data set is generated by sampling 5000 data points from 10 different overlapping Gaussians in ${\mathbb{R}}^5$, each with different mean and the same covariance matrix. The means for ten Gaussian are of the form $\frac{k}{\sqrt{5}}(1,1,1,1,1)$, where $k=1,2,\dots ,10$ with common covariance matrix $\frac{1}{20\sqrt{5}}{I}_{5\times 5}$. The 5-dimensional data are then padded with 0s to create data in ${\mathbb{R}}^{100}$, then rotated by a random orthogonal matrix, similar to the FS data. We label each point according to which Gaussian mean it is nearest; this accounts for the overlap in the Gaussians. The synthetic spectral data data is then arranged so that the first $25\times 20$ rectangle of synthetic spectra are sampled from the first Gaussian, the second $25\times 20$ rectangle are sampled from the second Gaussian, and so on. Therefore, the size of the data is $25\times 200$ and each class has 500 pixels; see Figure 4.

We also consider two real HSI data sets: the Salinas A and Pavia U data sets (http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes, accessed on 1 August 2019). Visualizations of the real HSI, along with their partial ground truth, are in Figure 5 and Figure 6, respectively. Note that both of these data sets contain a relatively small number of classes; in the case of Pavia U we chose to crop a small subregion to use for experiments, due to both the well-documented challenges of using too many ground truth classes for unsupervised HSI clustering of real data [46], and in order to ensure that most pixels in the image had ground truth labels.

4.1. Comparison Methods

We compare with four benchmark clustering methods, as well as five state-of-the-art methods. The four benchmark methods are:

• K-Means (KM) clustering [47];
• K-Means clustering on data that has been dimension-reduced with PCA by projecting the data onto the space defined by the first K principal components;
• Gaussian Mixture Models (GMM) [47];
• Spectral Clustering (SC) using Euclidean distance [8]

The five state-of-the-art methods are:

• Diffusion Learning (DL) (https://jmurphy.math.tufts.edu/Code/, accessed on 1 January 2020) [27,48];
• Density Peaks Clustering (DPC) (https://people.sissa.it/~laio/Research/Res_clustering.php, accessed on 1 January 2020) [15];
• Hierarchical Nonnegative Matrix Factorization (NMF) (https://sites.google.com/site/nicolasgillis/code, accessed on 1 January 2017) [22];
• Laplacian-Regularized Low-Rank Subspace Clustering (LLRSC) [20];
• Local Covariance Matrix Representation (LCMR) (https://github.com/henanjun/LCMR, accessed on 1 January 2020) [49]

The DL and NMF methods have, in particular, shown excellent performance on HSI while enjoying a high degree of theoretical interpretability. In Section 4.2, we assume the number of clusters K is known a priori. In Section 4.4, we show how the proposed method can estimate K.

We note the LCMR method is a supervised learning algorithm. After dimension reduction, the algorithm uses the cosine distance to compute the local neighboring data points, and applies the covariance matrix representation to each data point. Finally, an SVM uses the covariance matrices as the inputs to label the images. The algorithm uses a number of training labels equal to $5K$, where as always K is the number of classes in the ground truth. The purpose of including this supervised method amongst the unsupervised comparison methods is to demonstrate the effectiveness of SRUSC even compared to supervised ones which have access to labeled training data.

4.2. Clustering Accuracy

To perform quantitative comparisons, we align each clustered data set with the ground truth by solving a linear assignment problem with the Hungarian algorithm [50]. Then, three accuracy measures are computed: overall accuracy (ratio of correctly labeled pixels to total number of pixels), denoted OA; average accuracy (the average OA on each class), denoted AA; and Cohen’s $\kappa$ statistic [51]. Numerical results are in

Table 1. Results for clustering experiments. We see that across all methods and data sets, the proposed SRUSC method gives the best clustering performance.

Data Set	FS AA	TC AA	TG AA	SA AA	PU AA	FS OA	TC OA	TG OA	SA OA	PU OA	FS $\mathit{\kappa }$	TC $\mathit{\kappa }$	TG $\mathit{\kappa }$	SA $\mathit{\kappa }$	PU $\mathit{\kappa }$
KM	1.00	1.00	1.00	0.66	0.58	1.00	1.00	1.00	0.63	0.60	1.00	1.00	1.00	0.53	0.09
PCA	1.00	1.00	1.00	0.85	0.67	1.00	1.00	1.00	0.80	0.79	1.00	1.00	1.00	0.76	0.39
GMM	0.51	1.00	0.62	0.58	0.80	0.56	1.00	0.62	0.59	0.57	0.51	1.00	0.58	0.48	0.36
SC	1.00	1.00	0.58	0.72	1.00	1.00	1.00	0.58	0.76	1.00	1.00	1.00	0.53	0.69	1.00
DL	0.77	1.00	1.00	0.88	0.38	0.66	1.00	1.00	0.83	0.60	0.77	1.00	1.00	0.79	0.07
DPC	0.77	0.33	1.00	0.61	0.34	0.66	0.33	1.00	0.63	0.65	0.77	0.33	1.00	0.54	0.03
NMF	0.94	1.00	1.00	0.67	0.59	0.90	1.00	1.00	0.64	0.76	0.94	1.00	1.00	0.54	0.52
LLRSC	0.75	1.00	0.86	0.75	0.67	0.62	1.00	0.86	0.77	0.79	0.75	1.00	0.85	0.75	0.67
LCMR	0.94	0.62	0.89	0.79	0.99	0.94	0.62	0.89	0.76	0.99	0.95	0.62	0.88	0.71	0.98
SRUSC	1.00	1.00	1.00	0.89	1.00	1.00	1.00	1.00	0.85	1.00	1.00	1.00	1.00	0.81	1.00

, with visual results in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. Note that the accuracy metrics are only computed on pixels that have ground truth labels. Moreover, the alignments were made to maximize OA, and different alignments may be realized if AA or $\kappa$ are maximized.

We see that across all datasets, SRUSC outperforms all comparison methods. While many methods perform well on the synthetic data, only SRUSC performs well on both of the real data sets as well. Generally, SC and DL perform second best, which makes sense since they are also graph-based methods. Remarkably, the proposed method even outperforms the supervised LCMR method, which makes use of labeled training data to predict.

4.3. Discussion of Tunable Parameters

There are three major parameters to tune for the proposed method (Algorithm 3): $r,S,K_0$. The spatial radius r needs to be chosen large enough to capture important spatial patterns in the data, but not so large that many spatially disparate pixels in the image are connected. We found many choices of r were suitable for each data set, and that this was not a parameter to which SRUSC was extremely sensitive. The range of $\sigma$ values, S, should be chosen to cover the range of ${\rho }_{\infty }$ values at a relatively fine sampling rate. We found taking 20 equally sized steps between the minimal and maximal ${\rho }_{\infty }$-values worked well on all examples. Note that the larger $\left|S\right|$ is, the slower the proposed method. Similarly, we found taking $K_0=12$ allowed for efficient detection of K. Taking it larger would needlessly increase runtime by requiring more eigenvalues to be computed at each $\sigma \in S$. We note that no denoising was done on the Four Spheres and Three Cubes synthetic data, while pre-processing denoising on the Ten Gaussians ($T=0.22$), Salinas A ($T=290$), and Pavia U ($T=750$) was performed. These cutoffs were performed by visual inspection, noting that in all cases there was a clear gap between noisy outliers and inlying cluster points.

4.4. Estimation of Number of Clusters

While clustering accuracy when given K a priori is an important metric for clustering algorithm evaluation, it is not entirely realistic. Indeed, the estimation of K is an important yet poorly understood problem not just in HSI clustering, but in clustering more generally.

In Figure 12, the eigenvalues of the SRUSC Laplacian are shown for a range of scales $\sigma$. We see the eigengap (3) correctly estimates number of clusters for most of the data sets considered, for a range of $\sigma$ values. Only on Salinas A does the eigengap fail; it estimates 7 rather than 6 clusters. We note, however, that in this case one of the classes (in the bottom right) is obviously spectrally separable into two distinct regions. Since the algorithm is provided only with the unlabeled data, returning 7 as the number of clusters is arguably more reasonable than returning 6, the latter being the number of ground truth classes. Indeed, it is essentially impossible to link the split class based on the spectral data alone—supervision is required.

Overall, these results suggest that SRUSC is able to estimate (exactly or nearly) the number of clusters even on challenging, high-dimensional HSI.

Note that we also estimated the number of clusters using multiscale eigenvalues computed with the Euclidean Laplacian, with very poor results; see Figure 12f–j. Indeed, the Euclidean multiscale eigenvalues fail to reasonably estimate K in any of the examples considered. This suggests another important advantage of SRUSC compared to more classical graph-based clustering methods: it can estimate the number of clusters, making it nearly completely unsupervised.

4.5. Runtime

The runtimes for all algorithms are in

Table 2. Running time for different methods measured in seconds. The methods that require the computation of eigenvectors of a graph (SC, DL, SRUSC) are slower than methods that do not. However, all methods require only at most minutes to run, even on the largest datasets.

Data Set	FS	TC	TG	SA	PU
KM	0.7718	0.4352	0.1532	0.3206	0.1590
PCA	0.0472	0.0411	0.0372	0.0788	0.0479
GMM	3.4639	2.1814	0.6806	1.3530	0.1662
SC	563.8514	1832.7	9.3997	56.2373	2.0211
DL	870.0409	1036.8	23.7778	13.3009	1.2118
DPC	748.5418	1062.2	21.8215	9.6928	0.4860
NMF	0.4553	0.7978	0.6298	0.6593	0.3272
LLRSC	1.6171	1.0303	0.4702	1.15	0.4793
LCMR	240.5580	131.4040	4.55611	35.2812	3.5041
SRUSC	1402.1	2971.6	25.3597	97.4420	6.0195

. All experiments were performed on a Macbook Pro with a 3.5GHz Intel Core i7 processor and 16GB RAM. We see that the graph-based methods (SC, DL, SRUSC) are on a similar order of magnitude, and are considerably slower than simpler and less effective methods like KM and GMM.

5. Conclusions and Future Research

In this article, we showed that UPD are a powerful and efficient metric for the unsupervised analysis of HSI. When embedded in the spectral clustering framework and combined with suitable spatial regularization, state-of-the-art clustering performance is realized by the SRUSC algorithm on a range of synthetic and real data sets. Moreover, ultrametric spectral clustering is mathematically rigorous and enjoys theoretical understanding of its accuracy and robustness to parameters that many unsupervised learning algorithms lack.

Based on the success of unsupervised learning with ultrametric path distances, it is of interest to develop semisupervised UPD approaches for HSI. Path distances for semisupervised learning are effective in several contexts [52], and it is of interest to understand how the UPD perform in the context of high-dimensional HSI, specifically for active learning of HSI [53,54].

A related line of work is to regularize the ${\ell }^{\infty }$ geodesic not through spatial regularization, but through the addition of another metric (i.e., ${\ell }^1$ geodesic or Euclidean distance). This would have the effect of requiring the optimizing path in the HSI pixel space to be short in multiple sense, and is expected to improve robustness. For both this form of regularization and the spatial regularization proposed in this article, it is of interest to develop mathematical clustering performance guarantees depending on, for example, the joint spectral-spatial smoothness of the HSI.

It is also of interest to develop hierarchical clustering methods based on UPD, which will mitigate the challenge of using incompletely-labeled ground truth data to do algorithmic validation. Indeed, allowing for soft clusterings and multiscale labelings is closer to the practical use-case of HSI clustering algorithms, in which remote sensing scientists need to explore real data for which they have little or no knowledge of the underlying material classes. Developing methods and intrinsic clustering evaluation metrics (that do not require labeled ground truth) are the topic of ongoing research. A related line of inquiry pertains to intrinsic statistics that measure whether or not to split clusters or preserve them [55]. It is of interest to apply both classical methods (e.g., silhouette scores [56] and the Davies–Bouldin index (DBI) [57]) and also recent methods based on diffusion processes [58] to evaluate intrinsic cluster structure in the context of SRUSC. Indeed, balancing cohesion within and separation between clusters is an important underlying principle for clustering that will be explored via hierarchical methods.