Clustering of Rainfall Types Using Micro Rain Radar and Laser Disdrometer Observations in the Tropical Andes

Abstract

Lack of rainfall information at high temporal resolution in areas with a complex topography as the Tropical Andes is one of the main obstacles to study its rainfall dynamics. Furthermore, rainfall types (e.g., stratiform, convective) are usually defined by using thresholds of some rainfall characteristics such as intensity and velocity. However, these thresholds highly depend on the local climate and the study area. In consequence, these thresholds are a constraining factor for the rainfall class definitions because they cannot be generalized. Thus, this study aims to analyze rainfall-event types by using a data-driven clustering approach based on the k-means algorithm that allows accounting for the similarities of rainfall characteristics of each rainfall type. It was carried out using three years of data retrieved from a vertically pointing Micro Rain Radar (MRR) and a laser disdrometer. The results show two main rainfall types (convective and stratiform) in the area which highly differ in their rainfall features. In addition, a mixed type was found as a subgroup of the stratiform type. The stratiform type was found more frequently throughout the year. Furthermore, rainfall events of short duration (less than 70 min) were prevalent in the study area. This study will contribute to analyze the rainfall formation processes and the vertical profile.

1. Introduction

Precipitation is among the most important components of the hydrologic cycle because it triggers important processes that determine water distribution and availability [1,2,3]. In addition, precipitation is characterized by a high spatiotemporal variability. This is particularly true in the Tropical Andes, where complex topography is a key factor that influences rainfall processes [4]. Here, precipitation variability has been studied only at a certain extent [5,6,7]. This is because of the lack of high temporal resolution data, which is one of the main obstacles to understand the rainfall processes and dynamics in this area [8]. Usually, rainfall characteristics such as rain rate are used to study rainfall variability [6]. Moreover, microphysical characteristics (e.g., drop size distribution) and the study of the vertical profile of the rainfall allow to improve the knowledge about microphysical processes that govern the formation of the hydrometeors and to identify rainfall types. This rainfall variability can be captured by remote sensing observation with Micro Rain Radar (MRR) and laser disdrometers. The advantage of these instruments is that they not only enable to quantify the rainfall but also allow for the analysis of its microphysical attributes [9,10].

MRRs are instruments that measure the characteristics of the precipitation along its vertical profile. MRRs retrieve the reflectivity profile, drop size distribution (DSD), rain rate, velocity, and liquid water content (LWC) [9] for different atmospheric layers. These characteristics allow for the analysis of the vertical structure of the rain. They also allow to differentiate between rain types (convective and stratiform rain) and to identify the height of the Melting Layer (ML) [2,11,12,13]. Besides, disdrometers are instruments that retrieve characteristics as particle spectrum, the rain rate, the quantity, and the type of rain [10]. These instruments have been used to analyze the rainfall dynamic in mountain areas [4,12,14,15,16,17]. In the Tropical Andes, the diurnal dynamics of the precipitation were studied by Bendix et al. [16] using MRR data. The author found that rainfall is mostly of stratiform type and the afternoon events are influenced by local convection. A study in Peru and Bolivia using MRR data [12] showed the dominance of stratiform events during the night, and suggested that the height of ML is an indicator of climate change. Using microphysical data (e.g., mean volume diameter Dm) obtained from laser disdrometers, Orellana-Alvear et al. [4] analyzed rainfall types at three sites with different height in the Andes Cordillera in Ecuador. The authors found that convective type (rainfall associated with higher rain rate and Dm) was more common in the lower elevation sites while light rain was more frequent in higher sites. Seidel et al. [14] using MRR data, found that short events (less than 3 h) were dominant in the Tropical Andes and nocturnal precipitation is more of the stratiform type.

Previous studies highlight the importance of differentiating between rainfall types [3,17,18,19], principally to analyze the rainfall behavior and find patterns in the rainfall attributes. Furthermore, the definition of rainfall types is useful for improving the quantitative precipitation estimation (e.g., Z-R relation) [4]. Usually, rainfall types (e.g., stratiform and convective) are defined by using some rainfall characteristics thresholds such as rain rate [19,20,21]; DSD [22,23] and; reflectivity [24]. Furthermore, in the case of the reflectivity profile, it is used to determine the ML presence, which is also used to determine rainfall types [11,25]. However, these thresholds are site specific [21] and depend mainly on the local climate and the study area. This makes rainfall classification closely related to independent, arguably subjective decisions rather than the possibility of extracting knowledge only from the interactions between rainfall characteristics. This can be overcome using clustering analysis.

This is a machine learning tool that allows grouping objects with similar characteristics only based on the data. Clustering analysis based on the hierarchical and k-means algorithm had been successfully used to classify rainfall events in different studies such as Dilmi et al. [26], dos Santos et al. [27], Fang et al. [28], and Peng and Wang [29]. These studies were carried out in subtropical regions [26,28,29] and tropical semiarid regions [27]. However, there is no report of the application of these techniques in tropical high mountains up to date.

In this context, this study aims to analyze rainfall-event types in the Tropical Andes by using a clustering approach based on the k-means algorithm that allows accounting for the similarities of rainfall characteristics (e.g., duration, rain rate, drop size distribution) of each rainfall type. This will allow for the improvement of the knowledge of rainfall dynamics and its occurrence in the region.

2. Study Site and Data

2.1. Study Site

The study area Balzay (2°53′S, 79°02′W) is located at 2610 m above sea level (a.s.l), in the outskirts of the city of Cuenca in the Tropical Andes of southern Ecuador, as shown in Figure 1. Balzay is located in the inter-Andean depression [30] and shows a bimodal rainfall regime with two wet seasons in the months March-April-May and October. The mean annual precipitation is 969 mm [4] and the mean temperature is 14 °C [31]. The precipitation is mainly driven by the displacement of the Intertropical Convergence Zone (ITCZ) [32,33]. The ITCZ is defined as the zone in the vicinity of the equator, where the trade winds from the north and south converge [34]. The climate in Ecuador shows high variability in part due to the presence of the Andes Cordillera. In the inter-Andean depression, due to the impact of the ITCZ, the tropical Amazon air masses from the East and the Pacific coastal regimen from the West are the main factors that control the climatology of the area [35].

2.2. Instruments

The instruments used in this study are the Micro Rain Radar (MRR) [9] and the laser disdrometer (Thies Clima LPM—Laser Precipitation Monitor) [10]. A detailed explanation of the instruments’ operation is provided in the following sections.

2.2.1. Micro Rain Radar

The MRR is a vertically pointing frequency modulated continuous wave (FM-CW) doppler radar. It operates at 24.1 GHz and 12.5 mm wavelength. The radar transmits a signal along a vertical orientation in the atmosphere over the antenna [9,36].

The primary advantage of the MRR is its high sensitivity and temporal resolution to detect small amounts of precipitation (i.e., low rain rates) [9]. The MRR detects droplets with diameters between 0.25 to 6 mm [37], and it assumes water drops are spherical. The MRR retrieves basically the Doppler spectra of the falling droplets and radar reflectivity where parameters like the mean fall velocity, droplet concentration, rain liquid water content, and rain rate are derived from. The details of the parameters derivation can be found in [9,36,37,38]. The MRR records these parameters for all the vertical profile.

The vertical profile consists of 31 height steps (gates) whose maximum and minimum height resolution is defined by the user and range between 10 and 1000 m. In our case, the MRR was operated with a height resolution of 100 m and the data were captured with a 1-min frequency.

2.2.2. Disdrometer

The disdrometer used in this study is a Thies Clima Laser precipitation monitor (LPM) [10], which is based on a laser sensor that produces a horizontal light beam. This sensor has a wavelength of 785 nm and the measuring area is 45.6 cm². When a precipitation particle falls through the light beam, the receiving signal is attenuated. The particle diameter is estimated from the reduction in the signal amplitude while its fall velocity is calculated from the duration of the decreased signal. Each drop is assigned to one of 22 size bins and to one of 20 velocity bins. The size bins are between 0.125 and 8 mm and the velocity bins are between 0 and 10 m s⁻¹. Later, a telegram is sent every minute. This shows the number of drops that the LPM detected in each class depending on the bin combination (diameter-velocity). The LPM retrieves the particle spectrum, the rain rate, the quantity, and the type of precipitation. Data were captured with 5-min frequency, as a result of averaging 1-min observations.

2.3. Data Availability and Quality Control

Three years of data, from February 2017 to February 2020 of both instruments were used in this study. The performance of the disdrometer data has been evaluated in [39,40]. In spite of the good performance of the disdrometer, it shows some issues at high wind speeds (>15 m s⁻¹) [41], which, however, were not present in our disdrometer records [4]. Furthermore, to eliminate uncertainty measurements obtained from misclassification of particles, margin fallers and splashing effect, we employed the methodology used in Orellana-Alvear et al. [4]. Details regarding the quality control method can be found in Orellana-Alvear et al. [4] and Friedrich et al. [41]. In the case of the MRR, the data were averaged to 5-min. Several parameters of the MRR such as rain rate (mm h⁻¹), mean fall velocity (m s⁻¹), liquid water content (g m⁻³), droplet concentration (m⁻³ mm⁻¹), and radar reflectivity (dBZ) were used for the rainfall classification process.

The validity of the MRR data has been reported by many researchers [11,19,40,42,43]. These studies showed a good agreement between MRR and different types of disdrometer (OTT Parsivel, Joss-Waldvogel and LPM) through a correlation analysis. Thus, to ensure the validity of the MRR measurements, we compared the rain rate observed by the MRR at the lowest height (100m) with the rain rate obtained from the collocated disdrometer at 30-min cumulative interval (Figure 2). This comparison was performed by using the determination coefficient (R²). The coefficient of determination between MRR and LPM rain rate data was 0.74 (Figure 2). Therefore, we had a good fit in spite of the difference in height where each sensor is monitoring the rainfall (i.e., the disdrometer is located at ground level while the MRR first range of monitoring is 0–100 m).

As shown in Figure 2, the MRR tended to slightly underestimate the rainfall amount compared to disdrometer observations. Nevertheless, the MRR showed some outliers especially in higher values. Figure 2 also suggests that the MRR tend to overestimate the rainfall above 10 mm 30 min⁻¹. Sarkar et al. [40] found that the LPM and MRR had a good fit (R² = 0.74). The author suggested that over 60 mm h⁻¹, the MRR has a high probability of underestimating the measures of rain rate. In addition, Rollenbeck et al. [44] compared the precipitation measurements between five recording devices. The author found that the MRR underestimate the precipitation. The MRR had a high sensitivity to detect light rain, but it had problems detecting higher rain rates [44,45]. These studies agree with our results and show the good fit between both instruments. Thus, we derived the drop size distribution (m⁻³ mm⁻¹) from the disdrometer data. It was calculated from the number of drops for each size and velocity bins [10]. The details of the drop spectrum calculation can be found in [4,40,46].

3. Methods

First, we selected rainfall events from the available time series by using three criteria which are detailed in Section 3.1. Then, for each of them, we determined individual rainfall event characteristics (e.g., duration, maximum rain rate, etc.) derived from the MRR and LPM data. Finally, we applied the k-means algorithm that clusters these events based on their derived characteristics. A detailed explanation of the last steps is provided in Section 3.2.

3.1. Rainfall Events Selection

Representative data of the study period were obtained through the delineation of rainfall events using three criteria: (i) minimum interevent time, (ii) minimum total rainfall accumulation, and (iii) minimum duration. The minimum interevent time is defined as the minimum lapse of time for a dry period (i.e., no rainfall occurrence or less than a threshold) between rainfall events, which is necessary to classify two events as independent. In this study, we used the threshold of rain rate greater than 0.05 mm min⁻¹ for each time step. This threshold was identified using a sensitivity analysis by testing different values between 0.01 and 0.1 mm min⁻¹. The value of 0.05 mm min⁻¹ was selected because it eliminated the long tails and discontinuities that lower rain rate values showed in the events. The minimum total rainfall accumulation refers to the rainfall total during the event. The minimum duration is the time where the rainfall was continuous (without gaps) [47,48]. To identify the proper thresholds for these values we performed a sensitivity analysis which was carried out by using a variation between a range of values of each criterion (minimum interevent time, minimum total rainfall accumulation, and minimum duration) with the purpose of getting a probability distribution. This distribution was used to find a threshold where the number of events got steady for each criterion and thus, we got a trade-off between the number of events and their representativeness. The range of values to find the proper threshold were: (i) 20–60 min for minimum interevent time; (ii) 2–8 mm for minimum total rainfall accumulation per event and; (iii) 10–30 min for minimum duration. The methodology of Orellana-Alvear et al. [4] was used as a starting point to determine such thresholds. Finally, rainfall events that met the criteria were selected for the current study.

3.2. Rainfall Classification

3.2.1. Derivation of Rainfall Events Characteristics

Rainfall event characteristics are used to describe and synthesize the behavior of a rainfall event [26]. After the rainfall events were selected, several of their temporal (e.g., duration) and hydrometeorological (e.g., rainfall accumulation) characteristics were picked out for the rainfall classification process. However, there is no universally agreed set of characteristics to describe a rainfall event [26]. Generally, choosing the rainfall characteristics depends on the instrument, its measured variables, and the objective of the study. Here, we used the characteristics obtained from the MRR and the LPM; these include hydrological and microphysical information of the rainfall events (

Table A1. The 23 Rainfall events features determined for each event.

Number	Feature Name	Unit	Symbol	Instrument
1	Maximum Rain Rate	mm h−1	RRmax	MRR
2	Minimum Rain Rate	mm h−1	RRmin	MRR
3	Mean Rain Rate	mm h−1	RRmean	MRR
4	Median Rain Rate	mm h−1	RRmedian	MRR
5	Rainfall Accumulation	mm	Raccum	MRR
6	Maximum Velocity	m s−1	Vmax	MRR
7	Minimum Velocity	m s−1	Vmin	MRR
8	Mean Velocity	m s−1	Vmean	MRR
9	Median Velocity	m s−1	Vmedian	MRR
10	Event Duration	minutes	Dur	MRR
11	Maximum Reflectivity	dBZ	Rmax	MRR
12	Minimum Reflectivity	dBZ	Rmin	MRR
13	Mean Reflectivity	dBZ	Rmean	MRR
14	Median Reflectivity	dBZ	Rmedian	MRR
15	Melting Layer	-	ML	MRR
16	Maximum Liquid Water Content	g m−3	LWCmax	MRR
17	Minimum Liquid Water Content	g m−3	LWCmin	MRR
18	Mean Liquid Water Content	g m−3	LWCmean	MRR
19	Median Liquid Water Content	g m−3	LWCmedian	MRR
20	Maximum Mean Volume Diameter	mm	Dmmax	LPM
21	Minimum Mean Volume Diameter	mm	Dmmin	LPM
22	Mean Liquid Mean Volume Diameter	mm	Dmmean	LPM
23	Median Mean Volume Diameter	mm	Dmmedian	LPM

).

Derivation of MRR and Disdrometer Characteristics

We used four hydrological characteristics of rainfall events of the lower height bin of the MRR, namely rain rate (mm h⁻¹), mean fall velocity (m s⁻¹), liquid water content (g m⁻³), and radar reflectivity (dBZ). Moreover, rainfall accumulation and the duration of the event were calculated.

Regarding microphysical data, the LPM retrieved the drop spectra N(D) (m⁻³ mm⁻¹) and drop diameters D (mm). These characteristics are used to represent the Drop Size Distribution (DSD) [49] at each time step. Nonetheless, we needed to combine these characteristics to get a representative DSD for each rainfall event. So, we derived the mean volume diameter (Dm) in mm that represents the proportion between the fourth and third moment of the DSD, as defined by [50]. It is frequently used to represent the DSD of a rainfall event [4,26,43,51,52]. Finally, we analyzed the characteristic distribution and extracted the mean, maximum, minimum, and median value for characterizing the rainfall properties within each event.

Determination of the Melting Layer

The Melting Layer (ML) is an important characteristic, commonly used to identify rainfall classes [11,25,53]. The ML determination is based on the identification of a Bright Band (BB) signature in the vertical profile of the reflectivity. This BB detection consists in determining the prominent increase of the values in the reflectivity profile at specific gates, using the maximum slope found in the reflectivity profile [11,54,55]. This band is a combination of water, air, and ice that highly increase the reflectivity values at certain gates of the vertical profile. In addition, another factor that influences the increase in reflectivity is the density effect, which consists in the water (melted and snow) distribution in the particles [19,53,54,55].

A general solution to identify the ML is performing a visual inspection of the reflectivity profile [19,22]. Thus, the BB was identified for each event based on a visual inspection and the scheme of Fabry and Zawadski [55]. The scheme analyzed the vertical reflectivity profile of each event in order to determine the presence of the BB and to extract parameters such as the height of the BB. As a result, three possible scenarios related to the occurrence of the BB were found: (i) the BB is always present during the rainfall event, (ii) the BB is partially present along the event, and; (iii) the BB is absent. Thus, we used a three stage ML variable that can be set to 1 (BB always present), 0.5 (BB intermittent), and 0 (no BB present).

3.2.2. Clustering Approach: k-Means Algorithm

Clustering analysis is a statistical tool used to group objects with similar characteristics. The technique performs an unsupervised classification; thus, it is not based on the use of a priori labels to determine the clusters [26,56,57]. Therefore, by using a set of objects (instances from a data set), it finds their natural grouping that maximize the cohesion within the groups while ensuring higher separation from other clusters [57]. Clustering algorithms are divided into hierarchical and partitional [57]. In partitional algorithms as k-means clustering, the definition of the number of clusters and the feature selection are important conditions in the cluster formation [58].

The k-means algorithm was used for obtaining the rainfall event classes. This is accomplished by identifying different groups of instances (i.e., rainfall events) with similar features (i.e., the rainfall characteristics such as duration, DSD, etc.) within each group in a data set [59]. The main idea behind the k-means algorithm is grouping n points of m dimensions into k clusters, so that for each cluster, the square of the Euclidean distance between the x points that belongs to n and the centroid of the cluster is minimal (Equation (1)) [58,60,61].

$$\mathrm{J}={{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{k}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left|{\mathrm{x}}_{\mathrm{i}}-{\mathrm{c}}_{\mathrm{j}}\right|}^2,$$

(1)

where J is the Euclidean distance, x_i is each data point and c_j is the centroid of the cluster. The k-means algorithm is iterative, so the process is repeated until the Euclidean distance converges to the minimum value. In order to apply the k-means algorithm, it is needed to fulfill three conditions: determine the features (rainfall event characteristics) to use; standardize the features and define the number of clusters.

To begin this process, we decided to select a subset of features to diminish redundant information for the algorithm and for obtaining a parsimonious model. A number of techniques have been developed for feature-selection [62]. We chose each feature by performing a cross-correlation analysis between all features by means of the Pearson correlation coefficient. This aimed to highlight the features that contribute redundant information for the algorithm. With this, we removed these features and we got a parsimonious model with lower number of features.

In the case of the ML feature, it is worth mentioning that the identification of the ML and its corresponding feature derivation needed a great effort and was very time consuming because we had to visually check each one of the rainfall events. For these reasons, this feature was included and excluded from the original list of features with the purpose of determining its influence over the rainfall clusters formation.

Furthermore, the standardization of features is mandatory for the implementation of the k-means algorithm. This is because all features should have the same weight for calculating the Euclidean distance. While different methods have been proposed to standardize the features, Milligan and Cooper [63] found that standardizing by the range was the best method of eight standardization methods. So, we decided to use the range method (Equation (2)).

$$\mathrm{Z}=\frac{\mathrm{X}-\mathrm{Min}\left(\mathrm{X}\right)}{\mathrm{Max}\left(\mathrm{X}\right)-\mathrm{Min}\left(\mathrm{X}\right)},$$

(2)

where Z is the standardized feature, X is the feature, and Max and Min are the maximum and minimum value of X, respectively.

Finally, we aimed to select the optimal number of clusters for our data set. Milligan and Cooper [64] evaluated thirty procedures to determine the optimal number of clusters and they found that it highly depends on the data. For this study, we decided to run the algorithm a priori with two and three clusters because rainfall types are usually classified in two and three classes (stratiform, convective, and transition or mixed). Furthermore, we evaluated the quality of the cluster separation, so we decided to use the elbow method. Here, we needed to identify a sharp elbow between the sum of the squared errors as a function of the number of clusters [65]. In addition, this value usually indicates the optimal number of clusters. In our case we will include and exclude the ML feature in this analysis to identify its influence on the cluster’s separation.

4. Results

4.1. Rainfall Events Selection

We selected 92 rainfall events after finding the thresholds that met the criteria for the rainfall event separation. The thresholds of the three criteria were: 30 min for minimum interevent time, 3 mm for minimum total rainfall accumulation per event, and 15 min for minimum event duration.

Figure 3 illustrates the distribution of the rainfall event duration and occurrence in each month. The distribution of the rainfall events along the year is in agreement with the bimodal regime of precipitation in the study area as documented by Campozano et al. [33] and Célleri et al. [6]. The higher number of rainfall events occurred in March, May, and October whereas June, July, August, and September had the lowest number of rainfall events. However, no rainfall events accomplished the defined criteria (e.g., minimum interevent time, minimum total rainfall accumulation, and minimum duration) in July, which is one of the driest months of the year with a mean monthly precipitation of 7mm. Furthermore, the longest events duration was found in April and May, which are the wettest months with a mean monthly precipitation of 78 and 98 mm, respectively.

For the selected events, we found that the rainfall event duration was shorter than 3 h (Figure 3). In addition, we found that short rainfall events (i.e., <70 min) were predominant (around 70%) in the region during the study period. In addition, the mean duration at every month was less than 70 min.

4.2. Rainfall Event Features

Determination of the Melting Layer

With the aim of determining the ML feature, we analyzed the vertical reflectivity and velocity profile and well as their evolution along the rainfall event. Here we used data with 1 min frequency, as it was necessary to identify the variability of the rainfall characteristics along the event. We had three scenarios linked to the occurrence of the BB: (i) present, (ii) partially present, and (iii) absent.

Figure 4, Figure 5 and Figure 6 show the three scenarios (i–iii) about the BB identification. The event shown in Figure 4a,b shows a constant enhancement in the reflectivity and in the velocity profile around 2000 m above ground level (a.g.l), which evidence a BB. In the reflectivity profile, there is a clear increase of the reflectivity value around this height. In addition, a closer inspection of the velocity profile showed an extreme variation in the values around the 2000 m a.g.l. and in consequence supports the presence of the ML. In this case, the ML variable was set to 1.

In contrast, Figure 5a,b shows that the BB was not always present during the entire rainfall event as seen in the reflectivity and velocity profiles. Thus, the ML related feature was set to 0.5. The clear BB appeared from 15:00 h until the end of the event around 2000 m a.g.l. In the reflectivity and velocity profiles, we could see an increase of their values around this height from 15:00 h until the 15:35 h which is the end of the event. However, there is no previous signature of BB.

Finally, Figure 6a,b illustrates the absence of the BB along the entire event in the reflectivity and velocity profiles. There are no strong variations in the reflectivity and velocity profiles as in the previous scenarios. This means that the ML was not evident in the rainfall event. Here, we set the ML related feature to 0.

Furthermore, in Figure 4c, Figure 5c and Figure 6c, we differentiated between the rain rate range and the evolution of the event in the three scenarios of the BB.

In Figure 4c, we found that the rain rate ranged between 0 and 16 mm h⁻¹. In Figure 5c, the range was between 0 and 35 mm h⁻¹. In addition, the rain rate reveals two peaks before 15:00 h. Figure 6c shows that the rain rate ranged between 0 and 80 mm h⁻¹ and also has two peaks.

4.3. Clustering Using k-Means

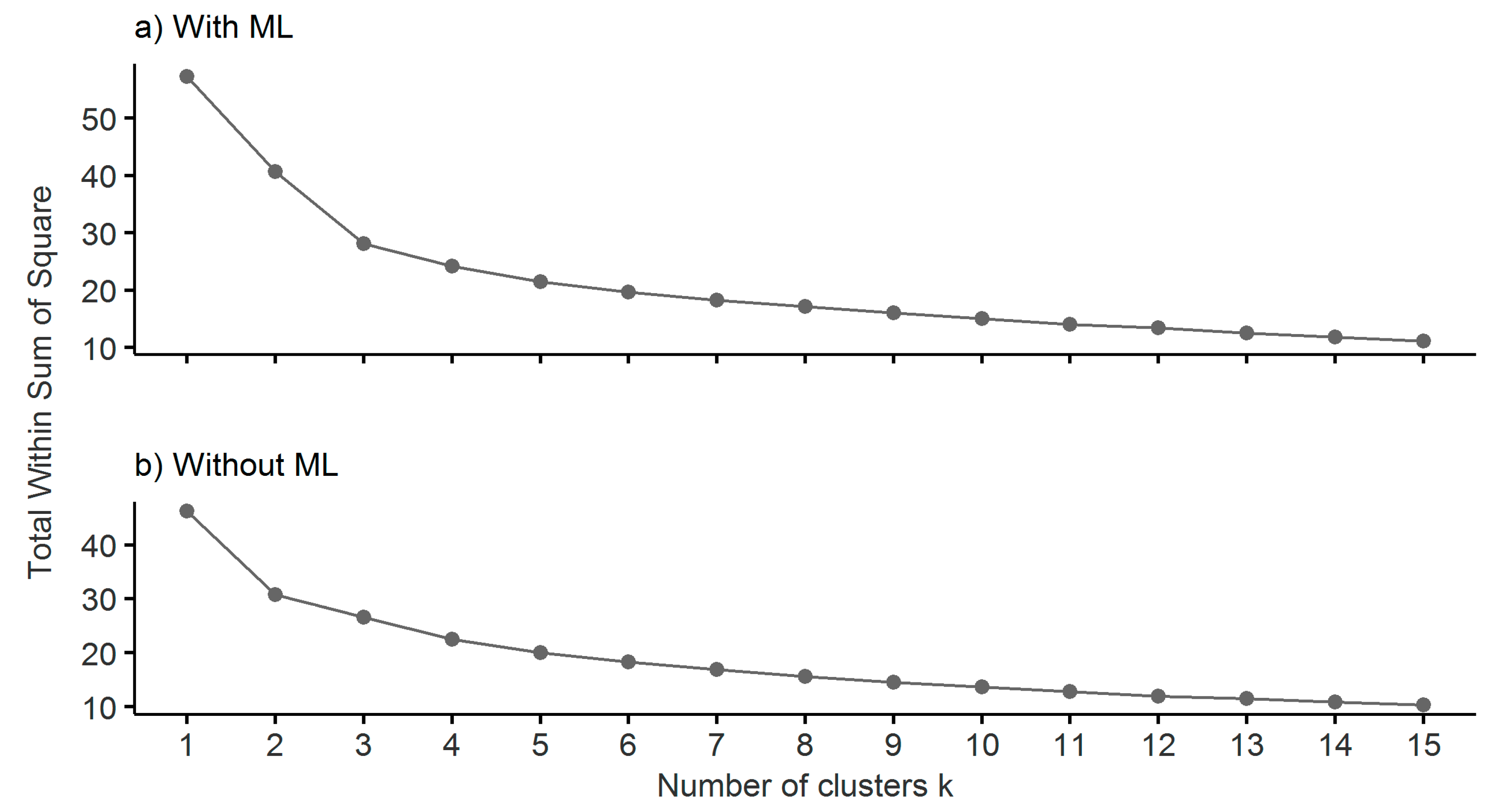
4.3.1. Features Selection

We analyzed the cross-correlation between the 23 features determined in Table A1. Results of the cross-correlation analysis are provided in Figure A1. From the cross-correlation analysis, we found that features as reflectivity and liquid water content are related especially with rain rate. Therefore, rain rate could explain these features in the algorithm. Furthermore, the median value distribution of all the features are linked in their majority with the mean value distribution of the same or other feature. Therefore, the features with a Pearson correlation coefficient higher than 0.8 are found to provide repetitive information in the clusters, so we kept only one feature and removed the related one(s). Thus, we determined that 12 features were the most important and these capture all the variability during the event (see

Table 1. Features selected for the cluster analysis.

Number	Variable Name	Unit	Symbol
1	Maximum Rain Rate	mm h−1	RRmax
2	Minimum Rain Rate	mm h−1	RRmin
3	Mean Rain Rate	mm h−1	RRmean
4	Rainfall Accumulation	mm	Raccum
5	Maximum Velocity	m s−1	Vmax
6	Minimum Velocity	m s−1	Vmin
7	Mean Velocity	m s−1	Vmean
8	Event Duration	minutes	Dur
9	Melting Layer	-	ML
10	Maximum Mean Volume Diameter	mm	Dmmax
11	Minimum Mean Volume Diameter	mm	Dmmin
12	Mean Liquid Mean Volume Diameter	mm	Dmmean

). In the case of Mean Rain Rate (RRmean), it had a Pearson correlation coefficient of 0.8 with the Maximum Rain Rate (RRmax) feature. However, we kept this feature because it is commonly considered to determine thresholds for rainfall types. The list of the selected features is provided in Table 1.

4.3.2. Features Standardization

As stated previously, standardization is mandatory for applying the k-means clustering algorithm. This ensures that all features are equally weighted in the process. This method compensates the differences among the range of all the features. For example, the RRmax values range between 5 and 100 mm h⁻¹ whereas the Dm values range between 0.30 and 5 mm.

Figure 7 shows the 12 features in a standardized mode. In the case of the rain rate related features (RRmax, RRmin and RRmean), we had a few events with high values, especially in RRmax. In this feature, around 80% of the events showed values below 0.5.

With respect to rainfall accumulation (Raccum), we had the same pattern as RRmax, but here around 70% of the events showed values below 0.25. In the case of Duration (Dur), short duration events (less than 0.5) were predominant. For the three velocity features, high values were dominant in all of the events. Finally, Dm max and Dm mean showed a similar distribution in their values.

4.3.3. Clustering with k = 2 and k = 3

The 12 standardized features and the a priori selected number of clusters (k = 2 and k = 3) were used to apply the k-means algorithm. In addition, by applying the elbow method, we found that k = 3 was the optimal k when we include the ML feature. However, when we exclude the ML feature, we find that k = 2 was the optimal k (see the Figure A2). So, these results agreed with our number of clusters selected a priori. To facilitate the graphical visualization of the clusters, we elaborated Figure 8 by using the two principal components from the principal component analysis (PCA); details regarding the methodology of PCA can be found in Abdi and Williams [66] and Wold et al. [67].

Figure 8 shows the results of the clustering approach by using k = 2 and k = 3. For each k we present the subsequent results of including or excluding the ML feature in the clusters formation. For simplicity we would refer as Class x (e.g., Class 1, Class 2) to every group resulting of the clustering process. Figure 8a,b with k = 2, present the Class 1 and Class 2. By excluding the ML feature, only two events shifted from Class 1 to Class 2. Also, this could be observed in the variation of the number of events in each Class (Cl).

Figure 8c,d with k = 3, present the Class 1, Class 2 and Class 3. By using k = 3, we found that 11 events shifted the class they belong initially. In addition, this could be observed in the variation of the number of events in each Cl.

Furthermore, when we increased the number of groups (i.e., k = 2 to k = 3) independently of the ML feature, it can be seen in Figure 8a–c and Figure 8b–d that Class 3 is formed principally by a splitting of Class 2. Besides, applying three classes (k = 3), we found a higher variability in the formation of the clusters.

Features Distribution Analysis per Each Class

Furthermore, we analyzed the distributions of the features obtained per each class in order to identify the thresholds of the features value for rainfall classification. Figure 9 shows the distribution of all the features using k = 2 and k = 3 and the influence of the presence or absence of the ML feature in the clusters formation.

In the clusters with k = 2 (Figure 9a), we found that the highest values of all features but the duration occurred in Class 1. Thus, in this class we had events with higher rain rate, velocity, Dm, and rainfall accumulation. However, the same events had the shortest duration in comparison with Class 2. On the other hand, Class 2 had events with lower values in all features, but these were also the events with the longest duration. Moreover, we observed that the ML feature has no effect in the clusters’ formation. This can be seen in the similarity of the feature distributions for both scenarios.

Similarly, we obtained comparable results in the clusters with k = 3 (Figure 9b). Class 1 showed events with higher values in the rain rate, velocity, rainfall accumulation, and Dm but shorter values in the event duration. However, in Class 2 and Class 3, it was difficult to define a tendency because there was not an evident pattern in all the features. For instance, in comparison with Class 2, Class 3 showed higher value in RRmax but shorter values in RRmin. However, Class 2 showed the highest value in the duration event feature.

Furthermore, in the clusters with k = 3, we observed a more notorious range difference regarding the values of the features when using the ML feature in comparison with their counterparts when using k = 2.

Distribution of Rainfall Classes along the Year

In order to analyze the rainfall events frequency, we calculated the events percentage by month from every cluster as seen in Figure 10.

Figure 10a,b present the events percentage when we included or not the ML feature with k = 2. In concordance with the Figure 8a,b, the 2 events that shifted of Class, belonged to January and May. For this reason, we found a slight variation in these months in the Figure 10a,b. In addition, these two events did have a BB and their rain rate showed a range between 0 and 60 mm h⁻¹ in 1min frequency.

Furthermore, we found that Class 1 was dominant (more than 50%) only in March and November. As a result, we had a predominance of the Class 2 along the year.

Figure 10c,d shows the events percentage by including or excluding the ML feature with k = 3. In Figure 10c,d, we found a different percentage of events in January, March, April, October, November, and December especially in the Class 2 and Class 3.

5. Discussion

Our study shows that we have a prevalence of short rainfall duration in the study area. These results about short rainfall duration support evidence from previous observations [4,14]. Orellana-Alvear et al. [4] analyzed the rainfall events duration using the LPM disdrometer and found that the mean event duration is around 3 h. In the same way, Seidel et al. [14] confirmed that the short duration events are dominant in this study area by using MRR data. Furthermore, the short duration of the events evidenced the necessity of high temporal resolution to capture their variability. However, the instruments’ time resolution (e.g., rain gauge) limit capturing the variability in these events [14,68]. Padrón et al. [68] already discussed the influence of different instrument time resolution (rain gauge and disdrometer laser) in rainfall data after finding that the rain gauge underestimates rainfall catch. In our case, with the MRR and LPM data, we could analyze the temporal variability (i.e., 1 min frequency) with respect to rain rate, velocity, reflectivity, liquid water content, rainfall accumulation, and mean volume diameter.

With respect to the rainfall characteristics, it is interesting to note that the events with a clear BB were related to the low rainfall rain rate range at the ground level. In addition, events with intermittent BB had an intermediate rainfall rain rate range between the other two scenarios of BB. This suggested that these events are mixed case of the other scenarios of BB. In the same way, events with no BB were related to the high rainfall rain rate range at the ground level. This finding was also reported by Das et al. [11], Seidel et al. [14], and Das and Maitra [19]. The authors related these scenarios of the BB to stratiform, transition, or mixed and convective classes. Furthermore, Seidel et al. [14] pointed out that the BB typically lies between 1700 and 2400 m a.g.l; this is in concordance with our results.

Furthermore, as can be seen in Figure 4, Figure 5 and Figure 6, rainfall starts forming at higher height gates (around 2000 m a.g.l), which is the height where we found the BB. Later, this rainfall comes to the ground gate with a lag time. This is named the boundary effect [14]. Moreover, Seidel et al. [14] identified that it could be a problem in its rainfall classification. So, to evaluate their rainfall classification method, the author employed other approaches that used different features (e.g., Dm).

Regarding the clustering method, previous studies [58,62,64] have noted the importance of defining the number of clusters and the features selected before applying the algorithm. In our case, we defined the number of clusters considering the typical rainfall classes (convective, stratiform, and mixed).

In the case of the features selected, we reduced from 23 to 12 features. Dilmi et al. [26] reduced the number of features from 23 to 5 using a genetic algorithm and self-organizing maps. Despite using different features than in this study, the rain rate, duration, and rainfall accumulation features belonged to the features selected. So, it suggests that these features are important in the rainfall classification. In relation to data standardization, our results are in agreement with [26,59,63], who found that data standardization is required to get the same weighting of the features before clustering.

Further by using the clustering method we conducted a classification of rainfall types. With respect to the number of clusters, one interesting finding is to note that the Class 3 and Class 2 (with k = 3) are principally part of the Class 2 (with k = 2) (Figure 8). So, the Class 3 could be considered like a subclass of the Class 2. These results are in agreement with Dilmi et al. [26] findings, which showed five subclasses of the two mainly rainfall types (convective and stratiform). Furthermore, our results suggest that with k = 2, we obtain remarkable features differences between the Class 1 and Class 2 (Figure 9a). These findings suggest that when we have another class (i.e., Class 3), it will be a result of splitting one of the main classes (k = 2). Besides, we analyzed the influence of including or excluding the ML feature in the cluster formation. In the case of k = 2, the results suggest that the ML feature did not affect the cluster formation. However, in k = 3, we had a shift of 11 events where more than 50% of these events change from Class 3 to Class 2 or vice versa. A possible explanation for this might be that the Class 3 and Class 2 (k = 3) are a subclass of the Class 2 (k = 2). So, the ML feature influenced in the cluster formation when we used three classes (k = 3).

Therefore, the features selected and determination of number of clusters play an important role in the cluster formation. For these reasons, these conditions should be defined carefully. In addition, we have to notice that k-means is an unsupervised method, so we did not evaluate the information a priori [57] to get these rainfall classifications.

For the purpose of determining the threshold values of the features for the rainfall classification, we assessed the features distribution. Rainfall is usually classified in stratiform, mixed, and convective rain. Stratiform rain is defined like a homogenous rain, with low rain rate, high duration, and low velocity [26]. Convective rain consists of variable rain types, with high rain rate, low duration, and high velocity [26]. Mixed rain is considered as a transition between convective and stratiform rain [19]. Several authors have identified rain rate and Dm thresholds for rainfall classification (

Table 2. Summary of rainfall features thresholds of Tropical Zones.

Feature (Units)	Author	Location	Rainfall Classification	Value
Rain Rate (mm h−1)	Tokay, (1999)	Marine Tropics	Convective	>10
			Stratiform	≈1.86
	Bendix, (2006)	Mountains South Ecuador	Mixed	≈2.4
	Das and Maitra, (2016)	Tropical Locations	Convective	8–12
			Stratiform	2–5
	This study	Tropical Andes	Class 1 (k = 2)	14.86 ± 0.20
			Class 2 (k = 2)	6.55 ± 0.08
			Class 1 (k = 3)	15.08 ± 0.32
			Class 2 (k = 3)	5.43 ± 1.06
			Class 3 (k = 3)	7.27 ± 0.14
Dm (mm)	Seidel, (2019)	Tropical Andes	Convective	≈1.66
			Stratiform	≈1.07
	This study	Tropical Andes	Class 1 (k = 2)	1.55 ± 0.01
			Class 2 (k = 2)	1.09 ± 0.01
			Class 1 (k = 3)	1.57 ± 0.02
			Class 2 (k = 3)	1.1 ± 0.05
			Class 3 (k = 3)	1.1 ± 0.01

).

Table 2 shows that Das and Maitra [19] and Tokay et al. [69] agreed that the convective rain type showed the highest values in comparison with the stratiform rain type. In the case of the mixed rain type, Caracciolo et al. [23] suggested that the values of rain rate between 2 and 10 mm h⁻¹ are complex to interpret because this range can show a mixed of convective and stratiform rainfall. In addition, Bendix et al. [16] found that mixed rain type had values of rain rate around 2.4 mm h⁻¹. Besides rain rate, Dm has also been related to rainfall type. Bringi et al. [70] found that events with larger Dm are considered convective. Seidel et al. [14] confirmed that convective events present values of Dm higher than stratiform events (Table 2). In this context, in our study, Class 1 events represent a convective rain type, Class 2 events are associated with stratiform rain type, and Class 3 events exhibit characteristics of a mixed rain type.

The analysis of the distribution of the rainfall classes along the year show that the stratiform type (Class 2) with k = 2 is not affected by the ML feature. Furthermore, the convective type (Class 1) for k = 3 showed a maximum value in March which may be related to the first ITCZ passage and a slightly higher value in October and November as a result of the secondary ITCZ. Nonetheless, in k = 3 the stratiform type (Class 2) and mixed type (Class 3) showed that the ML influenced the clusters formation. In addition, our results support the finding of Seidel et al. [14] that during most of the year the stratiform and mixed rain types are dominant.

The results obtained in this study are representative of the rainfall types in the high Tropical Andes, above 2400 m a.s.l. Since the land-sea contrast and related sea breezes have a great influence on the precipitation regime in the coastal lowlands, a different categorization of rainfall types may be found.

6. Conclusions

This is the first study that analyzed rainfall-event types in the Tropical Andes of Ecuador by using a data-driven clustering approach (k-means algorithm). The algorithm was efficient to identify rainfall types based on the similarities of rainfall attributes only. So, this method allowed disregarding subjective classification criteria of a human investigator. Furthermore, this methodology could be used to study rainfall classes in other areas because it is only based in data knowledge extraction. The investigation used common rainfall characteristics such as rain rate but also included microphysical data (e.g., DSD). Finally, it evaluated the influence of the Melting Layer (ML) as a feature in the clusters’ formation. From the study, the main conclusions are as follows:

• Rainfall types were identified by applying a clustering method and thus ensured an objective separation of rainfall events because the classification is based exclusively on the data (i.e., rainfall characteristics). The use of microphysical characteristics, which are not commonly used due to instrument limitations, allowed for the provision of additional insights about each rainfall type.
• Three rainfall classes were identified in the study area: convective, stratiform, and mixed. The rainfall classes show that the clustering method (k-means) works well to distinguish the different rainfall patterns and identify the rainfall types. The first two main classes, i.e., convective and stratiform, were obtained by first using the method with two classes (k = 2). Here, the two groups showed a clear difference in the features, especially in the mean values of rain rate, velocity, and Dm. In addition, the convective type (class 1) showed rainfall events with shorter duration and higher rain rate than the stratiform type (class 2). The inclusion/exclusion of the Melting Layer feature did not influence the clustering results. Thus, it proves that the other rainfall features are able to properly describe the differences between these two main groups. When using three classes (k = 3), the mixed type (class 3) resulted as a subgroup of one of the main groups (k = 2). So, the convective type remained almost invariable regarding its rainfall characteristics. With respect to the stratiform type and mixed type, their rainfall features are most similar between them. It suggests that the mixed type has a dominant stratiform behavior.
• Rainfall events with shorter duration of less than 70 min are more frequent in the study area. Furthermore, there is a prevalence of convective rainfall events in March and November, while rainfall events of the stratiform and mixed type are common during all the year.

The findings of this research provide insights about the rainfall dynamics in this tropical mountain setting and show that data with high temporal resolution is necessary to analyze the temporal variability in this area. Furthermore, these rainfall types identified here will be of interest to analyze the vertical profile of rainfall and identify the rainfall formation process. Applications that can benefit from rainfall classification include (i) Numerical Weather Prediction (NWP) verification regarding convective rainfall at high altitudes, (ii) the improvement of quantitative precipitation estimation from scanning weather radar, (iii) the parameterization of cloud microphysical processes in numerical models, and (iv) the analysis of rain-fed soil erosion.

This study allowed for the analysis of the rainfall-event types and their occurrence in the study area. Further analyses on the intraevent rainfall variability is suggested for future investigations.