Improved Mekong Basin Runoff Estimate and Its Error Characteristics Using Pure Remotely Sensed Data Products
Abstract
:1. Introduction
- (1).
- Passively sensed gridded data products, such as the normalized difference vegetation index (NDVI), are directly correlated with the in situ water level (or RD) at a nearby gridded point via a linear regression [7,8,9,10,11]. This method is simple and common; however, these data products have no direct causal relationship with RD.
- (2).
- Both actively and passively sensed water balance component data products, such as precipitation (P) from the Tropical Rainfall Measuring Mission (TRMM) [12] (hereinafter denoted TRMM-P), evapotranspiration (ET) from the Moderate Resolution Imaging Spectroradiometer (MODIS) [13] (hereinafter denoted MODIS-ET), and terrestrial water storage (S) from the Gravity Recovery and Climate Experiment (GRACE) [14] (hereinafter denoted GRACE-S), are aggregated over the entire basin or sub-basin individually before being correlated with the water level [15] or R [16]. This method is similar to the first method, but the difference lies in the use of the aggregated remotely sensed water balance data over the entire basin or sub-basin.
- (3).
- Passively sensed river width is inputted into hydraulic functional models to estimate the RD (e.g., [17,18,19,20,21]). Despite elegant models, high-resolution remote sensing imagery and an accurate in situ measured roughness coefficient are required [22,23,24]. Hence, this method is still dependent on the in situ measurements, which is not desirable.
- (4).
- An actively sensed water level (or so-called stage) measured from satellite altimetry is directly correlated with nearby in situ RD either via rating curves (e.g., [25,26,27]) or an ensemble-learning regression technique [28]. This method is direct; however, the nominal size of the radar altimetric footprint (i.e., between 3.5 km and 5 km (e.g., [29])) is normally larger than the river width. This results in an inaccurately sensed water level because the reflected radar signal is contaminated by the riverside (e.g., [30]).
- (5).
- Based on the terrestrial or combined land–atmosphere water balance equation, R can be estimated using a combination of a remotely sensed water balance component (RSWBC) and model-predicted data products [31,32,33,34]. This method is independent of in situ measurements; however, R accuracy is highly dependent on reliable model-predicted data.
2. Data and Methods
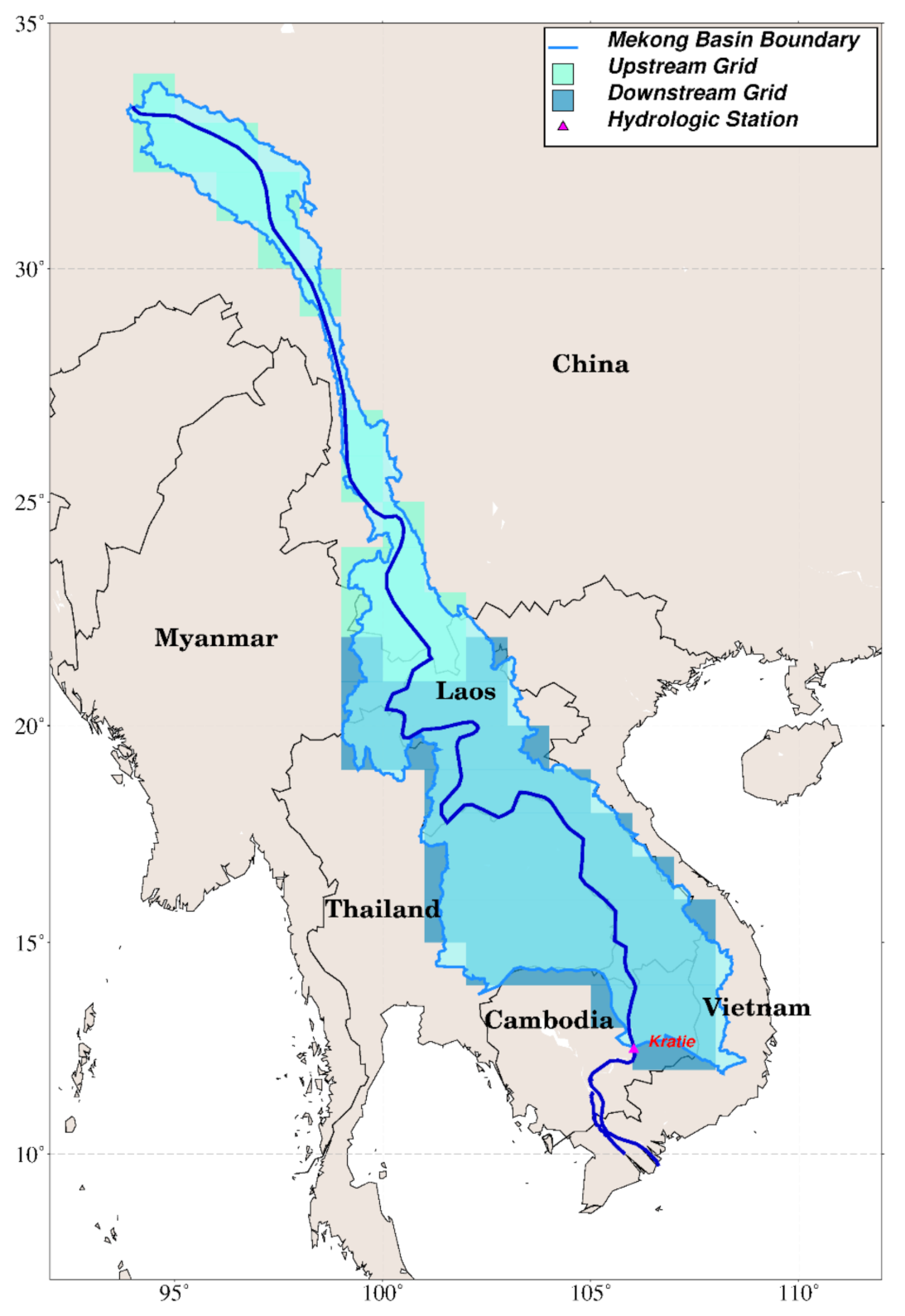
2.1. River Discharge Data
2.2. Water Balance Gridded Data Products
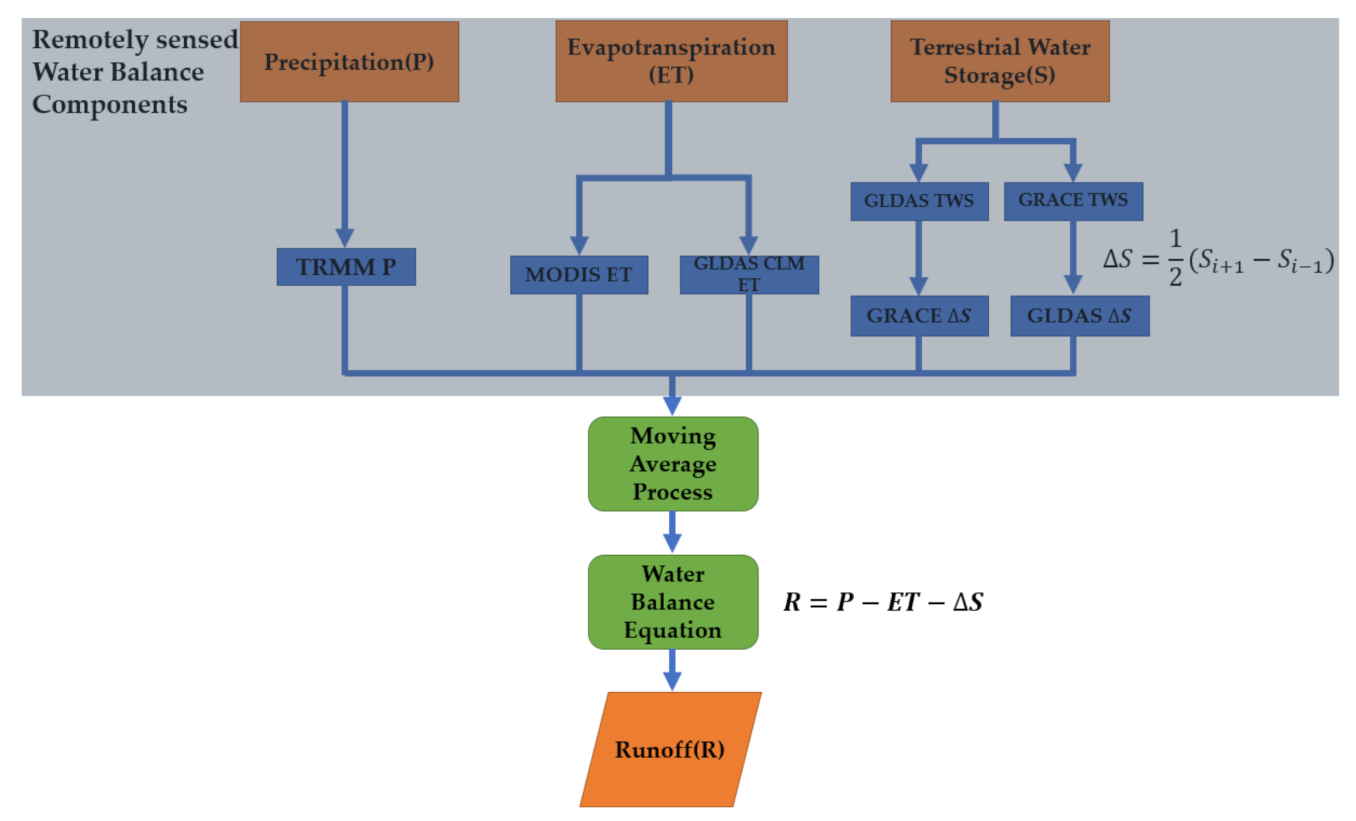
2.3. Methodology
2.4. Accuracy Evaluation Indicators
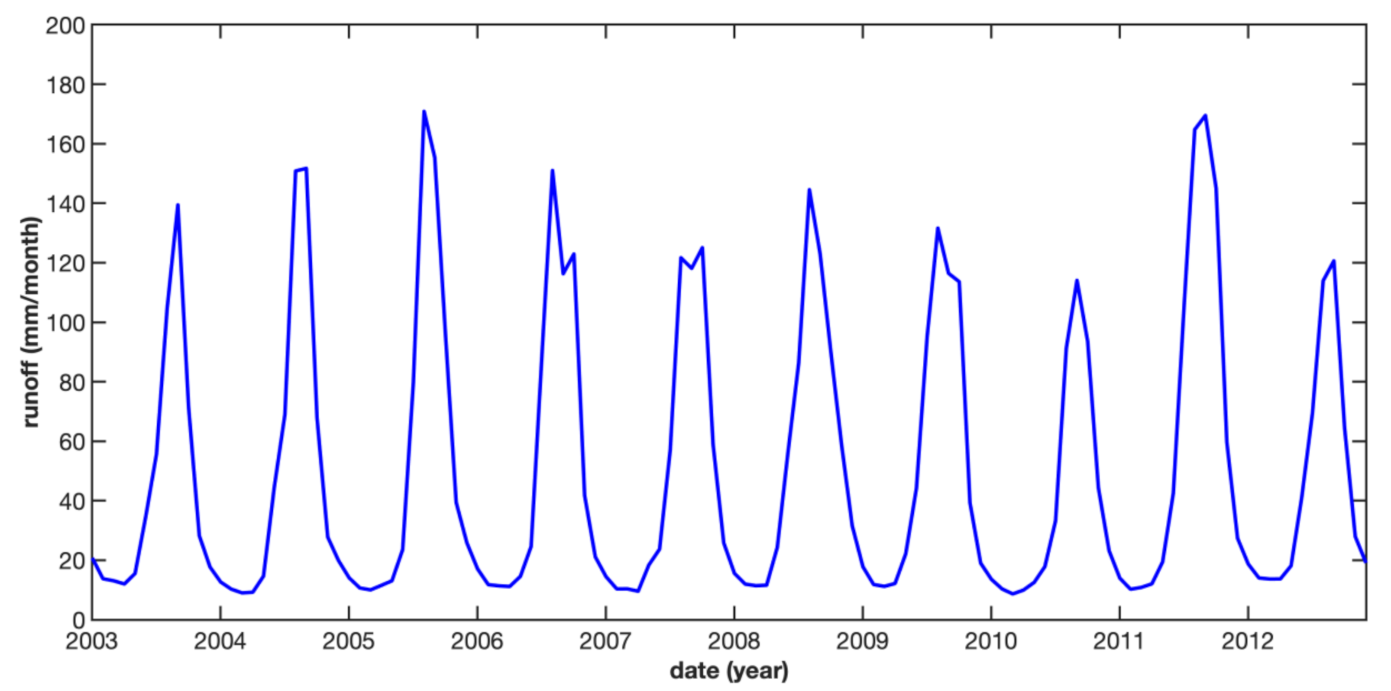
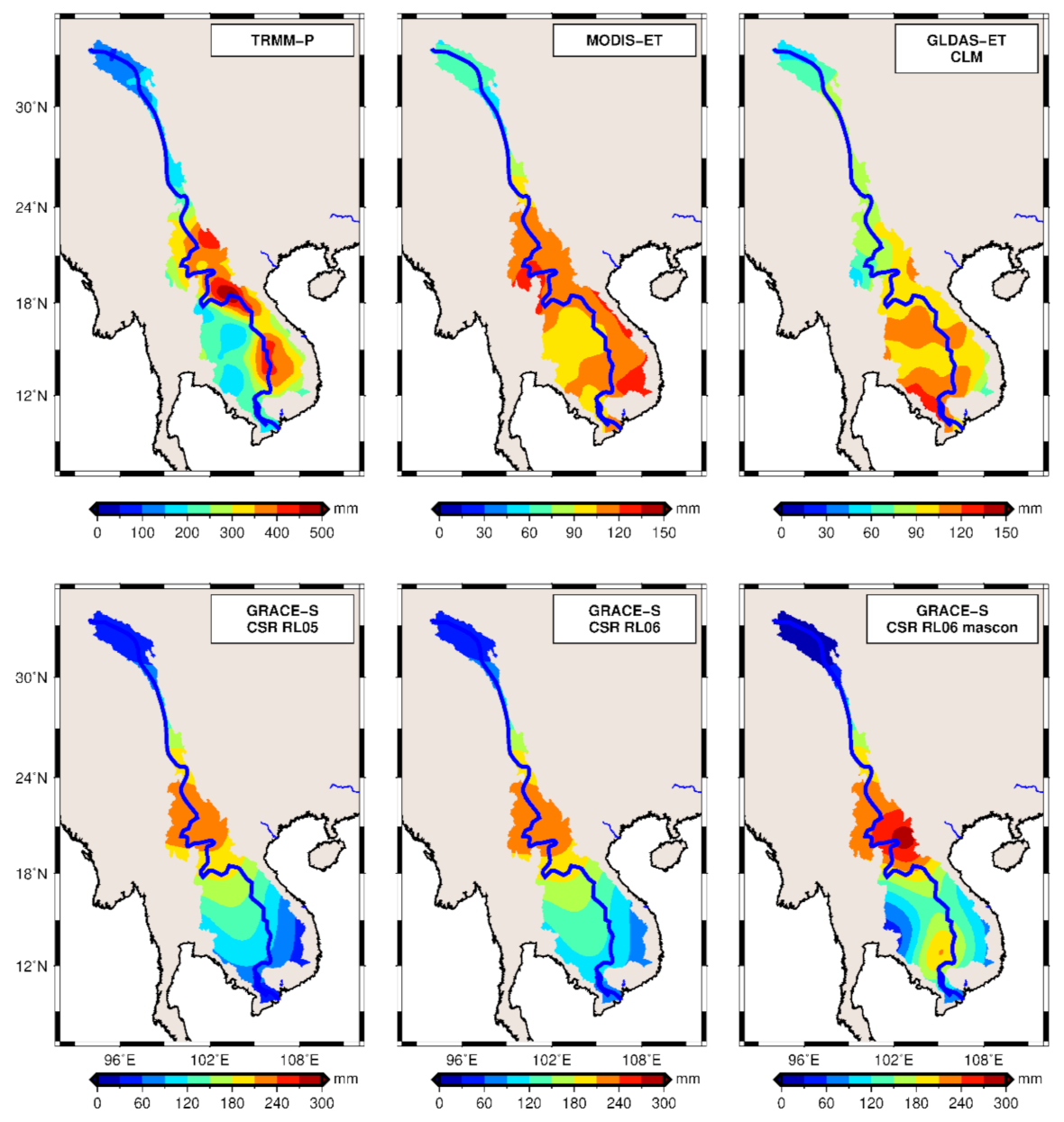
3. Results and Discussion
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Krysanova, V.; Zhai, J.; Su, B. Impact of intensive irrigation activities on river discharge under agricultural scenarios in the semi-arid Aksu river basin, northwest China. Water Resour. Manag. 2015, 29, 945–959. [Google Scholar] [CrossRef]
- Zampieri, M.; Carmona Garcia, G.; Dentener, F.; Gumma, M.; Salamon, P.; Seguini, L.; Toreti, A. Surface freshwater limitation explains worst rice production anomaly in India in 2002. Remote Sens. 2018, 10, 244. [Google Scholar] [CrossRef] [Green Version]
- Sneeuw, N.; Lorenz, C.; Devaraju, B.; Tourian, M.J.; Riegger, J.; Kunstmann, H.; Bardossy, A. Estimating runoff using hydro-geodetic approaches. Surv. Geophys. 2014, 35, 1333–1359. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Lettenmaier, D.P. Tracking fresh water from space. Science 2003, 301, 1491–1494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gleason, C.J.; Durand, M.T. Remote sensing of river discharge: A review and framing for the discipline. Remote Sens. 2020, 12, 1107. [Google Scholar] [CrossRef] [Green Version]
- Chiara, C.; Marco, M. Calibration and validation of a distributed energy–water balance model using satellite data of land surface temperature and ground discharge measurements. J. Hydrometeorol. 2012, 15, 376–392. [Google Scholar]
- Tarpanelli, A.; Brocca, L.; Lacava, T.; Melone, F.; Moramarco, T.; Faruolo, M.; Pergola, N.; Tramutoli, V. Toward the estimation of river discharge variations using MODIS data in ungauged basins. Remote Sens. Environ. 2013, 136, 47–55. [Google Scholar] [CrossRef]
- Lu, X.X.; Wang, J.; Higgitt, D.L. NDVI and its relationships with hydrological regimes in the upper Yangtze. Can. J. Remote Sens. 2000, 26, 418–427. [Google Scholar] [CrossRef]
- Li, C.H.; Yang, Z.F. Spatio-temporal changes of NDVI and their relations with precipitation and runoff in the Yellow River Basin. Geogr. Res. 2004, 23, 753–759. [Google Scholar]
- Xu, W.; Yang, D.; Li, Y.; Xiao, R. Correlation analysis of Mackenzie river discharge and NDVI relationship. Can. J. Remote Sens. 2016, 42, 292–306. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The tropical rainfall measuring mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Chen, J.; Seneviratne, S.I.; Viterbo, P.; Holl, S.; Wilson, C.R. Basin scale estimates of evapotranspiration using GRACE and other observations. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-variable gravity from GRACE: First results. Geophys Res Lett. 2004, 31, L11501. [Google Scholar] [CrossRef] [Green Version]
- Fok, H.S.; He, Q. Water Level Reconstruction Based on Satellite Gravimetry in the Yangtze River Basin. ISPRS Int. J. Geo Inf. 2018, 7, 286. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Fok, H.S.; Ma, Z.; Chen, Q. Upstream Remotely-Sensed Hydrological Variables and Their Standardization for Surface Runoff Reconstruction and Estimation of the Entire Mekong River Basin. Remote Sens. 2019, 11, 1064. [Google Scholar] [CrossRef] [Green Version]
- Bjerklie, D.M.; Moller, D.; Smith, L.C.; Dingman, S.L. Estimating discharge in rivers using remotely sensed hydraulic information. J. Hydrol. 2005, 309, 191–209. [Google Scholar] [CrossRef]
- LeFavour, G.; Alsdorf, D. Water slope and discharge in the Amazon river estimated using the shuttle radar topography mission digital elevation model. Geophys. Res. Lett. 2005, 32, L17404. [Google Scholar] [CrossRef] [Green Version]
- Neal, J.; Schumann, G.; Bates, P.; Buytaert, W.; Matgen, P.; Pappenberger, F. A data assimilation approach to discharge estimation from space. Hydrol. Process. 2010, 23, 3641–3649. [Google Scholar] [CrossRef]
- Pavelsky, T.M.; Durand, M.T.; Andreadis, K.M.; Beighley, R.E.; Paiva, R.C.D.; Allen, G.H.; Miller, Z.F. Assessing the potential global extent of SWOT river discharge observations. J. Hydrol. 2014, 519, 1516–1525. [Google Scholar] [CrossRef]
- Sichangi, A.W.; Wang, L.; Yang, K.; Chen, D.; Wang, Z.; Li, X.; Zhou, J.; Liu, W.; Kuria, D. Estimating continental river basin discharges using multiple remote sensing datasets. Remote Sens. Environ. 2016, 179, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Shih, S.F.; Rahi, G.S. Seasonal variations of Manning’s roughness coefficient in a subtropical marsh. Trans. ASABE 1982, 25, 116–119. [Google Scholar] [CrossRef] [Green Version]
- Mailapalli, D.R.; Raghuwanshi, N.S.; Singh, R.; Schmitz, G.H.; Lennartz, F. Spatial and temporal variation of Manning’s roughness coefficient in furrow irrigation. J. Irrig. Drain. Eng. 2008, 134, 185–192. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Hopson, T.M.; DeGroeve, T.; Brakenridge, G.R.; Gebremichael, M.; Restrepo, P.J. Upstream satellite remote sensing for river discharge forecasting: Application to major rivers in South Asia. Remote Sens. Envrion. 2013, 131, 140–151. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Barbetta, S.; Brocca, L.; Moramarco, T. River discharge estimation by using altimetry data and simplified flood routing modeling. Remote Sens. 2013, 5, 4145–4162. [Google Scholar] [CrossRef] [Green Version]
- Kouraev, A.V.; Zakharova, E.A.; Samain, O.; Mognard, N.M.; Cazenave, A. Ob’ river discharge from TOPEX/Poseidon satellite altimetry (1992–2002). Remote Sens. Environ. 2004, 93, 238–245. [Google Scholar] [CrossRef] [Green Version]
- Birkinshaw, S.J.; O’donnell, G.M.; Moore, P.; Kilsby, C.G.; Fowler, H.J.; Berry, P.A.M. Using satellite altimetry data to augment flow estimation techniques on the Mekong River. Hydrol. Process. 2010, 24, 3811–3825. [Google Scholar] [CrossRef]
- Kim, D.; Lee, H.; Chang, C.H.; Bui, D.D.; Jayasinghe, S.; Basnayake, S.; Chishtie, F.; Hwang, E. Daily river discharge estimation using multi-mission radar altimetry data and ensemble learning regression in the lower mekong river basin. Remote Sens. 2019, 11, 2684. [Google Scholar] [CrossRef] [Green Version]
- Phan, V.H.; Lindenbergh, R.; Menenti, M. ICESat derived elevation changes of Tibetan lakes between 2003 and 2009. Int. J. Appl. Earth Obs. 2012, 17, 12–22. [Google Scholar] [CrossRef]
- Sulistioadi, Y.B.; Tseng, K.H.; Shum, C.K.; Hidayat, H.; Sumaryono, M.; Suhardiman, A.; Setiawan, F.; Sunarso, S. Satellite radar altimetry for monitoring small rivers and lakes in Indonesia. Hydrol. Earth Syst Sc. 2015, 19, 341–359. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, V.G.; Gong, Z.; He, X.; Zhang, Y.; Andam-Akorful, S.A. Estimating total discharge in the Yangtze River Basin using satellite-based observations. Remote Sens. 2013, 5, 3415–3430. [Google Scholar] [CrossRef] [Green Version]
- Syed, T.H.; Famiglietti, J.S.; Chen, J.; Rodell, M.; Seneviratne, S.I.; Viterbo, P.; Wilson, C.R. Total basin discharge for the Amazon and Mississippi River basins from GRACE and a land-atmosphere water balance. Geophys. Res. Lett. 2005, 32, L24404. [Google Scholar] [CrossRef] [Green Version]
- Syed, T.H.; Famiglietti, J.S.; Chambers, D.P. GRACE-based estimates of terrestrial freshwater discharge from basin to continental scales. J. Hydrometeorol. 2009, 10, 22–40. [Google Scholar] [CrossRef]
- Seo, J.; Lee, S.I. Total discharge estimation in the Korean Peninsula using multi-satellite products. Water 2017, 9, 532. [Google Scholar]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef] [Green Version]
- Peixoto, J.P.; Oort, A.H. Physics of climate. N. Y. Am. Inst. Phys. 1992, 173, 415–423. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef] [Green Version]
- Dai, A.; Trenberth, K.E. Estimates of freshwater discharge from continents: Latitudinal and seasonal variations. J. Hydrometeorol. 2002, 3, 660–687. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol Soc. 2004, 3, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Fok, H.S.; Ma, Z.; Tenzer, R. Improved remote sensed total basin discharge and its seasonal error characterization in the Yangtze River Basin. Sensors 2019, 19, 3386. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.S.; Liaqat, U.W.; Baik, J.; Choi, M. Stand-alone uncertainty characterization of GLEAM, GLDAS and MOD16 evapotranspiration products using an extended triple collocation approach. Agric. For. Meteorol. 2018, 252, 256–268. [Google Scholar] [CrossRef]
- Xue, Z.; Liu, J.P.; Ge, Q. Changes in hydrology and sediment delivery of the Mekong River in the last 50 years: Connection to damming, monsoon, and ENSO. Earth Surf. Process. Landf. 2011, 36, 296–308. [Google Scholar] [CrossRef]
- Wang, B.; Lin, H. Rainy Season of the Asian–Pacific Summer Monsoon. J. Clim. 2002, 15, 386–398. [Google Scholar] [CrossRef] [Green Version]
- Räsänen, T.A.; Kummu, M. Spatiotemporal influences of ENSO on precipitation and flood pulse in the Mekong River Basin. J. Hydrol. 2013, 476, 154–168. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.P.; Saito, Y.; Nguyen, V.L. Recent evolution of the Mekong Delta and the impacts of dams. Earth Sci. Rev. 2017, 175, 1–17. [Google Scholar] [CrossRef]
- Onishi, K. Reassessing water security in the Mekong: The Chinese rapprochement with Southeast Asia. J. Nat. Resour. Policy Res. 2011, 3, 393–412. [Google Scholar] [CrossRef]
- Lu, X.X.; Li, S.; Kummu, M.; Padawangi, R.; Wang, J.J. Observed changes in the water flow at Chiang Saen in the lower Mekong: Impacts of Chinese dams? Quat. Int. 2014, 336, 145–157. [Google Scholar] [CrossRef]
- Cochrane, T.A.; Arias, M.E.; Piman, T. Historical impact of water infrastructure on water levels of the Mekong River and the Tonle Sap system. Hydrol. Earth Syst. Sci. 2014, 18, 4529–4541. [Google Scholar] [CrossRef] [Green Version]
- Lillesand, T.; Kiefer, R.W.; Chipman, J. Remote Sensing and Image Interpretation; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Peng, H.; Fok, H.S.; Gong, J.; Wang, L. Improving Stage–Discharge Relation in The Mekong River Estuary by Remotely Sensed Long-Period Ocean Tides. Remote Sens. 2020, 12, 3648. [Google Scholar] [CrossRef]
- Kummu, M.; Tes, S.; Yin, S.; Adamson, P.; Józsa, J.; Koponen, J.; Richey, J.; Sarkkula, J. Water balance analysis for the Tonle Sap Lake–floodplain system. Hydrol Process. 2014, 28, 1722–1733. [Google Scholar] [CrossRef]
- Colin, C.; Siani, G.; Sicre, M.A.; Liu, Z. Impact of the east Asian monsoon rainfall changes on the erosion of the mekong river basin over the past 25,000 yr. Mar. Geol. 2010, 271, 84–92. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Teng, W.; Kempler, S. Tropical Rainfall Measuring Mission (TRMM) precipitation data and services for research and applications. Bull. Am. Meteorol. Soc. 2012, 93, 1317–1325. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multi-satellite Precipitation Analysis: Quasi-Global, Multi-Year, Combined-Sensor Precipitation Estimates at Fine Scale. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Wu, X.; Ray, J.; van Dam, T. Geocenter motion and its geodetic and geophysical implications. J. Geodyn. 2012, 58, 44–61. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J. The unexpected signal in GRACE estimates of C20. J. Geod. 2017, 91, 897–914. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Lu, H.; Khem, S.; Yang, K.; Huang, X. Evaluation of Three Satellite-Based Precipitation Products Over the Lower Mekong River Basin Using Rain Gauge Observations and Hydrological Modeling. IEEE J-STARS 2019, 12, 2357–2373. [Google Scholar] [CrossRef]
- Oki, T.; Musiake, K.; Matsuyama, H.; Masuda, K. Global atmospheric water balance and runoff from large river basins. Hydrol. Process. 1995, 9, 655–678. [Google Scholar] [CrossRef]
- Wang, W.-C.; Chau, K.-W.; Cheng, C.-T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef] [Green Version]
- Fok, H.S.; Zhou, L.; Liu, Y.; Ma, Z.; Chen, Y. Upstream GPS vertical displacement and its standardization for Mekong river basin surface runoff reconstruction and estimation. Remote Sens. 2020, 12, 18. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Loc, H.H.; Do, Q.H.; Cokro, A.A.; Irvine, K.N. Deep neural network analyses of water quality time series associated with water sensitive urban design (WSUD) features. J. Appl. Water. Eng. Res. 2020, 1–20. [Google Scholar] [CrossRef]
- Ziv, G.; Baran, E.; Nam, S.; Rodríguez-Iturbe, I.; Levin, S.A. Trading-off fish biodiversity, food security, and hydropower in the Mekong River Basin. Proc. Natl Acad. Sci. USA 2012, 109, 5609–5614. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]





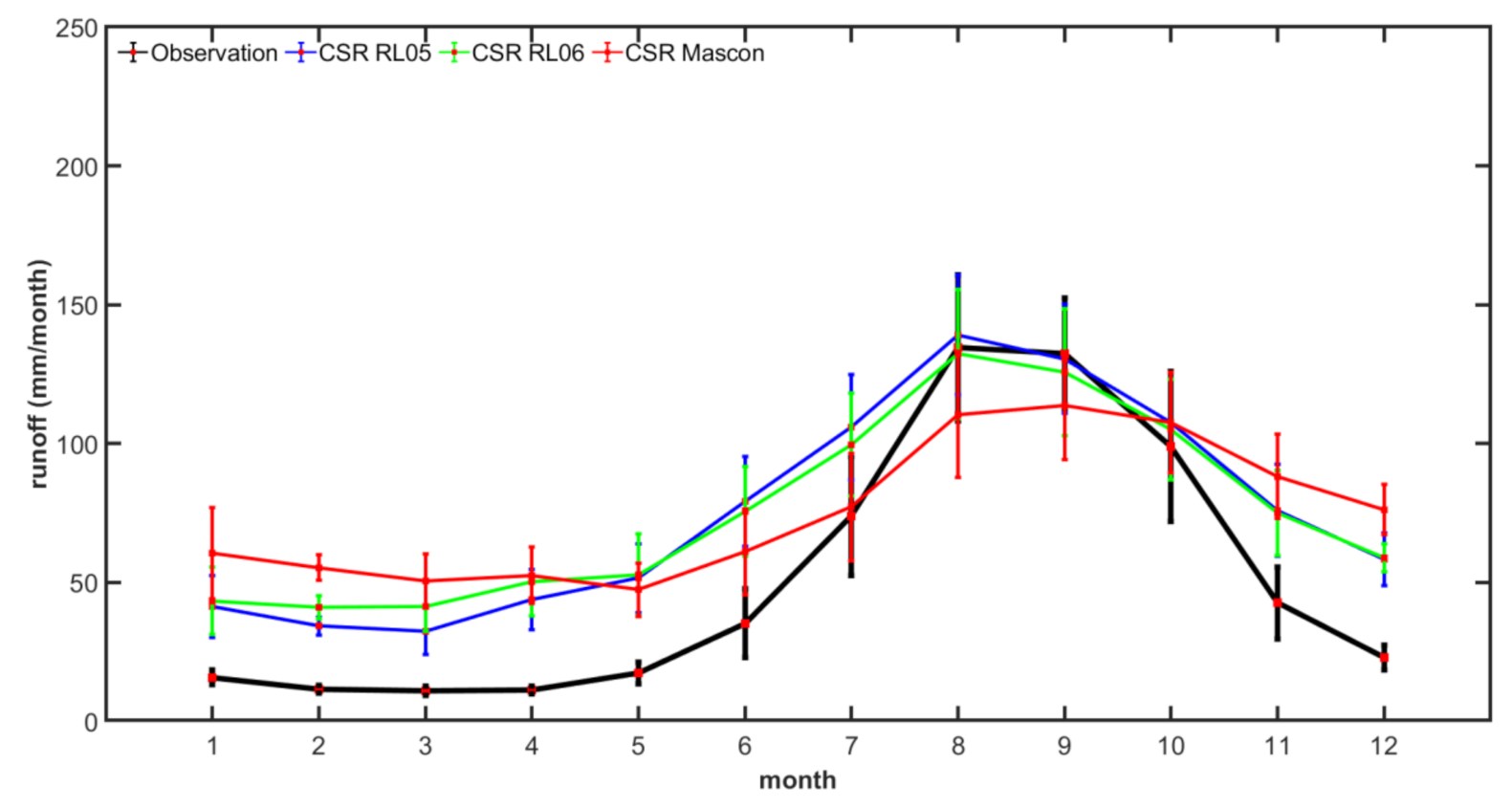
| Hydrological Component | Data Source | Spatial Resolution | Temporal Resolution |
|---|---|---|---|
| Precipitation | TRMM 3B43 v7 | 1 month | |
| Evapotranspiration | MOD16A2 | 1 month | |
| GLDAS CLM | 1 month | ||
| Terrestrial water storage change | GRACE | (mascon)/ (regular) | 1 month |
| GLDAS (CLM, Mosaic, VIC, and the Noah model) | 1 month | ||
| Runoff | Gauges | Point | 1 day |
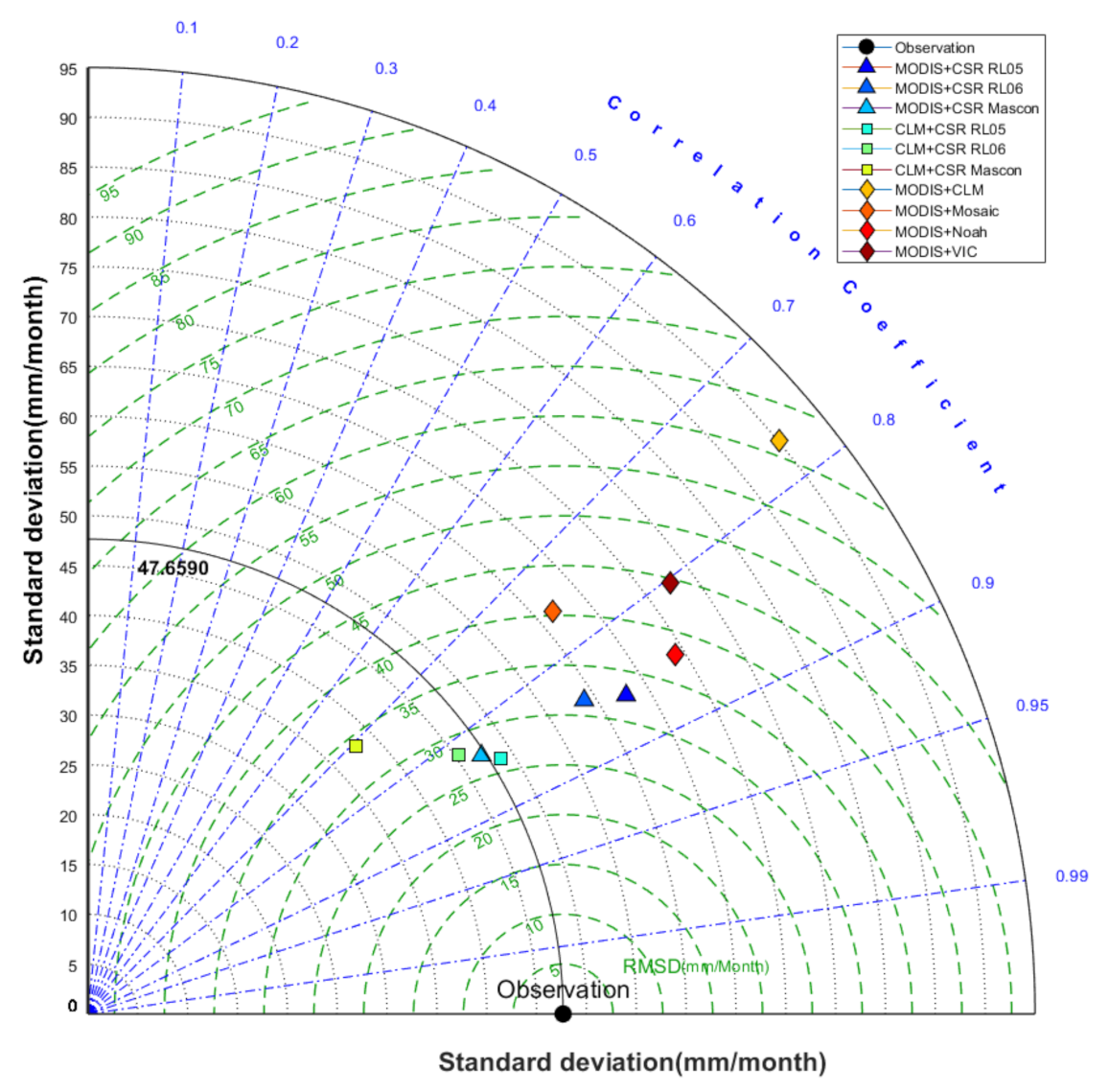
| Processing Strategy | Dataset Combinations | PCC | RMSE (mm/Month) | NSE | NRMSE | MAPE |
|---|---|---|---|---|---|---|
| None | MODIS + CSR RL05 | 0.860 | 32.798 | 0.522 | 0.202 | 1.055 |
| MODIS + CSR RL06 | 0.845 | 31.763 | 0.552 | 0.196 | 0.927 | |
| MODIS + CSR Mascon | 0.836 | 27.465 | 0.665 | 0.169 | 0.644 | |
| CLM + CSR RL05 | 0.851 | 35.963 | 0.426 | 0.222 | 1.255 | |
| CLM + CSR RL06 | 0.819 | 37.242 | 0.384 | 0.230 | 1.445 | |
| CLM + CSR Mascon | 0.707 | 41.878 | 0.221 | 0.258 | 1.805 | |
| MODIS + CLM | 0.770 | 61.371 | −0.672 | 0.378 | 2.136 | |
| MODIS + Mosaic | 0.756 | 40.464 | 0.273 | 0.249 | 1.263 | |
| MODIS + Noah | 0.853 | 37.883 | 0.363 | 0.234 | 1.258 | |
| MODIS + VIC | 0.803 | 44.689 | 0.113 | 0.275 | 1.578 | |
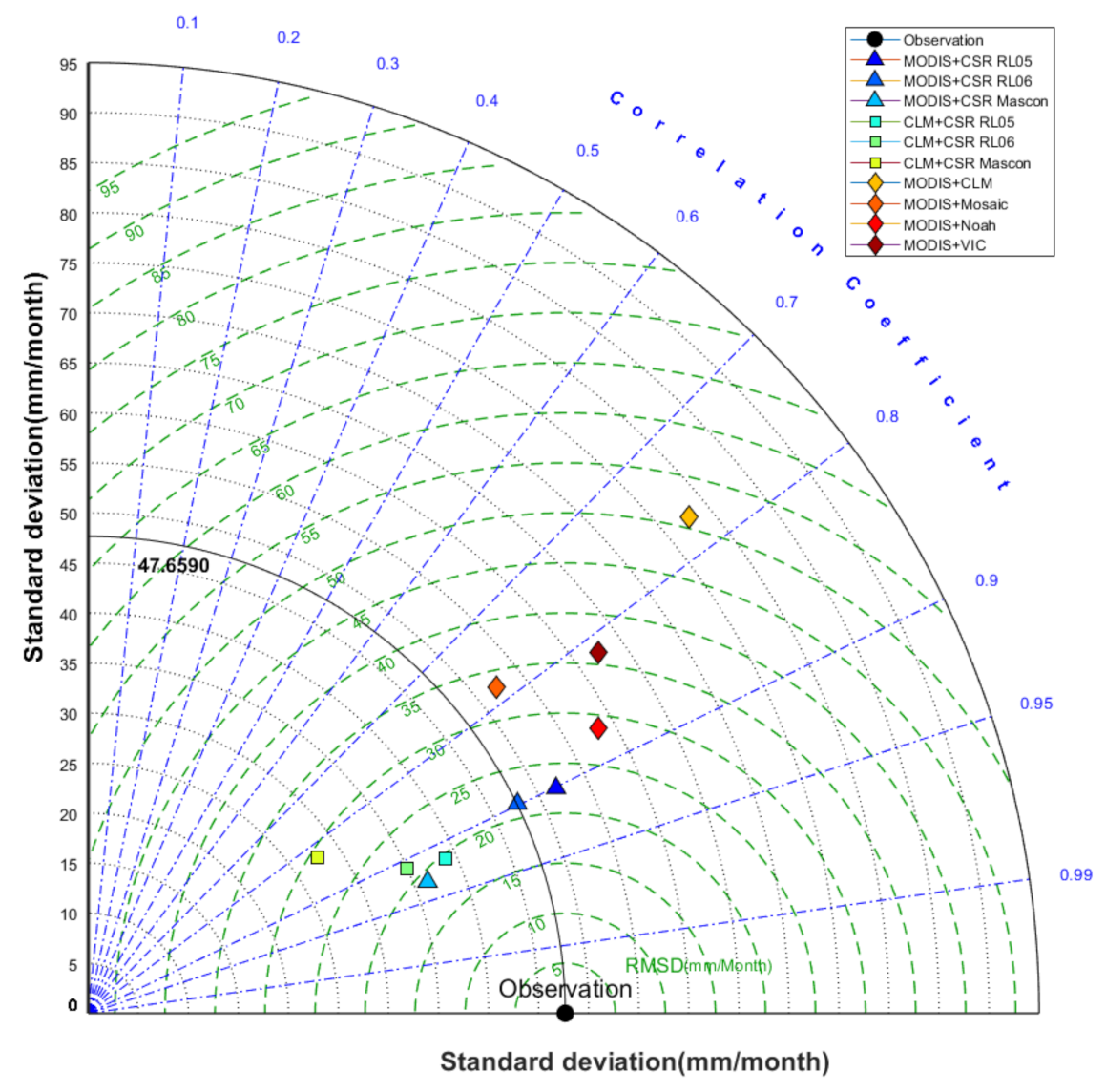
| Three-month average | MODIS + CSR RL05 | 0.901 | 22.966 | 0.766 | 0.142 | 0.816 |
| MODIS + CSR RL06 | 0.898 | 21.952 | 0.786 | 0.135 | 0.715 | |
| MODIS + CSR Mascon | 0.932 | 19.580 | 0.830 | 0.121 | 0.377 | |
| CLM + CSR RL05 | 0.918 | 31.165 | 0.569 | 0.192 | 1.312 | |
| CLM + CSR RL06 | 0.911 | 32.412 | 0.534 | 0.200 | 1.476 | |
| CLM + CSR Mascon | 0.828 | 38.000 | 0.359 | 0.234 | 1.793 | |
| MODIS + CLM | 0.771 | 51.175 | −0.163 | 0.315 | 1.934 | |
| MODIS + Mosaic | 0.781 | 33.536 | 0.501 | 0.207 | 1.137 | |
| MODIS + Noah | 0.873 | 29.046 | 0.625 | 0.179 | 1.070 | |
| MODIS + VIC | 0.816 | 36.483 | 0.409 | 0.225 | 1.376 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fok, H.S.; Chen, Y.; Wang, L.; Tenzer, R.; He, Q. Improved Mekong Basin Runoff Estimate and Its Error Characteristics Using Pure Remotely Sensed Data Products. Remote Sens. 2021, 13, 996. https://doi.org/10.3390/rs13050996
Fok HS, Chen Y, Wang L, Tenzer R, He Q. Improved Mekong Basin Runoff Estimate and Its Error Characteristics Using Pure Remotely Sensed Data Products. Remote Sensing. 2021; 13(5):996. https://doi.org/10.3390/rs13050996
Chicago/Turabian StyleFok, Hok Sum, Yutong Chen, Lei Wang, Robert Tenzer, and Qing He. 2021. "Improved Mekong Basin Runoff Estimate and Its Error Characteristics Using Pure Remotely Sensed Data Products" Remote Sensing 13, no. 5: 996. https://doi.org/10.3390/rs13050996
APA StyleFok, H. S., Chen, Y., Wang, L., Tenzer, R., & He, Q. (2021). Improved Mekong Basin Runoff Estimate and Its Error Characteristics Using Pure Remotely Sensed Data Products. Remote Sensing, 13(5), 996. https://doi.org/10.3390/rs13050996









