High-Resolution SMAP-Derived Root-Zone Soil Moisture Using an Exponential Filter Model Calibrated per Land Cover Type
Abstract
:1. Introduction
2. Data Description
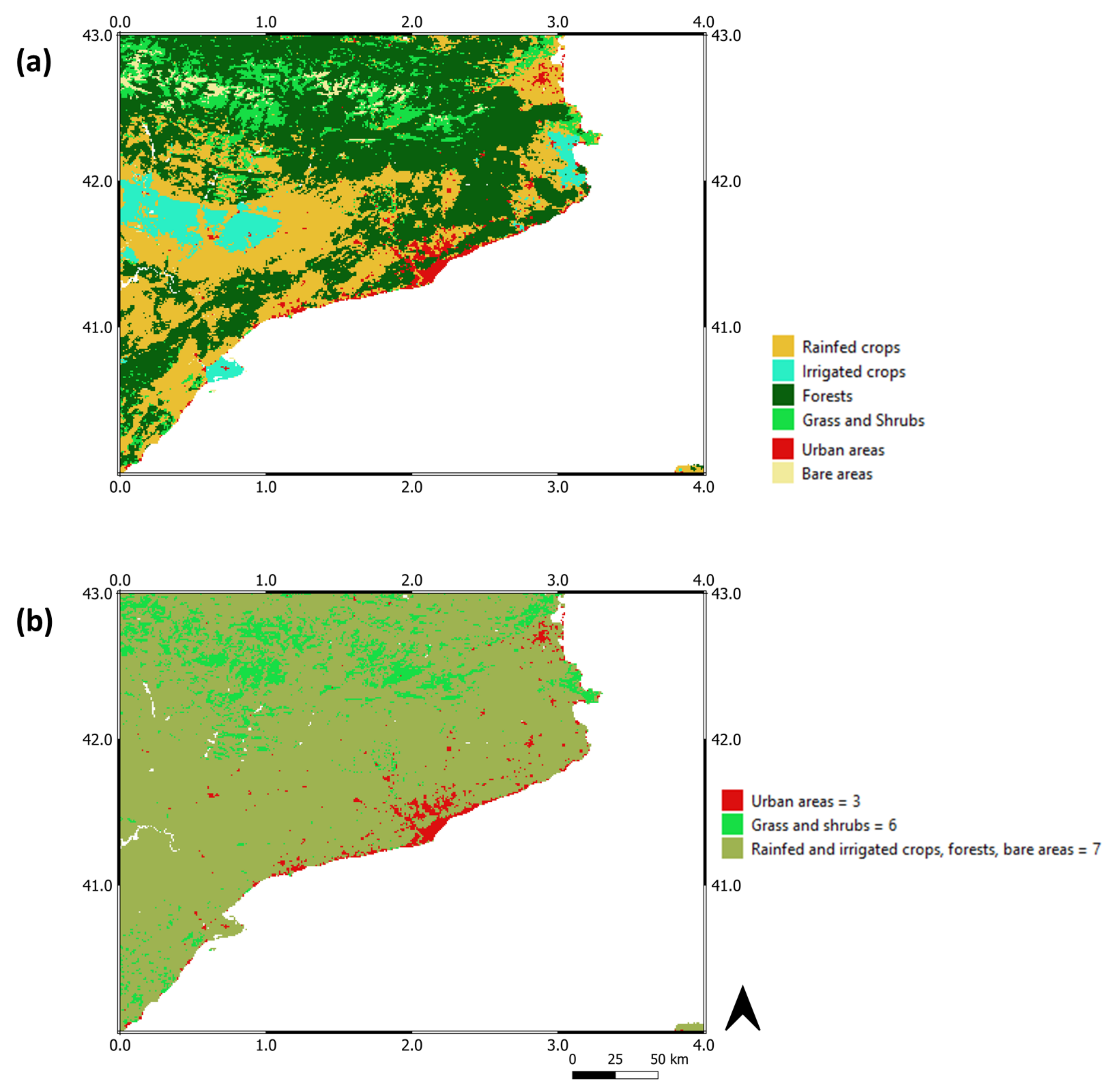
2.1. Validation Sites and In Situ Data
- Batea, Horta de Sant Joan and Poble de Massaluca: July 2019–June 2020
- Gandesa: July 2019–May 2020
- Observatori de l’Ebre: July 2018–June 2019
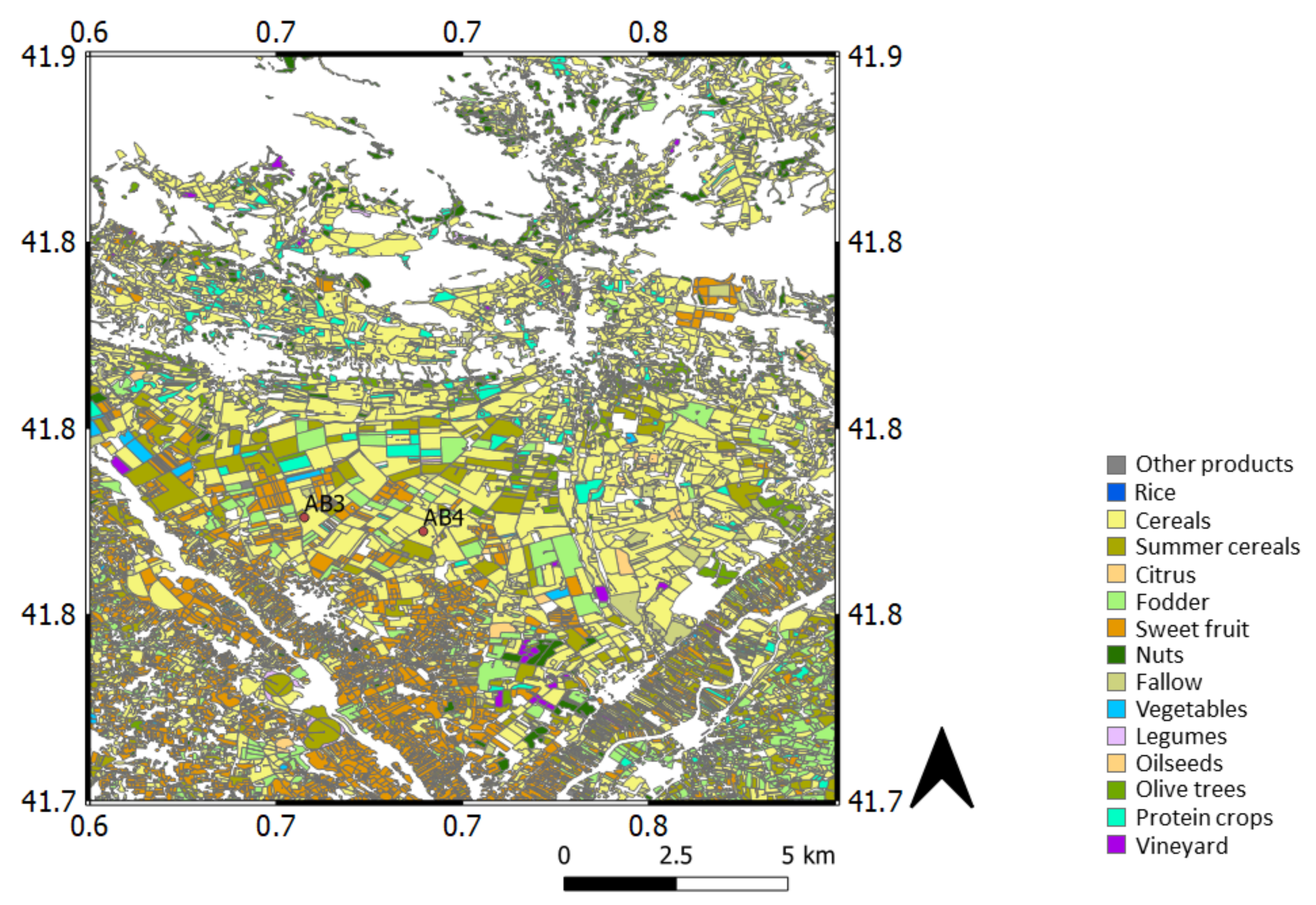
- For AB3: March 2017–December 2017 (hereby referred to as AB3_2017), January 2018–December 2018 (hereby referred to as AB3_2018), February 2020–September 2020 (hereby referred to as AB3_2020)
- For AB4: June 2017–November 2017 (hereby referred to as AB4_2017), January 2018– November 2018 (hereby referred to as AB4_2018), July 2019–December 2019 (hereby referred to as AB4_2019)
2.2. Remote Sensing Data
2.3. Land Surface Model Data
3. Methodology
3.1. Filter Model
3.2. Calibration of
4. Results
4.1. Validation of Calibration
4.2. —Depth Sensitivity Study
5. General Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pal, J.S.; Elthair, E.A.B. Pathways relating soil moisture conditions to future summer rainfall within a model of the land-atmosphere system. J. Clim. 2001, 14, 1227–1242. [Google Scholar] [CrossRef]
- Basara, J.B.; Crawford, K.C. Linear relationships between root-zone soil moisture and atmospheric processes in the planetary boundary layer. J. Geophys. Res. 2002, 107, 4274. [Google Scholar] [CrossRef] [Green Version]
- Daly, E.; Porporato, A. A Review of Soil Moisture Dynamics: From Rainfall Infiltration to Ecosystem Response. Environ. Eng. Science 2005. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements of the Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kerr, Y.H. Soil moisture from space: Where are we? Hydrogeol. J. 2007, 15, 117–120. [Google Scholar] [CrossRef]
- Wagner, W.; Bloschl, G.; Pampaloni, P.; Calvet, J.C.; Bizzari, B.; Wigneron, J.P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Nord. Hydrol. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Bazzi, H.; Zribi, M. Penetration analysis of SAR signals in the C and L bands for wheat, maize, and grasslands. Remote Sens. 2018, 11, 31. [Google Scholar] [CrossRef] [Green Version]
- El Hajj, M.; Baghdadi, N.; Zribi, M. Comparative analysis of the accuracy of surface soil moisture estimation from the C-and L-bands. J. Appl. Earth Obs. Geoinf. 2019, 82, 101888. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pasahaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Faridani, F.; Farid, A.; Ansari, H.; Manfreda, S. A modified version of the SMAR model for estimating root-zone soil moisture from time-series of surface soil moisture. Water SA 2017, 43, 492. [Google Scholar] [CrossRef] [Green Version]
- Deanmead, O.T.; Shaw, R.H. Availability of Soil Water to Plants as Affected by Soil Moisture Content and Meteorological Conditions. Agron. J. 1962, 54, 385–390. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Mirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating Soil Moistureclimate Interactions in a Changing Climate: A Review. Ph.D. Thesis, Wagenigen Univ., Wageningen, The Netherlands, 1986. [Google Scholar]
- Bolten, J.D.; Crow, W.T.; Zhan, X.; Jackson, T.J.; Reynolds, C.A. Evaluating the Utility of Remotely Sensed Soil Moisture Retrievals for Operational Agricultural Drought Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Seneviratne, S.I.; Nichols, N.; Easterling, D.; Goodess, C.M.; Kane, S.; Kossin, J.; Luo, Y.; Marengo, J.; McInnes, K.; Rahimi, M.; et al. Changes in Climate Extremes and their Impacts on the Natural Physical Environment. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambridge University Press: Cambridge, UK, 2012; pp. 109–230. [Google Scholar]
- Bindlish, R.; Crow, W.T.; Jackson, T.J. Role of Passive Microwave Remote Sensing in Improving Flood Forecasts. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; pp. 112–116. [Google Scholar]
- Bartsch, A.; Baltzer, H.; George, C. The influence of regional surface soil moisture anomalies on forest fires in Siberia observed from satellites. Environ. Res. Lett. 2009, 4, 045021. [Google Scholar] [CrossRef] [Green Version]
- Tobin, K.J.; Torres, R.; Crow, W.T.; Bennett, M.E. Multi-decadal analysis of root-zone soil moisture applying the exponential filter across CONUS. Hydrol. Earth Syst. Sci. 2017, 21, 4403–4417. [Google Scholar] [CrossRef] [Green Version]
- Ochsner, T.E.; Cosh, M.H.; Cuenca, R.H.; Draper, W.A.; Draper, C.S.; Hagimoto, Y.; Kerr, Y.H.; Njoku, E.G.; Small, E.E.; Zreda, M. State of the art in large-scale soil moisture monitoring. Soil Sci. Soc. Am. J. 2013, 77, 1888–1919. [Google Scholar] [CrossRef] [Green Version]
- Bolten, J.D.; Crow, W.T. Improved prediction of quasi-global vegetation conditions using remotely-sensed surface soil moisture. Geohpys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Ridler, M.E.; Madsen, H.; Stisen, S.; Bircher, S.; Fensholt, R. Assimilation of SMOS-derived soil moisture in a fully integrated hydrological and soil vegetation-atmosphere transfer model in Western Denmark. Water Resour. Res. 2014, 50, 8962–8981. [Google Scholar] [CrossRef]
- Lievens, H.; Tomer, S.K.; Al Bitar, A.; De Lannoy, G.J.; Drusch, M.; Dumedah, G.; Hendricks Franssen, H.-J.; Kerr, Y.H.; Martens, B.; Pang, M.; et al. SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia. Remote Sens. Environ. 2015, 168, 142–162. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, L.; Chen, Y.; Zhao, L.; Qin, J.; Lu, H.; Tang, W.; Han, M.; Ding, B.; Fang, N. Land surface model calibration through microwave data assimilation for improving soil moisture simulations. J. Hydrol. 2016, 533, 266–276. [Google Scholar] [CrossRef]
- Baldwin, D.; Manfreda, S.; Keller, K.; Smithwick, E.A.H. Predicting root zone soil moisture with soil properties and satellite near-surface moisture data across the conterminous United States. J. Hydrol. 2017, 546, 393–404. [Google Scholar] [CrossRef]
- Baldwin, D.; Manfreda, S.; Lin, H.; Smithwick, E.A. Estimating root zone soil moisture across the Eastern United Stateswith passive microwave satellite data and a simple hydrologic model. Remote Sens. 2019, 11, 2013. [Google Scholar] [CrossRef] [Green Version]
- Dumedah, G.; Walker, J.P.; Merlin, O. Root-zone soil moisture estimation from assimilation of downscaled Soil Moisture and Ocean Salinity data. Adv. Water Res. 2015, 84, 14–22. [Google Scholar] [CrossRef]
- Smith, A.B.; Walker, J.P.; Western, A.W.; Young, R.I.; Ellett, K.M.; Pipunic, R.C.; Grayson, R.B.; Siriwardena, L.; Chiew, F.H.S.; Richter, H. The Murrumbidgee soil moisture monitoring network data set. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Teuling, A.J.; Uijlenhoet, R.; Hupet, F.; van Loon, E.E.; Troch, P.A. Estimating spatial mean root—Zone soil moisture from point-scale observations. Hydrol. Earth Syst. Sci. 2006, 10, 1447–1485. [Google Scholar] [CrossRef] [Green Version]
- Vereecken, H.; Huisman, J.A.; Bogena, H.; Vanderborght, J.; Vrugt, J.A.; Hopmans, J.W. On the value of soil moisture measurements in vadose zone hydrology: A review. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Calvet, J.C.; Noilhan, J.; Bessemoulin, P. Retrieving the root-zone soil moisture from surface soil moisture or temperature estimates: A feasibility study based on field measurements. J. Appl. Meteorol. Climatol. 1998, 37, 371–386. [Google Scholar] [CrossRef]
- Dumedah, G.; Berg, A.A.; Wineberg, M. An integrated framework for a joint assimilation of brightness temperature and soil moisture using the non-dominated sorting genetic algorithm-II. J. Hydrometeorol. 2011, 12, 1596–1609. [Google Scholar] [CrossRef]
- Ford, T.W.; Harris, E.; Quiring, S.M. Estimating root zone soil moisture using near-surface observations from SMOS. Hydrol. Earth Syst. Sci. 2014, 18, 139–154. [Google Scholar] [CrossRef] [Green Version]
- Margulis, S.A.; McLaughlin, D.; Entekhabi, D.; Dunne, S. Land data assimilation and estimation of soil moisture using measurements from the southern great plains 1997 field experiment. Water Resour. Res. 2002, 38, 35-1–35-18. [Google Scholar] [CrossRef]
- Ragab, R. Towards a continuous operational system to estimate the root-zone soil moisture from intermittent remotely sensed surface moisture. J. Hydrol. 1995, 173, 1–25. [Google Scholar] [CrossRef]
- Dumedah, G.; Walker, J.P. Evaluation of model parameter convergence when using data assimilation in soil moisture estimation. J. Hydrometeorol. 2014, 15, 359–375. [Google Scholar] [CrossRef] [Green Version]
- Lia, F.; Crow, W.T.; Kustas, W.P. Towards the estimation root-zone soil moisture via the simultaneous assimilation of thermal and microwave soil moisture retrievals. Adv. Water Resour. 2010, 33, 201–214. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. Three-dimensional soil moisture profile retrieval by assimilation of near-surface measurements: Simplified kalman filter covariance forecasting and field application. Water Resour. Res. 2002, 38, 1301. [Google Scholar] [CrossRef] [Green Version]
- Entekhabi, D.; Nakamura, H.; Njoku, E.G. Solving the inverse problem for soil moisture and temperature profiles by sequential assimilation of multifrequency remotely sensed observations. IEEE Trans. Geosci. Remote Sens. 1994, 32, 438–448. [Google Scholar] [CrossRef]
- Houser, P.R.; Shuttleworth, W.J.; Famiglietti, J.S.; Gupta, H.V.; Syed, K.H.; Goodrich, D.C. Integration of Soil Moisture Remote Sensing and Hydrologic Modelling Using Data Assimilation. Water Resour. Res. 1998, 34, 3405–3420. [Google Scholar] [CrossRef] [Green Version]
- Calvet, J.C.; Noilhan, J. 2000: From Near-Surface to Root-Zone Soil Moisture Using Year-Round Data. J. Hydrometeor. 2000, 1, 393–411. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. One-dimensional soil moisture profile retrieval by assimilation of near-surface observations: A simplified soil moisture model and field application. J. Hydrometeorol. 2001, 2, 356–373. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. One-dimensional soil moisture profile retrieval by assimilation of near-surface observations: A comparison of retrieval algorithms. Adv. Water Resour. 2001, 24, 631–650. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.V.; Reichle, R.; Koster, R.T.; Crow, W.T.; Peters-Lidard, C.D. Role of subsurface physics in the assimilation of surface soil moisture observations. J. Hydrometeorol. 2010, 10, 1534–1547. [Google Scholar] [CrossRef]
- Sabater, J.M.; Jarlan, L.; Calvet, J.C.; Bouyssel, F.; De Rosnay, P. From near surface to root zone soil moisture using different assimilation techniques. J. Hydrometeorol. 2007, 8, 94–206. [Google Scholar] [CrossRef]
- Das, N.; Mohanty, B.P. Root zone soil moisture assessment using remote sensing and vadose zone modeling. Vadose Zone J. 2006, 5, 296–309. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.; Li, X.; Yu, Z.; Horton, R.; Zhu, Y.; Hao, Z.; Xiang, L. Using a H1 filter assimilation procedure to estimate root zone soil water content. Hydrol. Process. 2010, 24, 3648–3660. [Google Scholar] [CrossRef]
- Dumedah, G.; Coulibaly, P. Evolutionary assimilation of streamflow in distributed hydrologic modeling using in-situ soil moisture data. Adv. Water Resour. 2012, 53, 231–241. [Google Scholar] [CrossRef]
- Reichle, R.; Crow, W.T.; Koster, R.T.; Kimball, J.; De Lannoy, G. Algorithm Theoretical Basis Document (ATBD) SMAP Level 4 Surface and Root Zone Soil Moisture (L4_SM) Data Product. 2018. Available online: https://nsidc.org/sites/nsidc.org/files/files/data/smap/pdfs/l4_sm_initrel_v1_9.pdf (accessed on 25 May 2020).
- Clark, M.P.; Rupp, D.E.; Woods, R.A.; Zheng, X.; Ibbitta, R.P.; Slater, A.G.; Schmidta, J.; Uddstroma, M.J. Hydrological data assimilation with the ensemble Kalman filter: Use of streamflow observations to update states in a distributed hydrological model. Adv. Water Resour. 2008, 31, 1309–1324. [Google Scholar] [CrossRef]
- Albergel, C.; Rudiger, C.; Pellarin, T.; Calvet, J.C.; Fritz, N.; Suquia, D.; Petipa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 12, 1323–1337. Available online: https://hess.copernicus.org/articles/12/1323/2008/ (accessed on 25 May 2020). [CrossRef] [Green Version]
- Srivastava, S.K.; Yograjan, N.; Jayaraman, V.; Rao, P.N.; Chandrasekhar, M.G. On the relationship between ERS-1 SAR/backscatter and surface/sub-surface soil moisture variations in vertisols. Acta Astronaut. 1997, 40, 693–699. [Google Scholar] [CrossRef]
- Kornelsen, K.C.; Coulibaly, P. Root-zone soil moisture estimation using data-driven methods. Water Resour. Res. 2014, 50, 2946–2962. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Rüdiger, C.; Calvet, J.C.; Gruhier, C.; Holmes, T.R.; De Jeu, R.A.; Wagner, W. An Intercomparison of ERS-Scat and AMSR-E Soil Moisture Observations with Model Simulations over France. J. Hydrometeorol. 2009, 10, 431–448. [Google Scholar] [CrossRef] [Green Version]
- Ceballos, A.; Scipal, K.; Wagner, W.; Martínez-Fernández, J. Validation of ERS scatterometer-derived soil moisture data in the central part of the Duero Basin, Spain. Hydrol. Process. 2005, 19, 1549–1566. [Google Scholar] [CrossRef]
- De Lange, R.; Beck, R.; Van De Giesen, N.; Friesen, J.; De Wit, A.; Wagner, W. Scatterometer-Derived Soil Moisture Calibrated for Soil Texture with a One-Dimensional Water-Flow Model. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4041–4049. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Naeimi, V.; Bartalis, Z.; Hasenauer, S. Improving runoff prediction through the assimilation of the ASCAT soil moisture product. Hydrol. Earth Syst. Sci. 2010, 14, 1881–1893. [Google Scholar] [CrossRef] [Green Version]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Fernández, J.M.; Llorens, P.; Latron, J.; et al. Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. Remote Sens. Environ. 2011, 15, 3390–3408. [Google Scholar] [CrossRef]
- Brocca, L.; Tarpanelli, A.; Moramarco, T.; Melone, F.; Ratto, S.M.; Caduro, M.; Ferraris, S.; Berni, N.; Ponziani, F.; Wagner, W.; et al. Soil moisture estimation in alpine catchments through modeling and satellite observations. Vadose Zone Hydrol. 2013, 12, 1–10. [Google Scholar] [CrossRef]
- Barbu, A.L.; Calvet, J.C.; Mahfouf, J.F.; Albergel, C.; Lafont, T.S. Assimilation of Soil Wetness Indes and Leaf Area Index into the ISBA-A-gs land surface model: Grassland case study. Biogeosciences 2011, 8, 1971–1986. [Google Scholar] [CrossRef] [Green Version]
- Mishra, V.; Lee Ellenburg, W.; Markert, K.N.; Limaye, A.S. Performance evaluation of soil moisture profile estimation through entropy-based and exponential filter models. Hydrol. Sci. J. 2020, 65, 1036–1048. [Google Scholar] [CrossRef]
- Carlson, T.N.; Gillies, R.R.; Schmugge, T.J. An interpretation of methodologies for indirect measurement of soil water content. Agric. For. Meteorol. 1995, 77, 191–205. [Google Scholar] [CrossRef]
- Mahmood, R.; Hubbard, K.G. Relationship between soil moisture of near surface and multiple depths of the root zone under heterogeneous land uses and varying hydroclimatic conditions. Hydrol. Process. 2007, 21, 3449–3462. [Google Scholar] [CrossRef]
- Pellarin, T.; Calvet, J.C.; Wagner, W. Evaluation of ERS scatterometer soil moisture products over a half-degree region in southwestern France. Geophys. Res. Lett. 2006, 33, L17401. [Google Scholar] [CrossRef] [Green Version]
- Stroud, P. A Recursive Exponential Filter for Time-Sensitive Data. Los Alamos National Laboratory LAUR-99-5573. Available online: public.lanl.gov/stroud/ExpFilter/ExpFilter995573.pdf (accessed on 25 May 2020).
- Merlin, O.; Escorihuela, M.J.; Mayoral, M.A.; Hagolle, O.; Al Bitar, A.; Kerr, Y. Self-calibrated evaporation-based disaggregation of SMOS soil moisture: An evaluation study at 3 km and 100 m resolution in Catalunya, Spain. Remote Sens. Environ. 2013, 130, 25–38. [Google Scholar] [CrossRef] [Green Version]
- Merlin, O.; Rüdiger, C.; Al Bitar, A.; Richaume, P.; Walker, J.; Kerr, Y. Disaggregation of SMOS soil moisture in southeastern Australia. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1556–1571. [Google Scholar] [CrossRef] [Green Version]
- Wan, Z.; Hook, S.; Hulley, G. MOD11A1 MODIS/Terra Land Surface Temperature/Emissivity Daily L3 Global 1 km SIN Grid V006. NASA EOSDIS Land Process. DAAC 2015. [Google Scholar] [CrossRef]
- Wan, Z.; Hook, S.; Hulley, G. MYD11A1 MODIS/Aqua Land Surface Temperature/Emissivity Daily L3 Global 1 km SIN Grid V006. NASA EOSDIS Land Process. DAAC 2015. [Google Scholar] [CrossRef]
- Didan, K. MOD13A2 MODIS/Terra Vegetation Indices 16-Day L3 Global 1 km SIN Grid V006. NASA EOSDIS LP DAAC 2015. [Google Scholar] [CrossRef]
- Noilhan, J.; Planton, S. A simple parameterization of land surface processes for meteorological models. Mon. Weather Rev. 1989, 117, 536–549. [Google Scholar] [CrossRef]
- Mahfouf, J.F.; Noilhan, J. Inclusion of gravitationnal drainage in a land surface scheme based on the force-restore method. J. Appl. Meteor. 1996, 35, 987–992. [Google Scholar] [CrossRef] [Green Version]
- Masson, V.; Le Moigne, P.; Martin, E.; Faroux, S.; Alias, A.; Alkama, R.; Belamari, S.; Barbu, A.; Boone, A.; Bouyssel, F.; et al. The SURFEXv7.2 land and ocean surface platform for coupled or offline simulation of earth surface variables and fluxes. Geosci. Model Dev. 2013, 6, 929–960. [Google Scholar] [CrossRef] [Green Version]
- Boone, A. Modelisation des processus hydrologiques dans le schema de surface ISBA: Inclusion d’un Reservoir Hydrologique, du gel et Modelisation de la Neige. Ph.D. Thesis, University Paul Sabatier, Toulouse, France, 2000. [Google Scholar]
- Quintana-Segui, P.; Le Moigne, P.; Durand, Y.; Martin, E.; Habets, F.; Baillon, M.; Canellas, C.; Franchisteguy, L.; Morel, S. Analysis of near-surface atmospheric variables: Validation of the SAFRAN analysis over France. J. Appl. Meteorol. Climatol. 2008, 47, 92–107. [Google Scholar] [CrossRef]
- Quintana-Segui, P.; Peral, M.C.; Turco, M.; Llasat, M.C.; Martin, E. Meteorological Analysis Systems in North-East Spain: Validation of SAFRAN and SPAN. J. Environ. Inform. 2016, 27, 116–130. [Google Scholar] [CrossRef] [Green Version]
- Quintana-Segui, P.; Turco, M.; Herrera, S.; Miguez-Macho, G. Validation of a new SAFRAN-based gridded precipitation product for Spain and comparisons to Spain02 and ERA-Interim. Hydrol. Earth Syst. Sci. 2017, 21, 2187–2201. [Google Scholar] [CrossRef] [Green Version]
- Decharme, B.; Boone, A.; Delire, C.; Noilhan, J. Local evaluation of the Interaction between Soil Biosphere Atmosphere soil multilayer diffusion scheme using four pedotransfer functions. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Decharme, B.; Martin, E.; Faroux, S. Reconciling soil thermal and hydrological lower boundary conditions in land surface models. J. Geophys. Res. Atmos. 2013, 118, 7819–7834. [Google Scholar] [CrossRef]
- Merlin, O.; Malbéteau, Y.; Notfi, Y.; Bacon, S.; Er-Raki, S.; Khabba, S.; Jarlan, L. Performance Metrics for Soil Moisture Downscaling Methods: Application to DISPATCH Data in Central Morocco. Remote Sens. 2015, 7, 3783–3807. [Google Scholar] [CrossRef] [Green Version]
- Albergel, C.; Calvet, J.C.; Mahfouf, J.F.; Rudiger, C.; Barbu, A.L.; Lafont, S.; Roujean, J.L.; Walker, J.P.; Crapeau, M.; Wigneron, J.P. Monitoring of water and carbon fluxes using a land data assimilation system: A case study for southwestern France. Hydrol. Earth Syst. Sci. 2010, 14, 1109–1124. [Google Scholar] [CrossRef] [Green Version]
- Capehart, W.J.; Carlson, T.N. Decoupling of surface and near-surface soil water content: A remote sensing perspective. Water Resour. Res. 1997, 33, 1383–1395. [Google Scholar] [CrossRef]







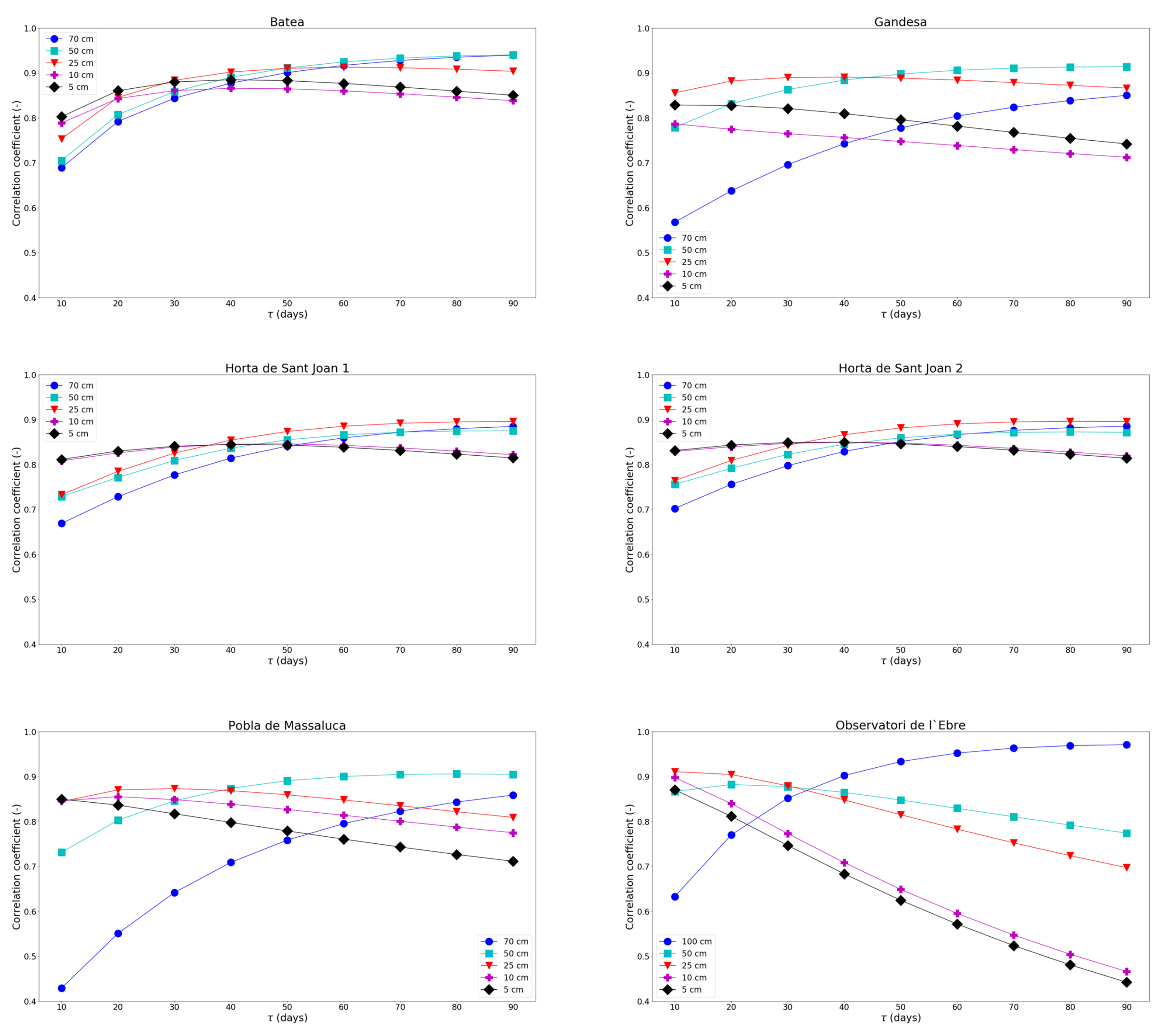
| Site | Depth (cm) | R | RMSE | Bias | Slope | NS |
|---|---|---|---|---|---|---|
| BA | 70 | 0.64 | 0.33 | 0.119 | 0.17 | 0.16 |
| (0.64) | (0.33) | (0.119) | (0.17) | (0.16) | ||
| 50 | 0.65 | 0.26 | 0.016 | 0.20 | 0.31 | |
| (0.65) | (0.26) | (0.016) | (0.20) | (0.31) | ||
| 25 | 0.71 | 0.21 | 0.001 | 0.26 | 0.39 | |
| (0.71) | (0.20) | (0.001) | (0.26) | (0.39) | ||
| 10 | 0.76 | 0.16 | −0.058 | 0.35 | 0.41 | |
| (0.76) | (0.16) | (−0.058) | (0.35) | (0.41) | ||
| 5 | 0.77 | 0.17 | −0.047 | 0.34 | 0.44 | |
| (0.75) | (0.17) | (−0.047) | (0.34) | (0.44) | ||
| GA | 70 | 0.54 | 0.28 | −0.112 | 0.25 | 0.16 |
| (0.54) | (0.28) | (−0.112) | (0.25) | (0.16) | ||
| 50 | 0.75 | 0.28 | 0.001 | 0.31 | 0.45 | |
| (0.75) | (0.28) | (0.001) | (0.31) | (0.45) | ||
| 25 | 0.84 | 0.25 | 0.063 | 0.37 | 0.51 | |
| (0.84) | (0.25) | (0.063) | (0.37) | (0.51) | ||
| 10 | 0.79 | 0.18 | −0.114 | 0.52 | 0.33 | |
| (0.79) | (0.18) | (−0.114) | (0.52) | (0.33) | ||
| 5 | 0.83 | 0.18 | −0.125 | 0.53 | 0.35 | |
| (0.83) | (0.18) | (−0.125) | (0.53) | (0.35) | ||
| HA1 | 70 | 0.64 | 0.29 | 0.046 | 0.28 | 0.36 |
| (0.64) | (0.29) | (0.046) | (0.28) | (0.36) | ||
| 50 | 0.71 | 0.24 | 0.025 | 0.35 | 0.45 | |
| (0.71) | (0.24) | (0.025) | (0.35) | (0.45) | ||
| 25 | 0.71 | 0.24 | 0.051 | 0.35 | 0.43 | |
| (0.71) | (0.24) | (0.051) | (0.35) | (0.43) | ||
| 10 | 0.80 | 0.19 | 0.061 | 0.44 | 0.54 | |
| (0.80) | (0.19) | (0.061) | (0.44) | (0.54) | ||
| 5 | 0.80 | 0.19 | 0.076 | 0.47 | 0.52 | |
| (0.80) | (0.19) | (0.076) | (0.47) | (0.52) | ||
| HA2 | 70 | 0.62 | 0.32 | −0.024 | 0.25 | 0.34 |
| (0.62) | (0.32) | (−0.024) | (0.25) | (0.34) | ||
| 50 | 0.71 | 0.26 | −0.094 | 0.35 | 0.37 | |
| (0.71) | (0.26) | (−0.094) | (0.35) | (0.37) | ||
| 25 | 0.79 | 0.21 | −0.111 | 0.45 | 0.42 | |
| (0.79) | (0.21) | (−0.111) | (0.45) | (0.42) | ||
| 10 | 0.81 | 0.17 | −0.092 | 0.54 | 0.49 | |
| (0.81) | (0.17) | (−0.092) | (0.54) | (0.49) | ||
| 5 | 0.84 | 0.17 | −0.006 | 0.48 | 0.63 | |
| (0.84) | (0.17) | (−0.006) | (0.48) | (0.63) | ||
| PM | 70 | 0.38 | 0.27 | −0.120 | 0.20 | −0.08 |
| (0.39) | (0.27) | (−0.072) | (0.20) | (−0.06) | ||
| 50 | 0.70 | 0.18 | −0.048 | 0.38 | 0.42 | |
| (0.71) | (0.18) | (−0.048) | (0.38) | (0.43) | ||
| 25 | 0.82 | 0.18 | 0.029 | 0.41 | 0.56 | |
| (0.83) | (0.18) | (0.029) | (0.41) | (0.56) | ||
| 10 | 0.83 | 0.17 | 0.002 | 0.42 | 0.58 | |
| (0.83) | (0.17) | (0.003) | (0.42) | (0.59) | ||
| 5 | 0.84 | 0.15 | −0.010 | 0.46 | 0.62 | |
| (0.85) | (0.15) | (−0.010) | (0.45) | (0.62) | ||
| OE | 100 | 0.57 | 0.28 | −0.003 | 0.30 | 0.33 |
| (0.55) | (0.28) | (−0.003) | (0.29) | (0.30) | ||
| 50 | 0.85 | 0.19 | −0.090 | 0.52 | 0.57 | |
| (0.84) | (0.19) | (−0.090) | (0.52) | (0.56) | ||
| 25 | 0.90 | 0.19 | −0.155 | 0.66 | 0.37 | |
| (0.89) | (0.19) | (−0.155) | (0.66) | (0.37) | ||
| 10 | 0.91 | 0.19 | −0.149 | 0.65 | 0.42 | |
| (0.91) | (0.19) | (−0.149) | (0.66) | (0.43) | ||
| 5 | 0.88 | 0.16 | −0.106 | 0.63 | 0.57 | |
| (0.88) | (0.16) | (−0.106) | (0.63) | (0.58) |
| Site | Depth (cm) | R | RMSE | Bias | Slope | NS |
|---|---|---|---|---|---|---|
| AB3_2017 | 50 | 0.21 | 0.31 | 0.196 | 0.05 | −0.59 |
| (0.21) | (0.31) | (0.196) | (0.05) | (−0.59) | ||
| 25 | 0.48 | 0.20 | 0.040 | 0.14 | 0.16 | |
| (0.48) | (0.20) | (0.040) | (0.14) | (0.16) | ||
| 5 | 0.48 | 0.38 | 0.327 | 0.14 | −2.13 | |
| (0.48) | (0.38) | (0.327) | (0.14) | (−2.13) | ||
| AB3_2018 | 50 | 0.54 | 0.30 | 0.203 | 0.18 | −0.39 |
| (0.54) | (0.30) | (0.203) | (0.18) | (−0.39) | ||
| 25 | 0.47 | 0.32 | 0.208 | 0.15 | −0.41 | |
| (0.47) | (0.32) | (0.208) | (0.15) | (−0.41) | ||
| 5 | 0.54 | 0.37 | 0.287 | 0.17 | −0.86 | |
| (0.54) | (0.37) | (0.287) | (0.17) | (−0.86) | ||
| AB3_2020 | 50 | 0.33 | 0.26 | 0.217 | 0.11 | −1.93 |
| (0.33) | (0.26) | (0.217) | (0.11) | (−1.93) | ||
| 25 | −0.16 | 0.37 | 0.301 | −0.04 | −2.57 | |
| (−0.16) | (0.37) | (0.301) | (−0.04) | (−2.57) | ||
| 5 | −0.01 | 0.35 | 0.259 | −0.00 | −1.31 | |
| (−0.01) | (0.35) | (0.259) | (−0.00) | (−1.31) | ||
| AB4_2017 | 50 | −0.02 | 0.32 | 0.118 | −0.00 | −0.26 |
| (−0.01) | (0.32) | (0.117) | (0.00) | (−0.24) | ||
| 25 | −0.56 | 0.34 | 0.101 | −0.16 | −0.54 | |
| (−0.52) | (0.34) | (0.100) | (−0.16) | (−0.54) | ||
| 5 | −0.53 | 0.33 | 0.098 | −0.16 | −0.53 | |
| (−0.50) | (0.33) | (0.096) | (−0.16) | (−0.52) | ||
| AB4_2018 | 50 | 0.46 | 0.28 | 0.148 | 0.15 | −0.13 |
| (0.47) | (0.27) | (0.147) | (0.16) | (−0.12) | ||
| 25 | 0.37 | 0.19 | −0.069 | 0.16 | 0.01 | |
| (0.39) | (0.19) | (−0.070) | (0.17) | (0.01) | ||
| 5 | 0.48 | 0.21 | 0.069 | 0.17 | 0.13 | |
| (0.51) | (0.21) | (0.068) | (0.19) | (0.15) | ||
| AB4_2019 | 50 | 0.27 | 0.21 | −0.025 | 0.06 | 0.06 |
| (0.29) | (0.21) | (−0.026) | (0.08) | (0.07) | ||
| 25 | 0.28 | 0.24 | −0.137 | 0.07 | −0.35 | |
| (0.30) | (0.24) | (−0.137) | (0.08) | (−0.34) | ||
| 5 | 0.19 | 0.27 | 0.008 | 0.03 | 0.03 | |
| (0.20) | (0.27) | (0.007) | (0.04) | (0.04) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefan, V.-G.; Indrio, G.; Escorihuela, M.-J.; Quintana-Seguí, P.; Villar, J.M. High-Resolution SMAP-Derived Root-Zone Soil Moisture Using an Exponential Filter Model Calibrated per Land Cover Type. Remote Sens. 2021, 13, 1112. https://doi.org/10.3390/rs13061112
Stefan V-G, Indrio G, Escorihuela M-J, Quintana-Seguí P, Villar JM. High-Resolution SMAP-Derived Root-Zone Soil Moisture Using an Exponential Filter Model Calibrated per Land Cover Type. Remote Sensing. 2021; 13(6):1112. https://doi.org/10.3390/rs13061112
Chicago/Turabian StyleStefan, Vivien-Georgiana, Gianfranco Indrio, Maria-José Escorihuela, Pere Quintana-Seguí, and Josep Maria Villar. 2021. "High-Resolution SMAP-Derived Root-Zone Soil Moisture Using an Exponential Filter Model Calibrated per Land Cover Type" Remote Sensing 13, no. 6: 1112. https://doi.org/10.3390/rs13061112
APA StyleStefan, V.-G., Indrio, G., Escorihuela, M.-J., Quintana-Seguí, P., & Villar, J. M. (2021). High-Resolution SMAP-Derived Root-Zone Soil Moisture Using an Exponential Filter Model Calibrated per Land Cover Type. Remote Sensing, 13(6), 1112. https://doi.org/10.3390/rs13061112







